Application of multiphoton imaging and machine learning to lymphedema tissue analysis

Abstract

The results of in-vivo two-photon imaging of lymphedema tissue are presented. The study involved 36 image samples from II stage lymphedema patients and 42 image samples from healthy volunteers. The papillary layer of the skin with a penetration depth of about 100 μm was examined. Both the collagen network disorganization and increase of the collagen/elastin ratio in lymphedema tissue, characterizing the severity of fibrosis, was observed. Various methods of image characterization, including edge detectors, a histogram of oriented gradients method, and a predictive model for diagnosis using machine learning, were used. The classification by “ensemble learning” provided 96% accuracy in validating the data from the testing set.

1. Introduction

The term lymphedema means chronic progressive disease of the lymphatic system, which is connected with insufficient lymph circulation and disorder of resorption and subsequent accumulation of high protein interstitial fluid, leading to inflammation, hypertrophy of adipose tissue and extension of fibrosis with irreversible structural damage [1,2]. It resembles swelling of tissue and eventual thickening and hardening of skin and soft tissue. Lymphedema involves not only lymphatics and nodes, but also the dermis, subcutaneous tissue, and fascia [1].

Lymphedema is divided into primary and secondary types. Primary lymphedema is related to a group of disorders, which are manifested in a congenital abnormality of the lymphatic system in combination with abnormal structural development caused by mutant genes [1]. Secondary lymphedema is acquired and has different origins, for example, the surgical removal of a lymph node, damage to a lymphatic vessel, malignant neoplasms, sequela of radiotherapy, parasitic infiltration, inflammation or infections [1]. The details of lymphedema occurrence, progression, and stage classification can be found elsewhere [1,2].

Various methods of lymphedema diagnosis are used to analyze the edema, lymphatic vessel state, lymph flow, and also tissue transformation [3].

Direct lymphography is based on injecting contrast agents directly into a lymphatic vessel [4]. Over time, this method has been avoided, because of the risk of damage to lymphatic vessels. Indirect lymphoscintigraphy is based on a radiolabeled contrast agent depot created in soft tissue or the parenchyma of an organ, with subsequent penetration into lymphatic vessels [5,6]. This method enables analysis of the lymphatic structure and lymph transport, but it suffers from a lack of standardization in respect to usage of different isotopes [7,8].

The technique for edema evaluation is based on recording an increase in the volume of a body part and includes the water displacement method, optoelectronic perometery, bioelectrical impedance and circumferential measurements [9,10]. For example, the water displacement method involves body part volume measurement by submerging it in a water container. Until recently, this approach was the “gold standard” for lymphedema diagnosis [9]. Unfortunately, the utility of such techniques for early lymphedema detection is questionable, because, by definition, the latent phase of lymphedema is that prior to detectable swelling [10].

Lately, ultrasound, magneto-resonance imaging (MRI), and computed tomography (CT), also in combination with a contrast agent, are using for lymphedema diagnosis. These methods enable analysis of fluid accumulation, fibrosis and tissue density variations [1,10]. Dual energy x-ray absorptiometry (DEXA) allows an assessment of the contribution of the fat component to overall tissue increase [11,12]. However, the aforementioned methods are either technologically complex (e.g., MRI or DEXA), or rather expensive, e.g., CT, and also have a radioactive hazard (e.g., isotopic indirect lymphoscintigraphy) [10].

Lymphochromy is infrared fluorescence imaging of lymphatic vessels using indocyanine green (ICG) dye, which provides visualization of even small lymphatic vessels, but it is also based on invasive injections of ICG dye into a lymphatic vessel [13–16].

Currently, very little is known at the most basic level about what exactly occurs in the tissue surrounding damaged lymph vessels, although it appears to resemble an inflammatory process. An experimental model of acute post-surgical lymphedema in tails of female hairless, immunocompetent SKH-1 mice was created and studied [17]. Lymphedema was shown by histology analysis to be characterized by the presence of marked acute inflammatory changes, both adjacent to the surgical site and within distal regions of the tail, remote from the site of surgical ablation. Intense inflammatory changes appeared in the dermis and the subdermis [18].

Morphological and histopathological evaluations were conducted for tissue samples collected from women with lower-extremity secondary lymphedema, which was caused by surgical intervention related to gynecological cancer. Lymphedema tissue was shown to have larger lobules of adipose tissue, surrounded by thick collagen fibers and interstitial lymphatic fluid. In lymphedema tissue, adipocytes displayed hypertrophic changes and more collagen fiber deposits. The number of capillary lymphatic channels was also found to be increased in the dermis of lymphedema limbs. These findings suggest that a long-term lymphatic volume overload can induce chronic tissue inflammation, progressive fibrosis, impaired homeostasis, altered remodeling of adipose tissue, impaired regenerative capacity and immunological dysfunction.

Chronic lymphedema was shown to be characterized by a change in the structure of skin collagen, since the development of lymphatic edema is accompanied by the development of fibrosis in the dermis [18].

The spatial structure of collagen in biological tissues is traditionally studied by histochemical, immunohistochemical and, in situ, hybridization methods [19,20].

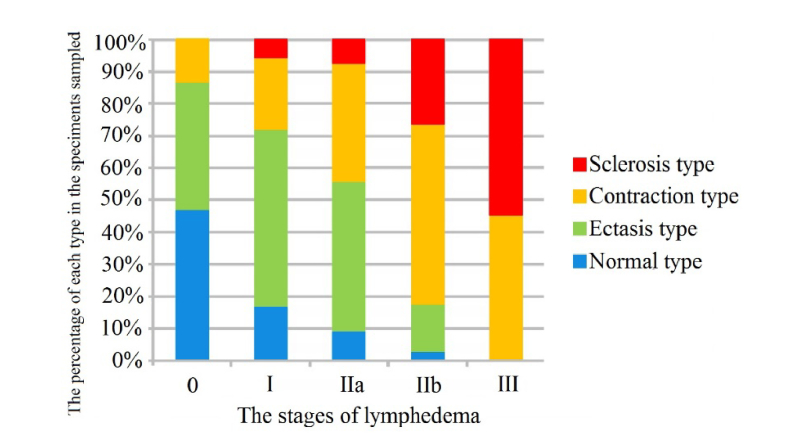
Electron microscopy of lymphatic vessels was conducted to examine the early stages of lymphedema [21]. Histochemical changes of collecting lymphatic vessels were categorized as follows: normal, ectasis, contraction, and sclerosis types (NECST). Here, the ectasis type was characterized by lymphatic vessel endothelial cells flattening. In the contraction type, smooth muscle cells were transformed into synthetic cells and promoted the growth of collagen fibers. Fibrous structure accounts for the majority of tissue in the sclerosis type. The association between the NECST and the lymphedema stage classification is shown in Fig. 1 [21]. Accordingly, fibrosis emerged before clinical manifestations of lymphedema.

Fig. 1.

Association between the NECST and the lymphedema stage classification [21]. The horizontal axis shows the stages of lymphedema. The vertical axis shows the percentage of the NECST in specimens sampled at each stage of the disease.

Histopathological examination provides detailed information about the process of lymphedema tissue remodeling, but has obvious disadvantages. Thus, methods of in-vivo tissue imaging with spatial resolution close to histology and the ability to analyze tissue reorganization during lymphedema development are of great importance.

Polarized light microscopy is routinely used to study collagen ex vivo (for example, in paraffin blocks). Highly oriented collagen fibers exhibit double refraction; thus, changes in the polarization of a light beam passing though the paraffin block with embedded tissue specimen can be used to indirectly assess the amount of collagen and its spatial organization in the specimen [22].

Multiphoton laser microscopy (MPM) provides instantaneous in-vivo tissue imaging at the cellular and subcellular levels. MPM uses the autofluorescence (AF) of endogenous fluorophores, such as elastin, and second harmonic generation (SHG) from matrix tissue components, such as collagen, providing functional and structural label-free tissue imaging [23]. Therefore, MPM can be used to measure the tissue “SHG-to-AF Aging Index of Dermis” value (SAAID) [24,25].

MPM is a powerful tool for fibrillar collagen imaging in a diverse range of tissues. MPM is highly sensitive to changes that occur in diseases such as cancer, fibrosis and connective tissue disorders [26]. MPM was used to analyze collagen architecture and its transformation during ovarian and breast cancer; accordingly, metrics provided based on collagen morphology allowed quantitative discrimination between normal and malignant tissues [27].

Typically, MPM provides high dimension visual data with no evident specific characteristics for a target disease. Similar data can hardly be analyzed directly with statistical methods, because extraction of preliminary image latent key parameters by an expert is required. Machine learning is a useful approach which does not require expert evaluation of hidden dependencies due to the ability to construct classification rules without explicit programming [28].

Machine learning data modeling is divided into supervised learning, based on the use of labeled data sets, and unsupervised learning, based on an analysis of data relations, clustering etc. Classifications are based on supervised learning. The most popular supervised learning algorithms are artificial neural networks, Support Vector Machine (SVM), Random Forest, Naïve Bayes, and boosting [29–32]. Because of the limited amount of available data we prefer SVM, which performs very good generalizations [33]. The concept behind the SVM method is the construction of a hyperplane in the feature space that represents the largest margin between the two classes of data. If the best margin between the classes is of a very complex shape then a nonlinear integral transformation of the input data is made by applying different kernel functions (kernel trick) [29].

The ensemble learning approach, in particular the “majority vote”, bagging procedures, etc., can improve the accuracy and robustness of classifications. The idea behind ensemble learning is to use several classifiers or different characteristics of an object jointly. Even in a case of not very high efficiency of every classifier employed, their combination can improve considerably the accuracy of the final classification.

This paper evaluates the potential of an approach to lymphedema diagnosis based on collagen reorganization estimation by MPM and machine learning.

2. Materials and methods

2.1 The groups under study

The study participants were recruited from among out-patients of the Scientific Research Institute of Microsurgery, Tomsk, Russia. The study protocol was approved by the Institutional Review Board. All participants gave their “informed consent” to the actions carried out.

The study involved a group of patients with II stage lymphedema of the limbs (target group) aged 23-68 years (34 image samples) and a group of healthy volunteers aged 19-65 (42 image samples).

The target group included 2 patients with primary lymphedema of the lower limbs, 2 patients with secondary lymphedema of the upper limbs (after axillary lymphadenectomy caused by breast cancer), and 4 patients with secondary lymphedema of the lower limbs of various causes, namely, extensive skin burns (1 case), after injury (1 case), and after surgical treatment of cervical cancer in combination with X-ray therapy (2 cases, one of which is shown in Fig. 2).

Fig. 2.

Photo of a patient with II stage lymphedema after surgical treatment of breast cancer.

Maximum edema in patients with primary lymphedema of the lower limbs was observed in the region of the rear feet and the lower thirds of the tibia. Maximum edema in patients with secondary lymphedema of the lower limbs was observed in the rear of the foot, in the region of the middle and upper third of the tibia. Maximum edema in patients with secondary lymphedema of the upper limbs was in the upper third of the forearm and in the shoulder area.

Erysipelatous inflammation and flushing and the integrity of the skin was not observed in the target group, but there was practically unvaried edema in all patients, and increased turgor of tissues was also observed.

2.2 The study protocol

Recording of tissue MPM images was carried out using an MPTflex two-photon microscope (Jenlab GmbH, Germany) [23]. The femtosecond Ti:Sapphire laser (Mai Tai, Spectra-Physics, USA) with a tuning range of 710 - 920 nm, 200fs pulse duration, repetition frequency of 80 MHz, and 2-50 mW in situ laser power was used as the optical radiation source. The receiver has a 1.3 numerical aperture and is equipped with focusing optics with 40x magnification. It has two detectors with wavelength ranges of 380 ± 7 nm and 409-660 nm. The lateral resolution is approximately 1 μm and the longitudinal resolution is no less than 2 μm.

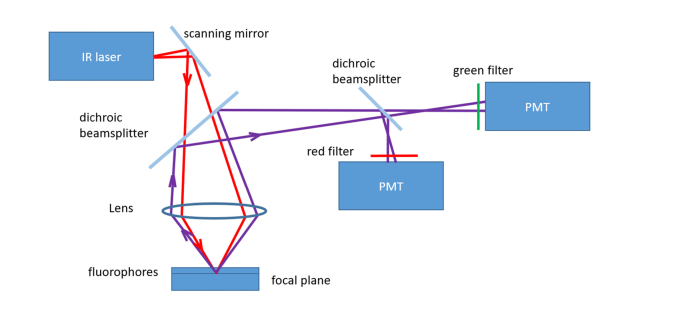
The block-scheme of the MPM device is depicted in Fig. 3.

Fig. 3.

Block-scheme of the MPM device. Here, the PMT is a photomultiplier tube.

Collagen molecules form the triple helix and therefore lack a symmetry center, which makes possible their visualization based on the SHG signal [33]. The narrow-band filter with a central wavelength of 380 nm allows the separation of the SHG signal from collagen fibers under laser pumping at 760 nm. The wide-band filter allows the separation of the autofluorescence signal (AF) from elastin pumped by the laser pulses on the same wavelength (760 nm). Thus, laser pumping at 760 nm is convenient for simultaneously analyzing the spatial distribution of collagen and elastin.

Since collagen fibers are hardly seen at a depth of 0–80 μm (they are located in the papillary dermis) and at a depth of ~150 μm the signal quality becomes poor even with increased power, the following algorithm of measurement was used. The first appearance of the stratum corneum was selected, then SHG and AF images were recorded at a depth of (100 ± 10) μm on a 512 × 512 pixels matrix. The image size was 75 × 75μm. The value of the depth interval was caused by limb skin thickness variations and by errors of initial position measurement. The scanning time and power (no greater than 35 mW) were chosen in order to obtain a quality signal without damage to the tissue. The shutter time was 0.046 ms, 23.9 ms per image scan line and 12.2s for the entire image.

2.3 Data preprocessing and analysis

Typical image processing includes image quality improving (denoising, smoothing, color and brightness normalization), image segmentation and region of interest (ROI) selection, feature extraction, and predictive model creation, which can be used for classifying new data.

Image segmentation techniques include region-based and contour-based approaches [33–36]. The region-based approach involves splitting the image into sets corresponding to coherent image properties such as brightness, color and texture. The contour-based approach usually starts with a first stage of edge detection, followed by a linking process that seeks to exploit curvilinear continuity.

The feature extraction techniques are necessary in order to build mathematical models of an image ROI (known as feature vectors) and classify them. These techniques can include gradients, textural, graph, and morphological features. The sharpness and orientation of collagen fibers can be estimated via different computer vision edge detector algorithms. State-of-the-art methods are based on first order (e.g. Sobel [37,38], Prewitt [39] operators), second order (e.g. Laplacian of Gaussian [40], difference of Gaussian [41]) derivatives, optimal procedure (Canny edge detector [42]) and mathematical morphology [43].

Convolution by a Sobel operator is one of the classic algorithms in computer vision for image edge highlighting. To provide this, an image is filtered by the Sobel operator G:

$$G=\sqrt{G_x^2+G_y^2};G_x=\left[\begin{array}{ccc}+1& 0& -1\\ +2& 0& -2\\ +1& 0& -1\end{array}\right];G_y=\left[\begin{array}{ccc}+1& +2& +1\\ 0& 0& 0\\ -1& -2& -1\end{array}\right],$$

where $G_x$, $G_y$ are kernels with which the original image convolved. Thus, each pixel contains a local spatial derivative of the initial image along the horizontal or vertical axis, respectively [44]. The Sobel operator evaluates the image brightness gradient over a 3x3 pixel matrix to decrease the influence of noise. The Prewitt operator works exactly the same way, but uses the following derivative approximations:

$$G_x=\left[\begin{array}{ccc}+1& 0& -1\\ +1& 0& -1\\ +1& 0& -1\end{array}\right];G_y=\left[\begin{array}{ccc}+1& +1& +1\\ 0& 0& 0\\ -1& -1& -1\end{array}\right].$$

The Laplacian of the Gaussian (LoG) method computes a second order derivative of the image and attempts to find zero-crossing points. Because second order derivatives are used, this approach is very sensitive to noise and thus requires preprocessing by noise removal algorithms (like the Gaussian filter). Commonly used kernels for the LoG filter are [45]:

$$\left[\begin{array}{ccc}+1& +1& +1\\ +1& -8& +1\\ +1& -1& +1\end{array}\right];\left[\begin{array}{ccc}-1& +2& -1\\ +2& -4& +2\\ -1& +2& -1\end{array}\right].$$

The Canny edge detector algorithm usually includes four basic steps. The first stage is image noise reduction, as a rule using the Gaussian filter. The second stage is selection of edges and directions. Directions are defined as the arctangent from the ratio of gradients obtained as a result of convolution. The third stage involves the removal from the image of all pixels that cannot be edges. During the last stage, a threshold is used for highlighting the edges on an image.

The idea of edge detection using mathematical morphology involves applying morphological dilatation and erosion to the input image. Then the eroded image is subtracted from the dilated one (“closing” operation) and finally the input image is subtracted from the result [43].

To classify images using their detected edges’ spatial structure, one must describe it in terms of its quantitative characteristics, which should compose a feature vector. The total edge length (TEL) of an image involves similar characteristics [46]. More sophisticated features of an image structure can be estimated using the histogram of oriented gradients (HOG) method. HOG is a very effective method for constructing an image feature descriptor, and it is very popular in computer vision and image processing, visual object detection and recognition. The HOG algorithm is based on an evaluation of the orientation field of brightness gradients over every image pixel [47].

To extract specific features of an image, the latter is usually divided into small parts called cells, and the descriptor is composed in the form of a concatenation of these histograms of gradient directions of every pixel in the cell. To compress data and to extract informative features, a spatial averaging of local HOG descriptors over a number of cells called a block is employed. A set of overlapping blocks forms an image patch. The number of gradients’ orientations used for discretization, size of cell, block and patch are dependent on image properties and should be evaluated consistently in machine learning.

The initial image analysis was performed using the software package of the Jenlab GmbH and Becker&Hickl. Statistical analysis of the results was carried out with the Statistica 8.0 software. Image processing was performed with the Matlab R2017b software.

3 Results

Examples of SHG images of the subsurface skin layer are shown in Fig. 4. “Hollow” areas of regular form inside papilla correspond to blood vessels [48]. Here the collagen fibers are bright. According to Fig. 4(b), not all tissues are uniformly morbid, there are several regions with a higher collagen disorganization degree: it has a sparser structure (increased number of “hollow” areas of irregular form) with sharply visible fibers. Next, to prove this statement we perform an analysis of the collagen to elastin ratio for healthy and lymphedema tissue. These visualizations correspond to the one in the animal model of lymphedema [18].

Fig. 4.

SHG image of healthy volunteers (a) and patients with II stage of lymphedema (b).

The estimation of the level of the SHG signal and AF signal (in relative units) in the image samples was shown in Table 1. The signals were averaged over image samples for every group separately. Here, the median value of SHG/AF ratio is significantly increased for lymphedema tissue. This most likely reflects the development of fibrosis in edematous tissue. An SHG signal is usually considered to reflect the collagen filling of a tissue; the same relation is considered between an AF signal and elastin filling of a tissue. The latter is not entirely correct due to the possible contribution of capillaries, lymphatic vessels, nerves, etc. to tissue autofluorescence [48,49].

Table 1. The estimation of collagen and elastin content in the tissues, Me [Q25; Q75].

Group Parameters	Healthy volunteers	Patients with II stage lymphedema
SHG signal, rel. units	100.48 [87.76; 111.49]	113.89 [100.39; 127.21]*
AF signal, rel. units	46.35 [39.84; 64.96]	42.15 [33.73; 48.90]*
Collagen/elastin ratio	1.96 [1.52; 2.55]	2.42 [2.25; 3.20]*

Note: *– p<0.05 compared with the group of volunteers (Mann-Whitney U Test)

The next stage was to obtain a quantitative estimation of the collagen structure disorganization in lymphedema tissue, which can be provided by an appropriate gradient image analysis. The visualization of the SHG image structure by a Sobel operator, Canny edge detector, morphology-based edge detector, and LoG operator is depicted in Fig. 5.

Fig. 5.

The results of the edge detection procedure, applied to lymphedema tissue (the upper row) and healthy tissue (the lower row); initial images (a, f), results of initial image filtering by: (b, g) - the Sobel operator, (c, h) - the Canny edge detector, (d, i) - the morphology method, (e, j) – Laplacian of Gaussian.

Sobel and LoG operators give a richer structure of gradients due to their sensitivity to noise, which complicates the estimation of a threshold. The Сanny and morphological algorithms give similar results with thinner edges in comparison to the Sobel and LoG operators.

The total number of gradient points might be used to compare the density of edges, but it fails to capture information about the gradients’ orientation. This result is consistent with those of other authors [40].

One of the trialed approaches was based on image TEL estimation using edge gradient methods. Each initial SHG image was divided into non-overlapping patches with a size of 32x32 pixels. The “empty” ones were removed (the mean brightness patch threshold was 80 in a gray scale varying from 0 to 255). The TEL was calculated as the ratio of the bright pixel quantity and the total pixel quantity in a patch. Next, a histogram of the TEL value for all patches of each image was constructed (Fig. 6). Regardless of the gradient method applied, the TEL histogram looks broader for lymphedema tissue in comparison with healthy tissue. An increase of the median value also takes place. This is most likely connected with disorganization of the collagen spatial structure.

Fig. 6.

The total edge length on the images of healthy and lymphedema tissue, calculated using the Sobel operator, the Canny edge detector, the morphology method, and the LoG operator.

SVM was used to create a predictive model for lymphedema and healthy tissue classification. To train SVM, positive and negative training sets should be formed. We took into account that healthy tissue has no morbid parts, while lymphedema tissue might have healthy parts so initial images were divided into patches. Images labeled as “healthy” formed a negative training set, while images labeled as “lymphedema” formed a positive set. As the SHG data set is relatively small, we used 80% of it for training and 20% for testing. Each image’s histogram of the TEL formed a feature vector used for classification. Multiple trials of SVM classification were performed and the best parameters estimated: the RBF kernel [29], regularization parameter equaled 0.1 and the gamma parameter (determining how far the influence of a single training example extends) equaled 1.0. Validation was performed using the N-1 leave procedure where N = 20 [50].

The mean and standard deviation (STD) of the sensitivity and the specificity values were calculated to estimate the accuracy of the classification, as follows:

$$\begin{array}{c}\mathit{\text{Sensitivity}}=\mathit{\text{TP}}/(\mathit{\text{TP}}+\mathit{\text{FN}});\mathit{\text{Specificity}}=\mathit{\text{TN}}/(\mathit{\text{TN}}+\mathit{\text{FP}});\\ \mathit{\text{Accuracy}}=(\mathit{\text{TP}}+\mathit{\text{TN}})/(\mathit{\text{TP}}+\mathit{\text{TN}}+\mathit{\text{FP}}+\mathit{\text{FN}}),\end{array}$$

where TP is the quantity of true positive classification results, and FN is the quantity of false negative classification results, TN is the quantity of true negative classification results, and FP is the quantity of false positive classification results. The results are presented in Table 2.

Table 2. Classification accuracy for the TEL feature on the images of healthy and lymphedema tissue.

Algorithm	Accuracy
	Mean	STD
Sobel operator	0.590	0.077
Canny edge detector	0.571	0.083
Morphology method	0.620	0.059
Laplacian of Gaussian	0.571	0.049

Evidently, the TEL value only roughly describes the structure of SHG images. To improve the accuracy of classifications, it is necessary to include additional image parameters such as a gradient orientation. The latter considers the HOG algorithm, which describes patch texture, using the local gradient’s spatial orientation structure [49,51,52].

Here, the principal issue in using HOG not for image recognition, but for group distinguishing, is to evaluate a rougher local gradient’s orientation field features, which are common for a whole group. For this purpose, model tests were carried out to construct a suitable feature vector based on HOG texture analysis to distinguish co-oriented and disorganized groups of “fibers”, which are a characteristic of a number of diseases, including lymphedema.

Collagen fibers in the human dermis exhibit an almost uniaxial structure, which tends to become gradually disordered with an increase in the probing area because of different directions mixing [53]. Collagen fibers were modeled by line segments of various length, width, orientation and color. Disorganization is mainly defined by the angle of the line segments, so at the first stage, we generated dominant orientations by choosing randomly a slope of the line in the slope-intercept form for all images. Next, for each image, the slope angle (number in range [0, 180)), width (number of pixels in range [1,5]), color value in range [0.6, 0.99]), x - coordinates of the starting and ending points in the pixel coordinates (x, y) (in range (0, image width)), the intercept of the line coefficient (integer in range [0, (image height)/2]) are generated randomly from uniform distribution.

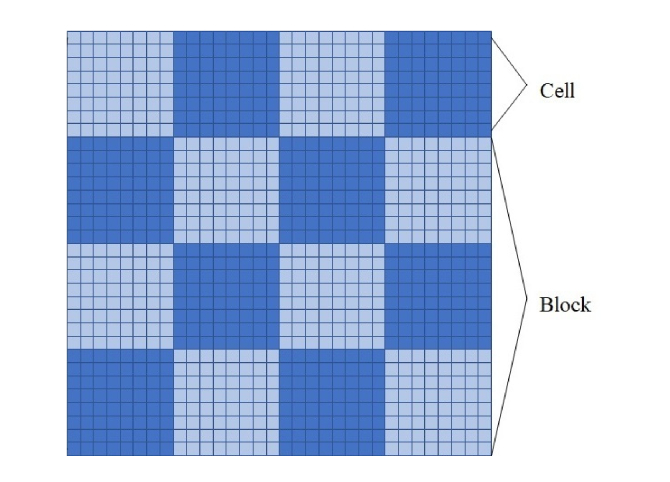
Finally, we defined the disorganization index, which corresponds to the tangent of the slope angle. If its magnitude varies in a small range, i.e. (0, 0.1), then such lines are considered ordered and if one varies in a range (0.1, 1) then they are disordered lines. The number of generated lines per image was 2000 in order to obtain a dense picture. Each model image had a size of 32x32 pixels. The latter was considered a patch. Each patch was divided into non-overlapping 8 × 8 pixel cells (16 cells in a patch; see the example in Fig. 7).

Fig. 7.

The image is divided into 32 × 32 pixel patches, each is divided into 8 × 8 pixel cells that are combined into a 24 × 24 pixel block.

The extracted features form a training and testing set for SVM binary classification. Each of them consists of positive and negative samples. The images filled with lines with a disorganization index defined in the range (0, 0.1) were considered as positive samples, the images with lines with a disorganization index in the range (0.1, 1.0) were considered as negative samples (see Fig. 8). The training image set included 28800 positive and 28800 negative randomly selected samples and the same number of samples was in the testing set. Such a ratio of test and training sets verifies that the trained classifier will not be overfitted [54]. This random separation of model samples into training and testing sets was repeated 50 times to estimate the influence of the means of data splitting on the results of classification. Again, multiple trials were performed in order to estimate the best parameters of SVM. They were: the RBF kernel, regularization parameter equaling 0.1 and the gamma parameter equaling 1.0.

Fig. 8.

Example of model data: (a) – organized fibers, positive samples, (b) – disorganized fibers, negative samples.

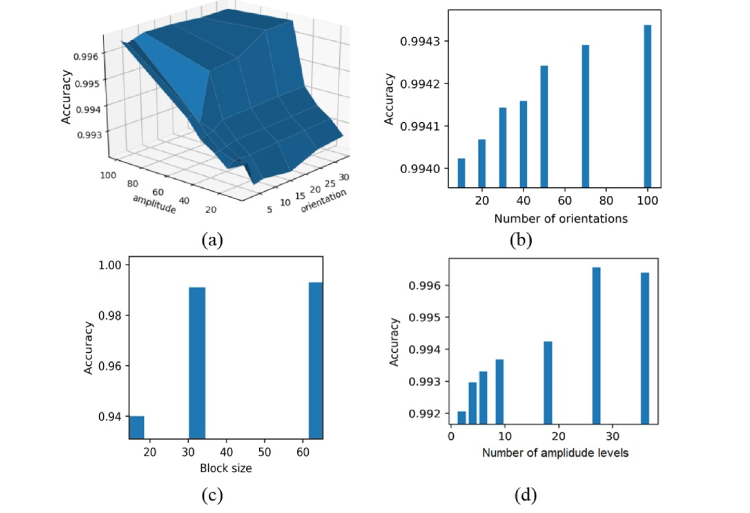
It should be pointed out that the accuracy of image coding by the HOG descriptor is defined by the discretization level of the brightness gradients amplitudes and orientations. It strongly influences the ability to distinguish image groups instead of individual image recognition. An analysis of accuracy in separating the positive and negative samples in dependence of the above mentioned discretization levels was carried out (see Fig. 9). Here the small variation of accuracy in detecting positive and negative samples under variation of the discretization levels is connected with the good spatial separation of the groups of samples in a feature space. In this case a small variation is significant.

Fig. 9.

Analysis of the optimal discretization level of the brightness gradient orientations and amplitudes together (a) and separately (b, d), and optimal block size (c).

Initially, the optimal number of brightness gradient orientations was estimated. According to the simulation results, it essentially does not depend on the discretization level of the brightness gradient amplitudes. Finally, 9 directions of orientations and 50 levels of brightness gradient amplitudes were followed in order obtain optimal results. These parameters were used for human SHG image analysis.

In order to apply the same approach to the analysis of human tissue, we divided the initial 512x512 pixel SHG images into 32x32 patches, removed those with low intensities (a mean brightness value lower than 80 in a gray scale) as shown in Fig. 10.

Fig. 10.

Selection of significant cells on an SHG tissue image

The studied SHG images consisted of 19968 patches in total. Only 3112 image patches were included for further consideration after brightness thresholding, 2500 of which were randomly selected for use in the training set and the remainder were allocated to the testing set. This splitting was repeated randomly 50 times to estimate the variation of classification accuracy.

Each image patch was divided into cells and block in the same manner as depicted in Fig. 7. Then, the gradient intensity in the range of [0, 180] degrees was calculated for every cell and it was routed along 9 directions (bins) with magnitudes as weights, which composed a 9-bin HOG. Then the magnitudes of bins were normalized to [0,1] range in order to provide invariance and were discretized on 50 levels. After that, 3 × 3 cells formed a block with a size of 24 × 24 pixels. Finally, 4 overlapping blocks covered a 32 × 32 pixel patch.

Contrary to the original usage of HOG which implies computation of one feature vector for the whole image as a concatenation of feature vectors for each patch, we did not merge HOG vectors but instead each one was used as a texture descriptor of the patch. So, each cell was described by a 9-bin HOG, 9 cells in 1 block, 4 blocks in 1 patch in total forming the HOG feature vector with 324 coordinates.

SVM was used to construct a classification rule. Lymphedema is a complex disease and experts cannot annotate every patch of an image. They can only state that the image was taken from the part of the body where lymphedema occurred. So, images from a lymphedema patient can contain both healthy and lymphedema tissues, which complicates classification. A combination of SVM and a “majority vote” method were used to solve this problem. The “majority vote” procedure was as follows: if the number of the image patches classified as “lymphedema tissue” exceeded the same for “healthy tissue”, this image was considered to correspond to lymphedema tissue. The idea of the approach is illustrated in Fig. 11.

Fig. 11.

Scheme of SHG image classification.

We tested different parameters of SVM and found that it worked better with the RBF kernel, the regularization parameter was equal to 1.0, and the gamma parameter was equal to 0.1. The best achieved quality of classification is sensitivity equaling 0.79 ± 0.11 and specificity equaling 0.77 ± 0.10.

Furthermore, we employed the idea of a bagging procedure, which is a machine learning ensemble meta-algorithm to improve the classification results [55,56]. Group classification of several SHG images of one participant was performed and subsequently the voting scheme was applied. This allowed us to achieve 96% accuracy. Instead of using different images of an object, different features and classifiers with a voting scheme can also be used. This can increase the robustness of the created classification rules [57].

4 Conclusion

Lymphedema development can cause an increase in adipose tissue lobules, hypertrophic changes in adipocytes, an increase in the number of capillary lymphatic channels, and disorganization of the spatial structure of skin collagen. The latter was used here as a diagnostic feature, because changes in size demands a calibration of the diagnosis method relative to the spatial scale. Also variation of cells or vessels quantity should be compared with a reference case. The advantages of an evaluation of the collagen spatial orientation structure are due to the existence of simple computer methods of image analysis for direct quantitative determination of collagen disorganization.

An approach to lymphedema diagnosis is proposed, which involves estimation of collagen disorganization in-vivo human tissue by MPM and machine learning.

Since collagen fibers are hardly seen at a depth of 0–80 μm (they are located in the papillary dermis) and at a depth of ~150 μm the signal quality becomes poor even with increased power, the AF and SHG images of tissue at (100 ± 10) μm depth were recorded.

The value of the SHG signal to the AF signal ratio, which is considered as the collagen to elastin ratio, was shown to be significantly increased for lymphedema tissue. This most likely reflects the development of fibrosis in edematous tissue.

A number of image edge detectors were used to provide quantitative estimation of disorganization in the collagen structure in lymphedema tissue. Regardless of the method, the image total edge length distribution was shown to become wider with a shift in the median of the distribution to larger values. This is most likely connected with disorganization of the collagen fiber spatial structure.

The histogram of oriented gradients (HOG) method was used for the SHG tissue image feature extraction. The combination of SVM and a “majority vote” method was applied for image classification. Averaged over 50 times random splitting of image patches into training and testing sets gave a value of 0.79 ± 0.11 for sensitivity and a value of 0.77 ± 0.10 for specificity. Therefore, we made a classifier based on texture information: if an image had mostly co-oriented collagen fiber pattern patches, it was classified as belonging to healthy tissue, otherwise it was classified as belonging to lymphedema tissue.

The classification results obtained from the tests performed show that HOG feature extraction following SVM can distinguish between different degrees of fiber disorganizations in SHG images.

The bagging procedure, based on a group classification of several SHG images of a participant was performed and the voting scheme was applied. This allowed us to achieve 96% accuracy.

Thus, lymphedema diagnosis based on collagen disorganization analysis by MPM and machine learning is very promising. Future research should be aimed at estimating the threshold of sensitivity of this approach during the emergence and development of lymphedema.

Funding

RFBR (grant No.17-00-00186); RFBR and Tomsk Region (Nº 18-42-703012).

Disclosures

The authors declare that there are no conflicts of interest related to this article.