On The Necessity of Abstraction

Abstract

A generally intelligent agent faces a dilemma: it requires a complex sensorimotor space to be capable of solving a wide range of problems, but many tasks are only feasible given the right problem-specific formulation. I argue that a necessary but understudied requirement for general intelligence is the ability to form task-specific abstract representations. I show that the reinforcement learning paradigm structures this question into how to learn action abstractions and how to learn state abstractions, and discuss the field’s progress on these topics.

1. Introduction

AI has recently produced a series of encouraging breakthroughs, particularly in reinforcement learning [1], which studies complete agents learning to act in an environment and therefore encapsulates the entirety of the AI problem. These results constitute undeniable progress in constructing generally intelligent AIs. However, one major aspect of general intelligence remains largely unaddressed. Consider chess.

AlphaZero essentially solves chess [2]. It does so purely by self-play, in approximately four hours, with no human intervention and without the benefit of specialist chess knowledge. That is a major achievement. But there is some human knowledge embedded here: it is in the problem formulation itself. AlphaZero takes as input a neural encoding of an abstract description of a chessboard as an 8 × 8 array of positions, each of which can be empty or contain one of six piece types of one of two colors; the actions available to it are legal moves for that abstract input: the pawn on e2 can be moved to e4. This abstract representation contains just the information relevant to playing chess and nothing else, and it is given to the agent as if it is a natural part of the environment. That is perfectly appropriate for a chess-playing agent, but it finesses a problem that must be solved by a general-purpose AI.

Consider one particular general-purpose agent that reasonably approximates a human—a robot with a native sensorimotor space consisting of video input and motor control output—and the chessboards shown in Figure 1. Those chessboards are actually perceived by the robot as high-resolution color images, and the only actions it can choose to execute are to actuate the motors attached to its joints. A general-purpose robot cannot expect to be given an abstract representation suitable for playing chess, just as it cannot expect to be given one that is appropriate for scheduling a flight, playing Go, juggling, driving cross-country, or composing a sonnet. Nevertheless, it should be able to do all of these things.

Figure 1:

Three different chessboards with the pieces in the same position.

The only computationally feasible way for a general AI to learn to play chess is to build a representation like that used by AlphaZero: an abstract representation of the board and the legal moves. The robot must be able to do this irrespective of the particular angle from which it views the board; varying sizes and colors of chess pieces, squares, and boards; different backgrounds, lighting conditions, and other extraneous information; how many joints it can actuate; and what gripper type it has. Those difficulties all have to do with the innate complexity of the robot, not the essential complexity of the task—the chessboards shown in Figure 1 are all in the same game position, despite their very different appearances, and irrespective of the details of the robot’s body. A general-purpose AI can only be effective when it is able to focus solely on the complexity of task. Consequently, a precondition for general AI is the ability to construct an appropriate—and problem-specific—abstract representation of a new problem. Humans do this effortlessly, even though such representations cannot be hard-wired into our brain—nothing remotely similar to chess, for example, appears in our evolutionary history.

2. Forms of Abstraction

Fortunately, the reinforcement learning formalization helps structure our reasoning about abstraction. Reinforcement learning problems are typically formalized as Markov Decision Processes (or MDPs), described by a tuple:

$$M=(S,A,R,T,\text{γ}),$$ (1)

where S is a set of states; A is a set of actions; R(s, a, s′) returns the reward obtained by executing action a from state s and arriving in state s′; and T(s′|s, a) encodes the task transition dynamics, a distribution over states s′ the agent may enter into after executing action a at state s; and $\text{γ}\in (0,1]$ is a discount factor expressing a preference for immediate over future reward. Of these, the reward function and discount factor describe the agent’s objectives, while the transition function describes the operation of the environment.

It is reasonable to model the operation of a generally intelligent agent as a single MDP—the base or root MDP—where the state and action space may be high dimensional and continuous, and the reward function (and possibly discount factor) can be varied to reflect the current task.¹ Then since the transition function depends on the state and action set, constructing an abstract task-specific MDP requires two types of abstraction: state abstraction, where an agent builds an abstract state set $\overline{S}$, and action abstraction, where it builds an abstract action set Ā.

3. Learning State Abstractions

Learning a state abstraction involves finding a mapping from the original state space S to another more compact space $\overline{S}$ that is sufficient for solving the task at hand. Such approaches have always been data-driven, and most are constructed to accurately but compactly represent some aspect of the agent’s learning process, either exactly [3] or with bounded loss [4, 5, 6].

The earliest state abstraction methods focused on constructing small discrete state spaces. Bisimulation approaches attempt to preserve the complete transition model of the task, either exactly [7] or approximately [8, 9, 10, 11]; unfortunately the resulting model minimization problem is NP-Hard [9]. Later state aggregation approaches [12, 13, 14, 15, 16, 17, 6] collapse sets of states from the original state space into undifferentiated single states in the abstract space, based on measures such as the topology of the original state space.

Several approaches find abstract representations by selectively ignoring state variables, for example by selecting an appropriate abstraction from a library [18, 19, 20, 21, 22], discarding irrelevant state variables [23, 24], or starting with no state relevant variables and adding some back in when necessary [25]. Such approaches became more principled with the introduction of feature selection methods drawn from linear regression [26, 27, 28, 29, 30, 31] to selectively include state features with the aim of learning accurate but compact representations.

Rather than discarding a subset of an existing state space, representation discovery approaches construct an entirely new compact state space that preserves some properties of the task. Example methods have centered on preserving the topology of the domain [32, 33], the ability to predict the next state [34, 35], and conformance with our prior knowledge of physical systems [36, 37]. Figure 2 shows an example learned state abstraction.

Figure 2:

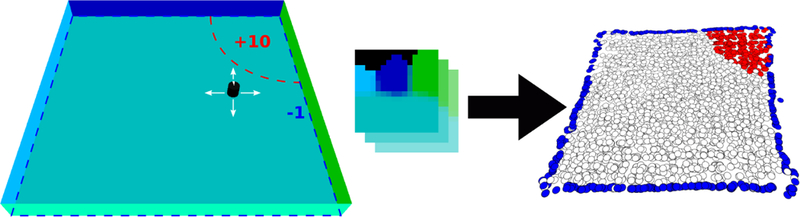
A robot operates in a square room, where its reward is −1 per step everywhere except the upper right corner, where it receives a positive reward (left). Its native state space is a short history of images observed with a front-facing camera (middle). Using a representation discovery algorithm based on physical priors [37], the robot discovers a low-dimensional representation that accurately reects the topology of the task (right) from its complex sensor space. Reused with permission from Jonschkowski and Brock [37].

A substantial shift occurred recently with the application of deep neural networks to reinforcement learning, which has in some cases successfully learned policies directly from raw sensorimotor data [38, 39]. The most impressive of these from a general AI standpoint is the use of a single network architecture and learning algorithm to master a large number of Atari games directly from raw pixel input [39]. At first blush, deep networks are just powerful function approximators, unrelated to state space abstraction. However, that view misses what makes them so powerful. Their deep structure forces state inputs to go through layers of processing, with policies depending only on the final layer. This structure strongly encourages the network to learn a highly processed transformation of the input state into a new representation [40] suitable for supporting a policy. The now-widespread use of autoencoders and pre-training [41, 42, 43, 38, 44, 45, 46]—where a deep network learns to compute a compact feature vector sufficient for reproducing its own input and the policy is learned as a function of that feature vector only—closely corresponds to representation discovery approaches. Therefore, while it may at first seem that deep networks successfully avoid state abstraction, it is likely that their success stems at least partly from their ability to do just that.

4. Learning Action Abstractions

Action abstraction involves constructing a set Ā of higher-level actions (sometimes called skills) out of an agent’s available low-level (also often called primitive) actions. Most research in this area has adopted the options framework [47], which provides methods for learning and planning using high-level options defined by a tuple $o=\left(I_o,{\pi }_o,{\beta }_o\right).$ The agent can execute option o in any state in the option’s initiation set $I_o\subseteq S$, whereafter the agent executes actions according to the option policy ${\pi }_o:S\to A,$ until option execution stops in some state s according the termination condition probability ${\beta }_o:S\to [0,1]$. The agent selects options in just the same way that it selects low-level actions.

The core question here has always been skill discovery—how to identify, from data or an explicit task description—a useful collection of options. In practice this amounts to identifying the termination condition β_o (often called a subgoal), around which the other components can be constructed: a synthetic reward function R_o that rewards entering β_o is used to learn the option policy (now just another reinforcement learning problem), and the initiation set includes only states from which that policy succeeds in reaching β_o.

The majority of work in skill discovery has centered on the somewhat heuristic identification of the desirable properties of subgoals, and then the development of algorithms for constructing options with those properties. Examples include a high likelihood of visiting high-reward or high-novelty states [48, 49, 50, 51], repeated subpolicies [52, 53], reaching various topological features of the state space like bottlenecks, graph clustering boundaries, and high between-ness states [54, 55, 12, 56, 57, 58, 59, 60, 15, 61], reaching specific discretized state-variable values [62, 13], generating diverse behavior [63, 64] or constructing skills that can be chained to solve the task [65, 66]. Figure 3 shows an example subgoal identification using between-ness centrality.

Figure 3:

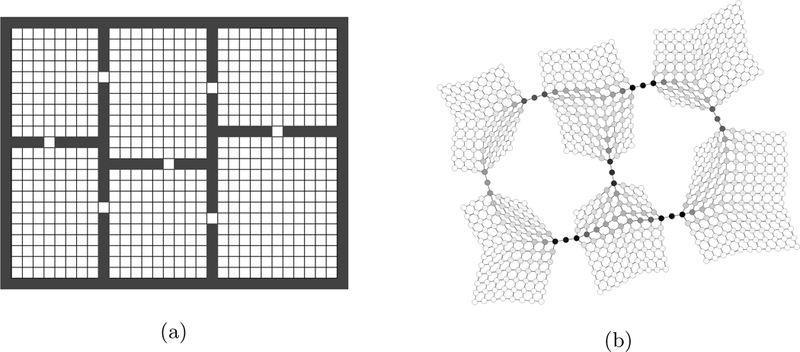
Skill discovery using between-ness centrality, a measure of the likelihood that a state lies on the shortest path between any two other states. When applied to a gridworld with multiple rooms (a), the doorways between rooms are local maxima of between-ness centrality (b), indicating that they might be useful subgoals. From S_im_sek [67], used with permission.

Unfortunately, however, there is evidence that poorly chosen options can slow learning [68]. Possibly stimulated by this result, a new wave of recent work—initiated by Solway et al. [69]—has defined an explicit performance cri-terion that adding options should improve, and sought to optimize it. This has been approached both by constructing algorithms with performance guarantees [69, 70, 71] and by adding parameters describing options to the agent’s learning task and directly optimizing them [72, 73, 16, 74, 75, 76]. Unfortunately recent complexity results have shown that even a very simple instantiation of the resulting problem is NP-Hard [71].

A critical distinction here is between approaches that aim to speed the learning of a single task, and those which may accept a temporary reduction in learning speed for one task with the aim of improving performance over future tasks, known as skill transfer [77, 78, 53]. The challenge in the single-task case is overcoming the additional cost of discovering the options; this results in a narrow opportunity for performance improvements, but a well-defined objective. In the skill transfer case, the key challenge is predicting the usefulness of a particular option to future tasks, given limited data.

5. Combined State and Action Abstraction

The vast majority of current research focuses on attacking state or action abstraction in isolation. This is a perfectly reasonable research strategy given the difficulty of each problem, but it seems unlikely to obtain a coherent model when both are required. A major question is therefore how one type of abstraction can drive the other.

State abstraction can drive action abstraction by first constructing a state abstraction and then building a corresponding action set, typically in the form of actions that move between abstract states. All skill discovery algorithms that rely on a clustering or partitioning of the state space already implicitly do this, while some (e.g., [12, 13, 15, 16, 17]) explicitly construct the resulting abstract MDP.

A second, much less explored alternative is to have action abstraction drive state abstraction: first discover abstract actions, and then build a state abstraction that supports planning with them [79, 80, 81, 82, 83]. My own recent work in this area [84] constructs an abstract representation that is provably necessary and sufficient for computing the probability that a sequence of given options can be executed (and the reward obtained if successful). The resulting framework is capable of learning abstract representations directly from sensorimotor experience, to solve a manipulation task on a complex mobile robot platform. An example abstract model of a skill, along with visualizations of the abstract symbolic propositions appearing in it, is shown in Figure 4.

Figure 4:

An abstract learned model (a) of the skill for opening a cupboard, along with the learned groundings for the symbols from which it is constructed. Each learned symbol is visu-alized using samples drawn from the corresponding sensor grounding, which is a probability distribution over the robot’s map location, joint positions, or the data reported by its depth sensor. Successfully executing the motor skill requires the robot’s location in the map to be in front of the cupboard (symbol1, b) with its arms in the stowed position, which indicates that it is not carrying an object (symbol3, c). Execution switches o_ symbol4, which indicates that the cupboard is closed (d), and switches on symbol5, indicating that it is open (e). The grounded symbolic vocabulary and the abstract model built using it are learned autonomously. Reused with permission from Konidaris et al. [84].

The key challenge in learning state-driven hierarchies is that it is easy to construct state abstractions for which no set of feasible options can be constructed. This occurs because options are constrained to be realizable in the environment—executing the option from the initiation set must result in the agent reaching the termination condition—but no such restrictions hold for state abstractions. This does not occur when learning action-driven hierarchies, where the agent is free to select an abstraction that supports the skills it has built, but then everything hinges on the skill discovery algorithm, which must solve a very hard problem.

6. Conclusions

The tension between narrow and general AI—between producing agents that solve specific problems extremely well, versus agents that can solve a wide variety of problems adequately—has always been a core dilemma in AI research. The modern AI paradigm [85] addresses this challenge by precisely formulating general classes of problems (e.g., MDPs) and designing algorithms targeting the entire class, rather than any specific instance of it. That approach led to the widespread development of powerful general-purpose algorithms, but it omits the key step of having the agent itself formulate a specific problem in terms of a general problem class as a precursor to applying a general algorithm—a step that is a necessary precondition for solving the AI problem.