Abstract
This paper presents an approach to surgical tool tracking using stereo vision for the da Vinci® Surgical Robotic System. The proposed method is based on robot kinematics, computer vision techniques and Bayesian state estimation. The proposed method employs a silhouette rendering algorithm to create virtual images of the surgical tool by generating the silhouette of the defined tool geometry under the da Vinci® robot endoscopes. The virtual rendering method provides the tool representation in image form, which makes it possible to measure the distance between the rendered tool and real tool from endoscopic stereo image streams. Particle Filter algorithm employing the virtual rendering method is then used for surgical tool tracking. The tracking performance is evaluated on an actual da Vinci® surgical robotic system and a ROS/Gazebo-based simulation of the da Vinci® system.
I. Introduction
This paper focuses on surgical instrument tracking for the da Vinci® surgical robotic system (Intuitive Surgical, Inc., Sunnyvale, CA) under stereo camera image streams. The long-term goal is to enable visual servo control [1],[2] of the surgical tools to perform precise visually guided manipulation tasks. For instance, given the 3D pose of a needle in the camera frame, let the robot arms pick up the needle and place the needle in a desired pose.
Tracking of surgical tools have attracted attention in the literature due to its essential role in a number of applications, ranging from surgical skill assessment to task automation in robotic surgery. Ren and Kazanzides [3] developed an integrated inertial and magnetic navigation system for attitude tracking of surgical tools inside the human body. Using a modified miniature integrated inertial sensing systems, the estimated gravity and magnetic field are utilized in an Extended Kalman Filter to estimate the orientation of the surgical instrument. Richa et al. [4] proposed a surgical tool tracking method and a retina disparity tracking method for detecting unintentional collisions between surgical tools and the retina using the visual feedback from the stereo cameras. The tool tracking is constructed as a direct 2D-3D image registration method based on a similarity metric measure called sum of the conditional variances, which extracts the position of the tools. Krupa et al. [5] designed a laser-pointing instrument holder that can be mounted by general surgical tools in minimal invasive surgery. One monocular camera is used to localize the optical markers on the tools and provide the 3-D positions of the tools, which are further applied to recover and center the tools in the image by means of a visual servoing algorithm. Staub, et al. [6] proposed a curve density algorithm that optimizes the separation of color statistics between the inner object and the background based on the initial kinematic pose prediction. Pezzementi, et al. [7] also developed their appearance model by extracting the color and texture features from the image which produced the class probability for maximum likelihood estimation. Choi [8] built contour templates using CAD models of the general objects and performed the object tracking using annealed particle filter and RANSAC algorithm. Reiter [9] considered the tool tracking problem from a pure computer vision perspective. By rendering the CAD model of surgical tools in various poses in a global manner, the localization of tools can be traced using a 3-D template matching algorithm called LINE-MOD [10] through a brute-force search. Similarly, Baek, et al. [11] provides a 7-DOF forceps tracking algorithm, where a database of the contour points of the forceps is built during pre-processing by projecting the 3-D geometry of the forceps onto the 2-D image plane under difference kinematic states. In this paper, we introduced a 9-DOF surgical tool contour rendering method from a graphical and geometrical point of view. Instead of generating the templates off-line and performing a brute-force search, we propose an on-line silhouette generation and rendering method in order to the dynamically adapt the appearance of each tool part, similar to [12], and a Bayesian adaptive filtering estimation scheme. In [12], the templates are defined using certain number (14) of keypoints on the tool parts and represented by bounding boxes, while a consensus-based verification approach is used for outliers rejection. In our work, the templates are modeled by the rendered geometrical silhouette of each tool part, and vision-based adaptive filtering is employed for correction of the kinematic-based rendering errors.
Bayesian approaches provide an estimation method for dealing with uncertainties in the system and the environment. As such, Bayesian state estimation is widely used in the literature. One non-parametric algorithm based on Bayesian inference is Particle Filter algorithm [13], [14]. The principle of Particle Filter is to represent the posterior probability density function using a finite number of random samples. Based on an importance sampling approach, particle filter uses a set of particles (or samples) to represent posterior distributions. As, the initial state and noise distributions can take any form required, particle filter can accommodate non-linear and non-Gaussian system. Particle filter has gained great popularity in computer vision applications [15], including, pose estimation on the SE(3) group [16].
The method proposed in this paper for robotic surgical tool tracking is a vision-based Bayesian state-estimation approach. The proposed method uses forward kinematics of the robotic surgical manipulator for state evolution, based on an approximate calibration of the robotic manipulator and the endoscopic surgical camera. Image streams acquired from the stereo endoscopic cameras are used as the sensing modality for the measurement updates in the Bayesian state-estimation. Specifically, as part of the method, an on-line virtual rendering algorithm is employed to create virtual images of the surgical tool by generating the silhouette of the defined tool geometry under the endoscopic camera view. The observation likelihoods used for Bayesian measurement updates are then estimated from the similarity of the virtual images of the tool pose hypotheses generated by the virtual rendering algorithms and the real images that are captured by the stereo vision system. A particle filter is used as the underlying Bayesian estimator, as the system is nonlinear and non-Gaussian. The tracking performance of the proposed method was evaluated on a simulation of the da Vinci® robotic surgery system (implemented in the Gazebo simulation environment of the Robot Operating System), and an actual physical da Vinci® robotic surgical system.
The rest of the paper is organized as follows. In Section II the silhouette generating algorithm and the virtual rendering algorithm are presented. The particle filter framework for surgical tool tracking is described in section III. The simulation-based and experimental validation results are presented in Section IV. And, finally, the conclusions are given in Section V.
II. Virtual Tool Rendering
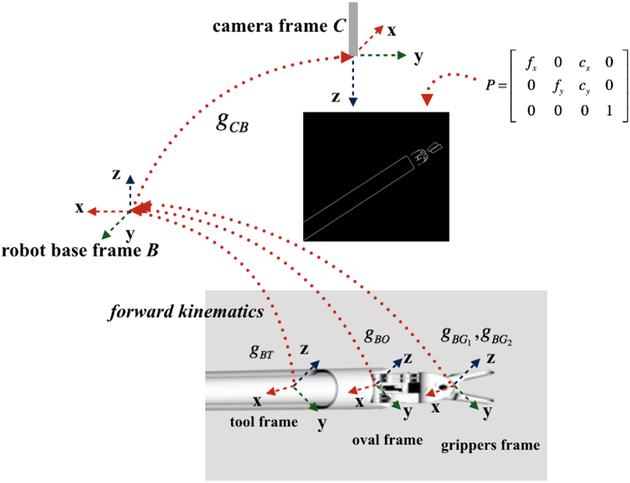
A key component of a Bayesian state estimation scheme is the underlying measurement model of the sensing system. In the proposed approach, a virtual rendering method, which generates a representation of the surgical tool as observed through the stereo endoscopic cameras of the system, is employed for constructing the measurement model (described in Section III-B). The tool geometries used in virtual rendering are based on the 3-dimensional (3D) CAD models of the real surgical tools, which provide triangulated surface mesh representations of the tool body parts and the constraints between the parts. Each 3D tool model is composed of a group of faces, which are represented as vertices and vertex normals in tool frame coordinates. Given a specific pose, the forward kinematics of the surgical manipulator [17] and the camera-robot calibration information are used to calculate the spatial configuration of the tools parts relative to the endoscopic camera. The virtual rendering method is then employed to generate the silhouette of the tool on a virtual image from the vertices and vertex normals that belong to the faces of the tool model. The obtained virtual image contains the rendered silhouette, which represents the contour of the tool from the endoscopes perspective. This approach can be easily applied to any surgical tool represented as a polygonal mesh.
A. Derivation of Tool Geometry Using Forward Kinematics
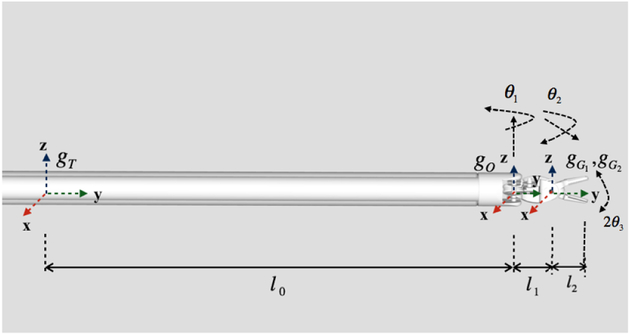
In this paper, an Endowrist® Large Needle Driver is used as the example surgical tool to be tracked. The needle driver tool model is decomposed to different parts with joint angle constraints, which we will refer to as cylinder (the tool shaft), oval (the intermediate oval shaped link in between the tool shaft and the gripper) and gripper (×2) parts (Fig. 1).
Fig. 1.
Definition of tool geometry, joint angle constraints, and the associated coordinate frames.
gBT, gBO, and are used to represent, respectively, the pose of the tool frame, oval frame and two gripper frames relative to the base frame (B) of the surgical manipulator (Fig. 1). Each tool body part i pose can be represented as one SE(3) matrix. For convenience, the tool frame T on the cylinder part is assumed to be located 10cm away from the oval joint along the tool shaft. Since the camera visual range is limited, the rest of the tool shaft is ignored to save computational time when preforming the rendering algorithm.
As the surgical tool has four body parts which are separated to render them in different poses, it is important to keep the geometry constraints of the four body parts. In Fig. 1, θ1 denotes the relative joint angle between oval part and the cylinder part along the Z-axis, θ2 describes the tilting angle of the gripper tip to the oval frame along the X-axis, and 2θ3 denotes the relative joint angle between two grippers. Therefore, the tool configuration can be represented by the pose of the tool frame along with the 3 joint angles. Specifically, the tool geometry can also be expressed in a constrained vector as showing in Fig. 1 as
| (1) |
where and denote, respectively, the position and orientation vectors of the tool shaft frame.
The pose of the tool frame relative to the base frame (gBT ∈ SE(3)) is given by the forward kinematics of the manipulator [18] from and as
| (2) |
where gBT denotes the transformation of the tool frame relative to robot base frame, and [18]. Then, the oval frame relative to robot base frame is then given by
| (3) |
Similarly, the gripper frames can be calculated as
| (4) |
| (5) |
where ϕ1 = θ2 + θ3 and ϕ2 = θ2 − θ3.
B. Silhouette Generation Using Surgical Tool Model
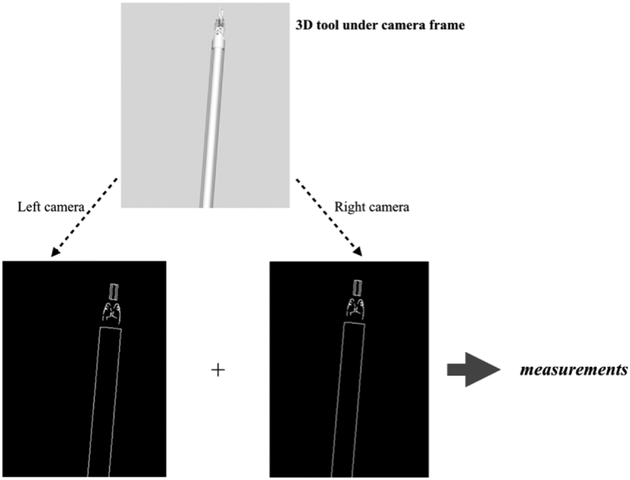
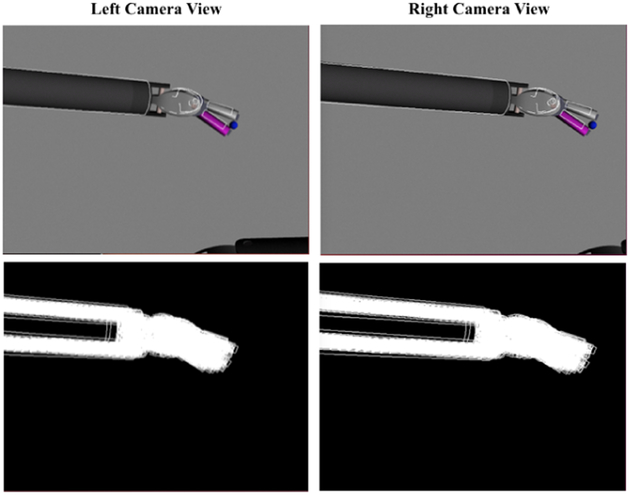
The silhouette generating algorithm aims to produce virtual images of the surgical tool for use as part of the measurement model of the Particle Filter algorithm. In this paper, a geometry-based approach [19], where the edges that separate the front facing and back facing faces of the tool model, is used to generate the silhouette of surgical tool as it is viewed from the pair of cameras of the stereo endoscope used in the da Vinci® robotic surgery system (Fig. 2). In this approach, first, the geometric model of the surgical tool’s body parts are transformed to their poses under the joint angle constraints, as described in the previous section. Then, the silhouette generation algorithm is executed for each tool part for rendering under the camera frames.
Fig. 2.
Virtual tool rendering under stereo camera view.
The CAD models of the surgical tools are defined in Alias/WaveFront Object (OBJ) file format [20]. The basic elements of each model file contain a set vertex definitions, along with vertex normals and vertex texture coordinates, and a set of face definitions. In the proposed silhouette extraction algorithm, the texture of the tool is ignored, and only the relative geometry information of the tool model is used. In the model, each face is defined by three vertices. The silhouette extraction algorithm generates the object silhouette by finding the adjoining edges of neighboring front- and back-facing faces based on the vertices and face normals. First, it is important to identify the front-facing faces and the back-facing faces. The OBJ file does not provide the face normal directly. Instead of estimating face normals from the vertex normals, face normals are computed from the relative positions of the three vertices of each of the faces. Meanwhile, it is critical to make sure that each face normal is pointing outwards from the object surface.
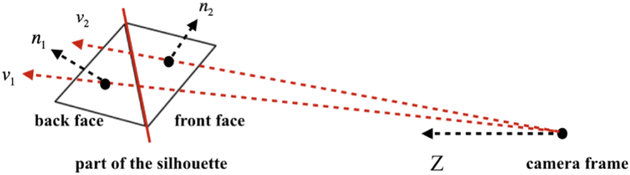
For a given model of the tool, the front-and back-facing faces are defined as shown in Fig. 3. It is easy to see that a front-facing face has a negative dot product of the face normal and view vector vi while a back-facing face has a positive one. An edge is drawn when it is the connecting edge of a back-facing and front-facing face, as determined by
| (6) |
Fig. 3.
Silhouette generation.
Using this method, the algorithm finds all of the silhouette edges of the object and the corresponding 3D positions of the edge vertices. All the edge vertices are then projected to the image by using the camera projection matrix given by
| (7) |
The 2D image point of each vertex is then given by
| (8) |
where XC denotes the vertex under camera frame. According to the relative transformation of each tool body part from equations (2)–(5), the edge points in pixel frame can be expressed as:
| (9) |
| (10) |
| (11) |
| (12) |
where gCB is the transformation of the robot arm base relative to camera frame, and, gBT is the transformation of the tool frame relative to the robot arm base. , and are the coordinates of each vertex in each of the tool body part frame, which are defined as shown in Fig. 1. and represent the image points on the silhouette of the rendered tool body part. For a given tool pose under the stereo camera frames, these image points can then be used to construct the silhouette of the tool model in a pair of 2D images and generate the virtual image that contains the emulation of the contour of the tool for further analysis.
The silhouette extraction algorithm, which generates the silhouette of the surgical tool model as viewed from a given camera pose, is summarized in Algorithm 1. The virtual tool rendering algorithm, which combines the silhouette extraction algorithm and the tool geometry computations, is given in Algorithm 2.
The virtual tool rendering algorithm is summarized in Fig. 4. The virtual tool rendering algorithm returns the virtual image virtual images with rendered silhouettes of the tool model, which is used in the measurement model of the Particle Filter algorithm (described in Section III). The experimental results of the virtual tool rendering algorithm are presented in Section IV, along with the tool tracking validation results.
Fig. 4.
Overview of virtual tool rendering.
III. Particle Filter for Tool Tracking
The principle of Particle Filter is to represent the posterior probability density function using a finite set of random samples. Each of the particles represents a state vector hypothesis, where the probability of a state hypothesis to be in the set is proportional to the posterior probability density.
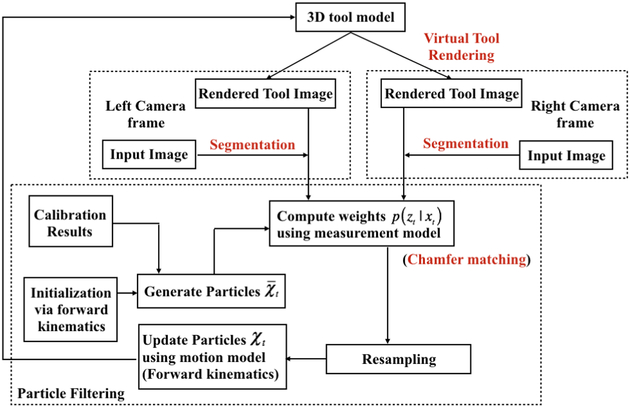
Importance resampling is employed in Particle Filters to transform the particles that are sampled from the prior into the posterior. In this work, low variance sampling is applied to reduce the degeneracy problem [21] in importance resampling. The details of the particle filter-based tool tracking under the stereo endoscope image stream is summarized in Fig. 5. The initial set of particles in the particle filter is obtained via the forward kinematics of the da Vinci® robot arm and the rough robot-camera calibration. This method provides a robust way for narrowing the search space, so that it is possible to get a relatively reliable initial guess set and avoid the time consuming global search to initialize the particles.
Fig. 5.
Particle filter-based tool tracking framework.
A. Motion Model
The motion model employed in this study assumes the state of the tool evolves incrementally based on the incremental joint displacement of the physical manipulator with additional Gaussian noise to account for uncertainty in calibration and robot motion. Thus the dynamic process noise has the form of a Gaussian with zero mean and joint angle variance , where noise for each of the joint angle components are assumed to be mutually independent [22]. Specifically,
| (13) |
where denotes the nominal joint displacement reported by the joint angle sensors for the time interval (t,t + Δt) and is the Gaussian process noise for joint i.1
B. Measurement Model
In the proposed approach, the measurement model quantifies the similarity or proximity between the virtual images of the tool pose hypotheses and the real images that are captured by the stereo vision system. The measurement likelihood p(zt|xt) [22] used is in the form
| (14) |
where η is the normalization constant that makes the measurement distribution integrate to 1, and v(·) denotes the measurement energy potential, which depends on the distance between the virtual image and real image. The correspondence between each set of virtual images that contain both left and right camera rendered tool and the real images are evaluated by the measurement energy potential function π(·). The proposed approach is based on edge-based tracking, where the distance function or the measurement energy potentials are calculated by a pixel-wise matching algorithm. In this study, the Chamfer distance map [23],[24] is used to describe the similarity between the two 2D images. Specifically, the Chamfer matching score is calculated to measure the distance between a virtual rendered tool image and a segmented image captured from the camera. In this paper, Canny edge detector [25], [26] is applied for the segmentation of the tool image, which is shown to be sufficient for the regular tracking scenes [11].
Let X denote the state vector, and the obtained Chamfer distance indicate the measurement error for each camera. Then we define s(X) as the matching score in order to map the measurement error to particle weight as
| (15) |
where τ is the sensitivity factor and dcm denotes the Chamfer distance. The measurement model π(X) is defined as
| (16) |
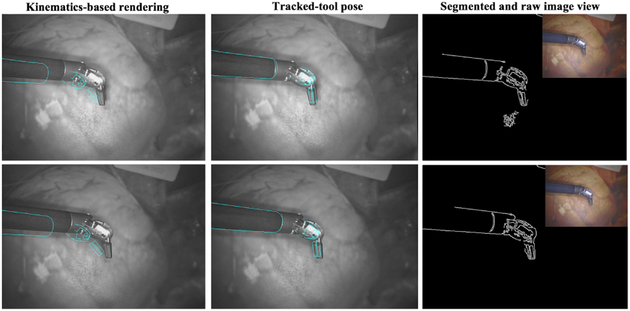
where and are the matching scores derived from the left and right camera, respectively [27]. The resulting particle filter based tracking algorithm is summarized in Algorithm 3 [28]. In the algorithm description, χ denotes the set of particles, z. denotes the measurement, i.e., the endoscopic images, and u denotes the input, i.e., the incremental motion of the surgical manipulator at the corresponding time steps. Fig. 6 gives an example of the robotic surgical tool pose estimation using the proposed tracking algorithm.
Fig. 6.
The kinematic-based silhouette rendering using the calibration and the recovered pose based on vision feedback of the da Vinci robot. Left camera view is given in first row, and right view is given in the second row.
IV. Experiment Results
The proposed surgical tool tracking algorithm was evaluated both in a simulation environment and on hardware.
A. Simulation-based Validation Results
For simulation based validation of the proposed method, a ROS/Gazebo-based simulation of the da Vinci® surgical robotic system was used. In the idealized world of the simulation, the endoscope to robot base transformation, robot forward kinematics, and the joint sensor feedback are exactly known, which provides an exact baseline to quantitatively evaluate the tracking performance. Noise was intentionally added to the joint sensor feedback to the particle filter algorithm, in order to create a validation scenario with realistic position and orientation errors.
Fig. 7 presents an example of surgical tool tracking results with the proposed algorithm in the Gazebo world using 200 particles. The projection of the best matched particle is superimposed by the white lines on the endoscopic images shown in the top row. Distribution of all of the particles are shown in the bottom row.
Fig. 7.
Surgical tool tracking in the Gazebo-based simulation environment: Top row shows the right and left camera images superimposed with best matched particle (white lines). Bottom row shows the distribution of all of the particles. In this particular simulation, the particle filter was initialized with an initial position error of 15mm and orientation error of 3.2°. After convergence of particles, the resulting position error was 0.6mm, and orientation error was 2.4°.
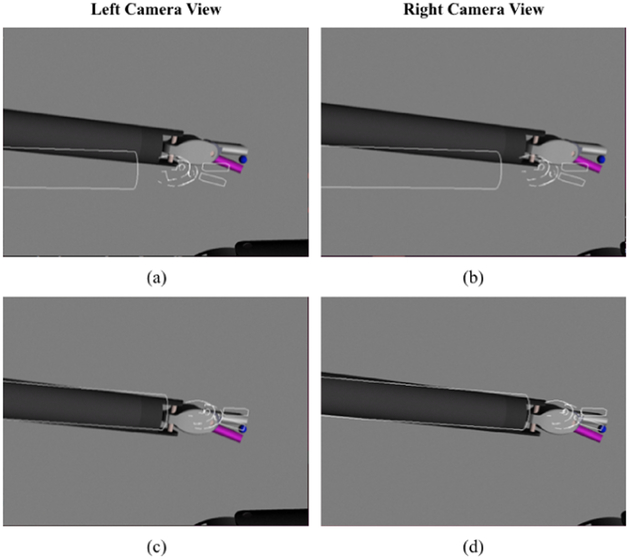
Fig. 8 presents a noised sample pose and the recovered tracking pose using 700 particles. The performance of the tracking was evaluated for 20 random selected initial poses with initial position and orientation errors of, respectively, 13mm and 10°. The resulting tracking errors averaged over 50 trials each are shown in Fig. 9.
Fig. 8.
Example tracking results in Gazebo-based simulation environment: Simulation starts with an initial position error of 10mm and an orientation error of 14°, as shown in (a) and (b). After convergence of the filter, the resulting position and orientation errors are, respectively, 2.6mm and 3.8°, as shown in (c) and (d).
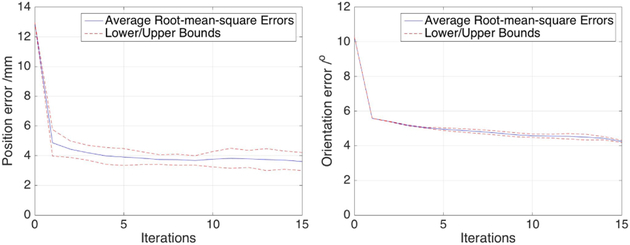
Fig. 9.
Average root-mean-square position and orientation errors in the Gazebo-based simulation environment using 700 particles.
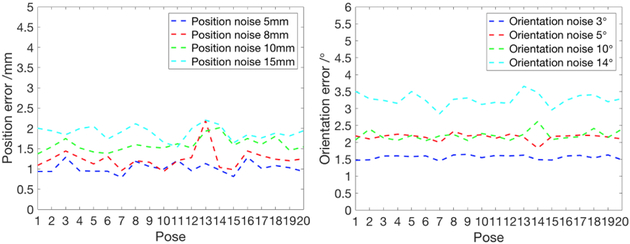
The robustness of the surgical tool tracking was also evaluated by varying the joint sensor noise variances in the simulation environment. The results, averaged over 50 trials for each noise level, starting from 20 randomly selected initial surgical tool configurations are reported in Fig. 10.
Fig. 10.
Performance of particle filter tool tracking with different joint sensor noise levels.
The simulation-based evaluation results demonstrate that the proposed algorithm, with relatively small number of particles (700 particles), results in robust surgical tool tracking for moderate initial position/orientation errors and joint sensor noise levels. The results also indicated that the tracking performance is sensitive to the pose of the oval part since it has relatively more noise than the cylinder and gripper parts for the segmentation algorithm to identify the contour.
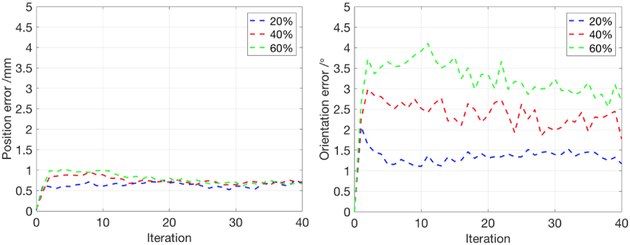
In order to test the robustness of the proposed method during dynamic tracking, the surgical tool was given a sequence of movement over 50 randomly selected trajectories in the Gazebo simulation environment [27]. At each trajectory, all particles were initialized with the true position and orientation. Three different noise levels were added to the joint sensor feedback during the motion of the robot arm. The position and orientation errors averaged over the 50 trials for each of the three noise level cases are presented in Fig. 11.
Fig. 11.
Tracking performance of various sequences of arm motions under three levels of joint sensor noise. The algorithm was tested with 50 different randomly generated trajectories. Here we chose 800 particles to compensate the highest noise level. The best particle position and orientation error were recorded at each iteration during the tracking for all 50 trajectories.
B. Experimental Evaluation on the Physical da Vinci® System
The hardware validation of the proposed method was performed on a da Vinci® IS-1200 Surgical Robotic System, upgraded with the open-source/open-hardware da Vinci Research Kit (dVRK) [17], which allows direct computer-based control of the system.
When executing the tracking algorithm in real robot system, the camera to robot base transformation is also corrupted by calibration uncertainty. Therefore, the camera-robot calibration errors were directly included as part of the system state used in the tracking algorithm. Specifically, the robot state defined in (1) is augmented as
| (17) |
| (18) |
where the transformation between the camera and robot base frames, gCB, is included in the state vector to estimate and compensate for the camera-robot calibration errors, along with all of the robot joint angles θ.
Experimental tracking results under 9 different example trials are shown in Fig. 12. In all of the hardware experiments, 500 particles are used in order to handle the uncertainty observed in the system while maintaining interactive tracking rates (please see Section V for a discussion on the computation times). In all trials, only one tool is tracked by the proposed algorithm. The second and/or the third tools of the da Vinci® system was moved inside the endoscope view in some of the trials, in order to make the background visually more complex during the experiments. Specifically, in trials 1–8, the additional tools were placed in locations and orientations that have the potential to create false positive matches, in order to validate if the tracking algorithm is capable of handling potential local optima in the matching function. Furthermore, in trials 2–8, the additional tools were placed above the target tool in different configuration, in order to evaluate tracking performance under occlusions.
Fig. 12.
Tracking results from hardware validation experiments for 9 different configurations (results referred to as trial 1–9, row-wise from top-left to bottom-right, in the text). Pairs of images show the left and right camera views from the da Vinci® system’s stereo endoscopes, overlaid with the best particles from the tracking algorithm rendered in cyan. In the experiments, only one surgical tool is being tracked, while manually controlled additional tools are placed in the view make the scene visually more complex.
The experimental results indicate that the proposed tracking algorithm is able to recover the tool pose from the real endoscope views, in highly noised environment with occlusions caused by surgical tools or other objects. Besides, the proposed algorithm generally tracks the target tool when the oval parts and grippers are entirely or partially covered, since the forward kinematics provides a relatively robust coarse guess to compensate for loss of vision feedback.
In order to further validate the tracking performance under occlusion during the tracking, a second tool was placed in different poses to block the target tool during the tracking process. Fig. 13 shows a time sequence of tracking results, where the target tool is occluded in several body parts. The results suggests that the proposed approach can recover from intermittent occlusions.
Fig. 13.
The sequence of tracking results under different occlusion conditions. The images (a-f) correspond to a time sequence of images from a single trial. The cyan lines mark the best particle overlaid on the images from the left and right endoscope views. In (d), the particles were briefly “distracted” by the tool in background due to the occlusion. However, the tracking algorithm was able to recover from the occlusion in the subsequent time steps.
Additional hardware tracking results are presented in the video attachment of the present paper.
V. Conclusions
This paper presented a particle filtering-based framework for tracking robotically controlled surgical tools under stereo vision based image streams. As part of the proposed framework, a virtual tool rendering algorithm is introduced and implemented to produce the silhouette of the surgical tool model. Using the virtual tool images generated by the virtual tool rendering algorithm, computer vision-based techniques are employed to construct the measurement model for the Particle Filter algorithm. The tracking performance was evaluated in a simulation environment and using the physical da Vinci® surgical robotic system.
The future work will proceed on several avenues. The current version of the algorithm is implemented as a serial algorithm on a CPU. Although the algorithm operates in real-time, it has a frame rate which is currently insufficient for closed-loop visual servo-control (at approximately 0.3 frames-per-second). The primary bottleneck in computation of the algorithm is the virtual tool rendering for the individual particles used in the filter. Fortunately, this part of the algorithm is parallelizable, since each of the particle hypotheses can be processed independently in parallel. As part of our future work, we are working on a GPU-based parallel implementation of the algorithm in order to speed up the tracking algorithm to a frame rate sufficient for visual servo control (~10 frames-per-second). Additionally, the tool models can be further refined to get more robust rendering results, potentially including color-based features. In order to perform the visually guided surgical manipulations with the da Vinci® robotic system, some additional pieces still need to be incorporated, such as motion planning algorithms for the da Vinci® arms and a needle tracking algorithm.
Acknowledgments
This work was supported in part by the National Science Foundation under grants CISE IIS-1524363 and CISE IIS-1563805, and National Institutes of Health under grant R01 EB018108.
Footnotes
If there is no information available about the nominal motion of the physical robot, the term for the nominal joint displacement can be excluded, and the variance for the Gaussian noise term increased. This would result in a Brownian motion model for the tool motion [16].
Contributor Information
Ran Hao, Email: rxh349@case.edu.
Orhan Özgüner, Email: oxo31@case.edu.
M. Cenk Çavuşoğlu, Email: mcc14@case.edu.
References
- [1].Feddema J and Mitchell O, “Vision-guided servoing with feature-based trajectory generation (for robots),” IEEE Transactions on Robotics and Automation, vol. 5, no. 5, pp. 691–700, 1989. [Google Scholar]
- [2].Vincze M, Schlemmer M, Gemeiner P, and Ayromlou M, “Vision for robotics: a tool for model-based object tracking,” IEEE Robotics Automation magazine, vol. 12, no. 4, pp. 53–64, 2005. [Google Scholar]
- [3].Hongliang R and Kazanzides P, “Investigation of attitude tracking using an integrated inertial and magnetic navigation system for hand-held surgical instruments,” IEEE/ASME Transactions on Mechatronics, vol. 17, no. 2, pp. 210–217, 2012. [Google Scholar]
- [4].Rogerio R, Balicki M, Sznitman R, Meisner E, Taylor R, and Hager G, “Vision-based proximity detection in retinal surgery,” IEEE Transactions on Biomedical Engineering, vol. 59, no. 8, pp. 2291–2301, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Krupa A, Gangloff J, Doignon C, de Mathelin MF, Morel G,Leroy J, Soler L, and Marescaux J, “Autonomous 3-d positioning of surgical instruments in robotized laparoscopic surgery using visual servoing,” IEEE Transactions on Robotics and Automation, vol. 19, no. 5, pp. 842–853, 2003. [Google Scholar]
- [6].Staub C, Lenz C, Panin G, Knoll A, and Bauernschmitt R, “Contour-based surgical instrument tracking supported by kinematic prediction,” in IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), 2010. [Google Scholar]
- [7].Pezzementi Z, Voros S, and Hager GD, “Articulated object tracking by rendering consistent appearance parts,” in IEEE International Conference on Robotics and Automation, 2009, pp. 3940–3947. [Google Scholar]
- [8].Choi C and Christensen H, “3d textureless object detection and tracking:an edge-based approach,” in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2012. [Google Scholar]
- [9].Reiter A, Allen PK, and Zhao T, “Marker-less articulated surgical tool detection,” Computer assisted radiology and surgery, 2012. [Google Scholar]
- [10].Hinterstoisser S, Holzer S, Cagniart C, Ilic S, Konolige K,Navab N, and Lepetit V, “Multimodal templates for real-time detection of texture-less objects in heavily cluttered scenes,” in IEEE International Conference on Computer Vision (ICCV), 2011. [Google Scholar]
- [11].Baek YM, Tanaka S, Harada K, Sugita N, Morita A, Sora S, and Mitsuishi M, “Robust visual tracking of robotic forceps under a microscope using kinematic data fusion,” IEEE/ASME Transactions on Mechatronics, vol. 19, no. 1, pp. 278–288, 2014. [Google Scholar]
- [12].Ye M, Zhang L, Giannarou S, and Yang G-Z, “Real-time 3d tracking of articulated tools for robotic surgery,” in International Conference on Medical Image Computing and Computer-Assisted Intervention, 2016, pp. 386–394. [Google Scholar]
- [13].Arulampalam M, Maskell S, Gordon N, and Clapp T, “A tutorial on particle filters for online nonlinear/non-gaussian bayesian tracking,” IEEE Transactions on signal processing, vol. 50, no. 2, pp. 174–188, 2002. [Google Scholar]
- [14].Breitenstein M, Reichlin F, Leibe B, Koller-Meier E, and Gool LV, “Robust tracking-by-detection using a detector confidence particle filter,” in IEEE 12th International Conference on Computer Vision, 2009. [Google Scholar]
- [15].Thrun S, “Particle filters in robotics,” in Proceedings of Eighteenth Conference on Uncertainty in Artificial Intelligence, 2002. [Google Scholar]
- [16].Choi C and Christensen H, “Robust 3d visual tracking using particle filtering on the special euclidean group: A combined approach of keypoint and edge features,” The International Journal of Robotics Research, vol. 31, no. 4, pp. 498–519, 2012. [Google Scholar]
- [17].Kazanzides P, Chen Z, Deguet A, Fischer GS, Taylor RH, and DiMaio SP, “An open-source research kit for the da vinci® surgical system,” in IEEE International Conference on Robotics and Automation (ICRA), 2014. [Google Scholar]
- [18].Murray R, Li Z, and Sastry SS, A mathematical introduction to robotic manipulation. CRC press, 1994. [Google Scholar]
- [19].Nucharee T and Lipikorn R, “Data reduction for finding silhouette edges on 3d-animated model,” International Journal of Computer and Communication Engineering, vol. 2, no. 5, p. 560, 2013. [Google Scholar]
- [20].Murray JD and vanRyper W, Encyclopedia of Graphics File Formats. Sebastopol, CA, USA: O’Reilly & Associates, Inc, 1994. [Google Scholar]
- [21].Wren R, Azarbayejani A, Darrell T, and Pentland A, “Pfinder: Real-time tracking of the human body,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 19, no. 7, pp. 780–785, 1997. [Google Scholar]
- [22].Petrovskaya A and Khatib O, “Global localization of objects via touch,” IEEE Transactions on Robotics, vol. 27, no. 3, pp. 569–585, 2011. [Google Scholar]
- [23].Liu M, Tuzel O, Veeraraghavan A, and Chellappa R, “Fast directional chamfer matching,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2010. [Google Scholar]
- [24].Ghafoor A, Iqbal R, and Khan S, “Image matching using distance transform,” Image Analysis, pp. 212–229, 2003. [Google Scholar]
- [25].Canny J, “A computational approach to edge detection,” IEEE Transactions on Pattern Analysis and Machine intelligence, vol. 6, pp. 679–698, 1986. [PubMed] [Google Scholar]
- [26].Arbelaez P, Maire M, Fowlkes C, and Malik J, “A computational approach to edge detection,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 33, no. 5, pp. 898–916, 2011. [DOI] [PubMed] [Google Scholar]
- [27].Özgüner O, Hao R, Jackson RC, Shkurti T, Newman W, and Çavuşoğlu MC, “Three-dimensional surgical needle localization and tracking using stereo endoscopic image streams,” in IEEE International Conference on Robotics and Automation, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Thrun S, Burgard W, and Fox D, Probabilistic robotics. MIT press, 2005. [Google Scholar]