Abstract
The emerging field of cancer radiomics endeavors to characterize intrinsic patterns of tumor phenotypes and surrogate markers of response by transforming medical images into objects that yield quantifiable summary statistics to which regression and machine learning algorithms may be applied for statistical interrogation. Recent literature has identified clinicopathological association based on textural features deriving from gray-level co-occurrence matrices (GLCM) which facilitate evaluations of gray-level spatial dependence within a delineated region of interest. GLCM-derived features, however, tend to contribute highly redundant information. Moreover, when reporting selected feature sets, investigators often fail to adjust for multiplicities and commonly fail to convey the predictive power of their findings. This article presents a Bayesian probabilistic modeling framework for the GLCM as a multivariate object as well as describes its application within a cancer detection context based on computed tomography. The methodology, which circumvents processing steps and avoids evaluations of reductive and highly correlated feature sets, uses latent Gaussian Markov random field structure to characterize spatial dependencies among GLCM cells and facilitates classification via predictive probability. Correctly predicting the underlying pathology of 81% of the adrenal lesions in our case study, the proposed method outperformed current practices which achieved a maximum accuracy of only 59%. Simulations and theory are presented to further elucidate this comparison as well as ascertain the utility of applying multivariate Gaussian spatial processes to GLCM objects.
Keywords: Bayesian prediction, cancer detection, gray-level co-occurrence matrix, Markov random field, radiomics, texture analysis
1. Introduction
Diagnostic radiologists in oncology settings encounter patients with diverse clinical pathways and heterogeneous tumor micro-environments making tissue characterization and diagnosis a challenge. Endeavoring to characterize tumor phenotypes through quantifications of intrinsic patterns of enhancement, texture, morphology, and shape, the subdiscipline of “cancer radiomics” has emerged with recent advances in scanning and high throughput computational technologies [27, 38]. Several authors have put forth particular types of quantitative mappings that facilitate the dimension reduction of delineated regions/volumes of interest into summary statistics (or features) that potentially elucidate the underlying composition or prognostication of solid masses suspect of malignant pathology [1, 5, 7, 20]. It’s often asserted that such analytical techniques yielded mineable image-derived feature sets facilitating subtyping schemes that capture patterns that are indistinguishable to the human eye.
Recent literature has identified clinicopathological association based on textural features deriving from gray-level co-occurrence matrices (GLCM) which facilitate evaluations of gray-level spatial dependence within a delineated region of interest. This article presents a Bayesian probabilistic modeling framework for the GLCM as a multivariate object as well as describes its application within a cancer detection context based on computed tomography. The methodology, which circumvents processing steps and avoids evaluations of reductive and highly correlated feature sets, uses latent Gaussian Markov random field structure to characterize spatial dependencies among GLCM cells and facilitates classification via predictive probability.
1.1. Texture Analysis in Oncology
Evaluation of gray-level spatial dependence through analysis of the Gray-Level Cooccurrence Matrix (GLCM), is perhaps the predominant technique for image texture analysis. A GLCM is a matrix defined over an image domain with cells comprised of counts that describe the distribution of co-occurring gray-scale valued pixels (or voxels) at a given offset and angle [12]. More specifically, the (i,j)th entry of a GLCM represents the frequency with which a {pixel with gray-level i was present in a spatial location either horizontally, vertically or diagonally to adjacent to a pixel with gray-level j. A GLCM is symmetric when considering all directions, summing over all angles using the same offset. Hereafter, we consider symmetric formulations of GLCM constructed from K gray-level bins which contain at most K(K + 1)/2 unique cell counts. The GLCM object, thereby, facilitates dimension reduction from the image space to a standardized data lattice consisting of K(K + 1)/2 structured, discrete random variables. Image standardization effectuated by a GLCM approach is useful in diagnostic oncology settings wherein targeted lesions may present with irregular shapes and sizes which preclude a common grid space to facilitate model formulation and analysis.
GLCMs are often analyzed through summary statistics which effectively reduce the lattice count data to sets of GLCM-based textural features. Several authors have noted that the resulting summary statistics are strongly correlated with each other, resulting in over-fitting [2, 18, 34, 35, 39]. Consequently, present practices invite scrutiny, challenge reproducibility, and encourage innovation. To illustrate, Table 1 presents five GLCM-derived features (correlation, energy, contrast, entropy, and homogeneity) commonly interrogated in cancer imaging settings at different angles and offsets. Interpretations of these features reflect those of conventional summary statistics commonly used to describe the empirical distributions of unstructured correlated random variables. For example, here Correlation denotes a measure of linear dependence in co-occurrence among the K gray-levels. Energy (also known as uniformity or the angular second moment) is defined as the sum of squared elements in the GLCM, representing the overall incidence of co-occurring gray-levels for the specific offset. Contrast measures local variation (also known as inertia), while homogeneity (or inverse difference moment) measures the overall smoothness of the gray-level distribution over the target region of interest (ROI), while entropy is the GLCM measure of non-informativeness. In a systematic study describing the discriminatory power GLCM-feature combinations based on Brodatz textures, Gotlieb and Kreyszig[11] found that a subset of four of these features (energy, contrast, entropy and homogeneity) yielded best classification performance. Wang et al.[36] suggested that energy and contrast were most efficient for describing textural patterns in their study. While, more recently, Mostaco-Guidolin et al.[22] argued on the basis of Fisher score criteria that all five features should be used for pattern detection.
Table 1.
Commonly used GLCM-based features.
| Statistic | Formula |
|---|---|
| Correlation | |
| Energy | |
| Contrast | |
| Entropy | |
| Homogeneity | |
Notes:
Pij = (ij)th entry in normalized GLCM
μi = mean of row i in normalized GLCM
μj = mean of column j in normalized GLCM
σi = standard deviation of row i in normalized GLCM
σj = standard deviation of column j in normalized GLCM
Several recent studies have endeavored to establish techniques for differentiating among tissue classes on the basis of texture-based statistical summaries. In a breast cancer study, Chan et al.[6] produced a GLCM-based feature classifier from 86 mam-mograms using a backpropagation artificial neural network (ANN). The authors were able to obtain an AUC of 0.88. Gibbs and Turnbull[9] used GLCM-based texture features obtained from post-contrast MRI images to discriminate benign and malignant breast tumors with logistic regression. In a study by Gletsos et al.[10], focal liver lesions from 147 patients were differentiated by four classes (normal, hepatic cysts, hemangioma, and hepatocellular carcinomas) using GLCM-based features derived from CT with ANN yielding high accuracy. Jirak et al.[17] extracted first order statistical and GLCM-based texture features from 43 patients using T2-weighted MRI images and implemented kNN (nearest neighbor) and ANN classifiers to discriminate between healthy and cirrhotic liver regions. Harshvardhan et al.[13] recently proposed a logistic regression classifier that uses GLCM-based features as predictors for early detection and recognition of glaucoma by ocular thermal images. Zulpe and Pawar[40] used artificial neural network techniques on GLCM texture features to classify brain tumors from MR images. More recently, Singh et al.[32] explored GLCM feature extraction on 330 mammograms concluding that random forest yielded the best classification performance in the breast cancer study. Tang et al.[33] used consensus and hierarchical clustering to develop a radiomics signature that characterizes the local immune pathology environment of non-small cell lung cancer patients treated with definitive resection.
1.2. Motivating Data,: Adrenal Malignant Lesion CT Images
Early identification and diagnosis of adrenal masses are considered pivotal clinically as it has implications for appropriate treatment selection as well as determining the prognostic status of a patient’s disease stage. Proper diagnosis of abdominal lesions is also critical in the metastatic setting to determine whether a patient has experienced distant migration. Yet, characterizing benign from malignant adrenal lesions is difficult on the basis of routine CT imaging at early stages [3, 37]. Our study of GLCM classifiers was motivated by an adrenal lesion study that comprised patients who had CT imaging available in the MD Anderson Cancer Center’s radiology picture archiving and communication system (PACS) and also underwent pathological diagnoses between January 2001 and January 2010 [23-25]. GLCM-derived classifiers were considered on the basis of both non-contrast (NC) and delayed post-contrast CT images (DL) using pixel-level data from the slice that exhibited the maximal axial cross-sectional area of the adrenal mass. Data was observed for a total of 210 adrenal lesions in 204 patients. Pathological analysis was available to establish benignity and malignancy. Of the 210 lesions, 114 were benign and 96 were malignant.
A range of CT scanners had been employed, with the following parameters: median mA, 265 mA (range, 86 630 mA); 120 kVp in 210 cases; median slice thickness, 2.5 mm (range, 2.5 - 5.0 mm). Scanner models were General Electric with various Light- Speeds including LightSpeed 16,LightSpeed VCT, LightSpeed Plus and LightSpeed QX/I. Contrast-enhanced CT scans had been obtained 60-70 seconds after intravenous administration of 100150 mL of nonionic contrast agent (iohexol 300 mgl/mL, GE Healthcare Inc., Princeton, NJ) at a rate of 2.0 - 3.0 mL/second by power injector. The images were reviewed using soft tissue windows (W=400; L=350), by a radiologist with more than 5 years of experience in abdominal CT imaging. For each lesion, a region of interest (ROI) was carefully drawn free-hand, with an electronic cursor and mouse, around the periphery of the adrenal lesion. As a precaution to avoid partial volume artifacts, the extreme edges of the mass were meticulously avoided. The ROI was saved and transposed onto the image of all other CT series containing the maximal cross-sectional area of the target lesion; translational adjustments to the ROI were made as necessary to correct any axial misalignments in any given image, but the shape and size of the original ROI was preserved. The same ROI was applied to both NC and DL scans. After robust evaluations of potential gray-level partitions, GLCMs were constructed from image ROIs as follows. Gray-level bins were constructed from the Hounsfield unit (HU) scale through evaluation of the empirical distribution of all pixels in the study, for NC alone and DL alone, separately. Pixel values below the 0.025 and above the 0.975 quantiles of this empirical distribution were scaled to gray- level 1 and the highest gray-level, respectively. The approach provided robustness to extreme low and high pixel outliers when projecting from the Hounsfield unit space to gray-level space. Additional pairs of empirical quantiles were also considered, the results for which are provided in Section B of Supplemental Material. Our case study partitioned the resultant range into 8 gray-level bins with equidistant quantiles. Mapping each pixel value into a gray-level bin, our analysis used GLCMs that counted the co-occurrences of gray-level pairs at adjacent pixels (1 grid-space in distant considering all direction) resulting in rotationally invariant mappings of the image enhancement values into GLCM counts.
Figure 1 depicts enhancement patterns on the Hounsfield unit domain of ROIs comprising adrenal lesions as well as their corresponding gray-level co-occurrence matrices. The top image reflects a high degree of co-occurrence at higher gray levels, which tends to be representative of cases of malignancies within our study. Conversely, the bottom image tends to be indicative of benign lesions. The central image, for which high co-occurrences were observed at middle gray-levels, depicts an intermediate case. Importantly, the GLCM cells exhibit high correlation with their adjacent neighbors, as depicted by the fairly smooth changes observed when transversing away from the peak cell counts. This suggests that lesion heterogeneity may be distinguished by the spatial pattern in the GLCM object with classifiers that leverage this dependence structure with an appropriate multivariate model. To model the multivariate count data observable within the GLCM lattice with a Gaussian process, normalization must be applied to the unique-valued diagonal and upper-diagonal GLCM cells. The model described in Section 2.1 is applied after transforming the co-occurrence counts into empirical rates in relation to the total number of co-occurrences observed in the image. Furthermore, in order to satisfy Gaussian distributional assumptions, the square-root transformation was applied to the observed empirical co-occurrence rates.
Figure 1. Illustrative patterns of GLCM in adrenal lesions from CT imaging for 3 representative subjects.
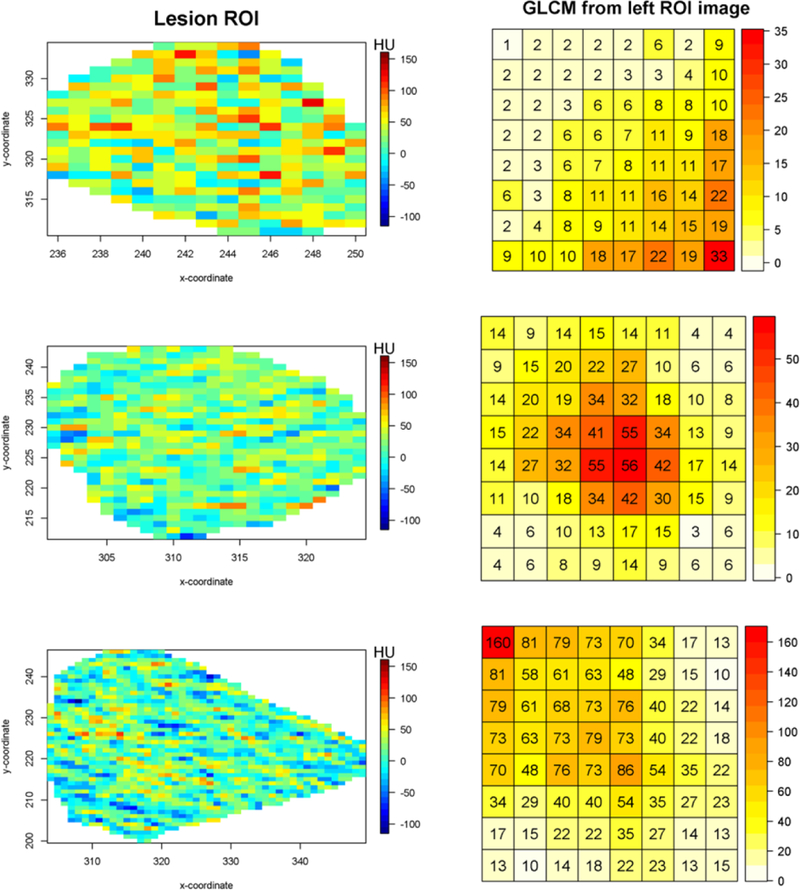
Pixel-level ROIs on the left, GLCMs on the right.The color grid of the left images reflect Hounsfield Unit(HU) domain.
However, the existing approaches aforementioned in section 1.1 should be considered limited. The GLCM object represents a specific type of structured count data. Analytical techniques that reduce this multivariate structure to a set of summary statistics effectuate information loss, potentially masking functional patterns that describe the density, perfusion, or morphology of the tumor microenvironment. As demonstrated in our simulation study, for example, the textural features are insensitive to rotations of the GLCM, which attenuates predictive power for pattern discrimination.
To overcome this limitation, we have formulated a Bayesian probabilistic method for predictive classification of GLCM objects and study its application to a retrospective database of patients with adrenal lesions scanned by computed tomography (CT) for which confirmatory pathology is available. The methodology, which circumvents feature processing steps and avoids model fitting in the presence of highly correlated feature sets, uses latent Gaussian Markov random fields to characterize GLCMs as multivariate objects. Specifically, by introducing a spatial Gaussian process to model spatial dependencies among the GLCM entries, the probability model characterizes distributional assumptions that pertain to the space of the entire normalized GLCM as a multivariate response surface. Thus, each independent unit (lesions in our case study) contributes an entire GLCM as the dependent variable. Therefore, our context represents a departure from the traditional disease mapping setting for which the aggregated random variable is observed at varying spatial locations spanning the patient population. The modeling approach yields a Bayesian spatial Gaussian process classifier (BSGC), which we applied in the cancer detection setting to discriminate malignant and benign adrenal lesions based on CT scans with and without administration of contrast. Correctly predicting the underlying pathology of 81% of the adrenal lesions in our case study, the GLCM Bayesian multivariate classifier outperformed classifiers based on GLCM-derived features with regression and machine learning algorithms which achieved a maximum accuracy of only 59% in our case study. Simulations and theory are presented to further elucidate this comparison as well as ascertain the utility of applying multivariate Gaussian spatial processes to GLCM objects.
This article is organized as follows. Section 1 discusses the applications of texture analysis in oncology settings and describes our motivating abdominal imaging study. The proposed hierarchical Bayesian modeling framework and resultant Bayesian GLCM classifier are presented in Section 2. Section 3 uses simulation to compare diagnostic properties of the method to feature-based classification. Our case study comparison is also presented in this section. Section 4 concludes this paper.
2. Hierarchical Statistical Framework
An observable GLCM object represents structured multivariate count data. Existing literature on methods for spatial count data mostly relies on Poisson distribution which is limited by the restriction of having one parameter to control both location and scale of the distribution [4, see e.g.]. Alternatives have been proposed, such as copula models, to estimate dependencies among multivariate count random variables [26]. Computation with these models, however, can be very challenging which limits their scalability to ‘big data’ environments, such as those encountered with classification and prediction among hundreds of images. This section describes the utilization of Gaussian Markov random field (GMRF) priors in a hierarchical Bayesian model formulated to capture patterns of dependence within the GLCM structure and yield probabilistic- based measures for prediction and classification.
2.1. Model formulation
We start by transforming the observed GLCM counts to normalized counts by dividing each cell of an observed GLCM by the total sum of cell counts. The modeling of normalized GLCMs offers the advantage of seamless adjustment for heterogeneity in lesion size, which impact the GLCM count total but is unrelated to textural pattern. Additionally, the use of normalized counts enables Gaussian process assumptions, which facilitate posterior mixing and reduce computational complexity. Let i denote a lesion index, and let (s1, s2,sn) denote the finite collection of GLCM location indices spanning the unique cells of the symmetric matrix. Let denote the vectorized values of normalized GLCM counts for the ith lesion. A multivariate model for the GLCM of patient i can be formulated by assuming a linear mean function for the normalized GLCM counts, y, with an additive random error term
such that the vector characterizes cell-specific effects corresponding to unique gray-levels of the GLCM that are assumed to be shared by all patients, and defines a collection of spatial random effects capturing spatial dependencies among the GLCM cells. Without loss of generality, the general case can be extended to accommodate multiple predictors by incorporating subject level design matrix and corresponding regression coefficient vector λ. For example, where λ is p - dimensional coefficient vector shared by all subjects and a dimensional design matrix adjusting the GLCM cells for subject i in relation to subject-level characteristics that describe the tumor or scanning technique. The vector ϵi denotes random noise (arising from unknown sources of variation), which is assumed to follow a n-dimensional normal distribution with zero mean and diagonal covariance matrix with variance .
In this paper, we propose to model the spatial dependence encoded by GLCMs for adrenal lesions by using a GMRF prior. GMRF models have been studied extensively as tools for characterizing the spatial variation of observable areal data as well as unobservable latent variables in hierarchical models. Spatial models for areal data, such as disease mapping of aggregated measures of prevalence or incidence within administrative districts, commonly employ GMRF models. In particular, the conditional specification of a GMRF known as the conditional autoregressive (CAR) model is often used in such settings.
The standard formulation of a GMRF model for areal data assumes that any element of ηi, depends only on its neighboring elements. Neighbors in this context are defined as elements represented by areas that share a common spatial border. Additional neighboring schemes were considered but yielded indiscernible results. This is discussed further in Section D of the Supplementary Material. We formulate a GMRF among adjacent cells within the structured GLCM lattice through specification of full conditional distributions for random effect vector ηi. Specifically, we assume that ηi arises from the following multivariate Gaussian distribution
where Bk is a normalizing factor; Tn is a precision parameter and Wkd represents a “weight” characterizing the strength of dependence between lattice elements k and d, k ≠ d. Through Brook’s Lemma [4, see e.g.], the resultant joint distribution is proportional to W is an adjacency matrix with entry Wkd indicating whether lattice elements k and d are adjacent neighbors, and B as a diagonal matrix with kth entry Bk = Dk + q denotes the number of neighbors for lattice element k, and q > 0 denotes a diagonal offset term. It should be noted that our GLCM GMRF specification resembles the one used in the INLA construction instead than the conventional CAR model formulation [4, 31, see e.g.]. In Section C of the Supplemental Material, we prove two theorems which provide mild conditions for such prior to be well defined, and with fully identifiable hyper-parameters.
To complete the conditional sampling model, given specification of the model parameters and latent, spatially correlated random effects, the observed normalized GLCM for lesion i assumes the following Gaussian distribution
Prior specification for ni follows from the GMRF formulation,
Hierarchical model specification is complete upon assuming prior distributions for the prior parameters. The conditionally conjugate prior specification is most commonly utilized with this type of Gaussian process. We denote the conjugate Gaussian prior for β with mean m0 and covariance Σ0. Conjugate gamma priors were assumed for precision parameters Tϵ and Tη with hyper-parameters a, d and b, g respectively. Moreover, the Gaussian Markov random field is properly defined in accordance with the diagonal offset term q being positive, which can be implemented based on a prior distribution π (q) that has strictly positive support, resulting in the following specification:
Posterior inference on the parameters of interest is conducted by using Markov Chain Monte Carlo (MCMC) techniques (see the Supplementary Material). However, the primary interest of the field investigators is often to provide a more accurate classification of tumor tissues, which may be improved by taking fully into consideration the spatial dependencies observed in the GLCMs.
2.2. Predictive Discriminant Analysis for GLCMs
Unlike regression-based classifiers, which rely on linear predictors, in the presence of collinearity the Bayesian paradigm facilitates class prediction through probabilistic- based measures that characterize the distributions of interdependent observable predictors under candidate classes. Bayesian discriminant-type predictive classifiers are fully specified through the predictive density of an observable predictor and the prior probability of each class. Denote the observed GLCM of a new, heretofore unclassified object by yN+1 Additionally, let c = {c\, c2,ch} denote the set of all possible classes to which object yN+1could be assigned. The classification probability for any class configuration follows from our model specification as proportional to the product of the prior probability of class ck and the value of the conditional predictive distribution for yN+1 under class ck,
| (1) |
where
is computed by averaging over posterior samples obtained from MCMC. The prior values for P(c = ck) can be specified based on the frequency of class ck observed in a training sample or through other available information. Class labels can be assigned in accordance with the highest class probability (1), which is used as the basis for evaluation in our simulation and case studies using a leave-one-out cross-validation (LOOCV) strategy.
3. Application of the proposed methodology to GLCM objects
3.1. Simulation Study: performance versus comparator classifiers
3.1.1. Simulation Design
A simulation study was devised to evaluate and compare the Bayesian GLCM classifier to four approaches to texture analysis based on GLCM features applied in recent cancer imaging literature (see e.g. Section 1.2). Specifically, comparator classifiers were based on the five GLCM-derived texture features described in Table 1 using the methods of logistic regression, support vector machine (SVM), artificial neural network (ANN) and random forest [13, 14, 16, 19, 28, 29, 32]. To formulate an appropriate sampling model capable of effectuating characterizations of spatial patterns of GLCMs that were evident in our diagnostic cancer study of adrenal lesions, we considered GLCMs constructed from 8 gray-levels with normalized element-wise probability densities arising from a bivariate normal distribution with and where we considered a wide range of values for c and s for extensive simulation scenarios. We further smoothed the Gaussian-derived empirical rate surface, calculated in proportion to the number of generated points in each grid with respect to the total number of generated points of the entire grid surface. In addition, to effectuate the discrete GLCM space, we scaled the rate surface by a random integer sampled uniformly from the range of total co-occurrence counts (50 to 2000) observed in our case study to account for heterogeneity with respect to image size. Simulation scenarios were then constructed by considering distributions of GLCMs generated under different choices of mean shift parameter c and variance scale parameter s. Specifically, c ϵ {0, 0.5,1,1.5, 2, 2.5, 3, 3.5, 4}, was chosen for a given s, such that the center of the generating bivariate normal ellipsoid shifts gradually from north-west toward south-east along the 135° diagonal of GLCM lattice, and thereby reflected the varying patterns observed in our case study pertaining to the spatial clustering of dense versus non-dense tissues (Figure 2). We also varied s, where s ϵ {5,10,12,15}, with each s representing the extent to which the noise covers the true signal the underlying spatial patterns intrinsic to each class. For example, increasing the value of s diminishes the extent to which the two spatial patterns are differentiable by any method.
Figure 2. Simulation scenarios for comparing GLCM-based classifiers.
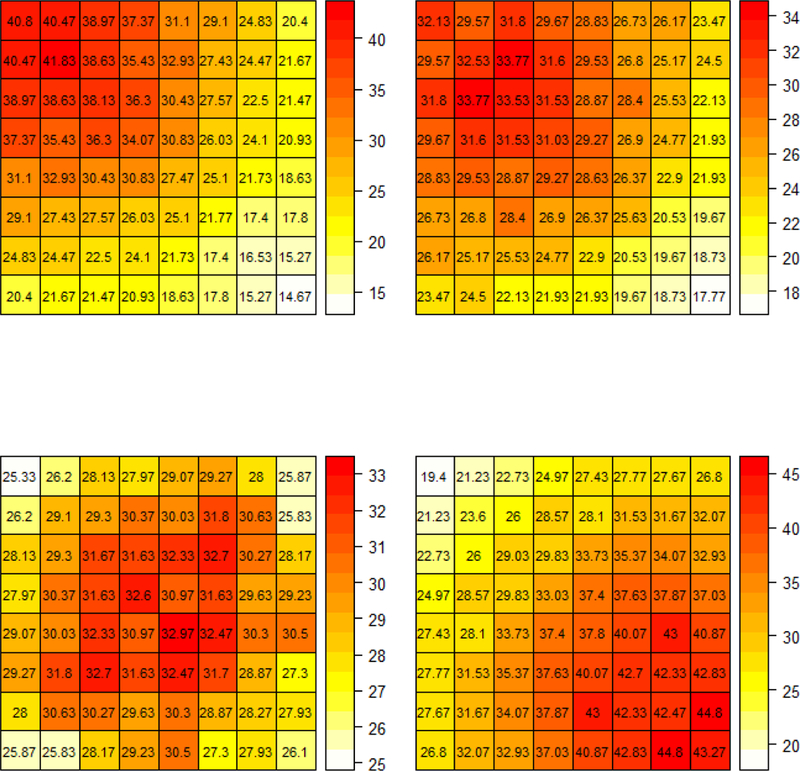
Each figure depicts the assumed mean rate surface used to simulate GLCM-derived patterns with different choices of c under s = 10. The upper-left is generated with c = 0, the upper-right is generated with c = 1, the lower-left is generated with c = 2, the lower-right is generated with c = 3.5
Analyses of each simulated cohort of lesion GLCMs was conducted assuming a vague prior for , to promote maximal data learning. Hyperparameters were set to conform to the recommendations putforth by Banerjee et al.[4] such that a = d = 0.001, b = g = 0.1. For computational efficiency, we show here the results obtained when setting q = 0.01, although the results appeared robust to the choice of priors with small variance. Bayesian posterior inference was conducted through Markov chain Monte Carlo (MCMC) sampling and post-MCMC computation of the predictive density. Details pertaining to Bayesian computation are provided in Section A of Supplemental Material. MCMC was implemented with 10,000 iterations, the First 5,000 of which were discarded as burn-in. Convergence was assessed by visual inspection and by evaluation of commonly used diagnostic tests, e.g. the Geweke diagnostic [8] with implementation using the R package ‘coda’. Convergence issues were not evident from the statistics. We simulated 30 lesion GLCMs for each c and a given s. Class assignments were predicted for each simulated lesion under each method using a LOOCV approach, with 2 lesion class, 60 subjects in total. In particular, at each step, one observed GLCM or derived GLCM-based features from a single lesion were omitted from the training cohort, the posterior inference was implemented using the remaining 59 lesion GLCMs. Thereafter, a predicted class (benign or malignant) is obtained for the lesion GLCM contributed by this omitted patient for each method and compared with each lesion’s true known status. Simulated lesion GLCM from the reference (or benign class) was assumed to arise with c = 0 for all scenarios.
3.1.2. Simulation Results
Figure 3 depicts the resultant smoothed classification accuracy obtained in our simulation study as a function of the mean shift parameter c ϵ {0.5,1,1.5, 2, 2.5, 3, 3.5, 4} for four choices of the dispersion parameter s, respectively.
Figure 3.
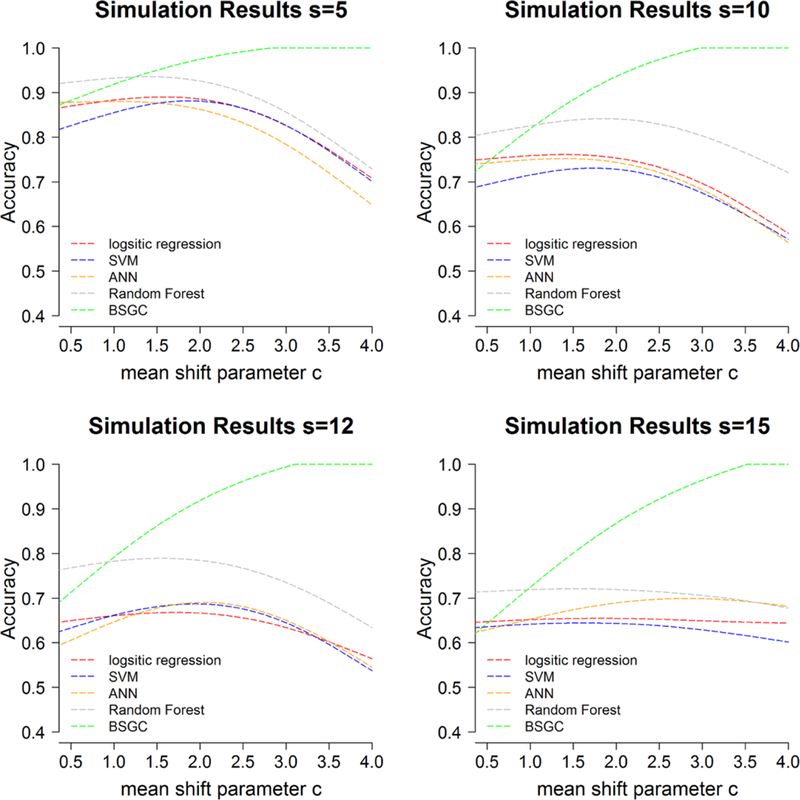
Simulation results. Classification accuracy obtained from prediction under LOOCV.
The best performance for feature-based approaches was random forest which obtained a maximum of 93% accuracy at c = 1.7 and s = 5. Logistic regression, SVM and ANN yield similar best performance of 89% accuracy at c = 1.8, 88% accuracy at c = 2,1 and 88% accuracy at c = 1.4, respectively, with s = 5. In all simulated scenarios, random forest yield the best classification performance among other feature-based approaches considered in this study, which is consistent to previous conclusion by Singh et al.[32].
Overall the proposed BSGC method outperformed methods used in current literature which reduce the multivariate lattice structure intrinsic to GLCMs to a set of summary statistics. Trends in diagnostic performance for the BSGC conformed to our intuition with mean shifts in peak count rates and random noise. As the distance in true mean peaks increased between the classes with larger values of c, the patterns conveyed in malignant GLCMs were more separable from the reference group. This resulted in enhanced discrimination accuracy for the BSGC method which leverages the spatial location information. In the presence of high signal-to-noise in the rate densities, as characterized by small values of s, performance for BSGC was comparable to feature-based classifier only for very small mean shifts. BSGC yielded the best predictive classification performance, however, for c > 1.4, c > 1.1, c > 0.9 and c > 0.9 for s = 5, s = 10, s = 12 and s = 15, respectively; and resulted in 100% classification accuracy with c ≥ 2.8 for the highest signal-to-noise scenario with s = 5. As the variance scale parameter s increases, the distinction of spatial pattern between c close to 0 and c = 0 is diminished, as a result, the overall classification accuracy of all methods decreases. The BSGC was globally optimal for these low signal-to- noise scenarios, however, with s > 10 wherein the performance of feature-based was considerably diminished by comparison.
Interestingly, naive to the spatial arrangements of GLCM cell counts, the competing GLCM feature-based classifiers failed to yield monotonic trends as the distance between mean peak increased with c. The feature-based approaches tended to achieve best performance near c = 2, corresponding to GLCMs with mean peak rate of co-occurrences at moderate gray levels. Considering the symmetry inherent to GLCMs that characterize all directions, these methods resulted in diminished predictive performance for increasing values of c due to the fact that 180° counterclockwise rotations produce similar GLCM-derived summary statistics thereby attenuating the true extent of data-signal between classes of c = 0 and c = 4. By way of contrast, the BSGC classifier characterizes the positional information of peak counts via the adjacency matrix which results in robustness to shifts in the mean count surface, enhancing separability with increasing c. Thus, when functional structure is present in the underlying GLCM generating process, then the proposed BSGC appears to be more efficient and robust when compared with the feature-based classification approaches.
3.2. Case Study: Dection of Adrenal Malignant Lesions
This section applies the classifiers to the diagnostic study of adrenal lesion data presented in section 2. Recall that the objective is lesion discrimination on the basis of ROIs obtained from both non-contrast and contrast CT imaging. Specifically, both BSGC and the GLCM feature-based classifiers were applied to predict the true pathological status of the lesion in our study (malignant from benign) from enhancement patterns observed from CT, using both NC and DL phase scans. In order to satisfy the Gaussian distributional assumptions, the square-root transformation was applied to the observed empirical co-occurrence rates before applying the BSGC. The analyses used the specification of values for the hyperparameters , and that was described in Section 3.1.1. Moreover, we utilized a uniform distribution prior for q such that any value within the positive support is equally likely a priori. MCMC was implementedwith 50,000 iterations, the first 25,000 of which were discarded as burn-in. Convergence was assessed by visual inspection and by evaluation of commonly used diagnostic tests, e.g. the Geweke diagnostic [8] with implementation using the R package ‘coda’. Convergence issues were not evident from the statistics.
The classification accuracy of all methods, reported in Table 2, was assessed by LOOCV. LOOCV was implemented as follows: at each step, the observables (either GLCM or GLCM-derived features) from a single lesion were omitted from the training set, while estimation was implemented using data from the remaining lesions. Thereafter, a class (benign or malignant) was predicted for each lesion ROI contributed by the omitted patient for each method and compared with the true underlying pathology.
Table 2. Case study results.
Classification accuracy obtained from prediction under LOOCV for non-contrast (NC) and delay (DL) scans, separately
| BSGC | Logistic Regression | SVM | ANN | Random Forest | |
|---|---|---|---|---|---|
| NC | 0.809 | 0.514 | 0.505 | 0.524 | 0.562 |
| DL | 0.771 | 0.571 | 0.467 | 0.538 | 0.495 |
Failing to leverage the functional patterns in GLCMs, feature-based methods attained maximum predictive power of only 57% with logistic regression based on DL scans. By contrast, the Bayesian spatial Gaussian process classifier correctly predicted the pathological status of 81% and 77% of lesions in our case with NC and DL scans, respectively. The multivariate GLCM-based classifier effectuated improved prediction accuracies of 38% to 73% when compared to methods currently utilized in cancer radiomics settings.
In addition, we also compared the methods with classification rules based on both NC and DL scans. Two classification schemes were considered reflecting differential preferences between false negative and false positive findings. Rule a) assigned the status of malignancy given that resultant predictors yielded a malignancy assignment for both NC and DL scans, protecting specificity. Conversely, a malignancy assignment resulted for rule b) given the prediction of malignancy status at least one of the scans, reflecting a preference for sensitivity.
Similar performance was observed, with the GLCM-based classifier outperforming the existing textural feature-based classifiers under both schemes (Table 3). Note that, although classification rules a) and b) yielded similar accuracy, they represent differing sensitivity and specificity trade-offs. Rule a) attained sensitivity 0.750 and specificity 0.816, while rule b) resulted in higher sensitivity, 0.948, and lower specificity, 0.675.
Table 3. Case study results.
Classification accuracy obtained from prediction under LOOCV for NC and DL combined
| BSGC | Logistic Regression |
SVM | ANN | Random Forest |
|
|---|---|---|---|---|---|
| a) favors False Positive | 0.786 | 0.548 | 0.500 | 0.586 | 0.567 |
| b) favors False Negative | 0.800 | 0.538 | 0.486 | 0.519 | 0.481 |
4. Discussion
Recent emphasis on improving characterizations of tumor phenotypes based on scanning technologies have produced numerous types of radiomics-based subtyping schemes that utilize summary statistics obtained from gray-level co-occurrence matrices. In this manuscript, we demonstrated that the GLCM object can be modelled as a multivariate outcome using a Bayesian Gaussian spatial process formulation, and thereby it can be used to characterize spatial patterns in the distribution of co-occurring gray- levels among tumor clinicopathological subtypes. Additionally, the BSGC approach avoids the processing and analysis of potentially redundant feature-sets which require variable selection with each application reducing their reproducibility. Moreover, the BSGC model effectuates probabilistic-based classification through a predictive density. In both simulation and case studies, modeling GLCM objects based on the Bayesian spatial framework yielded considerable improvements in predictive accuracy when compared to feature-based approaches currently utilized by the biomedical imaging communities. The methodology offers insights into the manner in which imaging data may be better utilized to identify complex patterns that characterize the intrinsic heterogeneity observed in tumor pathology.
A few limitations should be noted. Applications pursued thus far used R [30] to implement both the MCMC and machine learning algorithms. Bayesian models are generally more computationally intensive than the alternative machine learning algorithms considered in our simulation and case studies. Most of the computational burden can be ascribed to full posterior inference with MCMC of the training set, for which our case study required approximately 80 minutes using the Red Hat Linux 6.4 2.67GHZ single-core processor system. Model training, however, needs to be performed only once. Individual lesion prediction with the BSGC approach can be parallelized, requiring less than 5 minutes to obtain each predictive probability via compositional sampling. The less accurate machine learning algorithms required approximately 1 minute to complete the classification process. Our clinical collaborators have indicated that the run time would be acceptable for actual use, considering the increased accuracy of the classification and current practices. Further computational benefit, however, may result by taking advantage of more efficient programming techniques and GPU computation infrastructure.
The extent to which classification performance may be improved by the proposed BSGC depends upon the extent to which functional patterns in the GLCM lattice are separable among class objects. Neglecting to consider the existing spatial information leads to a decrease in performance of all the algorithms considered here. If instead the original data were to present weak correlation, the MRF parameter would adjust accordingly to reflect the weaker correlation. However, the classification performance would be affected by the resulting decreased separability of functional patterns in the GLCM objects, similarly as for the commonly employed machine learning algorithms, which fail to leverage spatial information.
As intrinsic to all Bayesian approaches, both prior and hyperprior specification is required for inference. In addition, to use the method for prediction, one must specify subjective prior class probabilities often set with equal weight or to reflect the objects prevalence within the sampled population. Alternatively, the class prior probabilities could be formulated on a case-by-case basis to reflect the extent to which morphological features associated with malignancies are conspicuous to the image reader. Rather than modeling the counts, we considered transformed count data with Gaussian approximation. The assumption of Gaussian distribution for the normalized GLCM avoids posterior computational intractability, thereby facilitating posterior mixing and reducing computational burden. If the normalized counts fail to satisfy Gaussian distributional assumptions, however, one can conceive of several approaches to formulate a non-Gaussian model. The non-spatial vector of errors ϵi may be assigned a robust distribution, e.g. a n-dimensional multivariate t-distribution. As an alternative, it may be possible to relax the Gaussian assumption when directly modeling the spatial dependence. While non-Gaussian Markov random fields are usually reserved to categorical or count data, a possibility might be to employ recently developed copula-based methods (see Hughes[15]). Bayesian nonparametric models for areal data have also been proposed in the literature, especially for boundary detection (see e.g. Li et al.[21] and references therein). Normalizing GLCM counts may result in information loss and thus could fail to capture over/under dispersed scenarios. More flexible methods should be considered to handle correlated multivariate count data as well as address over- and under-dispersion.
Supplementary Material
Acknowledgements
Footnotes
Disclosure statement
The authors declare no conflict of interests.
References
- [1].Aerts HJ, Velazquez ER, Leijenaar RT, Parmar C, Grossmann P, Carvalho S, Bussink J, Monshouwer R, Haibe-Kains B, Rietveld D, et al. , Corrigendum: Decoding tumour phenotype by noninvasive imaging using a quantitative radiomics approach, Nature communications 5 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Albregtsen F, et al. , Statistical texture measures computed from gray level coocurrence matrices, Image processing laboratory, department of informatics, university of oslo; 5 (2008). [Google Scholar]
- [3].Altinmakas E, Hobbs BP, Ye H, Grubbs EG, Perrier ND, Prieto VG, Lee JE, and Ng CS, Diagnostic performance of 18-F-FDG-PET-CT in adrenal lesions using histopathology as reference standard,, Abdominal Radiology (2016), pp. 1–8. [DOI] [PubMed] [Google Scholar]
- [4].Banerjee S, Carlin BP, and Gelfand AE, Hierarchical modeling and analysis for spatial data, Crc Press, 2014. [Google Scholar]
- [5].Buvat I, Orlhac F, and Soussan M, Tumor texture analysis in pet: where do we stand?, Journal of Nuclear Medicine 56 (2015), pp. 1642–1644. [DOI] [PubMed] [Google Scholar]
- [6].Chan HP, Sahiner B, Petrick N, Helvie MA, Lam KL, Adler DD, and Good- sitt MM, Computerized classification of malignant and benign microcalcifications on mammograms: texture analysis using an artificial neural network, Physics in medicine and biology 42 (1997), p. 549. [DOI] [PubMed] [Google Scholar]
- [7].Cook GJ, Siddique M, Taylor BP, Yip C, Chicklore S, and Goh V, Radiomics in pet: principles and applications, Clinical and Translational Imaging 2 (2014), pp. 269–276. [Google Scholar]
- [8].Geweke J, Evaluating the accuracy of sampling-based approaches to calculating posterior moments, in Bayesian Statistics 4, Bernardo JM, Berger J, Dawid AP, and Smith JFM, eds., Oxford University Press, Oxford, 1992, pp. 169–193. [Google Scholar]
- [9].Gibbs P and Turnbull LW, Textural analysis of contrast-enhanced mr images of the breast, Magnetic resonance in medicine 50 (2003), pp. 92–98. [DOI] [PubMed] [Google Scholar]
- [10].Gletsos M, Mougiakakou SG, Matsopoulos GK, Nikita KS, Nikita AS, and Kelekis D, A computer-aided diagnostic system to characterize ct focal liver lesions: design and optimization of a neural network classifier, IEEE transactions on information technology in biomedicine 7 (2003), pp. 153–162. [DOI] [PubMed] [Google Scholar]
- [11].Gotlieb CC and Kreyszig HE, Texture descriptors based on co-occurrence matrices, Computer Vision, Graphics, and Image Processing 51 (1990), pp. 70–86. [Google Scholar]
- [12].Haralick RM, Shanmugam K, et al. , Textural features for image classification, IEEE Transactions on systems, man, and cybernetics (1973), pp. 610–621. [Google Scholar]
- [13].Harshvardhan G, Venkateswaran N, and Padmapriya N, Assessment of Glaucoma with ocular thermal images using GLCM techniques and Logistic Regression classifier, in Wireless Communications, Signal Processing and Networking (WiSPNET), International Conference on. IEEE, 2016, pp. 1534–1537. [Google Scholar]
- [14].Hassan I, Kotrotsou A, Bakhtiari AS, Thomas GA, Weinberg JS, Kumar AJ, Sawaya R, Luedi MM, Zinn PO, and Colen RR, Radiomic Texture Analysis Mapping Predicts Areas of True Functional MRI Activity, Scientific reports 6 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Hughes J, copcar: A flexible regression model for areal data, Journal of Computational and Graphical Statistics 24 (2015), pp. 733–755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Jafarpour S, Sedghi Z, and Amirani MC, A robust brain MRI classification with GLCM features, Int. J. Comput. Appl 37 (2012), pp. 1–5. [Google Scholar]
- [17].Jirak D, Dezortova M, Taimr P, and Hajek M, Texture analysis of human liver, Journal of Magnetic Resonance Imaging 15 (2002), pp. 68–74. [DOI] [PubMed] [Google Scholar]
- [18].Kassner A and Thornhill R, Texture analysis: a review of neurologic mr imaging applications, American Journal of Neuroradiology 31 (2010), pp. 809–816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Kumari R, SVM Classification an Approach on Detecting Abnormality in Brain MRI Images, International Journal of Engineering Research and Applications 3 (2013), pp. 1686–1690. [Google Scholar]
- [20].Lambin P, Rios-Velazquez E, Leijenaar R, Carvalho S, van Stiphout RG, Granton P, Zegers CM, Gillies R, Boellard R, Dekker A, et al. , Radiomics: extracting more information from medical images using advanced feature analysis, European journal of cancer 48 (2012), pp. 441–446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Li P, Banerjee S, Hanson TA, and McBean AM, Bayesian models for detecting difference boundaries in areal data, Statistica Sinica (2015), pp. 385–402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Mostaco-Guidolin LB, Ko ACT, Wang F, Xiang B, Hewko M, Tian G, Major A, Shiomi M, and Sowa MG, Collagen morphology and texture analysis: from statistics to classification, Scientific reports 3 (2013), p. 2190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Ng CS, Altinmakas E, Wei W, Ghosh P, Li X, Grubb EG, and Hobbs BP, Combining washout and noncontrast data from adrenal protocol ct: improving diagnostic performance., Academic Radiology In press. [DOI] [PubMed] [Google Scholar]
- [24].Ng CS, Wei W, Altinmakas E, Ghosh P, Li X, Grubb EG, Perrier NA, Lee JE, Prieto VG, and Hobbs BP, Utility of intermediate-delay washout ct images for differentiation of malignant and benign adrenal lesions: A multivariate analysis., American Journal of Roentgenology In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Ng CS, Wei W, Altinmakas E, Ghosh P, Li X, Grubb EG, Perrier NA, Prieto VG, Lee JE, and Hobbs BP, Differentiation of malignant and benign adrenal lesions with delayed ct imaging: multivariate analysis and prediction models., American Journal of Roentgenology 210 (2018), pp. W156–W163. [DOI] [PubMed] [Google Scholar]
- [26].Nikoloulopoulos AK and Karlis D, Modeling multivariate count data using copulas, Communications in Statistics-Simulation and Computation 39 (2009), pp. 172–187. [Google Scholar]
- [27].Parekh V and Jacobs MA, Radiomics: a new application from established techniques, Expert Review of Precision Medicine and Drug Development 1 (2016), pp. 207–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Pawar M, Sharma DK, and Giri R, Multiclass skin disease classification using Neural Network, International Journal of Computer Science and Information Technology Research 2 (2014), pp. 189–193. [Google Scholar]
- [29].Preethi G and Sornagopal V, MRI image classification using GLCM texture features, in Green Computing Communication and Electrical Engineering (ICGCCEE), 2014 International Conference on. IEEE, 2014, pp. 1–6. [Google Scholar]
- [30].R Core Team R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria: (2017). Available at http://www.R-project.org/. [Google Scholar]
- [31].Rue H, Martino S, and Chopin N, Approximate bayesian inference for latent gaussian models by using integrated nested laplace approximations, Journal of the royal statistical society: Series b (statistical methodology) 71 (2009), pp. 319–392. [Google Scholar]
- [32].Singh VP, Srivastava A, Kulshreshtha D, Chaudhary A, and Srivastava R, Mammogram Classification Using Selected GLCM Features and Random Forest Classifier, International Journal of Computer Science and Information Security 14 (2016), p. 82. [Google Scholar]
- [33].Tang C, Hobbs BP, Amer A, Li X, Behrens C, Rodriguez-Canales J, Parra E, Villalobos P, Fried D, Chang JY, Hong D, Welsh JW, Sepesi B, Court L, Wistuba I, and Koay EJ, Development of an immune-pathology informed radiomics model for non-small cell lung cancer., Scientific Reports 8 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Thibault G, Angulo J, and Meyer F, Advanced statistical matrices for texture characterization: application to cell classification, IEEE Transactions on Biomedical Engineering 61 (2014), pp. 630–637. [DOI] [PubMed] [Google Scholar]
- [35].Ulaby FT, Kouyate F, Brisco B, and Williams TL, Textural infornation in sar images, IEEE Transactions on Geoscience and Remote Sensing (1986), pp. 235–245. [Google Scholar]
- [36].Wang Z, Bovik AC, and Lu L, Why is image quality assessment so difficult?, in Acoustics, Speech, and Signal Processing (ICASSP), 2002 IEEE Internationa! Conference on, Vol. 4. IEEE, 2002, pp. IV–3313. [Google Scholar]
- [37].Wanis KN and Kanthan R, Diagnostic and prognostic features in adrenocortical carcinoma: a single institution case series and review of the literature, World Journal of Surgical Oncology 13 (2015), p. 117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Yip SS and Aerts HJ, Applications and limitations of radiomics, Physics in medicine and biology 61 (2016), p. R150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Zhang J, Tong L, Wang L, and Li N, Texture analysis of multiple sclerosis: a comparative study, Magnetic resonance imaging 26 (2008), pp. 1160–1166. [DOI] [PubMed] [Google Scholar]
- [40].Zulpe N and Pawar V, GLCM textural features for brain tumor classification (2012). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


