Abstract
The determination of the integral molecular weight distribution (MWD) of the linear polyethylene sample (SRM 1475) by means of gel permeation chromatography (GPC) is described. Both the experimental and mathematical details of column calibration and sample analysis are included.
Keywords: Gel permeation chromatography (GPC), linear polyethylene, molecular weight distribution (MWD), number average, weight average
1. Introduction
Heretofore the molecular weight characterization of polymer samples issued by the National Bureau of Standards has been primarily limited to the reporting of the number average molecular weight, Mn, and the weight average molecular weight, Mw. This paper describes the determination of the integral molecular weight distribution (MWD) of the linear polyethylene sample (SRM 1475) using the technique of gel permeation chromatography (GPC).
Prior to 1964 the determination of the MWD of a polymer was a tedious, time-consuming task. The first step was to fractionate the polymer using either batch fractionation or elution chromatographic techniques, both of which take advantage of changes in solution properties as a function of molecular weight. Then Mn and Mw measurements were made on each fraction, and, by knowing the weight percent of each fraction and by making certain simplifying assumptions about the molecular weight distribution of each fraction, the MWD was constructed.
In 1964, J. C. Moore first published his work on a process which he called gel permeation chromatography [1].1 In GPC a dissolved sample of polymer is carried into and through a packed column by an appropriate solvent stream. The packing is such that the polymer is separated by molecular size, the larger molecules eluting first. By using the appropriate sensing devices, a function of the quantity of each molecular species is graphically displayed on a strip-chart recorder against the volume of solution emerging from the column (elution volume).
Thus, providing the system has been calibrated, one can determine the MWD for a given polymer sample in a very short time (usually less than one day). In the past, for each polymer system, the calibration procedure has required the use of well-characterized fractions of the polymer. This paper describes the techniques for the use of such fractions to provide a calibration curve, as well as the methods used to determine the MWD of our linear polyethylene whole polymer (SRM 1475). This Standard Reference Material, with its certified MWD, may then be used to calibrate other gel permeation chromatographs without requiring the use of fractions.
2. Description of Apparatus
The particular gel permeation chromatographic apparatus used was the Waters Model 200 (analytical scale) GPC.2,3 This instrument is designed to analyze samples in the milligram range. The range of molecular weights which can be analyzed is dependent upon column selection. The pertinent features of the apparatus include, in order of flow: (1) a solvent reservoir, (2) a solvent degasser and preheaters, and (3) a precision metering pump with an adjustable pumping rate. The solvent flow emerging from the pump is split, one portion going into a set of columns being used for sample injection, and the other portion flowing through a second set of columns (reference set). Multi-port valving is used to inject the dissolved sample into the appropriate set of columns for analysis. The materials emerging from the two sets of columns pass through the two sides of a differential refractometer cell. The refractometer is stated by the manufacturer to be capable of detecting a difference of 10−7 in refractive index. The electronic output from the refractometer is recorded on a chart recorder, providing a continuous record of the difference in refractive index between the two streams. From the refractometer the sample-solvent mixture flows directly into a dump-syphon (5 ml capacity). When the syphon empties a spike is displayed on the recorder trace. In GPC language each spike or pip is referred to as a “count,” and the sample injection is timed to coincide with a count, labeled the zeroth one. Temperature controls are provided for regulating the temperature throughout the column, detector, and syphon system. The one modification made to the Model 200 GPC was to provide a Teflon cover for the top of the syphon, to minimize solvent evaporation.
In the Model 200 GPC, each column is a 4-foot long, thin (3/8 in diameter) stainless steel tube packed with beads of a rigid, crosslinked polystyrene gel. The gel was prepared, characterized, and packed in the columns by Waters Associates, Inc. Five such columns were connected in series to form the column set used for the analysis. The columns had nominal exclusion limits of 1 × 107, 1 × 106 1 × 105, 1 × 104, and 1 × 103 angstroms. This particular nomenclature [1] describes the minimal length in angstroms of a polystyrene molecule which will be excluded from permeation into the pores of the particular bead packing. The reference column set was a five column set having similar nominal exclusion limits.
3. Column Broadening Effects
From the cursory information in the introduction one might assume that a sample of monodisperse material injected into the GPC column would emerge from the column without change in concentration, producing a rectangular area as a recorder trace, having a base length equal to the volume of the sample injected. However, as is well known [2], in any chromatographic procedure the elution profile is broadened due to longitudinal diffusion in the column, producing, in the case of a single component, a bell-shaped curve. Therefore, in the case of a polydisperse polymer the height of the chromatogram at any point is due to the cumulative effect of the presence of many neighboring molecular weights. The amount of broadening observed is a function of the molecular weight, becoming larger as the molecular weight increases. The observed width is due to: (1) the actual MWD, (2) the spreading which occurs during flow through connecting tubing, (3) the effect due to spreading in the interstitial volume of the column packing, (4) the diffusional spreading within the pores, and (5) the effects of any adsorption within the system. The combined result may be not only spreading or broadening, but also skewing of the chromatogram.
Attempts to obtain analytical and numerical corrections for column broadening have been made by Tung and others [3–5], and the general state-of-the-art of GPC correction of broadening and skewing has been discussed by Hamielec [6, 7]. Fortunately, these effects tend to cancel out when the molecular weight distribution of a relatively broad material is obtained on a GPC column calibrated with much narrower fractions of the same material. Since the work reported here meets this condition, throughout this paper we assume that column broadening effects can be neglected. The validity of this assumption is discussed in section 9.
4. The Molecular Weight Distribution
In this section we describe the method used to calibrate the GPC. As stated in the preceding section, we assume that column broadening effects are not significant. In the notation of Frank [8], the calibration curve and the elution ehromatogram are respectively:
| (1) |
| (2) |
In (1) the molecular weight, m, is a function of the elution volume, v. Z(m) is the number of molecules in the particular sample having molecular weights which are greater than m; conversely N(v) is the number of molecules in the sample which elute at volumes which are less than or equal to v. We define z(m)dm as the number of molecules having molecular weights between m and m + dm, such that:
| (3) |
where m’ is the slope of the calibration curve, m(v) versus v.
For this development we assume that the height, h, of the chromatogram from the base line results solely from the presence of molecules all having the same molecular weight, m, for each corresponding elution volume, v. In particular it is assumed that the detector responds linearly to the mass of the sample. Thus:
| (4) |
Combining (3) with (4), we obtain:
| (5) |
Here k is an unknown instrumental scaling factor. The number-, weight-, and z-average molecular weights Mn, Mw, and Mz are given by:
| (6) |
| (7) |
| (8) |
The integral MWD is obtained in the following fashion. We define a function w(m) by
| (9) |
Then the cumulative weight percent, i.e., the weight percent of polymer of molecular weight less than M, is given by
The integral MWD is usually given as cumulative weight percent versus log molecular weight.
5. The Calibration Curve
In this section we will presuppose that the column selection has been made such that log m is a nearly linear function of v in the molecular weight range of interest. Further, we will assume that we already have a calibration curve for polystyrene using the same column set.
The development of the calibration curve for any particular polymer usually starts from the preparation and characterization of narrow molecular weight fractions. The molecular weight range covered by the fractions should at least encompass the expected distribution of any samples to be subsequently analyzed. By classical characterization methods such as osmometry and light scattering, the average molecular weights Mn and Mw are determined for each fraction. One of two general methods is then used in producing a reliable calibration. In the first method we define M0 as being that molecular weight species which elutes at the peak of a chromatogram, and we assume that a reasonable value of M0 can be assigned by knowing both Mn and Mw. In the second method we assume that, for each fraction, we know the general form of the calibration curve, eq (1).
A. Method One
In this development we assume that the peak molecular weight, M0, can be approximated by:
| (11) |
This assumption would appear reasonable to a first approximation providing that the polydispersity, Mw/Mn, is sufficiently close to unity, and that the chromatogram is symmetrical and single-peaked. From the individual chromatograms of the fractions we can determine the elution volume v0 corresponding to M0.
A preliminary calibration curve is constructed using the pairs of M0 and v0 values, and a least-squares fitting routine is employed to determine whether the points can be best described by a first, a second, or a third degree polynomial. Comparison of this preliminary calibration curve with the polystyrene calibration curve obtained with the same column set, should show qualitative similarity, i.e., the inflection points and general curvature at all elution volumes should be similar. Next equations (6) and (7), in conjunction with the preliminary calibration curve, are used to calculate Mn’s and Mw’s from the GPC chromatograms of the individual fractions, and from the preliminary calibration curve we determine the corresponding elution volumes. We now use the values of Mn and Mw (classically determined) together with the elution volumes (GPC determined) and plot these points on the preliminary calibration curve. This type of plot should reveal that most of the calculated points fall on or near the calibration curve. However, if all the number-average molecular weight points lie on one side of the curve and all of the weight-average molecular weight points lie on the other side, this is usually an indication of extreme broadening and skewness of the chromatograms resulting from poor column selection or poorly chosen operational parameters.
Assuming that this latter possibility did not arise, we now refit the data, using only the classically determined Mn’s and Mw’s and their calculated elution volumes (GPC), and at this point we consider that the best fit has been obtained.
B. The Second Calibration Method
In this method we assume that for our narrow distribution fractions (Mw/Mn from 1.1 to 1.7) the portion of the calibration curve for each fraction will be adequately represented by the relationship:
| (12) |
Of course we do not assume that the parameters a and b are the same for all fractions. Again following the development by Frank [8], we incorporate eq (11) into eqs (6) and (7). By using eq (11) in the denominator of (6) and in the numerator of (7), we obtain two expressions for the parameter a:
| (13) |
and
| (14) |
After equating an with aw, simultaneous solution of eqs (12) and (13) yields unique values for the parameters a and b. If this were done for each fraction, a plot using eq (11) over the particular molecular weight range involved should result in a collection of straight lines which define the calibration curve exactly.
Both the first and second methods herein described have the disadvantage that Mn and Mw have to be known for each fraction; further, an error in either Mn or Mw seriously affects the calculation. A modification of the second method allows calibrational information to be obtained when only Mn or only Mw is known for a fraction, and, in addition, may provide insight into the question of whether or not error exists in Mn or Mw as determined classically.
Rather than solving eqs (12) and (13) simultaneously to obtain a unique pair of values for the parameters a and b, we can, by treating each equation separately, obtain the functional dependence of an and aw on b over the range of values for which b may be expected to lie. Either equation (12) or equation (13) implies a functional relationship between a and b, i.e., a = a(b). The calibration curve (or rather, our estimate of it based on one determination of Mn or Mw) is then one of the family of curves.
| (15) |
and must therefore be tangent to the envelope of the family at some point. The envelope is easily obtained, in the usual way, as the simultaneous solution of eq (14) and the result of partial differentiation of eq (14) with respect to b at constant m and v, i.e.,
| (16) |
For each point (v, m(v)) on the calibration curve, the abscissa v is given by eq (15) and the ordinate m(v) by eq (14). A calibration curve may then be estimated from measurements of Mn and/or Mw on a series of fractions by plotting the envelope obtained for each measurement and requiring that the calibration curve be tangent or nearly so to each envelope at some point. Since this technique uses each experimental value of Mn and Mw independently, it can be useful in identifying individual molecular weight measurements which may be in error.
6. Experimental Procedures
All samples were dissolved in nitrogen-saturated, 1,2,4-trichlorobenzene (TCB) (filtered technical grade) at 135 °C using magnetic stirring. They were then filtered under nitrogen pressure through regenerated cellulose filters having an average pore size of 0.45 microns. The GPC column oven was operated at approximately 135 °C, and nitrogen-saturated TCB was used. Five hundredths of one percent by weight of 2,6-di-tert.-butyl-4-methylphenol was added to the TCB as an antioxidant.
We assumed that the calibration curve for polyethylene would be similar to that for polystyrene and hence selected the column combinations used herein because they produced a nearly linear polystyrene calibration curve.
The degree of replication which can be achieved in successive chromatograms resulting from a series of identical experiments appears to be almost totally dependent upon base-line stability. Of the various factors affecting this stability, we found that the constancy of both fluid flow and temperature was the most important. We were fortunate in that our GPC was in an area in which both the air temperature and air circulation were well controlled, and this, coupled with stable line voltages, gave good temperature stability throughout the system. We found that the constancy of solvent flow could be improved upon by keeping both of the column throttle valves in their open position, regulating solvent flow solely by adjustment of the pumping stroke. Under these conditions a point by point comparison of the heights of the chromatograms resulting from supposedly identical experiments showed maximum deviations of approximately ± 1 percent, and a comparison of the areas of the chromatograms showed a maximum deviation of less than ± 2 percent. Uncertainties of this magnitude could be explained almost completely by the observed base-line instability.
A change in operating parameters may result in a change of the chromatogram obtained with gel permeation chromatography. Ideally, perhaps, one would like to use samples of very small size and of vanishing concentration together with very small flow rates, but, practically, one compromises by using samples whose size and concentration are such that good detector response is obtained, and a flow rate such that the experiment can be run in a reasonable amount of time. A large number of experiments were run, varying each of the operating parameters in turn. We found that between the extremes of 0.2 and 2.0 ml/minute no discernible change occurred in the chromatograms resulting from replicate experiments. We therefore chose to use 0.5 ml/minute as the flow rate which would be used. With the whole polymer (SRM 1475) a change in the concentration from 0.02 to 0.2 weight percent caused no observable change in the calculated weight versus elution volume distribution. We therefore chose to use a 0.1 weight percent concentration for the whole polymer. The acceptable range of concentration varied for each fraction, but we found that the use of concentrations such that the resulting viscosities were similar to that of the 0.1 weight percent of the whole polymer was a good workable rule. The detector response was such that for a 0.1 weight percent concentration of whole polymer, an injection time of two minutes was required to produce a 1/2 to 2/3 full scale deflection of the recorder pen at the peak elution, and this injection time was used throughout.
For the final calibration, three independently prepared concentrations of each calibrating material were used. For each material, the three concentrations were such as to cause peak heights of nearly full scale, one-half of full scale, or one-quarter of full scale. When any two chromatograms within each triplicate set were compared in respect to height ratio at each elution volume, or in respect to area ratios, these were, within the precision of the experiment, identical to the ratios of the known concentrations. Therefore, within the limits of our sensitivity, we believe that there was no dn/dc (refractive index change in respect to concentration) dependence with molecular weight. This observation is not in conflict with paper VII of this series [9], wherein, when greater sensitivity and precision was used, there indeed was shown to be a dn/dc dependence with molecular weight.
The integration of the chromatograms was performed numerically using Simpson’s one-third rule, using an elution increment of 0.2 count.
7. Determination of the Calibration Curve
We used both polyethylene fractions and linear hydrocarbon samples in the determination of the calibration curve. Zone-refined samples of n-C36H74 and n-C94H190 were used. The values assigned to the hydrocarbon samples were the calculated molecular weights, and these calculated molecular weights were assigned to the peak elution volumes. Table 1 lists these materials together with the Mn and Mw values associated with each. These were determined by membrane osmometry and light scattering experiments. For details of the fractionation and of the determination of the molecular weights see papers VI, VIII and IX of this series [10–12]. Included also in table 1 are the GPC determined moments using the final calibration curve.
Table 1.
Classic versus gel permeation chromatographic analysis of polyethylene fractions used in calibration procedure
| Sample | Mn × 10−4 a | Mw × 10−4 b | Mw/Mn | GPC analysisc | ||
|---|---|---|---|---|---|---|
| Mn × 10−4 | Mw × 10−4 | Mw/Mn | ||||
| PE600 | 35.5 | 68.8 | 1.9 | 39 | 67 | 1.7 |
| PE350 | 24.1 | d 52.0 | 2.2 | 26 | 40 | 1.5 |
| PE200 | 20.1 | 21 | 32 | 1.5 | ||
| PE180 | 14.3 | 21.0 | 1.5 | 14.0 | 21 | 1.5 |
| PE120 | 11.2 | 17.0 | 1.5 | 12.2 | 16 | 1.3 |
| PE60 | 6.1 | d 8.22 | 1.3 | 6 | 6.9 | 1.2 |
| PE40 | 4.97 | 4.94 | 1.0 | 4.6 | 5.2 | 1.1 |
| PE20 | 2.07 | 2.2 | 2.5 | 1.1 | ||
| PE15 | 1.35 | 1.91 | 1.4 | 1.4 | 1.6 | 1.1 |
| (1.00) | 0.146 | 0.154 | 1.05 | |||
| (1.00) | .047 | .049 | 1.04 | |||
= results from membrane osmometry.
= results from light scattering.
= results of using the samples to calibrate the GPC, then analyzing the samples using calculated calibration curve.
Not employed in construction of calibration curve. See text.
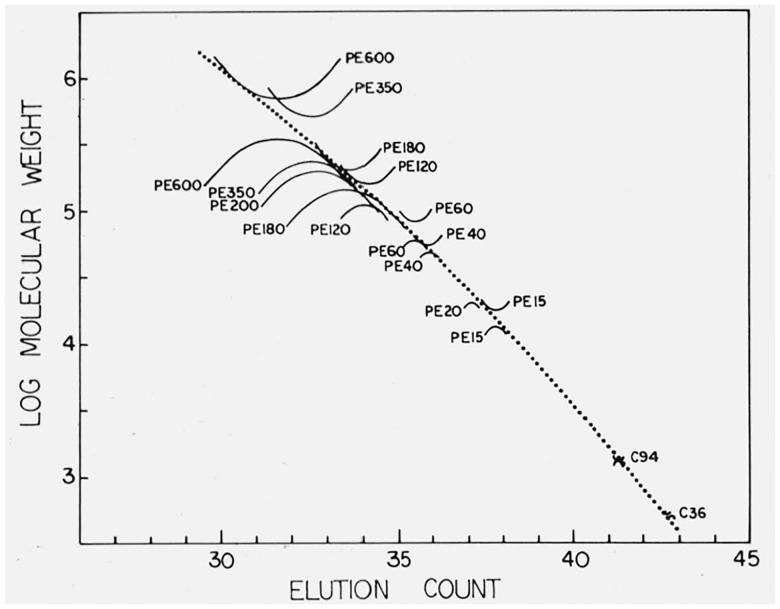
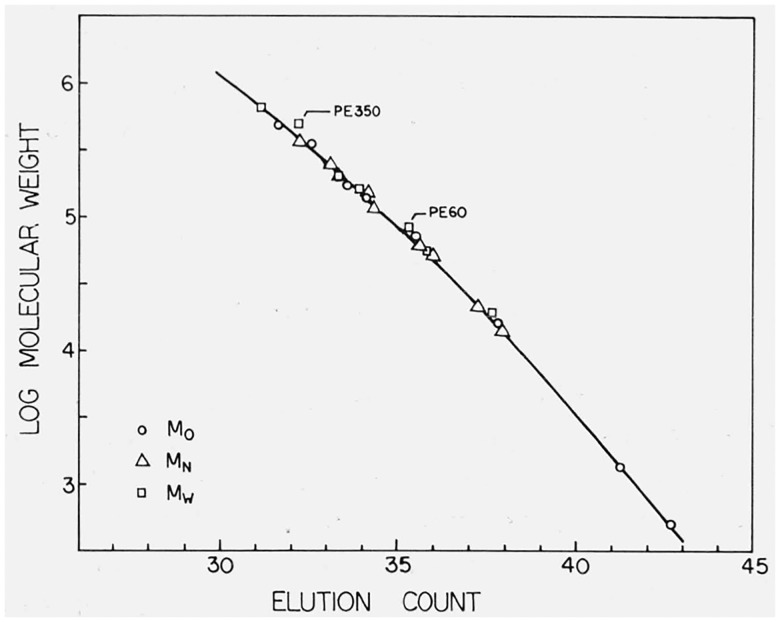
The calibration curve used in this work was determined by the use of method 1. For the preliminary determination of the calibration curve the chromatograms of the hydrocarbon samples and those of the fractions for which both Mn and Mw had been determined were used. As can be seen from table 1, the differences between the classical and GPC values of Mw for PE 350 and PE 60 do not appear consistent with those for the other fractions. The same discrepancies are shown when method 2 is employed (see fig. 2), and as a result we did not use the Mw values for these two fractions in the final determination of the calibration curve. In addition the Mw values for PE 200 and PE 20 were not available and only Mn values were employed. A plot of the final calibration curve is shown in figure 1, together with the points corresponding to M0, Mn, and Mw for the fractions and the hydrocarbons.
Figure 2.
The calibration curve derived by use of Method One (dotted line) together with the calculated envelopes for each calibration sample.
Figure 1.
The calibration curve derived by use of Method One, showing all calibration points.
The best least squares fit, using Method 1, was found to be a quadratic of the form (log M = a + bv + cv2), having the following coefficients and standard deviations:
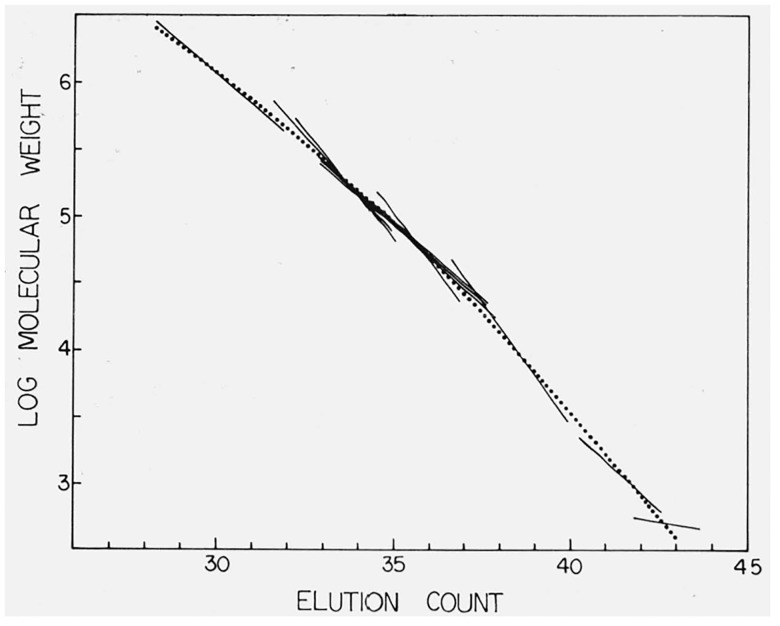
The standard deviation of the molecular weight was ± 0.047 log M units. The volume v is in units of count. Method 2 was also investigated. Figure 2 shows the calibration curve as derived by method 1, together with the envelope plots for each material used in the calibration. Figure 3 shows the same calibration curve, superimposed on which are the individual line segments calculated for the individual calibrating materials. The unusual behavior associated with the two hydrocarbon samples results from using their calculated molecular weight to describe both Mn and Mw in eqs (12) and (13), and the slopes of these lines probably reflect the column dispersion. While the calibration curve was determined solely by method 1, it is obvious from figures 2 and 3 that method 2 would have produced a nearly identical curve.
Figure 3.
The calibration curve derived by use of Method One (dotted line) together with the calculated line segments for each calibration sample for which both Mn and Mw are known.
It was interesting to note that the polyethylene calibration curve remained unchanged for approximately a year of continuous running. Immediately after starting up there would be an apparent shift of calibration, but the columns would return to their previous state after approximately 48 hours of running time. During this year the solvent and the general operational parameters were not changed.
8. Analysis of SRM 1475
The data in table 2 result from the analysis of twelve samples of SRM 1475, listed as samples 1 through 12. Each of the twelve samples was prepared from 25–75 pellets as described in section 6. The mean values and sample standard deviations of the mean for Mn, Mw, and Mz are those shown on the certificate for SRM 1475.
Table 2.
Gel permeation chromatographic analysis of SRM 1475
| Sample number | Mn× 10−4 | Mw × 10−4 | Mz × 10−5 |
|---|---|---|---|
| 1 | 1.833 | 5.503 | 1.518 |
| 2 | 1.789 | 5.309 | 1.490 |
| 3 | 1.681 | 5.013 | 1.291 |
| 4 | 1.726 | 5.247 | 1.369 |
| 5 | 1.921 | 5.451 | 1.351 |
| 6 | 2.019 | 5.149 | 1.200 |
| 7 | 2.068 | 5.400 | 1.243 |
| 8 | 1.820 | 5.065 | 1.220 |
| 9 | 1.883 | 5.538 | 1.534 |
| 10 | 1.789 | 5.310 | 1.489 |
| 11 | 1.657 | 5.032 | 1.277 |
| 12 | 1.789 | 5.669 | 1.583 |
| Mean | 1.831 | 5.307 | 1.380 |
| Estimated standard deviation | 0.125 | 0.214 | 0.127 |
| Estimated standard deviation of mean | .036 | .062 | .037 |
Samples 1 through 4 were also subjected to a modified treatment, in order to check the effects of the handling procedure. After the solutions had been made up as described in section 6, and aliquots taken for the original chromatograms, the remaining portions of the solutions were allowed to cool to room temperature, precipitating the polymer, reheated and stirred as before to redissolve the material, and fresh aliquots rerun on the GPC column. The results obtained for the original and rerun materials are shown in table 3. If degradation or other modification of the sample occurred in the handling procedure, one might expect to find trends in the results for the original and rerun materials. No such trends are apparent, and the differences between original and rerun values are not inconsistent with the sample-to-sample spreads implied by the sample standard deviations given in table 2. We conclude that the effects of our sample handling procedure are not observable.
Table 3.
Effect of rerunning SRM 1475 samples
| Sample Number | Mn × 10−4 | Mw × 10−4 | Mz × 10−5 |
|---|---|---|---|
| 1 | 1.833 | 5.503 | 1.518 |
| 1, rerun | 1.852 | 5.374 | 1.363 |
| 2 | 1.789 | 5.309 | 1.490 |
| 2, rerun | 1.741 | 5.296 | 1.469 |
| 3 | 1.681 | 5.013 | 1.291 |
| 3, rerun | 1.674 | 5.196 | 1.410 |
| 4 | 1.726 | 5.247 | 1.369 |
| 4, rerun | 1.745 | 5.276 | 1.395 |
The integral MWD was obtained by summing the chromatograms for samples 1 through 12. In view of the lack of trend in the reruns of samples 1 through 4 described above, the rerun chromatograms were included in the final sums. The resulting molecular weight distribution is given in table 4 and on the certificate for SRM 1475. Since this distribution is based on an “average” chromatogram, the values of Mn, Mw, and Mz obtained from it will not necessarily agree precisely with those quoted in table 2, which are obtained by averaging molecular weights from the individual chromatograms. From the MWD, we obtain values of 17,900, 52,900, and 139,000 respectively for Mn, Mw, and Mz. These may be compared with the values 18,310, 53,070, and 138,000, respectively, shown in table 2.
Table 4.
Cumulative molecular weight distribution of SRM (1475) by gel permeation chromatography
| log M | Wt. percent | log M | log M percent | log M | Wt. percent |
|---|---|---|---|---|---|
| 2.800 | 0.0 | 4.014 | 15.2 | 5.065 | 90.7 |
| 2.865 | .005 | 4.070 | 18.1 | 5.113 | 92.2 |
| 2.929 | .020 | 4.126 | 21.5 | 5.161 | 93.7 |
| 2.992 | .052 | 4.182 | 25.2 | 5.209 | 94.8 |
| 3.056 | .105 | 4.237 | 29.3 | 5.256 | 95.8 |
| 3.119 | .185 | 4.292 | 33.7 | 5.303 | 96.6 |
| 3.181 | .343 | 4.346 | 38.5 | 5.349 | 97.3 |
| 3.243 | .475 | 4.400 | 43.4 | 5.395 | 97.9 |
| 3.305 | .706 | 4.454 | 48.5 | 5.440 | 98.4 |
| 3.366 | .999 | 4.507 | 53.5 | 5.485 | 98.7 |
| 3.427 | 1.38 | 4.560 | 58.3 | 5.530 | 99.1 |
| 3.488 | 1.88 | 4.612 | 62.9 | 5.574 | 99.3 |
| 3.548 | 2.51 | 4.664 | 67.3 | 5.618 | 99.5 |
| 3.607 | 3.30 | 4.715 | 71.4 | 5.662 | 99.7 |
| 3.667 | 4.28 | 4.776 | 75.1 | 5.705 | 99.8 |
| 3.725 | 5.46 | 4.817 | 78.5 | 5.789 | 99.9 |
| 3.784 | 6.87 | 4.868 | 81.6 | 5.87 | 100.0 |
| 3.842 | 8.56 | 4.918 | 84.4 | ||
| 3.900 | 10.50 | 4.967 | 86.7 | ||
| 3.957 | 12.7 | 5.016 | 88.9 |
9. Discussion and Conclusion
For both calibration and analysis, no corrections have been applied to take into account the effects of column broadening in the GPC system. While such effects are obviously present, it would appear that in this particular case, they do not significantly affect the validity of the analysis. Evidence to this effect may be found in the general agreement between values of Mw/Mn obtained from the chromatograms of the individual fractions and the classically determined ratios. Since SRM 1475 is substantially broader than the individual fractions, we conclude that column broadening effects are not likely to introduce serious errors into the molecular weight distribution obtained for SRM 1475.
The internal consistency of the experiment was checked by comparing chromatograms obtained from sixteen fractions of a sample of SRM 1475 with the chromatogram of the whole polymer. The polymer was fractionated into sixteen fractions using a conventional column elution technique [10]. The fractions were analyzed using GPC, and the areas under the resulting chromatograms were normalized to the weight of the respective fraction. These normalized curves were summed. When this reconstructed “whole polymer” was analyzed, the number- and weight-average molecular weights were calculated to be 17,400 and 53,300 respectively, whereas the best GPC values for the whole polymer were calculated as 18,300 and 53,100.
The results given herein reflect primarily on the precision of the measurement. A statement as to the absolute accuracy is impossible at this time; however, it is our opinion that the errors reflected in the uncertainty of the GPC analysis are largely those associated with the light scattering and membrane osmometry analyses of the calibrating samples.
Individual credit has not been given to some of the specific experimental and analytical details used herein. In many instances original credit is not known, but a great many of these details are to be found in references [8, 13, and 14].
Footnotes
Figures in brackets indicate the literature references at the end of this paper.
Certain commercial materials and equipment are identified in this paper in order to specify adequately the experimental procedures. In no case does such indentification imply recommendation or endorsement by the National Bureau of Standards, nor does it imply that the material or equipment is necessarily the best available for the purpose.
Waters Associates, 61 Fountain Street, Framingham, Mass. 01701
10. References
- [1].Moore J. C., J. Polymer Sci. A 2, 835 (1964). [Google Scholar]
- [2].Determan H., Gel Chromatography, Chap. 3 (Springer-Verlag, New York, N.Y. 1968). [Google Scholar]
- [3].Tung L. H., J. Appl. Polymer Sci. 10, 375 (1966). [Google Scholar]
- [4].Tung L. H., Moore J. C., and Knight G. W., J. Appl. Polymer Sci. 10, 1261 (1966). [Google Scholar]
- [5].Hess M., and Kratz R., J. Polymer Sci. A 2, 4, 731 (1966). [Google Scholar]
- [6].Hamielec A., Proceedings of the 6th International GPC Seminar, Miami Beach, Fla (1968). [Google Scholar]
- [7].Duerksen J. H., and Hamielec A. C., J. Polymer Sci. C 21, 83 (1968). [Google Scholar]
- [8].Frank F. O., Ward I. M., and Williams T., Proceedings of the 5th International GPC Seminar, London (1968). [Google Scholar]
- [9].Wagner H. L, J. Res. Nat. Bur. Stand. (U.S.), 76A (Phys. and Chem.), No. 2, 151–155 (Mar-Apr 1972). Paper VII of this series. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Christensen R. G., J. Res. Nat. Bur. Stand. (U.S.), 76A, (Phys. and Chem.), No. 2, 149–150 (Mar-Apr 1972). Paper VI of this series. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Frolen L. J., Ross G. S., Wims A., and Verdier P. H., J. Res. Nat. Bur. Stand. (U.S.). 76A (Phys. and Chem.), No. 2, 156–160 (Mar-Apr 1972). Paper VIII of this series. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Brown J. E. and Verdier P. H., J. Res. Nat. Bur. Stand. (U.S.), 76A (Phys. and Chem.), No. 2, 161–163 (Mar-Apr 1972). Paper IX of this series. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Moore J. C., Proceedings of the 4th International GPC Seminar, Miami Beach, Fla (1967). [Google Scholar]
- [14].Yau W. W., Suchan H. L., Malone C. P., and Fleming S. W., Proceedings of the 5th International GPC Seminar, London (1968). [Google Scholar]