Abstract
Light-scattering measurements have been made on a series of linear polyethylene fractions and a linear polyethylene standard reference material (SRM 1475). All measurements were made in 1-chloronaphthalene at 135 °C. and over an angular range from 45° to 135°. The data were analyzed to obtain the weight average molecular weights, second virial coefficients and root-mean square end-to-end distances.
Keywords: End-to-end distance, light scattering, linear polyethylene, polyethylene fractions, Mw, second virial coefficient, solution properties
1. Introduction
Several investigators [1, 2]1 have used the technique of light scattering to obtain weight-average molecular weights, second virial coefficients and radii of gyration for polyethylene in dilute solutions. In this paper, we report the results of light scattering studies on a series of linear polyethylene fractions with molecular weight ranging from about 1.9 × 104 to about 6.9 × 105. The weight-average molecular weights reported here were employed in the calibration of a gel permeation chromatograph used [3] to obtain the molecular weight distribution of Standard Reference Material 1475, Linear Polyethylene. We also report the direct determination of weight-average molecular weight for SRM 1475 by light scattering.
2. Experimental Procedure
2.1. Apparatus
The light scattering photometer described by McIntyre and Doderer [4] was used for most of the studies reported here. However, a few measurements were made on a modified Brice-Phoenix Photometer (Phoenix Precision Instrument Company, Philadelphia, Pa.).2 Consistent results were obtained from the two instruments, and data from both instruments are included in the analysis of results.
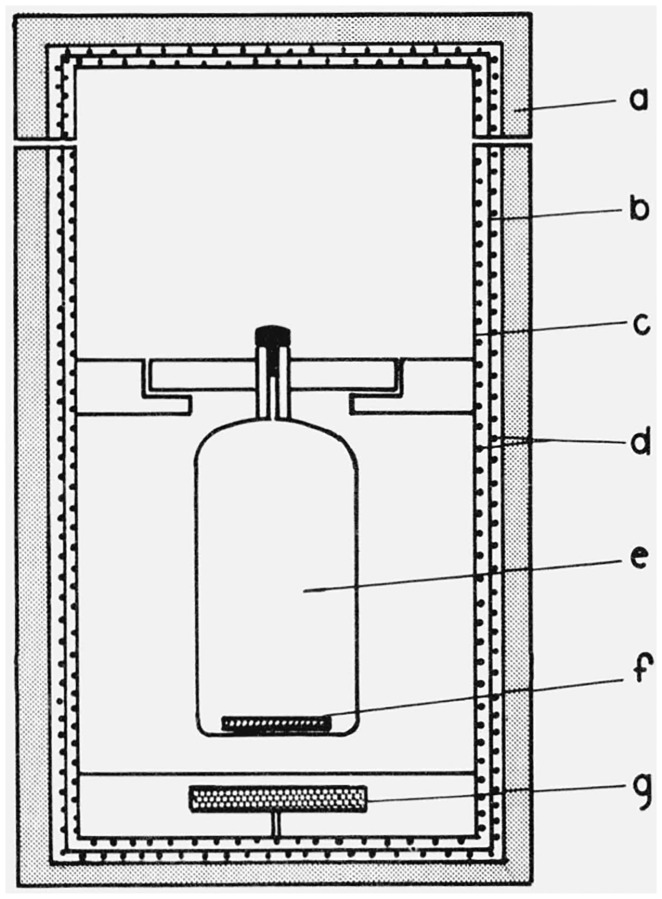
All measurements on polyethylene solutions were made at 135 °C, using a heated cell holder [5] designed and constructed in this laboratory. A schematic drawing of the cell holder is shown in figure 1. It consists of two concentric cylinders wrapped with heating wire, insulated with alternating layers of balsa wood and aluminum foil bonded together with silicone rubber adhesive. A slot, not shown in the figure, extends slightly more than halfway around the oven at the height of the sample cell to provide paths for the incident, transmitted and scattered light. A small rotatable magnet under the sample cell permits stirring when desired. The scattering cells used with the oven are clear Pyrex cylindrical cells fitted with capillary necks and Teflon stoppers to minimize contamination by dust.
Figure 1. Schematic drawing of high temperature oven for light scattering cells.
a. Insulation, b. outer cylinder, c. inner cylinder, d. heating wire, e. light scattering cell, f. stirring bar. g. rotatable magnet.
Measurements on polyethylene were made with the outer cylinder heated to 130 °C and the temperature of the inner cylinder controlled to maintain the sample at 135 °C. No attempt was made to monitor the temperature of the solutions in the light scattering cell while measurements were being taken. However, in preliminary tests, the temperature at various points in the stirred solvent was monitored with thermocouples. The liquid attained a steady temperature of 135° in 15 minutes and thereafter showed temperature variations of less than ± 0.05 °C during a period of one hour.
A solution of polystyrene in toluene was used as a working standard to calibrate the instrument. Measurements of absolute scattering on the working standard were made at room temperature (about 25 °C) in a semi-octagonal sample cell with a clear (unblackened) back surface. The temperature control employed for the higher-temperature measurements on polyethylene was felt to be unnecessary for the room-temperature reference measurements. The oven and cell holder described above were therefore not used for the reference measurements.
2.2. Preparation of Samples
The preparation of the linear polyethylene fractions is described in paper VI of this series [6]. The solvent employed was Fisher Reagent Grade 1-chloronaphthalene which was passed through activated 28–200 mesh silica gel before use. Gas chromatographic analysis of the solvent showed less than 0.1 percent observable impurity. Before being filled with solution, the light scattering cells were cleaned with hot chromic acid, rinsed with distilled water, dried in a dust-free atmosphere, and rinsed from three to five times with filtered 1-chloronaphthalene.
Each sample was prepared by adding approximately 10 cm3 of solvent to a weighed amount of polyethylene, stirring at 130–135 °C until the polyethylene dissolved (usually 1 to 11/2 h) and weighing the resulting solution. The sample was then filtered as described below into a weighed scattering cell. After light scattering measurements had been taken, second and third concentrations were prepared for measurement by adding approximately 5 cm3 increments of filtered solvent, weighing the scattering cell before and after each addition. Weight per unit volume concentrations were calculated from the weights of solvent and solute, solvent density, and partial specific volume [7] of polyethylene in 1-chloronaphthalene. For some representative samples, the final concentration was checked by evaporating 10 cm3 of the solution and weighing the residue. In all cases, the concentration so obtained agreed with that calculated from the known dilutions to within 1 percent.
The samples were filtered with a heated 40 cm3 hypodermic syringe fitted with a “Swinney Adapter” filter holder (Millipore Corp., Bedford, Mass. 01730). A ball joint sealed to the top of the syringe allowed the rate of filtration to be controlled with nitrogen gas under pressure. The nitrogen pressure was adjusted to give a flow rate of approximately 1 drop per second. Faster flow rates resulted in less clean samples as determined by their erratic scattering at low angles. Two Metricel type, Alpha–6 filter discs with a nominal pore size of 0.4 μm (Gelman Instrument Co., Ann Arbor, Mich. 48106) were used for each filtration. These discs had been found to be resistant to 1-chloronaphthalene and could be used at temperatures up to 150°C without apparent damage. They were rinsed with the material to be filtered before use, and were changed after each filtration.
During filtration, the syringe was heated by placing it in a glass tube wrapped with heating wire and maintained at 135–140 °C. The needle of the syringe was inserted into the capillary neck of the light-scattering cell, and the filtration was carried out in a stagnant air box to minimize contamination by dust.
2.3. Scattering Measurements
Scattered intensities were measured at eleven scattering angles ranging from 45° to 135°. Measurements on SRM 1475 were made at 25 concentrations, in the range from 1.7 × 10−3 to 20.8 × 10−3 g/cm3. Measurements on each of the seven fractions listed in table 1 were made at six concentrations. The concentrations chosen varied with the molecular weights of the fractions, from a range of 1.8 × 10−2 to 5.7 × 10−2 g/cm3 for PE 15 to a range of 0.7 × 10−3 to 2.6 × 10−3 g/cm3 for PE 600. Measurements were also made on pure solvent. The incident illumination in all cases was the mercury green line of wavelength 5461 Å, plane-polarized with its electric vector perpendicular to the scattering plane.
Table 1. Weight-average molecular weights Mw, second virial coefficients A2, and rms end-to-end lengths 〈L2〉1/2, for linear polyethylenes in 1-chloronaphthalene at 135 °C.
The uncertainties shown are estimates of the standard deviations obtained from linear least squares analyses of the corrected experimental scattering intensities, as described in the text.
| Sample | dn/dc, ml/g | Mw × 10−3g/mol | A2 × 103, mol • cm3/g2 | 〈L2〉1/2 × 10−3, Å |
|---|---|---|---|---|
| PE 15 | −0.193 | 19.1 ± 2.4 | 1.9 | 0.4 |
| PE 40 | −.191 | 49.4 ± 2.0 | 1.6 | .6 |
| PE 60 | −.190 | 82.2 ± 7.1 | 1.6 | .6 |
| PE 120 | −.188 | 170 ±16 | 1.4 | .7 |
| PE 180 | −.188 | 210 ±30 | 1.2 | .9 |
| PE 350 | −.188 | 520 ±42 | 1.3 | 1.4 |
| PE 600 | −.188 | 688 ±67; | 1.2 | 2.1 |
| SRM 1475 | − .193 | 52.0± 2.0 |
As mentioned previously, a solution of polystyrene in toluene was used as a working standard. The absolute scattering of the working standard at 90° was first determined. As each polyethylene solution was measured, the scattered intensity from the working standard at 90° was also recorded. Thus, the quantity actually obtained was the ratio of the scattering from the solution (or solvent) at each angle to that of the working standard at 90°.
3. Treatment of the Data
The use of light scattering to determine molecular weight and size parameters of macromolecules in dilute solution is well established [8]. At sufficiently low concentrations and small scattering angles, the ratio of solution concentration to scattered light intensity may be expanded in a Taylor series in concentration and in the sine of half the scattering angle. For plane-polarized monochromatic light scattered through an angle θ, the result for a solution of monodisperse material may be expressed in the form [9]:
| (1) |
with:
| (2) |
| (3) |
and
| (4) |
where
c is solution concentration (weight per unit volume),
M is the molecular weight of the solute,
RG is the radius of gyration of the solute,
A2 is the second virial coefficient of the solution,
λ0 is the wavelength in vacuo of the radiation,
n is the index of refraction of the solvent at wavelength λ0,
λ = λ0/n is the wavelength of the radiation in the solvent,
NA is Avogadro’s number,
dn/dc, the so-called differential refractive index, is the derivative (at constant temperature and pressure and in the limit of zero concentration) of solution refractive index with respect to concentration,
θ is the angle between the incident and scattered wave vectors,
ψ is the angle between the electric vector of the incident radiation and the plane containing the incident and scattered wave vectors,
I0 is the intensity of the incident radiation,
I(θ,c) is the scattered intensity at angle θ for a solution of concentration c,
r is the distance from the scattering center to the point at which the scattered intensity is observed, and
v = v(n,θ) is the volume of solution from which the scattered radiation is observed.
For the special cases ψ = π/2 and ψ = 0 (so-called vertical and horizontal polarization), the last factor in eq (2) becomes unity and cos2θ, respectively. (The usually-quoted result for unpolarized incident radiation is obtained by averaging over all possible values of ψ, in which case the factor becomes (l + cos2θ)/2.)
For a solution of polydisperse material, it can be shown [10, 11] that eq (1) still holds at sufficiently small scattering angle and low concentration, provided M is replaced by Mw, the weight-average molecular weight, is replaced by its z-average, [12], and A2 is replaced by an “effective” value without simple interpretation [11].
In order to use eqs(1)–(4) to relate observed scattering to molecular parameters, it is necessary to know the functional dependence of the scattering volume, v, upon n and θ. For the geometry of our instrument, the scattering volume is inversely proportional to the square of the index of refraction of the material in the scattering cell [13,14]. A simple geometrical argument suggests that for scattering angles not too close to 0° or 180°, the scattering volume should vary as the cosecant of the scattering angle. (The validity of the approximation was established for the present work, in the course of checking the alignment of the instrument, by measurements on fluorescein solutions.) Thus we can write
| (5) |
Finally, the observed intensities must be corrected for the effects of reflections at the entrances and exits of the scattering cells, as discussed by Kratohvil [15]. When light impinges perpendicularly upon an interface between two regions with indices of refraction n1 and n2, the fraction f reflected is given by Fresnel’s formula: f = [(n1− n2)/(n1 + n2)]2. In the light-scattering experiment, such interfaces occur at both the inside and the outside surfaces of the walls of the scattering cells. If we make the usual assumption that the difference between the index of refraction of the solution inside the scattering cell and the index of the glass in the cell walls is so small as to cause negligible reflection, we are left with only the interfaces between the cell walls and the air outside the cell to consider. By counting up the various possible paths resulting from multiple reflections of the incident and scattered beams, we can readily show that for a circularly cylindrical scattering cell, the observed intensity I′(θ,c) is related to the “true” intensity I(θ,c) (i. e., that which would be observed in the absence of reflections) by
| (6) |
where f = [(ng− 1)/(ng + 1)]2, and ng is the index of refraction of the cell wall glass. Equation (6) is in agreement, to first order in f, with the approximate result obtained by Kratohvil [15] for this case.
For the semioctagonal cell used to determine absolute scattering by the working standard, only the intensity of the beam scattered through an angle θ = π/2 and the intensity I0 of the incident (unscattered) beam need be considered. For right-angle scattering, the light paths for this cell are identical with those for a circularly cylindrical cell, and the special case I = I′ obtained from eq (6) for θ = π/2 also applies to this cell. For the incident beam, observed after passage through the semioctagonal cell, it can easily be shown that
| (7) |
For the present work, the quantity Rπ/2, s = r2Is/(vI0), where we denote by Is the intensity of right-angle scattering from the working standard, was first determined as described by McIntyre [13]. The intensity ratio Is/I0 was measured with the use of a set of calibrated filters, and was corrected for reflections as described above. For the semioctagonal cell employed, the quantities r and v0 were obtainable from the instrument geometry, and the scattering volume v was obtained from eq (5).
For measurements made on the working standard at 90° in the circularly cylindrical scattering cells, we can use the definition of Rπ/2, s and eq (5) to write
| (8) |
where ns is the index of refraction of the working standard. With the use of eqs (2)–(6), the left-hand side of eq (1) can be rewritten in the form
| (9) |
Thus, measurement of the scattering of the solution relative to that of the working standard (the last factor on the right-hand side of eq (9)), together with the value of dn/dc for the solution, yields Kc/Rθ. Equation (1) may then be used to determine Mw, , and A2 from the dependence of Kc/Rθ upon c and θ.
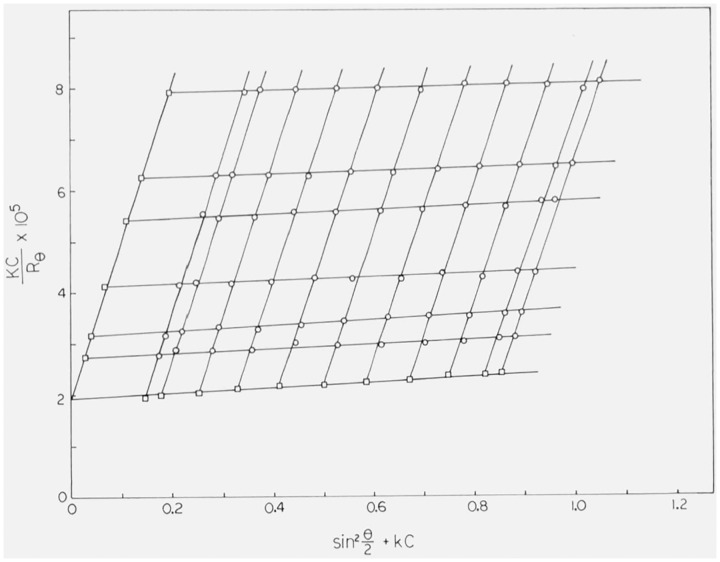
In order to extract molecular parameters from experimental values of Kc/Rθ, we employ the well-known Zimm method [16]. If we plot Kc/Rθ as a function of sin2(θ/2) + kc, where k is a constant chosen for convenience, we obtain an array of points through which lines of constant concentration and lines of constant angle can be drawn, as exemplified in figure 2. Extrapolation of each of the constant-concentration lines to zero angle gives a set of points which constitute a plot of Kc/R0 versus kc. According to eq (1), such a plot intersects the Kc/Rθ-axis at 1/Mw, with a limiting slope of 2A2/k. In the same way, extrapolation of each of the constant-angle lines to zero concentration yields a plot of lim c→0 [Kc/Rθ] versus sin2(θ/2). Combining eqs (1) and (4), we find:
Figure 2. Typical Zimm plot (Kc/Rθ versus sin2(θ/2) + kc) obtained for linear polyethylene in 1-chloronaphthalene at 135 °C. The concentration c is expressed in g/cm3; the arbitrary constant k was chosen to have a value of 10 cm3/g.
The other symbols are explained in the text. The circles are experimental values; the squares are extrapolations to zero angle at constant concentration and to zero concentration at constant angle.
The intercept is therefore again 1/Mw, and the limiting slope is a measure of . In the special case of a linear random-coil chain one can estimate the mean-square distance, 〈L2〉, between the ends of the chain by using the relation [17] , although this relation has been established only for chains with Gaussian random-flight statistics.
4. Results
The results obtained for the linear polyethylene fractions and for SRM 1475 are summarized in table 1, together with the values of dn/dc used in calculating Kc/Rθ. For SRM 1475 and the fractions with Mw less than 200,000, measured values [7] of dn/dc were used. For fractions with Mw greater than 200,000, measured values of dn/dc were not available, but measurements on the lower-molecular-weight fractions appeared to suggest that by this point, dn/dc had reached a constant value of −0.188 ml/g independent of molecular weight. This value of dn/dc was therefore used in calculating Kc/Rθ for the fractions of Mw above 200,000.
Values of Kc/Rθ for each fraction and for SRM 1475 were analyzed by the Zimm technique, as described in the preceding section. In all cases, plots of Kc/Rθ versus sin2(θ/2) + kc were found to be linear throughout the entire angular range. A typical plot, obtained for SRM 1475, is shown in figure 2. For clarity, the plot shows the data for only six of the 25 concentrations actually employed. The lack of downward curvature in the plots suggests that the samples were adequately cleaned [18].
The linear extrapolations necessary to obtain Mw, , and A2 were carried out by unweighted linear least-squares analyses. The results are given in table 1, together with estimates of the standard deviation in Mw inferred from the least-squares analyses. The values of the rms end-to-end length, 〈L2〉1/2, given in table 1 were obtained from the values found for by use of the approximate relation , as described in the preceding section. It is clear from the lack of smoothness in the variation of A2 and 〈L2〉1/2 with molecular weight that they are to be regarded as no more than crude estimates. Estimates of the standard deviations in and A2 from the least-squares analyses were unrealistically low (typically, about 5 per cent for A2 and 50–100 Å for 〈L2〉1/2), and are therefore not shown in the table. Values of and A2 were not calculated for SRM 1475.
Footnotes
Present address: General Motors Research Laboratory, Warren, Michigan 48092
Figures in brackets indicate the literature references at the end of this paper
Certain commercial equipment, instruments, or materials are identified in this paper in order to adequately specify the experimental procedure. In no case does such identification imply recommendation or endorsement by the National Bureau of Standards, nor does it imply that the material or equipment identified is necessarily the best available for the purpose.
5. References
- [1].DeLaCusta M. O., and Billmeyer F. W. Jr., J. Polymer Sci. A1, 1721 (1963). [Google Scholar]
- [2].Chiang R., J. Phys. Chem. 69, 1645 (1965). [Google Scholar]
- [3].Ross G. S., and Frolen L. J., J. Res. Nat. Bur. Stand. (U.S.), 76A (Phys. and Chem.), No. 2, 163–170 (Mar.–Apr. 1972), Paper X of this series. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].McIntyre D., and Doderer G. C., J. Res. Nat. Bur. Stand. (U.S.), 62, 153 (1959). [Google Scholar]
- [5].Wims A., and Ross G. S., unpublished work.
- [6].Christensen R. G., J. Res. Nat. Bur. Stand. (U.S.), 76A, (Phys. and Chem.). No. 2, 149–150 (Mar.–Apr. 1972). Paper VI of this series. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Wagner H. L., J. Res. Nat. Bur. Stand. (U.S.), 76A, (Phys. and Chem.), No. 2, 151–155 (Mar.–Apr. 1972). Paper VII of this series. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].See, for example. Kerker M., The Scattering of Light (Academic Press, New York, 1969): [Google Scholar]; Tanford C., Physical Chemistry of Macromolecules, John Wiley and Sons, New York, 1961; [Google Scholar]; Flory P. J., Principles of Polymer Chemistry (Cornell University Press, Ithaca, New York, 1953). [Google Scholar]
- [9].The notation used here is essentially that used by Kerker (op. cit., Ch. 8). but is written for plane-polarized incident radiation rather than for unpolarized radiation.
- [10].Kerker, op. cit., Ch. 8.
- [11].Fujita H., Mathematical Theory of Sedimentation Analysis, p. 268 f. (Academic Press, New York, 1962). [Google Scholar]
-
[12]. We define the z-average of the square of the radius of gyration of a polydisperse material as
where ni is the number of molecules of the i-th component, of molecular weight Mi and radius of gyration RGi. - [13].McIntyre D. , J. Res. Nat. Bur. Stand. (U.S.), 68A, (Phys. and Chem.) 87 (1964). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Herman J. J. and Levinsnn S., J. Opt. Soc. Am. 41, 460 (1951). [Google Scholar]
- [15].Kratohvil J. P., Colloid J. and Interface Science 21, 498 (1966). [Google Scholar]
- [16].Zimm B. H., J. Chem. Phys. 16, 1099 (1948). [Google Scholar]
- [17].See, for example, Flory P. J., op. cit.
- [18].Muus L. T., and Billmeyer F. W. Jr., J. Am. Chem. Soc. 79, 5079 (1957). [Google Scholar]