The Formation of Curved Polymer Crystals: Poly (4-methylpentene-1)

F Khoury; J D Barnes

doi:10.6028/jres.076A.027

. 1972 May-Jun;76A(3):225–252. doi: 10.6028/jres.076A.027

The Formation of Curved Polymer Crystals: Poly (4-methylpentene-1)

F Khoury ¹, J D Barnes ¹

PMCID: PMC6706570 PMID: 34565860

Abstract

An optical and electron microscopical study is described of the habits exhibited by poly(4-methylpentent-1) crystals (Modification I tetragonal unit cell) grown at temperatures between 50 and 90 °C from 0.1 percent solutions of the polymer in equivolume mixtures of xylene and amyl acetate. A distinct trend in the effect of crystallization temperature (supercooling) on the habits of the crystals is illustrated and discussed. The lamellar crystals formed in that temperature range are all the more pronouncedly curved the lower the crystallization temperature. To indicate but the extremes in this trend, the crystals varied from essentially planar ones whose constitutent square shaped chain-folded lamellae (bounded laterally by {100} faces and up to 20 μm on a side) are four-sectored and only very slightly buckled as previously indicated by Bassett et al., to distinctly curved four-fold symmetrical hollow bowl shaped ones having a radius of curvature of about 2.5 μm and in which the surface of the curved multilayered wall of which they are constituted changes in orientation through 180° from the base (pole) to the periphery. In contrast with the four-sectored character of the lamellae in the aforementioned essentially planar crystals, the constituent lamellae in all the distinctly dished and bowl-like crystals formed in the temperature range 50 to 90 °C are multiseetored. their lateral development being characterized by the formation at their periphery during growth of successive arrays of {100} microfaceted sectored outgrowths. The reasons why the lamellar crystals of poly (4-methylpentene-1) are all the more pronouncedly curved the lower the crystallization temperature are explored and discussed. Conjectures concerning the origins of this phenomena are advanced in the form of a working ‘model.’

Keywords: Chain-folded; crystal, curved; electron microscopy; lamellar; optical microscopy; poly-(4-methylpentene-1); polymer; solution-grown

1. Introduction

Investigations of the crystal habits exhibited by poly(4-methylpentene-1) (P4MP), polychlorotrifluoroethylene, and polyoxymethylene when these polymers are crystallized from dilute solutions have led us to the observation that, broadly speaking, whereas at high crystallization temperatures the solutions yield lamellar crystals which are planar or nearly planar in character, at lower crystallization temperatures multilayered lamellar crystals are formed which exhibit distinctly curved shapes and which are all the more pronouncedly curved, i.e., they have a smaller radius of curvature, the lower the crystallization temperature [1].¹ Indeed, at high supercoolings the polymer solutions yield hollow bowl-shaped crystals. This paper, which consists of two parts, concerns the formation of curved crystals of P4MP. First, a description will be presented of the formation, habits, and fine structural characteristics of curved crystals of P4MP grown from 0.1 percent solutions of the polymer in equi-volume mixtures of xylene and amyl acetate at temperatures between 90 and 50 °C. Second, considerations based on the observations derived from this study regarding the origins of the curved habits exhibited by these crystals and why they are all the more pronouncedly curved the lower the crystallization temperature will be advanced and discussed.

As background to the study of P4MP reported herein, previously published investigations on the structure and crystallization habits of this polymer are summarized below.

The crystal structure of P4MP was reported several years ago by Frank, Keller and O’Connor [2] who determined, on the basis of an x-ray and electron diffraction study of solution grown crystals of P4MP which had been formed by slowly cooling hot polymer solutions to room temperature, that the unit cell is tetragonal, the cell parameters being a = b = 18.66 Å, c = 13.80 Å. Four chains, each in a 7/2 helical conformation, pass through the unit cell which contains twenty-eight monomer units. The axes of the helices are parallel to the c axis of the cell. According to Frank et al. [2], and later Bassi et al. [3], the space group is probably $P \bar{4}$ . This unit cell structure which is that most commonly exhibited by crystalline P4MP has since been referred to as Modification I in view of subsequent reports of the existence of two other less stable crystalline modifications of P4MP [4–8]. The habits of P4MP crystals grown from solution were first described by Frank, Keller, and O’Connor [2]. These were crystals from the same preparations used in the determination of the unit cell structure of P4MP (Mod I) mentioned above. The simplest crystals observed by Frank et al. [2] were thin square-shaped lamellae of P4MP which are bounded laterally by {100} faces at which growth occurs through the accretion of the chain molecules along correspondingly parallel {200} planes. These lamellae are composed of four sectors (fold domains)² which are distinguished by the {200} planes along which the molecules are folded as shown schematically in figure 1. Electron diffraction patterns obtained from these crystals indicated that the chain molecules are oriented normal to the plane of these seemingly flat lamellae. Bassett [9] and Bassett et al. [10] have more recently reported that the otherwise ideally tetragonal unit cell is slightly distorted in the constituent sectors of such four-sectored lamellae. Evidence of the distortion of the unit cell was derived from an analysis of Moiré patterns exhibited in the electron microscope by bilayered crystals (in which each of the two superimposed chain-folded lamellae or layers is four-sectored) which indicated that the spacing of the {200} planes in each of the four constituent sectors in individual layers differs by ~ 0.1 percent according to whether or not they are fold planes [9]. This asymmetric distortion of the unit cell in each sector has been attributed to the bulkiness of the chain folds. Furthermore, the dark field {200} diffraction contrast characteristics exhibited by these bilayered crystals in the electron microscope indicated that their constituent lamellae, as grown, are not perfectly planar but suggested instead that they possess a very slight “conicalness” [9, 10]. According to Bassett et al. [9, 10], this latter feature (which escapes detection under the optical microscope [10]). is associated with the distortion of the unit cell in the constituent sectors of the chain-folded lamellae. On the basis of the magnitude of the unit cell distortion and assuming to a first approximation that the lamellae are conical, their angle of inclination was estimated to be ~ 2°.

In addition to the simple four-sectored lamellae referred to above, Frank et al. [2] observed in the same preparations numerous tetragonal crystals (all of Modification I) which exhibited under the electron microscope ample evidence of having undergone substantial pleating and folding over when they sedimented upon the carbon substrate. Indeed, the majority of the crystals in their preparations exhibited such features. In many instances the corners of the basal lamella were observed to have folded over onto the interior of the crystal. Similar crystals have been observed by Woodward [11] who suggested that such crystals are hollow pyramidal in character, having steep sides and “deformed square bases.” Further insight into the growth habits and fine structures of crystals of P4MP which exhibit evident collapse features such as those mentioned above when they sediment upon a flat substrate is provided by the combined optical and electron microscope investigation reported herein of the crystallization of P4MP.

2. Experimental Details

2.1. Materials and Preparative Methods

Poly(4-methylpentene-l) in powder form and having an intrinsic viscosity η = 4.6 dl/g [12] was used throughout this study. According to Hoffman, Fries and Condit [13] the relationship between η and the number average molecular weight (M_n) of P4MP is

η = 1.94 \times 10^{- 4} {(M_{n})}^{0.81}

which gives M_n = 252,000 for the above polymer.

The poly(4-methylpentene-1) was crystallized from solution in equivolume mixtures of xylene (good solvent) and amyl acetate (poor solvent). Both solvents were distilled independently prior to use. Solutions with a concentration of 0.1 percent (w/v) of the polymer in the mixed solvent system (50 ml) were prepared by heating appropriate quantities of P4MP mixed with solvent at 140 °C for half an hour. The resulting solutions were then transferred to baths held isothermally, within ±0.1 °C, at temperatures in the range 50 and 90 °C (i.e., 50, 70, 80, and 90 °C) for from 1 to 3 days, during which periods the polymer crystallized in the form of crystals in suspension in solvent. In order to prevent further crystallization of polymer still in solution when the preparations are finally cooled from the crystallization temperature to room temperature, the mother liquor was in all instances isothermally exchanged, prior to cooling, with fresh equivolume mixtures of xylene and amyl acetate preheated to the temperature of each preparation. The following procedure was followed in each instance: Each preparation was rapidly transferred from the crystallization bath and poured into an isothermally controlled filtration vessel maintained at a temperature corresponding to that of the crystallization bath. The type of filtration vessel used was essentially similar in design to a filtering apparatus previously described by Bassett et al. [14]. Uncrystallized polymer was eliminated by alternate filtration and addition of fresh preheated (to the temperature of the preparation) solvent mixture to the suspension of crystals, care being taken to ensure that the crystals were continuously immersed in liquid and not allowed to dry between successive additions of fresh solvent mixture to the suspension. Two to three exchanges of the solvent medium were carried out in each instance. After a final addition of a fresh preheated solvent mixture to the suspension of crystals, the filtration vessel containing the latter suspension was allowed to cool to room temperature.

In a few experiments which will be mentioned later in the paper (sec. 3.5) a self-nucleating procedure analogous in principle to that used by Blundell, Keller and Kovacs [15] in the case of polyethylene was adopted to crystallize P4MP from 0.1 percent solutions of the polymer in equivolume mixtures of xylene and amyl acetate. The thermal histories of the self-nucleated solutions were as follows: 140 °C (1/2 hr) → 70 °C (1 hr) → 130 °C (1/2 hr) → T °C, where T °C = 50 °C and 90 °C were the chosen crystallization temperatures after redissolving at 130 °C. Following crystallization at T °C the preparations were subjected to isothermal filtering and washing in the manner described above.

2.2. Microscopy

a. General

Both optical and the electron microscopy were necessary in order fully to characterize the shapes as well as the fine structural details of the curved crystals discussed in ensuing sections. These crystals collapse and flatten very readily when they are sedimented and allowed to dry on a flat carbon substrate as required for electron-microscopic observations. Although some information regarding the as-grown shapes of the crystals could be derived from the nature of the collapse features they exhibit under the electron microscope, detailed characterization of their as-grown shapes could only be derived by observing them under the optical microscope while in suspension in liquid.

b. Optical Microscopy

The as-grown shapes of the crystals were determined by examining them as they tumbled or were induced to tumble slowly while in suspension in solvent at room temperature under a microscope using phase contrast optics. Glass slides having a shallow central well in which droplets containing crystals in suspension were deposited and subsequently covered with a thin cover-glass were used for this purpose. Examination of the crystals was facilitated by diluting the solvent medium with a liquid having a refractive index sufficiently different from that of the crystals which is ~ 1.46 in order to enhance contrast. Dilution with a Cargille³ liquid of refractive index 1.70, which did not affect the crystals, was found most convenient particularly for recording and exhibiting the salient features of the crystals photographically.

c. Electron Microscopy

For transmission electron microscopy, droplets of each preparation containing crystals in suspension were deposited on electron microscope grids covered with a film of carbon. The solvents were allowed to evaporate at room temperature, after which the dried crystals were shadowed in vacuo with a platinum-palladium alloy (80% Pt/20% Pd). In instances in which crystals were too thick to allow their fine structure to be observed in transmission (e.g., see sec. 3.4) shadow transfer replicas of the crystals were prepared. In such instances drops of the preparation containing crystals in suspension were deposited on a microscope slide; the crystals were allowed to dry at room temperature, after which they were shadowed with metal (Pt/Pd). A backing layer of carbon was then evaporated onto the shadowed crystals. The composite carbon-metal “film” was then floated off the slide on distilled water. The crystals were found to adhere to the “film.” portions of which were picked up on electron microscope grids and allowed to dry in air. The crystals were then dissolved by immersing the grids supporting the replicas in xylene for two hours at 139 to 140 °C.

The electron microscope used in most of this study was a JEM 6a³ which was operated at 80 kV using the double condenser system.

3. Observations on the Morphologies of Poly(4-methylpentene-1) Crystals

3.1. General

A description is presented in succeeding subsections (3.2–3.4) of the morphologies exhibited by P4MP crystals which are formed when 0.1 percent solutions of the polymer initially maintained at 140 °C are subsequently transferred to baths held at temperatures between and including 90 and 50 °C within which range crystallization occurs. In anticipation of what follows it may be noted at this stage that electron diffraction patterns obtained from selected areas of individual crystals formed within that range of temperatures as well as x-ray powder patterns obtained from samples from each preparation were consistent with the Modification I tetragonal unit cell structure proposed by Frank et al. [2], A typical x-ray powder pattern is shown in figure 2 in which the 200; the 220; the composite 311, 212; the 321; the 411; and the composite 331, 420, 322, 203; rings may be discerned. The corresponding measured spacings are 9.3₁, 6.6₀, 5.2₉, 4.8₃, 4.3₀, 4.1₄ Å. This particular pattern was obtained from a sample of crystals from a 50 °C preparation.

Figure 2. — This particular pattern was obtained from a sample of crystals from a 50 °C preparation. Proceeding from the center outwards the rings which may be readily discerned are the 200; the 220; the composite 311, 212; the 321; the 411; and the composite 331, 420, 322, 203.

3.2. Crystals Formed at 90 °C

The onset of faint cloudiness in the solutions, indicating the occurrence of crystallization, was observed 30 to 40 min after transfer to the 90 °C bath. The developing crystals are initially well dispersed in the mother liquor which exhibits uniform cloudiness. In time, however, they tended to agglomerate in random clusters consisting of several crystals which tended to adhere to one another due to some intergrowing which occurs between vicinal crystals within each cluster.

A mixed population of lamellar cystals differing in both size and shape are formed at this temperature. Interestingly a correlation was observed between the relative sizes of the crystals and their respective habits and fine structures. Before proceeding with more detailed descriptions of the morphological characteristics of the various crystals, it may be pointed out from the outset that whereas the smaller crystals among the entire population were essentially planar in character, the larger crystals had detectably curved overall shapes which, however, as will be seen later, were less pronouncedly curved than crystals formed at lower temperatures.

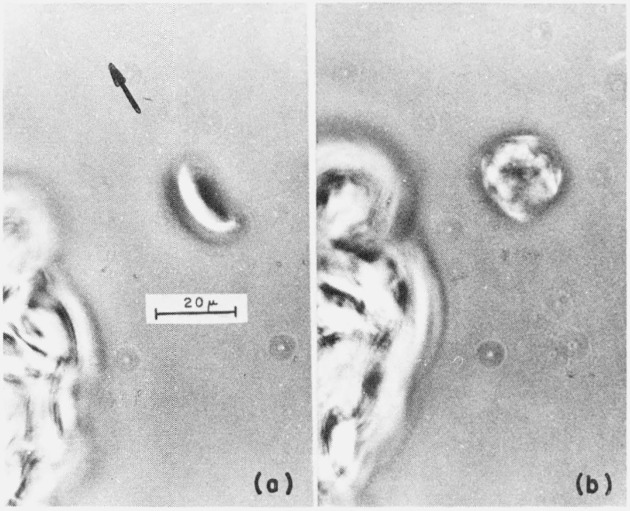
The smaller crystals formed at 90 °C were mono- or multilayered, their habit being identical to that of the simplest very nearly planar four-sectored chain-folded lamellae previously observed by other workers [2, 8–11]. An example of such a crystal is shown in figure 3. The morphological characteristics of this species of crystal as seen under the optical and electron microscopes bear to be recapitulated here since they provide a useful basis of reference with respect to which the morphologies of the larger and more complex crystals formed at 90 °C, as well as the crystals formed at lower temperatures, may be compared. The constituent lamellae in these smaller crystals are square-shaped and are bounded laterally by {100} faces. Furthermore superimposed layers frequently develop in a spiral-like fashion through the agency of screw dislocations in the basal lamella, as may be seen in figure 3. The essentially planar character of these crystals is readily revealed when they are viewed edge-on while in suspension in liquid under the optical microscope using phase contrast. An edge-on perspective of such a crystal is shown in figure 4 in which it may be seen to exhibit an essentially linear profile. It is not possible unequivocally to resolve under the optical microscope the very slight “conicalness” which it has been suggested [9, 10] these crystals possess. Nevertheless, morphological evidence which is consistent with Bassett et al.’s [9, 10] interpretation of dark field electron images which indicate that these crystals are not perfectly planar and that they collapse on drying on a substrate is provided by an examination of shadowed crystals under the electron microscope. Shadowing characteristically reveals faintly discernible ridges which may be traced along the diagonals of each square-shaped lamella as may be seen in figure 5. These ridges correspond to the boundaries between the four constituent sectors or fold domains in each lamella. Figure 5a represents a region near the bottom left-hand corner of the basal lamella in the crystal shown in figure 3 viewed at higher magnification. Figure 5b represents a region further upfield in the same crystal where three lamellae overlap and the three arrows point to the sector delineating ridge in each lamella. Such sector delineating ridges which have been previously observed by Woodward [11] suggest that the lamellae undergo slight localized pleating at the sector boundaries as the crystals collapse upon the substrate. For the purpose of later comparison (e.g., see figs. 9–10 onwards) the essentially smooth character of the edges of the lamellae in this crystal may also be noted in figure 5.

It has been pointed out above that the crystals formed at 90 °C tended to cluster and intergrow while in suspension in the solvent at the crystallization temperature. The species of crystals described in the previous paragraph, which represent the smaller fraction of the total crystal population, were generally observed to be situated at the periphery of clusters consisting of other larger and more complex crystals. This latter observation coupled with the fact that they are the smallest among the entire population of crystals, their edges being about 20 μm or less in length, indicates that they developed during the more advanced stages of the depletion of polymer from solution.

We turn now to a consideration of the morphological characteristics of the larger and more complex crystals formed at 90 °C. These larger crystals are multilayered, the sides of their basal lamella being up to 45 μm or so long; furthermore, these crystals are distinctly curved. This latter feature is readily perceived when they are examined edge-on while in suspension in liquid. When viewed in this latter perspective they characteristically exhibit a crescent-like profile, as shown in figure 6 in which such crystals oriented edge-on with respect to the field of view may be seen. It should also be pointed out that some large multilayered crystals were observed which consisted of two families of lamellae which were curved in opposite directions.

Figure 6. — The crystals are in suspension in liquid and exhibit a crescent-like profile when viewed in this orientation. Phase contrast, × 490.

An example of a large curved crystal as observed in the electron microscope at low magnification is shown in figure 7 in which its multilayered character may be clearly seen (notwithstanding the fact that there is another overlapping crystal in the upper left hand part of the micrograph). In addition, the incidence of appreciable pleating which results from the collapse of these nonplanar crystals when they sediment upon the substrate may be seen in figure 7.

An electron diffraction pattern which was obtained from a crystal similar to those in figures 6 and 7 is shown in figure 8a, and the corresponding selected area near the periphery of the crystal is shown in figure 8b (note the pleats). The diffraction pattern in figure 8a corresponds to the zero layer (i.e., the a*b* plane where a* = b* in P4MP) of the reciprocal lattice net of P4MF, the innermost and most intense spots being 200 and the next most intense are 220 and 420 in accordance with Frank et al. [2]. It is evident from the disposition of the 200 reflections along directions normal to the edges of the lamellae that the chain folded layers in these larger crystals are also bound laterally by {100} growth faces as is the case in the smaller crystals discussed in previous paragraphs. However, examination under the electron microscope of the periphery of the curved lamellae in these crystals reveals a profusion of pronounced step-like reentrances. This feature may be readily seen in figures 9 and 10 depicting portions along the sides of the basal lamella in two such crystals in which well developed orthogonally reentrant facets are evident. This is in contrast with the relatively smooth character of the lateral edges of the smaller four-sectored crystals (figs. 5a, 5b). In short the {100} sides of the lamellae in the larger crystals are distinctly microfaceted; the microfacets are {100}. The existence of well developed reentrant {100} microfacets suggests in itself that the lamellae in these crystals are multisectored, i.e., that they consist of a mosaic of fold domains, neighboring domains being subtended at the edges of the lamellae during the process of growth by adjacent {100} microfacets which are orthogonal to one another and along both of which chain-folding occurs. The multisectored (as distinct from four-sectored) character of the lamellae in these larger curved crystals is further substantiated by the fact that when they are shadowed with metal and examined under the electron microscope, a network of faintly discernible domain delineating ridges is revealed on their upper surface. Such ridges are pointed to in figures 9–10. These ridges can usually be traced from leading microcorners, formed by adjacent {100} microfacets at the periphery of the lamellae, inwards often along paths oriented at ~ 45° to the sides of the lamellae, although this angle does vary from 45° (barbed arrows in figure 9 and figure 10 point to such cases) as a result of situations which arise at the periphery where new chain folded planes are formed more rapidly along a {100} microfacet facing the surrounding medium than along an adjacent reentrant {100} microfacet. As has been advanced earlier in the case of four-sectored lamellae, these ridges presumably result from the occurrence of slight localized pleating along the fold domain boundaries when the lamellae collapse on drying in addition to the much more pronounced pleating and overfolding which these larger curve lamellae undergo as pointed out earlier with reference to figure 7.

We shall in due course consider further the nature of the as-grown character of the larger curved crystals formed at 90 °C in the light of observations derived from crystals grown at lower temperatures. This will be done in section 4 in which inter alia the matter of the differences between the larger and smaller crystals formed at 90 °C will also be broached. It will suffice at this stage to point out that the observations derived from the combination of optical and electron microscopic observations on the population of crystals formed at 90 °C which are described above are suggestive in themselves of a phenomenological correlation between the fine (domain) structure and the as-grown conformation of the constituent lamellae in the crystals. It is of interest to note that the lamellae in the larger crystals are multisectored and that these lamellae are perceptibly curved, whereas the smaller crystals whose constituent lamellae are four-sectored are essentially planar and correspondingly they do not exhibit any pronounced collapse features upon sedimentation as is the case with the larger curved crystals. As will be seen in subsequent subsections, crystallization at lower temperatures leads exclusively to the formation of crystals whose constituent lamellae are multisectored as well as curved.

Finally it may be noted that the thickness of the lamellae in the crystals formed at 90 °C as determined from a low angle x-ray diffraction pattern obtained from a mat of such crystals (using a Rigaku-Denki low angle camera with pinhole collimation) with the plane of the mat parallel to the x-ray beam was found to be 139 Å.

3.3. Crystals Formed from Solutions Cooled at 80 °C

Crystallization occurs rapidly when solutions initially held at 140 °C are transferred to a bath at 80 °C. The lapse of time corresponding to the onset of cloudiness coincides closely to the time taken (~ 10 min) by the solution to cool from 140 to 80 °C. Under these conditions an essentially uniform population of lamellar crystals is yielded. Considerably less in situ clustering of the crystals occurred in these preparations than was the case at 90 °C. When they are viewed edge-on under the optical microscope, while they are in suspension in liquid, the crystals exhibit crescent-like profiles as shown in figure 11, in short, these crystals are curved. A representative crystal in suspension in liquid is also shown in figure 12, in which it is depicted as seen in two different perspectives. Figure 12a represents the crystal as viewed edge-on; its crescent shaped profile may be readily discerned. In figure 12b the same crystal is shown after it had rotated through 90° about an axis oriented at ~ 30° with respect to the vertical in the field of view (see arrow). In this latter perspective, in which the crystal is viewed along a direction very nearly parallel to its central axis, it may be seen to exhibit an essentially square-shaped peripheral profile which is, however, rounded at the corners. Furthermore, it can be noted that the crystal also exhibits more pronounced contrast or scatter of light in the vicinity of its apparently rounded corners than is evident elsewhere along its periphery. These two features are characteristic of all the crystals formed at 80 °C when they are viewed along their central axis. They bear revealingly on the nature of the as-grown curved shape of these crystals. In order to discuss their significance in this respect more comprehensibly however, it is necessary first to consider the morphology of the crystals as observed under the electron microscope.

Figure 11. — Note their crescent-like profiles. Phase contrast, × 900.

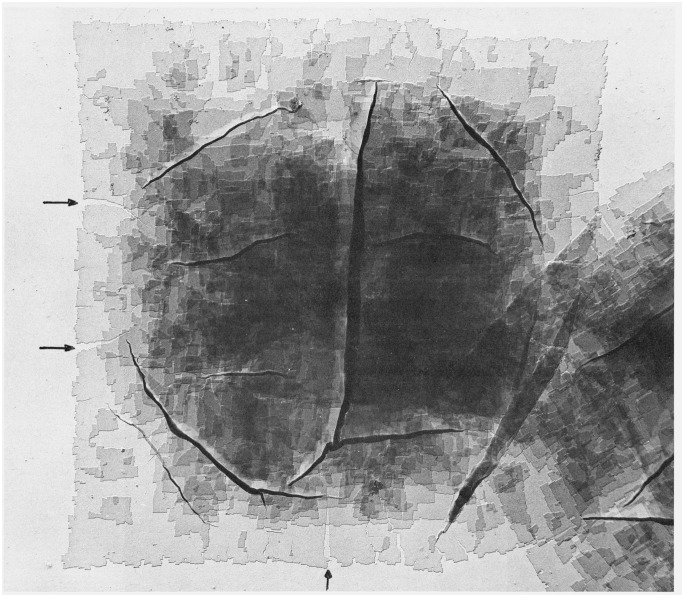
Electron micrographs of two representative crystals formed on cooling the polymer solutions to 80 °C are shown in figures 13–14. As may be seen in these two figures the crystals formed under these conditions are characteristically multilayered, the sides of their basal lamella being about 20 μm to 25 μm. A selected area electron diffraction pattern obtained from a portion of such a crystal is shown in figure 15a, the corresponding selected region in the crystal is shown in figure 15b. The disposition in electron diffraction patterns obtained from such crystals of the 200 reflections relative to the crystals clearly indicates that the lamellae are bounded laterally by {100} growth ‘faces’; however, as is the case in the larger curved crystals formed at 90 °C, these faces are pronouncedly microfaceted as may be discerned in figures 13–14, and in more detail at higher magnification in figure 16 in which pronounced reentrant steps are evident at the edges of the basal lamella in such a crystal; in short the microfacets are {100}. In addition, shadowing the crystals with metal reveals, as was the case in the large curved crystals formed at 90 °C, faintly discernible ridges at the surface of the lamellae. Although some such ridges can be traced from leading corners formed by adjacent {100} microfacets at the periphery of the lamellae, inwards along paths at 45° to the lamella edges, they are very often discontinuous, badly defined and cannot be traced to a particular peripheral corner, in addition to the fact that they often deviate from the 45° orientation relative to the sides of the lamellae (some more evident ridges are pointed out in figure 16). There is no question however from the distinctly microfaceted character of the periphery of the lamellae in these crystals that their constituent curved lamellae are multisectored.

Figure 13. — Arrows point to cracks incurred in the basal lamella upon sedimentation and drying on the substrate. It can also be seen that the crystal has undergone pronounced pleating and buckling upon sedimentation. Pt/Pd shadowed, × 5900.

Figure 16. — Arrows point to faint ridges on the surface of the lamella. Pt/Pd shadowed, × 13900.

These curved crystals undergo deformations of a pronounced character when they collapse upon drying on a substrate. Thus, cracks are frequently observed in the peripheral regions of the basal lamella in collapsed crystals, as may be seen in figures 13–14. These cracks generally extend from the periphery inwards roughly at right angles to the sides of the basal lamella; furthermore, as would be expected from this manner of deformation which involves “cleaving” across some fold-domains in the lamella in which the chain molecules are folded along planes at right angles to the cleavage direction, the cracks are characteristically traversed by fine fibrils which extend between the adjoining undeformed portions of the lamella. This latter feature is readily discernible at high magnifications as shown in figure 17. The cracks and associated fibrillation which occur upon sedimentation in the evidently non-planar basal lamella are no doubt a consequence of its tendency to spread out upon the substrate as it collapses during drying. The crystals also undergo pronounced pleating and folding when they collapse upon the substrate. The pronouncedly pleated and folded portions of the crystals shown in figures 13–14 may be clearly discerned as somewhat narrow extended regions which exhibit substantial opacity to the incident electron beam. While the disposition of such pleating and folding varied somewhat from one crystal to another, particularly in the central portions of the crystals, opaque regions corresponding to such deformations were always observed which “subtended” the four apices of the basal lamella. Such regions, oriented at ~ 45° to the sides of the basal lamella are evident in the crystals shown in figures 13–14.

In addition to undergoing the deformations described in the previous paragraph, several sedimented crystals were observed which exhibited yet another type of deformation in that the apical (corner) portions of the basal lamella were doubled back onto (or tucked under) the collapsed interior of the crystals, as may be seen at (A), (B), and (C) in the crystal shown in figure 18, in which three of the corners of the basal lamella have folded back inwards and collapsed part way towards the central axis. The fourth corner (D). whose right angled character is evident, did not fold back completely in this instance; that it tended to do so is evidenced however by the manner in which the crystal is pleated back and forth at (E). It is of interest to note that those portions of the outline of this collapsed crystal, which subtend the folded apical regions of the basal lamella, i.e., at (A), (B), and (C) are rounded in character. This latter feature which is clearly consistent with the fact that the crystal, as grown, has a curved conformation, was characteristically observed in all instances in which the corners of the basal lamella had folded backwards during the process of sedimentation and drying. The very fact that the corners of the basal lamella do occasionally fold over also has a bearing on the conformation of these curved crystals. Its relevance in this latter respect is examined, in conjunction with other features described in the foregoing paragraphs, in the ensuing further discussion of the conformational characteristics of the crystals.

Having established that the crystals are curved, that they are multilayered, and that their constituent chain-folded lamellae, which are bounded laterally by {100} growth faces, are multisectored and collapse readily when the crystals are sedimented upon a substrate, we turn at this stage to the consideration of an aspect of the shape of the crystals which has not been specifically discussed so far, namely, the nature of the as-grown conformation of the periphery of their leading basal lamella whose lateral edges define the rim of these distinctly dished objects. It has been clearly shown that the basal lamella is bounded laterally by {100} faces and that the four apices (corners) of that lamella are right-angled and not rounded, as may be seen for example in figures 13–14 and figure 16. It has also been pointed out previously, however, with reference to figure 12b, that when one views one of these crystals in the uncollapsed state along its central axis, it exhibits a profile corresponding to a square which is rounded at the corners. On the basis of this latter feature, and since it is evident that the periphery of the basal lamella is not rounded at the corners, it can be readily concluded with reference to figure 19, that the apical portions of the basal lamella in the crystals as-grown must be appreciably upturned as shown schematically in figure 19c, and that, as is also illustrated in the same diagram, the sides of that lamella must be bowed with respect to the plane of reference (FG) (see fig. 19a) which is tangential to the surface of the crystal at its ‘pole’ (H). In other words, both the inclination of the basal lamella and hence the vertical displacement of its periphery with respect to the plane of reference FG are maximal at the four corners of the lamella and least pronounced at the midpoints along its lateral edges. The model shown in figure 19c is further substantiated by yet another feature which has also been pointed out earlier with reference to the phase contrast optical micrograph shown in figure 12b, namely, that in addition to appearing rounded at the corners, the crystals, when viewed in the uncollapsed state along their central axis, exhibit more pronounced contrast, and hence greater effective thickness with respect to the direction of observation, in the vicinity of their apparently rounded corners than elsewhere along their four-fold symmetrical outline. Such an effect is implicit in the model shown in figure 19c on the basis of which one would also anticipate that the apical portions of the basal lamella would exhibit a tendency to fold backwards when the crystal is sedimented and dried. The occasional folding of the basal lamella in the latter manner has been pointed out above, and while this feature, which has also been previously observed by Frank, Keller, and O’Connor [2] and Woodward [11] in some sedimented crystals of P4MP. is not conclusive in itself, it is, to say the least, consistent with the model shown in figure 19c.

Further substantiation that the apical portions of the crystals which are yielded on cooling the polymer solutions to 80 °C are preferentially ‘curled,’ in accordance with figure 19c, and ‘head’ the remainder of the crystal in its propagation in a curved fashion relative to the plane of reference (FG) (fig. 19a), is provided by the manifestation of this feature in an unequivocally detectable and more dramatic fashion in crystals formed at lower temperatures, as will be seen in the ensuing section.

It may finally be noted that the thickness of the lamellae in the crystals formed at 80 °C as determined from a low angle x-ray diffraction pattern obtained from a mat of such crystals with the plane of the mat parallel to the x-ray beam was found to be 124 A.

3.4. Crystals Formed at Temperatures Below 80 C

The species of crystals described in this subsection were formed when polymer solutions initially held at 140 °C were subsequently transferred to baths maintained at 70 and 50 °C. Crystallization is extremely rapid at these temperatures, the onset of cloudiness was observed to occur (at ~ 70–75 °C) before thermal equilibrium was attained. It may be pointed out from the outset that the crystals yielded in these preparations exhibited shapes which were similar to one another but that their sizes differed depending on thermal history. Thus, the solutions cooled to 70 °C yielded the largest, and those cooled to 50° yielded the smallest crystals.

An example is shown in figure 20 of several randomly oriented crystals formed on cooling a solution to 70 °C. This phase contrast micrograph depicts the crystals as seen while in suspension in liquid. They are hollow fishbowl-like objects which collapse very readily when they are allowed to sediment and dry on a substrate. When they are examined (in the collapsed state) in transmission in the electron microscope, they exhibit, due to the thickness of their wall, an overall opacity to the electron beam which frustrates the examination of their fine structure directly. Replicas of collapsed crystals prepared by the shadow transfer technique described earlier (section 2.2c) revealed, not unexpectedly, that they possess a lamellar morphology, their curved wall being constituted of numerous superimposed chain-folded lamellae. A replica of a collapsed crystal is shown in figure 21 in which the layered (lamellar) morphology of the crystal can be seen. Such replicas also reveal that the sides of the constituent lamellae in these crystals are profusely microfaceted, indicating that the lamellae are multisectored. No sector delineating ridges are observed however. As may also be seen in figure 21, adjacent microfacets are orthogonal to one another, in short it may be readily surmised that these lateral growth facets are {100} as is the case in the crystals formed at higher temperatures. Bearing in mind the lamellar texture of these crystals we now turn to a more detailed description and analysis of their overall shape.

Figure 21. — Arrow points to region in which the lamellar character of the wall is evident as is the microfaceted character of the edges of the lamellae, × 11,000.

Three differently oriented crystals which are representative of the type formed on cooling the polymer solutions to 70 °C are shown in figure 22. Figure 22a represents the characteristic appearance exhibited by these bowl-like objects when they are viewed, while in suspension in liquid, flat-on, i.e., along their central axis (in this instance the central axis of the crystal is actually slightly inclined to the direction of observation). In this perspective the crystals exhibit a circular outline whose diameter is 12 μm to 15 μm. One may also readily detect within the outline of the crystal shown in figure 22a the characteristic tetracuspid profile exhibited by its rim (i.e., the open end of the bowl) in this perspective. This feature indicates quite clearly that these crystals develop in a coherent four-fold symmetrical fashion about their central axis. A side (edge-on) view of a crystal similar to that shown in figure 22a may be seen in the lower part of figure 22b, and a crystal whose orientation with respect to the direction of viewing lies between the flat-on and edge-on extremes may be seen in the upper part of figure 22b.

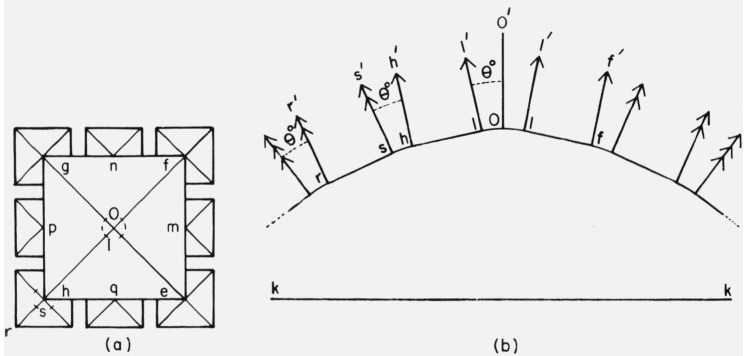
For the sake of clarity in discussing further the conformational characteristics of these bowl-like crystals and attempting to characterize their habit in crystallographic terms, the edge-on and flat-on perspectives of these hollow bowl-shaped crystals are reproduced schematically in figure 23a and figure 23b. respectively, in which (J) represents the pole of the crystal, (KL) is a plane of reference which is tangential to the surface of the crystal at (J), and (M_1–4) denote the symmetrically disposed leading extremities of the rim of the crystal which lie along four equispaced “longitudes” of preferential development (JM_1–4). Consideration of the crystals shown in figure 22 and schematically in figure 23 indicates that on progressing from J along the surface of the crystal to any of the extremities M, the orientation of the surface of the lamellar envelope of which these objects are constituted changes progressively through 180° or more with respect to the plane (KL), whereas at intermediate “longitudes” (JN) along which growth is seemingly slowest, the change in orientation tapers to about 90°.

Figure 23. — (KL) is a plane tangential to the outer surface of the crystal at its pole (J). (M_1–4) are the four symmetrically disposed leading extremities of the curved lamellar wall. (N) denotes positions along the rim of the crystal which are intermediate between the leading extremities (M).

This four-fold symmetrical disparity in the growth and curling of the lamellar envelope along the (JM) relative to the (JN) longitudes provides a basis for characterizing the habit of these crystals more specifically, namely, in terms of the orientation of the unit cell at their pole (J) relative to the disposition of the (JM) and (JN) longitudes. This relationship may be deduced from a consideration of the conformational characteristics of the crystals formed at 80 °C coupled with the reasonable expectation that under the conditions of higher undercooling which govern the development of crystals from solutions cooled at 70°C, growth will tend to occur (in dendritic fashion) preferentially at the corners of an initially formed lamellar precursor crystal bounded laterally by {100} faces. Briefly, it may be readily surmised, as shown schematically in figure 24 (and with reference to figure 23). that at the pole (J) the (JM) longitudes coincide with 〈110〉 whereas the (JN) longitudes coincide with 〈100〉 and that [001] (i.e. the c axis of the unit cell) is normal to the surface of the crystal throughout as shown in figure 24a. The orientation of the tetragonal unit cell at the pole (J) relative to the crystal as it is viewed along its central axis of four-fold symmetry is outlined in figure 24b.

Confirmation of the crystallographic assignment depicted in figure 24 from which it is evident that growth along each of the (JM) longitudes involves an 180° (or more) change in orientation of the stems of the folded molecules (c axis) in the lamellar envelope relative to the plane (KL), was obtained from crystals grown on cooling polymer solutions to 50 °C. As pointed out earlier, these crystals were smaller than those formed on cooling to 70 °C but possessed similar shapes and, more pertinently, had a wall consisting of fewer superimposed lamellae thus permitting their direct examination in transmission in the electron microscope.

A general view including numerous randomly oriented crystals (suspended in liquid) which were formed on transferring a 0.1 percent solution initially held at 140 °C to a bath at 50 °C is shown in figure 25 in which the variation in the sizes of the crystal formed is evident. Their diameter when viewed along their central axis of four-fold symmetry was between 5 μm −10 μm. Figure 26 is an electron micrograph showing several such crystals after they had collapsed on a carbon substrate. The similarity in shape between these smaller and thinner walled crystals and those formed on cooling the solutions to 70 °C is revealed in the crystals (P), (Q), and (R) which evidently initially impinged upon the substrate with their central axis of four-fold symmetry oriented by chance at right angles to the carbon film and subsequently collapsed upon the film on drying in an essentially uniform fashion corresponding to a mere flattening about their central axis. The circular outline of these collapsed crystals may be clearly seen in figure 26, as can the inner essentially tetracuspid-shaped boundary between the less transparent outer portions (where the lamellar envelope is doubled on itself) and the more transparent central (polar) portion of the flattened lamellar envelope. This boundary delineates in effect the projected outline of the rim of these crystals upon the substrate prior to collapse, allowance being made for some distortion about the central axis as the crystal flattens. The similarity between these crystals and those yielded by the 70° preparation is further demonstrated in figure 27 in which a large and a smaller crystal (suspended in liquid) from the 50 °C preparation, are shown which are respectively oriented with their central axis normal and parallel to the field of view. The tetracuspid profile of the rim of the appropriately oriented former crystal is discernible, but faintly so due to the relatively thinner nature of the wall of the crystal, as compared to those formed on cooling to 70 °C.

Figure 25. — The crystals are in suspension in liquid. Phase contrast, × 1000.

Figure 26. — (P), (Q) and (R) denote crystals which have collapsed relatively uniformly about their central axis upon drying. Unshadowed, × 3900.

Figure 27. — The crystals are in suspension in liquid. The larger one is seen in flat-on perspective and the smaller one in edge-on perspective. Phase contrast, × 1400.

Having demonstrated the similarity in the shape of the crystals formed on cooling the polymer solutions to 70 and 50 °C, we turn to a consideration of the electron diffraction characteristics exhibited by crystals yielded in the latter instance when these crystals have collapsed about their central axis in the essentially uniform fashion exhibited by crystals (P), (Q), and (R) in figure 26. Such a crystal is shown in figure 28b, the corresponding diffraction pattern (electron beam normal to the field of view) is shown in figure 28a. The disposition of the 200 and the 220 reflections in figure 28a relative to the tetracuspid profile formed by the folded over portions in the flattened crystal clearly confirms the relationship indicated in figure 24 between the lattice orientation at the pole of these bowl-like objects relative to their overall four-fold symmetrical shape. In addition, the diffraction pattern is consistent with the observed preferred orientation of the {100} microfacets in the lamellar terraces in the central protion of the crystal, as indicated by the cross in the right-hand side of figure 28b.

The {100} microfaceted (and hence multisectored) character of the constituent lamellae in the crystals formed at 50 °C can be seen in the crystal shown in figure 29 which tended to tear outwards upon collapsing thus revealing (see arrow) a portion of its periphery (rim). No sector delineating ridges were observed even at high magnifications in the constituent terraces of the crystals grown in the 50 °C preparations.

Figure 29. — The crystal tended to tear outwards upon collapsing on the substrate revealing a portion of its periphery (see arrow). Pt/Pd shadowed, × 10000.

Finally, it may be noted that the thickness of the lamellae in the crystals formed on cooling the polymer solutions to 50 °C as determined from a low angle x-ray diffraction pattern obtained from a mat of such crystals with the x-ray beam parallel to the plane of the mat was found to be 121 Å.

3.5. Further Comments on, and Summary of, the Main Characteristics of the P4MP Crystals Described in Sections 3.2 to 3.4

The purpose of this section is to summarize the main features of the experimental observations reported in sections 3.2 to 3.4 as a preliminary to the considerations and conjectures pertaining to the origins and “mechanism of development” of curved crystals of P4MP which are discussed in section 4. In addition we shall comment further herein on the formation of both planar four-sectored and perceptibly curved multisectored lamellar crystals at 90 °C.

In considering the influence of crystallization conditions on the habits of P4MP crystals, it may be noted from the outset that, with the exception of those smaller crystals formed at 90 °C whose constituent lamellae are essentially planar and four-sectored, the larger crystals formed at 90 °C (e.g. figures 6–10) as well as those formed at lower temperatures exhibit under the optical microscope distinctly detectable curved shapes; furthermore, the constituent lamellae in these distinctly curved crystals are multisectored.

A consideration of ssections 3.2 to 3.4 also reveals that the lower the crystallization temperature the more pronouncedly curved are the crystals yielded in suspension in solvent. It is also evident that all the distinctly curved multisectored lamellar crystals are multilayered (i.e., they consist of two or more superimposed chain folded layers) and exhibit four-fold symmetrical shapes which are specifically related to one another. Thus, for example, the hollow bowl-shaped crystals formed on cooling the polymer solutions to 50 °C (figs. 25–29) are simply miniature versions (with respect to overall shape) of those formed on cooling the polymer solutions to 70 °C (figs. 20–22). The radius of these bowls as measured at right angles to their central axis of four-fold symmetry provides a rough measure of the curvature of their lamellar wall. The radii of the hollow bowls formed on cooling the polymer solutions to 50 and 70 °C were found to be between 2.5 μm and 5 μm, and between 6 μm to 7.5 μm, respectively.⁴ In considering the lamellar crystals formed at temperatures above 70 °C, it may be readily visualized that had the curved crystals formed at 80 °C (figs. 11–19) and the large (multisectored) species of curved crystals formed at 90 °C (figs. 6–10) not stopped growing due to the depletion of polymer from the mother liquor, they would have developed further and would have eventually curled back toward their central axis of four-fold symmetry with the corners of the basal lamella leading the way, so to speak, as shown in figure 19 (it may be reasonably assumed that this latter feature is also manifested in the large curved crystals formed at 90 °C but is not readily detectable due to the less pronounced curvature of these crystals). It may be roughly estimated from their respective edge-on profiles, that if the curved multisectored lamellar crystals formed at 80 and 90 °C had indeed continued to grow as envisaged above the radius of the resulting bowl-shaped objects measured at right angles to their central axis of four-fold symmetry would be about 15 μm and about 30–40 μm, respectively.

While it is evident from the foregoing that lower crystallization temperatures, which favor more rapid lateral growth of chain folded polymer lamellae, lead to the formation of more pronouncedly curved crystals of P4MP, it should be noted that crystallization at 90 °C yielded a mixed population of crystals among which two types were readily distinguishable, namely, the smaller essentially planar crystals whose constituent lamellae are four-sectored, and the largest perceptibly curved ones whose constituent lamellae are multisectored. While both these types of crystals are less pronouncedly curved than those formed at lower temperatures, and thus conform with the overall trend to more pronounced curvature the lower the crystallization temperature, the formation of these differing crystals in the same preparation at 90 °C prompts further comment. Noting that these preparations were filtered at the temperature of crystallization (see section 2.1) it is significant that it is the smallest crystals (basal lamella up to about 20 μm on a side), and hence those formed during the more advanced stages of depletion of polymer from the mother liquor, which are essentially planar and whose constituent lamellae are four-sectored, whereas the largest members of the population (basal lamella ~ 40 μm to 45 μm on a side) whose constituent lamellae are multisectored are perceptibly curved. The difference between the fine structures of the smaller crystals (four-sectored) and the larger crystals (multisectored) may be attributed to a combination of two factors, namely, the continuous depletion of polymer from the mother liquor as well as to fractionation [16], the latter factor leading progressively to a continuing decrease in the molecular weight of the polymer still in solution during the process of crystallization. Both of these factors would be expected to lead to a progressive decrease in the rate of lateral propagation of developing chain folded lamellae over the duration of their growth. In short, the average rate of lateral growth of the initially formed multisectored basal lamella in the largest perceptibly curved crystals formed at 90 °C would be expected to be greater than that of the four-sectored lamellae in the smaller essentially planar crystals. This is substantiated by the nature of the respective fine structures of the lamellae in the larger and smaller crystals. It is common experience that conditions which favor more rapid lateral growth rates in chain-folded polymer lamellae lead to multisectoring. That this is the case is certainly born out by the fact that the constituent lamellae in the P4MP crystals formed at lower temperatures than 90 °C are all multisectored. While one may thus reasonably attribute the fact that the constituent lamellae in the smallest crystals formed at 90 °C are four-sectored to their propagation laterally at slower overall growth rates as compared to the larger crystals, it is evident that the continuously changing rate of lateral growth of both the large and small crystals must be the same and diminish coincidentally in both types during the period corresponding to the development of the smaller crystals which propagate in a four-sectored fashion. Since it is evident that the outer regions of the basal lamella in the larger crystals are multisectored, we must conclude that notwithstanding the slower growth conditions under which these regions must have developed, the ambient conditions were not sufficient to lead progressively to a total “smoothing out” of their {100} growth faces and thus to overcoming of the earlier multisectored manner of propagation of these lamellae.

After the work described in sections 3.1 to 3.4 had been completed Blundell Keller and Kovacs [15] have described a “self-seeding” technique for growing polyethylene crystals from solution which yielded crystals of uniform size. Using a similar technique we were able to obtain a uniform population of four-sectored lamellar crystals of P4MP at 90 °C. The preparation details are given in section 2.1 we shall therefore only mention here that the final step in the procedure involved taking a 0.1 percent solution of P4MP held at 130 °C and immersing it in a bath at 90 °C. Four-sectored chain-folded monolayers as well as crystals consisting of more than one four-sectored chain-folded layer were formed. The monolayers and the basal lamella in the multilayered crystals were similar in size (~ 10 μm on a side). Evidently all the crystals had started to grow simultaneously from predetermined nuclei, presumably residual crystal nuclei which had not been dissolved at 130 °C. A corner portion of a crystal formed under these conditions is shown in figure 30 in which a diagonally oriented domain delineating ridge and the essentially smooth character of the lateral edges of the lamella can be seen. An electron micrograph depicting a distinct crack near the periphery of a crystal formed in this preparation is shown in figure 31. As would be expected from the four-sectored character of the crystal, that portion (unbarbed arrow) of the crack which runs parallel to the crystal edge is not traversed by fibrils, whereas fibrils can be seen in the short portion of the crack which runs at an angle to the edge (barbed arrow). The crystals formed in this self-seeded preparation exhibited, not unexpectedly, no detectable curvature when viewed edge-on in suspension in liquid in the optical microscope. The fact that by the time crystallization was essentially completed the crystals formed at 90 °C in this self-seeded preparation were considerably smaller than those formed in the unseeded preparation at the same temperature may be attributed to the large number of heterogeneous nuclei available for growth, the net effect of which nuclei is to lead to a more rapid rate of depletion of the polymer in solution and hence to a slower average rate of lateral propagation of the crystals under these circumstances as compared to that which prevails during the earlier stages of propagation of the considerably larger multisectored crystals formed in the unseeded preparation at the same temperature. This would account for the fact that all the crystals yielded in the self-seeded preparation are four-sectored. We have not pursued this matter further. It suffices for our present purposes to note that our accounting earlier of the presence of both four-sectored and multisectored crystals in unseeded preparations crystallized at 90 °C in terms of different rates of lateral propagation prevailing during their formation is plausible in the light of the differences we have observed between unseeded and seeded preparations. As a further check of the observation derived from the unseeded preparations crystallized between 90 and 50 °C that lower crystallization temperatures lead to the formation of curved P4MP crystals from solution, a self-seeded 0.1 percent solution (see sec. 2.1) was prepared using the same procedure as that used in the self-seeded preparation crystallized at 90 °C which was mentioned above, it was however transferred from a bath at 130 °C to one held at 50 °C. Under those conditions the population of crystals was indistinguishable from that obtained on cooling unseeded solutions to 50 °C and consisted of hollow bowl-like crystals whose constituent lamellae were multisectored. The radius of individual bowls as measured at right angles to their central axis of four-fold symmetry was in the range 2.5 μm to 5 μm.

Figure 30. — Arrow points to diagonal ridge which delineates domain boundary. Pt/Pd shadowed, × 12000.

Figure 31. — Unharhed arrow points to a portion of a crack which runs parallel to the edge of the crystal. No fibrils traverse this portion of the crack. Barbed arrow points to fibrils in the portion of the crack which is not parallel to the edge of the crystal. Gold decorated, × 31000.

4. On the Origins and Mechanism of Formation of Curved Crystals of P4MP

4.1. Summary of, and Comments on, Previous Observations on Four-Sectored Lamellar Crystals of P4MP

Before attempting to discuss why it is as has been illustrated in sections 3.2–3.5 that lamellar crystals of P4MP formed between 90 and 50 °C from 0.1 percent solutions of the polymer in an equivolume mixture of xylene and amyl acetate are all the more pronouncedly curved the lower the temperature at which they are formed, it is relevant to first dwell on the nature of the as-grown shape of four-sectored lamellar crystals of P4MP which in our experience are formed from solution at low supercooling, i.e., under conditions which favor slower lateral propagation of the lamellae. As pointed out in section 3.2, these crystals exhibit an essentially linear profile when they are viewed edge-on while in suspension in liquid; it bears reiterating here that they are however not perfectly flat, as has been previously pointed out by Bassett et al. [9, 10], although their departure from planarity is relatively minimal and escapes detection under the optical microscope. The deduction due to Bassett et al. [9, 10], that four-sectored lamellae are not perfectly planar stems from the diffraction contrast characteristics exhibited by these crystals in dark-field electron micrographs formed by imaging the {200} planes. A dark-field electron micrograph of a four-sectored monolayer crystal formed at 90 °C (this particular crystal was grown in the self-seeded preparation mentioned in section 3.5) is shown in figure 32a. For the sake of clarity a schematic representation of such a crystal is shown in figure 32b in which the four constituent sectors are identified. The {200} planes which are imaged in the dark-field electron micrograph shown in figure 32a are those which run vertically in the field of view as indicated by the arrow in the top right-hand corner of the micrograph. The four-sectored character of the crystal is clearly revealed in this dark-field image, in which it may be readily seen that the upper and lower sectors or fold-domains (S₁, S₂ fig. 32b) in which the {200} planes which are being imaged are not fold planes are darker than the other two sectors (S₃, S₄ fig. 32b) in which the {200} planes which are being imaged are fold planes. In addition, darker non-diffracting streaks which traverse sectors (S₁, S₂) at right angles to the corresponding outer edges which subtend these sectors may be readily seen. This systematic difference in contrast between those sectors in which the {200} planes which are being imaged are not fold planes, and those sectors in which the corresponding planes are fold planes is a characteristic feature exhibited by four-sectored lamellae which was first observed by Bassett et al. [9, 10]. If the {200} planes which run horizontally in figure 32a had been imaged, sectors (S₃, S₄) would have appeared darker than sectors (S₁, S₂) and furthermore non-diffracting streaks would have been observed in (S3, S4), these streaks being oriented at right angles to the outer edges of the crystal which subtend the S₃ and S₄ sectors. Clearly, if these four-sectored lamellae were perfectly flat as-grown, the molecular stems in their four-constituent domains would be expected to be parallel to one another throughout the lamellae and oriented at right angles to the plane of the lamellae, consequently no difference in contrast between the constituent sectors should be observed in dark field images and the appearance (contrast) of the lamellae in {200} dark-field images should be uniform throughout. The observed diffraction contrast characteristics described above however indicate, according to Bassett et al. [9, 10], that in the four-sectored crystals, sedimented upon a flat substrate, the molecular stems in the crystals are not perfectly parallel to one another throughout but rather that the stems in each sector are slightly tilted about an axis normal to the corresponding {100} face which subtends that sector, i.e., about an axis which is parallel to the {200} planes which are not fold planes in each sector. The extent of this tilt within each sector in the sedimented crystal is not uniform as evidenced by the darker non-diffracting streaks observed in dark-field images in the darker sectors (S₁, S₂ fig. 32a) in which the {200} planes which are imaged are not fold planes.

The evidence summarized above has been interpreted by Bassett el al. [9, 10], as indicating that the crystals as grown are not perfectly planar, the tilt of the molecules in each sector about an axis perpendicular to the corresponding {100} growth face suggesting that the lamellae as grown possess a slight “conicalness.” Before dwelling on this latter aspect further it is necessary first to consider another feature of four-sectored lamellae which bears on the possible origin of their nonplanar character. An analysis due to Bassett [9] of dark field Moiré patterns exhibited by bilayer crystals of P4MP in which the two superimposed chain-folded layers are four-sectored and slightly rotated relative to one another about an axis normal to the plane of the lamellae has indicated that there is a very small fractional difference of ~ 10⁻³ in the spacing between those {200} planes in each sector which are fold planes and those which are not. For the sake of brevity in what ensues these planes will henceforth be referred to as {200}_f and {200}_nf planes respectively (f = fold, nf = non-fold). In short, the idealized tetragonal subcell in each sector is slightly distorted. This feature has been attributed to the asymmetric bulkiness of the chain folds by Bassett et al. [9, 10], who have suggested that the nonplanar character of four-sectored lamellae of P4MP is due to buckling consequent to the inherent distortion of the subcell in their constituent domains resulting from the bulkiness of the chain folds. It is not unreasonable to presume that stresses which arise within the lattice, particularly at the sector boundaries where the mismatch in spacing between the {200}_f planes in one sector and the {200}_nf planes in adjoining ones must be accommodated, as well as stresses at the fold surfaces [17], cause an overall slight buckling of the lamella. If one proceeds on the assumption that d_{200}f > d_{200}nf then on the basis of the magnitude of the difference of ~ 0.1 percent between the spacings it may be roughly estimated, geometrically, that the buckled lamella, as grown, is slightly conical in character and has an angle of elevation which is probably not greater than ~ 2°. This estimate is arrived at as follows: Imagine an idealized flat four-sectored crystal in which d_{200}f = d_{200}nf as shown in figure 33. It may be readily calculated that if a fractional difference of ~ 10⁻³ is applied to each sector such that d_{200}f > d_{200}nf then this would lead to an angular deficit of ~ 3′ between adjacent sectors and hence to a total angular deficit of 12′ on circumnavigating the lamella [9, 10], as shown in exaggerated form in figure 33 (full lines). A reconstruction of the lamella from these distorted sectors such that there be continuity between sectors at the center 0 as well as across sector boundaries, may be accomplished by simultaneously lifting the sectors out of the plane of the diagram at (0) where they are initially in contact. However, if the elevated sectors are kept flat, there would result in view of their thickness a V-shaped groove along the boundaries between the sectors. This feature may be overcome by bending or buckling the individual sectors so that contact between adjacent sectors is made throughout their thickness, hence the conicalness of the lamella. By the same token it may be visualized that the lamella is rounded at the apex (0) so that continuity is maintained between the sectors at (0) as shown in figure 34 which represents schematically a central cross-sectional view of two opposite sectors in the lamella. The angle of inclination θ° of such a quasi-conical lamella may be estimated to be ~ 2° [12, 13]. It is envisaged that the molecular stems are oriented normal to the surface of the lamella throughout. Upon sedimentation and drying on a substrate such a crystal would tend to flatten and spread on the substrate and it is in that state that it exhibits the faint diagonal fold-domain boundary delineating ridges mentioned previously and the {200} dark field diffraction contrast characteristics which have been pointed out above with reference to figure 32.

The considerations which have been advanced above concerning the nonplanar character of four-sectored lamellae are based on the assumption that in each sector d_{200}f > d_{200}nf. One cannot however distinguish from Moiré patterns which of these spacings is the larger. In short the possibility cannot be discounted that d_{200} < d_{200}nf. If the latter were indeed the case, then it can be seen that the application of a corresponding fractional difference of ~ 10⁻³ between these spacings to an idealized four-sectored lamella (d_{200}f = d_{200}nf) results in a total angular excess of 12′ between sectors in which case on the basis of admittedly simplified model building (from paper sectors) it can be envisaged that the lamella would be buckled, but rather than being quasi-conical it could conceivably adopt a four-fold symmetrical wavy or corrugated conformation such as shown in perspective in figure 35 in which the molecular stems are also envisaged as being normal to the surface of the lamella throughout. Alternatively, the lamella could adopt a somewhat distorted but yet essentially conical shape.

In short, then, while there is no question that four-sectored lamellae are not perfectly planar but are instead slightly buckled there is some uncertainty about their exact as-grown shape. The fact that one observes sector boundary delineating ridges in sedimented crystals can be accounted for as resulting from a tendency of each sector to spread in a direction parallel to the corresponding growth face when the crystal collapses as shown by the arrows in figure 36. This can be expected to occur both whether the crystal has a slight conicalness or whether it has a four-fold symmetrical wavy conformation such as shown in figure 35. The question then is: can one differentiate between the two cases on the basis of the dark field diffraction contrast images? These clearly indicate that whereas in the collapsed state the {200}_f planes in each sector satisfy most closely the Bragg condition for diffraction the {200}_nf planes in each sector deviate from that condition and are tilted relative to that condition about an axis perpendicular to the corresponding {100} edges. While the extent of this tilting is not uniform it is significant as may be noted in figure 32 that all regions in sectors S₁ and S₂ in which the {200} planes which contribute to the image are not fold planes are consistently darker than sectors S₃S₄. This feature can be viewed as favoring conicalness in the crystals as grown, as opposed to the model shown in figure 35, the argument being that in the latter case one would expect to see some strongly diffracting streaks in sectors S₁ and S₂ comparable in intensity to that of sectors S₃ and S₄. The absence of such streaks while favoring conicalness is not unequivocal proof of this feature as opposed to the model shown in figure 35 nor can it be taken as definitely establishing that d{200}_f > d{200}_nf since the possibility cannot be ruled out that the lamella could also adopt a conical-like shape if d{200}_f < d{200}_nf.

Having pointed out that some uncertainty exists concerning the exact as-grown shape of four-sectored lamellae which are no doubt buckled we shall nonetheless proceed in what follows with a discussion of the variation of the curvature of multisectored lamellar crystals of P4MP with crystallization temperature based on the assumption that four-sectored lamellae possess a very slight conicalness.

4.2. Preliminary Considerations and Outline of Discussion on the Origins of the Dependence of the Curvature of P4MP Crystals on Temperature of Crystallization

The factors summarized above concerning four-sectored crystals provide a basis, or at any rate a starting point, for considerations pertaining to why it is, as has been described in sections 3.2–3.5, that P4MP crystals are all the more pronouncedly curved the lower the temperature at which they are formed. Interestingly, the constituent lamellae in all the P4MP crystals which are distinctly curved, such as the larger crystals formed at 90 °C (unseeded preparation, figs. 6–10)), as well as all those crystals formed at lower temperatures, are not four-sectored but are multisectored. The multisectored lamellae in these crystals have one feature in particular in common with four-sectored lamellae, namely, the chain molecules in their constituent sectors or fold domains are also folded along {200} planes. It is consequently not unreasonable to consider, first, that as is apparently the case in four-sectored lamellae, interfold interactions leading to a distortion (d_{200}f ≠ d_{200}nf) of the subcell in each fold domain also occur in the multisectored lamellae in the curved crystals formed in the range 90 to 50 °C,⁵ and second, that this feature induces each component domain in these lamellae to buckle under the influence of stresses resulting from the accommodation across domain boundaries of the respective subcell distortions in adjoining domains, as well as due to stresses at the fold surfaces. On the basis of these two premises, a multisectored lamella may be visualized as a mosaic structure whose building blocks, i.e., its constituent fold domains, are inherently slightly curved or buckled due to the bulkiness of the chain folds, and contribute incrementally to the overall curvature of the lamella. Accepting in principle that the overall curvature of a multisectored lamella is a cumulative consequence of the inherent nonplanar character of its constituent fold domains, one is still left with the problem of explaining the fact that the lower the crystallization temperature the more pronouncedly curved are the multisectored lamellar crystals of P4MP formed in suspension in solvent. We shall advance in what ensues a simple working hypothesis or model on the basis of which the observed trend in the dependence of the curvature of the P4MP crystals on supercooling is explained qualitatively in terms of the combined influence of two factors. These factors are: the inherent buckling of fold domains caused by the bulkiness of the chain folds, and the average lateral size of the fold domains in the multisectored lamellae which is governed by the supercooling dependent development of new fold domains at the periphery of a developing lamella throughout its growth. For the sake of simplicity in the exposition of the conjectures upon which this hypothesis is based we will initially discuss the development of a curved multisectored monolayer and proceed from there to the case of curved crystals which consist of two or more superimposed multisectored chain-folded terraces. We will assume that d_{200}f > d_{200}nf in the constituent fold domains of the multisectored lamellae and that the fractional difference between these interplanar spacings is the same (~ 10⁻³) as that found by Bassett [9] in four-sectored lamellae irrespective of the crystallization conditions. This hypothesis and its limitations will then be discussed.

4.3. Hypothetical Model Pertaining to the Origins of Curvature and Its Variation in P4MP Crystals

In keeping with the outline given above we shall first consider the propagation of a single multisectored lamella developing from a four-sectored precursor crystal assuming that d_{200}f > d_{200}nf and that the fractional difference between these spacings, 10⁻³ [9], is the same in both the precursor and the multisectored lamella which evolves therefrom. It is also envisaged as indicated in the earlier discussion of Bassett’s observations that the four-sectored precursor possesses a slight conicalness and has an angle of inclination θ ~ 2°, that it is rounded at the pole, and that the molecular stems are oriented at right angles to the surface throughout this (conically shaped) lamellar precursor. A plan view representing such a precursor crystal is shown schematically in figure 37a (efgh) and a side view depicting the cross-section of the crystal corresponding to a cut along one of its diagonals (fOh in figure 37a) is shown in figure 37b in which (O′O) is the normal to the surface of the lamella at its pole. (O′O) coincides with the axis of four-fold symmetry of the lamella and is also normal to the plane of reference (kk) (figure 37b): The normals to the surface of the lamella at (f) and (h) are (f′f) and (h′h), respectively.

In accordance with the visualization indicated above that the four-sectored precursor is rounded at the pole, it is assumed as shown in figure 37b, that on proceeding from its pole (O) to its periphery following radial paths outwards along the surface, e.g., along the diagonal path (Oh) there occurs within a small distance (O1) where (O1) < < (Oh), a gradual inclination of θ° of the lamella relative to the plane kk and that beyond (1) the inclination of the lamella with respect to (kk) remains essentially constant. In other words, it is assumed that the angle between the surface normals at (O) and (h) is equal to the angle of inclination θ° referred to earlier, and that the normals to the surface of the lamella at (1) and (h) are parallel to one another. The molecular stems are considered to be normal to the lamellar surface throughout.

Bearing the above features attributed to a four-sectored lamella in mind, the formation is imagined (as a consequence of multiple nucleation) of sectored outgrowths centered about the corners (efgh) as well as the midpoints (mnpq) along the sides of such a precursor lamella, as shown in figure 37a. In essence then figure 37a is intended to represent an early stage in the evolution of a multisectored lamella from a four-sectored precursor crystal. As pointed out earlier, we will assume in what follows that d{200}_f > d_{200}nf and that the fractional difference (~ 10⁻³) between these interplanar spacings is independent of the crystallization conditions and is the same both in the fold domains of the precursor four-sectored crystal as well as in the constituent fold domains of the sectored outgrowths which develop therefrom. Accordingly, each tri- or tetra-sectored outgrowth shown in figure 37a may be considered to have a slight “conicalness” akin to that of the central four-sectored precursor. This conicalness is not centered however about the normal to the lamella at the pole (O) but, rather, about the corresponding surface normals at e, f, g, h, and m, n, p, q about which the outgrowths develop. As shown cross-sectionally in figure 37b this latter feature is envisaged to lead to a corresponding increase in the inclination of the peripheral regions of the developing lamella relative to the plane (kk) by an additional increment of θ° (this increment could be as large as 2θ as is the case between opposite sectors in the four-sectored precursor). By analogy with the four-sectored precursor, this additional inclination is depicted in figure 37b as occurring close to the center of initiation of each outgrowth e.g., between (h) and (s) where (hs) is much smaller than (hr). Thus, the total inclination of the developing multisectored lamella relative to the reference plane (kk) on proceeding outwards from (O) to (r) along the surface of the crystal is envisaged in the model depicted in figure 37b to be 2θ°, i.e., an increase of θ° in the inclination of the growing lamella relative to the plane (kk) over that of the four-sectored precursor has resulted from the nucleation and development of the inherently nonplanar sectored outgrowth centered about the precursor’s periphery at (h). The same argument applies to the other sectored outgrowths shown in figure 37a. It may be visualized that the nucleation and development of a new set of sectored outgrowths centered about the corners and sides of the previous ones shown in figure 37a will lead to a further inclination θ° of the lamella relative to the plane (kk) and hence, cumulatively, to a total inclination of 3 θ° of the surface of the lamella (and hence the orientation of the molecular stems) relative to the plane (kk) on proceeding from the pole (O) to the periphery of the newest sectored outgrowth, and so forth.

The thrust of this hypothetical representation of the development of a curved multisectored lamella of P4MP given above is that the evolving lamella grows in a curved fashion as a cumulative consequence of the combined effects of two factors namely, the intrinsic conicalness of about θ° (due to the asymmetric bulkiness of chain folds) of new sectored outgrowths which are generated intermittently at the periphery of the lamella during growth, and the frequency per unit path length from pole to periphery at which the new sectored outgrowths are formed. This latter feature determines according to the model depicted in figure 37b the number of small quasi-discreet inclinations of θ° which occur per unit path length along longitudinal paths traced from the pole of the monolayer to its periphery and thus governs the radius of curvature of the lamella. Conceptually then, for a constant conicalness of θ° in sectored outgrowths one would expect that the smaller the lateral dimensions which sectored outgrowths attain before new outgrowths develop therefrom in a multisectored lamella, the larger will be the number of inclinations of θ° per unit path length from pole to periphery, consequently the average radius of curvature of the lamella will be correspondingly smaller. We shall discuss, qualitatively the matter of sectored outgrowth sizes in curved crystals of P4MP formed at the different temperatures in relation to the curvature of the crystals in due course. Before doing so however it is pertinent to dwell first on two aspects of the multisectored mode of propagation of P4MP lamellae which have been omitted in the exposition of the model given above pertaining to why such lamellae are curved. These aspects have a bearing on this latter feature, and although their influence on the curvature of the lamellae is indeterminate their existence and possible roles in this connection must be raised in association with the hypothetical considerations which were advanced above.

First, it should be borne in mind that the growth of the lamellae in a multisectored fashion involving the intermittent development of new sectored outgrowths at its periphery entails the occurrence of distinct reentrant corners as depicted schematically in figure 38 (this feature is evident in the electron micrographs of the periphery of such lamellae shown in sections 3.2–3.4), as well as the accretion of chain molecules in folded conformation along the {100} facets which subtend such corners. This results in the generation of diagonal fold domain or sector boundaries which terminate at these corners. Such boundaries are depicted in figure 38 (arrows T). One would expect that the same disparity in spacing between the {200}_f and the {200}_nf planes due to the asymmetric bulkiness of the chain folds will occur across such boundaries as has been indicated earlier occurs across the fold domain boundaries which terminate at leading corners in sectored outgrowths. The effect of the accommodation of the disparity in spacing between the {200}_f and {200}_nf planes along fold domain boundaries terminating at reentrant corners on the conicalness (angle θ°) which it has been suggested sectored outgrowths intrinsically tend to adopt, remains indeterminate.

Second we have omitted in the preceding discussion to take into consideration the influence which the lateral impingement of adjoining sectored outgrowths may have on the manner of propagation of a multisectored lamella possessed, according to the conjectures advanced above, of an intrinsic tendency to develop in a cumulatively curved fashion due to the innate conicalness of the sectored outgrowths. In addition to imparting, cumulatively, curvature in a multisectored lamella, it may he envisaged that the intrinsic conicalness of sectored outgrowths causes imperfections in registry (see below) to occur between adjoining sectored outgrowths when they impinge as they propagate laterally, thus giving rise to the question of how these additional imperfections influence in turn the mode of propagation of the lamella. We shall consider and discuss this matter below following a brief indication of the nature of these imperfections.

The impingement of neighboring sectored outgrowths as they propagate laterally at the periphery of a developing multisectored lamella gives rise to the occurrence of 〈100〉 boundaries between impinging domains in the lamella as indicated schematically in figure 38 (boundary denoted U). Because of the inherent conicalness of the sectored outgrowths as well as the resulting cumulatively curved character which this feature imparts to the developing lamella it can be expected that impinging fold-domains belonging to adjoining sectored outgrowths will not always be in crystallographic registry and that slight mis-orientations, as well as disinclinations of the impinging {100} facets relative to one another, will occur. We shall, henceforth, refer to such imperfections as “imperfections in crystallographic registry.” Another likely type of situation which also can be expected to arise is the occurrence, in association with the aforementioned imperfections in crystallographic registry, of differences in height between neighboring sectored outgrowths relative to one another along a direction normal to the surface of the crystal. The consequence of such relative displacements is that when the sectored outgrowths impinge, steps are created at the upper and lower surfaces of the lamella. We shall henceforth refer to such situations which simulate a shearing of the lamella at right angles to its surface corresponding in effect to the generation of a screw-dislocation, as “imperfections in height registry” between impinging domains, with the understanding that such imperfections in height registry also involve imperfect crystallographic registry between the impinging {100} facets involved.

The following considerations may be raised concerning the possible influence of the aforementioned imperfections in registry at 〈100〉 boundaries between impinging sectored outgrowths upon the curvature of a multi-sectored lamella. It may be envisaged that the accommodation of imperfections in crystallographic registry at the periphery of a developing multisectored lamella gives rise to localized internal stresses which could possibly entail a modification of the innately buckled character of the constituent fold domains in adjoining sectored outgrowths when these outgrowths impinge as they propagate laterally. The gist of this consideration is that imperfections in crystallographic registry, of the type indicated above, could have a modifying influence on the innate conicalness of sectored outgrowths thus leading effectively to either increases or decreases in their angle of inclination θ by say dθ. The resulting “radius of curvature” of a particular multisectored lamella would accordingly be expected to be: (a) smaller, (b) larger, or (c) essentially unaffected, relative to what the radius would be in the absence of any modifying influence due to outgrowth impingement, depending respectively on whether this latter feature always leads (a) to an effective average increase to (θ + dθ), or (b) to an effective average decrease to (θ − dθ), in the angle of inclination of sectored outgrowths relative to their innate angle θ, or (c) to the occurrence with equal probability of increases and decreases in angle of inclination relative to θ in which case dθ would be effectively zero. The same considerations also apply to imperfections in height registry.

Whether the curvature of multisectored lamellae is influenced to any appreciable extent, if at all, by the two types of imperfections indicated above, namely imperfections in crystallographic and height registry at 〈100〉 boundaries between impinging sectored outgrowths, is an open question.

In summary then, the main features of the discussion presented so far on the origins of the curature of P4MP crystals are: Conjectures were first advanced to the effect that: (i) a multisectored lamella develops in a curved fashion as a consequence of the cumulative influence of one type of imperfection, namely the intrinsically slightly conical nature (due to the bulkiness of chain folds which lead to a disparity in spacing between {200}_f and {200}_nf planes) of sectored outgrowths which develop in successive arrays at its periphery during growth, and (ii) that the curvature of the lamella will vary depending on the frequency per unit path length, from its pole to its periphery, of the development of new sectored outgrowths each of which contributes incrementally to its overall curvature. An indication was then given of some additional imperfections which can be envisioned to arise in the multisectored lamella during the process of growth. The possible modifying influence which these additional imperfections might have on the curvature which the lamella derives in the first instance from the intrinsic conicalness of sectored outgrowths were indicated but are indeterminate.

Before discussing the observed variation of the curvature of multisectored lamellar crystals of P4MP with crystallization temperature in the light of the synthesis embodied in the hypothetical model represented schematically in figure 37, it is appropriate to digress at this juncture and to dwell briefly on a feature which all the perceptibly curved multisectored crystals of P4MP exhibit in common, namely they are all multilayered, i.e., they all consist of two or more superposed chain-folded layers. On the basis of the aforementioned model this latter feature may be attributed in the first instance to the incidence of imperfections in height registry between impinging sectored outgrowths at the periphery of their leading multisectored lamella throughout growth [18]. The likelihood of the occurence at the periphery of a growing curved multisectored lamella of such imperfections which simulate in effect screw dislocations has been pointed out above. In short, the steps which are envisioned to be generated at the upper and lower surfaces of such a multisectored lamella at its periphery during growth act as sources for the development of additional chain-folded multisectored layers.

A consideration of the electron micrographs of the large curved multisectored lamellar crystals formed at 90 °C and the crystals formed at 80 °C clearly reveals that new chain-folded terraces are generated at the periphery of the leading (basal) lamella throughout its growth (see for example figs. 7, 13, 14). In addition examination of the periphery of such crystals (see for example the higher magnification electron micrographs shown in fig. 10 and fig. 16) shows that, as is common in polymer crystal growth, the propagation of new chain-folded layers or terraces from the leading lamella involves a relative displacement during growth of adjoining peripheral portions of that lamella relative to one another at right angles to the surface of the lamella through a distance equal to the thickness of the lamella. These additional terraces in such crystals of P4MP do not exhibit a propensity for continuing to grow in a spiral-like fashion resulting in the development of several superimposed layers centered about the screw dislocation-like imperfection. It appears rather, judging from the electron micrographs, that the formation of the numerous superimposed terraces in these crystals is contributed to in large measure by the generation of new curved terraces at the periphery of each additional curved multisectored terrace which develops during the growth of the crystal, due to the incidence of imperfections in height registry between impinging sectored outgrowths at the periphery of each terrace as is the case in the leading (basal) lamella. Furthermore, similar terrace initiating imperfections in height registry probably occur as a result of imperfect height registry between neighboring terraces when they impinge laterally.

In addition to the aspects of the multilayered character of the 90 °C and 80 °C curved crystals discussed above, it should be pointed out that healing, i.e., a return in height registry between overlapping terraces (as would result from two dislocation-like defects of opposite hand [18a]), also occurs at the periphery of these crystals. Whether such healing is a consequence of internal stress buildup resulting from the initial imperfections in height registry, which give rise to the generation of the additional terraces or whether it is primarily a statistical feature associated with the formation of successive arrays of new sectored outgrowths at the periphery of multisectored lamella, remains an open question.

Although the hollow bowl shaped crystals formed at 70 and 50 °C do not lend themselves to as detailed an examination as the curved crystals formed at 90 and 80 °C insofar as their multilayered character is concerned, available evidence indicates that their development in a multilayered fashion is similar to that of the crystals formed at higher temperatures. The fact that the hollow-bowl shaped crystals formed at 50 °C consist of fewer superimposed chain-folded layers than those formed at 70 °C is most probably an effect of polymer depletion from solution associated with the formation of a relatively larger number of simultaneously growing crystals at 50 than at 70 °C.

Returning to the matter of the variation of the curvature of P4MP crystals with crystallization temperature, we refer back to the hypothetical model depicted in figure 37. The explanation which is embodied in that model of the curvature of a multisectored chain folded monolayer may be readily considered to apply to each constituent multisectored lamellar terrace in a multilayered crystal. Accordingly, on the basis of that model, in which it is assumed that sectored outgrowths possess an intrinsic conicalness θ°, the overall curvature of a multilayered crystal will still depend on the frequency, per unit longitudinal path length, at which new sectored outgrowths are formed at the periphery of its leading lamella during growth. The higher that frequency the larger the number of incremental inclinations of θ° per unit path length and hence the smaller will be the radius of curvature of the multilayered crystal. Furthermore the higher that frequency the smaller will be the average lateral dimensions attained by sectored outgrowths before new ones develop therefrom, and hence the smaller will be the lateral extent of individual fold domains in the constituent chain-folded layers in the crystal.

Qualitatively, a consideration of the periphery of the basal lamella in the crystals formed at different temperatures indicates that sectored outgrowths tend to be smaller the lower the temperature at which the crystals are formed. This may be judged, for example, from a comparison of the peripheral regions in the basal lamella in the large curved crystals formed at 90 °C, such as shown in figures 9 and 10, and that portion of the periphery of the basal lamella in the collapsed crystal grown in a 50 °C preparation which is shown in figure 29 (region pointed to by arrow). Taking the sizes of leading {100} microfacets (i.e., microfacets facing outwards as distinct from reentrant microfacets) as a rough indication of the lateral dimensions of sectored outgrowth which develop in successive arrays at the periphery of the lamellae in these crystals, it may be seen that the larger leading {100} microfacets in figures 9 and 10 are ~ 0.5 μm to 1 μm long, whereas the leading {100} microfacets in the peripheral region pointed to in the crystal shown in figure 29 are not larger than 0.2 μm long.⁶ There are, however, substantial uncertainties involved in: (a) attempting to derive – from an examination of the topography of the lateral edges of the multisectored lamellae formed at the different temperatures – a rigorous quantitative measure of the lateral dimensions which sectored outgrowths attain⁷ on average before new ones develop therefrom and before they impinge laterally with nearest neighbors,⁸ and (b) estimating the radii of curvature of the large distinctly dished crystals formed at 90 °C as well as the dished crystals formed at 80 °C from their edge-on profiles. These uncertainties impede a fruitful quantitative analysis of the relationship between the curvature of the crystals formed at different temperatures and the multisectored character of their constituent lamellae. Such an analysis would provide a more rigorous verification of the hypothetical model (depicted in fig. 37) which has been advanced above and used as a basis for explaining the observed increasingly curved character which P4MP crystals exhibit the lower the crystallization temperature. Alternatively, such an analysis could shed some tangible indications of additional factors, not considered so far, which it may be envisaged could possibly contribute to the increased curvature of the crystals the lower the temperature at which they are formed. Some such factors are indicated below.

We have assumed in our discussion so far that the disparity (attributed to the asymmetric bulkiness of chain folds) in spacing between the {200}_f planes and the {200}_nf planes in the sectored outgrowths which develop in successive arrays at the periphery of multisectored lamellae does not vary with crystallization temperature and that the intrinsic conicalness (angle of inclination θ°) which sectored outgrowths adopt is the same at all temperatures. The possibility must be considered that the fractional disparity in spacing between the {200}_f and the {200}_nf planes, which as determined by Bassett [9] is about 10⁻³ in four-sectored lamellae, may differ intrinsically from this value depending on the crystallization conditions. Thus, it may be envisaged that at low crystallization temperatures, which lead to the formation of multisectored lamellae and which favor a more rapid folding of the chain molecules along their periphery during growth the lower the temperature, the folds may tend to be less regular and hence have bulkier conformations (giving rise correspondingly to larger differences between d_{200}f and d_{200}nf) causing the sectored outgrowths to be intrinsically more pronouncedly buckled. In other words, the intrinsic conicalness of the sectored outgrowths could conceivably tend to be larger the lower the crystallization temperature. In short, in terms of the hypothetical model depicted in figure 37, it may be envisaged that multisectored lamellae will be more pronouncedly curved the lower the crystallization temperature not only, as discussed earlier, because of the larger frequency at which new sectored outgrowths are formed and corresponding incremental inclinations of θ° occur per unit path length from pole to periphery, but also because these incremental inclinations may tend to be intrinsically larger the lower the crystallization temperature. To this consideration must be added the possibility that even for a constant fold conformation the buckling of sectored outgrowths may tend to be enhanced in some degree at lower crystallization temperatures due to the thinner character of the lamellae.

In view of the multiplicity of factors such as those indicated in the previous paragraph as well as those pointed out in the earlier discussion of the hypothetical model depicted in figure 37 (e.g., the occurrence and effect of imperfections in lateral and height registry on the intrinsic conicalness of impinging sectored outgrowths) which it may be envisaged could contribute to the curvature of the multisectored lamellar crystals of P4MP formed at different temperatures but whose roles in this connection are quantitatively indeterminate at present, the simple qualitative explanation of the observed variation of the curvature of P4MP crystals with crystallization temperature which was advanced earlier in this subsection (4.3) with reference to figure 37 remains speculative at this stage as do the assumptions and conjectures on which it is based. To recapitulate briefly, these assumptions and conjectures are: (i) The primary souce of the curvature of a multisectored lamella of P4MP is an intrinsic conicalness (angle of inclination θ° of the order of 2°) in the sectored outgrowths which develop in successive arrays at its periphery; (ii) the intrinsic conicalness in sectored outgrowths is a consequence of buckling under the influence of the bulkiness of the chain folds which leads to a fractional difference of 10⁻³ [9] between d_{200}f and d_{200}nf in their constituent folds domains; (iii) the overall curvature of a multisectored lamella is a cumulative consequence of the intrinsic conicalness of the sectored outgrowths which develop in successive arrays at its periphery and is governed by the frequency per unit path length from pole to periphery at which new sectored outgrowths are generated during the growth of the lamella, the higher that frequency the smaller the radius of curvature of the lamella. These assumptions and conjectures serve in themselves to set off the complexities which underlie the quantitative elucidation of the phenomenon described in this paper and provide thereby a foundation for the further study of its origins.

Acknowledgments

The authors wish to express their gratitude to R. K. Eby, E. Passaglia, and D. H. Reneker for their encouragement as well as for the benefit of helpful discussions during the course of this work.

Footnotes

Figures in brackets indicate the literature references at the end of this paper.

The terms sector and fold-domain will be used synonymously throughout this paper.

Trade name used only for the purpose of identification and in no way implies endorsement or recommendation by NBS.

⁴

That lower crystallization temperatures lead to the formation of more pronouncedly curved lamellar crystals is also reflected by the character of the individual bowl-shaped crystals grown in the preparations cooled to 70 °C. Thus, it has been pointed out in section 3.4 that crystallization is extremely rapid at 70 °C and that consequently the onset of crystal growth occurs before temperature equilibrium is attained at 70 °C, when the solutions are cooled to that temperature. Accordingly, as may be seen for example from the edge on profile of the bowl-shaped crystals (e.g., fig. 22b) the initially formed polar regions of the bowls which develop at higher ambient temperature during the cooling of the solutions to 70 °C are less pronouncedly curved than the peripheral regions which develop at a more advanced stage of thermal equilibrium.

⁵

The direct determination of the existence, or otherwise, of a suheell distortion in multisectored lamellae using Moiré techniques is frustrated by many factors including the deformation of the curved crystals when they collapse, as well as by the small sizes of their constituent domains which does not lend itself to the use of these techniques whose success depends on the ability of obtaining extensive Moiré patterns in which the separation and orientation of Moiré lines can be readily related to the domain boundaries in superimposed terraces.

⁶

It may be noted that, taking the roughly estimated radius of curvature of the larger curved crystals formed at 90 °C as being 35 μm it can be calculated that incremental inclinations, assumed to be θ = 2°, along longitudinal paths from pole to periphery would occur at intervals (representing the lateral dimensions of sectored outgrowths) of about 1.2 μm, whereas in the case of the crystals formed at 50 °C whose observed radii vary between 2.5 μm and 5 μm the corresponding intervals would be about 0.09 μm and 0.17 μm, respectively.

⁷

As distinct from the dimensions they exhibit in the process of development to full size.

⁸

It is evident from a consideration of the electron micrographs, e.g., figures 9, 10, 16, that there are substantial variations in the sizes of both leading and reentrant {100} microfacets at the periphery of the multisectored lamellae.

5. References and Notes

[1].Barnes J. D., and Khoury F., Bull. Am. Phys. Soc. 10, 366 (1965); HG3. HG4, ibid. 11, 248 (1966); FA10, FA11. ibid 12, 385 (1967). GD2. [Google Scholar]
[2].Frank F. C., Keller A., and O’Connor A., Phil. Mag. 4, 200 (1959). [Google Scholar]
[3].Bassi I. W., Bonsignori O., Lorenzi G. P., Pino P., Corradini P., and Temussi P. A., J. Polym. Sci. A2, 9, 193 (1971). [Google Scholar]
[4].Tanda Y., Kawasaki N., Imada K., and Takayanagi M., Rept. Progr. Polymer Phys. Japan 9, 165 (1966). [Google Scholar]
[5].Tanda Y., Imada K., and Takayanagi M., Kogyo Kagaku Zasshi 69, 1971 (1966). [Google Scholar]
[6].Kawasaki N., and Takayanagi M., Rept. Progr. Polymer Phys. Japan 10, 337 (1967). [Google Scholar]
[7].Takayanagi M., and Kawasaki N., J. Maeromol. Sci. B1, 741 (1967). [Google Scholar]
[8].Nakajima A., Hayashi S., Taka T., and Utsumi N., Kolloidzschr. Z. Polymere 234, 1097 (1969). [Google Scholar]
[9].Bassett D. C., Phil. Mag. Ser. VIII, 10, 595 (1964). [Google Scholar]
[10].Bassett D. C., Dannnont F. R., and Salovey R., Polymer Lond. 5, 579 (1964). [Google Scholar]
[11].Woodward A. E., Polymer Lond. 5, 293 (1964). [Google Scholar]
[12].Hiltz A. A., private communication.
[13].Hoffman A. S., Fries B. A., and Condit P. C., J. Polymer Sci. Pt. C., No. 4 109 (1964). [Google Scholar]
[14].Bassett D. C., and Keller A., Phil. Mag. 7, 1553 (1962). [Google Scholar]
[15].Blundell D. J., Keller A., and Kovacs A. J., J. Polymer Sci. B4, 481 (1966). [Google Scholar]
[16].Sadler D. M., J. Polvme r Sci. A2, 9, 779 (1971). [Google Scholar]
[17].It should be noted that the occurrence of stresses at the fold surfaces of chain-folded lamellae due to sterie interactions between neighboring folds has been previously invoked in a suggested explanation of the incidence of twist in the constituent radiating lamellae in polyethylene spherulites.; Hoffman J. D.and Lauritzen J. L. Jr., J. Res. Nat. Bur. Stand. (U.S.), 65A (Phys. and Chern.), No. 4, 297–336 (1961). [DOI] [PMC free article] [PubMed] [Google Scholar]
[18].The generation of new terraces resulting from either built-in or accidental displacements in height registry between adjoining portions at the periphery of multiseetored chain-folded lamellae is a common feature in polymer crystal growth e.g., see; (a) Reneker D. H., and Geil P. H., J. Appl. Phys. 31, 1916 (1960); [Google Scholar]; (b) Bassett D. C, and Keller A., Phil. Mag. 7, 1553 (1962); [Google Scholar]; (c) Keith H. D., J. Appl. Phys. 35, 3115 (1964). [Google Scholar]

[R1] [1].Barnes J. D., and Khoury F., Bull. Am. Phys. Soc. 10, 366 (1965); HG3. HG4, ibid. 11, 248 (1966); FA10, FA11. ibid 12, 385 (1967). GD2. [Google Scholar]

[R2] [2].Frank F. C., Keller A., and O’Connor A., Phil. Mag. 4, 200 (1959). [Google Scholar]

[R3] [3].Bassi I. W., Bonsignori O., Lorenzi G. P., Pino P., Corradini P., and Temussi P. A., J. Polym. Sci. A2, 9, 193 (1971). [Google Scholar]

[R4] [4].Tanda Y., Kawasaki N., Imada K., and Takayanagi M., Rept. Progr. Polymer Phys. Japan 9, 165 (1966). [Google Scholar]

[R5] [5].Tanda Y., Imada K., and Takayanagi M., Kogyo Kagaku Zasshi 69, 1971 (1966). [Google Scholar]

[R6] [6].Kawasaki N., and Takayanagi M., Rept. Progr. Polymer Phys. Japan 10, 337 (1967). [Google Scholar]

[R7] [7].Takayanagi M., and Kawasaki N., J. Maeromol. Sci. B1, 741 (1967). [Google Scholar]

[R8] [8].Nakajima A., Hayashi S., Taka T., and Utsumi N., Kolloidzschr. Z. Polymere 234, 1097 (1969). [Google Scholar]

[R9] [9].Bassett D. C., Phil. Mag. Ser. VIII, 10, 595 (1964). [Google Scholar]

[R10] [10].Bassett D. C., Dannnont F. R., and Salovey R., Polymer Lond. 5, 579 (1964). [Google Scholar]

[R11] [11].Woodward A. E., Polymer Lond. 5, 293 (1964). [Google Scholar]

[R12] [12].Hiltz A. A., private communication.

[R13] [13].Hoffman A. S., Fries B. A., and Condit P. C., J. Polymer Sci. Pt. C., No. 4 109 (1964). [Google Scholar]

[R14] [14].Bassett D. C., and Keller A., Phil. Mag. 7, 1553 (1962). [Google Scholar]

[R15] [15].Blundell D. J., Keller A., and Kovacs A. J., J. Polymer Sci. B4, 481 (1966). [Google Scholar]

[R16] [16].Sadler D. M., J. Polvme r Sci. A2, 9, 779 (1971). [Google Scholar]

[R17] [17].It should be noted that the occurrence of stresses at the fold surfaces of chain-folded lamellae due to sterie interactions between neighboring folds has been previously invoked in a suggested explanation of the incidence of twist in the constituent radiating lamellae in polyethylene spherulites.; Hoffman J. D.and Lauritzen J. L. Jr., J. Res. Nat. Bur. Stand. (U.S.), 65A (Phys. and Chern.), No. 4, 297–336 (1961). [DOI] [PMC free article] [PubMed] [Google Scholar]

[R18] [18].The generation of new terraces resulting from either built-in or accidental displacements in height registry between adjoining portions at the periphery of multiseetored chain-folded lamellae is a common feature in polymer crystal growth e.g., see; (a) Reneker D. H., and Geil P. H., J. Appl. Phys. 31, 1916 (1960); [Google Scholar]; (b) Bassett D. C, and Keller A., Phil. Mag. 7, 1553 (1962); [Google Scholar]; (c) Keith H. D., J. Appl. Phys. 35, 3115 (1964). [Google Scholar]

PERMALINK

The Formation of Curved Polymer Crystals: Poly (4-methylpentene-1)

F Khoury

J D Barnes

Abstract

1. Introduction

2. Experimental Details

2.1. Materials and Preparative Methods

2.2. Microscopy

a. General

b. Optical Microscopy

c. Electron Microscopy

3. Observations on the Morphologies of Poly(4-methylpentene-1) Crystals

3.1. General

Figure 2. A modification 1 x-ray pattern typical of those obtained with a powder camera from samples of crystals formed at temperatures between 90 and 50 °C.

3.2. Crystals Formed at 90 °C

Figure 3. Electron micrograph showing an example of one of the smaller essentially planar lamellar crystals of P4MP formed at 90 °C, Pt/Pd shadowed, × 3500.

Figure 4. Edge-on view under the optical microscope of one of the smaller essentially planar (compare with subsequent optical micrographs) lamellar crystals of P4MP formed at 90 °C. The crystal (center of micrograph) is in suspension in liquid. Phase contrast, × 1300.

Figure 6. Edge-on view under the optical microscope of some larger species of crystals (center of micrograph) formed at 90 °C.

Figure 7. Electron micrograph showing an example of the larger perceptibly curved crystals of P4MP formed at 90 °C.

3.3. Crystals Formed from Solutions Cooled at 80 °C

Figure 11. Several P4MP crystals formed at 80 °C viewed edge-on in suspension in liquid under the optical microscope.

Figure 13. Electron micrograph of a typical P4MP crystal formed at 80 °C.

Figure 14. Electron micrograph of typical P4MP crystal formed at 80 °C.

Figure 16. Portion of the basal lamella in a P4MP crystal formed at 80 °C.

Figure 17. A portion near the periphery of the basal lamella in a P4MP crystal formed at 80 °C showing a large crack traversed by fibrils.

Figure 18. A crystal of P4MP formed at 80 °C in which the corners of the basal lamella have folded or tended to fold back towards the interior of the crystal upon sedimentation and drying, see text.

Figure 19. Schematic representation of P4MP crystal formed at 80 °C. (a) Edge-on view; (F G) is a plane of reference which is tangential to the surface of the crystal at its pole (H). (b) Flat-on view, (c) Three dimensional perspective.

3.4. Crystals Formed at Temperatures Below 80 C

Figure 20. Optical micrograph showing four hollow bowl-shaped crystals of P4MP typical of those formed on cooling the solutions to 70 °C.

Figure 21. Electron micrograph of replica of a portion of the surface of a collapsed hollou bowl-shaped type of P4MP crystals formed on cooling the polymer solution to 70 °C.

Figure 23. Schematic representation of (a) Edge-on view and (b) flat-on view of hollow bowl-shaped crystals formed on cooling solutions to 70 °C.

Figure 25. Optical micrograph showing several P4MP bowl-shaped crystals formed on cooling a polymer solution to 50 °C.

Figure 26. Electron micrograph showing several collapsed bowl-shaped crystals of P4MP formed on cooling a polymer solution to 50 °C.

Figure 27. Optical micrographs of two bowl-shaped crystals of P4MP formed on cooling a polymer solution to 50 °C.

Figure 29. Electron micrograph of a crystal formed on cooling a polymer solution to 50 °C.

3.5. Further Comments on, and Summary of, the Main Characteristics of the P4MP Crystals Described in Sections 3.2 to 3.4

Figure 30. Electron micrograph of a corner of a four-sectored P4MP crystal grown at 90 °C using self-seeding procedure.

Figure 31. Region near the edge of a four-sectored lamella showing cracks.

4. On the Origins and Mechanism of Formation of Curved Crystals of P4MP

4.1. Summary of, and Comments on, Previous Observations on Four-Sectored Lamellar Crystals of P4MP

Figure 33. Schematic representation of an idealized four-sectored crystal in which d{200}f = d{200}nf in each sector (– – –), and distorted sectors in which d{200}f > d{200}nf (——).

Figure 34. Schematic representation of central cross-sectional view of two opposite sectors in a slightly conical four-sectored lamella.

Figure 35. Three dimensional perspective of a possible four-sectored lamella having a four-fold symmetrical wavy conformation resulting from d{200}f < d{200}nf in each sector.

Figure 36. Schematic representation of the possible origin of the ridges which delineate sector boundaries in collapsed four-sectored crystals, see text.

4.2. Preliminary Considerations and Outline of Discussion on the Origins of the Dependence of the Curvature of P4MP Crystals on Temperature of Crystallization

4.3. Hypothetical Model Pertaining to the Origins of Curvature and Its Variation in P4MP Crystals

Figure 38. Schematic representation of the generation of sector boundaries (T) which terminate at reentrant corners in a developing muItisectored lamellae, as well as the generation of 〈100〉 sector boundaries (U) between impinging sectored outgrowths.

Acknowledgments

Footnotes

5. References and Notes

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Figure 33. Schematic representation of an idealized four-sectored crystal in which d_{200}f = d_{200}nf in each sector (– – –), and distorted sectors in which d_{200}f > d_{200}nf (——).

Figure 35. Three dimensional perspective of a possible four-sectored lamella having a four-fold symmetrical wavy conformation resulting from d_{200}f < d_{200}nf in each sector.