Detection and classification of bearing faults in industrial geared motors using temporal features and adaptive neuro-fuzzy inference system

Abstract

This paper concerns the automatic diagnosis of ball bearing defects in industrial geared motor based on statistical indicators and the Adaptive Neuro-Fuzzy Inference System (ANFIS). The approach consists of three essential steps: the first is the extraction of statistical indicators from the root mean square (RMS) of the raw vibration signals measured experimentally for different states of the bearing (healthy and in the presence of defects). The second step consists of the selection of the more relevant indicators, and finally the introduction of these indicators to the ANFIS network in order to classify the various defects in the bearing (inner and outer race faults, and combined fault). A test campaign was conducted on an industrial installation (Wheeled Conveyor) to collect data as the RMS trend of the raw vibrations using adequate instrumentation in order to verify the validity of the method in real test conditions. The obtained results show that the proposed approach can reliably detect and classify various faults at different speeds of rotation of the electric motor. The effectiveness of the proposed method was also approved by using additional test data.

1. Introduction

Induction machine-based electrical drives are widely used in industrial applications because of their robustness, reliability and low cost. The availability of the machine is a main objective in the industrial domain which requires to design a good maintenance plan based on the monitoring of the state of the machine and diagnosing the defects starting from the measurements taken using different techniques either by the analysis of the machine electric current signature, thermography, oil analysis, vibration analysis, temperature ... etc. In the context of preventive maintenance, vibration analysis is the most common technique in the industrial field for the detection of defects in rotating machinery [1, 2]. According to the study of Electric Power Research Institute EPRI, 41–42 % of the failures of the induction motor are due to defects in bearings and 36 % are defects related to the stator [3, 4]. The appearance of incipient defects in the bearing does not lead to immediate breakdown, but their increase over time will generate a critical failure in the machine that requires expensive intervention. These issues have prompted many researchers to propose several diagnosis methods by analyzing the signal acquired with various methods such as temporal analysis [5, 6], frequency analysis [7] and time-frequency analysis [8]. The temporal analysis is widely used due to its effective results, it uses time-based indicators such as: root mean square [9], kurtosis [10], peak value, skewness [11], high-order statistics [12]. The analysis in the time domain has the advantage of simple and faster calculations. However, the insensitivity to initial defects and deeply distributed defects are the major drawbacks of this approach.

The spectral or frequency analysis approach is the most classical method for detecting faults in rotating machines. Indeed, this approach allows the conversion of the temporal signal into the frequency domain. It also gives detailed and early information about the state of the machine when compared with the time domain analysis. Consequently, several methods are based on using the spectrum of the temporal signal, such as the Hilbert transformation method [13], the high-frequency shock and friction forces method [14], the bearing defect frequencies analysis technique [15, 16], and the envelope spectrum method [17]. This approach is sensitive and robust for detecting bearing faults and identifying the location of damage. However, its accuracy depends on the dimensions of the bearing and the speed of rotation. In addition, all methods using the frequency domain require intelligent selection of the frequency band to be effective, as the information is often submerged in noise which is characterized by a higher energy. Therefore, it is difficult to identify the defect in the spectra using the conventional frequency-based methods.

The time-frequency domain analysis approach allows the provision of useful information for the stationary and non-stationary signals, which represents its main advantage over the temporal and frequency based techniques [18]. Several methods of analysis in the time-frequency domain have been proposed, such as short-term Fourier Transform (STFT) [19], Wigner-Ville distribution (WVD), wavelet transforms [20]. It should be noted that in many cases and in particular in variable speed and load systems, a simple inspection of the monitoring index does not provide reliable information about the state of the machine.

This work concerns the detection and classification of faults in rotating machines by means of artificial intelligence. Several methods using this approach have been used: in [21] the authors used neural networks for fault diagnosis using time and frequency characteristics. In [22], a spectral-based diagnosis approach using fuzzy logic has been proposed. In [23], a Neuro-Fuzzy-based (ANFIS) approach has been suggested for fault classification. The work presented in [24], showed diagnosis efficiency using multi-scale entropy and ANFIS. An overview of the development and application choices of the wavelet was given in [25]. As for the authors in [26], they proposed an intelligent method for fault diagnosis based on neural networks combined with intelligent filters (RNFC). On the other hand, in [27], an approach based firstly on the extraction of characteristics in the time and frequency domain, then the construction of a basic classifier by applying a genetic algorithm is presented. A novel method combining "Adaptive Feature Extraction" and "Multi-scale entropy" using "Support Vector Machine" (SVM) has been proposed in [28]. In the research work [29], the faults signature extraction is based on the frequency domain analysis using the envelope power spectrum. In [30], the proposed approach is based on the wavelet transform and Artificial Neural Networks (ANN) for the detection and classification of faults. A feature selection and diagnosis method based on Ensemble Empirical Mode Decomposition (EEMD) and optimized by the algorithm Elman_AdaBoost was suggested in [31].

The aim of this work is the integration and validation of an intelligent automated approach for the detection and classification of geared motor bearing faults in an industrial field using only the RMS trend signals. The method is based on using temporal statistical indicators and Adaptive Neuro-Fuzzy Inference System (ANFIS) [32]. The features are calculated from the acquired signals in the form of the Root Mean Square (RMS) trend of the raw vibration signals issued from an accelerometer installed on a rotating machine in operation. Such choice gives fast features calculations as it uses simple equations compared with other techniques and does not require complex denoising procedures. The experimental tests are carried out using several bearing sets with different states and operating at various speeds of rotation.

2. Theory/ calculation

2.1. Feature extraction and classification

The acquired vibration data represents the root mean square (RMS) of the original vibration data which is the available form of measurement from the acquisition device. These signals are then subject to a moving window calculations of statistical features in order to extract intrinsic characteristics.

2.1.1. Feature extraction

Statistical features are calculated from the dataset of each state of the bearing with a length of 2400 points. The used features are (mean, standard deviation (std), maximum, minimum, geometric mean) which are given in Table 1 as Eqs. (1), (2), (3), (4), and (5) applied to an input signal x(k) with a window of length N.

Table 1.

Statistical features extraction.

$F_1=\frac{1}{N}\sum _{k=1}^{N}x\left(k\right)$	mean	(1)
$F_2=\sqrt{\frac{1}{N-1}\sum _{k=1}^N{\left(x\left(k\right)-F_1\right)}^2}$	standard deviation	(2)
$F_3=\underset{1\le k\le N}{\max }\left(x\left(k\right)\right)$	maximum	(3)
$F_4=\underset{1\le k\le N}{\min }\left(x\left(k\right)\right)$	minimum	(4)
$F_5={\left(\prod _{k=1}^{N}x\left(k\right)\right)}^{\frac{1}{N}}$	geometric mean	(5)

2.1.2. Adaptive neuro-fuzzy inference system

The ANFIS algorithm was first introduced by Jang [32], which consists of a network characterized by inputs that are fuzzified using a chosen membership functions and a training algorithm that adjusts the weighting parameters and membership functions to give a fuzzy inference system that mimics a desired input-output mapping. The fuzzy inference system is composed of rules of the following form:

$$\text{If}x\text{is}{A}_i\text{and}y\text{is}{B}_i\text{then}{z}_i=p_{i}x+q_{i}y+r_i$$

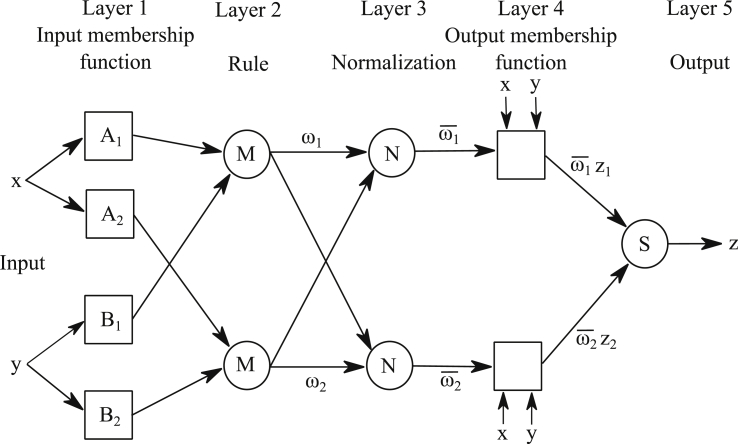
Where A_i and B_i are fuzzy sets, x and y are system input output desired mapping, z_i output of each rule with design parameters p_i, q_i and r_i. The structure of the ANFIS network is given in Fig. 1.

Fig. 1.

ANFIS architecture.

2.1.2.1. Input membership function layer

Each node $i$ in this layer is an adaptive node with a node function. Hence $O_i^1$ is a membership grade of the fuzzy set ($A_1,A_2,B_1,B_2$) which are given in Eqs. (6) and (7)

$$O_i^1={\mu }_{Ai}\left(x\right),i=1,2.$$ (6)

$$O_i^1={\mu }_{Bi-2}\left(x\right),i=3,4.$$ (7)

μ_Ai(x) and μ_Bi-2(x) are fuzzy membership functions given in Eq. (8). The used membership functions in the previous nodes are chosen to be the bell-shaped functions with an upper limit of one and a minimum of zero, it is given as follows:

$${\mu }_{Ai}\left(x\right)=\frac{1}{1+{\left[{\left(\frac{x-c_i}{a_i}\right)}^2\right]}^{b_i}},i=\mathrm{1,2}.$$ (8)

Where a_i, b_i and c_i are the parameters of the bell shaped membership function.

2.1.2.2. Rule layer

Each node in this layer is a fixed node labeled M. The output is a product of all the input signals. The outputs in Eq. (9) represent the weights ${\omega }_i$for each rule as:

$$O_i^2={\omega }_i={\mu }_{Ai}\left(x\right).{\mu }_{Bi}\left(y\right),i=\mathrm{1,2}.$$ (9)

2.1.2.3. Normalization layer

The nodes in this layer are fixed nodes labeled N. The $ith$ node calculates the ratio of the$ith$ rule's weight to the sum of all rule's weights are given as given in Eq. (10).

$$\sum _{i=1}^2{\omega }_i,i=\mathrm{1,2}.$$ (10)

The outputs for this layer are normalized weights calculated using Eq. (11).

$$O_i^3={\overline{\omega }}_i=\frac{{\omega }_i}{{\sum }_{i=1}^2{\omega }_i},i=\mathrm{1,2}.$$ (11)

2.1.2.4. Output membership function layer

Each node $i$ in this layer is an adaptive node with the node function in Eq. (12).

$$O_i^4={\overline{\omega }}_i.z_i={\omega }_i\left[p_{i}x+q_{i}y+r_i\right],i=\mathrm{1,2}.$$ (12)

q_i,p_i and r_i are the adaptive parameters set of this node.

2.1.2.5. Output layer

The output node is labeled S, which calculates the overall output using the sum of all input signals as in Eq. (13).

$$O_i^3=z=\sum _{i=1}^2{\overline{\omega }}_i{z}_i=\frac{{\sum }_{i=1}^2{\omega }_i{z}_i}{{\sum }_{i=1}^2{\omega }_i}$$ (13)

The algorithm used for the training of the ANFIS network is a combination of a gradient descent method and the least squares estimation algorithm that comprises two stages for better training efficiency and bypass the possibility of being trapped in local minima. In the first step, the parameters are supposed to be fixed. The resulting parameters are then given to the least squares estimation algorithm. In the next step, the parameters are also supposed to be fixed. The parameters are then updated using the back propagation gradient descent method, on the basis of the error values.

The used classification algorithm is based on a modified faster version of the original ANFIS classifier [32] that has been proposed in [33]. The speed-up of the supervised learning algorithm has been achieved by estimating one of the first-order gradients from the previously calculated gradients without using the training dataset. To estimate this gradient, a least square error estimator has been calculated. The cost in time for the execution of the estimator has been proven to be smaller than the computation complexity of original algorithm especially for large-scale datasets [33].

3. Experimental

3.1. Experimental setup

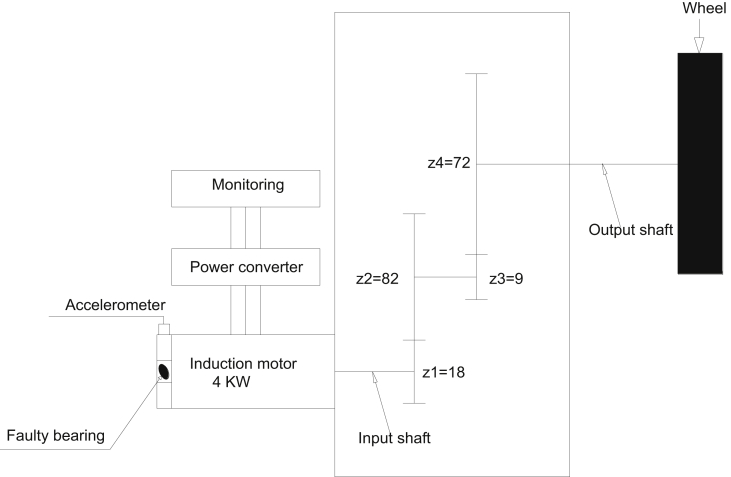
As it is well known in the literature [3, 4], bearings faults have a higher occurrence rate in rotating machinery compared to other types of faults. Consequently, this study is carried out in an industrial field in order to propose a fault diagnosis algorithm for the bearing components. The tests are performed in welded steel pipes manufacturing factory, destined for the transport of gas and hydrocarbons. The displacement of these pipes in the workshop is performed using wheeled gear motors as illustrated in Fig. 2.

Fig. 2.

Pipe coating process.

Fig. 2 shows the importance of the gear motor as a strategic equipment in the production line of the workshop. Its shutdown due to failure may have devastating economic consequences on the production process. To remedy to such problem (unexpected shutdown) as part of preventive maintenance plan, we have conducted a series of experimental tests on the behavior of the bearing (fan side) of the geared motor in different states (without defects and faulted). These tests were performed at different speeds of the electric motor.

The technical characteristics and the kinematic diagram of the gear motor are respectively shown in Table 2 and Fig. 3.

Table 2.

Technical characteristics of the tested geared motor.

Rated Power	4.0 kW
Supply frequency	50 HZ
Rated speed	1455 rpm
Rated voltage between phases	400 V
Rated current	8.4 A
Power factor	0.80
Nominal torque reduction	932 N.m

Fig. 3.

Kinematic chain of the geared motor.

The tests were carried out on the bearing (type 6306-2RS1/C3) of the electric motor (fan side) in different states (healthy and in the presence of defects) and at variable speeds (460, 840, 1220 and 1570 rev/min). The defects (Ø 4.5mm drilled holes) are created artificially on three different bearings. The first bearing has a defect on the outer race, the second on the inner race and the third on the outer and inner race simultaneously (combined) (Fig. 4 b, c, d). The drilled holes (defects) were made using a metal carbide drill.

Fig. 4.

Different states of the bearing: (a) Healthy, (b) outer race fault, (c) inner race fault and (d) combined fault.

Vibration analysis is used technique for fault detection. The vibrations were acquired at a variable acquisition frequency using a VM 6360 digital vibrometer interfaced with a computer. The latter has an accelerometer-type vibration sensor placed on the motor fan bearing in the vertical direction (Fig. 5). The vibration variables measured by the acquisition device are expressed as the RMS value of the acceleration. Numeric data is collected for each state of the bearing with an acquisition length of 2400 samples which represents the concatenation of 600 samples of the vibration signals for a fixed operation condition and rotating speed.

Fig. 5.

Vibration measurement experimental setup.

4. Results and discussion

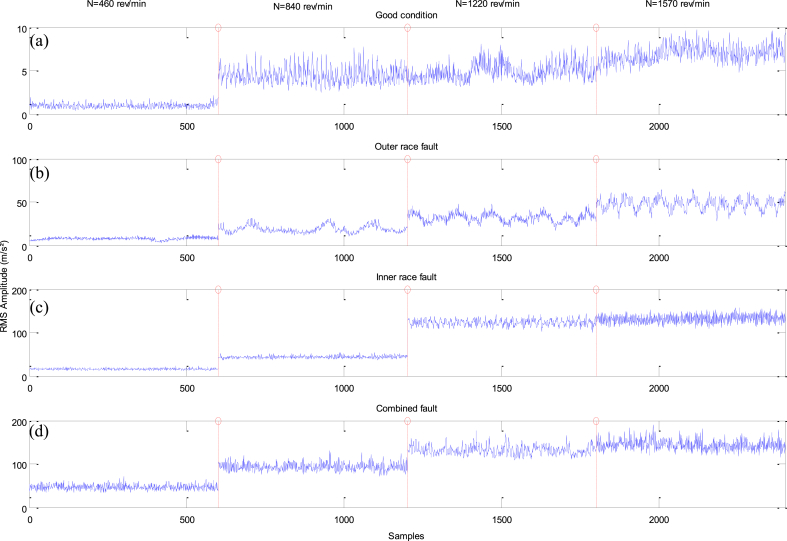
In order to study the effects of bearing defects on the gear motor vibrations, vibration signals have been collected in the healthy state and at various faulted states by varying the rotation speed of the geared motor as shown in (Fig. 6). The data collected for each bearing condition contains 2400 samples.

Fig. 6.

Results of acquired vibrations for different bearing states and different speeds: (a) healthy, (b) outer race fault, (c) inner race fault, (d) combined defect.

The analysis of the obtained results (Fig. 6) shows that the combined defect (d) is characterized by relatively higher vibrations compared to other defects and this is valid for the different speeds of rotation of the geared motor. In addition, it is also noted that the defect of the inner ring (c) causes vibrations lower than those of the combined defect, but higher than those caused by the defect of the outer race (b). The analysis also shows that the vibrations caused by the failure of the outer race are relatively higher compared to those generated by the bearing in the healthy state (a).

The intensity of the vibrations is more pronounced as the frequency of rotation of the gear motor increases. By referring to the previous analysis, it appears that: the impact of defects (b, c, d) and rotational speeds on the amplitude of vibrations (RMS) has a considerable influence. Indeed, the quantification of this influence by the ratio of each defect to the healthy state gives us the following ratios: (8–49), (4–21), (6–27) and (7–20) times, respectively for 460, 840, 1220 and 1580 rpm.

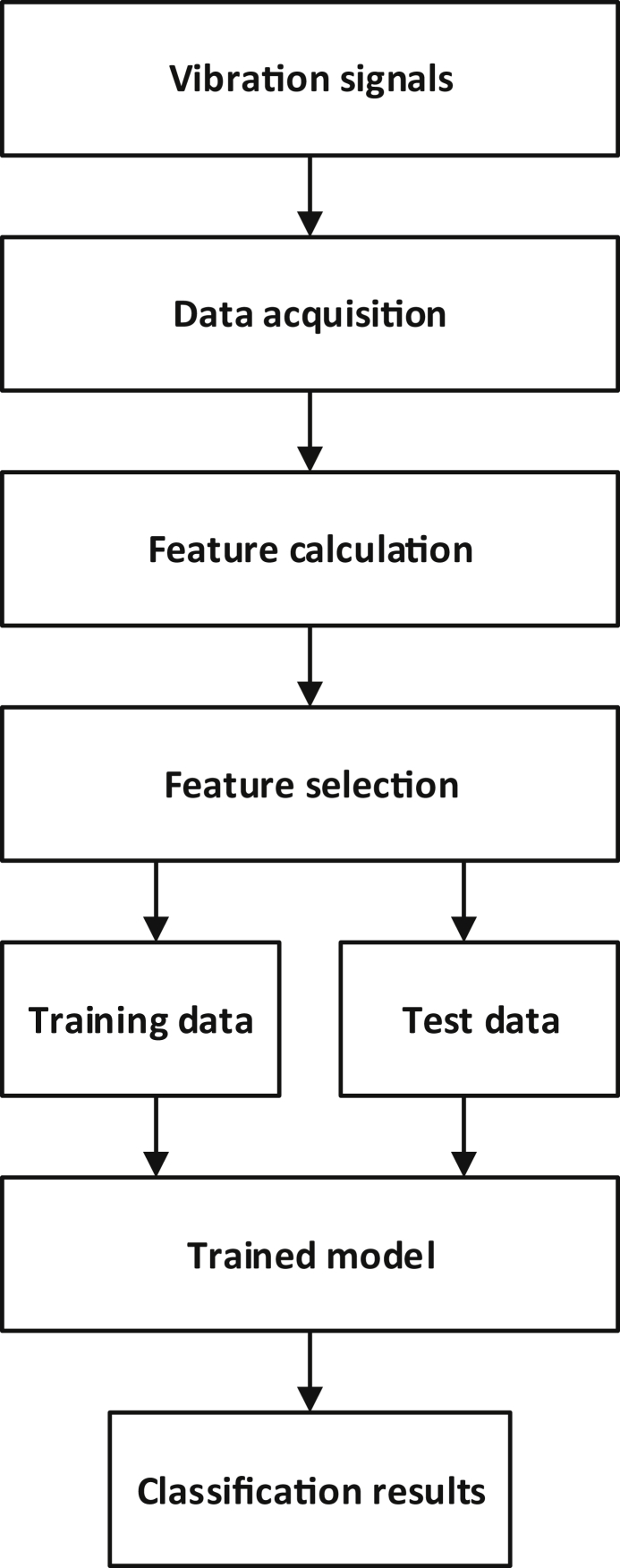
The visual distinction between the vibration signals in the time domain at the different rolling states is difficult. In order to overcome this difficulty, we proceed to the extraction of different statistical indicators, which will be analyzed later for each type of defect. This will make possible the definition of relevant indicators which will be the input vectors of the defect classification approach, according to the flowchart Fig. 7.

Fig. 7.

Steps for detection and classification of defects.

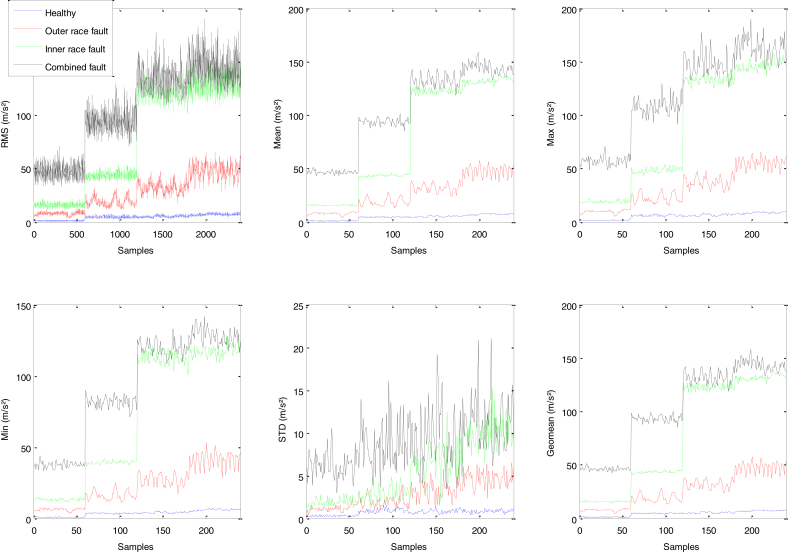
The conventional indicators to be studied for the different bearing conditions are extracted from the vibration signals in order to test their ability to identify each of the defects. These indicators are illustrated in Fig. 8.

Fig. 8.

Scalar indicators extracted from vibration signals.

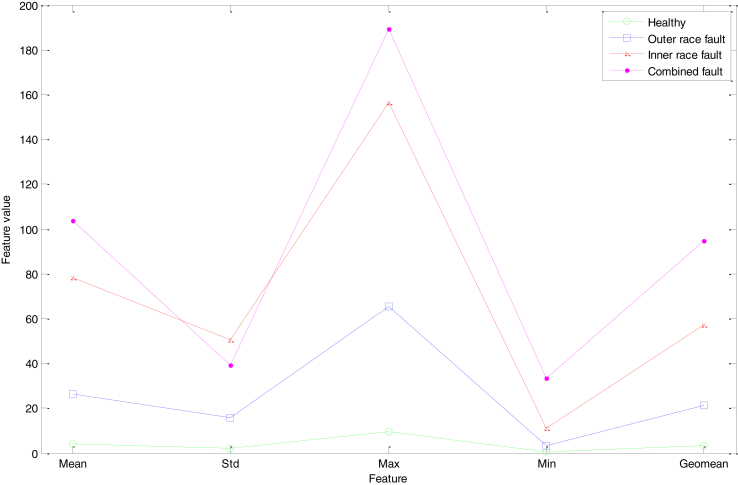
The analysis of Fig. 8 shows that the curves of the various defects of the STD indicator overlap, therefore this makes possible the detection of faults without being able to identify them. On the other hand, the curves of the other indicators (Mean, Max, Min, Geomean) are quite distinct for the different states, which makes possible the detection and identification the presence of failures. In order to illustrate the influence of each bearing fault on the scalar indicators, Fig. 9 clearly shows their evolution.

Fig. 9.

Sensitivity of indicators to different types of bearing faults.

The in-depth analysis of the scalar indicators of Fig. 9 shows that only the STD indicator has an overlap between the combined defect and the defect of the inner race which confirms the analysis previously discussed (Fig. 8).

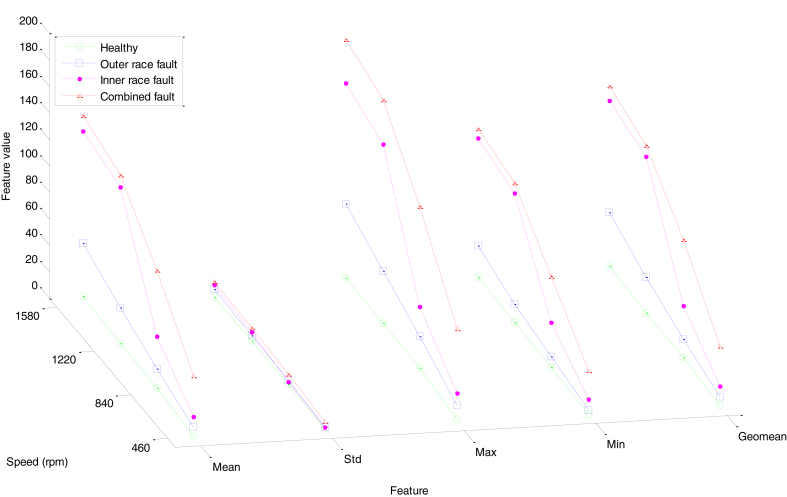
In addition, the confirmation of the choice of relevance of the indicators was highlighted by expressing the effect of the speed of rotation on the studied scalar indicators (Fig. 10). It appears that only the STD indicator has an overlap.

Fig. 10.

Evolution of the statistical indicators for the different bearing states as a function of speed.

From the indicator analysis results shown in Figs. 8, 9, and 10, it is clear that the STD indicator is unreliable for fault detection and identification due to the overlapping curves. On the other hand, the remaining indicators allow the detection and identification of the studied defects.

After identifying relevant indicators as feature vectors and for the aim of facilitating industrial exploitation, an adaptive neuro-fuzzy inference system (ANFIS) will be configured to perform automated fault diagnosis in order to minimize uncertainty in the diagnosis process. For this purpose, the four characteristic indicators as input vectors (Mean, Max, Min, Geomean) and gear motor rotational speed were used for neuro-fuzzy structure training and testing.

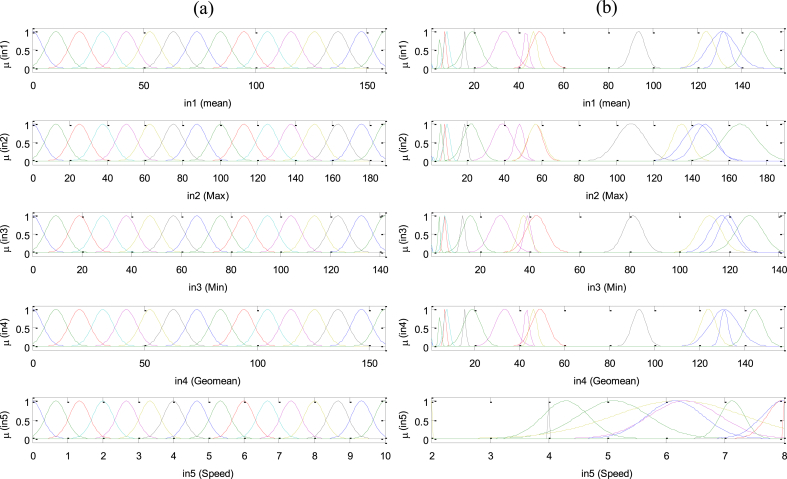
The database is separated to form a set of training data (960 samples) and test data (280 samples). The ANFIS model is trained using the training data set, so that the fuzzy logic inference is able to give the expected results. The input domain is partitioned using the membership function into sixteen segments. Modifications of the bell-shaped membership functions after training from the initial membership functions are given in Fig. 11.

Fig. 11.

Membership functions: (a) before training, (b) after training.

Fig. 11 (a) shows the initial membership functions for the inputs of the ANFIS network with 16 Gaussian membership functions for each input. The final membership functions of each entry after training are shown in Fig. 11 (b). Examination of the initial and final membership functions indicates that the membership functions can be modified according to the current condition of the training data and the training process. The changes in the membership functions after training is proportional to the effect of the corresponding indicator (Mean, Max, Min, Geomean). The larger the change in membership function contributes also to better classification results.

In the test phase, the membership functions resulting from the training procedure are used to give the evaluation of each input. The classification accuracy of the trained ANFIS structure is estimated using the testing data. The purpose of the classification is to determine an input/output mapping that estimates the operating conditions studied in this work. The results of the classification procedure applied for fault diagnosis is divided in two evaulations: one for the same training data is shown in Fig. 12 and the other classification for test set which is not included in the training data (Fig. 13).

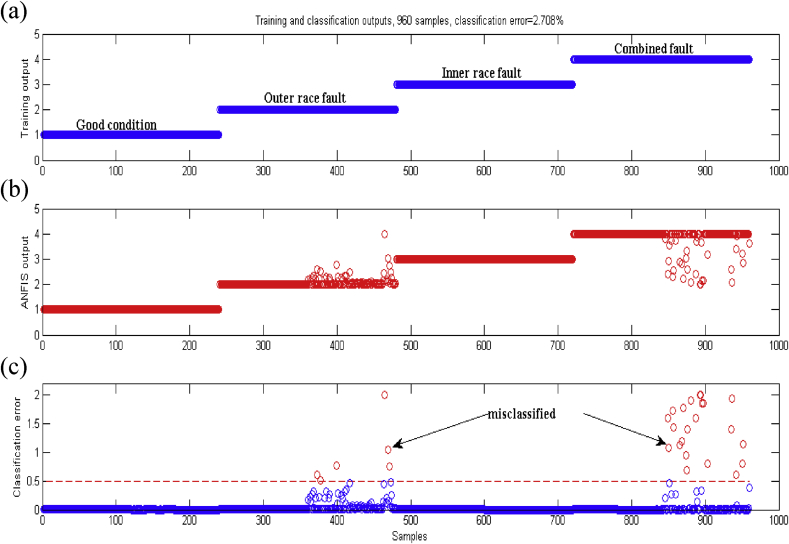
Fig. 12.

Classification results using the trained ANFIS structure using 960 training samples: (a) Desired outputs, (b) ANFIS outputs, (c) classification absolute error.

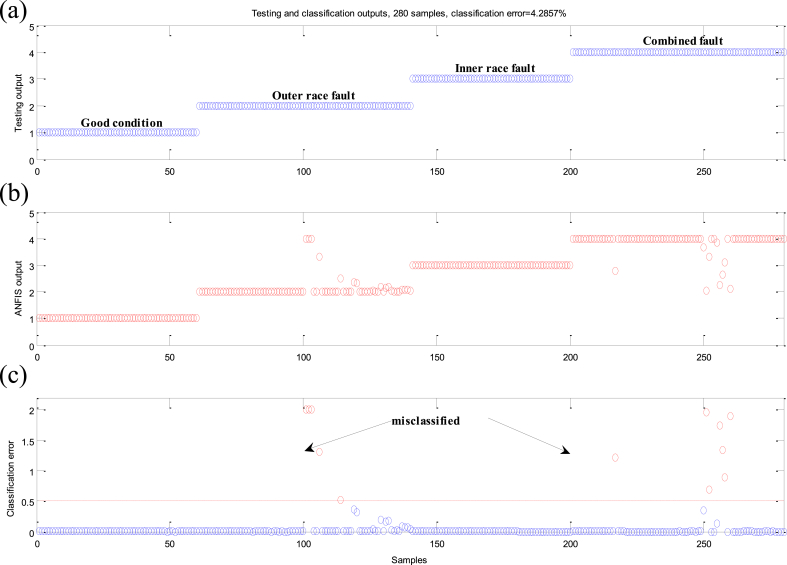
Fig. 13.

Classification results using the trained ANFIS structure using 280 testing samples: (a) Desired training outputs, (b) ANFIS outputs, (c) Classification absolute error.

Fig. 12 (a) shows the desired classes and the corresponding output of the ANFIS structure. Fig. 12 (b) shows the calculated absolute error between the desired output and the ANFIS output which is equal to 2.708 %. When the absolute error is greater than or equal to 0.5, the corresponding sample is considered as misclassified (Fig. 12b). Indeed, for the second level (outer race fault) there are 6 samples (red) misclassified, while for the fourth level (combined defect), 20 samples are misclassified. The total precision of the classification of the proposed approach for all of the training and test data is in the order of 97.3%. Table 3 shows detailed classification results for the training data.

Table 3.

Confusion matrix for the training data.

	Desired class
ANFIS output		1	2	3	4
	1	240	0	0	0
	2	0	234	0	8
	3	0	5	240	12
	4	0	1	0	220

The second classification for the test database is illustrated in Fig. 13. Knowing that these data are other than the training data. Fig. 13 (b) shows the absolute error of the ANFIS output relative to the desired output which is equal to 4.285 %. As a result, the total accuracy of the proposed approach classification for the test data set is 95.71%.Table 4 shows the confusion matrix for the test data with detailed classification samples.

Table 4.

Confusion matrix for test data.

	Desired class
ANFIS output		1	2	3	4
	1	70	0	0	0
	2	0	65	0	3
	3	0	2	70	4
	4	0	3	0	63

A comparison with previous research works that uses the ANFIS classifier for bearing faults diagnosis is given in Table 5. The current study uses a time-based approach that accelerates the processing of the feature extraction procedure as it does not require the calculation of the spectrum of the raw data as in other spectral based methods. In addition the features used in this work are characterized by simple formulas which do not require long processing time compared to entropy-based techniques. The obtained results show excellent performance for a variable speed drive operating in industrial production line.

Table 5.

Comparison of the proposed technique with other ANFIS-based works.

Paper	Considered fault	Domain	Used Features	Results	Remarks
[23]	Bearings: Outer race, Ball, Inner race	Time, Spectral	N.A.	Training: 94.78% Testing: 83.42%	Variable severity, fixed speed. Case Western database.
[35]	Bearings: Outer race, Ball, Inner race	Spectral	Frequency of detects, Spectrum peak ratio	Training: 97%	Variable severity and speed. Case Western database.
[36]	Bearings: Outer race, Ball, Inner race	Time	Multi-scale Permutation Entropy	Training: 92.5%	Variable severity and speed. Case Western database.
Current study	Bearings: Outer race, Inner race, Combined	Time	Mean, Max, Geomean, Min, Speed	Training: 97.3% Testing: 95.71%	Variable speed. Industrial equipment.

5. Conclusion

This paper applies a soft computing approach to the diagnosis of bearing faults in a geared motor of a strategic equipment in an industrial welded steel pipe factory. The approach is based on the extraction of statistical indicators from the acquired vibration signals and then the classification of faults using a trained adaptive neuro-fuzz inference system ANFIS.

The experimental results obtained at the different bearing states (healthy and in the presence of faults) clearly show that the proposed ANFIS approach to the detection and classification of bearing state of operation in real industrial applications is reliable. The total classification accuracy of the proposed approach for all training and testing data is in the order of 97.38%.

Declarations

Author contribution statement

CHOUG Abdelkrim, Meridjet Mohamed Salah, BOUTASSETA Nadir & Boulanouar Lakhdar: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.