Abstract
Mitochondrial DNA (mtDNA) mutations cause severe congenital diseases but may also be associated with healthy aging. mtDNA is stochastically replicated and degraded, and exists within organelles which undergo dynamic fusion and fission. The role of the resulting mitochondrial networks in the time evolution of the cellular proportion of mutated mtDNA molecules (heteroplasmy), and cell-to-cell variability in heteroplasmy (heteroplasmy variance), remains incompletely understood. Heteroplasmy variance is particularly important since it modulates the number of pathological cells in a tissue. Here, we provide the first wide-reaching theoretical framework which bridges mitochondrial network and genetic states. We show that, under a range of conditions, the (genetic) rate of increase in heteroplasmy variance and de novo mutation are proportionally modulated by the (physical) fraction of unfused mitochondria, independently of the absolute fission–fusion rate. In the context of selective fusion, we show that intermediate fusion:fission ratios are optimal for the clearance of mtDNA mutants. Our findings imply that modulating network state, mitophagy rate, and copy number to slow down heteroplasmy dynamics when mean heteroplasmy is low could have therapeutic advantages for mitochondrial disease and healthy aging.
Keywords: mitochondrial DNA, mitochondrial networks, heteroplasmy variance, cellular noise
MITOCHONDRIAL DNA (mtDNA) encodes elements of the respiratory system vital for cellular function. Mutation of mtDNA is one of several leading hypotheses for the cause of normal aging (López-Otín et al. 2013; Kauppila et al. 2017), as well as underlying a number of heritable mtDNA-related diseases (Schon et al. 2012). Cells typically contain hundreds, or thousands, of copies of mtDNA per cell: each molecule encodes crucial components of the electron transport chain, which generates energy for the cell in the form of ATP. Consequently, the mitochondrial phenotype of a single cell is determined, in part, by its fluctuating population of mtDNA molecules (Wallace and Chalkia 2013; Stewart and Chinnery 2015; Aryaman et al. 2019; Johnston 2019). The broad biomedical implications of mtDNA mutation, combined with the countable nature of mtDNAs and the stochastic nature of their dynamics, offer the opportunity for mathematical understanding to provide important insights into human health and disease (Aryaman et al. 2019).
An important observation in mitochondrial physiology is the threshold effect, whereby cells may often tolerate relatively high levels of mtDNA mutation until the fraction of mutated mtDNAs (termed heteroplasmy) exceeds a certain critical value where a pathological phenotype occurs (Rossignol et al. 2003; Picard et al. 2014; Stewart and Chinnery 2015; Aryaman et al. 2017). Fluctuations within individual cells mean that the fraction of mutant mtDNAs per cell is not constant within a tissue (Figure 1A), but follows a probability distribution which changes with time (Figure 1B). Here, motivated by a general picture of aging, we will largely focus on the setting of nondividing cells, which possess two mtDNA variants (although we will also consider de novo mutation using simple statistical genetics models). The variance of the distribution of heteroplasmies gives the fraction of cells above a given pathological threshold (Figure 1B). Therefore, heteroplasmy variance is related to the number of dysfunctional cells above a phenotypic threshold within a tissue, and both heteroplasmy mean and variance are directly related to tissue physiology. Increases in heteroplasmy variance also increase the number of cells below a given threshold heteroplasmy, which can be advantageous in, e.g., selecting low-heteroplasmy embryos in preimplantation genetic diagnosis for treating mitochondrial disease (Burgstaller et al. 2014b; Johnston et al. 2015).
Figure 1.
A simple model bridging mitochondrial networks and genetics yields a wide-reaching, analytically obtained description of heteroplasmy variance dynamics. (A) A population of cells from a tissue exhibit intercellular heterogeneity in mitochondrial content: both mutant load (heteroplasmy) and copy number. (B) Intercellular heterogeneity implies that heteroplasmy is described by a probability distribution. Cells above a threshold heteroplasmy (, black dashed line) are thought to exhibit a pathological phenotype. The low-variance distribution (black line) has fewer cells above a pathological threshold heteroplasmy than the high-variance distribution (red line). Heteroplasmy is depicted as an approximately normal distribution, as this is the regime in which our approximations below hold: i.e., when the probability of fixation is small. (C) The chemical reaction network we use to model the dynamics of mitochondrial DNA (see main text for a detailed description). mtDNAs are assigned a genetic state of mutant (M) or wild type (W), and a network state of singleton (i.e., unfused, S) or fused (F). (D) The central result of our work is, assuming that a cell at time is at its (deterministic) steady state, heteroplasmy variance approximately increases with time (t), mitophagy rate (μ), and the fraction of mitochondria that are unfused , and decreases with mtDNA copy number (n). Importantly, does not depend on the absolute magnitude of the fission–fusion rates. Also see Table S1 for a summary of our key findings.
Mitochondria exist within a network which dynamically fuses and fragments. Although the function of mitochondrial networks remains an open question (Hoitzing et al. 2015), it is often thought that a combination of network dynamics and mitochondrial autophagy (termed mitophagy) act in concert to perform quality control on the mitochondrial population (Twig et al. 2008; Aryaman et al. 2019; Johnston 2019). Observations of pervasive intramitochondrial mtDNA mutation (Morris et al. 2017) and universal heteroplasmy in humans (Payne et al. 2012) suggest that the power of this quality control may be limited. It has also been suggested that certain mtDNA mutations, such as deletions (Kowald and Kirkwood 2013, 2014, 2018) and some point mutations (Samuels et al. 2013; Ye et al. 2014; Li et al. 2015; Lieber et al. 2019), are under the influence of selective effects. However, genetic models without selection have proven valuable in explaining the heteroplasmy dynamics both of functional mutations (Elson et al. 2001; Taylor et al. 2003; Wonnapinij et al. 2008) and polymorphisms without dramatic functional consequences (Birky et al. 1983; Ye et al. 2014), and in common cases where mean heteroplasmy shifts are small compared to changes in variances [for instance, in germline development (Johnston et al. 2015) and postmitotic tissues (Burgstaller et al. 2014a)]. Mean changes seem more likely in high-turnover tissues and when mtDNA variants are genetically distant (Burgstaller et al. 2014a; Pan et al. 2019), suggesting that neutral genetic theory may be useful in understanding the dynamics of the set of functionally mild mutations which accumulate during aging. Furthermore, there currently exists limited evidence for pronounced, universal, selective differences of mitochondrial variants in vivo (Stewart and Larsson 2014; Hoitzing 2017). Neutral genetic theory also provides a valuable null model for understanding mitochondrial genetic dynamics (Chinnery and Samuels 1999; Poovathingal et al. 2009; Johnston and Jones 2016), potentially allowing us to better understand and quantify when selection is present. There is thus a set of open questions about how the physical dynamics of mitochondria affect the genetic populations of mtDNA within and between cells under neutral dynamics.
A number of studies have attempted to understand the impact of the mitochondrial network on mitochondrial dysfunction through computer simulation (reviewed in Kowald and Klipp 2014). These studies have suggested the following: that clearance of damaged mtDNA can be assisted by high and functionally selective mitochondrial fusion, or by intermediate fusion and selective mitophagy (Mouli et al. 2009); that physical transport of mitochondria can indirectly modulate mitochondrial health through mitochondrial dynamics (Patel et al. 2013); that fission–fusion dynamic rates modulate a trade-off between mutant proliferation and removal (Tam et al. 2013, 2015); and that if fission is damaging, decelerating fission–fusion cycles may improve mitochondrial quality (Figge et al. 2012).
Despite providing valuable insights, these previous attempts to link mitochondrial genetics and network dynamics—while important for breaking ground—have centered around complex computer simulations, making it difficult to deduce general laws and principles. Here, we address this lack of a general theoretical framework linking mitochondrial dynamics and genetics. We take a simpler approach in terms of our model structure (Figure 1C), allowing us to derive explicit, interpretable, mathematical formulas which provide intuitive understanding, and give a direct account for the phenomena which are observed in our model (Figure 1D). This simplified approach ensures that our results hold for a range of variant model structures. Simplified approaches using stochastic modeling have shown success in understanding mitochondrial physiology from a purely genetic perspective (Chinnery and Samuels 1999; Capps et al. 2003; Johnston and Jones 2016). Our basic approach also differs from previous modeling attempts, since our model is neutral with respect to genetics (no replicative advantage or selective mitophagy) and the mitochondrial network (no selective fusion). Evidence for negative selection of particular mtDNA mutations has been observed in vivo (Ye et al. 2014; Morris et al. 2017); we therefore extend our analysis to explore selectivity in the context of mitochondrial quality control using our simplified framework.
Here, we reveal the first general mathematical principle linking (physical) network state and (genetic) heteroplasmy statistics (Figure 1D). Our models potentially allow rich interactions between mitochondrial genetic and network dynamics, yet we find that a simple link emerges. For a broad range of situations, the expansion of mtDNA mutants is strongly modulated by network state, such that the rate of increase of heteroplasmy variance, and the rate of accumulation of de novo mutation, is proportional to the fraction of unfused mitochondria. We discover that this result stems from the general notion that fusion shields mtDNAs from turnover, since autophagy of large fragments of the mitochondrial network are unlikely, and consequently rescales time. Importantly, we used our model for network dynamics to show that heteroplasmy variance is independent of the absolute magnitude of the fusion and fission rates due to a separation of timescales between genetic and network processes (in contrast to Tam et al. 2015). Surprisingly, we find the dependence of heteroplasmy statistics upon network state arises when the mitochondrial population size is controlled through replication, and vanishes when it is controlled through mitophagy, shedding new light on the physiological importance of the mode of mtDNA control. We show that when fusion is selective, intermediate fusion:fission ratios are optimal for the clearance of mutated mtDNAs (in contrast to Mouli et al. 2009). When mitophagy is selective, complete fragmentation of the network results in the most effective elimination of mitochondrial mutants (in contrast to Mouli et al. 2009). We also confirm that mitophagy and mitochondrial DNA copy number affect the rate of accumulation of de novo mutations (Johnston and Jones 2016), see Supplemental Material, Table S1 for a summary of our key findings. We suggest that pharmacological interventions which promote fusion, slow mitophagy, and increase copy number earlier in development may slow the rate of accumulation of pathologically mutated cells, with implications for mitochondrial disease and aging.
Materials and Methods
Stochastic modeling of the coupling between genetic and network dynamics of mtDNA populations
Our modeling approach takes a chemical master equation perspective by combining a general model of neutral genetic drift (for instance, see Chinnery and Samuels 1999 and Johnston and Jones 2016) with a model of mitochondrial network dynamics. We seek to understand the influence of the mitochondrial network upon mitochondrial genetics. The network state itself is influenced by several factors including metabolic poise and the respiratory state of mitochondria (Szabadkai et al. 2006; Hoitzing et al. 2015; Mishra and Chan 2016), which we do not consider explicitly here. We consider the existence of two mitochondrial alleles, wild-type (W) and mutant (M), existing within a postmitotic cell without cell division, with mtDNAs undergoing turnover [or “relaxed replication” (Stewart and Chinnery 2015)]. mtDNAs exist within mitochondria, which undergo fusion and fission. We therefore assign mtDNAs a network state: fused (F) or unfused (we term “singleton,” S). This representation of the mitochondrial network allows us to include the effects of the mitochondrial network in a simple way, without the need to resort to a spatial model or consider the precise network structure, allowing us to make analytic progress and derive interpretable formulas in a more general range of situations.
Our model can be decomposed into three notional blocks (Figure 1C). First, the principal network processes denote fusion and fission of mitochondria containing mtDNAs of the same allele
| (1) |
| (2) |
| (3) |
where X denotes either a wild-type (W) or a mutant (M) mtDNA (therefore a set of chemical reactions analogous to Equations 1–3 exist for both DNA species). γ and β are the stochastic rate constants for fusion and fission respectively.
Second, mtDNAs are replicated and degraded through a set of reactions termed genetic processes. A central assumption is that all degradation of mtDNAs occur through mitophagy, and that only small pieces of the mitochondrial network are susceptible to mitophagy; for parsimony we take the limit of only the singletons being susceptible to mitophagy:
| (4) |
| (5) |
| (6) |
where λ and μ are the replication and mitophagy rates, respectively, which are shared by both W and M resulting in a so-called “neutral” genetic model. Equation 6 denotes removal of the species from the system. The effect of allowing nonzero degradation of fused species is discussed in the Supplemental Material (see Equation S68 and Figure S3E). Replication of a singleton changes the network state of the mtDNA into a fused species, since replication occurs within the same membrane-bound organelle. An alternative model of singletons which replicate into singletons, thereby associating mitochondrial replication with fission (Lewis et al. 2016), leaves our central result (Figure 1D) unchanged (see Equation S67). The system may be considered neutral since both W and M possess the same replication and degradation rates per molecule of mtDNA at any instance in time.
Finally, mtDNAs of different genotypes may interact through fusion via a set of reactions we term network cross-processes:
| (7) |
| (8) |
| (9) |
Any fusion or fission event which does not involve the generation or removal of a singleton leaves our system unchanged; we term such events as nonidentity-changing processes, which can be ignored in our system (see Rate renormalization in the Supplemental Material for a discussion of rate renormalization). We have neglected de novo mutation in the model description above (although we will consider de novo mutation using a modified infinite sites Moran model below).
We found that treating as a constant led to instability in total copy number (see Constant rates yield unstable copy numbers for a model describing mtDNA genetic and network dynamics in the Supplemental Material), which is not credible. We therefore favored a state-dependent replication rate such that copy number is controlled to a particular value, as has been done by previous authors (Chinnery and Samuels 1999; Capps et al. 2003; Johnston and Jones 2016). Allowing lower-case variables to denote the copy number of their respective molecular species, we will focus on a linear replication rate of the form (Hoitzing 2017; Hoitzing et al. 2019):
| (10) |
where is the total wild-type copy number, and similarly for . The lower-case variables , , , and denote the copy numbers of the corresponding chemical species (, , , and ). b is a parameter which determines the strength with which total copy number is controlled to a target copy number, and κ is a parameter which is indicative of (but not equivalent to) the steady-state copy number. δ indicates the relative contribution of mutant mtDNAs to the control strength and is linked to the “maintenance of wild-type” hypothesis (Durham et al. 2007; Stewart and Chinnery 2015). When , and both mutant and wild-type species are present, mutants have a lower contribution to the birth rate than wild types. When wild types are absent, the population size will be larger than when there are no mutants: hence mutants have a higher carrying capacity in this regime. We have modeled the mitophagy rate as constant per mtDNA. We do, however, explore relaxing this constraint below by allowing mitophagy to be a function of state, and also affect mutants differentially under quality control. λ may be rewritten as for constants , and so only consists of three independent parameters. However we will retain λ in the form of Equation 10 since the parameters μ, b, κ, and δ have the distinct physiological meanings described above (Hoitzing 2017; Hoitzing et al. 2019). Furthermore, λ may in general also depend on other cellular features such as mitochondrial reactive oxygen species. Here, we seek to explain mitochondrial behavior under a simple set of governing principles, but our approach can naturally be combined with a description of these additional factors to build a more comprehensive model. Analogs of this model (without a network) have been applied to mitochondrial systems (Chinnery and Samuels 1999; Capps et al. 2003). Overall, our simple model consists of 4 species , 6 independent parameters, and 15 reactions, and captures the central property that mitochondria fragment before degradation (Twig et al. 2008).
Throughout this work, we define heteroplasmy as the mutant-allele fraction per cell of a mitochondrially encoded variant (Wonnapinij et al. 2008; Samuels et al. 2010; Aryaman et al. 2019):
| (11) |
where is the state of the system (not to be confused with mitochondrial “respiratory states”). Hence, a heteroplasmy of denotes a cell with 100% mutant mtDNA (i.e., a homoplasmic cell in the mutant allele). Arguably, mutant-allele fraction would be a more precise description of Equation 11 but we retain the use of heteroplasmy for consistency. To convert to a definition of heteroplasmy which is maximal when the mutant allele fraction is 50%, one may simply use the conversion .
Statistical analysis
In Figure S3B and Figure S4, A–I, we compare Equation 13 and Equation S72 to stochastic simulations for various parameterizations and replication/degradation rates. To quantify the accuracy of these equations in predicting , we define the following error metric
| (12) |
where is the time derivative of heteroplasmy variance with subscripts denoting theory (Th) and simulation (Sim). An expectation over time is taken for the stochastic simulations, whereas is a scalar quantity for Equation 13 and Equation S72.
Data availability
Code for simulations and analysis can be accessed at https://GitHub.com/ImperialCollegeLondon/MitoNetworksGenetics. Supplemental material available at FigShare: https://doi.org/10.25386/genetics.8343830.
Results
Mitochondrial network state rescales the linear increase of heteroplasmy variance over time, independently of fission–fusion rate magnitudes
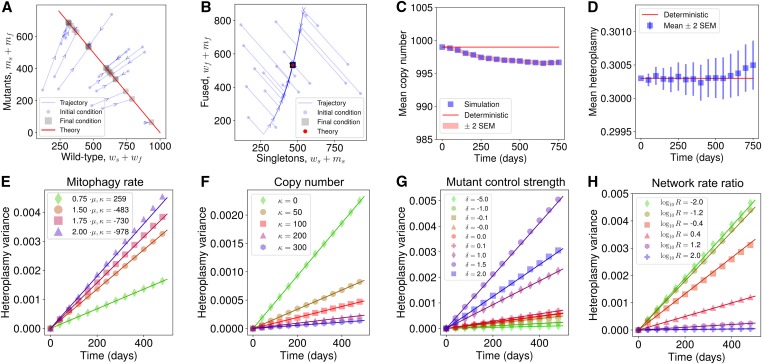
We first performed a deterministic analysis of the system presented in Equations 1–10 by converting the reactions into an analogous set of four coupled ordinary differential equations (see Equations S29–S32) and choosing a biologically motivated approximate parameterization (which we will term the “nominal” parameterization, see Choice of nominal parametrization in the Supplemental Material and Table S2). Figure 2, A and B, show that copy numbers of each individual species change in time such that the state approaches a line of steady states (Equations S34–S36), as seen in other neutral genetic models (Capps et al. 2003; Hoitzing 2017). Upon reaching this line, total copy number remains constant (Figure S2A) and the state of the system ceases to change with time. This is a consequence of performing a deterministic analysis, which neglects stochastic effects, and our choice of replication rate in Equation 10 which decreases with total copy number when and vice versa, guiding the total population to a fixed total copy number. Varying the fission (β) and fusion (γ) rates revealed a negative linear relationship between the steady-state fraction of singletons and copy number (Figure S2B).
Figure 2.
General mathematical principles linking heteroplasmy variance to network dynamics. (A) Wild-type and mutant copy numbers and (B) fused and unfused copy numbers both move toward a line of steady states under a deterministic model, as indicated by arrows. In stochastic simulation, (C) mean copy number is initially slightly perturbed from the deterministic treatment of the system and then remains constant, while (D) mean heteroplasmy remains invariant with time (see Equation S61). (E–H) We show that Equation 13 holds across many cellular circumstances: lines give analytic results, points are from stochastic simulation. Heteroplasmy variance behavior is successfully predicted for varying (E) mitophagy rate, (F) steady-state copy number, (G) mutation sensing, and (H) fusion rate. In H, fusion and fission rates are redefined as and where M and R denote the relative magnitude and ratio of the network rates, and denote the nominal parameterizations of the fusion and fission rates, respectively (see Table S2). Figure S3D shows a sweep of M over the same logarithmic range when . See Figure S4, A–I, and Table S3 for parameter sweeps numerically demonstrating the generality of the result for different mtDNA control modes.
We may also simulate the system in Equations 1–9 stochastically, using the stochastic simulation algorithm (Gillespie 1976), which showed that mean copy number is slightly perturbed from the deterministic prediction due to the influence of variance upon the mean (Grima et al. 2011; Hoitzing 2017) (Figure 2C). The stationarity of total copy number is a consequence of using for our nominal parameterization (i.e., the line of steady states is also a line of constant copy number). Choosing results in a difference in carrying capacities between the two species and nonstationarity of mean total copy number, as trajectories spread along the line of steady states to different total copy numbers. Copy number variance initially increases since trajectories are all initialized at the same state, but plateaus because trajectories are constrained in their copy number to remain near the attracting line of steady states (Figure S3A). Mean heteroplasmy remains constant through time under this model (Figure 2D; see Birky et al. 1983). This is unsurprising since each species possesses the same replication and degradation rate, so neither species is preferred.
From stochastic simulations we observed that, for sufficiently short times, heteroplasmy variance increases approximately linearly through time for a range of parameterizations (Figure 2, E–H), which is in agreement with recent single-cell oocyte measurements in mice (Burgstaller et al. 2018). Previous work has also shown a linear increase in heteroplasmy variance through time for purely genetic models of mtDNA dynamics (see Johnston and Jones 2016). We sought to understand the influence of mitochondrial network dynamics upon the rate of increase of heteroplasmy variance.
To this end, we analytically explored the influence of mitochondrial dynamics on mtDNA variability. Assuming that the state of the system above is initialized at its deterministic steady state , we took the limit of large mtDNA copy numbers (mtCNs), fast fission–fusion dynamics, and applied a second-order truncation of the Kramers–Moyal expansion (Gardiner 1985) to the chemical master equation describing the dynamics of the system (see Supplemental Material). This yielded a stochastic differential equation for heteroplasmy, via Itô’s formula (Jacobs 2010). Upon forcing the state variables onto the steady-state line (Constable et al. 2016), we derived Equation S63, which may be approximated for sufficiently short times as
| (13) |
Here, is the variance of heteroplasmy, μ is the mitophagy rate, is the total copy number, and is the fraction of unfused (singleton) mtDNAs, and is thus a measure of the fragmentation of the mitochondrial network. is the (deterministic) steady state of the system. Equation 13 demonstrates that mtDNA heteroplasmy variance increases approximately linearly with time (t) at a rate scaled by the fraction of unfused mitochondria, mitophagy rate, and inverse population size. We find that Equation 13 closely matches heteroplasmy variance dynamics from stochastic simulation, for sufficiently short times after initialization, for a variety of parameterizations of the system (Figure 2, E–H, and Figure S5).
To our knowledge, Equation 13 reflects the first analytical principle linking mitochondrial dynamics and the cellular population genetics of mtDNA variance. Its simple form allows several intuitive interpretations. As time progresses, replication and degradation of both species occurs, allowing the ratio of species to fluctuate; hence we expect to increase with time according to random genetic drift (Figure 2, E–H). The rate of occurrence of replication/degradation events is set by the mitophagy rate μ, since degradation events are balanced by replication rates to maintain population size; hence, random genetic drift occurs more quickly if there is a larger turnover in the population (Figure 2E). We expect to increase more slowly in large population sizes, since the birth of, e.g., one mutant in a large population induces a small change in heteroplasmy (Figure 2F). The factor of encodes the state dependence of heteroplasmy variance, exemplified by the observation that if a cell is initialized at or , heteroplasmy must remain at its initial value (since the model above does not consider de novo mutation, see below) and so heteroplasmy variance is zero. Furthermore, the rate of increase of heteroplasmy variance is maximal when a cell’s initial value of heteroplasmy is 0.5. In Figure 2G, we show that Equation 13 is able to recapitulate the rate of heteroplasmy variance increase across different values of δ, which are hypothesized to correspond to different replicative sensing strengths of different mitochondrial mutations (Hoitzing 2017). We also show in Figure S3, B and C, that Equation 13 is robust to the choice of feedback control strength b in Equation 10. , , and in Equation 13 are not independent degrees of freedom in this model: they are functions of the state vector x, where x is determined by the parameterization and initial conditions of the model. Hence, the parameter sweeps in Figure 2, E–H, and Figure S3, B and C, also implicitly vary over these functions of state by varying the steady state .
In Equation 6, we have made the important assumption that only unfused mitochondria can be degraded via mitophagy, as seen by Twig et al. (2008), hence the total propensity of mtDNA turnover is limited by the number of mtDNAs which are actually susceptible to mitophagy. Strikingly, we find that the dynamics of heteroplasmy variance are independent of the absolute rate of fusion and fission, only depending on the fraction of unfused mtDNAs at any particular point in time (see Figure 2H and Figure S3D). This observation, which contrasts with the model of Tam et al. (2013, 2015) (see Discussion), arises from the observation that mitochondrial network dynamics are much faster than replication and degradation of mtDNA, by around a factor of (see Table S2), resulting in the existence of a separation of timescales between network and genetic processes. In the derivation of Equation 13, we have assumed that fission–fusion rates are infinite, which simplifies into a form which is independent of the magnitude of the fission–fusion rate. A parameter sweep of the magnitude and ratio of the fission–fusion rates reveals that, if the fusion and fission rates are sufficiently small, Equation 13 breaks down and gains dependence upon the magnitude of these rates (see Figure S4A). This regime only appears, however, for network rates which are ∼100-times smaller than the biologically motivated nominal parameterization shown in Figure 2, A–D, where the fission–fusion rate becomes comparable to the mitophagy rate. Since fission–fusion takes place on a faster timescale than mtDNA turnover, we may neglect this region of parameter space as being implausible.
Equation 13 can be viewed as describing the “quasi-stationary state” where the probability of extinction of either allele is negligible (Johnston and Jones 2016). On longer timescales, or if mtDNA half-life is short (Poovathingal et al. 2012), the probability of fixation becomes appreciable. In this case, Equation 13 overestimates as heteroplasmy variance gradually becomes sublinear with time (see Figure S5, C and D). This is evident through inspection of Equation S63, which shows that cellular trajectories which reach or cease to diffuse in heteroplasmy space, and so heteroplasmy variance cannot increase indefinitely. Consequently, the depiction of heteroplasmy variance in Figure 1, B and D, as being approximately normally distributed corresponds to the regime in which our approximation holds, and is a valid subset of the behaviors displayed by heteroplasmy dynamics under more sophisticated models [e.g., the Kimura distribution (Kimura 1955; Wonnapinij et al. 2008)]. Further analytical developments may be possible to take into account extinction (e.g., see Wonnapinij et al. 2008 and Assaf and Meerson 2010). However, the linear regime for heteroplasmy variance has been observed to be a substantial component of mtDNA dynamics in, e.g., mouse oocytes (Burgstaller et al. 2018).
The influence of mitochondrial dynamics upon heteroplasmy variance under different models of genetic mtDNA control
To demonstrate the generality of this result, we explored several alternative forms of cellular mtDNA control (Johnston and Jones 2016). We found that when copy number is controlled through the replication rate function [i.e., , constant], when the fusion and fission rates were high and the fixation probability [ or ] was negligible, Equation 13 accurately described across all of the replication rates investigated (see Figure S4, A–F). The same mathematical argument to show Equation 13 for the replication rate in Equation 10 may be applied to these alternative replication rates where a closed-form solution for the deterministic steady state may be written down (see Deriving an ODE description of the mitochondrial network system in the Supplemental Material). Interestingly, when copy number is controlled through the degradation rate [i.e., , heteroplasmy variance loses its dependence upon network state entirely and the term is lost from Equation 13 (see Equation S72 and Figure S4, G–I). A similar mathematical argument was applied to reveal how this dependence is lost (see Proof of heteroplasmy relation for linear feedback control in the Supplemental Material).
To provide an intuitive account for why control in the replication rate vs. control in the degradation rate determines whether or not heteroplasmy variance has network dependence, we investigated a time-rescaled form of the Moran process (see A modified Moran process may account for the alternative forms of heteroplasmy variance dynamics under different models of genetic mtDNA control in the Supplemental Material). The Moran process is structurally much simpler than the model presented above, to the point of being unrealistic, in that the mitochondrial population size is constrained to be constant between consecutive time steps. Despite this, the modified Moran process proved to be insightful. We find that, when copy number is controlled through the replication rate, the absence of death in the fused subpopulation means the timescale of the system (being the time to the next death event) is proportional to . In contrast, when copy number is controlled through the degradation rate, the presence of a constant birth rate in the entire population means the timescale of the system (being the time to the next birth event) is independent of (see Equation S84 and surrounding discussion).
Control strategies against mutant expansions
In this study, we have argued that the rate of increase of heteroplasmy variance, and therefore the rate of accumulation of pathologically mutated cells within a tissue, increases with mitophagy rate (μ), decreases with total mtCN per cell (n), and increases with the fraction of unfused mitochondria (termed singletons, ), see Equation 13. Below, we explore how biological modulation of these variables influences the accumulation of mutations. We use this new insight to propose three classes of strategy to control mutation accumulation and hence address associated issues in aging and disease, and discuss these strategies through the lens of existing biological literature.
Targeting network state against mutant expansions:
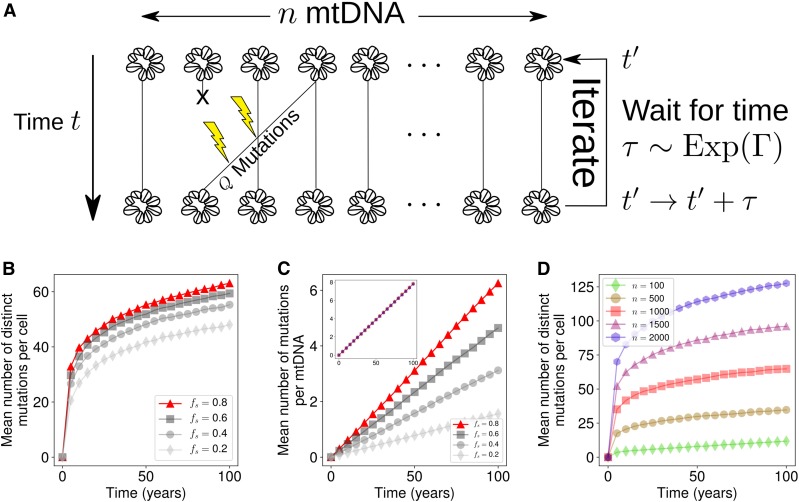
To explore the role of the mitochondrial network in the accumulation of de novo mutations, we invoked an infinite sites Moran model (Kimura 1969) (see Figure 3A). Single cells were modeled over time as having a fixed mitochondrial copy number (n), and at each time step one mtDNA is randomly chosen for duplication and one (which can be the same) for removal. The individual replicated incurs Q de novo mutations, where Q is binomially distributed according to
| (14) |
where is a binomial random variable with N trials and probability p of success. is the length of mtDNA in base pairs and is the mutation rate per base pair per doubling (Zheng et al. 2006); hence each base pair is idealized to have an equal probability of mutation upon replication. In Equation S83 we argue that when population size is controlled in the replication rate, the interevent rate of the Moran process is effectively rescaled by the fraction of unfused mitochondria, i.e., , which we apply here.
Figure 3.
Rate of de novo mutation accumulation is sensitive to the network state/mitophagy rate and copy number for a time-rescaled infinite sites Moran model. (A) An infinite sites Moran model where Q mutations occur per Moran step (see Equation 14). (B–D) Influence of our proposed intervention strategies. (B) Mean number of distinct mutations increases with the fraction of unfused mitochondria. This corresponds to a simple rescaling of time, so all but one of the parameterizations are shown in gray. (C) The mean number of mutations per mtDNA also increases with the fraction of unfused mitochondria. Inset shows that the mean number of mutations per mtDNA is independent of the number of mtDNAs per cell; values of n are the same as in D. (D) Mean number of mutations per cell increases according to the population size of mtDNAs. Standard error in the mean is too small to visualize, so error bars are neglected, given realizations.
Figure 3B shows that in the infinite sites model, the consequence of Equation S83 is that the rate of accumulation of mutations per cell reduces as the mitochondrial network becomes more fused, as does the mean number of mutations per mtDNA (Figure 3C). These observations are intuitive: since fusion serves to shield the population from mitophagy, mtDNA turnover slows down, and therefore there are fewer opportunities for replication errors to occur per unit time. Different values of in Figure 3, B and C, therefore correspond to a rescaling of time, i.e., stretching of the time axis. The absolute number of mutations predicted in Figure 3B may overestimate the true number of mutations per cell (and of course depends on our choice of mutation rate), since a subset of mutations will experience either positive or negative selection. However, quantification of the number of distinct mitochondrial mutants in single cells remains underexplored, as most mutations will have a variant allele fraction close to 0 or 100% (Birky et al. 1983), which are challenging to measure, especially through bulk sequencing.
A study by Chen et al. (2010) observed the effect of deletion of two proteins which are involved in mitochondrial fusion (Mfn1 and Mfn2) in mouse skeletal muscle. Although knock-out studies present difficulties in extending their insights into the physiological case, the authors observed that fragmentation of the mitochondrial network induced severe depletion of mtCN (which we also observed in Figure S2B). Furthermore, the authors observed that the number of mutations per base pair increased upon fragmentation, which we also observed in the infinite sites model where fragmentation effectively results in a faster turnover of mtDNA (Figure 3C).
Our models predict that promoting mitochondrial fusion has a twofold effect: first, it slows the increase of heteroplasmy variance (see Equation 13 and Figure 2H); second, it reduces the rate of accumulation of distinct mutations (see Figure 3, B and C). These two effects are both a consequence of mitochondrial fusion rescaling the time to the next turnover event, and therefore the rate of random genetic drift. As a consequence, this simple model suggests that promoting fusion earlier in development (assuming mean heteroplasmy is low) could slow down the accumulation and spread of mitochondrial mutations, and perhaps slow aging.
If we assume that fusion is selective in favor of wild-type mtDNAs, which appears to be the case at least for some mutations under therapeutic conditions (Suen et al. 2010; Kandul et al. 2016), we predict that a balance between fusion and fission is the most effective means of removing mutant mtDNAs (see below), perhaps explaining why mitochondrial networks are often observed to exist as balanced between mitochondrial fusion and fission (Sukhorukov et al. 2012; Zamponi et al. 2018). In contrast, if selective mitophagy pathways are induced then promoting fragmentation is predicted to accelerate the clearance of mutants (see below).
Targeting mitophagy rate against mutant expansions:
Alterations in the mitophagy rate μ have a comparable effect to changes in in terms of reducing the rate of heteroplasmy variance (see Equation 13) and the rate of de novo mutation (Figure 3, B and C) since they both serve to rescale time. Our theory therefore suggests that inhibition of basal mitophagy may be able to slow down the rate of random genetic drift, and perhaps healthy aging, by locking in low levels of heteroplasmy. Indeed, it has been shown that mouse oocytes (Boudoures et al. 2017) as well as mouse hematopoietic stem cells (de Almeida et al. 2017) have comparatively low levels of mitophagy, which is consistent with the idea that these pluripotent cells attempt to minimize genetic drift by slowing down mtDNA turnover. A previous modeling study has also shown that mutation frequency increases with mitochondrial turnover (Poovathingal et al. 2009).
Alternatively, it has also been shown that the presence of heteroplasmy, in genotypes which are healthy when present at 100%, can induce fitness disadvantages (Acton et al. 2007; Sharpley et al. 2012; Bagwan et al. 2018). In cases where heteroplasmy itself is disadvantageous, especially in later life where such mutations may have already accumulated, accelerating heteroplasmy variance increase to achieve fixation of a species could be advantageous. However, this will not avoid cell-to-cell variability, and the physiological consequences for tissues of such mosaicism is unclear.
Targeting copy number against mutant expansions:
To investigate the role of mtCN on the accumulation of de novo mutations, we set such that (i.e., a standard Moran process). We found that varying mtCN did not affect the mean number of mutations per molecule of mtDNA (Figure 3C, inset). However, as the population size becomes larger, the total number of distinct mutations increases accordingly (Figure 3D). In contrast to our predictions, a recent study by Wachsmuth et al. (2016) found a negative correlation between mtCN and the number of distinct mutations in skeletal muscle. However, Wachsmuth et al. (2016) also found a correlation between the number of distinct mutations and age, in agreement with our model. Furthermore, the authors used partial regression to find that age was more explanatory than mtCN in explaining the number of distinct mutations, suggesting age as a confounding variable to the influence of copy number. Our work shows that, in addition to age and mtCN, turnover rate and network state also influence the proliferation of mtDNA mutations. Therefore, one would ideally account for these four variables jointly, to fully constrain our model.
A study of single neurons in the substantia nigra of healthy human individuals found that mtCN increased with age (Dölle et al. 2016). Furthermore, mice engineered to accumulate mtDNA deletions through faulty mtDNA replication (Trifunovic et al. 2004) display compensatory increases in mtCN (Perier et al. 2013), which potentially explains the ability of these animals to resist neurodegeneration. It is possible that the observed increase in mtCN in these two studies is an adaptive response to slow down random genetic drift (see Equation 13). In contrast, mtCN reduces with age in skeletal muscle (Wachsmuth et al. 2016), as well as in a number of other tissues such as pancreatic islets (Cree et al. 2008) and peripheral blood cells (Mengel-From et al. 2014). Given the beneficial effects of increased mtCN in neurons, long-term increases in mtCN could delay other age-related pathological phenotypes.
Optimal mitochondrial network configurations for mitochondrial quality control
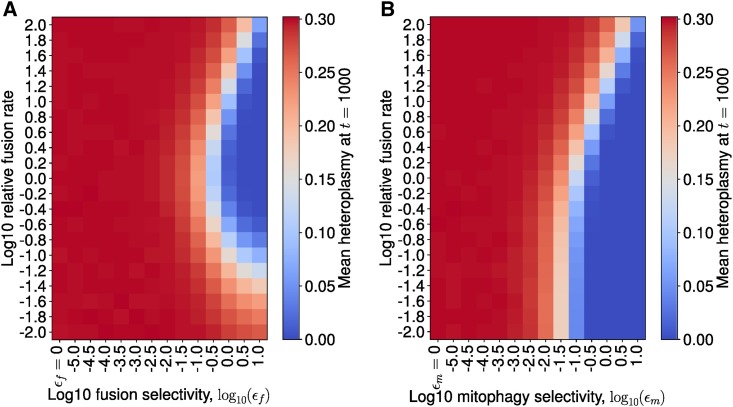
While the above models of mtDNA dynamics are neutral (i.e., m and w share the same replication and degradation rates), it is often proposed that damaged mitochondria may experience a higher rate of degradation (Kim et al. 2007; Narendra et al. 2008). There are two principal ways in which selection may occur on mutant species. First, mutant mitochondria may be excluded preferentially from the mitochondrial network in a background of unbiased mitophagy. If this is the case, mutants would be unprotected from mitophagy for longer periods of time than wild types, and therefore be at greater hazard of degradation. We can alter the fusion rate (γ) in the mutant analogs of Equations 1 and 2 and Equations 7–9 by writing
| (15) |
for all fusion reactions involving one or more mutant mitochondria where . The second potential selective mechanism we consider is selective mitophagy. In this case, the degradation rate of mutant mitochondria is larger than wild types, i.e., we modify the mutant degradation reaction to
| (16) |
for .
In these two settings, we explore how varying the fusion rate for a given selectivity ( and ) affects the extent of reduction in mean heteroplasmy. Figure 4A shows that, in the context of selective fusion and nonselective mitophagy the optimal strategy for clearance of mutants is to have an intermediate fusion:fission ratio. This was observed for all fusion selectivities investigated (see Figure S7). Intuitively, if the mitochondrial network is completely fused then, due to mitophagy only acting upon smaller mitochondrial units, mitophagy cannot occur, so mtDNA turnover ceases and heteroplasmy remains at its initial value. In contrast, if the mitochondrial network completely fissions, there is no mitochondrial network to allow the existence of a quality control mechanism: both mutants and wild types possess the same probability per unit time of degradation, so mean heteroplasmy does not change. Since both extremes result in no clearance of mutants, the optimal strategy must be to have an intermediate fusion:fission ratio.
Figure 4.
Selective fusion implies intermediate fusion rates are optimal for mutant clearance, whereas selective mitophagy implies complete fission is optimal. Numerical exploration of the shift in mean heteroplasmy for varying fusion:fission ratio, across different selectivity strengths. Stochastic simulations for mean heteroplasmy, evaluated at 1000 days, with an initial condition of and ; the state was initialized on the steady-state line for the case of , for iterations. (A) For selective fusion (see Equation 15), for each value of fusion selectivity , the fusion rate (γ) was varied relative to the nominal parameterization (see Table S2). When , the largest reduction in mean heteroplasmy occurs at intermediate values of the fusion rate; a deterministic treatment reveals this to be true for all fusion selectivities investigated (see Figure S7). (B) For selective mitophagy (see Equation 16), when mitophagy selectivity , a lower mean heteroplasmy is achieved and the lower the fusion rate (until mean heteroplasmy = 0 is achieved). Hence, complete fission is the optimal strategy for selective mitophagy.
In contrast, in Figure 4B, in the context of nonselective fusion and selective mitophagy , the optimal strategy for clearance of mutants is to completely fission the mitochondrial network. Intuitively, if mitophagy is selective, then the more mtDNAs which exist in fragmented organelles, the greater the number of mtDNAs which are susceptible to selective mitophagy, the greater the total rate of selective mitophagy, and the faster the clearance of mutants.
Discussion
In this work, we sought to unify our understanding of three aspects of mitochondrial physiology—the mitochondrial network state, mitophagy, and copy number—with genetic dynamics. The principal virtue of our modeling approach is its simplified nature, which makes general, analytic, quantitative insights available for the first time. In using parsimonious models, we are able to make the first analytic link between the mitochondrial network state and heteroplasmy dynamics. This is in contrast to other computational studies in the field, whose structural complexity makes analytic progress difficult and accounting for their predicted phenomena correspondingly more challenging.
Our bottom-up modeling approach allows for potentially complex interactions between the physical (network) and genetic mitochondrial states of the cell, yet a simple connection emerged from our analysis. We found, for a wide class of models of postmitotic cells, that the rate of linear increase of heteroplasmy variance is modulated in proportion to the fraction of unfused mitochondria (see Equation 13). The general notion that mitochondrial fusion shields mtDNAs from turnover, and consequently serves to rescale time, emerges from our analysis. This rescaling of time only holds when mitochondrial copy numbers are controlled through a state-dependent replication rate, and vanishes if copy numbers are controlled through a state-dependent mitophagy rate. We have presented the case of copy-number control in the replication rate as being a more intuitive model than control in the degradation rate. The former has the interpretation of biogenesis being varied to maintain a constant population size, with all mtDNAs possessing a characteristic lifetime. The latter has the interpretation of all mtDNA molecules being replicated with a constant probability per unit time, regardless of how large or small the population size is, and changes in mitophagy acting to regulate population size. Such a control strategy seems wasteful in the case of stochastic fluctuations resulting in a population size which is too large, and potentially slow if fluctuations result in a population size which is too small. Furthermore, control in the replication rate means that the mitochondrial network state may act as an additional axis for the cell to control heteroplasmy variance (Figure 2) and the rate of accumulation of de novo mutations (Figure 3, B and C). Single-mtDNA tracking through confocal microscopy in conjunction with mild mtDNA depletion could shed light on whether the probability of degradation per unit time per mtDNA varies when mtCN is perturbed, and therefore provide evidence for or against these two possible control strategies.
Our observations provide a substantial change in our understanding of mitochondrial genetics, as it suggests that the mitochondrial network state, in addition to mitochondrial turnover and copy number, must be accounted for to predict the rate of spread of mitochondrial mutations in a cellular population. Crucially, through building a model that incorporates mitochondrial dynamics, we find that the dynamics of heteroplasmy variance is independent of the absolute rate of fission–fusion events, since network dynamics occur ∼-times faster than mitochondrial turnover, inducing a separation of timescales. The independence of the absolute rate of network dynamics makes way for the possibility of gaining information about heteroplasmy dynamics via the mitochondrial network, without the need to quantify absolute fission–fusion rates (for instance through confocal micrographs to quantify the fraction of unfused mitochondria). By linking with classical statistical genetics, we find that the mitochondrial network also modulates the rate of accumulation of de novo mutations, also due to the fraction of unfused mitochondria serving to rescale time. We find that, in the context of mitochondrial quality control through selective fusion, an intermediate fusion:fission ratio is optimal due to the finite selectivity of fusion. This latter observation perhaps provides an indication for the reason why we observe mitochondrial networks in an intermediate fusion state under physiological conditions (Sukhorukov et al. 2012; Zamponi et al. 2018).
We have, broadly speaking, considered neutral models of mtDNA genetic dynamics. It is, however, typically suggested that increasing the rate of mitophagy promotes mtDNA quality control and therefore shrinks the distribution of heteroplasmies toward 0% mutant (see Equations 15 and 16). If mitophagy is able to change mean heteroplasmy, then a neutral genetic model appears to be inappropriate, as mutants experience a higher rate of degradation. Biological examples of non-neutral behavior include the observation that the PINK1/Parkin pathway can select against deleterious mtDNA mutations in vitro (Suen et al. 2010) and in vivo (Kandul et al. 2016), as has repression of the mTOR pathway via treatment with rapamycin (Dai et al. 2013; Kandul et al. 2016). However, the necessity of performing a genetic/pharmacological intervention to clear mutations via this pathway suggests that the ability of tissues to selectively remove mitochondrial mutants under physiological conditions is weak. Consequently, neutral models such as our own are useful in understanding how the distribution of heteroplasmy evolves through time under physiological conditions. Indeed, it has been recently shown that mitophagy is basal (McWilliams et al. 2016) and can proceed independently of PINK1 in vivo (McWilliams et al. 2018), perhaps suggesting that mitophagy has nonselective aspects—although this is yet to be verified conclusively.
We have paid particular attention to the case of postmitotic tissues, since these tissues are important for understanding the role of mitochondrial mutations in healthy aging (Khrapko and Vijg 2009; Kauppila et al. 2017). A typical rate of increase of heteroplasmy variance predicted by Equation 13 given our nominal parameterization (Table S2) is day−1 . This value accounts for the accumulation of heteroplasmy variance which is attributable to turnover of the mitochondrial population in a postmitotic cell. However, in the most general case, cell division is also able to induce substantial heteroplasmy variance. For example, has been measured in model organism germlines to be ∼ day−1 in Drosophila (Solignac et al. 1987; Johnston and Jones 2016), day−1 in NZB/BALB mice (Wai et al. 2008; Wonnapinij et al. 2008; Johnston and Jones 2016), and day−1 in single Lehsten (LE) and Hohenberg (HB) mouse oocytes (Burgstaller et al. 2018). We see that these rates of increase in heteroplasmy variance are approximately an order of magnitude larger than predictions from our model of purely quiescent turnover, given our nominal parameterization. While larger mitophagy rates may also potentially induce larger values for (see Poovathingal et al. 2012, and Figure S5C, corrsponding to day−1) it is clear that partitioning noise [or “vegetative segregation” (Stewart and Chinnery 2015)] is also an important source of variance in heteroplasmy dynamics (Johnston et al. 2015). Quantification of heteroplasmy variance in quiescent tissues remains an underexplored area, despite its importance in understanding healthy aging (Kauppila et al. 2017; Aryaman et al. 2019).
Our findings reveal some apparent differences with previous studies which link mitochondrial genetics with network dynamics (see Table S4). First, Tam et al. (2013, 2015) found that slower fission–fusion dynamics resulted in larger increases in heteroplasmy variance with time, in contrast to Equation 13 which only depends on fragmentation state and not absolute network rates. The simulation approach of Tam et al. (2013, 2015) allowed for mitophagy to act on whole mitochondria, where mitochondria consist of multiple mtDNAs. Faster fission–fusion dynamics tended to form heteroplasmic mitochondria, whereas slower dynamics formed homoplasmic mitochondria. It is intuitive that mitophagy of a homoplasmic mitochondrion induces a larger shift in heteroplasmy than mitophagy of a single mtDNA, hence slower network dynamics form more homoplasmic mitochondria. However, this apparent difference with our findings can naturally be resolved if we consider the regions in parameter space where the fission–fusion rate is much larger than the mitophagy rate, as is empirically observed to be the case (Cagalinec et al. 2013; Burgstaller et al. 2014a). If the fission–fusion rates are sufficiently large to ensure heteroplasmic mitochondria, then further increasing the fission–fusion rate is unlikely to have an impact on heteroplasmy dynamics. Hence, this finding is potentially compatible with our study, although future experimental studies investigating intramitochondrial heteroplasmy would help constrain these models. Tam et al. (2015) also found that fast fission–fusion rates could induce an increase in mean heteroplasmy, in contrast to Figure 2D which shows that mean heteroplasmy is constant with time. We may speculate that the key difference between our treatment and that of Tam et al. (2013, 2015) is the inclusion of cellular subcompartments which induces spatial effects which we do not consider here. The uncertainty in accounting for the phenomena observed in such complex models highlights the virtues of a simplified approach which may yield interpretable laws and principles through analytic treatment.
The study of Mouli et al. (2009) suggested that, in the context of selective fusion, higher fusion rates are optimal. This initially seems to contrast with our finding which states that intermediate fusion rates are optimal for the clearance of mutants (Figure 4A). However, the high fusion rates in that study do not correspond directly to the highly fused state in our study. Fission automatically follows fusion in Mouli et al. (2009), ensuring at least partial fragmentation, and the high fusion rates for which they identify optimal clearing are an order of magnitude lower than the highest fusion rate they consider. In the case of complete fusion, mitophagy cannot occur in the model of Mouli et al. (2009), so there is no mechanism to remove dysfunctional mitochondria. It is perhaps more accurate to interpret the observations of Mouli et al. (2009) as implying that selective fusion shifts the optimal fusion rate higher, when compared to the case of selective mitophagy alone. Therefore, the study of Mouli et al. (2009) is compatible with Figure 4A. Furthermore, Mouli et al. (2009) also found that when fusion is nonselective and mitophagy is selective, intermediate fusion rates are optimal, whereas Figure 4B shows that complete fragmentation is optimal for clearance of mutants. Optimality of intermediate fusion in the context of selective mitophagy in the model of Mouli et al. (2009) likely stems from two aspects of their model: (1) mitochondria consist of several units which may or may not be functional, and (2) the sigmoidal relationship between number of functional units per mitochondrion and mitochondrial “activity” (the metric by which optimality is measured). Points (1) and (2) imply that small numbers of dysfunctional mitochondrial units have very little impact on mitochondrial activity, so fusion may boost total mitochondrial activity in the context of small amounts of mutation. So while Figure 4B remains plausible in light of the study of Mouli et al. (2009) if reduction of mean heteroplasmy is the objective of the cell, it is also plausible that nonlinearities in mitochondrial output under cellular fusion (Hoitzing et al. 2015) result in intermediate fusion being optimal in terms of energy output in the context of nonselective fusion and selective mitophagy. Future experimental studies quantifying the importance of selective mitophagy under physiological conditions would be beneficial for understanding heteroplasmy variance dynamics. The ubiquity of heteroplasmy (Payne et al. 2012; Ye et al. 2014; Morris et al. 2017) suggests that a neutral-drift approach to mitochondrial genetics may be justified, which contrasts with the studies of Tam et al. (2013, 2015) and Mouli et al. (2009) which focus purely on the selective effects of mitochondrial networks.
To fully test our model, further single-cell longitudinal studies are required. For instance, the study by Burgstaller et al. (2018) found a linear increase in heteroplasmy variance through time in single oocytes. Our work here has shown that measurement of the network state, as well as turnover and copy number, are required to account for the rate of increase in heteroplasmy variance. Joint longitudinal measurements of , μ, and n, with heteroplasmy quantification, would allow verification of Equation 13 and aid in determining the extent to which neutral genetic models are explanatory. This could be achieved, for instance, using the mito-QC mouse (McWilliams et al. 2016) which allows visualization of mitophagy and mitochondrial architecture in vivo. Measurement of , μ, and n, followed by, e.g., destructive, single-cell, whole-genome sequencing of mtDNA would allow validation of how μ, n, and influence and the rate of de novo mutation (see Figure 3). One difficulty is sequencing errors induced through, e.g., PCR, which hampers our ability to accurately measure mtDNA mutation within highly heterogeneous samples (Woods et al. 2018). Morris et al. (2017) have suggested that single cells are highly heterogeneous in mtDNA mutation, with each mitochondrion possessing 3.9 single-nucleotide variants on average. Error-correction strategies during sequencing may pave the way toward high-accuracy mtDNA sequencing (Salk et al. 2018; Woods et al. 2018), and allow us to better constrain models of heteroplasmy dynamics.
Acknowledgments
We thank Hanne Hoitzing, Thomas McGrath, Abhishek Deshpande, and Ferdinando Insalata for useful discussions. Simulations were performed using the Imperial College High Performance Computing Service. J.A. acknowledges grant support from the Biotechnology and Biological Sciences Research Council (BB/J014575/1) and the Medical Research Council Mitochondrial Biology Unit (MC_UP_1501/2). N.S.J. acknowledges grant support from the British Heart Foundation (RE/13/2/30182) and Engineering and Physical Sciences Research Council (EP/N014529/1). I.G.J. acknowledges funding from European Research Council StG 805046 (EvoConBiO) and a Turing fellowship from the Alan Turing Institute.
Footnotes
Supplemental material available at FigShare: https://doi.org/10.25386/genetics.8343830.
Communicating editor: L. Wahl
Literature Cited
- Acton B., Lai I., Shang X., Jurisicova A., Casper R., 2007. Neutral mitochondrial heteroplasmy alters physiological function in mice. Biol. Reprod. 77: 569–576. 10.1095/biolreprod.107.060806 [DOI] [PubMed] [Google Scholar]
- Aryaman J., Johnston I. G., Jones N. S., 2017. Mitochondrial DNA density homeostasis accounts for a threshold effect in a cybrid model of a human mitochondrial disease. Biochem. J. 474: 4019–4034. 10.1042/BCJ20170651 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aryaman J., Johnston I. G., Jones N. S., 2019. Mitochondrial heterogeneity. Front. Genet. 9: 718 10.3389/fgene.2018.00718 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assaf M., Meerson B., 2010. Extinction of metastable stochastic populations. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 81: 021116 10.1103/PhysRevE.81.021116 [DOI] [PubMed] [Google Scholar]
- Bagwan N., Bonzon-Kulichenko E., Calvo E., Lechuga-Vieco A. V., Michalakopoulos S., et al. , 2018. Comprehensive quantification of the modified proteome reveals oxidative heart damage in mitochondrial heteroplasmy. Cell Rep. 23: 3685–3697.e4. 10.1016/j.celrep.2018.05.080 [DOI] [PubMed] [Google Scholar]
- Birky C. W., Maruyama T., Fuerst P., 1983. An approach to population and evolutionary genetic theory for genes in mitochondria and chloroplasts, and some results. Genetics 103: 513–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boudoures A. L., Saben J., Drury A., Scheaffer S., Modi Z., et al. , 2017. Obesity-exposed oocytes accumulate and transmit damaged mitochondria due to an inability to activate mitophagy. Dev. Biol. 426: 126–138. 10.1016/j.ydbio.2017.04.005 [DOI] [PubMed] [Google Scholar]
- Burgstaller J. P., Johnston I. G., Jones N. S., Albrechtová J., Kolbe T., et al. , 2014a. MtDNA segregation in heteroplasmic tissues is common in vivo and modulated by haplotype differences and developmental stage. Cell Rep. 7: 2031–2041. 10.1016/j.celrep.2014.05.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgstaller J. P., Johnston I. G., Poulton J., 2014b. Mitochondrial DNA disease and developmental implications for reproductive strategies. Mol. Hum. Reprod. 21: 11–22. 10.1093/molehr/gau090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgstaller J. P., Kolbe T., Havlicek V., Hembach S., Poulton J., et al. , 2018. Large-scale genetic analysis reveals mammalian mtDNA heteroplasmy dynamics and variance increase through lifetimes and generations. Nat. Commun. 9: 2488 10.1038/s41467-018-04797-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cagalinec M., Safiulina D., Liiv M., Liiv J., Choubey V., et al. , 2013. Principles of the mitochondrial fusion and fission cycle in neurons. J. Cell Sci. 126: 2187–2197. 10.1242/jcs.118844 [DOI] [PubMed] [Google Scholar]
- Capps G. J., Samuels D. C., Chinnery P. F., 2003. A model of the nuclear control of mitochondrial DNA replication. J. Theor. Biol. 221: 565–583. 10.1006/jtbi.2003.3207 [DOI] [PubMed] [Google Scholar]
- Chen H., Vermulst M., Wang Y. E., Chomyn A., Prolla T. A., et al. , 2010. Mitochondrial fusion is required for mtDNA stability in skeletal muscle and tolerance of mtDNA mutations. Cell 141: 280–289. 10.1016/j.cell.2010.02.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chinnery P. F., Samuels D. C., 1999. Relaxed replication of mtDNA: a model with implications for the expression of disease. Am. J. Hum. Genet. 64: 1158–1165. 10.1086/302311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Constable G. W., Rogers T., McKane A. J., Tarnita C. E., 2016. Demographic noise can reverse the direction of deterministic selection. Proc. Natl. Acad. Sci. USA 113: E4745–E4754. 10.1073/pnas.1603693113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cree L., Patel S., Pyle A., Lynn S., Turnbull D., et al. , 2008. Age-related decline in mitochondrial DNA copy number in isolated human pancreatic islets. Diabetologia 51: 1440–1443. 10.1007/s00125-008-1054-4 [DOI] [PubMed] [Google Scholar]
- Dai Y., Zheng K., Clark J., Swerdlow R. H., Pulst S. M., et al. , 2013. Rapamycin drives selection against a pathogenic heteroplasmic mitochondrial DNA mutation. Hum. Mol. Genet. 23: 637–647. 10.1093/hmg/ddt450 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Almeida M. J., Luchsinger L. L., Corrigan D. J., Williams L. J., Snoeck H. W., 2017. Dye-independent methods reveal elevated mitochondrial mass in hematopoietic stem cells. Cell Stem Cell 21: 725–729.e4. 10.1016/j.stem.2017.11.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dölle C., Flønes I., Nido G. S., Miletic H., Osuagwu N., et al. , 2016. Defective mitochondrial DNA homeostasis in the substantia nigra in Parkinson disease. Nat. Commun. 7: 13548 10.1038/ncomms13548 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durham S. E., Samuels D. C., Cree L. M., Chinnery P. F., 2007. Normal levels of wild-type mitochondrial DNA maintain cytochrome c oxidase activity for two pathogenic mitochondrial DNA mutations but not for m.3243A→G. Am. J. Hum. Genet. 81: 189–195. 10.1086/518901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elson J., Samuels D., Turnbull D., Chinnery P., 2001. Random intracellular drift explains the clonal expansion of mitochondrial DNA mutations with age. Am. J. Hum. Genet. 68: 802–806. 10.1086/318801 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Figge M. T., Reichert A. S., Meyer-Hermann M., Osiewacz H. D., 2012. Deceleration of fusion–fission cycles improves mitochondrial quality control during aging. PLoS Comput. Biol. 8: e1002576 10.1371/journal.pcbi.1002576 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardiner C., 1985. Stochastic Methods: A Handbook for the Natural and Social Sciences (Springer Series in Synergetics). Springer-Verlag, Berlin. [Google Scholar]
- Gillespie D. T., 1976. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 22: 403–434. 10.1016/0021-9991(76)90041-3 [DOI] [Google Scholar]
- Grima R., Thomas P., Straube A. V., 2011. How accurate are the nonlinear chemical Fokker-Planck and chemical Langevin equations? J. Chem. Phys. 135: 084103 10.1063/1.3625958 [DOI] [PubMed] [Google Scholar]
- Hoitzing, H., 2017 Controlling mitochondrial dynamics: population genetics and networks. Ph.D. Thesis, Imperial College London, London. [Google Scholar]
- Hoitzing H., Johnston I. G., Jones N. S., 2015. What is the function of mitochondrial networks? A theoretical assessment of hypotheses and proposal for future research. BioEssays 37: 687–700. 10.1002/bies.201400188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoitzing H., Gammage P. A., Johnston I. G., Minczuk M., Jones N. S., 2019. Energetic costs of cellular and therapeutic control of stochastic mitochondrial DNA populations. PLoS Comput Biol 15: e1007023 10.1371/journal.pcbi.1007023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobs K., 2010. Stochastic Processes for Physicists: Understanding Noisy Systems. Cambridge University Press, Cambridge, UK: 10.1017/CBO9780511815980 [DOI] [Google Scholar]
- Johnston I. G., 2019. Tension and resolution: dynamic, evolving populations of organelle genomes within plant cells. Mol. Plant 12: 764–783. 10.1016/j.molp.2018.11.002 [DOI] [PubMed] [Google Scholar]
- Johnston I. G., Jones N. S., 2016. Evolution of cell-to-cell variability in stochastic, controlled, heteroplasmic mtDNA populations. Am. J. Hum. Genet. 99: 1150–1162. 10.1016/j.ajhg.2016.09.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston I. G., Burgstaller J. P., Havlicek V., Kolbe T., Rülicke T., et al. , 2015. Stochastic modelling, bayesian inference, and new in vivo measurements elucidate the debated mtDNA bottleneck mechanism. eLife 4: e07464 10.7554/eLife.07464 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kandul N. P., Zhang T., Hay B. A., Guo M., 2016. Selective removal of deletion-bearing mitochondrial DNA in heteroplasmic drosophila. Nat. Commun. 7: 13100 10.1038/ncomms13100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kauppila T. E., Kauppila J. H., Larsson N.-G., 2017. Mammalian mitochondria and aging: an update. Cell Metab. 25: 57–71. 10.1016/j.cmet.2016.09.017 [DOI] [PubMed] [Google Scholar]
- Khrapko K., Vijg J., 2009. Mitochondrial DNA mutations and aging: devils in the details? Trends Genet. 25: 91–98. 10.1016/j.tig.2008.11.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim I., Rodriguez-Enriquez S., Lemasters J. J., 2007. Selective degradation of mitochondria by mitophagy. Arch. Biochem. Biophys. 462: 245–253. 10.1016/j.abb.2007.03.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M., 1955. Solution of a process of random genetic drift with a continuous model. Proc. Natl. Acad. Sci. USA 41: 144–150. 10.1073/pnas.41.3.144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M., 1969. The number of heterozygous nucleotide sites maintained in a finite population due to steady flux of mutations. Genetics 61: 893–903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kowald A., Kirkwood T. B., 2013. Mitochondrial mutations and aging: random drift is insufficient to explain the accumulation of mitochondrial deletion mutants in short-lived animals. Aging Cell 12: 728–731. 10.1111/acel.12098 [DOI] [PubMed] [Google Scholar]
- Kowald A., Kirkwood T. B., 2014. Transcription could be the key to the selection advantage of mitochondrial deletion mutants in aging. Proc. Natl. Acad. Sci. USA 111: 2972–2977. 10.1073/pnas.1314970111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kowald A., Kirkwood T., 2018. Resolving the enigma of the clonal expansion of mtdna deletions. Genes (Basel) 9: 126 10.3390/genes9030126 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kowald A., Klipp E., 2014. Mathematical models of mitochondrial aging and dynamics. Prog. Mol. Biol. Transl. Sci. 127: 63–92. 10.1016/B978-0-12-394625-6.00003-9 [DOI] [PubMed] [Google Scholar]
- Lewis S. C., Uchiyama L. F., Nunnari J., 2016. ER-mitochondria contacts couple mtDNA synthesis with mitochondrial division in human cells. Science 353: aaf5549 10.1126/science.aaf5549 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M., Schröder R., Ni S., Madea B., Stoneking M., 2015. Extensive tissue-related and allele-related mtDNA heteroplasmy suggests positive selection for somatic mutations. Proc. Natl. Acad. Sci. USA 112: 2491–2496. 10.1073/pnas.1419651112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieber T., Jeedigunta S. P., Palozzi J. M., Lehmann R., Hurd T. R., 2019. Mitochondrial fragmentation drives selective removal of deleterious mtDNA in the germline. Nature 570: 380–384. 10.1038/s41586-019-1213-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- López-Otín C., Blasco M. A., Partridge L., Serrano M., Kroemer G., 2013. The hallmarks of aging. Cell 153: 1194–1217. 10.1016/j.cell.2013.05.039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McWilliams T. G., Prescott A. R., Allen G. F., Tamjar J., Munson M. J., et al. , 2016. mito-QC illuminates mitophagy and mitochondrial architecture in vivo. J. Cell Biol. 214: 333– 345 10.1083/jcb.201603039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McWilliams T. G., Prescott A. R., Montava-Garriga L., Ball G., Singh F., et al. , 2018. Basal mitophagy occurs independently of PINK1 in mouse tissues of high metabolic demand. Cell Metab. 27: 439–449.e5. 10.1016/j.cmet.2017.12.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mengel-From J., Thinggaard M., Dalgård C., Kyvik K. O., Christensen K., et al. , 2014. Mitochondrial DNA copy number in peripheral blood cells declines with age and is associated with general health among elderly. Hum. Genet. 133: 1149–1159. 10.1007/s00439-014-1458-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishra P., Chan D. C., 2016. Metabolic regulation of mitochondrial dynamics. J. Cell Biol. 212: 379–387. 10.1083/jcb.201511036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris J., Na Y.-J., Zhu H., Lee J.-H., Giang H., et al. , 2017. Pervasive within-mitochondrion single-nucleotide variant heteroplasmy as revealed by single-mitochondrion sequencing. Cell Rep. 21: 2706–2713. 10.1016/j.celrep.2017.11.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mouli P. K., Twig G., Shirihai O. S., 2009. Frequency and selectivity of mitochondrial fusion are key to its quality maintenance function. Biophys. J. 96: 3509–3518. 10.1016/j.bpj.2008.12.3959 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narendra D., Tanaka A., Suen D.-F., Youle R. J., 2008. Parkin is recruited selectively to impaired mitochondria and promotes their autophagy. J. Cell Biol. 183: 795–803. 10.1083/jcb.200809125 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan J., Wang L., Lu C., Zhu Y., Min Z., et al. , 2019. Matching mitochondrial DNA haplotypes for circumventing tissue-specific segregation bias. iScience 13: 371–379. 10.1016/j.isci.2019.03.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patel P. K., Shirihai O., Huang K. C., 2013. Optimal dynamics for quality control in spatially distributed mitochondrial networks. PLoS Comput. Biol. 9: e1003108 10.1371/journal.pcbi.1003108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payne B. A., Wilson I. J., Yu-Wai-Man P., Coxhead J., Deehan D., et al. , 2012. Universal heteroplasmy of human mitochondrial DNA. Hum. Mol. Genet. 22: 384–390. 10.1093/hmg/dds435 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perier C., Bender A., García-Arumí E., Melia M. J., Bove J., et al. , 2013. Accumulation of mitochondrial DNA deletions within dopaminergic neurons triggers neuroprotective mechanisms. Brain 136: 2369–2378. 10.1093/brain/awt196 [DOI] [PubMed] [Google Scholar]
- Picard M., Zhang J., Hancock S., Derbeneva O., Golhar R., et al. , 2014. Progressive increase in mtDNA 3243A>G heteroplasmy causes abrupt transcriptional reprogramming. Proc. Natl. Acad. Sci. USA 111: E4033–E4042. 10.1073/pnas.1414028111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poovathingal S. K., Gruber J., Halliwell B., Gunawan R., 2009. Stochastic drift in mitochondrial DNA point mutations: a novel perspective ex silico. PLoS Comput. Biol. 5: e1000572 10.1371/journal.pcbi.1000572 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poovathingal S. K., Gruber J., Lakshmanan L., Halliwell B., Gunawan R., 2012. Is mitochondrial DNA turnover slower than commonly assumed? Biogerontology 13: 557–564. 10.1007/s10522-012-9390-7 [DOI] [PubMed] [Google Scholar]
- Rossignol R., Faustin B., Rocher C., Malgat M., Mazat J., et al. , 2003. Mitochondrial threshold effects. Biochem. J. 370: 751–762. 10.1042/bj20021594 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salk J. J., Schmitt M. W., Loeb L. A., 2018. Enhancing the accuracy of next-generation sequencing for detecting rare and subclonal mutations. Nat. Rev. Genet. 19: 269–285. 10.1038/nrg.2017.117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samuels D. C., Wonnapinij P., Cree L., Chinnery P. F., 2010. Reassessing evidence for a postnatal mitochondrial genetic bottleneck. Nat. Genet. 42: 471–472. 10.1038/ng0610-471 [DOI] [PubMed] [Google Scholar]
- Samuels D. C., Li C., Li B., Song Z., Torstenson E., et al. , 2013. Recurrent tissue-specific mtDNA mutations are common in humans. PLoS Genet. 9: e1003929 10.1371/journal.pgen.1003929 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schon E. A., DiMauro S., Hirano M., 2012. Human mitochondrial DNA: roles of inherited and somatic mutations. Nat. Rev. Genet. 13: 878–890. 10.1038/nrg3275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharpley M. S., Marciniak C., Eckel-Mahan K., McManus M., Crimi M., et al. , 2012. Heteroplasmy of mouse mtDNA is genetically unstable and results in altered behavior and cognition. Cell 151: 333–343. 10.1016/j.cell.2012.09.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solignac M., Génermont J., Monnerot M., Mounolou J.-C., 1987. Drosophila mitochondrial genetics: evolution of heteroplasmy through germ line cell divisions. Genetics 117: 687–696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart J. B., Chinnery P. F., 2015. The dynamics of mitochondrial DNA heteroplasmy: implications for human health and disease. Nat. Rev. Genet. 16: 530–542. 10.1038/nrg3966 [DOI] [PubMed] [Google Scholar]
- Stewart J. B., Larsson N.-G., 2014. Keeping mtDNA in shape between generations. PLoS Genet. 10: e1004670 10.1371/journal.pgen.1004670 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suen D.-F., Narendra D. P., Tanaka A., Manfredi G., Youle R. J., 2010. Parkin overexpression selects against a deleterious mtDNA mutation in heteroplasmic cybrid cells. Proc. Natl. Acad. Sci. USA 107: 11835–11840. 10.1073/pnas.0914569107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sukhorukov V. M., Dikov D., Reichert A. S., Meyer-Hermann M., 2012. Emergence of the mitochondrial reticulum from fission and fusion dynamics. PLoS Comput. Biol. 8: e1002745 10.1371/journal.pcbi.1002745 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szabadkai G., Simoni A. M., Bianchi K., De Stefani D., Leo S., et al. , 2006. Mitochondrial dynamics and Ca2+ signaling. Biochim. Biophys. Acta 1763: 442–449. 10.1016/j.bbamcr.2006.04.002 [DOI] [PubMed] [Google Scholar]
- Tam Z. Y., Gruber J., Halliwell B., Gunawan R., 2013. Mathematical modeling of the role of mitochondrial fusion and fission in mitochondrial DNA maintenance. PLoS One 8: e76230 10.1371/journal.pone.0076230 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tam Z. Y., Gruber J., Halliwell B., Gunawan R., 2015. Context-dependent role of mitochondrial fusion-fission in clonal expansion of mtDNA mutations. PLoS Comput. Biol. 11: e1004183 10.1371/journal.pcbi.1004183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor R. W., Barron M. J., Borthwick G. M., Gospel A., Chinnery P. F., et al. , 2003. Mitochondrial DNA mutations in human colonic crypt stem cells. J. Clin. Invest. 112: 1351–1360. 10.1172/JCI19435 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trifunovic A., Wredenberg A., Falkenberg M., Spelbrink J. N., Rovio A. T., et al. , 2004. Premature ageing in mice expressing defective mitochondrial DNA polymerase. Nature 429: 417–423. 10.1038/nature02517 [DOI] [PubMed] [Google Scholar]
- Twig G., Elorza A., Molina A. J., Mohamed H., Wikstrom J. D., et al. , 2008. Fission and selective fusion govern mitochondrial segregation and elimination by autophagy. EMBO J. 27: 433–446. 10.1038/sj.emboj.7601963 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wachsmuth M., Hübner A., Li M., Madea B., Stoneking M., 2016. Age-related and heteroplasmy-related variation in human mtDNA copy number. PLoS Genet. 12: e1005939 10.1371/journal.pgen.1005939 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wai T., Teoli D., Shoubridge E. A., 2008. The mitochondrial DNA genetic bottleneck results from replication of a subpopulation of genomes. Nat. Genet. 40: 1484–1488. 10.1038/ng.258 [DOI] [PubMed] [Google Scholar]
- Wallace D. C., Chalkia D., 2013. Mitochondrial DNA genetics and the heteroplasmy conundrum in evolution and disease. Cold Spring Harb. Perspect. Biol. 5: a021220 10.1101/cshperspect.a021220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wonnapinij P., Chinnery P., Samuels D., 2008. The distribution of mitochondrial DNA heteroplasmy due to random genetic drift. Am. J. Hum. Genet. 83: 582–593. 10.1016/j.ajhg.2008.10.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woods D. C., Khrapko K., Tilly J. L., 2018. Influence of maternal aging on mitochondrial heterogeneity, inheritance, and function in oocytes and preimplantation embryos. Genes (Basel) 9: 265 10.3390/genes9050265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye K., Lu J., Ma F., Keinan A., Gu Z., 2014. Extensive pathogenicity of mitochondrial heteroplasmy in healthy human individuals. Proc. Natl. Acad. Sci. USA 111: 10654–10659. 10.1073/pnas.1403521111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zamponi N., Zamponi E., Cannas S. A., Billoni O. V., Helguera P. R., et al. , 2018. Mitochondrial network complexity emerges from fission/fusion dynamics. Sci. Rep. 8: 363 10.1038/s41598-017-18351-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng W., Khrapko K., Coller H. A., Thilly W. G., Copeland W. C., 2006. Origins of human mitochondrial point mutations as DNA polymerase γ-mediated errors. Mutat. Res. 599: 11–20. 10.1016/j.mrfmmm.2005.12.012 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Code for simulations and analysis can be accessed at https://GitHub.com/ImperialCollegeLondon/MitoNetworksGenetics. Supplemental material available at FigShare: https://doi.org/10.25386/genetics.8343830.