Heritability in Plant Breeding on a Genotype-Difference Basis

Abstract

In plant breeding, heritability is often calculated (i) as a measure of precision of trials and/or (ii) to compute the response to selection. It is usually estimated on an entry-mean basis, since the phenotype is usually an aggregated value, as genotypes are replicated in trials, which stands in contrast with animal breeding and human genetics. When this was first proposed, assumptions such as balanced data and independent genotypic effects were made that are often violated in modern plant breeding trials/analyses. Due to this, multiple alternative methods have been proposed, aiming to generalize heritability on an entry-mean basis. In this study, we propose an extension of the concept for heritability on an entry-mean to an entry-difference basis, which allows for more detailed insight and is more meaningful in the context of selection in plant breeding, because the correlation among entry means can be accounted for. We show that under certain circumstances our method reduces to other popular generalized methods for heritability estimation on an entry-mean basis. The approach is exemplified via four examples that show different levels of complexity, where we compare six methods for heritability estimation on an entry-mean basis to our approach (example codes: https://github.com/PaulSchmidtGit/Heritability). Results suggest that heritability on an entry-difference basis is a well-suited alternative for obtaining an overall heritability estimate, and in addition provides one heritability per genotype as well as one per difference between genotypes.

THE idea behind measures of heritability as used in plant breeding is relatively simple: they express the proportion of the total phenotypic variance that is attributable to the average effects of genes, which in turn determines the degree of resemblance between relatives (Falconer and Mackay 2005, chapter 10). Lourenço et al. (2017) phrase it as “the extent to which a phenotype is genetically determined.” A phenotype is the composite of an organism’s observable traits. It results from (i) the expression of the organism’s genotype, (ii) the influence of environmental factors, and (iii) the interactions between both. Thus, heritability investigates the relationship between observed/phenotypic values with phenotypic variance ${\sigma }_p^2$ and their respective underlying true genotypic values $\left(\mathit{g}\right)$ with genotypic variance ${\sigma }_g^2$. We can furthermore dissect $\mathit{g}$ and ${\sigma }_g^2$ into additive, dominance, and epistasis components to extract average effects of alleles and breeding values $\left(\mathit{a}\right)$, with variance ${\sigma }_a^2$. Depending on whether genotypic values or breeding values are considered, we refer to broad-sense heritability $\left(H^2\right)$ or narrow-sense heritability $\left(h^2\right)$, respectively (e.g., Xu 2013). Accordingly, there is a clear distinction between $H^2$ and $h^2$. However, note that the approach presented in this article is relevant for both measures, which is why we will refer to heritability in general throughout this article, unless it is necessary to refer to one of the two specifically. The true genotypic/breeding values (and their variances) are of course unknown, but can be estimated/predicted from phenotypic data.

Piepho and Möhring (2007) pointed out that heritability was originally proposed in the context of animal breeding where the observations are collected from individuals, and are used in mixed models to estimate genetic parameters or breeding values by utilizing the additive genetic relationship of all individuals. It is important to note that in animal breeding, each individual usually has its own and unique genotype. Hence, an animal and a genotype refer to the same thing: a single individual. Naturally, this means that genotypes/animals cannot be truly replicated in or across environments. Instead, the same genotype/animal may only be measured repeatedly over time (Mrode and Thompson 2014, chapter 1.3.2) and/or via its progeny/relatives (Mrode and Thompson 2014, chapter 3.4). Repeated observations of individuals are either modeled by adding a random uncorrelated permanent environment effect to the mixed model or by treating repeated observations as different traits.

However, in plant breeding, we usually have crop cultivars/lines/varieties that are represented by a large group of individual plants with exactly the same genotype. This is mainly because most crop cultivars are clones, inbred lines, or hybrids. Thus, in contrast to animal breeding, a genotype in plant breeding does not refer to just a single individual, but to all individual plants belonging to the same cultivar and thus sharing the same genotype. In other words, a genotype in animal breeding is a single, genetically unique individual, whereas a genotype in plant breeding is usually a group of genetically identical individuals (though there are exceptions; see the Discussion). This allows for true replication of a genotype in and across multiple environments, even at a single time point and thus without repeated measurements in time. Notice that plant breeders may also decide to have repeated measures over time and/or account for observations of related genotypes, but the salient feature of plant genotypes as opposed to animal genotypes is the availability of true replication.

As a consequence, the multiple observations of the same cultivar are usually aggregated to obtain a single phenotypic value. Levels of aggregation range from individual plants to means of many plants, with the same genotype tested across several locations and years in designed experiments. The need for this aggregation in plant breeding results is an additional step that is not necessary in animal breeding. Since we do not consider analyses of individual plants in this article, the phenotypic value for a genotype will always be assumed to be some sort of mean value. In this context, heritability is referred to as heritability on an entry-mean (i.e., genotype-mean) basis, which stands in contrast with heritability in animal breeding and human genetics. This difference can also be deduced from the level of the heritability, which is usually much lower for complex traits in humans and animals compared to the entry-mean heritability of complex traits in plant breeding. Nowadays, the aggregation of the multiple observations into a mean phenotypic value per genotype is usually either done by best linear unbiased estimation (BLUE) or best linear unbiased prediction (BLUP). Note that the use of BLUPs here is not the same as in the framework of breeding value estimation typical for animal breeders (see Materials and Methods). The choice between BLUE and BLUP in plant breeding depends on the goal of the analysis and both are commonly used in practice [see Piepho et al. (2008), for more information and a review on the decision-making].

In early work on measures of heritability for plant breeding trials (e.g., Hanson and Robinson 1963), it was assumed that (i) the trial design is completely balanced/orthogonal, (ii) genotypic effects are independent, and (iii) variances and covariances are constant, so that the arithmetic mean across all observations for a genotype is the natural choice to aggregate to a single phenotypic value. We will from now on refer to such a scenario as the simple, balanced setting. Only in a simple, balanced setting does heritability have multiple direct interpretations. Specifically, $H^2$ is (I) the ratio of genetic variance to phenotypic variance, (II) the slope coefficient of a linear regression of the genotypic values on the phenotypic values $\left[{\gamma }_{ap}\right]$, (III) the squared correlation between genotypic values and phenotypic values $\left[r_{ap}^2\right]$, and (IV) the ratio of response to selection $\left[\text{Δ}G\right]$ to selection differential $\left[S\right]$ [see Falconer and Mackay (2005), pages 160 and 186]. For the simple, balanced setting, these interpretations can be represented by

$$H^2=\stackrel{I}{\overbrace{\frac{{\sigma }_{\mathit{g}}^2}{{\sigma }_p^2}}}=\stackrel{II}{\overbrace{{\gamma }_{gp}}}=\stackrel{III}{\overbrace{r_{gp}^2}}=\stackrel{IV}{\overbrace{\frac{\text{Δ}G}{S}}},$$ (1)

where $\text{Δ}G$ is often also referred to as the genetic gain and $S$ is the mean phenotypic value of the selected genotypes, expressed as a deviation from the population mean. Note that when heritability is estimated via (1)-IV, it is referred to as the realized heritability, as it requires $\text{Δ}G$ to be known, which means that selection has already occurred and that the offspring have been observed. By rewriting (1)-IV, we obtain the more directly interpretable breeder’s equation:

$$\text{Δ}G=H^{2}S,$$ (2)

which allows the prediction of the expected response to selection and is the key reason why heritability plays such an important role in plant (and animal) breeding. Hanson and Robinson (1963, page 128) get to the heart of it: “Heritability has value primarily as a method of quantifying the concept of whether progress from selection for a plant character is relatively easy or difficult to make in a breeding program. A plant breeder, through experience, can perhaps rate a series of characters on their response to selection. Heritability gives a numerical description of this concept.”

The standard method of estimating $H^2$ for phenotypic mean values is by plugging estimates for ${\sigma }_g^2$ and ${\sigma }_p^2$ into (1)-I. Given the simple, balanced setting, these variances can easily be estimated from mean squares and their respective expected mean squares of a conventional ANOVA (Yan 2014, chapter 1). For a single environment, where $n_g$ genotypes are tested in $n_r$ replicates in a completely randomized design (CRD), the observed data may be modeled as

$$y_{ik}=\mu +g_i+{\epsilon }_{ik},$$ (3)

where $y_{ik}$ is the $k$th observation of the $i$th genotype, $\mu$ is the intercept, $g_i$ is the effect for the $i$th genotype, and ${\epsilon }_{ik}$ is the plot error effect corresponding to $y_{ik}$. The phenotypic value of genotype $i$ can be obtained as the arithmetic mean across replicates, ${\overline{y}}_{i\cdot }$, which is also the BLUE in this simple, balanced setting. Assuming that $g_i$ and ${\epsilon }_{ik}$ are random, with independent distribution, zero mean, and variances ${\sigma }_g^2$ and ${\sigma }_{\epsilon }^2$, respectively, we can calculate the phenotypic variance of ${\overline{y}}_{i\cdot }$ as:

$${\sigma }_p^2={\sigma }_g^2+\frac{{\sigma }_{\epsilon }^2}{n_r}.$$ (4)

When genotypes are tested in a multienvironment trial (MET), where an environment denotes a year-by-location combination and CRDs are used at all environments, the observed data may be modeled as

$$y_{ikt}=\mu +g_i+e_t+{\left(ge\right)}_{it}+{\epsilon }_{ikt},$$ (5)

where $y_{ikt}$ is the $k$th observation of the $i$th genotype at the $t$th environment, $\mu$ is the intercept, $g_i$ is the main effect for the $i$th genotype, $e_t$ is the main effect for the $t$th environment, ${\left(ge\right)}_{it}$ is the $it$th genotype-by-environment interaction effect, and ${\epsilon }_{ikt}$ is the plot error effect corresponding to $y_{ikt}$. Again, since we have a simple, balanced setting, we can obtain phenotypic values as ${\overline{y}}_{i\cdot \cdot }=BLUE\left(\mu +g_i\right)$. Assuming that $g_i$, $e_t$, ${\left(ge\right)}_{it}$, and ${\epsilon }_{ikt}$ are random, with independent distributions, zero mean, and variances ${\sigma }_g^2$, ${\sigma }_e^2$, ${\sigma }_{ge}^2$ and ${\sigma }_{\epsilon }^2$, respectively, one may then calculate the phenotypic variance as

$${\sigma }_p^2={\sigma }_g^2+\frac{{\sigma }_{ge}^2}{n_e}+\frac{{\sigma }_{\epsilon }^2}{n_e{n}_r},$$ (6)

where $n_e$ is the number of environments (Hallauer et al. 2010, page 59). This approach assumes a single variance for genotype-by-environment interactions $\left(g\times e\right)$, even when multiple locations were tested across multiple years. In the latter case, one may instead model the environmental effects via separate year, and location main and interaction effects as

$$y_{ikmq}=\mu +g_i+f_m+l_q+{\left(fl\right)}_{mq}+{\left(gf\right)}_{im}+{\left(gl\right)}_{iq}+{\left(gfl\right)}_{imq}+{\epsilon }_{ikmq},$$ (7)

where $y_{ikmq}$ is the $k$th observation of the $i$th genotype in the $m$th year and the $q$th location, $\mu$is the intercept, $g_i$ is the main effect of the $i$th genotype, $f_m$ is the main effect for the $m$th year, $l_q$ is the main effect for the $q$th location, ${\left(fl\right)}_{mq}$ is the $mq$th year-by-location interaction effect, ${\left(gf\right)}_{im}$ is the $im$th genotype-by-year interaction effect, ${\left(gl\right)}_{iq}$ is the $iq$th genotype-by-location interaction effect, ${\left(gfl\right)}_{imq}$ is the $imq$th genotype-by-year-by-location interaction effect, and ${\epsilon }_{ikmq}$ is the plot error effect corresponding to $y_{ikmq}$. Once more, we have the phenotypic values for each genotype as ${\overline{y}}_{i\cdot \cdot \cdot }=BLUE\left(\mu +g_i\right)$. Assuming $g_i$, $f_m$, $l_q$, ${\left(fl\right)}_{mq}$, ${\left(gf\right)}_{im}$, ${\left(gl\right)}_{iq}$, ${\left(gfl\right)}_{imq}$, and ${\epsilon }_{ikmq}$ are random, with independent distribution, zero mean, and variances ${\sigma }_g^2$, ${\sigma }_f^2$, ${\sigma }_l^2$, ${\sigma }_{fl}^2$, ${\sigma }_{gf}^2$, ${\sigma }_{gl}^2$, ${\sigma }_{gfl}^2$, and ${\sigma }_{\epsilon }^2$, respectively, we can calculate the phenotypic variance as:

$${\sigma }_p^2={\sigma }_g^2+\frac{{\sigma }_{gl}^2}{n_l}+\frac{{\sigma }_{gf}^2}{n_f}+\frac{{\sigma }_{gfl}^2}{n_l{n}_f}+\frac{{\sigma }_{\epsilon }^2}{n_l{n}_f{n}_r},$$ (8)

where $n_f$ and $n_l$ are the number of years and locations, respectively (Becker 2011; Yan 2014). Note that when a MET is conducted either at multiple locations within a single year or at a single location but across multiple years, (8) simplifies to (6). We will refer to heritability estimates involving (4), (6), or (8) and (1)-I as the standard heritability $\left(H_{Std}^2\right)$.

By examining (4), (6), and (8), it can be seen that the calculation of ${\sigma }_p^2$ always involves the genotypic variance and all $g\times e$ variances. However, it does not incorporate purely environmental variance components, such as ${\sigma }_e^2$ in the context of (6), and ${\sigma }_f^2$, ${\sigma }_l^2$, and ${\sigma }_{fl}^2$ in the context of (8) [but see Yan (2014, page 3)]. Hence, referring to ${\sigma }_p^2$ as the phenotypic variance may be considered misleading, as it neglects the purely environmental effects and therefore is definitely not the variance of phenotypic mean values. However, a key feature of the perspective on heritability put forward in this paper is that ${\sigma }_p^2$, as defined in (3)–(8), actually coincides with half the variance of a difference between two phenotypic mean values in the simple, balanced setting. Taking (5) as an example, the variance of a genotype mean is

$$var\left({\overline{y}}_{i\cdot \cdot }\right)={\sigma }_g^2+\frac{{\sigma }_e^2}{n_e}+\frac{{\sigma }_{ge}^2}{n_e}+\frac{{\sigma }_{\epsilon }^2}{n_e{n}_r}\ne {\sigma }_p^2,$$ (9)

whereas the variance of a difference between means of genotypes $i$ and $j$ is $var\left({\overline{y}}_{i\cdot \cdot }\right)+var\left({\overline{y}}_{j\cdot \cdot }\right)-2cov\left({\overline{y}}_{i\cdot \cdot },{\overline{y}}_{j\cdot \cdot }\right)$, which in this simple, balanced setting reduces to

$$var\left({\overline{y}}_{i\cdot \cdot }-{\overline{y}}_{j\cdot \cdot }\right)=2\left({\sigma }_g^2+\frac{{\sigma }_{ge}^2}{n_e}+\frac{{\sigma }_{\epsilon }^2}{n_e{n}_r}\right)=2{\sigma }_p^2.$$ (10)

It can be argued that this focus on genotype “differences” makes more sense than a focus on genotype means or effects themselves, since the goal is to select the best-performing genotype(s) to maximize $\text{Δ}G$ and the ranking of genotypes is uniquely determined by all pairwise differences, whereas the individual genotypic effects and the absolute (mean) performance level as such do not inform about the ranking (Searle et al. 1992; Piepho et al. 2008). Accordingly, the correct ranking of genotypes and thus the precision of estimating genotype differences is more relevant than the precision of the genotype effect estimates. Furthermore, we found that especially in some older publications, the definitions of heritability refer to differences: Knight (1948) defines heritability as “the portion of the observed variance for which differences in heredity are responsible,” while Hanson and Robinson (1963, page 125) state that the “concept of heritability originated as an attempt to describe whether differences actually observed between individuals arose from the differences in genetic makeup between the individuals or resulted from different environmental forces.” Finally, it is no coincidence that two published alternative heritability estimation methods also involve the variance of a difference between genotypes: Cullis et al. (2006) proposed to calculate heritability as

$$H_{Cullis}^2=1-\frac{{\overline{v}}_{\text{Δ}\cdot \cdot }^{BLUP}}{2{\sigma }_g^2},$$ (11)

where ${\overline{v}}_{\text{Δ}\cdot \cdot }^{BLUP}$ is the mean variance of a difference of two BLUPs for the genotypic effect and ${\sigma }_g^2$ is the genotypic variance. The BLUE counterpart was suggested by Piepho and Möhring (2007) as

$$H_{Piepho}^2=\frac{{\sigma }_g^2}{{\sigma }_g^2+{\overline{v}}_{\text{Δ}\cdot \cdot }^{BLUE}/2},$$ (12)

where ${\overline{v}}_{\text{Δ}\cdot \cdot }^{BLUE}$ is the mean variance of a difference of two genotypic BLUEs and ${\sigma }_g^2$ is the genotypic variance. Both measures reduce to $H_{Std}^2$ in the simple, balanced setting.

These considerations suggest that heritability is best defined in terms of pairwise comparisons among genotypes, and this is in fact the key perspective taken in this paper. We aim to provide two things. First, an elaboration of how a heritability on an entry-difference basis $\left(H_{\text{Δ}}^2/h_{\text{Δ}}^2\right)$ can be defined. Second, a comparison of how the application of $H_{\text{Δ}}^2/h_{\text{Δ}}^2$ compares to other published methods for estimating heritability on an entry-mean basis. To do so, we give a derivation of $H_{\text{Δ}}^2$ and subsequently apply it alongside six other heritability measures in four example analyses with real data.

Materials and Methods

Mixed model theory

We assume a standard linear mixed model for the observed data vector $\mathit{y}$, which is of the form

$$\mathit{y}=\mathit{X\beta }+\mathit{Zu}+\mathit{\epsilon },$$ (13)

where $\mathit{\beta }$ and $\mathit{u}$ are vectors of fixed and random effects, respectively, $\mathit{X}$ and $\mathit{Z}$ are the associated design matrices, and $\mathit{\epsilon }$ is a vector of random residual errors. The random effects $\mathit{u}$ and $\mathit{\epsilon }$ are assumed to be independently distributed as $\mathit{u}\sim MVN\left(0,\mathit{G}\right)$ and $\mathit{\epsilon }\sim MVN\left(0,\mathit{R}\right)$, such that $\mathit{y}\sim MVN\left(\mathit{X\beta },\mathit{V}\right)$, where $MVN\left(.,.\right)$ denotes the multivariate normal distribution with a mean vector given as the first argument and a variance–covariance matrix as the second. To obtain estimates for $\mathit{\beta }$ as well as predictions for $\mathit{u}$, the mixed model equations (Henderson 1986; Searle et al. 1992) can be solved as

$$\left[\begin{array}{c}BLUE\left(\mathit{\beta }\right)\\ BLUP\left(\mathit{u}\right)\end{array}\right]=\mathit{C}\left[\begin{array}{c}{\mathit{X}}^{\prime }{\mathit{R}}^{-1}\mathit{y}\\ {\mathit{Z}}^{\prime }{\mathit{R}}^{-1}\mathit{y}\end{array}\right],$$ (14)

where

$$\mathit{C}=\left[\begin{array}{cc}{\mathit{C}}_{11}& {\mathit{C}}_{12}\\ {\mathit{C}}_{21}& {\mathit{C}}_{22}\end{array}\right]={\left[\begin{array}{cc}{\mathit{X}}^{\prime }{\mathit{R}}^{-1}\mathit{X}& {\mathit{X}}^{\prime }{\mathit{R}}^{-1}\mathit{Z}\\ {\mathit{Z}}^{\prime }{\mathit{R}}^{-1}\mathit{X}& {\mathit{Z}}^{\prime }{\mathit{R}}^{-1}\mathit{Z}+{\mathit{G}}^{-1}\end{array}\right]}^{-}.$$ (15)

Note that we will explicitly use the words “estimate/estimator” and “predict/predictor” for BLUEs and BLUPs, respectively. In the context of variety trials, genotype effects $\mathit{g}$ may be considered to be fixed or random. The choice between these two options depends on the goal of the analysis and both are commonly used in practice [see Piepho et al. (2008) for a review on decision-making as well as Appendix A]. Accordingly, we consider both as complementing cases in this article.

If $\mathit{g}$ is assumed to be a fixed effect, we obtain genotypic BLUEs $\left({\widehat{\mathit{g}}}^{BLUE}\right)$ as a subset of $BLUE\left(\mathit{\beta }\right)$ with $var\left({\widehat{\mathit{g}}}^{BLUE}|\mathit{g}\right)={\mathit{C}}_{11\left(\mathit{g}\right)}$ as the submatrix of ${\mathit{C}}_{11}$ associated with $\mathit{g}$. If $\mathit{g}$ is assumed to be a random effect, we obtain genotypic BLUPs $\left({\widehat{\mathit{g}}}^{BLUP}\right)$ as a subset of $BLUP\left(\mathit{u}\right)$ with $var\left({\widehat{\mathit{g}}}^{BLUP}|\mathit{g}\right)={\mathit{C}}_{22\left(\mathit{g}\right)}$ as the submatrix of ${\mathit{C}}_{22}$ associated with $\mathit{g}$. Note that in the case where $\mathit{g}$ is the only fixed/random effect in the model, its estimators/predictors and their variance matrices are not subsets of, but equal to, $BLUE\left(\mathit{\beta }\right)/BLUP\left(\mathit{u}\right)$ and ${\mathit{C}}_{11}/{\mathit{C}}_{22}$, respectively. Notice further that BLUPs can always be computed from entry means (BLUEs) using a stage-wise approach (see Appendix A). Only in the simple, balanced setting is the correlation of genotypic BLUEs and BLUPs equal to unity, and thus the ranking of genotypes does not change. On a side note, it should be mentioned that one may want to use linear combinations of $BLUE\left(\mathit{\beta }\right)$, such as, e.g., least squares means (SAS Institute Inc. 2013) or estimated marginal means (Searle et al. 2012) as phenotypic mean values instead. While this certainly results in different estimated values and (co)variances, it does not affect the heritability measures proposed in this article. This is because for all methods that rely on ${\widehat{\mathit{g}}}^{BLUE}$, the focus lies on differences, and any additional variance brought in via the linear combination with nongenetic effects cancels out when computing differences.

Example data sets

To exemplify the approach proposed in this article, we use four examples that show different levels of complexity. In examples 1 and 2, a single-environment data set (Wright 2017) is analyzed, while in example 3 a subset (i.e., a single environment) of the MET data set in example 4 (Hadasch et al. 2016) is analyzed.

Example 1:

The R-package agridat (Wright 2017) provides yield data from an oat trial at a single environment. The trial had 24 genotypes and was laid out as an $\alpha$-design, with three complete replicates and six incomplete blocks of size four within each replicate. Yet, in this first example, we will analyze the data as if the trial were laid out as CRD, and thus ignore the information about the complete replicates and incomplete blocks. Therefore, the model is simply

$$y_{ik}=\mu +g_i+{\epsilon }_{ik},$$ (16)

where $y_{ik}$ is the $k$th observation of the $i$th genotype, $\mu$ is the intercept, $g_i$ is the effect for the $i$th genotype, and ${\epsilon }_{ik}$ is the plot error effect corresponding to $y_{ik}$ with $var\left(\mathit{\epsilon }\right)={\mathit{I}}_{72}{\sigma }_{\epsilon }^2$. Accordingly, this example is a simple, balanced setting.

Example 2:

Here, we analyzed the same data set as in example 1, but included effects accounting for the trial’s design in the model

$$y_{iko}=\mu +g_i+r_k+b_{ko}+{\epsilon }_{iko},$$ (17)

where $y_{iko}$ is the observation of the $i$th genotype in the $o$th block of the $k$th replicate, $\mu$ is the intercept, $g_i$ is the effect for the $i$th genotype, $r_k$ is the effect for the $k$th replicate, $b_{ko}$ is the effect for the $o$th block in the $k$th replicate, and $e_{iko}$ is the plot error effect corresponding to $y_{iko}$ with $var\left(\mathit{\epsilon }\right)={\mathit{I}}_{72}{\sigma }_{\epsilon }^2$. To recover interblock information, $b_{ko}$ was modeled as random with $var\left(\mathit{b}\right)={\mathit{I}}_{18}{\sigma }_b^2$, whereas $r_k$ was taken as fixed.

Example 3:

This data set was taken from Hadasch et al. (2016). It comprises plot data of 89 lettuce varieties (i.e., “geno1”–“geno89”) tested at three environments (i.e., “env1”–“env3”), each laid out as a randomized complete block design (RCBD). The measured trait was resistance to downy mildew scored on a scale ranging from 0 to 5. We note that despite the acknowledged discreteness of this response variable, residual plots did not indicate an appreciable deviation of residuals from the normal distribution. All 89 varieties were genotyped with a total of 300 markers [i.e., 95 single nucleotide polymorphisms and 205 amplified fragment length polymorphism markers, see Hayes et al. (2014) for details] so that a marker matrix ${\mathit{M}}_{89\times 300}$ was provided. The biallelic marker $M_{iw}$ for the $i$th genotype, and the $w$th marker with alleles $A_1$ (i.e., the reference allele) and $A_2$, was coded as 1 for $A_1{A}_1$, −1 for $A_2{A}_2$, and 0 for $A_1{A}_2$ and $A_2{A}_1$. The kinship matrix $\mathit{K}$ was obtained as

$$\mathit{K}=\mathit{M}{\mathit{M}}^{\prime }.$$ (18)

We note that for our purposes, the scaling of M is largely immaterial, but see Appendix D for different scaling options of M and the associated interpretations of genetic variance. In this example, we analyzed only the second environment (“env2”) and thus have 89 genotypes at a single environment laid out as RCBD with three replicates, which we modeled as

$$y_{ik}=\mu +a_i+r_k+{\epsilon }_{ik},$$ (19)

where $y_{ik}$ is the observation of the $i$th genotype in the $k$th replicate, $\mu$ is the intercept, $a_i$ is the additive effect for the $i$th genotype, $r_k$ is the effect for the $k$th replicate, and ${\epsilon }_{ik}$ is the plot error effect corresponding to $y_{ik}$ with $var\left(\mathit{\epsilon }\right)={\mathit{I}}_{267}{\sigma }_{\epsilon }^2$. For simplicity, we assume here that there are no genetic effects for dominance or epistasis, but an extension of the model to cover this case is straightforward (Wellmann and Bennewitz 2011; Dias et al. 2018; Viana et al. 2018).

Example 4:

In contrast to example 3, we here analyzed all three environments jointly. The data set is not completely balanced, as (i) environment env1 has two complete replicates, while environments env2 and env3 have three, (ii) there are no observations for genotypes geno38 and geno49 at environment env1, and (iii) there are no observations for genotype geno81 at either env1 or env3. The linear mixed model used for this analysis was

$$y_{ikt}=\mu +a_i+e_t+{\left(ge\right)}_{it}+r_{kt}+{\epsilon }_{ikt},$$ (20)

where $y_{ikt}$ is the observation of the $i$th genotype in the $k$th replicate at the $t$th environment, $\mu$ is the intercept, $a_i$ is the additive effect for the $i$th genotype, $e_t$ is the effect for the $t$th environment, ${\left(ge\right)}_{it}$ is the $it$th genotype-by-environment interaction, $r_{kt}$ is the effect for the $k$th replicate at the $t$th environment, and ${\epsilon }_{ikt}$ is the plot error effect corresponding to $y_{ikt}$. We allowed for heterogeneous error variances between environments, assuming $var\left(\mathit{\epsilon }\right)={\mathbf{\oplus }}_{t=1}^{n_e}{\mathit{I}}_{{\mathit{n}}_{\mathit{obs}\left(\mathit{t}\right)}}{\sigma }_{{\epsilon }_t}^2$, where $\mathbf{\oplus }$ is the direct sum operator, and $n_{obs\left(t\right)}$ and ${\sigma }_{{\epsilon }_t}^2$ are the number of observations and plot error variance at the $t$th environment, respectively. Finally, $e_t$ and $r_k$ were taken as fixed effects, while ${\left(ge\right)}_{it}$ was taken as random with $var\left(\mathit{ge}\right)={\mathit{I}}_{263}{\sigma }_{ge}^2$.

Modeling of genotypic main effect in all examples:

Note that some of the heritability measures used in this article require estimates from both the model with a fixed genotype main effect as well as the model with a random genotype main effect. For example, $H_{Piepho}^2$ in (12) needs an estimate for ${\overline{v}}_{\text{Δ}\cdot \cdot }^{BLUE}$ as well as for ${\sigma }_g^2$. Thus, in this article we always fit both potential models in parallel, and accordingly obtain both ${\widehat{\mathit{g}}}^{BLUE}$ and ${\widehat{\mathit{g}}}^{BLUP}$ for the same example. For models where $\mathit{g}$ is assumed to be a random effect, we assume $var\left(\mathit{g}\right)={\mathit{I}}_{{\mathit{n}}_{\mathit{g}}}{\sigma }_g^2$. Additionally, we make use of the marker information in examples 3 and 4, and thus estimate additive genotypic effects $\mathit{a}$ by assuming $var\left(\mathit{a}\right)=\mathit{K}{\sigma }_a^2$.

Further, notice that for each example the variance components in the model with the fixed genotype main effect are fixed to the corresponding estimates in the model where $\mathit{g}$ is assumed to be a random effect. This is done to rule out the potential influence of an estimation error on variance component estimation between the two models (Schmidt et al. 2019).

Pairwise heritability

As shown in (1), heritability can be interpreted and thus estimated in multiple ways. To derive a pairwise heritability or heritability on an entry-difference basis $\left(H_{\text{Δ}}^2/h_{\text{Δ}}^2\right)$, we can exploit and slightly alter (1)-III so that it applies to phenotypic and genotypic differences instead of their respective mean values. We here first derive $H_{\text{Δ}}^2$ under the assumption of independent genotypic effects with constant variance and afterward generalize $H_{\text{Δ}}^2$ to correlated genotypic effects with nonconstant (co)variances. For both scenarios, we differentiate between ${\widehat{\mathit{g}}}^{BLUE}$ and ${\widehat{\mathit{g}}}^{BLUP}$.

Independent genotypic effects with constant variance:

Given independent genotypic effects with constant variance ${\sigma }_g^2$ (as in the simple, balanced setting), and irrespective of whether ${\widehat{\mathit{g}}}^{BLUE}$ or ${\widehat{\mathit{g}}}^{BLUP}$ is used, the variance of the true difference between genotypes $i$ and $j$ is

$$var\left(g_i-g_j\right)=2{\sigma }_g^2.$$ (21)

As stated before, the conditional variance, or prediction error variance, of the predicted BLUPs given the observed data is $var\left({\widehat{\mathit{g}}}^{BLUP}|\mathit{g}\right)={\mathit{C}}_{22\left(\mathit{g}\right)}$. However, notice that the marginal variance of ${\widehat{\mathit{g}}}^{BLUP}$is $var\left({\widehat{\mathit{g}}}^{BLUP}\right)={\mathit{G}}_{\left(\mathit{g}\right)}-{\mathit{C}}_{22\left(\mathit{g}\right)}$, where ${\mathit{G}}_{\left(\mathit{g}\right)}$ is the submatrix of $\mathit{G}$ associated with $\mathit{g}$ (see Searle et al. 1992, chapter 7.4.d.). As a result, we find that the variance of a difference between two BLUPs of genotypes $i$ and $j$ is

$$var\left({\widehat{g}}_i^{BLUP}-{\widehat{g}}_j^{BLUP}\right)=2{\sigma }_g^2-v_{\text{Δ}ij}^{BLUP},$$ (22)

where $v_{\text{Δ}ij}^{BLUP}$ is the prediction error variance of a difference between BLUPs of genotypes $i$ and $j$, and can be obtained via ${\mathit{C}}_{22\left(\mathit{g}\right)}$. Furthermore, we find the covariance to be

$$cov\left(g_i-g_j,{\widehat{g}}_i^{BLUP}-{\widehat{g}}_j^{BLUP}\right)=2{\sigma }_g^2-v_{\text{Δ}ij}^{BLUP}.$$ (23)

Hence, making use of (21), (22), and (23), the squared correlation between the true difference and its predictor, which is the heritability of the predictor of the difference $\left(g_i-g_j\right)$, is found to be

$$H_{\text{Δ}i{j}_{BLUP}}^2={\left(\frac{2{\sigma }_g^2-v_{\text{Δ}ij}^{BLUP}}{\sqrt{2{\sigma }_g^2\left(2{\sigma }_g^2-v_{\text{Δ}ij}^{BLUP}\right)}}\right)}^2=\frac{2{\sigma }_g^2-v_{\text{Δ}ij}^{BLUP}}{2{\sigma }_g^2}.$$ (24)

This pairwise heritability is a quantity that explicitly accounts for unbalanced data, is analogous to the coefficient of determination (CD) (Piepho 2019), and can be reported in its own right. Yet, as the number of genotypes increases, the number of genotype differences $n_{\text{Δ}}$ can quickly get very large $\left(n_{\text{Δ}}=n_g\left[n_g-1\right]/2\right)$. Thus, it is not a convenient statistic to report. However, the statistic can be averaged per genotype, so that a genotype-specific average heritability is obtained, i.e.

$${\overline{H}}_{\text{Δ}i{\cdot }_{BLUP}}^2=\frac{1}{n_g-1}{\displaystyle \sum _{j\ne i}{H}_{\Delta i{j}_{BLUP}}^2}.$$ (25)

Note that (25) is similar in spirit to the repeatability for an individual genotype’s BLUP as is commonly reported in animal breeding (Laloë 1993; Mrode and Thompson 2014). Finally, if we go further and instead average (24) across all pairs of genotypes, we obtain a single average pairwise heritability as

$${\overline{H}}_{\text{Δ}\cdot {\cdot }_{BLUP}}^2=\frac{2}{n_g\left(n_g-1\right)}{\displaystyle \sum _i{\displaystyle \sum _{j<i}{H}_{\Delta i{j}_{BLUP}}^2}}.$$ (26)

Hence, ${\overline{H}}_{\text{Δ}\cdot {\cdot }_{BLUP}}^2$ has the interpretation of an arithmetic mean of all pairwise heritabilities $H_{\Delta i{j}_{BLUP}}^2$ and is (given independent genotypic effects with constant variance) the algebraically equivalent simplification of $H_{Cullis}^2$, since the pairwise heritability in (24) has a constant denominator.

If ${\widehat{\mathit{g}}}^{BLUE}$ is used, we take the marginal variance of a difference between two BLUEs of genotypes $i$ and $j$ as

$$var\left({\widehat{g}}_i^{BLUE}-{\widehat{g}}_j^{BLUE}\right)=2{\sigma }_g^2+v_{\text{Δ}ij}^{BLUE},$$ (27)

where $v_{\text{Δ}ij}^{BLUE}$ is the variance of a difference between BLUEs of genotypes $i$ and $j$, and can be obtained via ${\mathit{C}}_{11\left(\mathit{g}\right)}$. Moreover,

$$cov\left(g_i-g_j,{\widehat{g}}_i^{BLUE}-{\widehat{g}}_j^{BLUE}\right)=2{\sigma }_g^2.$$ (28)

Analogous to (24), only this time applying (21), (27), and (28), the squared correlation between the true difference and its estimator, which is the heritability of the estimator of the difference $\left(g_i-g_j\right)$, is found to be

$$H_{\Delta i{j}_{BLUE}}^2={\left(\frac{2{\sigma }_g^2}{\sqrt{2{\sigma }_g^2\left(2{\sigma }_g^2+v_{\text{Δ}ij}^{BLUE}\right)}}\right)}^2=\frac{2{\sigma }_g^2}{2{\sigma }_g^2+v_{\text{Δ}ij}^{BLUE}}.$$ (29)

In accordance with (25) and (26), we could now take the arithmetic mean of $H_{\Delta i{j}_{BLUE}}^2$ per genotype and across all pairs. However, the inconvenient difference compared to ${\overline{H}}_{\text{Δ}\cdot {\cdot }_{BLUP}}^2$ in (24) is that the pairwise heritabilities in (29) do not have a constant denominator. As a result, taking the arithmetic mean across all $H_{\Delta i{j}_{BLUE}}^2$ does not lead to the algebraically equivalent simplification of $H_{Piepho}^2$. However, if we take the harmonic mean instead of the arithmetic mean for all pairwise heritabilities as

$${\overline{H}}_{\text{Δ}\cdot {\cdot }_{BLUE}}^2=\frac{n_g\left(n_g-1\right)}{2{\displaystyle {\sum }_i{\displaystyle {\sum }_{i<j}\frac{1}{H_{\Delta i{j}_{BLUE}}^2}}}},$$ (30)

the resulting average does indeed coincide with $H_{Piepho}^2$. Correspondingly, we take the harmonic mean per genotype as:

$${\overline{H}}_{\text{Δ}i{\cdot }_{BLUE}}^2=\frac{n_g-1}{{\displaystyle {\sum }_{i<j}\frac{1}{H_{\Delta i{j}_{BLUE}}^2}}}.$$ (31)

Notice that since we here assume independent genotypic effects with constant variance, both ${\overline{H}}_{\Delta \cdot {\cdot }_{BLUP}}^2$ and ${\overline{H}}_{\Delta \cdot {\cdot }_{BLUE}}^2$ can, in fact, also be obtained by averaging the numerator and denominator in (24) and (29) separately across pairs (see Appendix B).

Generalization to correlated genotypic effects with nonconstant variances:

So far, we have assumed independent genotypic effects with constant variance ${\sigma }_g^2$. Yet, the approach outlined above naturally extends to the case where effects have nonconstant variance, (i.e., $var\left(g_i\right)={\sigma }_{g\left(i,i\right)}^2$) and/or are correlated (i.e., $cov\left(g_i,g_j\right)={\sigma }_{g\left(i,j\right)}$), e.g., due to pedigree- or marker-based kinship. The variance of the true difference between genotypes $i$ and $j$ then becomes

$$var\left(g_i-g_j\right)={\sigma }_{g\left(i,i\right)}^2+{\sigma }_{g\left(j,j\right)}^2-2{\sigma }_{g\left(i,j\right)}.$$ (32)

When BLUP is used, the pairwise heritability in (24) accordingly generalizes to

$$H_{\Delta i{j}_{BLUP}}^2=\frac{var\left(g_i-g_j\right)-v_{\text{Δ}ij}^{BLUP}}{var\left(g_i-g_j\right)}=\frac{{\sigma }_{g\left(i,i\right)}^2+{\sigma }_{g\left(j,j\right)}^2-2{\sigma }_{g\left(i,j\right)}-v_{\text{Δ}ij}^{BLUP}}{{\sigma }_{g\left(i,i\right)}^2+{\sigma }_{g\left(j,j\right)}^2-2{\sigma }_{g\left(i,j\right)}}.$$ (33)

When BLUE is used, the pairwise heritability in (29) generalizes to

$$H_{\Delta i{j}_{BLUE}}^2=\frac{var\left(g_i-g_j\right)}{var\left(g_i-g_j\right)+v_{\text{Δ}ij}^{BLUE}}=\frac{{\sigma }_{g\left(i,i\right)}^2+{\sigma }_{g\left(j,j\right)}^2-2{\sigma }_{g\left(i,j\right)}}{{\sigma }_{g\left(i,i\right)}^2+{\sigma }_{g\left(j,j\right)}^2-2{\sigma }_{g\left(i,j\right)}+v_{\text{Δ}ij}^{BLUE}}.$$ (34)

These pairwise heritabilities can be averaged as before, i.e., as per Equations (25) and (26) for BLUP, and Equations (31) and (30) for BLUE, to obtain $H_{\text{Δ}i\cdot }^2$ and $H_{\text{Δ}\cdot \cdot }^2$. Unfortunately, the average over all pairwise heritabilities cannot generally be simplified algebraically for either BLUE or BLUP, since in both cases neither the denominator nor the numerator of the pairwise heritability is constant. But a simplification is forthcoming if, as an approximation, we average the numerator and denominator of the pairwise heritability separately (see Appendix C).

Other proposals to compute heritability

Besides $H_{Std}^2$, $H_{Cullis}^2$ (11), and $H_{Piepho}^2$ (12), we calculated three additional generalized heritability measures that are in common usage.

H² Oakey:

An alternative measure of heritability, which is sometimes referred to as the generalized heritability, can be traced back to Laloë (1993) and was proposed by Oakey et al. (2006) in the context of plant breeding. It has gained popularity due to its ability to account for heterozygosity/covariances in ${\mathit{G}}_{\left(\mathit{g}\right)}$ (e.g., Mathews et al. 2008; Rodríguez-Álvarez et al. 2018). In this approach, contrasts of the true and predicted genotypic effects are defined as ${\mathit{c}}^{\prime }\mathit{g}$ and ${\mathit{c}}^{\prime }{\widehat{\mathit{g}}}^{BLUP}$, respectively. Note that, unlike for $H_{\text{Δ}}^2$ where all differences/contrasts between genotype pairs are considered, the contrast vector $\mathit{c}$ can be any linear combination of genotypic effects where the elements of $\mathit{c}$ sum to 0. This allows different genotypic effects to have different heritabilities, while at the same time reducing to a single scalar quantity. Similar to our derivation, they make use of (1)-III, with the difference that it applies to ${\mathit{c}}^{\prime }\mathit{g}$ and ${\mathit{c}}^{\prime }{\widehat{\mathit{g}}}^{BLUP}$, and thus represents the squared correlation between the true and predicted genotypic contrasts defined by $\mathit{c}$. The vector $\mathit{c}$ is then chosen so that this squared correlation (i.e., the heritability) is maximized. Components of the full heritability are defined as

$$\mathit{\lambda }={\left(\frac{cov\left({\mathit{c}}^{\prime }\mathit{g},\mathit{ }{\mathit{c}}^{\prime }{\widehat{\mathit{g}}}^{BLUP}\right)}{\sqrt{var\left({\mathit{c}}^{\prime }\mathit{g}\right)var\left({\mathit{c}}^{\prime }{\widehat{\mathit{g}}}^{BLUP}\right)}}\right)}^2=\frac{{\mathit{c}}^{\prime }{\mathit{G}}_{\left(\mathit{g}\right)}\left({\mathit{I}}_{{\mathit{n}}_{\mathit{g}}}-{\mathit{G}}_{\left(\mathit{g}\right)}^{-1}{\mathit{C}}_{22\left(\mathit{g}\right)}\right)\mathit{c}}{{\mathit{c}}^{\prime }{\mathit{G}}_{\left(\mathit{g}\right)}\mathit{c}}=\frac{{\mathit{c}}^{\prime }{\mathit{G}}_{\left(\mathit{g}\right)}\mathit{Dc}}{{\mathit{c}}^{\prime }{\mathit{G}}_{\left(\mathit{g}\right)}\mathit{c}},$$ (35)

where $\mathit{c}$ is an eigenvector of the matrix $\mathit{D}={\mathit{I}}_{{\mathit{n}}_{\mathit{g}}}-{\mathit{G}}_{\left(\mathit{g}\right)}^{-1}{\mathit{C}}_{22\left(\mathit{g}\right)}$ with constraint ${\mathit{c}}^{\prime }{\mathit{G}}_{\left(\mathit{g}\right)}\mathit{c}=1$ and $\mathit{\lambda }$ is the associated eigenvalue. The largest among the eigenvalues, ${\lambda }_{\zeta }$ $\left(\zeta =\left\{1,\dots ,n_{\lambda }\right\}\right)$, equals the maximized squared correlation of ${\mathit{c}}^{\prime }\mathit{g}$ and ${\mathit{c}}^{\prime }{\widehat{\mathit{g}}}^{BLUP}$. Note that $n_{\lambda }=n_g$ and due to constraints on ${\widehat{\mathit{g}}}^{BLUP}$, $n_z<n_g$ eigenvalues will be zero. The generalized heritability is then defined as the mean of all nonzero eigenvalues:

$$H_{Oakey}^2=\frac{{\displaystyle {\sum }_{\zeta =1}^{n_g}{\lambda }_{\zeta }}}{n_g-n_z}=\frac{{\displaystyle {\sum }_{\zeta =n_z+1}^{n_g}{\lambda }_{\zeta }}}{n_g-n_z}.$$ (36)

In more recent work, Rodríguez-Álvarez et al. (2018) show how random spatial variation in plant breeding experiments can be analyzed using tensor product P-splines, which is a two-dimensional smoothing technique. In this context, they denote the trace of $\mathit{D}$ as the effective dimension of the genotypic effects and reexpress $H_{Oakey}^2$ as:

$$H_{Oakey}^2=\frac{trace\left(\mathit{D}\right)}{n_g-n_z}.$$ (37)

They point out that the notion of effective dimension is well known in the smoothing context, where it can be interpreted as a complexity measure for a given model and its component effects.

Simulated:

This method was proposed by Piepho and Möhring (2007), and is also based on the squared correlation between $\mathit{g}$ and ${\widehat{\mathit{g}}}^{BLUP}$ in (1)-III. It first defines the variance–covariance matrix of all random effects $\mathit{u}$ and the target genotypic effects $\mathit{g}$ as

$$var\left(\begin{array}{c}\mathit{g}\\ \mathit{u}\end{array}\right)=\left(\begin{array}{cc}{\mathit{G}}_{\left(\mathit{g}\right)}& \mathit{U}\\ {\mathit{U}}^{\prime }& \mathit{G}\end{array}\right),$$ (38)

so that $\mathit{U}=cov\left(\mathit{g},\mathit{u}\right)$. They then define $\mathit{\Omega }$ as the variance–covariance matrix of the joint distribution of the true and predicted genotypic effects:

$$\mathit{\Omega }=var\left(\begin{array}{c}\mathit{g}\\ {\widehat{\mathit{g}}}^{BLUP}\end{array}\right)=\left(\begin{array}{cc}{\mathit{G}}_{\left(\mathit{g}\right)}& \mathit{F}{\mathit{G}}^{-1}\left(\mathit{G}-{\mathit{C}}_{22}\right){\mathit{G}}^{-1}{\mathit{F}}^{\prime }\\ \mathit{F}{\mathit{G}}^{-1}\left(\mathit{G}-{\mathit{C}}_{22}\right){\mathit{G}}^{-1}{\mathit{F}}^{\prime }& \mathit{F}{\mathit{G}}^{-1}\left(\mathit{G}-{\mathit{C}}_{22}\right){\mathit{G}}^{-1}{\mathit{F}}^{\prime }\end{array}\right) ,$$ (39)

where $\mathit{F}=\left(\begin{array}{cc}{\mathit{G}}_{\left(\mathit{g}\right)}& \mathit{U}\end{array}\right)$. Subsequently, $\mathit{\Omega }$ can be decomposed as $\mathit{\Omega }=\mathit{\Gamma }{\mathit{\Gamma }}^{\prime }$ by singular value decomposition or Cholesky decomposition. Finally, values for $\mathit{g}$ and ${\widehat{\mathit{g}}}^{BLUP}$ can be simulated (i.e., ${\mathit{g}}_{\mathit{sim}}$ and ${\widehat{\mathit{g}}}_{\mathit{sim}}^{\mathit{BLUP}}$) for an experiment, with the same design and genotypic relationships as those underlying the actual data $\mathit{y}$, as

$${\mathit{d}}_{\mathit{sim}}=\left(\begin{array}{c}{\mathit{g}}_{\mathit{sim}}\\ {\widehat{\mathit{g}}}_{\mathit{sim}}^{\mathit{BLUP}}\end{array}\right)=\mathit{\Gamma }{\mathit{z}}_{\mathit{sim}},$$ (40)

where ${\mathit{z}}_{\mathit{sim}}$ is a vector with $2n_g$ simulated random independent standard normal deviates. Thus, for each of the $n_{sim}=\left\{1, \dots ,s\right\}$ simulation runs, a new vector ${\mathit{z}}_{\mathit{sim}}$ of independent standard normal deviates is randomly generated, so that we can obtain ${\mathit{d}}_{\mathit{sim}}$, and compute the squared sample correlation $\left(r_s^2\right)$ of ${\mathit{g}}_{\mathit{sim}}$ and ${\widehat{\mathit{g}}}_{\mathit{sim}}^{\mathit{BLUP}}$. By running a large number of simulations, we can obtain the simulated expected squared correlation of predicted and true genotypic effects as

$$H_{sim}^2=\frac{1}{n_{sim}}{\displaystyle \sum _{s=1}^{n_{sim}}{r}_s^2}.$$ (41)

Notice that even in the simple, balanced setting, this method is not exactly identical to $H_{Std}^2$, but it is asymptotically equivalent for an increasing number of genotypes:

$$H_{sim}^2=E\left(r_{g,\widehat{g}}^2\right)\approx {\left(\frac{cov\left(\mathit{g},{\widehat{\mathit{g}}}^{BLUP}\right)}{\sqrt{var\left(\mathit{g}\right)var\left({\widehat{\mathit{g}}}^{BLUP}\right)}}\right)}^2=H_{Std}^2.$$ (42)

It can be argued that $H_{sim}^2$ is preferable over, e.g., $H_{Piepho}^2$ or $H_{Cullis}^2$, as it captures the entire variance–covariance structure in the data in a more comprehensive manner (Piepho and Möhring 2007; Schmidt et al. 2019). Further notice that this approach also allows direct simulation of the response to selection (see Appendix E).

Reliability:

In animal breeding and thus mostly in the context of a single observation per genotype, the reliability $\left(r^2\right)$, also known as the CD, is a popular statistic expressing the squared correlation between predicted and true breeding value, and is closely related to heritability (Laloë et al. 1996; Laloë and Phocas 2003; Kuehn et al. 2007; Piepho 2019). We can estimate the reliability for the (genotypic/breeding value of the) $i$th entry as

$$r_i^2=1-\frac{var\left({\widehat{g}}_i^{BLUP}\right)}{var\left(g_i\right)},$$ (43)

where $var\left({\widehat{g}}_i^{BLUP}\right)$ is the $i$th diagonal element of the ${\mathit{C}}_{22\left(\mathit{g}\right)}$ matrix and $var\left(g_i\right)$ is $i$th diagonal element of the ${\mathit{G}}_{\left(\mathit{g}\right)}$ matrix (Mrode and Thompson 2014, chapter 9.3.4.). Accordingly, $r_i^2$ does not account for the off-diagonal elements of either ${\mathit{C}}_{22\left(\mathit{g}\right)}$ or ${\mathit{G}}_{\left(\mathit{g}\right)}$ [but see Mrode and Thompson (2014), Appendix D]. We can further obtain the mean reliability as

$${\overline{r}}_{\cdot }^2=\frac{1}{n_g}{\displaystyle \sum _{i=1}^{n_g}{r}_i^2}.$$ (44)

Computation of heritability measures:

As summarized in Table 1, we computed eight overall heritability measures ($H_{Std}^2$,${\overline{H}}_{\text{Δ}\cdot {\cdot }_{BLUE}}^2$, $H_{Piepho}^2$, ${\overline{H}}_{\text{Δ}\cdot {\cdot }_{BLUP}}^2$, $H_{Cullis}^2$, $H_{Oakey}^2$, ${\overline{r}}_{\cdot }^2$, and $H_{Sim}^2$), three genotype-wise heritability measures (${\overline{H}}_{\text{Δ}i{\cdot }_{BLUE}}^2$, ${\overline{H}}_{\text{Δ}i{\cdot }_{BLUP}}^2$, and $r_i^2$), and two pair-wise heritability measures ($H_{\Delta i{j}_{BLUE}}^2$ and $H_{\Delta i{j}_{BLUP}}^2$) for each of the four examples. When assuming $var\left(\mathit{a}\right)=\mathit{K}{\sigma }_a^2$ for examples 3 and 4, we are estimating narrow-sense heritabilities, otherwise broad-sense heritabilities were computed. The former is not possible for $H_{Std}^2$, $H_{Cullis}^2$, and $H_{Piepho}^2$, however, as these measures implicitly assume a constant genotypic variance and no covariances. We therefore based estimates of these heritability measures on the alternative model that assumes $var\left(\mathit{g}\right)={\mathit{I}}_{{\mathit{n}}_{\mathit{g}}}{\sigma }_g^2$ and accordingly completely ignores marker information. Finally, we used an ad hoc solution to compute $H_{Std}^2$ via (6) in example 4, where we had slightly unbalanced data and environment-specific error variance estimates. Although only 86 out of 89 genotypes were present at all three environments, and one environment only had two replicates instead of three, we considered $n_e=n_r=3.$ Thus, we took the respective maximum value, which is often done in practice. Furthermore, we computed the mean error variance as ${\sigma }_{\epsilon }^2={\displaystyle \sum {\sigma }_{{\epsilon }_t}^2/n_e}$.

Table 1. Summary of heritability measures.

Heritability measure			Accounts for heteroscedasticity/covariances
Overall	Per genotype	Per pair	In ${\mathit{G}}_{\left(\mathit{g}\right)}$	In ${\mathit{C}}_{11\left(\mathit{g}\right)}$	In ${\mathit{C}}_{22\left(\mathit{g}\right)}$
$H_{Std}^2$	—	—	No/no	No/no	—
${\overline{H}}_{\text{Δ}\cdot {\cdot }_{BLUE}}^2$	${\overline{H}}_{\text{Δ}i{\cdot }_{BLUE}}^2$	$H_{\Delta i{j}_{BLUE}}^2$	Yes/yes	Yes/yes	—
$H_{Piepho}^2$	—	—	No/no	Yes/yes	—
${\overline{H}}_{\text{Δ}\cdot {\cdot }_{BLUP}}^2$	${\overline{H}}_{\text{Δ}i{\cdot }_{BLUP}}^2$	$H_{\Delta i{j}_{BLUP}}^2$	Yes/yes	—	Yes/yes
$H_{Cullis}^2$	—	—	No/no	—	Yes/yes
$H_{Oakey}^2$	—	—	Yes/yes	—	Yes/yes
${\overline{r}}_{\cdot }^2$	$r_i^2$	—	Yes/no	—	Yes/no
$H_{sim}^2$	—	—	Yes/yes	—	Yes/yes

Software:

All statistical analyses were done by REML with the mixed model package ASReml-R version 3.0 (Gilmour et al. 2009) in the R Statistical Computing Environment (R Core Team 2015) and SAS 9.4 (SAS Institute Inc. 2013).

Data availability

The data used in examples 1 and 2 are the “john.alpha” data set provided in the R package agridat (Wright 2017), which is available at https://cran.r-project.org/web/packages/agridat/index.html. Supplemental material and the data used in examples 3 and 4 are available at https://figshare.com/articles/Lettuce_trial_phenotypic_and_marker_data_/8299493. R code is available at https://github.com/PaulSchmidtGit/Heritability.

Results

In this section, we present overall heritability estimates first, followed by genotype-wise and finally pairwise heritability estimates. The results are accompanied by minimal interpretations, whereas an elaboration on general reasons for differences between estimates of the different methods is provided in the Discussion.

Overall heritability

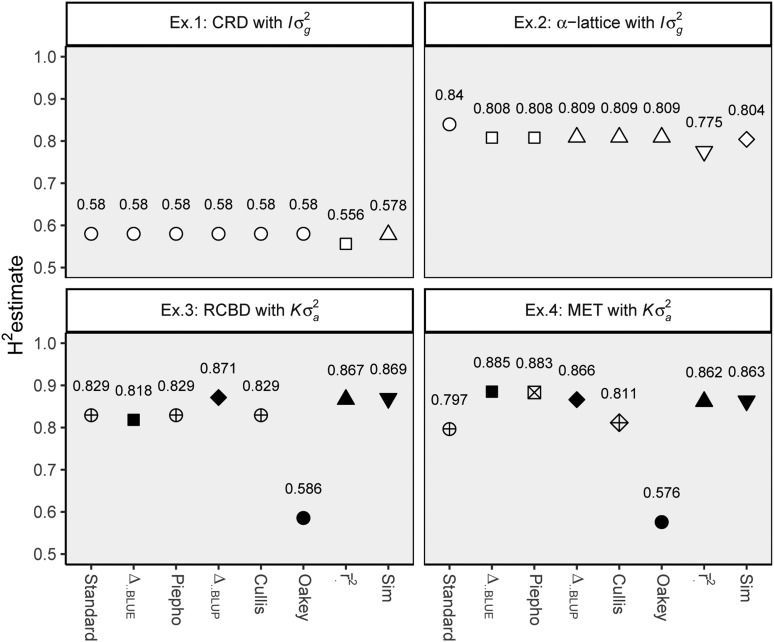
Figure 1 shows estimates for overall heritability obtained via all eight methods for all examples. As expected for the simple, balanced setting of example 1, all estimates are identical, except for the slightly smaller estimates obtained for ${\overline{r}}_{\cdot }^2$ and $H_{sim}^2$. A similar picture is found for example 2, with the exception of $H_{Std}^2$ displaying a notably larger estimate than the rest, which is due to the method’s inability to account for the variance of the random incomplete block effect. Examples 3 and 4 show a more heterogeneous picture, with $h_{Oakey}^2$ displaying estimates that are strikingly lower than the rest.

Figure 1.

Overall heritability estimates for each method and example. For clearer comparison, (i) estimated values are shown above each symbol and (ii) within each experiment identical values show the same symbol. Black symbols indicate that $var\left(\mathit{a}\right)=\mathit{K}{\sigma }_a^2$ was assumed for the estimation, whereas for white symbols $var\left(\mathit{g}\right)=\mathit{I}{\sigma }_g^2$ was assumed. BLUE, best linear unbiased estimation; BLUP, best linear unbiased prediction; CRD, completely randomized design; Ex, example; RCBD, randomized complete block design.

Genotype-wise heritability

In example 1, estimates for the pairwise heritability measures $H_{\text{Δ}i{j}_{BLUE}}^2$ and $H_{\text{Δ}i{j}_{BLUP}}^2$ were constant across all pairs (≈0.580), and hence equal to ${\overline{H}}_{\text{Δ}i{\cdot }_{BLUE}}^2$, ${\overline{H}}_{\text{Δ}i{\cdot }_{BLUP}}^2$, ${\overline{H}}_{\text{Δ}\cdot {\cdot }_{BLUE}}^2$, and ${\overline{H}}_{\text{Δ}\cdot {\cdot }_{BLUP}}^2$, which in turn were equal to $H_{Std}^2$, $H_{Cullis}^2$, and $H_{Oakey}^2$. Analogously, the slightly lower $r_i^2$ estimates were also constant (≈0.556) across genotypes and, therefore, equal to ${\overline{r}}_{\cdot }^2$.

In example 2, estimates for genotype-wise heritability measures were no longer constant, neither between nor within each method. Instead, each method found two unique, but relatively similar, estimates and each one for half of the genotypes, respectively, i.e., 0.80792 and 0.80801 for ${\overline{H}}_{\text{Δ}i{\cdot }_{BLUE}}^2$, 0.80911 and 0.80916 for ${\overline{H}}_{\text{Δ}i{\cdot }_{BLUP}}^2$, and 0.77537 and 0.77547 for $r_i^2$.

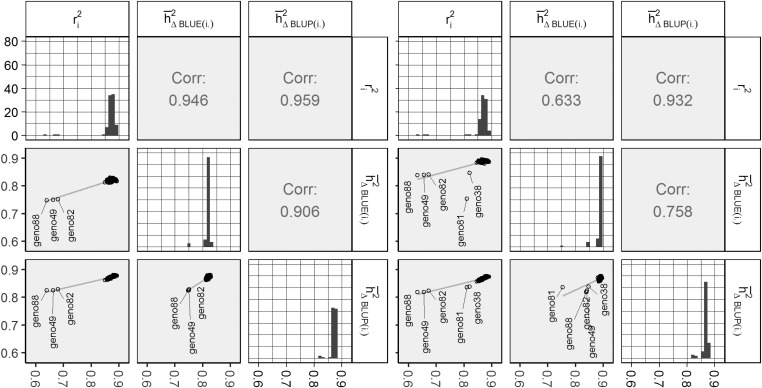
Figure 2 details the heritability estimates per genotype for examples 3 and 4. It can be seen that the estimates are much more heterogeneous compared to examples 1 and 2. In fact, all of the 89 genotype-wise estimates per method were different from each other in both example 3 and example 4. In both of the latter, and irrespective of the heritability method, genotypes geno49, geno82, and geno88 showed noticeably lower estimates than the rest. This is related to the fact that the additive variances of these three genotypes stand out with a size of only ≈30% of the average (results not shown). We additionally found relatively low estimates for geno49 and geno81 (i.e., two of the genotypes with missing observations) in example 4 (Figure 2).

Figure 2.

Summary plot for genotype-wise heritability estimates for example 3 (left) and example 4 (right). Plots on the bottom left show scatter plots with simple linear regression lines and genotype-labels for outlying estimates. The plots on the diagonal show histograms for the respective column. The upper right corner displays the Pearson correlation estimate. BLUE, best linear unbiased estimation; BLUP, best linear unbiased prediction; Corr, correlation.

In example 3, estimates between the three methods all showed correlations larger than 0.9, with ${\overline{h}}_{\text{Δ}i{\cdot }_{BLUP}}^2$ and $r_i^2$ displaying the highest correlation of ∼0.959. In example 4, the correlation between these two was still high (≈0.932), while the other two correlation estimates dropped below 0.76 (Figure 2).

Pairwise heritability

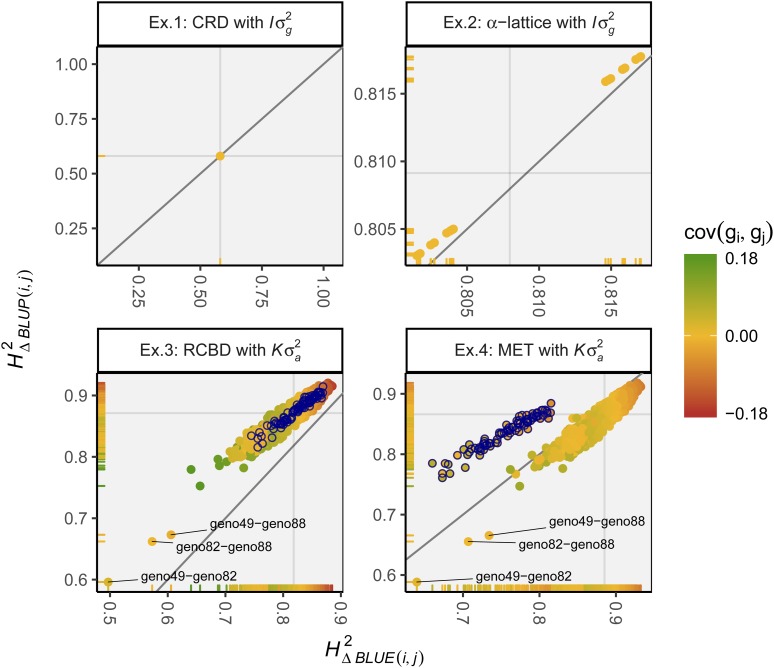
Figure 3 details the estimated pairwise heritability measures for all examples. As mentioned above, estimates for $H_{\Delta i{j}_{BLUE}}^2$ and $H_{\Delta i{j}_{BLUP}}^2$ in example 1 were constant across all $n_{\text{Δ}}=276$ genotype pairs (≈0.580). In example 2, estimates for each method split into two clusters, respectively, yet even the overall estimate ranges were relatively small (0.802–0.817 for $H_{\Delta i{j}_{BLUE}}^2$ and 0.803–0.818 for $H_{\Delta i{j}_{BLUP}}^2$). The heterogeneous estimates in example 2 are due to the recovery of interblock information via the random incomplete block effect in (17). It results from the varying number of times two genotypes (or even their neighboring genotypes) appear together in the same incomplete block and thus can be compared directly (John and Williams 1995).

Figure 3.

All pairwise heritability estimates. Color indicates covariance in ${\mathit{G}}_{\left(\mathit{g}\right)}$ for the respective pair. Circles with blue border are pairs with genotype “geno81,” which is only present at a single environment. Vertical and horizontal gray lines represent ${\overline{H}}_{\text{Δ}\cdot {\cdot }_{BLUE}}^2$ and ${\overline{H}}_{\text{Δ}\cdot {\cdot }_{BLUP}}^2$ for examples 1 and 2, and ${\overline{h}}_{\text{Δ}\cdot {\cdot }_{BLUE}}^2$ and ${\overline{h}}_{\text{Δ}\cdot {\cdot }_{BLUP}}^2$ for examples 3 and 4. BLUE, best linear unbiased estimation; BLUP, best linear unbiased prediction; CRD, completely randomized design; Ex, example; MET, multienvironment trial; RCBD, randomized complete block design.

Estimates in example 3 mostly form a single cluster for both methods, respectively, ranging from ∼0.70–0.88 for $H_{\Delta i{j}_{BLUE}}^2$ and 0.80–0.92 for $H_{\Delta i{j}_{BLUP}}^2$, so that the cluster is located left of/above the diagonal in Figure 3. There are three exceptionally low estimates for both methods, which are those of the differences geno49–geno82, geno49–geno88, and geno82–geno88, i.e., the three genotypes with relatively small additive variances as mentioned before. Generally speaking, genotype pairs with a lower additive genotypic covariance $cov\left(g_i,g_j\right)$ tend to show higher estimates for both $H_{\Delta i{j}_{BLUE}}^2$ and $H_{\Delta i{j}_{BLUP}}^2$ (Figure 3).

In most aspects, results from example 4 are similar to those in example 3. The most striking difference is the second cluster of lower pairwise heritability estimates. As highlighted in Figure 3, this cluster consists only of the 88 differences from/to genotype geno81, i.e., the genotype present only at a single of the three environments. Notice that while not highlighted, the differences from/to the two genotypes present at only two of the environments (i.e., geno38 and geno49) also form similar clusters, but they are merely located at the lower left border of the main cluster and thus do not stand out as drastically. Furthermore, the main cluster here lies more or less on the diagonal. Finally, the range of estimates for $cov\left(g_i,g_j\right)$ is smaller than in example 3. This is mostly due to the $g\times e$ variance that for example 4 in (20) could be estimated separately via the genotype-by-environment interaction effect ${\left(ge\right)}_{it}$ as $var\left(\mathit{ge}\right)={\mathit{I}}_{263}{\sigma }_{ge}^2$, whereas fo example 3 the $g\times e$ variance is confounded within the variance of the genotype main effect, since there is no genotype-by-environment interaction effect in (19), as data from only a single environment are present.

Discussion

Variations of the mixed model for replicated plant data

A consequence of having multiple individuals represent the same genotype is that the definition of the genetic variance ${\sigma }_g^2$ requires careful consideration; rather unproblematic are genetically completely homogeneous cultivars such as inbred lines, doubled-haploid (DH) lines, clones, or hybrids. Yet, it should be noted that when it comes to genetically heterogeneous population cultivars in rye, for example, the matter is no longer straightforward (Bernal-Vasquez et al. 2017). Note that estimates for ${\overline{h}}_{\text{Δ}\cdot {\cdot }_{BLUE}}^2$, ${\overline{h}}_{\text{Δ}\cdot {\cdot }_{BLUP}}^2$ increased with decreasing covariance $cov\left(g_i,g_j\right)$ as seen in the Results section for pairwise heritability. Note further that when we assumed $var\left(\mathit{a}\right)=\mathit{K}{\sigma }_a^2$ for the (additive) genotype main effect in the analysis of example 4, for simplicity we did not correspondingly make use of $\mathit{K}$ for modeling the genotype–environment interaction effect, but instead assumed $var\left(\mathit{ge}\right)={\mathit{I}}_{263}{\sigma }_{ge}^2$. Yet, to account for marker-by-environment interaction, one may instead assume e.g., $var\left(\mathit{ge}\right)=\mathit{K}\mathbf{\otimes }{\mathit{I}}_3{\sigma }_{ge}^2$, where $\mathbf{\otimes }$ denotes the Kronecker product. Although Schulz-Streeck et al. (2012) found that the improvement of accounting for marker-by-environment interaction can be negligible, the reader may easily decide to include $\mathit{K}$ for random genotype-interaction effects and it may actually be advisable if the variances for those effects are expected to be relatively large (Bernal-Vasquez et al. 2017).

Relatedness of heritability methods

When both ${\mathit{G}}_{\left(\mathit{g}\right)}$ and ${\mathit{C}}_{22\left(\mathit{g}\right)}$ are proportional to identity matrices, all heritability measures give identical estimates. However, this only holds for a linear random model, since even a single fixed effect [e.g., $\mu$ in (16)] results in nonzero off-diagonal elements in ${\mathit{C}}_{22\left(\mathit{g}\right)}$. Yet, it should be noted that such a purely random model is not practically relevant in plant (and animal) breeding.

When ${\mathit{G}}_{\left(\mathit{g}\right)}={\mathit{I}}_{{\mathit{n}}_{\mathit{g}}}{\sigma }_g^2$ and ${\mathit{C}}_{22\left(\mathit{g}\right)}$ have compound symmetry structure (i.e., simple, balanced setting), all methods except $H_{Sim}^2$ and ${\overline{r}}_{\cdot }^2$ give identical estimates, which we confirmed in the simple, balanced setting of example 1. Furthermore, both $H_{\text{Δ}}^2$ methods display that same value across all genotypes and pairs. Since we always had to assume ${\mathit{G}}_{\left(\mathit{g}\right)}={\mathit{I}}_{{\mathit{n}}_{\mathit{g}}}{\sigma }_g^2$ for $H_{Std}^2$, $H_{Piepho}^2$, and $H_{Cullis}^2$, example 3 technically reduces to a simple, balanced setting for these measures as well, since it involves a single environment laid out as RCBD with balanced data. Accordingly, these three methods yielded identical estimates in that scenario as well (Figure 1). The estimates for ${\overline{r}}_{\cdot }^2$ differ, because off-diagonal elements are ignored in its estimation. However, notice that with increasing $n_g$, the off-diagonal elements of ${\mathit{C}}_{22\left(\mathit{g}\right)}$ approach 0, and thus ${\overline{r}}_{\cdot }^2$ approaches the other measures and, as stated before, so does $H_{Sim}^2$.

In the case where ${\mathit{G}}_{\left(\mathit{g}\right)}={\mathit{I}}_{{\mathit{n}}_{\mathit{g}}}{\sigma }_g^2$ and ${\mathit{C}}_{22\left(\mathit{g}\right)}$ is an unstructured matrix, ${\overline{H}}_{\Delta \cdot {\cdot }_{BLUP}}^2$ and $H_{Cullis}^2$ give identical estimates. This is analogously true for ${\overline{H}}_{\Delta \cdot {\cdot }_{BLUE}}^2$ and $H_{Piepho}^2$, and for ${\mathit{C}}_{11}$ (rather than ${\mathit{C}}_{22\left(\mathit{g}\right)}$) being an unstructured matrix. Rodríguez-Álvarez et al. (2018) show a connection between ${\overline{r}}_{\cdot }^2$ and $H_{Oakey}^2$. They point out that given ${\mathit{G}}_{\left(\mathit{g}\right)}={\mathit{I}}_{{\mathit{n}}_{\mathit{g}}}{\sigma }_g^2$, the mean reliability can be expressed as ${\overline{r}}_{\cdot }^2=\frac{1}{n_g}{\displaystyle \sum _{i=1}^{n_g}{r}_i^2}=trace\left({\mathit{I}}_{{\mathit{n}}_{\mathit{g}}}-{\mathit{G}}_{\left(\mathit{g}\right)}^{-1}{\mathit{C}}_{22\left(\mathit{g}\right)}\right)/n_g=trace\left(\mathit{D}\right)/n_g$ and thus as a special case of $H_{Oakey}^2$, ignoring the number of zero eigenvalues. This is in agreement with Laloë (1993), and our results confirm this relationship for examples 1 and 2 (results not shown). However, we did not find it to be true for examples 3 and 4, where ${\mathit{G}}_{\left(\mathit{g}\right)}\ne {\mathit{I}}_{{\mathit{n}}_{\mathit{g}}}{\sigma }_g^2$. Note that in their article Rodríguez-Álvarez et al. (2018) refer to the mean reliability $\left({\overline{r}}_{\cdot }^2\right)$ as $H_C^2$ in Cullis et al. (2006), even though the latter method is based on differences [see (11)], whereas the former is based on individual genotypes [see (43)].

Interestingly, though not practically very relevant, $r_i^2$ and ${\overline{H}}_{\Delta i{\cdot }_{BLUP}}^2$ give identical estimates per genotype for diagonal ${\mathit{G}}_{\left(\mathit{g}\right)}$ and ${\mathit{C}}_{22\left(\mathit{g}\right)}$.

Finally, when ${\mathit{G}}_{\left(\mathit{g}\right)}$ displays covariances (e.g., as ${\mathit{G}}_{\left(\mathit{g}\right)}=\mathit{K}{\sigma }_g^2$) and ${\mathit{C}}_{22\left(\mathit{g}\right)}$ is an unstructured matrix, none of the five measures that are appropriate for this case (i.e., ${\overline{h}}_{\text{Δ}\cdot {\cdot }_{BLUE}}^2$, ${\overline{h}}_{\text{Δ}\cdot {\cdot }_{BLUP}}^2$, $h_{Oakey}^2$, ${\overline{r}}_{\cdot }^2$, and $h_{Sim}^2$) give identical results. Nevertheless, with the exception of $h_{Oakey}^2$, heritability estimates within examples 3 and 4 were relatively similar (Figure 1). This is true even for the methods that did not include kinship information (i.e., $H_{Std}^2$, $H_{Piepho}^2$, and $H_{Cullis}^2$). Yet, when Ould Estaghvirou et al. (2013) simulated phenotypic and marker data for a single location, they found that these three methods gave lower estimates than the rest.

The most striking results are those for $h_{Oakey}^2$ in examples 3 and 4. Notice that Lourenço et al. (2017) also found outstandingly low estimates for $h_{Oakey}^2$ in models with ${\mathit{G}}_{\left(\mathit{g}\right)}=\mathit{K}{\sigma }_g^2$ for two real data sets and one simulated data set. This raises the question whether $H_{Oakey}^2$ is suited for cases where ${\mathit{G}}_{\left(\mathit{g}\right)}=\mathit{K}{\sigma }_g^2$. While it is true that $H_{Oakey}^2$ estimates are equal to $H_{Std}^2$ in the simple, balanced setting (of example 1), this is only a necessary, but not a sufficient, condition for $H_{Oakey}^2$ to be generally applicable also with correlated genotypes. It can be argued that $H_{Oakey}^2$ and ${\overline{H}}_{\text{Δ}\cdot \cdot }^2$ are similar in the sense that both are based on contrasts between genotypes. However, the important difference is that for ${\overline{H}}_{\text{Δ}\cdot \cdot }^2$ the contrasts of interest (i.e., all genotype pairs) are chosen according to the breeders’ goals, while the contrasts in $H_{Oakey}^2$ are determined by the data set. Laloë (1993) shows that the smallest and largest nonzero eigenvalues, ${\lambda }_{\zeta }$, are the lower and upper limit for the heritability of all possible contrasts of genotypes. Accordingly, they are also the lower and upper limit for all $H_{\text{Δ}ij}^2/h_{\text{Δ}ij}^2$, which is confirmed by our results (Figure 4). It may be noted that $H_{Oakey}^2$ is a simple average of “canonical” heritabilities (eigenvalues) corresponding to canonical contrasts and derived from the canonical decomposition of covariance matrices. As such, low heritabilities indicate a low design efficiency, as the smallest eigenvalue appears to be a good indicator of the robustness of the design and a measure of the part of the genetic trend that can be predicted (Laloë and Phocas 2003). In contrast, a pairwise difference is a combination of low and high heritability contrasts that corresponds to the weighted mean of canonical heritabilities. This may go some way toward explaining the observed discrepancies in estimates of $h_{Oakey}^2$ and the alternatives considered here.

Figure 4.

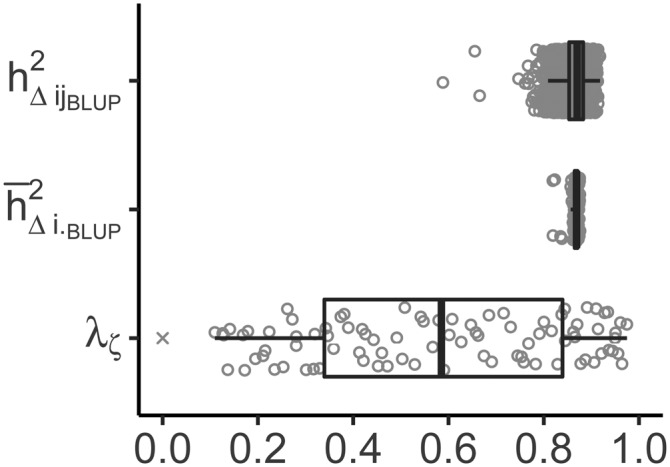
Individual estimates and boxplots for $h_{\Delta i{j}_{BLUP}}^2$, ${\overline{h}}_{\Delta i{\cdot }_{BLUP}}^2$, and ${\lambda }_{\zeta }$ (i.e., eigenvalues needed for $h_{Oakey}^2$) from example 4. The zero eigenvalue is denoted by the symbol ×. BLUP, best linear unbiased prediction.

Genotype-specific information gained from $H_{\text{Δ}}^2$

Figure 2 and Figure 3 are good examples of how $H_{\text{Δ}}^2/h_{\text{Δ}}^2$ can give a more in-depth insight into the outcome of a plant breeding trial. More precisely, the results show that investigating genotype-specific, or even genotype-contrast-specific, heritability measures can (i) summarize how variable/ambiguous an overall heritability estimate is and (ii) point out individual genotypes that stand out.

The first point may seem obvious by now, but it must be realized that whenever only a single (overall) heritability estimate is obtained, there is no information whatsoever about the dispersion of that estimate, only about its central tendency. We argue that investigating ${\overline{H}}_{\Delta i\cdot }^2/{\overline{h}}_{\Delta i\cdot }^2$ and/or $H_{\Delta ij}^2/h_{\Delta ij}^2$ gives more comprehensive insight, since they explicitly show the variability across genotypes and thus, bringing us to the second point, point out exceptional genotypes such as geno38, geno49, geno81, geno82, and geno88 in example 4. Notice that we identified two separate reasons for why these five genotypes were exceptional (low additive variance and missing observations; see Results section). Moreover, looking at the cluster of estimates for geno81 in example 4 in Figure 3, it becomes clear how a single genotype can display notably lower pairwise heritability estimates than the rest. These estimates are obviously decreasing the overall heritability estimate for this example, which would be especially unfavorable in a scenario where the breeder does not have great interest in this particular genotype. In the end, none of this would become apparent by only looking at overall heritability estimates (Figure 1).

What do we really want heritability for and how does $H_{\text{Δ}}^2$ help?

There are two main reasons why heritability on an entry-mean basis is of interest in plant breeding. On one hand, it is plugged into the breeder’s Equation (2) to predict the response to selection. On the other hand, it is a descriptive measure used to assess the usefulness and precision of results from cultivar evaluation trials. In the simple, balanced setting, heritability is suited for both purposes. However, whenever we depart from the simple, balanced setting, $H_{Std}^2$ is no longer suited for either of the two purposes. Furthermore, any alternative measure can ultimately only aim to generalize heritability as a descriptive measure. Regarding the purpose of heritability as a mean to estimate the response to selection, we reiterate the view of Piepho and Möhring (2007): instead of trying to approximate heritability using some ad hoc measure, one should simulate the response to selection directly. As stated before, this can be done via the same simulation-based approach used to obtain $H_{Sim}^2$ and is exemplified in their work (also see Appendix E).

In terms of the descriptive function of heritability, we believe that $H_{\text{Δ}}^2$ is a valuable extension of heritability on an entry-mean basis, because its genotype-wise and pair-wise estimates give more detailed insight, and ultimately allow for better decision-making by the breeder. Furthermore, we would like to argue that its derivation, calculation, and interpretation is rather intuitive, which makes us optimistic about its acceptance in practice. Our view is further supported by Laloë (1993), who also suggested extending reliability to pairwise contrasts in the animal breeding framework.

Conclusions

Irrespective of whether a breeder ultimately decides to apply $H_{\text{Δ}}^2$, we think that understanding the idea behind it alone raises awareness for the mentioned problems with heritability outside the scope of simple, balanced settings and thus can potentially improve the use of heritability in breeding programs. In the end, all heritability measures aim to inform about the same underlying subject matter, and, albeit via different methodologies, they all do. What should therefore be held above all, especially given the mentioned ambiguity problems in a nonsimple, unbalanced setting, is to report how heritability was estimated. Hanson and Robinson (1963, page 612) put it in this crucial context of reproducible science by pointing out that “One must extrapolate in the real world, and one must use estimates of heritability derived by someone else, especially with new crops in new environments. Therefore, it is important to specify exactly how published estimates were obtained in order that others may extrapolate.”

Appendix

Appendix A: Computing ${\widehat{\mathit{g}}}^{\mathit{BLUP}}$ From ${\widehat{\mathit{g}}}^{\mathit{BLUE}}$ in a Stage-Wise Approach

Consider the analysis of a series of trials where the aim is to obtain ${\widehat{\mathit{g}}}^{BLUP}$. One may use a single-stage analysis with a random genotype main effect. Alternatively, it is also possible to use a stage-wise analysis, where the first stage obtains ${\widehat{\mathit{g}}}^{BLUE}$ from which ${\widehat{\mathit{g}}}^{BLUP}$ are predicted in the second stage. Both approaches are equivalent, if variance components are known. In practice, small differences are encountered, as variances need to be estimated (Piepho et al. 2012a).

Single-stage analysis

Assume that we can write the general single-stage model in (13) as

$$\mathit{y}={\mathit{X}}_{\mathit{A}}{\mathit{\beta }}_{\mathit{A}}+{\mathit{Z}}_{\mathit{A}}{\mathit{u}}_{\mathit{A}}+{\mathit{Z}}_{\mathit{B}}{\mathit{u}}_{\mathit{B}}+{\mathit{Z}}_{\mathit{W}}{\mathit{u}}_{\mathit{W}}+\mathit{\epsilon },$$ (45)

where ${\mathit{\beta }}_{\mathit{A}}$ is a vector of fixed across-environment effects (subscript $A$), ${\mathit{u}}_{\mathit{A}}$ is a vector of random across-environment effects with ${\mathit{u}}_{\mathit{A}}\sim \left(0,{\mathit{G}}_{\mathit{A}}\right)$, ${\mathit{u}}_{\mathit{B}}$ is a vector of random between-environment effects (subscript $B$) with ${\mathit{u}}_{\mathit{B}}\sim \left(0,{\mathit{G}}_{\mathit{B}}\right)$, ${\mathit{u}}_{\mathit{W}}$ is a vector of random within-environment effects (subscript $W$) with ${\mathit{u}}_{\mathit{W}}\sim \left(0,{\mathit{G}}_{\mathit{W}}\right)$, $\mathit{\epsilon }$ is a vector of plot errors with $\mathit{\epsilon }\sim \left(0,\mathit{R}\right)$, and $\mathit{y}$ is the observed data vector with $\mathit{y}\sim \left(0,\mathit{V}\right)$, where $\mathit{V}={\mathit{Z}}_{\mathit{A}}{\mathit{G}}_{\mathit{A}}{\mathit{Z}}_{\mathit{A}}^{\mathit{T}}+{\mathit{Z}}_{\mathit{B}}{\mathit{G}}_{\mathit{B}}{\mathit{Z}}_{\mathit{B}}^{\mathit{T}}+{\mathit{Z}}_{\mathit{W}}{\mathit{G}}_{\mathit{W}}{\mathit{Z}}_{\mathit{W}}^{\mathit{T}}+\mathit{R}$ [see Piepho et al. (2012a)]. Thus, $\mathit{G}$ here is a block diagonal matrix with blocks ${\mathit{G}}_{\mathit{A}}$, ${\mathit{G}}_{\mathit{B}}$, and ${\mathit{G}}_{\mathit{W}}$ on its diagonal. Given a MET similar to example 4, ${\mathit{X}}_{\mathit{A}}{\mathit{\beta }}_{\mathit{A}}$ would be a general intercept, ${\mathit{u}}_{\mathit{A}}$ the random genotype main effect (i.e. $\mathit{g}$), ${\mathit{u}}_{\mathit{B}}$ the random environment main effect and random genotype-by-environment interaction effect, ${\mathit{u}}_{\mathit{W}}$ the random block effect at each environment, and $\mathit{\epsilon }$ the plot error. Accordingly, ${\mathit{G}}_{\mathit{A}}$ would correspond to the kinship matrix $\mathit{K}$, whereas ${\mathit{G}}_{\mathit{B}}$ and ${\mathit{G}}_{\mathit{W}}$ would be proportional to identity matrices.

Two-stage analysis

Model (45) has a two-stage representation, with the first stage model given by

$$\mathit{y}={\mathit{X}}_{\mathit{A}1}{\mathit{\beta }}_{\mathit{A}1}+{\mathit{Z}}_{\mathit{B}}{\mathit{u}}_{\mathit{B}}+{\mathit{Z}}_{\mathit{W}}{\mathit{u}}_{\mathit{W}}+{\mathit{\epsilon }}_1,$$ (46)

where effects are defined as in (45), while the subscript $1$ denotes that the corresponding parameters are estimated in this first stage and thus ${\mathit{V}}_1={\mathit{Z}}_{\mathit{B}}{\mathit{G}}_{\mathit{B}}{\mathit{Z}}_{\mathit{B}}^{\mathit{T}}+{\mathit{Z}}_{\mathit{W}}{\mathit{G}}_{\mathit{W}}{\mathit{Z}}_{\mathit{W}}^{\mathit{T}}+{\mathit{R}}_1$. Notice that in contrast to (45), ${\mathit{Z}}_{\mathit{A}}{\mathit{u}}_{\mathit{A}}$ is missing here, since the genotype main effect needs to be taken as fixed at this stage (Piepho et al. 2012a) and is therefore comprised in ${\mathit{X}}_{\mathit{A}1}{\mathit{\beta }}_{\mathit{A}1}$. For simplicity, we can assume that here the genotypic main effects are the only fixed effects so that ${\mathit{\beta }}_{\mathit{A}1}$ are the genotype means. Accordingly, we can obtain genotypic BLUEs as

$$BLUE\left({\mathit{\beta }}_{\mathit{A}1}\right)={\widehat{\mathit{g}}}^{BLUE}={\left({\mathit{X}}_{\mathit{A}1}^{\prime }{\mathit{V}}_1^{-1}{\mathit{X}}_{\mathit{A}1}\right)}^{-1}{\mathit{X}}_{\mathit{A}1}^{\prime }{\mathit{V}}_1^{-1}\mathit{y},$$ (47)

with variance

$$var\left({\widehat{\mathit{g}}}^{BLUE}\right)={\left({\mathit{X}}_{\mathit{A}1}^{\prime }{\mathit{V}}_1^{-1}{\mathit{X}}_{\mathit{A}1}\right)}^{-1}={\mathit{R}}_2.$$ (48)

In the second stage we then have

$${\widehat{\mathit{g}}}^{BLUE}={\mathit{X}}_{\mathit{A}2}{\mathit{\beta }}_{\mathit{A}2}+{\mathit{Z}}_{\mathit{A}2}{\mathit{u}}_{\mathit{A}}+{\mathit{\epsilon }}_2,$$ (49)

where ${\mathit{\epsilon }}_2\sim \left(0,{\mathit{R}}_2\right)$ and just like in (45), the random genotype main effect $\mathit{g}={\mathit{u}}_{\mathit{A}}\sim \left(0,{\mathit{G}}_{\mathit{A}}\right)$ where ${\mathit{G}}_{\mathit{A}}$ corresponds to the kinship matrix $\mathit{K}$. Notice that ${\mathit{X}}_{\mathit{A}2}{\mathit{\beta }}_{\mathit{A}2}=1_{{\mathit{n}}_{\mathit{g}}}\mu$ and ${\mathit{Z}}_{\mathit{A}2}={\mathit{I}}_{{\mathit{n}}_{\mathit{g}}}$. Accordingly, we have ${\mathit{V}}_2={\mathit{Z}}_{\mathit{A}2}{\mathit{G}}_{\mathit{A}}{\mathit{Z}}_{\mathit{A}2}^{\mathit{T}}+{\mathit{R}}_2$ and for the mixed model equations we find

$${\left[\begin{array}{cc}{\mathit{X}}_{\mathit{A}2}^{\prime }{\mathit{R}}_2^{-1}{\mathit{X}}_{\mathit{A}2}^{\prime }& {\mathit{X}}_{\mathit{A}2}^{\prime }{\mathit{R}}_2^{-1}{\mathit{Z}}_{\mathit{A}2}\\ {\mathit{Z}}_{\mathit{A}2}^{\prime }{\mathit{R}}_2^{-1}{\mathit{X}}_{\mathit{A}2}& {\mathit{Z}}_{\mathit{A}2}^{\prime }{\mathit{R}}_2^{-1}{\mathit{Z}}_{\mathit{A}2}+{\mathit{G}}_{\mathit{A}}^{-1}\end{array}\right]}^{-}\left[\begin{array}{c}{\widehat{\mathit{\beta }}}_{\mathit{A}2}\\ {\widehat{\mathit{g}}}^{BLUP}\end{array}\right]=\left[\begin{array}{c}{\mathit{X}}_{\mathit{A}2}^{\prime }{\mathit{R}}_2^{-1}{\widehat{\mathit{g}}}^{BLUE}\\ {\mathit{Z}}_{\mathit{A}2}^{\prime }{\mathit{R}}_2^{-1}{\widehat{\mathit{g}}}^{BLUE}\end{array}\right].$$ (50)

It is important to note that we can write

$${\mathit{X}}_{\mathit{A}}={\mathit{X}}_{\mathit{A}1}{\mathit{X}}_{\mathit{A}2}$$ (51)

and

$${\mathit{Z}}_{\mathit{A}}={\mathit{X}}_{\mathit{A}1}{\mathit{Z}}_{\mathit{A}2}.$$ (52)

Finally, plugging in (48) and (49) into (50), while making use of (51) and (52), it can be seen that the mixed model equation solutions for the second stage are equivalent to those for the single-stage analysis.

Appendix B: An Alternative Estimation for ${\overline{\mathit{H}}}_{\mathit{\Delta }\cdot \cdot }^2$ in the Case of Independent Genotypic Effects with Constant Variance by Averaging Separately Across Numerator and Denominator

Given independent genotypic effects with constant variance, averaging numerator and denominator of $H_{\Delta i{j}_{BLUP}}^2$ in (24) separately first leads to the algebraically equivalent simplification

$${\overline{H}}_{\text{Δ}\cdot {\cdot }_{BLUP}}^2=\frac{{\displaystyle {\sum }_i{\displaystyle {\sum }_{j<i}\text{var}\left(g_i-g_j\right)}}-v_{\text{Δ}ij}^{BLUP}}{{\displaystyle {\sum }_{\text{i}}{\displaystyle {\sum }_{j<i}\text{var}\left(g_i-g_j\right)}}}=\frac{2{\sigma }_g^2-\frac{2}{n_g\left(n_g-1\right)}{\displaystyle {\sum }_i{\displaystyle {\sum }_{j<i}{v}_{\text{Δ}ij}^{BLUP}}}}{2{\sigma }_g^2}=\frac{2{\sigma }_g^2-{\overline{v}}_{\text{Δ}\cdot \cdot }^{BLUP}}{2{\sigma }_g^2}=1-\frac{{\overline{v}}_{\text{Δ}\cdot \cdot }^{BLUP}}{2{\sigma }_g^2}=H_{Cullis}^2.$$ (53)

Analogously, we find for $H_{\Delta i{j}_{BLUE}}^2$ in (29) that

$${\overline{H}}_{\text{Δ}\cdot {\cdot }_{BLUE}}^2=\frac{{\displaystyle {\sum }_i{\displaystyle {\sum }_{j<i}\text{var}\left(g_i-g_j\right)}}}{{\displaystyle {\sum }_i{\displaystyle {\sum }_{j<i}\text{var}\left(g_i-g_j\right)}}+v_{\text{Δ}ij}^{BLUE}}=\frac{2{\sigma }_g^2}{2{\sigma }_g^2+\frac{2}{n_g\left(n_g-1\right)}{\displaystyle {\sum }_i{\displaystyle {\sum }_{j<i}{v}_{\text{Δ}ij}^{BLUE}}}}=\frac{2{\sigma }_g^2}{2{\sigma }_g^2+{\overline{v}}_{\text{Δ}\cdot \cdot }^{BLUE}}=\frac{{\sigma }_g^2}{{\sigma }_g^2+{\overline{v}}_{\text{Δ}\cdot \cdot }^{BLUE}/2}=H_{Piepho}^2.$$ (54)

Appendix C: An Approximation for ${\overline{\mathit{H}}}_{\mathit{\Delta }\cdot \cdot }^2$ in the General Case

It can be shown (Ould Estaghvirou et al. 2013, Additional Files 1) that

$${\displaystyle \sum _i{\displaystyle \sum _{j<i}{v}_{\text{Δ}ij}^{BLUE}}}=trace\left(n_g{\mathit{P}}_{\mathit{\mu }}{\mathit{C}}_{11\left(\mathit{g}\right)}\right),$$ (55)

where ${\mathit{P}}_{\mathit{\mu }}={\mathit{I}}_{\mathit{n}}{}_{\mathit{g}}-n_g^{-1}{1}_{{\mathit{n}}_{\mathit{g}}}{1}_{{\mathit{n}}_{\mathit{g}}}^{\mathit{T}}$ with $1_{{\mathit{n}}_{\mathit{g}}}$ being a vector of ones. Thus, ${\mathit{P}}_{\mathit{\mu }}$ is a matrix that centers for the overall mean, such that ${\overline{v}}_{\text{Δ}\cdot \cdot }^{BLUE}=\frac{2}{n_g\left(n_g-1\right)}trace\left(n_g{\mathit{P}}_{\mathit{\mu }}{\mathit{C}}_{11\left(\mathit{g}\right)}\right)$. Analogously, we have

$${\displaystyle \sum _i{\displaystyle \sum _{j<i}{v}_{\text{Δ}ij}^{BLUP}}}=trace\left(n_g{\mathit{P}}_{\mathit{\mu }}{\mathit{C}}_{22\left(\mathit{g}\right)}\right),$$ (56)

such that ${\overline{v}}_{\text{Δ}\cdot \cdot }^{BLUP}=\frac{2}{n_g\left(n_g-1\right)}trace\left(n_g{\mathit{P}}_{\mathit{\mu }}{\mathit{C}}_{22\left(\mathit{g}\right)}\right)$ and finally

$${\displaystyle \sum _i{\displaystyle \sum _{j<i}var\left(g_i-g_j\right)}}=trace\left(n_g{\mathit{P}}_{\mathit{\mu }}{\mathit{G}}_{\left(\mathit{g}\right)}\right),$$ (57)

such that ${\overline{v}}_{\text{Δ}\cdot \cdot }^g=\frac{2}{n_g\left(n_g-1\right)}trace\left(n_g{\mathit{P}}_{\mathit{\mu }}{\mathit{G}}_{\left(\mathit{g}\right)}\right)$. By inserting (55), (56), and (57) into (34), we get

$${\overline{\overline{H}}}_{\Delta \cdot {\cdot }_{BLUE}}^2=\frac{trace\left({\mathit{P}}_{\mathit{\mu }}{\mathit{G}}_{\left(\mathit{g}\right)}\right)}{trace\left({\mathit{P}}_{\mathit{\mu }}{\mathit{G}}_{\left(\mathit{g}\right)}\right)+trace\left({\mathit{P}}_{\mathit{\mu }}{\mathit{C}}_{11\left(\mathit{g}\right)}\right)},$$ (58)

where, loosely speaking, $trace\left({\mathit{P}}_{\mathit{\mu }}{\mathit{G}}_{\left(\mathit{g}\right)}\right)$ captures the genotypic variance, $trace\left({\mathit{P}}_{\mathit{\mu }}{\mathit{C}}_{11\left(\mathit{g}\right)}\right)$ captures the environmental variance, and hence $trace\left({\mathit{P}}_{\mathit{\mu }}{\mathit{G}}_{\left(\mathit{g}\right)}\right)+trace\left({\mathit{P}}_{\mathit{\mu }}{\mathit{C}}_{11\left(\mathit{g}\right)}\right)$ captures the phenotypic variance. Notice that (58) coincides with Method 4 of Ould Estaghvirou et al. (2013). Based on (33), we find correspondingly

$${\overline{\overline{H}}}_{\Delta \cdot {\cdot }_{BLUP}}^2=\frac{trace\left({\mathit{P}}_{\mathit{\mu }}{\mathit{G}}_{\left(\mathit{g}\right)}\right)-trace\left({\mathit{P}}_{\mathit{\mu }}{\mathit{C}}_{22\left(\mathit{g}\right)}\right)}{trace\left({\mathit{P}}_{\mathit{\mu }}{\mathit{G}}_{\left(\mathit{g}\right)}\right)} .$$ (59)

Appendix D: A Standardization of $\mathit{M}$ To Directly Capture the Total Genotypic Variance

As shown in Appendix C, ${\overline{v}}_{\text{Δ}\cdot \cdot }^g$ captures the average genotypic variance of a difference between two genotypes. In accordance with the notion of this article, we could obtain half the average variance of a difference as an estimate for the total genotypic variance. Notice that this approach is in line with the average semi variance $\left({\sigma }_{g(asv)}^2\right)$ used by Piepho (2019) and can be defined as

$${\sigma }_{g\left(asv\right)}^2=0.5{\overline{v}}_{\text{Δ}\cdot \cdot }^g=\frac{trace\left({\mathit{P}}_{\mathit{\mu }}{\mathit{G}}_{\left(\mathit{g}\right)}\right)}{n_g-1}.$$ (60)

In the case of ${\mathit{G}}_{\left(\mathit{g}\right)}=\mathit{M}{\mathit{M}}^{\prime }{\sigma }_a^2=\mathit{K}{\sigma }_a^2$, we can do some useful rearrangements:

$$\begin{array}{l}{\sigma }_{g\left(asv\right)}^2=\frac{trace\left({\mathit{P}}_{\mathit{\mu }}\mathit{M}{\mathit{M}}^{\prime }\right){\sigma }_g^2}{n_g-1}=\frac{trace\left({\mathit{P}}_{\mathit{\mu }}{\mathit{P}}_{\mathit{\mu }}\mathit{M}{\mathit{M}}^{\prime }\right){\sigma }_g^2}{n_g-1} \\ =\frac{trace\left({\mathit{P}}_{\mathit{\mu }}\mathit{M}{\mathit{M}}^{\prime }{\mathit{P}}_{\mathit{\mu }}\right){\sigma }_g^2}{n_g-1}=\frac{trace\left(\stackrel{\sim }{\mathit{M}}{\stackrel{\sim }{\mathit{M}}}^{\prime }\right){\sigma }_g^2}{n_g-1},\end{array}$$ (61)

where $\stackrel{\sim }{\mathit{M}}={\mathit{P}}_{\mathit{\mu }}\mathit{M}$ is column mean-centered. Notice that $\stackrel{\sim }{\mathit{M}}$ is equal to what is referred to as $\mathit{Z}$ in VanRaden (2008) (page 4416). Notice further that the standardization presented here works for an arbitrary coding of markers and arbitrary scale. As a result, the trace of ${\stackrel{\sim }{\mathit{G}}}_{\left(\mathit{g}\right)}=\stackrel{\sim }{\mathit{M}}{\stackrel{\sim }{\mathit{M}}}^{\prime }\stackrel{\sim }{{\sigma }_a^2}=\stackrel{\sim }{\mathit{K}}\stackrel{\sim }{{\sigma }_a^2}$ directly returns${\widehat{\sigma }}_{g(asv)}^2$. We can standardize further:

$$\overline{\overline{M}}=\frac{\stackrel{\sim }{\mathit{M}}}{\sqrt{\frac{trace\left(\stackrel{\sim }{\mathit{M}}{\stackrel{\sim }{\mathit{M}}}^{\prime }\right)}{n_g-1}}}$$ (62)

and define ${\overline{\overline{\mathit{G}}}}_{\left(\mathit{g}\right)}=\overline{\overline{\mathit{M}}}{\overline{\overline{\mathit{M}}}}^{\prime }\overline{\overline{{\sigma }_a^2}}=\overline{\overline{\mathit{K}}}\overline{\overline{{\sigma }_a^2}}$. Now the total genotypic variance simplifies to

$${\sigma }_{g\left(asv\right)}^2=\frac{trace\left({\mathit{P}}_{\mathit{\mu }}\overline{\overline{\mathit{M}}}{\overline{\overline{\mathit{M}}}}^{\prime }\overline{\overline{{\sigma }_a^2}}\right)}{n_g-1}=\overline{\overline{{\sigma }_a^2}},$$ (63)

which simplifies (58) and (59) to

$${\overline{h}}_{\text{Δ}BLUE}^2=\frac{\overline{\overline{{\sigma }_a^2}}}{\overline{\overline{{\sigma }_a^2}}+trace\left(n_g{\mathit{P}}_{\mathit{\mu }}{\mathit{C}}_{11\left(\mathit{g}\right)}\right)}$$ (64)

and

$${\overline{h}}_{\text{Δ}BLUP}^2=\frac{\overline{\overline{{\sigma }_a^2}}-trace\left(n_g{\mathit{P}}_{\mathit{\mu }}{\mathit{C}}_{22\left(\mathit{g}\right)}\right)}{\overline{\overline{{\sigma }_a^2}}}.$$ (65)

Thus, if $\overline{\overline{\mathit{M}}}$ is standardized as shown above, the genotypic variance we are trying to capture is conveniently estimated directly as the variance for $\mathit{a}$. However, it should be noted that both $\stackrel{\sim }{\mathit{K}}$ and $\overline{\overline{\mathit{K}}}$ are singular, and thus may lead to problems depending on the statistical software being used: ASReml-R 3.0 (Gilmour et al. 2009) will show an error message, while PROC MIXED in SAS 9.4 (SAS Institute Inc. 2013) will effectively compute a modified version of the mixed model equations (Piepho et al. 2012b; SAS Institute Inc. 2017).

We would like to point out that neither $\stackrel{\sim }{\mathit{K}}$ nor $\overline{\overline{\mathit{K}}}$ are equal to the genomic relationship matrices proposed in VanRaden (2008). Their first method obtains the general relationship matrix as:

$${\mathit{K}}_{\mathit{VanRaden}1}=\frac{\stackrel{\sim }{\mathit{M}}{\stackrel{\sim }{\mathit{M}}}^{\prime }}{{\displaystyle {\sum }_{w=1}^{n_m}2{\mathit{p}}_{\mathit{w}}\left(1-{\mathit{p}}_{\mathit{w}}\right)}},$$ (66)

where ${\mathit{p}}_{\mathit{w}}$ are the mean frequencies of the second allele across all genotypes at marker $\mathit{w}=\left\{1,\dots ,n_m\right\}$ and can also be expressed as ${\mathit{p}}_{\mathit{w}}=\frac{1_{{\mathit{n}}_{\mathit{g}}}^{\mathit{T}}\mathit{M}}{2n_g}$. Their second method obtains the matrix as ${\mathit{K}}_{\mathit{VanRaden}2}=\stackrel{\sim }{\mathit{M}}\mathit{L}{\stackrel{\sim }{\mathit{M}}}^{\prime }$ where $\mathit{L}$ is a diagonal with elements

$$L_{w,w}=\frac{1}{n_m\left[2{\mathit{p}}_{\mathit{w}}\left(1-{\mathit{p}}_{\mathit{w}}\right)\right]}.$$ (67)

Since we have $\stackrel{\sim }{\mathit{K}}=\stackrel{\sim }{\mathit{M}}{\stackrel{\sim }{\mathit{M}}}^{\prime }$, we find that opposed to $\stackrel{\sim }{\mathit{K}}$ and therefore $\overline{\overline{\mathit{K}}}$, (66) and (67) additionally require a division involving allele frequencies. It may also be pointed out that in a population with Hardy–Weinberg equilibrium, $trace\left(\mathit{M}{\mathit{M}}^{\prime }\right)$ corresponds to the heterozygosity of the markers. However, it should be kept in mind that completely genetically homogeneous cultivars—such as inbred lines, DH-lines, clones, or hybrids—are definitely not in Hardy–Weinberg equilibrium. Finally, note that if we approximate ${\overline{h}}_{\Delta \cdot {\cdot }_{BLUE}}^2$ via (59) and implement ${\widehat{\sigma }}_{g\left(asv\right)}^2$ into $h_{Piepho}^2$, we find that ${\overline{\overline{h}}}_{\Delta \cdot {\cdot }_{BLUE}}^2=h_{Piepho}^2$ even in the general case. Analogously, we have ${\overline{\overline{h}}}_{\Delta \cdot {\cdot }_{BLUP}}^2=h_{Cullis}^2$.

Appendix E: Directly Simulate Response to Selection

As proposed by Piepho and Möhring (2007), one may directly simulate the response to selection via the same approach used to obtain $H_{Sim}^2$ in this article. Since in (40) we simulate $n_g$ pairs of true $\left({\mathit{g}}_{\mathit{sim}}\right)$ and predicted $\left({\widehat{\mathit{g}}}_{\mathit{sim}}^{\mathit{BLUP}}\right)$ genotypic values, we can select a subset with the best values for ${\widehat{\mathit{g}}}_{\mathit{sim}}^{\mathit{BLUP}}$ and compute the response to selection for the $s$th simulation run as

$$R_s=\frac{{\displaystyle {\sum }_{i\in {\varphi }_s}{\mathit{g}}_{\mathit{sim}}}}{n_{sel}},$$ (68)

where ${\varphi }_s$ is the selected subset of genotypes in the $s$th simulation run and $n_{sel}$ is the number of selected genotypes (i.e. $n_{sel}\le n_g$). Analogous to (41), we can then obtain the simulated expected response to selection as

$$R_{sim}=n_{sim}^{-1}{\displaystyle \sum _{s=1}^{n_{sim}}{R}_s}.$$ (69)

Note that, in principle, the simulation-based approach could also be adapted to simulate the joint distribution of true $\left({\mathit{g}}_{\mathit{sim}}\right)$ and estimated $\left({\widehat{\mathit{g}}}_{\mathit{sim}}^{\mathit{BLUE}}\right)$ genotypic values. Furthermore, one could then compare the simulated expected response to selection values from both simulation approaches to determine whether to ultimately model the genotypic main effect as fixed or random. Yet, not least because of the ability to account for kinship information, we generally expect an analysis with random genotypic effects to be more useful than one with fixed genotypic effects [see Piepho et al. (2008)].