Multi-Model Sensor Fault Detection and Data Reconciliation: A Case Study with Glucose Concentration Sensors for Diabetes

Abstract

Erroneous information from sensors affect process monitoring and control. An algorithm with multiple model identification methods will improve the sensitivity and accuracy of sensor fault detection and data reconciliation (SFD&DR). A novel SFD&DR algorithm with four types of models including outlier robust Kalman filter, locally weighted partial least squares, predictor-based subspace identification, and approximate linear dependency-based kernel recursive least squares is proposed. The residuals are further analyzed by artificial neural networks and a voting algorithm. The performance of the SFD&DR algorithm is illustrated by clinical data from artificial pancreas experiments with people with diabetes. The glucose-insulin metabolism has time-varying parameters and nonlinearities, providing a challenging system for fault detection and data reconciliation. Data from 17 clinical experiments collected over 896 hours were analyzed; the results indicate that the proposed SFD&DR algorithm is capable of detecting and diagnosing sensor faults and reconciling the erroneous sensor signals with better model-estimated values.

Introduction

Accuracy in data collected by sensors is crucial for effective process monitoring and control. Data from sensors offer on-line information to assess the state of a process and to calculate the values of manipulated variables by the controller. Hence, sensor data quality and accuracy strongly affect product quality and process safety. Sensor signals need to be treated and reconciled to eliminate the effects of sensor faults on process operation. We use multiple methods to detect sensor faults and provide estimates for erroneous sensor signal replacement to implement data reconciliation.

Sensor errors can be divided into two main categories: hard failure (complete hardware failure) and soft failure such as bias, drift, and outliers.¹ Hard failures are typically easy to detect, though expensive to resolve since they may require hardware replacement. Soft failures, in contrast, can often be readily resolved through sensor fault detection, and data reconciliation (SFD&DR) systems at low cost, though handling soft sensor faults can be challenging if appropriate dynamic models are not available to exploit analytical redundancies.²

Early efforts in handling sensor faults mostly focused on detection and data reconciliation with linear models and steady-state operating conditions,³ and significantly expanded over the years to encompass nonlinear, dynamic, and stochastic conditions.^4,5 Model uncertainty is of particular concern as process and measurement noise can obscure the sensor faults, resulting in sensor faults remaining undetected. To incorporate the stochastic elements of models in the fault handling schemes, the extended Kalman filter (KF) has been proposed to explicitly consider system uncertainty and modeling inaccuracies.⁶ The Akaike information criterion (AIC) minimization is often used as an objective function to evaluate the accuracy of sensor signal estimates.⁷ More recently, the outlier-robust Kalman filter (ORKF)^8–10 is proposed as an on-line smoother to automatically remove inconsistent data from the sensor signals. Fault detection and data reconciliation (FD-DR) can be implemented by using either fundamental (first-principles) models that provide good predictive capability over wide operating ranges, or data-driven models that best characterize the data for specific operation ranges which are similar to the database used in model development. In contrast to first-principles-model-based techniques, the data-driven approaches, such as subspace identification (SID)^11,12, are more appealing when the model structure is complex or unknown. Data-driven models such as locally weighted partial least squares^13,14 (LW-PLS) and kernel least squares¹⁵ (KLS) can also provide computationally efficient, robust, and accurate models with reliable prediction ability. More detailed discussion about the fault detection and diagnosis methods can be found in various review papers^16–18.

As various models developed using different techniques possess unique advantages, FD-DR algorithms that simultaneously integrate multiple methods are proposed to pool their strengths. A bank of KFs is proposed where each filter is tuned to be sensitive to a particular type of sensor error.^{11, 19} One complication that arises from the aggregation of multiple models is the appropriate consolidation of the respective output predictions for FD-DR. For instance, faulty signal values should be reconstructed with the most accurate model estimates. One approach for integrating the various models is to employ machine learning techniques such as artificial neural networks (ANN) that can automatically analyze the residuals.^20–22 As ANN algorithm development accelerated and improved network structure specification and training approaches have been proposed,²³ ANNs have become more amenable to on-line use.^24,25 The ANNs can therefore readily analyze the generated residuals to classify the operating conditions (normal or a certain type of fault) and reconcile the faulty measurements with the most accurate model predictions.

Motivated by the above considerations, an SFD&DR algorithm for faults in sensor measurements is proposed in this work to leverage multiple data-driven models and generate residual signals that are analyzed by ANNs for FD-DR. Four different modeling techniques have been used in the SFD&DR algorithm: ORKF, LW-PLS, Predictor-Based Subspace method (PBSM), and approximate-linear-dependency-criterion-based kernel recursive least squares (ALD-KRLS). Each method has its unique characteristics, ORKF relies more on the smoothness of the current signal (if there is any abnormal rapid change). LW-PLS is based on historical data (if the current signal tendency is same as the historical reference in the database). PBSM can use subspace identification and recursive calculation to partially solve the system nonlinearity and the proposed algorithm include a stability check module to guarantee the stability of the model. And ALD-KRLS is able to provide a reclusively database update to include new features of sensor signal to the dictionary. The residuals (the differences between sensor data and predicted values) of all four methods are categorized by an ANN to different sensor signal conditions. Finally, the erroneous signals are substituted by estimated values by the models developed.

The performance of the SFD&DR algorithm is evaluated by using continuous glucose monitoring (CGM) sensor data collected from people with type 1 diabetes that used an artificial pancreas during clinical experiments. Overall 896 hours of CGM data in 17 clinical experiments were used, and the results indicate that the new SFD&DR algorithm is capable of detecting and categorizing the sensor faults and reconciling the erroneous sensor signals with the better model estimated values.

The remainder of the article is structured as follows. The four techniques (ORKF, LW-PLS, PBSM, and ALD-KRLS), and the SFD&DR algorithm using ANN and the four models are described. A case study and results of the SFD&DR algorithm performance with data from clinical experiments are given. Discussion of results and conclusions are provided in the two final sections.

Method

In a previous work, ORKF and LW-PLS were used to develop an SFD&DR algorithm.¹⁴ A predesigned threshold of one-step-ahead model error was used to determine whether a sensor signal is faulty. While a SFD algorithm based on one-step-ahead prediction error can reconcile the sensor signal at the same step when the sensor fault is detected, it is challenged if the sensor fault is a gradual bias such as drift change. Recursively updated models track better the dynamic change of a system with time-varying parameters. If the sensor fault is too small to be tracked at the beginning, the model may follow the wrong signal trend which will make the fault detection in the following samples more difficult. In this paper, instead of using a threshold for one-step-ahead prediction, a longer prediction horizon is used for each model as the input of an ANN to determine the condition (normal or a certain type of fault) of sensor signals and the beginning of the sensor fault if the condition is classified as faulty. Two more models, PBSM and ALD-RKLS have been added to the SFD&DR algorithm. These two methods use different ways of model identification, and their unique characteristics provide a more robust decision making when used in the SFD&DR algorithm. For example, the PBSM can provide a time-varying state space model which guarantees the stability of the model, while the ALD-RKLS uses a kernel-based method which requires a large data size for model training but provides predictions with high accuracy.

Outlier-robust Kalman filter

ORKF detects an outlier when the sensor residual is beyond the expected sensor noise estimated by using past signal samples and the detected erroneous signals will have a smaller weight for updating the Kalman model. The ORKF method has been used to solve outlier-related sensor problems in various fields such as GPS data analysis⁸ and robotic systems⁹.

Sensor data ${\mathit{y}}_k\in {\mathfrak{R}}^{d_1}$ can be described by Kalman filter equations with states ${\mathit{x}}_k\in {\mathfrak{R}}^{d_2}$ where d₁ and d₂ are the dimensions of outputs (number of sensors) and state variables:

$${\mathit{y}}_k=\mathit{C}{\mathit{x}}_k+{\mathit{v}}_k$$ (1)

$${\mathit{x}}_k=\mathit{A}{\mathit{x}}_{k-1}+{\mathit{s}}_k$$ (2)

where $\mathit{C}\in {\mathfrak{R}}^{d_1\times d_2}$ is the observation matrix, $\mathit{A}\in {\mathfrak{R}}^{d_2\times d_2}$ is the state transition matrix, ${\mathit{v}}_k\in {\mathfrak{R}}^{d_1\times 1}$ is the observation noise at time step k, and ${\mathit{s}}_k\in {\mathfrak{R}}^{d_2\times 1}$ is the state noise at time step k. v_k and s_k are assumed uncorrelated mean-zero Gaussian noise: ${\mathit{v}}_k~ Normal\left(0,\mathit{R}\right)\mathrm{ },\mathrm{ }{\mathit{s}}_k~ Normal\left(0,\mathit{Q}\right).\mathrm{ }\mathit{R}\in {\mathfrak{R}}^{d_1\times d_1}$ and $\mathit{Q}\in {\mathfrak{R}}^{d_2\times d_2}$ are covariance matrices for observation and state noise respectively. A, C, Q, and R are recursively calculated at each sampling time. The measurement error (y_k − CAx_k−1) is compared to the expected measurement error (R_k) so that if the measurement error is larger than expected, a smaller weight is assigned to this measurement and the model will not be updated to follow the wrong tendency¹⁴.

Locally weighted partial least squares

Locally weighted regression (LWR)²⁶ constructs a local model by prioritizing samples in a database according to the similarity between them and a query sample. Many sample sets paired with their prediction values are stored in the database. Locally weighted partial least squares (LW-PLS) compares the current sample with samples in the database, gives a weight for each sample in the database according to its similarity with the query sample, and uses the weighted samples to generate a partial least squares (PLS) model to compute a prediction for the query sample.

LW-PLS¹⁴ can construct a model capable of providing accurate prediction over a long horizon if the conditions of the current signal samples is similar to the data in the database. The database of LW-PLS should be fault free. If it contains noisy signals, a denoising filter such as Savitzky-Golay filter (SGF)²⁷ can be used to filter the noise for building the LW-PLS models offline.

Predictor-based subspace model

Subspace identification methods provide an efficient framework for identifying linear state-space models from input and output measurements. A predictor-based subspace model (PBSM) implementing recursive model identification to track time-varying linear systems is proposed²⁸. PBSM is modified with a constrained optimization solver to guarantee the stability of the recursive models²⁹ and implemented in a multivariable artificial pancreas system.

Consider a vector auto-regressive model with exogenous variables (VARX):

$$\widehat{y}\left(k|k-1\right)={\sum }_{i=0}^P{\theta }_1^{u\left(k-i\right)}u\left(k-i\right)+{\sum }_{i=0}^P{\theta }_1^{y\left(k-i\right)}y\left(k-i\right)$$ (3)

where $\widehat{y}\left(k|k-1\right)$ is the predicted output for time instant k using the inputs at time instants k, …, k − p and the outputs at time instants k − 1,…, k − p, with p denoting the length of the past window. The coefficients ${\theta }_1^{u\left(k-i\right)}$ and ${\theta }_1^{y\left(k-i\right)}$ are estimated though recursive least squares (RLS) techniques at each sampling time.

The coefficients ${\theta }_1^{u\left(k-i\right)}$ and ${\theta }_1^{y\left(k-i\right)}$ are used to estimate the states in the Kalman filter through the following procedure:

$${\Omega }_u\left(k\right)=\left[\begin{array}{cccc}{\theta }_1^{u\left(k-p\right)}& {\theta }_1^{u\left(k-p+1\right)}& \cdots & {\theta }_1^{u\left(k-1\right)}\\ 0& {\theta }_1^{u\left(k-p\right)}& \cdots & {\theta }_1^{u\left(k-2\right)}\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\theta }_1^{u\left(k-f\right)}\end{array}\right]$$ (4)

$${\Omega }_y\left(k\right)=\left[\begin{array}{cccc}{\theta }_1^{y\left(k-p\right)}& {\theta }_1^{y\left(k-p+1\right)}& \cdots & {\theta }_1^{y\left(k-1\right)}\\ 0& {\theta }_1^{y\left(k-p\right)}& \cdots & {\theta }_1^{y\left(k-2\right)}\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\theta }_1^{y\left(k-f\right)}\end{array}\right]$$ (5)

$$\widehat{x}\left(k\right)=W[{\Omega }_u\left(k\right)U_P\left(k\right)+{\Omega }_y\left(k\right)Y_P\left(k\right)]$$ (6)

where f is the future data window length and W is a weighting matrix²⁸, $\widehat{x}\left(k\right)\in {\mathfrak{R}}^n$ denotes the predicted state vector. Let U_P(k) = [u(k − p) u(k − p + 1) ⋯ u(k − 1)]^T and Y_P(k) = [y(k − p) y(k − p + 1) ⋯ y(k − 1)]^T.

After calculating $\widehat{x}\left(k\right)$, two recursive least squares (RLS) with stability check procedure are used to estimate the state-space matrices [C(k), D(k)] and [A(k), B(k), K(k)]:

$$\widehat{x}\left(k+1\right)=A\left(k\right)\widehat{x}\left(k\right)+B\left(k\right)u\left(k\right)+K\left(k\right)e\left(k\right)$$ (7)

$$\widehat{y}\left(k\right)=C\left(k\right)\widehat{x}\left(k\right)+D\left(k\right)u\left(k\right)+e\left(k\right)$$ (8)

where K(k) is the Kalman gain matrix and $e\left(k\right)=y\left(k\right)-\widehat{y}\left(k\right)$.

Approximate linear dependency criterion based kernel recursive least squares

A novel sparse filtering algorithm was recently proposed by integrating the approximate linear dependency (ALD) criterion with the kernel recursive least squares (KRLS) method.³⁰ The proposed approach leverages the concepts formalized by reproducing kernel Hilbert spaces, which are widely employed to transform linear algorithms expressed only in terms of inner products into their nonlinear versions. For example, kernels are used to develop nonlinear extensions for principal components analysis and Fisher discriminant analysis.

Let $\kappa :\mathcal{U}\times \mathcal{U}\to \mathbb{R}$ be a kernel and $\mathcal{H}$ be the associated reproducing kernel Hilbert space. The commonly used kernels include the Gaussian kernel and the polynomial kernel. The kernel is incorporated in the least-squares problem to determine a function $\psi \left(·\right)$ of $\mathcal{H}$ to transform the data u_i into the feature space ψ(u_i). Subsequent to the nonlinear mapping, the weight vector ω_i is computed to minimize the sum of squares of the residuals between the samples d_i of the desired response and the corresponding data u_i in the higher dimensional space ψ(u_i) = 〈ψ(·), κ(·,u_i)〉, which can be written as

$${\text{min}}_{{\omega }_i}{\sum }_{j=1}^i{\left|d_i-{\omega }_i\psi \left(u_i\right)\right|}^2+\lambda {‖{\omega }_i‖}^2$$ (9)

where λ denotes the regularization parameter. The above least squares optimization problem needs to be solved recursively to capture the time-varying relationships among the data. However, the repetitive solution cannot be efficiently obtained because the dimensionality increases as the number of sampling instances increases. Specifically, the incremental augmentation of the kernel matrix at each sampling instance results in increased computational complexity and amplified memory requirements for information storage. Moreover, the higher dimension of the weight vector ω_i may lead to overfitting. By combining the KRLS algorithm with the ALD sparsification criterion, the proposed ALD-KRLS filtering algorithm can overcome the computational tractability drawbacks by effectively preventing the size of kernel functions from becoming prohibitively large.

Several sparsification criteria for selecting a finite proper dictionary to define a summary of the training data are employed in KRLS algorithms. The sparse kernel can be written as

$$\psi \left(·\right)={\sum }_{i=1}^m{\omega }_i\kappa \left(u_i,·\right)$$ (10)

where the sparsified dataset {u₁,…,u_m} is a subset of the original dataset {u₁,…,u_m} with m < n. The new finite dictionary is specified such that it is sufficient for capturing the relationships among the variables in the complete data. For this purpose, the ALD criterion is employed, which determines whether a newly available data sample u_i+1 can be written as an approximate linear combination of the previous data {u₁,…,u_m} as follows:

$${\alpha }_{i+1}={\min }_{{\omega }_i}\Vert \kappa \left(u_{i+1},·\right)-{\sum }_{j=1}^m{\omega }_i\kappa \left(u_i,·\right){\Vert }^2$$ (11)

where α_i denotes the ALD criterion that must be less than or equal to the threshold parameter ε for determining the level of sparsity. If the ALD condition holds, the new sample k(u_i+1,·) can be approximated within a squared error ∈ by some linear combination of the current dictionary members. If α_i > ∈, then the new sample should be included in the finite dictionary, with the oldest sample discarded to maintain the finite size m, while retaining the newest m samples that best represent the system. As such, the ALD-KRLS approach develops a kernel-based filtering algorithm that uses only a finite number of training samples for the recursive least squares estimation that are sufficient for characterizing the system using a linear model identified in the high dimensional kernel space.

Artificial neural networks for sensor signal characterization

Model prediction errors (MPE) which indicate the distance between the model prediction and the measured value are often used for sensor fault detection. A threshold method can report a fault if the magnitude of MPE is larger than a threshold. In order to track the dynamic changes in systems with time-varying parameters, the recursively updated models may be used to calculate the predictions. Using a simple threshold method may cause three challenges for sensor fault detection. First, it is hard to distinguish the real dynamic change in the system and sensor bias (type 2 error). Second, for a slowly changing sensor fault such as drift change, the recursive model may follow the erroneous signal trace without showing a large model prediction error. Third, it is often difficult to identify the type of the sensor fault directly through MPE. To address these problems, the ANN is used to further analyze the model prediction error and categorize the sensor signal into different conditions including normal condition and types of the sensor fault.

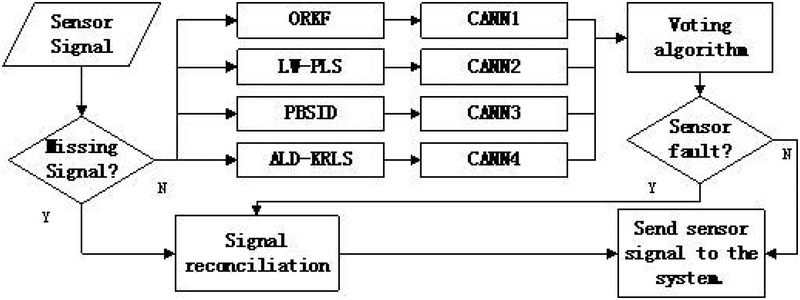
The category ANN (CANN) is a feedforward network with an input layer, a hidden layer, and an output layer. The input is multi-step MPE, and the output is the conditions of the sensor signal. The Neural Network Toolbox³¹ in MATLAB is used to design the CANN. The numbers of neurons in the input and output layer are determined by the prediction horizon of the MPE and the numbers of conditions (normal operation and types of sensor error), respectively. The number of neurons in the hidden layer is selected in the training step to optimize the accuracy of classification. A separate CANN is designed for each model type used in fault detection. The output of each model is a scalar between 0 to 1 indicating the possibility of each condition. The CANN outputs from four different models are used in a voting algorithm (summation of the outputs) to decide the condition of the sensor signal (the condition is indicated by the largest output values). A missing signal is not analyzed by CANN since missing signal detection is trivial. A missing signal reading is automatically reported for data reconciliation. After a sensor fault is detected, a moving window method is used to evaluate which method has the best accuracy to replace the erroneous sensor signal with the value predicted by a model (Figure 1).

Figure 1.

Flowchart of SFD&DR using four model identification methods and CANN

Implementation of SFD&DR in Artificial Pancreas

Artificial pancreas and continuous glucose monitoring

The artificial pancreas (AP) is a treatment alternative for people with type 1 diabetes (T1D) to maintain their blood glucose concentration (BGC) at a desired level. A typical AP has three components: a continuous glucose monitoring (CGM) sensor which measures the subcutaneous glucose concentration to infer BGC at high frequency (sampling time of 5 minutes³²); a controller which uses the CGM signals as input to calculate the insulin infusion rate for regulating the BGC, and an insulin pump which delivers the insulin amount calculated by the controller to the patient. BGC dynamics in the body can be affected by many factors such as meals and exercise³³ and their effects on the BGC may not be easy to quantify, can vary from patient to patient and also over time for the same patient.

The reliability and accuracy of CGM sensors directly influence the performance of an AP system. The CGM values reported may be affected by various types of sensor faults and interruptions in signal transmission (missing values). If the CGM sensor is biased, the controller may suggest less or more insulin which may cause hyperglycemia (high BGC) or hypoglycemia (low BGC), respectively. The sensor signal may also become noisy or be affected by pressure-induced sensor attenuations (PISA)³⁴. Finally, if the signal is missing, the entire AP system may need to pause its operation or use old data.

The proposed SFD&DR algorithm is implemented in the AP system for CGM sensor signal fault detection and signal reconciliation. Seventeen clinical experiments with T1D subjects were conducted. Each experiment lasted continuously for 54 hours; each subject was wearing a CGM sensor (Dexcom G4³²), an insulin pump and an armband (BodyMedia³⁵) which provides energy expenditure (EE) and galvanic skin response (GSR) information to the AP system. All data sets of CGM, EE, GSR, and insulin infusion rates were collected every 5 minutes.

Data processing

For LW-PLS, a database contains clinical data including CGM readings, change in CGM values, insulin infusion rate, EE, and GSR as input X and with NP steps into the future CGM as output Y. The nth column of X and Y are denoted by x_n and y_n, respectively:

$${\mathit{x}}_n={\left[\begin{array}{c}{G}_{k-\mathrm{\alpha }}, G_{k-\mathrm{\alpha }+1}, \dots , G_{k-1}, {\Delta G}_{k-\mathrm{\alpha }}, {\Delta G}_{k-\mathrm{\alpha }+1}, \dots , {\Delta G}_{k-1},{\mathrm{ }ins}_{k-\mathrm{\alpha }}, {ins}_{k-\mathrm{\alpha }+1}, \dots , {ins}_{k-1}, \\ {EE}_{k-\mathrm{\alpha }}, {EE}_{k-\mathrm{\alpha }+1}, \dots , {EE}_{k-1}, {\mathrm{ }GSR}_{k-\mathrm{\alpha }}, {GSR}_{k-\mathrm{\alpha }+1}, \dots , {GSR}_{k-1}\end{array}\right]}^{\mathrm{T}}$$ (12)

$${\mathit{y}}_n=[G_k,\mathrm{ }{G}_{k+1},\mathrm{ }\dots ,\mathrm{ }{G}_{k+NP-1}{]}^{\mathrm{T}}$$ (13)

where G_k is the CGM value at time step k, ΔG_k = G_k − G_{k − 1}, and ins_k, EE_k, and GSR_k are the insulin infusion rate, EE, and GSR at step k, respectively. The CGM sensor signals in the LW-PLS database should be noise free. The original CGM signal was first filtered with Savitzky-Golay filter²⁷ (SGF) to generate the noise-free signal. The database of LW-PLS contains 5184 pairs of input and output samples.

CANN1 through CANN4 are trained by using the predictions and conditions of the CGM sensor signals from the corresponding estimation method. For each CANN, the input (${IN}_k^m$) is the MPEs (14) from one kind of model identification method, and the output is a vector with all its elements ranging from 0 to 1 to indicate the possibility of conditions of CGM sensors. The CGM conditions information is defined as normal (${\mathrm{C}}_k^1$), signal stuck (${\mathrm{C}}_k^2$), spike (${\mathrm{C}}_k^3$), drift change (${\mathrm{C}}_k^4$), step change (${\mathrm{C}}_k^5$), and PISA (${\mathrm{C}}_k^6$).

$${\mathrm{M}\mathrm{P}\mathrm{E}}_{k|k-\mathrm{t}}^{\mathrm{m}}=\left\{\begin{array}{cc}[{\widehat{\mathrm{G}}}_{k|k-1}^{\mathrm{m}}-{\mathrm{G}}_k]& t=1\\ [{\widehat{\mathrm{G}}}_{k-1|k-2}^{\mathrm{m}}-{\mathrm{G}}_{k-1},{\widehat{\mathrm{G}}}_{k|k-2}^{\mathrm{m}}-{\mathrm{G}}_{\mathrm{k}}]& t=2\\ [{\widehat{\mathrm{G}}}_{k-t+1|k-t}^{\mathrm{m}}-{\mathrm{G}}_{k-\mathrm{t}+1},{\widehat{\mathrm{G}}}_{k-\mathrm{t}+2|\mathrm{k}-t}^{\mathrm{m}}-{\mathrm{G}}_{k-t+2},\mathrm{ }\dots ,\mathrm{ }{\widehat{\mathrm{G}}}_{k|k-t}^{\mathrm{m}}-{\mathrm{G}}_k]& t>2\end{array}\right.$$ (14)

$${IN}_k^m=[{\mathrm{M}\mathrm{P}\mathrm{E}}_{k|k-1}^m,\mathrm{ }{\mathrm{M}\mathrm{P}\mathrm{E}}_{k|k-2}^m,\dots ,\mathrm{ }{\mathrm{M}\mathrm{P}\mathrm{E}}_{k|k-NP}^m,{]}^{\mathrm{T}}$$ (15)

$${OUT}_k^m=[{\mathrm{C}}_k^1,\mathrm{ }{\mathrm{C}}_k^2,\mathrm{ }\dots ,\mathrm{ }{\mathrm{C}}_k^6]$$ (16)

where G_k is the CGM sensor signal at step k. The superscript m indicates the model identification method (1: ORKF, 2: LW-PLS, 3: PBSM and 4: ALD-RKLS). ${\widehat{\mathrm{G}}}_{k|k-t}^m$ denotes the prediction of CGM value at step k by using method m based on the information available at step k − t. NP is the maximum prediction horizon that the models need to provide to generate the input of CANN. For the training data, at step k, one value of the ${OUT}_k^m$ is set equal to 1 and other elements are set to 0, depending on the known CGM fault in the training data.

Data sets from 8 clinical experiments were used to generate the training data of CANNs. First, the original CGM signals were filtered with SGF to generate the noise-free signal. Second, the noise-free signals were used by the four model identification methods to generate model predictions (${\widehat{\mathrm{G}}}_{k|k-t}^m$). It is very difficult to identify various types of faults in the original clinical data. Missing signals are obvious but, drifts, small biases, PISA are elusive. Hence, various types of errors are added to the noise-free signal to build a database that would enable the evaluation of the performance of the algorithms proposed. The following relations are used to generate CGM sensor signals with faults:

Signal stuck:

$$\begin{gathered} \left[G_{e,k},\mathrm{ }{G}_{e,k+1},\dots , G_{e,k+{Du}_e-1}\right]=[G_k,\mathrm{ }{G}_k,\dots ,G_k] \\ s.t.{Du}_e\in [1, 2, 3, 4] \end{gathered}$$ (17)

Spike:

$$G_{e,k}=G_k+ {Di}_e{M}_e{G}_k$$ (18)

Drift change:

$$\begin{gathered} \left[G_{e,k},\mathrm{ }{G}_{e,k+1},\dots ,\mathrm{ }{G}_{e,k+{Du}_e-1}\right]=\left[G_k,\mathrm{ }{G}_{k+1},\dots ,\mathrm{ }{G}_{k+{Du}_e-1}\right]+{Di}_e{M}_e{G}_k[1,\mathrm{ }2,\mathrm{ }\dots ,\mathrm{ }{Du}_e]/{Du}_e \\ \mathrm{s}.\mathrm{t}.\mathrm{ }{Du}_e\in [2,\mathrm{ }3,\mathrm{ }4,\mathrm{ }5]\mathrm{ } \end{gathered}$$ (19)

Step change:

$$\begin{gathered} \left[G_{e,k},\mathrm{ }{G}_{e,k+1},\dots , G_{e,k+{Du}_e-1}\right]=\left[G_k,\mathrm{ }{G}_{k+1},\dots , G_{k+{Du}_e-1}\right]+{Di}_e{M}_e{G}_k \\ \mathrm{s}.\mathrm{t}.\mathrm{ }{Du}_e\in [2,\mathrm{ }3,\mathrm{ }4,\mathrm{ }5]\mathrm{ } \end{gathered}$$ (20)

PISA³⁴:

$$\begin{gathered} G_{e,k+t}=\left\{\begin{array}{c}\begin{array}{cc}{G}_{k+t}-M_e\mathrm{*}\left(1-\text{exp}\left(\frac{-5t}{\tau }\right)\right)& \mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }if\mathrm{ }t\le \frac{D}{5}\end{array}\\ G_{k+t}\begin{array}{cc}+M_e\left(1-\text{exp}\left(\frac{-5t+D}{\tau }\right)\right)-M_e\left(1-\text{exp}\left(\frac{-5t}{\tau }\right)\right)\mathrm{ }& if\mathrm{ }\frac{D}{5}<t<{Du}_e\end{array}\end{array}\right. \\ \mathrm{s}.\mathrm{t}.\mathrm{ }\mathrm{ }\mathrm{ }{Du}_e=\frac{D+3\tau }{5},\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }t\in \left[1,\mathrm{ }{Du}_e\right],\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\tau \in \left[5,\mathrm{ }10,\mathrm{ }15,\mathrm{ }20\right],\mathrm{ }\mathrm{ }D\in \left[15,\mathrm{ }20,\mathrm{ }25,\mathrm{ }30\right] \end{gathered}$$ (21)

where G_e(k) is the faulty CGM measurement generated by the sensor error generator using the original CGM value G(k). Failures of CGM sensor are mainly due to sensor-receiver connection problem (missing signal and signal stuck) and biomechanical issues of the sensor-tissue interface³⁶, such as motion of the subjects (spike and step change), scar tissue growth around the CGM sensor or degradation of sensor materials (drift change), and PISA³⁴. The duration, direction (positive or negative) and magnitude of the errors are noted as Du_e, Di_e, and M_e, respectively. These error types, magnitudes and durations are randomly selected, and the error appearance rate (EAR) is every 18 samples so that no fault will be overlapped. Note that the EAR used in training data is much higher than the frequency of errors in real life since the purpose of training data is to make CANN recognize as many different faulty situations as possible. In this way, each clinical data set will generate 50 faulty CGM signals and the input and output of training data can be constructed by (14) – (16). Overall, the training data for each CANN contains 259,200 pairs of input and output samples.

After a certain type of fault is detected, a moving window of N_MW sampling times is used to estimate the MPE for each method and the model with the best accuracy is used for data reconciliation. Assume the fault is continuously reported in N_f number of samples:

$${\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}_k^m={\sum }_{j=1}^{N_{\mathrm{M}\mathrm{W}}}\left|{\mathrm{M}\mathrm{P}\mathrm{E}}_{k-N_f-j|k-2N_f-j}^{\mathrm{m}}\right|$$ (22)

$$G_k={\widehat{\mathrm{G}}}_{k|k-N_f}^{\mathrm{m}}\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }such that\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }{\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}_k^m\mathrm{ }\mathrm{i}\mathrm{s}\mathrm{ }\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{ }\mathrm{s}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{e}\mathrm{s}\mathrm{t}$$ (23)

The size of moving window is determined by minimize the difference between the noise free signal and the estimated signal ${\widehat{\mathrm{G}}}_{k|k-N_f}^{\mathrm{m}}$ in the training dataset, the search range of N_MW is [1, 2, 3, …, 12]. In this case, N_MW = 8 is selected for the window length.

Voting algorithm

BGC level is directly related to carbohydrate consumption and plasma insulin concentration (PIC). The training data from clinical experiments includes several meal consumptions and insulin infusion rate adjustments that affect the PIC. Models without meal announcement may classify rapid CGM increases caused by carbohydrate consumption and rapid decreases driven by large PIC as sensor faults. The sensor signal based on a meal detection module³⁷ and a PIC estimation module³⁸ developed in our research group can provide on-line meal information and PIC information, respectively. The meal signal and PIC are integrated into the voting algorithm to reduce the number of false positives (FP) caused by meal consumption and high PIC values. The detailed voting algorithm is described in the following procedure:

$$\begin{gathered} {\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{l}}_k^m=\left\{\begin{array}{cc}0.5& {\mathrm{i}\mathrm{f}\mathrm{ }\mathrm{ }\mathrm{M}\mathrm{P}\mathrm{E}}_{k|k-1}^m<0 \&{\mathrm{F}\mathrm{l}\mathrm{a}\mathrm{g}}_k^{\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{l}}=1\\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right. \\ m\in [\mathrm{O}\mathrm{R}\mathrm{K}\mathrm{F},\mathrm{ }\mathrm{L}\mathrm{W}-\mathrm{P}\mathrm{L}\mathrm{S},\mathrm{ }\mathrm{P}\mathrm{B}\mathrm{S}\mathrm{M},\mathrm{ }\mathrm{A}\mathrm{L}\mathrm{D}-\mathrm{K}\mathrm{R}\mathrm{L}\mathrm{S}] \end{gathered}$$ (24)

$$\begin{gathered} {\mathrm{P}\mathrm{I}\mathrm{C}}_k^m=\left\{\begin{array}{cc}0.5& {\mathrm{i}\mathrm{f}\mathrm{ }\mathrm{ }\mathrm{M}\mathrm{P}\mathrm{E}}_{k|k-1}^m>0 \& {\mathrm{P}\mathrm{I}\mathrm{C}}_k>25mU {\mathrm{L}}^{-1}\\ 0& \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array}\right. \\ m\in [\mathrm{O}\mathrm{R}\mathrm{K}\mathrm{F},\mathrm{ }\mathrm{L}\mathrm{W}-\mathrm{P}\mathrm{L}\mathrm{S},\mathrm{ }\mathrm{P}\mathrm{B}\mathrm{S}\mathrm{M},\mathrm{ }\mathrm{A}\mathrm{L}\mathrm{D}-\mathrm{K}\mathrm{R}\mathrm{L}\mathrm{S}] \end{gathered}$$ (25)

$$\begin{gathered} {\mathrm{S}\mathrm{C}}_k^V=\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{d}(\mathrm{m}\mathrm{a}\mathrm{x}(\sum \frac{{\mathrm{O}\mathrm{U}\mathrm{T}}_k^m+{\left[{\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{l}}_k^m+{\mathrm{P}\mathrm{I}\mathrm{C}}_k^m,\mathrm{ }0,\mathrm{ }0,\mathrm{ }\mathrm{ }0,\mathrm{ }0,\mathrm{ }0\right]}^{\mathrm{T}}}{4}\left)\right) \\ m=[\mathrm{O}\mathrm{R}\mathrm{K}\mathrm{F},\mathrm{ }\mathrm{L}\mathrm{W}-\mathrm{P}\mathrm{L}\mathrm{S},\mathrm{ }\mathrm{P}\mathrm{B}\mathrm{S}\mathrm{M},\mathrm{ }\mathrm{A}\mathrm{L}\mathrm{D}-\mathrm{K}\mathrm{R}\mathrm{L}\mathrm{S}] \end{gathered}$$ (26)

where ${\mathrm{F}\mathrm{l}\mathrm{a}\mathrm{g}}_k^{\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{l}}$ is a binary variable provided by the meal detection module³⁷ indicates the meal effect (1: meal effect exists, 0: meal effect does not exist) at step k. And PIC_k at step k is indicated by the PIC estimation module³⁸. ${\mathrm{S}\mathrm{C}}_k^V$ is the number of the largest element of the sensor condition vector. The first element of ${OUT}_k^m$ indicates the normal condition, additional values will be added to the normal condition when a meal is detected and MPE is negative or PIC is high and MPE is positive. The reduction of FP by integrating meal detection and PIC estimation module in the voting algorithm is illustrated in Figure 2.

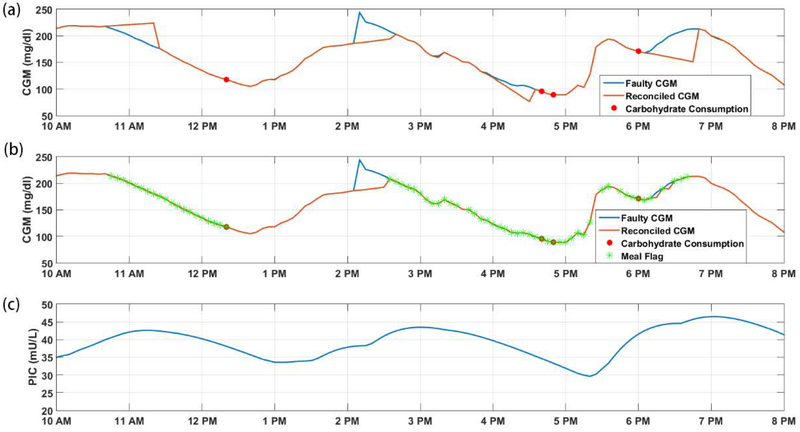
Figure 2.

Comparison between SFD&DR algorithm with and without PIC and meal detection module. (a) PIC and meal detection modules are not used, (b) PIC and meal detection modules are used, (c) PIC estimates.

Figure 2a shows the results when no meal detection and PIC information is used. Without the meal detection module, the rapid increase in CGM caused by carbohydrate consumption from 6:00 PM to 7:00 PM, and the rapid reduction of CGM caused by the large value of PIC during 10:45 AM to 11:20 AM and 3:50 PM to 4:40 PM are detected as sensor faults and reconciled with model estimations. In Figure 2b, the voting algorithm with meal flag and PIC estimates generated by meal detection and PIC estimation modules eliminated these FPs after meals, while the real sensor fault around 2:10 PM to 2:40 PM can still be detected and reconciled.

To illustrate the contribution of CANN, PIC estimation and meal detection modules, the same testing data are used for four different SFD&DR algorithms: (1) without CANN, PIC estimation and meal detection modules; (2) with CANN but without PIC estimation and meal detection modules; (3) with PIC estimation and meal detection modules but without CANN; and (4) with CANN, PIC estimation and meal detection modules.

For SFD&DR algorithm with CANN but without PIC estimation and meal detection module, the voting algorithm in (26) is changed to (27):

$$\begin{gathered} {\mathrm{S}\mathrm{C}}_k^{\mathrm{V}}=\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{d}\left(\mathrm{m}\mathrm{a}\mathrm{x}\right(\sum \frac{{\mathrm{O}\mathrm{U}\mathrm{T}}_k^m}{4}\left)\right) \\ m\in [\mathrm{O}\mathrm{R}\mathrm{K}\mathrm{F},\mathrm{ }\mathrm{L}\mathrm{W}-\mathrm{P}\mathrm{L}\mathrm{S},\mathrm{ }\mathrm{P}\mathrm{B}\mathrm{S}\mathrm{M},\mathrm{ }\mathrm{A}\mathrm{L}\mathrm{D}-\mathrm{K}\mathrm{R}\mathrm{L}\mathrm{S}] \end{gathered}$$ (27)

For SFD&DR algorithm without CANN, will use a threshold method to detect the sensor error, hence its condition report contains only two conditions, normal and faulty. The binominal index, threshold-based error (TBE_k) equal to 1 or 0 indicates the sensor signal is faulty or normal, respectively:

$$\begin{gathered} E_k^m=\left\{\begin{array}{c}1, if \left|{\mathrm{ }\mathrm{M}\mathrm{P}\mathrm{E}}_{k|k-1}^m\right|>{\mathrm{T}}^m\\ 0, if \left|{\mathrm{ }\mathrm{M}\mathrm{P}\mathrm{E}}_{k|k-1}^m\right|\le {\mathrm{T}}^m\end{array}\right. \\ m\in [\mathrm{O}\mathrm{R}\mathrm{K}\mathrm{F},\mathrm{ }\mathrm{L}\mathrm{W}-\mathrm{P}\mathrm{L}\mathrm{S},\mathrm{ }\mathrm{P}\mathrm{B}\mathrm{S}\mathrm{M},\mathrm{ }\mathrm{A}\mathrm{L}\mathrm{D}-\mathrm{K}\mathrm{R}\mathrm{L}\mathrm{S}] \end{gathered}$$ (28)

$${\mathrm{T}\mathrm{B}\mathrm{E}}_k=\left\{\begin{array}{c}1, \sum _m{E}_k^m\ge 2\\ 0, \sum _m{E}_k^m<2\end{array}\right.$$ (29)

The threshold T^m is set equal to ${\mathrm{M}\mathrm{P}\mathrm{E}}_{mean}^m+{\mathrm{M}\mathrm{P}\mathrm{E}}_{std}^m$, where ${\mathrm{M}\mathrm{P}\mathrm{E}}_{mean}^m$ and ${\mathrm{M}\mathrm{P}\mathrm{E}}_{std}^m$ are the mean and standard deviation of $\left|{\mathrm{ }\mathrm{M}\mathrm{P}\mathrm{E}}_{k|k-1}^m\right|$, respectively. If the ${\mathrm{ }\mathrm{M}\mathrm{P}\mathrm{E}}_{k|k-1}^m$ follow a standard normal distribution, the acceptable signal range is about 84%, since there is a voting algorithm for fault detection, the acceptable signal range will become even larger to reduce false alarms. For SFD&DR algorithm with PIC estimation and meal detection module and without CANN, Eqs. 28 and 29 are modified as:

$$E_k^m=\{\begin{array}{ll}1,\hfill & if \left|{\text{MPE}}_{k|k-1}^m\right|>{\text{T}}^m and {\text{ Meal}}_k^m=0 and {\text{ PIC}}_k^m=0\hfill \\ 0,\hfill & otherwise m\in \left[\text{ORKF},\text{ LW}-\text{PLS},\text{ PBSM},\text{ ALD}-\text{KRLS}\right]\hfill \end{array}$$ (30)

$${\mathrm{T}\mathrm{B}\mathrm{E}}_k=\left\{\begin{array}{c}1, \sum _m{E}_k^m\ge 2\\ 0, \sum _m{E}_k^m<2\end{array}\right.$$ (31)

Results

Eight datasets from the clinical experiments were used for building the database for LW-PLS and training the CANNs, and the other 9 data sets are used for testing. The testing data sets were analyzed by a clinical specialist with expertise on the effects of carbohydrates, exercise, insulin infusion rate, and PISA to label the changes in the CGM signal. The PISA is conducted by letting the subject lie on a towel-covered cardboard to simulate the pressure introduced to the sensor. The time for PISA is known to the clinical specialist but unknown to the SFD&DR algorithm. The sensor error conditions identified by the clinical specialist are listed as “condition announced” (CA). The conditions reported by SFD&DR algorithm are listed as “condition reported” (CR).

The results of the SFD&DR algorithm are illustrated with three parameters: type accuracy (TA), sensitivity (S), and false detection ratio (FDR). The formula for computing S, TA, and FDR percentages are

$$\mathrm{S}=100\mathrm{ }\frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}\mathrm{ }\mathrm{\%}$$ (32)

$$\mathrm{T}\mathrm{A}=100\mathrm{ }\frac{Samples\mathrm{ }where\mathrm{ }CR\mathrm{ }and\mathrm{ }CA\mathrm{ }are\mathrm{ }the\mathrm{ }same\mathrm{ }condition}{\mathrm{S}\mathrm{C}\mathrm{A}}\mathrm{ }\mathrm{\%}$$ (33)

$$\mathrm{F}\mathrm{D}\mathrm{R}=100\mathrm{ }\frac{Samples\mathrm{ }that\mathrm{ }CR\mathrm{ }declared\mathrm{ }as\mathrm{ }one\mathrm{ }type\mathrm{ }of\mathrm{ }fault\mathrm{ }but\mathrm{ }CA\mathrm{ }as\mathrm{ }normal}{Samples\mathrm{ }that\mathrm{ }CR\mathrm{ }declared\mathrm{ }as\mathrm{ }one\mathrm{ }type\mathrm{ }of\mathrm{ }fault}\mathrm{ }\mathrm{\%}$$ (34)

where TP and FN are true positive and false negative for a certain type of fault (when CR and CA declare the same sensor fault, the sample is considered as TP) and SCA indicates samples that are announced by clinical specialist as normal or one type of sensor fault.

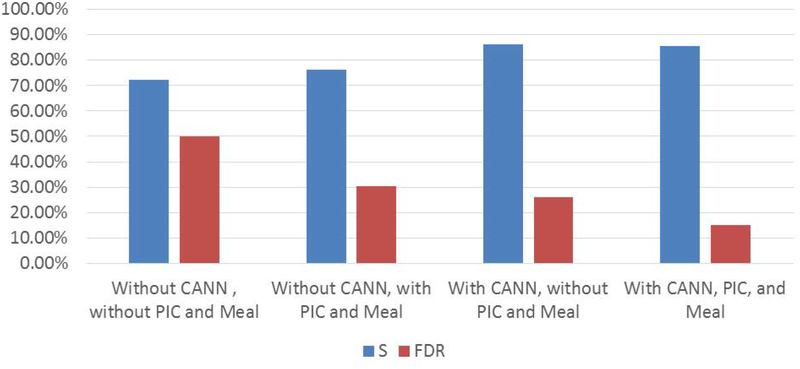
The summary of sensor signal condition classification of SFD&DR with CANN is displayed in Table 1 and Table 2 where the condition reported by the algorithm (CR), and the condition announced by the clinical expert (CA) are listed. For example, the value 15 in the array element for column ‘drift change’ and row ‘spike’ (row 2 column 1) indicates that 15 one-sample errors that are reported as drift change were spikes in CGM values. The comparison between the performances of the four different SFD&DR is displayed in Figure 3.

Table 1.

Summary of Sensor Signal Condition Classification of SFD&DR with CANN but without PIC Estimation and Meal Detection Module

CR CA	Spike	Drift Change	Step Change	Signal Stuck	PISA	Missing Signal	Normal	SCA	TA (%)	S (%)
Spike	81	15	32	0	6	0	31	165	49.09	81.21
Drift Change	15	189	5	0	18	0	50	277	68.23	81.95
Step Change	18	1	86	1	19	0	14	139	61.87	89.93
Signal Stuck	0	4	12	47	5	0	8	76	61.84	89.47
PISA	17	39	29	0	212	0	40	337	62.91	88.13
Missing Signal	0	0	0	0	0	33	0	33	100	100
Normal	40	142	49	12	67	0	3997	4307	92.80	---
FDR (%)	23.39	36.41	23.00	20.00	20.49	0	---	---	---	---

Table 2.

Summary of Sensor Signal Condition Classification of SFD&DR with CANN, PIC Estimation and Meal Detection Module

CR CA	Spike	Drift Change	Step Change	Signal Stuck	PISA	Missing Signal	Normal	SCA	TA (%)	S (%)
Spike	81	15	32	0	6	0	31	165	49.01	81.03
Drift Change	15	188	3	0	18	0	53	277	67.72	80.94
Step Change	18	1	86	1	19	0	14	139	61.49	89.64
Signal Stuck	0	4	12	47	5	0	8	76	62.07	89.66
PISA	16	37	29	0	212	0	43	337	62.84	87.16
Missing Signal	0	0	0	0	0	33	0	33	100	100
Normal	7	42	19	10	57	0	4214	4349	96.88	---
FDR (%)	5.23	14.61	10.31	17.64	18.07	0	---	---	---	---

Figure 3.

Comparison of sensitivity S and false detection ratio (FDR) for four different SFD&FR algorithms

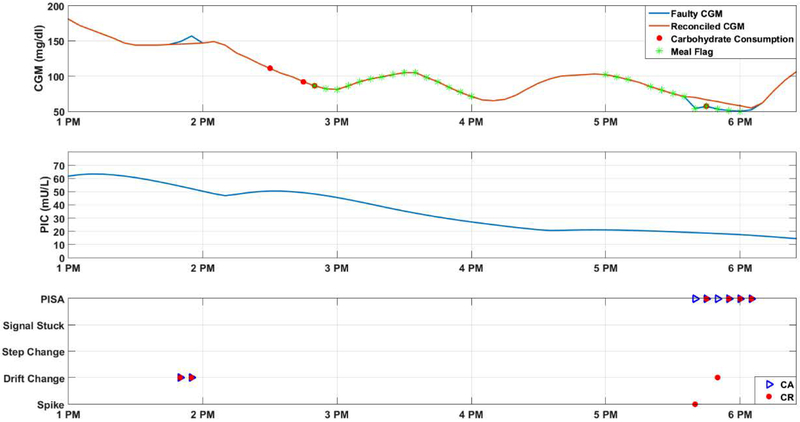
Figure 4 illustrates the decisions reached by SFD&DR with CANN, PIC estimation and meal detection modules for one data set. Between 1:45 PM to 1:55 PM there is a large amount of insulin active in the body based on the PIC estimates, but there is no carbohydrate consumption (no meal flag) by the subject. As a result, the increase of CGM is diagnosed as a drift (sensor error), and the signals are reconciled with model estimations. Between 5:35 PM to 6:05 PM, an induced PISA is recorded in the experiment notes. The SFD&DR reports the CGM data as a spike at the first sample and as PISA and drift at the second and third samples, respectively. Thereon, PISA is reported correctly for the fourth to sixth samples.

Figure 4.

Example of SFD&DR with CANN, PIC estimation, and meal detection module

In Figure 4, the PISA is started at 5:40 PM. At the first sampling time, it is diagnosed and reported as a spike since a large reduction is detected. At the second and third sampling times, PISA and drift change are reported, respectively. At the beginning of PISA, the fault is similar to a decreasing drift. Starting with the fourth sampling time, the SFD&DR can confirm with more confidence that the type of sensor fault is PISA. For a continuous error such as PISA, the SFD&DR algorithm may not able to report the correct error at the beginning since some types of error may look similar at the onset. One way to improve the TA is to modify the error reports if the fault diagnosis reports indicate that the sensor signal has another type of error as the error persists. As an example, the following rules are added to SFD&DR with CANN, PIC estimation, and meal detection module:

• At step k:

  • If ${\mathrm{S}\mathrm{C}}_{k-1}^V\left(3\right)=1$ and ${\mathrm{S}\mathrm{C}}_k^V\left(1\right)\ne 0$:

    • ${\mathrm{S}\mathrm{C}}_{k-1}^V={\mathrm{S}\mathrm{C}}_k^V$
  • For j=[2,4,5,6]:

    • If $\sum _{i=0}^2{\mathrm{S}\mathrm{C}}_{k-i}^V\left(j\right)=3$:

      • t = 2
      • While ${\mathrm{S}\mathrm{C}}_{k-t}^V\left(1\right)\ne 1$:

        • $t=t+1,\mathrm{ }{\mathrm{S}\mathrm{C}}_{k-t}^V={\mathrm{S}\mathrm{C}}_k^V$

At each step k, if a spike is reported at step k − 1 but the current signal is not at normal condition, the ${\mathrm{S}\mathrm{C}}_{k-1}^V$ will be changed to be the same as the current sensor signal condition, since a spike is a discrete sensor error. If for three consecutive sampling times the sensor signal conditions are reported as one type of continuous error, the previous sensor signal condition will be synchronized as the same type of sensor error one by one until ${\mathrm{S}\mathrm{C}}_{k-t}^V$ indicates a normal condition. The summary of sensor signal condition classification of the modified SFD&DR is listed in Table 3.

Table 3.

Summary of Sensor Signal Condition Classification of SFD&DR with Rules and CANN, PIC Estimation, and Meal Detection Module

CR CA	Spike	Drift Change	Step Change	Signal Stuck	PISA	Missing Signal	Normal	SCA	TA (%)	S (%)
Spike	68	21	33	0	12	0	31	165	41.2	81.21
Drift Change	3	211	3	0	7	0	53	277	76.17	80.87
Step Change	7	1	111	1	5	0	14	139	79.86	89.93
Signal Stuck	0	4	8	51	5	0	8	76	67.11	89.47
PISA	0	15	14	0	265	0	43	337	78.64	87.24
Missing Signal	0	0	0	0	0	33	0	33	100	100
Normal	7	42	19	10	57	0	4214	4349	96.90	---
FDR (%)	8.24	14.29	10.11	16.13	16.24	0.00	---	---	---	---

Discussion

In Table 1 and Table 2, the TA and S for missing signal are 100% since it is easy to detect. The missing signal fault is reported when no sensor signal is received for one sampling time. The TA for the spike is relatively low because for many other sensor faults such as PISA the signal behavior is the same as a spike (a single signal jump) at the first sample.

As expected, drift change is the most difficult sensor fault to detect, because the sensor signal change is slow and it may look like an increase caused by carbohydrate consumption or by decreasing PIC especially when a drift change happens during the effective meal period. PISA can only happen when there is pressure introduced (induced) to the sensor, and it often lasts for multiple samples. Some normal CGM signals fluctuations are similar to parts of PISA samples which may cause incorrect classification. Introducing other sensors to indicate the body position may help in improving the detection accuracy. For example, if the subject is lying down, PISA is more likely to occur than if the subject is sitting or standing.

TA and S in Table 1 and Table 2 are almost the same (the difference is less than 1%), but the FDR is reduced significantly, especially for the spike, step change, and drift change decreased by more than half. Using PIC estimation and meal detection modules can provide additional information about the sensor signal dynamics, which reduced the number of FP reported by the SFD&DR algorithm. The PIC estimation and meal detection modules are providing additional known information about the dynamics of the sensor signals, and the CANN can determine some hidden relationships between the MPE and sensor. In Figure 3, both the use of CANN or PIC and meal modules can improve the sensitivity and reduce the FPs. The expected times between false alarms for four different SFD&DR algorithms, as the sequence of Figure 3 are 2.3h, 3.7h, 3.9h, and 4.5h. And the SFD&DR algorithm with CANN, PIC estimation, and meal detection modules achieve the best results by combining high sensitivity and low FDR. In previous work¹⁴, a more complicated threshold setting is proposed, but the FDR is still higher than SFD&FR algorithm with CANN. One the advantage of using CANN is to simplify the threshold determination.

Comparing Table 2 and Table 3, the TA for all the types of sensor faults except spike are shown to improve significantly after introducing rules for continuous sensor signal report modification. The TA of spike was reduced, because some of the TP of the spike may change to another type of error if followed by FPs. The additional rules will not change S and FDR because it only changes the type of error reported, the number of negatives and positives reported by SFD&DR remain the same.

Observability should be checked before the sensor fault detection and data reconciliation system is developed. In this paper, the focus is on how to systematically use different methods for SFD&DR. All the four method is data driven model, we assume the input and output signals are significantly correlated so that the sensor signal can be estimated.

Conclusions

The proposed smart multiple-model SFD&DR combined four different model identification methods (ORKF, LW-PLS, PBSM, and ALD-KRLS) with CANN voting algorithm, and rules for continuous sensor error reporting and data reconciliation. This SFD&DR is able to detect and classify the faults and reconcile the erroneous sensor signal with model-estimated values. The performance of the SFD&DR is illustrated with CGM sensor faults in an AP system. The results illustrate that the SFD&DR is capable of successfully detecting most sensor faults with a small number of false alarms and reconciling the readings with model estimations that are closer to expected values.

Notation

Di_e

direction of faulty CGM measurement

Du_e

duration of faulty CGM measurement

EE_k

energy expenditure at step k

FDR

false detection ratio

${\mathrm{F}\mathrm{l}\mathrm{a}\mathrm{g}}_k^{\mathrm{M}\mathrm{e}\mathrm{a}\mathrm{l}}$:

a binary variable provided by the meal detection module at step k (1: meal effect exists, 0: meal effect does not exist)

FN

false negative

G_k

CGM value at step k

G_e,k

faulty CGM measurement at step k

${\widehat{\mathrm{G}}}_{k|k-t}^m$:

prediction of CGM value at step k by using method m

GSR_k

galvanic skin response at step k

ins_k

insulin infusion rate at step k

${IN}_k^m$:

input of CANN at step k by using method m

m

index for different model identification method (1: ORKF, 2: LW-PLS, 3: PBSM and 4: ALD-KRLS)

M_e

magnitude of faulty CGM measurement

${\mathrm{M}\mathrm{P}\mathrm{E}}_{k|k-1}^m$:

model prediction error of method m at step k

N_f

steps of a fault continuously reported by SFD&DR algorithm

NP

maximum prediction horizon that the models need to provide to generate the input of CANN

${OUT}_k^m$:

output of CANN at step k by using method m

PIC_k

PIC estimation at step k

S

sensitivity

SCA

samples that are announced by clinical specialist as one specific condition

${\mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}}_k^m$:

Score used to determine which model prediction will be used for signal reconciliation at step k

${\mathrm{S}\mathrm{C}}_k^V$:

index for sensor condition report (1: normal, 2: signal stuck, 3: spike, 4: drift change, 5: step change, and 6: PISA)

T^m

threshold of $\left|{\mathrm{ }\mathrm{M}\mathrm{P}\mathrm{E}}_{\mathrm{k}|\mathrm{k}-1}^{\mathrm{m}}\right|$

TA

type accuracy

TBE_k

threshold-based error (1 or 0 indicates the sensor signal is faulty or normal)

TP

true positive