Spin-orbit torque flips the perpendicular magnetic moment of a 2D van der Waals magnet.
Abstract
The recent discovery of ferromagnetism in two-dimensional (2D) van der Waals (vdW) materials holds promises for spintronic devices with exceptional properties. However, to use 2D vdW magnets for building spintronic nanodevices such as magnetic memories, key challenges remain in terms of effectively switching the magnetization from one state to the other electrically. Here, we devise a bilayer structure of Fe3GeTe2/Pt, in which the magnetization of few-layered Fe3GeTe2 can be effectively switched by the spin-orbit torques (SOTs) originated from the current flowing in the Pt layer. The effective magnetic fields corresponding to the SOTs are further quantitatively characterized using harmonic measurements. Our demonstration of the SOT-driven magnetization switching in a 2D vdW magnet could pave the way for implementing low-dimensional materials in the next-generation spintronic applications.
INTRODUCTION
Emerging phenomena arising from the interfaces and heterostructures of conventional magnetic thin films (1, 2), such as exchange bias (3), interfacial perpendicular magnetic anisotropy (PMA) (4, 5), spin-transfer torque (6–8), and spin-orbit torques (SOTs) (9, 10), have greatly advanced the development of spintronic applications (8, 11). However, the pursuit of new magnetic materials with better interfacial properties and thinner thicknesses is still one of the main themes in spintronic studies. van der Waals (vdW) materials offer a versatile platform for exploring novel phenomena and can provide high-quality interfaces at the atomic scale. Their intersection with spintronics has just been properly established with the recently found two-dimensional (2D) magnetism (12–22). It is believed that spintronic devices harnessing vdW magnets may inherit many advantages of 2D materials such as the gate tunability, flexibility, low-cost/large-scale growth, etc. However, manipulating the magnetic order parameter of vdW magnets via spintronic approaches, which is essential for practical applications, have been rarely studied so far.
A feasible scheme to spintronically control the magnetization of vdW magnets is to combine their PMA with the effect of SOTs, using an additional heavy metal layer next to the magnetic layer. In this work, we demonstrate an SOT-driven perpendicular magnetization switching in a bilayer structure of few-layered Fe3GeTe2 (FGT) and Pt (Fig. 1, A and B). FGT is currently one of the most attractive 2D magnetic vdW materials due to its gate-tunable Curie temperature Tc (up to room temperature) and PMA (21, 22), which are both important for high-density information storage applications (4). The crossover between magnetic vdW materials and SOTs opens the possibilities to push spintronic devices to the 2D limit with faster speed and lower energy consumption.
Fig. 1. Schematic view and characterizations of FGT/Pt bilayer.
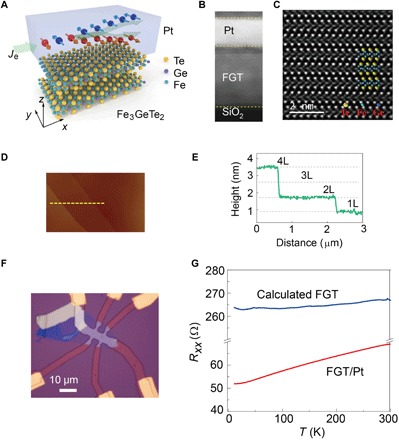
(A) Schematic view of the bilayer structure. Pt layer (top) is sputtered on top of the exfoliated FGT (bottom). The green arrow represents the in-plane current flowing in the Pt layer, which generates a spin current flowing in the z direction. The accumulated spins at the bottom (top) Pt surface are indicated by the red (blue) arrows. The spin current exerts torques on the magnetization of FGT and can switch it in the presence of an in-plane magnetic field. (B) Cross-sectional STEM image of the FGT/Pt device fabricated on a Si/SiO2 substrate. The total thickness of FGT is 12.6 nm. (C) High-resolution STEM image of an FGT (87 nm)/Pt (6 nm) bilayer on a Si/SiO2 substrate. (D) Top view of the FGT exfoliated from the bulk material measured by atomic force microscopy. (E) The atomic steps profile taken along the yellow dashed lines in (D). An atomic layer step of 0.8 nm is observed. (F) The optical image of the measured Hall bar device. (G) Temperature-dependent longitudinal resistance of the FGT/Pt bilayer device and FGT only.
RESULTS
We fabricated the FGT/Pt device by first exfoliating few-layered FGT flakes from a high-quality bulk crystal onto Si/SiO2 substrates. Characterizations of the magnetic properties and the structure of bulk FGT are shown in section S1. Figure 1C shows a representative high-angle annular dark-field scanning transmission electron microscopy (STEM) image of the as-exfoliated FGT. Atomic arrangements in the [100] axes are in agreement with the crystal structure of FGT. Each layer is constituted by the alternately arranged Te─Fe─Ge(Fe)─Fe─Te atomic planes. The vdW gaps (dark area) are visible between different layers. The exfoliated FGT flakes show a minimum step height of 0.8 nm on the surface (Fig. 1, D and E), which matches an atomic layer thickness of FGT. After exfoliating the FGT flakes, we immediately transferred the substrates into a high-vacuum sputtering system and then deposited a 6-nm-thick Pt layer on top of FGT. We then patterned the FGT/Pt bilayers into Hall bar devices (see Fig. 1F) by the processes described in section S2.
We first measured the resistance of the device as a function of temperature, as shown in Fig. 1G. The bilayer device exhibits a metallic behavior. To elucidate the resistance behavior of FGT, we separately characterize the temperature-dependent resistivity of Pt layer by measuring a Hall bar control device prepared on a Si/SiO2 substrate. Considering the geometry and thickness of the Pt layer in the FGT/Pt device, the resistance contribution from the Pt layer can be deducted (see fig. S14) so that the resistance of FGT can be roughly extracted (see Fig. 1G). The temperature dependence of the FGT resistance is similar to the previous reports for FGT with four to six layers (3.2 to 4.8 nm) (21). The actual layer number observed by TEM is larger, as shown in Fig. 1B. We attribute this difference to the oxidization of FGT.
We then characterized the magnetic properties of our devices by measuring the Hall resistances. Figure 2A shows the Hall resistance as a function of the out-of-plane magnetic fields at various temperatures. Because of the intrinsic magnetization of FGT, anomalous Hall resistance dominates over the total Hall resistance below Tc as indicated by the square-shaped loops. The hysteresis loop gradually disappears, and the Hall resistance curve becomes more linear with increasing the temperature. The Tc of our device is determined to be ~158 K by performing the Arrott plots (21, 23), as shown in Fig. 2B. Compared to the previously reported layer-dependent Tc (21), the obtained Tc in our FGT corresponds to approximately five layers (4 nm). This thickness value is in consistent with the estimations from the resistance measurements and the TEM image. Below Tc, the device exhibits PMA, as manifested by the much larger saturation field in the in-plane direction than that in the out-of-plane direction (Fig. 2C).
Fig. 2. Magnetic properties of FGT/Pt bilayer.
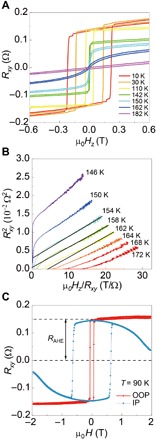
(A) Hall resistance as a function of magnetic field at different temperatures. (B) Arrott plots of the Hall resistance of the FGT/Pt device. The determined Tc is 158 K. (C) RAHE as a function of in-plane (IP) and out-of-plane (OOP) magnetic field at 90 K.
Next, we show that a current flowing in the bilayer can generate SOTs, which are originated from the spin Hall effect in Pt and/or the interfacial effects. The SOTs are characterized through harmonic measurements (24, 25). For the harmonic measurements, a small ac is applied to the device in the presence of an in-plane external magnetic field along the longitudinal (transverse) direction for measuring longitudinal (transverse) effective fields. Figure 3 shows the measured harmonic voltages under longitudinal (HL) (A and B) and transverse (HT) (D and E) external magnetic fields, which are fitted by parabolic and linear functions, respectively. The ratios corresponding to damping-like and field-like torques can be calculated as . Here, Vω and V2ω are the first and second harmonic voltage, respectively. The current-induced effective fields in the longitudinal and transverse directions can then be extracted on the basis of (26) ΔHL(T) = (BL(T) ± 2βBT(L))/(1 − 4β2). Here, β is the ratio between the planar Hall resistance (RP) and the anomalous Hall resistance (RAHE), and β = RP/RAHE = 0.12. The obtained effective fields versus current density are ΔHL = 53.4 ± 4.7 mT per 107 A/cm2 and ΔHT = 24.3 ± 2.3 mT per 107 A/cm2, respectively. Note that the contributions from thermal effect and Oersted field have been carefully considered (see section S3).
Fig. 3. Characterization of the current-induced effective fields.
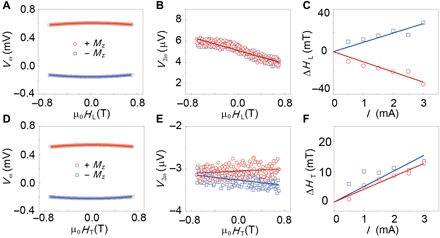
(A and B) First and second harmonic voltages for the longitudinal effective field. HL is the applied longitudinal magnetic field along the current direction (x axis). (D and E) First and second harmonic voltages for the transverse effective field. HT is the applied transverse magnetic field transverse to the current direction (y axis). (C and F) Plots of the longitudinal and transverse field as a function of the peak current. The solid lines represent the linear fitting result with zero intercept. The red circles (blue squares) are data points for the Mz > 0 (Mz < 0). In the bilayer device, applying a current of 1 mA corresponds to a current density of 1.85 × 1010 A/m2 in the Pt layer.
In general, the SOT can be evaluated by the spin torque efficiency (27, 28): , where Tint is the interfacial spin transparency (Tint < 1), θSH is the spin Hall angle, e is the electron charge, ħ is the reduced Planck constant, μ0 is the vacuum permeability, Ms is the saturation magnetization, is the effective thickness of FGT, and Je is the current density. It is difficult to get ξ without knowing the value of Ms for few-layered FGT. However, as ξ is only determined by the spin Hall angle of the heavy metal and the interface quality, it may shed a light on estimating the upper limit of Ms for few-layered vdW magnets. If the spin torque efficiency ξ = 0.12 (in the case with a transparent interface and the spin Hall angle of Pt is 0.12), which is in consistent with the previously reported ξ values for Pt (27, 28), is assumed, then we can approximately estimate the upper limit value of Ms to be 1.6 × 104 A/m. This value is notably smaller than the bulk Ms value (3.21 × 105 A/m; see fig. S7), which might be due to the finite size effect, strong surface modification in ultrathin magnetic films (29, 30), and oxidation of FGT.
Last, we show that the generated SOTs can be used to switch the perpendicularly magnetized FGT in the bilayer devices with the assistance of an in-plane magnetic field to break the mirror symmetry (31). Figure 4 (A and B) shows the current-induced magnetization switching of FGT with the in-plane magnetic field Hx = 50 and −50 mT at 100 K, respectively. The magnetization of FGT can be switched from one state to the other by sweeping the electric current. Two distinct states can be well sustained at the zero current. The switching polarity is anticlockwise (clockwise) for the positive (negative) in-plane field, indicating a positive spin Hall angle of Pt here, which is consistent with previous works. Similar behaviors can be observed from 10 to 130 K (see section S4), suggesting a large temperature window for switching. The switching behavior disappears around 140 K (still below Tc), which is likely due to the gradual loss of squareness of the hysteresis loops and the resulting absence of two distinct remanence states.
Fig. 4. SOT-driven perpendicular magnetization switching in the FGT/Pt bilayer device.
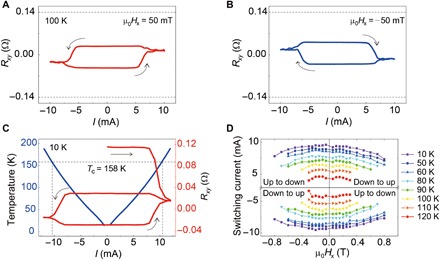
Current-driven perpendicular magnetization switching for in-plane magnetic fields of 50 mT (A) and −50 mT (B) at 100 K. The switching polarity is anticlockwise and clockwise, respectively. The dashed lines correspond to the RAHE at saturated magnetization states. (C) Current-driven perpendicular magnetization switching with a 300-mT in-plane magnetic field at 10 K (red). The arrows indicate the current sweeping direction. The initial state is saturated in the positive direction. The current increases gradually in the positive direction, and the RAHE jumps down to an intermediate state. The two states in the switching loop do not correspond to the saturated states. The device temperature during the application of switching current (blue) is obtained by comparing the measured longitudinal resistance and the measured RxxT curve (fig. S14). The dashed line corresponds to the Tc obtained from the Arrott plots. (D) Switching-phase diagram with respect to the in-plane magnetic fields and critical switching currents at different temperatures. The critical switching current decreases with increasing temperature. In the bilayer device, applying a current of 1 mA corresponds to a current density of 1.85 × 1010 A/m2 in the Pt layer.
DISCUSSION
It is noted that the two observed resistance states during the switching are not fully saturated (indicated by the dashed lines in Fig. 4, A and B). This incomplete switching can be ascribed to a Joule heating effect. As shown in Fig. 4C, starting from a fully saturated initial state (polarized in the positive direction), the magnetization of FGT (represented by the Hall resistance Rxy) begins to decrease once the applied current exceeds 8 mA. In our device, the positive current favors a positive magnetization under a positive in-plane magnetic field, so Rxy should not decrease with increasing the current. Moreover, the decreasing behavior is independent of the initial state (section S5), indicating its thermal origin. We have further extracted the temperature of the device under applied current pulses (with a duration of 50 ms) by monitoring the resistance of the device (blue curves in Fig. 4C) (32). An evident thermal effect is observed, as the device temperature is approaching Tc under a current of 8 mA and exceeding Tc under a current of 10.5 mA. When the device temperature is close to Tc, the magnetic interactions of FGT are not sufficient to fight against the thermal fluctuations and maintain a single domain state. Thus, a multidomain state is formed under large applied current pulses, which results in the unsaturated resistance sates. Further increasing the current to above 10.5 mA also does little to help in realizing a complete switching since the temperature rises above Tc.
To further prove that the switching is originated from the current-induced SOT, we have also fabricated FGT/Ta bilayer devices and observed similar switching behavior but with opposite switching polarity due to the opposite sign of the spin Hall angle in Ta (see section S6). Figure 4D shows the switching diagram for various temperatures. The switching current decreases with the increase in temperature. We attribute the reduction of switching current to the simultaneous decrease in Ms (manifested by the decrease in RAHE) and effective PMA field (Hk) (see section S7).
In summary, an SOT-driven perpendicular magnetization switching has been demonstrated in an FGT/Pt bilayer device. Our proof-of-concept SOT devices highlight the potential of magnetic vdW materials and their compatibilities with spintronic technologies. Further work is still needed to push the FGT down to the monolayer limit. Other than the Pt or Ta used in this work, vdW materials with strong spin-orbit coupling and nontrivial electronic properties can also be used as SOT sources, leading to the possible all-vdW magnetic memories. The large family of vdW materials and numerous combinations of vdW heterostructures remarkably extend the material choices and can be visioned as new building blocks for spintronic applications in the near future.
MATERIALS AND METHODS
Growth and characterization of FGT bulk crystal
Single crystals of FGT were prepared by chemical vapor transport (CVT) method with iodine as the transport agent. High-purity (99.99%) Fe, Ge, and Te were milled into powder form with a stoichiometric molar proportion of 3:1:2 (Fe:Ge:Te) in an agate mortar.
Device fabrication
We obtained few-layered FGT flakes with a freshly cleaved surface on Si/SiO2 substrate by our new developed scratching method (refer to section S2) through our home-made transfer station. Next, we deposited a 6-nm-thick Pt [or Ta (6 nm)/Pt (1.5 nm)] layer on the FGT surface, and the obtained FGT/Pt bilayer is air-stable and this could confirm the subsequent fabrication process. The Pt/FGT bilayer was patterned as Hall geometry by a standard e-beam lithography process, and excrescent areas were etched by ion milling. Last, the electrodes were fabricated by Ti (3 nm)/Au (50 nm) through e-beam evaporation.
Characterizations
We used aberration-corrected STEM to image the cross sections directly. The cross-sectional samples were fabricated by focused ion beam cutting along the [100] axes of FGT. All the electrical measurements were performed in a Physical Property Measurement System (PPMS) system with magnetic fields of up to 9 T and temperatures down to 1.8 K. Multiple lock-in amplifiers (Stanford SR830 and SR850) and Keithley source meters (Keithley 2400, 2182, and 6221) were connected to the PPMS, enabling comprehensive transport measurements for the Hall bar devices. A constant of 200 μA dc was applied for the Hall measurement. In the switching measurement, large current pulses (write current, 50 ms) were first applied. After a time interval of 100 ms, we subsequently applied another small current (read current, 0.1 mA for 50 ms), during which the Hall voltage signal was picked up. The device temperature during the application of write pulse was extracted by monitoring the longitudinal resistance. The temperature increased during the application of read pulse was negligible.
Supplementary Material
Acknowledgments
Funding: G.Y. and X.H. thank the National Key Research and Development Program of China (grant nos. 2017YFA0206200, 2018YFB0407600, 2016YFA0300802, and 2017YFA0206302), the National Natural Science Foundation of China (NSFC; grant nos.11874409, 11804380, 11434014, and 51831012), the NSFC–Science Foundation Ireland (SFI) Partnership Programme (grant no. 51861135104), and the 1000 Youth Talents Program for financial support. G.Z. thanks NSFC (grant nos. 61734001, 11834017, and 51572289), the Strategic Priority Research Program (B) of CAS (grant no. XDB30000000), the Key Research Program of Frontier Sciences of CAS (grant no. QYZDB-SSW-SLH004), the National Key R&D Program of China (grant no. 2016YFA0300904) for financial support. Y.L. acknowledges support from the Institute of Physics, Chinese Academy of Sciences through the International Young Scientist Fellowship (grant no. 2018001). J.Z. and Xixiang Zhang acknowledge the financial support from the King Abdullah University of Science and Technology (KAUST), Office of Sponsored Research (OSR) under the award no. OSR-2017-CRG6-3427. G.Y. and Y.L. acknowledge fruitful discussion with J. Yu and J. Zang. Author contributions: G.Y. conceived the project. X.X. grew and characterized the bulk FGT crystal with the help from the latter X.L. J.T. exfoliated the FGT thin films and fabricated the devices with the help from X.W., C.H., M.L., the former X.L., R.Y., and D.S. X.W. performed the electrical measurements with the help from C.W., C.F., C.G., W.Y., Y.G., the former X.Z., H.X., J.W., J.F., and H.W. J.Z. performed the TEM measurements with the help from Y.P. and the latter X.Z. G.Y. drafted the paper and revised the paper with the help from Y.L., Z.H., G.Z. The study was performed under the supervision of G.Y. and X.H. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/8/eaaw8904/DC1
Section S1. Crystal growth and characterization
Section S2. Exfoliation of FGT thin flakes and fabrication of FGT/Pt bilayer devices
Section S3. Correction of current-induced effective fields
Section S4. Current-driven switching at different temperatures
Section S5. Current-driven magnetization switching
Section S6. Current-driven magnetization switching and measurement of effective fields corresponding the current-induced torques
Section S7. Temperature dependence of PMA
Fig. S1. Single crystals of FGT at the colder side in a sealed quartz tube (diameter of the tube is 1.5 cm).
Fig. S2. Characterization of FGT single crystal grown by CVT method.
Fig. S3. Zero-field–cooling and field-cooling curves of the FGT crystals (grown by CVT) measured from 10 to 300 K with the external magnetic field (H = 0.1 T) parallel to the c axis.
Fig. S4. Hysteresis loops measured of the FGT crystals (grown by CVT) at various temperatures with the external magnetic field parallel to the c axis.
Fig. S5. Zero-field–cooling and field-cooling curves of the FGT crystals (grown by CVT method) measured from 10 to 300 K with the external magnetic field (H = 0.1 T) parallel to the ab plane.
Fig. S6. Hysteresis loops of the FGT crystals (grown by CVT method) measured at various temperatures with the external magnetic field parallel to the ab plane.
Fig. S7. Zero-field–cooling and field-cooling curves of the FGT crystals (grown by CVT) measured from 10 to 300 K with the external magnetic field (H = 0.1 T) parallel to the c axis and the ab plane.
Fig. S8. Characterization of FGT single crystal grown by flux method.
Fig. S9. Zero-field–cooling and field-cooling curves of the FGT crystals (grown by flux method) measured from 10 to 300 K with the external magnetic field (H = 0.1 T) parallel to the c axis.
Fig. S10. Hysteresis loops measured of the FGT crystals (grown by flux method) at various temperatures with the external magnetic field parallel to the c axis.
Fig. S11. Schematic view of FGT exfoliation, transfer, and device fabrication process.
Fig. S12. Atomic force microscopy image of the obtained FGT flakes on SiO2 substrate through two strategies.
Fig. S13. Optical image of the device fabrication process.
Fig. S14. Estimation of the temperature dependence of the resistance of FGT layers.
Fig. S15. Schematic diagram of measurement setup and coordinate system.
Fig. S16. Current-driven switching at 10 K.
Fig. S17. Current-driven switching at 20 K.
Fig. S18. Current-driven switching at 30 K.
Fig. S19. Current-driven switching at 40 K.
Fig. S20. Current-driven switching at 50 K.
Fig. S21. Current-driven switching at 60 K.
Fig. S22. Current-driven switching at 70 K.
Fig. S23. Current-driven switching at 80 K.
Fig. S24. Current-driven switching at 90 K.
Fig. S25. Current-driven switching at 100 K.
Fig. S26. Current-driven switching at 110 K.
Fig. S27. Current-driven switching at 120 K.
Fig. S28. Current-driven switching at 130 K.
Fig. S29. Rxy as a function of current under different in-plane magnetic field at 140 K.
Fig. S30. Current-driven magnetization switching for different initial states.
Fig. S31. Current-driven switching in an FGT/Ta bilayer.
Fig. S32. Characterization of the current-induced effective fields in an FGT/Ta device.
Fig. S33. Hall resistance as a function of in-plane magnetic field.
Fig. S34. Temperature dependence of effective anisotropy field (μ0Hk), coercivity (μ0Hc), and saturation anomalous Hall resistance.
REFERENCES AND NOTES
- 1.Hellman F., Hoffmann A., Tserkovnyak Y., Beach G. S. D., Fullerton E. E., Leighton C., MacDonald A. H., Ralph D. C., Arena D. A., Dürr H. A., Fischer P., Grollier J., Heremans J. P., Jungwirth T., Kimel A. V., Koopmans B., Krivorotov I. N., May S. J., Petford-Long A. K., Rondinelli J. M., Samarth N., Schuller I. K., Slavin A. N., Stiles M. D., Tchernyshyov O., Thiaville A., Zink B. L., Interface-induced phenomena in magnetism. Rev. Mod. Phys. 89, 025006 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Soumyanarayanan A., Reyren N., Fert A., Panagopoulos C., Emergent phenomena induced by spin-orbit coupling at surfaces and interfaces. Nature 539, 509–517 (2016). [DOI] [PubMed] [Google Scholar]
- 3.Nogués J., Schuller I. K., Exchange bias. J. Magn. Magn. Mater. 192, 203–232 (1999). [Google Scholar]
- 4.Dieny B., Chshiev M., Perpendicular magnetic anisotropy at transition metal/oxide interfaces and applications. Rev. Mod. Phys. 89, 025008 (2017). [Google Scholar]
- 5.Ikeda S., Miura K., Yamamoto H., Mizunuma K., Gan H. D., Endo M., Kanai S., Hayakawa J., Matsukura F., Ohno H., A perpendicular-anisotropy CoFeB-MgO magnetic tunnel junction. Nat. Mater. 9, 721–724 (2010). [DOI] [PubMed] [Google Scholar]
- 6.Slonczewski J. C., Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mater. 159, L1–L7 (1996). [Google Scholar]
- 7.Berger L., Emission of spin waves by a magnetic multilayer traversed by a current. Phys. Rev. B 54, 9353–9358 (1996). [DOI] [PubMed] [Google Scholar]
- 8.Brataas A., Kent A. D., Ohno H., Current-induced torques in magnetic materials. Nat. Mater. 11, 372–381 (2012). [DOI] [PubMed] [Google Scholar]
- 9.Miron I., Garello K., Gaudin G., Zermatten P. J., Costache M. V., Auffret S., Bandiera S., Rodmacq B., Schuhl A., Gambardella P., Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–193 (2011). [DOI] [PubMed] [Google Scholar]
- 10.Liu L., Pai F., Li Y., Tseng H. W., Ralph D. C., Buhrman R. A., Spin-torque switching with the giant spin Hall effect of tantalum. Phys. Rev. Lett. 336, 555–558 (2012). [DOI] [PubMed] [Google Scholar]
- 11.Ikeda S., Hayakawa J., Lee Y. M., Matsukura F., Ohno Y., Hanyu T., Ohno H., Magnetic tunnel junctions for spintronic memories and beyond. IEEE Trans. Electron. Dev. 54, 991–1002 (2007). [Google Scholar]
- 12.Huang B., Clark G., Navarro-Moratalla E., Klein D. R., Cheng R., Seyler K. L., Zhong D., Schmidgall E., McGuire M. A., Cobden D. H., Yao W., Xiao D., Jarillo-Herrero P., Xu X., Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 546, 270–273 (2017). [DOI] [PubMed] [Google Scholar]
- 13.Gong C., Li L., Li Z., Ji H., Stern A., Xia Y., Cao T., Bao W., Wang C., Wang Y., Qiu Z. Q., Cava R. J., Louie S. G., Xia J., Zhang X., Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265–269 (2017). [DOI] [PubMed] [Google Scholar]
- 14.Klein D. R., MacNeill P., Lado J. L., Soriano D., Navarro-Moratalla E., Watanabe K., Taniguchi T., Manni S., Canfield P., Fernández-Rossier J., Jarillo-Herrero P., Probing magnetism in 2D van der Waals crystalline insulators via electron tunneling. Phys. Rev. Lett. 360, 1218–1222 (2018). [DOI] [PubMed] [Google Scholar]
- 15.Song T. C., Cai X., Tu M. W., Zhang X., Huang B., Wilson N. P., Seyler K. L., Zhu L., Taniguchi T., Watanabe K., McGuire M. A., Cobden D. H., Xiao D., Yao W., Xu X., Giant tunneling magnetoresistance in spin-filter van der Waals heterostructures. Phys. Rev. Lett. 360, 1214–1218 (2018). [DOI] [PubMed] [Google Scholar]
- 16.Kim H. H., Yang B., Patel T., Sfigakis F., Li C., Tian S., Lei H., Tsen A. W., One million percent tunnel magnetoresistance in a magnetic van der Waals heterostructure. Nano Lett. 18, 4885–4890 (2018). [DOI] [PubMed] [Google Scholar]
- 17.Sivadas N., Okamoto S., Xiao D., Gate-controllable magneto-optic Kerr effect in layered collinear antiferromagnets. Phys. Rev. Lett. 117, 267203 (2016). [DOI] [PubMed] [Google Scholar]
- 18.Huang B., Clark G., Klein D. R., MacNeill D., Navarro-Moratalla E., Seyler K. L., Wilson N., McGuire M. A., Cobden D. H., Xiao D., Yao W., Jarillo-Herrero P., Xu X., Electrical control of 2D magnetism in bilayer CrI3. Nat. Nanotechnol. 13, 544–548 (2018). [DOI] [PubMed] [Google Scholar]
- 19.Jiang S. W., Shan J., Mak K. F., Electric-field switching of two-dimensional van der Waals magnets. Nat. Mater. 17, 406–410 (2018). [DOI] [PubMed] [Google Scholar]
- 20.Wang Z., Zhang T., Ding M., Dong B., Li Y., Chen M., Li X., Huang J., Wang H., Zhao X., Li Y., Li D., Jia C., Sun L., Guo H., Ye Y., Sun D., Chen Y., Yang T., Zhang J., Ono S., Han Z., Zhang Z., Electric-field control of magnetism in a few-layered van der Waals ferromagnetic semiconductor. Nat. Nanotechnol. 13, 554–559 (2018). [DOI] [PubMed] [Google Scholar]
- 21.Deng Y. J., Yu Y., Song Y., Zhang J., Wang N. Z., Sun Z., Yi Y., Wu Y. Z., Wu S., Zhu J., Wang J., Chen X. H., Zhang Y., Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2. Nature 563, 94–99 (2018). [DOI] [PubMed] [Google Scholar]
- 22.Fei Z. Y., Huang H., Malinowski P., Wang W., Song T., Sanchez J., Yao W., Xiao D., Zhu X., May A. F., Wu W., Cobden D. H., Chu J. H., Xu X., Two-dimensional itinerant ferromagnetism in atomically thin Fe3GeTe2. Nat. Mater. 17, 778–782 (2018). [DOI] [PubMed] [Google Scholar]
- 23.Arrott A., Criterion for ferromagnetism from observations of magnetic isotherms. Phys. Rev. 108, 1394–1396 (1957). [Google Scholar]
- 24.Garello K., Miron I. M., Avci C. O., Freimuth F., Mokrousov Y., Blügel S., Auffret S., Boulle O., Gaudin G., Gambardella P., Symmetry and magnitude of spin-orbit torques in ferromagnetic heterostructures. Nat. Nanotechnol. 8, 587–593 (2013). [DOI] [PubMed] [Google Scholar]
- 25.Pi U. H., W. Kim K., Bae J. Y., Lee S. C., Cho Y. J., Kim K. S., Seo S., Tilting of the spin orientation induced by Rashba effect in ferromagnetic metal layer. Appl. Phys. Lett. 97, 162507 (2010). [Google Scholar]
- 26.Hayashi M., Kim J., Yamanouchi M., Ohno H., Quantitative characterization of the spin-orbit torque using harmonic Hall voltage measurements. Phys. Rev. B 89, 144425 (2014). [Google Scholar]
- 27.Nguyen M.-H., Ralph D. C., Buhrman R. A., Spin torque study of the spin hall conductivity and spin diffusion length in platinum thin films with varying resistivity. Phys. Rev. Lett. 116, 126601 (2016). [DOI] [PubMed] [Google Scholar]
- 28.Pai C. F., Ou Y. X., Vilela-Leao L. H., Ralph D. C., Buhrman R. A., Dependence of the efficiency of spin Hall torque on the transparency of Pt/ferromagnetic layer interfaces. Phys. Rev. B 92, 064426 (2015). [Google Scholar]
- 29.Zhang R. J., Willis R. F., Thickness-dependent Curie temperatures of ultrathin magnetic films: Effect of the range of spin-spin interactions. Phys. Rev. Lett. 86, 2665–2668 (2001). [DOI] [PubMed] [Google Scholar]
- 30.Vaz C. A. F., Bland J. A. C., Lauhoff G., Magnetism in ultrathin film structures. Rep. Prog. Phys. 71, 056501 (2008). [Google Scholar]
- 31.Yu G. Q., Upadhyaya P., Fan Y., Alzate J. G., Jiang W., Wong K. L., Takei S., Bender S. A., Chang L. T., Jiang Y., Lang M., Tang J., Wang Y., Tserkovnyak Y., Amiri P. K., Wang K. L., Switching of perpendicular magnetization by spin-orbit torques in the absence of external magnetic fields. Nat. Nanotechnol. 9, 548–554 (2014). [DOI] [PubMed] [Google Scholar]
- 32.Razavi S. A., Razavi A., Wu D., Yu G., Lau Y.-C., Wong K. L., Zhu W., He C., Zhang Z., Coey J. M. D., Stamenov P., Amiri P. K., Wang K. L., Joule heating effect on field-free magnetization switching by spin-orbit torque in exchange-biased systems. Phys. Rev. Appl. 7, 024023 (2017). [Google Scholar]
- 33.Avci C. O., Garello K., Gabureac M., Ghosh A., Fuhrer A., Alvarado S. F., Gambardella P., Interplay of spin-orbit torque and thermoelectric effects in ferromagnet/normal-metal bilayers. Phys. Rev. B 90, 224427 (2014). [Google Scholar]
- 34.Kim J., Sinha J., Hayashi M., Yamanouchi M., Fukami S., Suzuki T., Mitani S., Ohno H., Layer thickness dependence of the current-induced effective field vector in Ta/CoFeB/MgO. Nat. Mater. 12, 240–245 (2013). [DOI] [PubMed] [Google Scholar]
- 35.Kong W. J., Wan C. H., Tao B. S., Fang C., Huang L., Guo C. Y., Irfan M., Han X. F., Study of spin-orbit torque induced magnetization switching in synthetic antiferromagnet with ultrathin Ta spacer layer. Appl. Phys. Lett. 113, 162402 (2018). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/8/eaaw8904/DC1
Section S1. Crystal growth and characterization
Section S2. Exfoliation of FGT thin flakes and fabrication of FGT/Pt bilayer devices
Section S3. Correction of current-induced effective fields
Section S4. Current-driven switching at different temperatures
Section S5. Current-driven magnetization switching
Section S6. Current-driven magnetization switching and measurement of effective fields corresponding the current-induced torques
Section S7. Temperature dependence of PMA
Fig. S1. Single crystals of FGT at the colder side in a sealed quartz tube (diameter of the tube is 1.5 cm).
Fig. S2. Characterization of FGT single crystal grown by CVT method.
Fig. S3. Zero-field–cooling and field-cooling curves of the FGT crystals (grown by CVT) measured from 10 to 300 K with the external magnetic field (H = 0.1 T) parallel to the c axis.
Fig. S4. Hysteresis loops measured of the FGT crystals (grown by CVT) at various temperatures with the external magnetic field parallel to the c axis.
Fig. S5. Zero-field–cooling and field-cooling curves of the FGT crystals (grown by CVT method) measured from 10 to 300 K with the external magnetic field (H = 0.1 T) parallel to the ab plane.
Fig. S6. Hysteresis loops of the FGT crystals (grown by CVT method) measured at various temperatures with the external magnetic field parallel to the ab plane.
Fig. S7. Zero-field–cooling and field-cooling curves of the FGT crystals (grown by CVT) measured from 10 to 300 K with the external magnetic field (H = 0.1 T) parallel to the c axis and the ab plane.
Fig. S8. Characterization of FGT single crystal grown by flux method.
Fig. S9. Zero-field–cooling and field-cooling curves of the FGT crystals (grown by flux method) measured from 10 to 300 K with the external magnetic field (H = 0.1 T) parallel to the c axis.
Fig. S10. Hysteresis loops measured of the FGT crystals (grown by flux method) at various temperatures with the external magnetic field parallel to the c axis.
Fig. S11. Schematic view of FGT exfoliation, transfer, and device fabrication process.
Fig. S12. Atomic force microscopy image of the obtained FGT flakes on SiO2 substrate through two strategies.
Fig. S13. Optical image of the device fabrication process.
Fig. S14. Estimation of the temperature dependence of the resistance of FGT layers.
Fig. S15. Schematic diagram of measurement setup and coordinate system.
Fig. S16. Current-driven switching at 10 K.
Fig. S17. Current-driven switching at 20 K.
Fig. S18. Current-driven switching at 30 K.
Fig. S19. Current-driven switching at 40 K.
Fig. S20. Current-driven switching at 50 K.
Fig. S21. Current-driven switching at 60 K.
Fig. S22. Current-driven switching at 70 K.
Fig. S23. Current-driven switching at 80 K.
Fig. S24. Current-driven switching at 90 K.
Fig. S25. Current-driven switching at 100 K.
Fig. S26. Current-driven switching at 110 K.
Fig. S27. Current-driven switching at 120 K.
Fig. S28. Current-driven switching at 130 K.
Fig. S29. Rxy as a function of current under different in-plane magnetic field at 140 K.
Fig. S30. Current-driven magnetization switching for different initial states.
Fig. S31. Current-driven switching in an FGT/Ta bilayer.
Fig. S32. Characterization of the current-induced effective fields in an FGT/Ta device.
Fig. S33. Hall resistance as a function of in-plane magnetic field.
Fig. S34. Temperature dependence of effective anisotropy field (μ0Hk), coercivity (μ0Hc), and saturation anomalous Hall resistance.


