TCR–pMHC kinetics under force in a cell-free system show no intrinsic catch bond, but a minimal encounter duration before binding

Significance

T lymphocytes use their T cell receptors (TCRs) to discriminate between similar peptide-MHC (pMHC) antigens. The mechanisms employed to achieve this discrimination are debated. The TCR–pMHC interaction is subjected to forces, and recent work in live T cells has suggested that force paradoxically increases TCR–pMHC bond lifetimes for activating peptides, forming so-called “catch bonds,” facilitating discrimination from nonactivating peptides. A question is whether this behavior is intrinsic to the TCR–pMHC bond or a cellular response. We measured TCR–pMHC lifetimes under force in a cell-free system: lifetimes correlated well with activation potency of the TCR–pMHC bonds, while no catch bonds were observed. However, a minimum encounter duration is necessary for bond formation, which could increase specificity.

Abstract

The T cell receptor (TCR)–peptide-MHC (pMHC) interaction is the only antigen-specific interaction during T lymphocyte activation. Recent work suggests that formation of catch bonds is characteristic of activating TCR–pMHC interactions. However, whether this binding behavior is an intrinsic feature of the molecular bond, or a consequence of more complex multimolecular or cellular responses, remains unclear. We used a laminar flow chamber to measure, first, 2D TCR–pMHC dissociation kinetics of peptides of various activating potency in a cell-free system in the force range (6 to 15 pN) previously associated with catch–slip transitions and, second, 2D TCR–pMHC association kinetics, for which the method is well suited. We did not observe catch bonds in dissociation, and the off-rate measured in the 6- to 15-pN range correlated well with activation potency, suggesting that formation of catch bonds is not an intrinsic feature of the TCR–pMHC interaction. The association kinetics were better explained by a model with a minimal encounter duration rather than a standard on-rate constant, suggesting that membrane fluidity and dynamics may strongly influence bond formation.

T lymphocyte activation begins with the binding of the T cell receptor (TCR) on the lymphocyte surface to an antigenic peptide carried by a major histocompatibility complex (pMHC) molecule on the antigen-presenting cell (APC) surface, triggering a cascade of signaling events. The TCR is the only antigen-specific molecule of the T lymphocyte activation, making the TCR–pMHC interaction a decisive step. A long-standing problem was to understand the basis of the exquisite specificity of T lymphocytes. While discrimination between different pMHCs seems based on quantitative properties of the TCR–pMHC bond such as its lifetime (1), bond rupture is a stochastic event, making a single lifetime measurement insufficient to discriminate between peptides forming bonds with only limited lifetime difference (2). Several studies using surface plasmon resonance mostly reported a correlation between a TCR–pMHC bond off-rate measured in solution (3D) and its lymphocyte activation potency (1, 3–6), leading to the kinetic proofreading model (7). However, as the TCR–pMHC interaction takes place between 2 cell surfaces, it is subjected both to a disruptive force and to 2D motions linked to membrane fluidity and dynamics, which may profoundly change the kinetics of molecular interactions (8–11). Furthermore, TCR triggering is sensitive to mechanical forces (12–16). Multiple bond lifetime measurements might be needed by the cell to overcome the stochasticity of bond rupture (17). However, due to the duration needed for such repeated assays and the time constraint of T lymphocyte activation, it has been proposed that force application might be a way to strongly reduce the lifetime of the TCR–pMHC bonds, to allow numerous, repeated measurements in a short time (17, 18). Force might also be exploited by the cell to test additional discriminating parameters such as bond sensitivity to force, further improving discrimination between pMHC, while also reducing the variability of bond lifetimes (18). For these reasons, efforts have been made to measure TCR–pMHC 2D dissociation kinetics and the effect of mechanical force thereon. Independent studies using the biomembrane force probe (BFP) (19–22) or optical tweezers (23) on live cells, or using optical tweezers in cell-free experimental setup (23, 24) reported that activating TCR–pMHC interactions exhibit a decrease in off-rate when exposed to mechanical force in the 10- to 15-pN range, i.e., catch bonds. It was therefore suggested that T cells might probe the TCR–pMHC bond by exerting a pull on the order of 10 pN, with activating peptides displaying a nonintuitive increase bond lifetime that made it 10-fold higher than the lifetime of nonactivating peptides (19). This raises 2 questions: 1) bonds formed by T cells and APCs are not only bimolecular interactions but depend on complex cellular processes (10, 11). Thus, a cell-free system is necessary to check that the catch bond effect is a cause, not a consequence, of high activation by efficient agonists. We previously measured dissociation kinetics of TCR and observed increases in off-rate with force, i.e., slip bonds. However, the forces applied were higher than 15 pN, precluding a direct comparison with aforementioned results (25). 2) Since T cell discrimination may involve multiple TCR–pMHC interactions, measuring the kinetics of bond formation as well as dissociation is necessary to fully assess the properties of TCR–pMHC interaction.

While several groups have examined 2D dissociation kinetics, studies of the 2D association kinetics of the TCR and pMHC are scarce and were limited by the methods used. Two-dimensional association measurements need a quantification of both the binding events and the distribution of the durations of the molecular encounters that may lead to binding; these encounter durations need to be in a physiologically relevant range. Before pulling, both BFP and optical tweezers bring into contact TCR and pMHC-bearing surfaces for durations of several hundreds of milliseconds, much longer than membrane fluidity and dynamics would allow (11, 23). The thermal fluctuation assay relies on spontaneous membrane fluctuations bringing into contact both surfaces (19). While contact durations may be much shorter than in BFP or optical tweezers, neither duration of encounter nor applied force are controlled. In contrast, our laminar flow chamber enables control of a distribution of encounter durations in the millisecond range (26, 27) and is thus well suited for 2D association measurements after molecular encounters of short duration. The description of 2D bond formation is usually based on on-rates, corresponding to 1 free energy barrier leading to 1 free energy well. Probability of bond formation as a function of the duration $t_e$ during which a receptor can interact with its ligand (referred later as “encounter duration”) can be written as $P\left(t_e\right)=f_E\times \left(1-\exp \left(-k_{\mathrm{on}}\times t_e\right)\right)$, where $f_E$ is a proportionality factor and $k_{\mathrm{on}}$is the on-rate (27). Using the laminar flow chamber, we observed that description of antibody–antigen association through an on-rate was not appropriate. We proposed a minimal encounter duration model (26, 28) where bond formation results from crossing a rough initial part of the energy landscape, which occurs as a slow diffusion process, before a free energy well; probability of bond formation can be written as $P\left(t_e\right)=f_E\times erfc\sqrt{t_{\mathrm{on}}/t_e}$, where $f_E$ is a proportionality factor, $erfc$ is the complementary error function, and $t_{\mathrm{on}}$ is a characteristic time of the bond describing a minimal encounter duration for association. The similarities between TCR and antibodies suggest that this model might also describe TCR–pMHC association. We measured at the single-molecular level in the laminar flow chamber the association and dissociation kinetics of 5 different agonist TCR–pMHC bonds under force from 6 to 45 pN, in the range where catch bonds were observed by other groups. These TCR–pMHC interactions did not form catch bonds, but their dissociation kinetics correlated well with their activation potency. Minimal encounter durations $\left(t_{\mathrm{on}}\text{model}\right)$ described bond formation better than on-rates $\left(k_{\mathrm{on}}\text{model}\right)$.

Results

Demonstration of Single-Molecular TCR–pMHC Association and Rupture under 2D Conditions.

Single bond measurements were demonstrated using the usual method for laminar flow chamber experiments (25) with 2 necessary conditions that are sufficient if both are realized: First, if single molecular bonds are observed, increasing the amount of ligand on the chamber surface must increase proportionally the binding linear density (BLD); second, survival curves must remain unchanged for the different amounts of ligand on the chamber surface as the same binding events are measured. Here, for each pMHC, flow chamber experiments were performed on substrates coated either without ligand as a negative control, or coated with 8 different amounts of ligand, doubling from 1 condition to the next, thus varying the ligand amount 128-fold. For each pMHC, for 3 consecutive amounts of ligand (forming a 4-fold range) plus a negative control, BLD varied proportionally to the amount of deposited ligand. This is shown by the high correlation coefficient of BLD versus amount of deposited ligand for these 4 conditions, with R² = 0.97 for 3A, R² = 0.97 for H74, R² = 0.98 for 9V, R² = 0.80 for 3Y, and R² = 0.92 for 9L (SI Appendix, Fig. S1). Survival curves remained unchanged at least for the 2 highest consecutive amounts of ligand in this range (SI Appendix, Fig. S2); arrests were therefore considered to be the consequence of formation of single molecular bonds.

Activating pMHCs Do Not Necessarily Form Catch Bonds with TCRs.

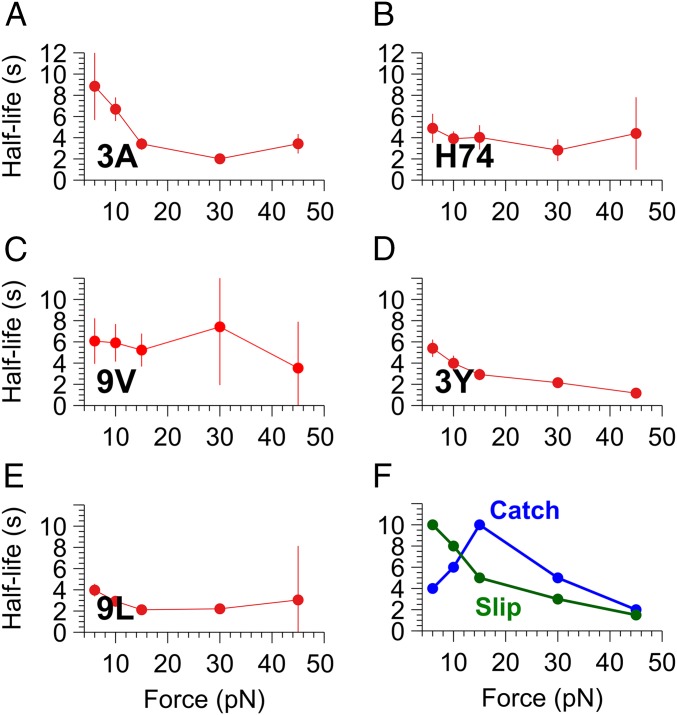
We measured the dissociation kinetics of the 5 agonist TCR–pMHC pairs under force ranging from 6 to 45 pN. The slope of survival curves (where the logarithm of the fraction of surviving bonds is plotted versus time; SI Appendix, Figs. S2 and S3) is equal to the off-rate. To account simply for the change of slope with time suggesting a bond strengthening (SI Appendix, Fig. S3), we chose to consider the average slope, or off-rate, on the 5 first seconds. This was justified by calculating for each force the correlation between the peptide activation potency and the average off-rate calculated at variable intervals (SI Appendix, Fig. S4). An interval of 5 s ensured a maximal correlation coefficient at each force. The corresponding average half-lives are calculated from the average off-rate between 0 and 5 s [k_{off(0–5 s)}] as equal to ln(2)/k_{off(0–5 s)}. Fig. 1 shows the half-lives plotted versus force: 3A, 3Y, and 9L behave as slip bonds, with off-rate increasing with force. H74 and 9V are little influenced by force in this range.

Fig. 1.

(A–E) Effect of varying forces (6 to 45 pN) on half-life of agonist TCR–pMHC bonds. Half-lives of bonds calculated from off-rate measured between 0 and 5 s (Left) are plotted versus force (Bottom). Error bars are experimental SEM. (F) Schematics illustrating examples of typical slip bonds (green) and catch bonds (blue).

Dissociation Kinetics Show Good Correlation with Activation Potency from 6 to 15 pN.

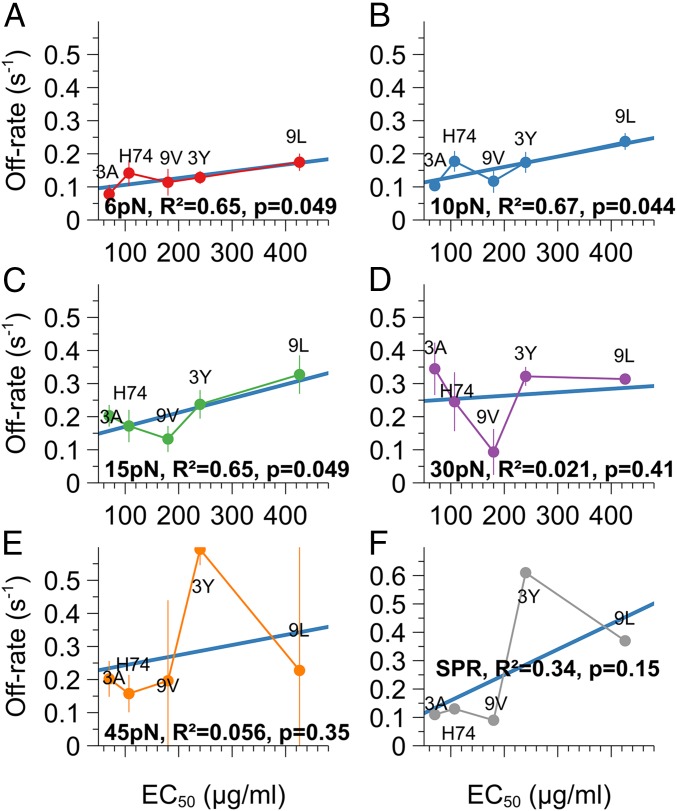
Activation potency was measured previously (5) as an EC₅₀, being the amount of pMHC on a surface necessary to trigger 50% of the maximum γ-IFN production by 1G4 T lymphocytes. Here, off-rates were significantly correlated with activation potency of each pMHC under 6-, 10-, and 15-pN force (Fig. 2). It then reduced sharply at 30 and 45 pN. A poor correlation was also observed here between off-rate measured in solution (3D) earlier by surface plasmon resonance and activation potency. The 2D and 3D series of off-rate values remain in the same order of magnitude.

Fig. 2.

Off-rates of TCR–pMHC bonds between 0 and 5 s for force increasing from 6 to 45 pN for each pMHC (A–E), plotted versus corresponding activation potencies measured as the EC₅₀ for γ-IFN production. Errors bars are experimental SEM. In F, off-rates were measured in surface plasmon resonance and plotted versus corresponding activation potencies. R² is the square Pearson correlation coefficient, and P is the result of a Student test on Pearson coefficient.

Association Kinetics Supports a Minimum Encounter Duration Model.

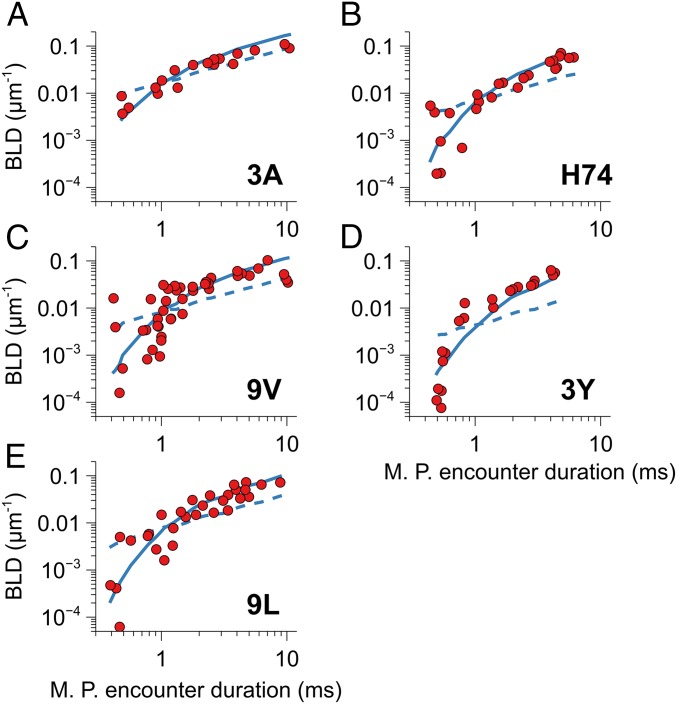
The BLD were measured for the 5 TCR–pMHC interactions with different values of shear stress. The distribution of encounter durations for these shear stresses was calculated using a numerical simulation of microspheres and binding sites motion (SI Appendix, Fig. S5). The calculation of distributions of encounter durations allowed us to compare the ability of 2 different bond models to describe bond formation. One model uses a classical on-rate k_on, and a second model uses a minimal encounter duration described by a t_on as described in our previous works; both use a single adjustable parameter. Our assumptions on the geometry of the bonds were checked by systematically varying in the simulation the maximal solid angle of diffusion φ_max and the maximal variability in radial length ΔR_max. Calculated association kinetics changed in a limited way except for very narrow angles (SI Appendix, Fig. S6). The classical on-rate model $\left(k_{\mathrm{on}}\right)$ fitted the data poorly (Fig. 3) except for the 3A pMHC, while the minimal encounter duration model $\left(t_{\mathrm{on}}\text{model}\right)$ gave better fits. $t_{\mathrm{on}}$ values were 0.46 ms for 3A, 0.72 ms for H74, 0.65 ms for 9 V, 0.91 ms for 3Y, and 0.69 ms for 9L.

Fig. 3.

Binding linear density (BLD) of each experiment plotted versus most probable encounter duration (red dots) for each pMHC (A–E). Most probable (MP) encounter duration D_e was calculated as D_e = L/V_avg, where L = 35 nm is the molecular length of the bond, including intermediate antibodies, and V_avg is the peak of the microspheres’ velocity distribution. Data fits for 2 bond models are shown: The dashed lines show the fit with the classical k_on model, while the full lines show the fit with the minimal encounter duration model (t_on model).

Discussion

What Is the Physiological Relevance of Single TCR–pMHC Bond Measurements under Force?

In physiology, both TCR and pMHC are linked to actively motile cell membranes, where they are surrounded by adhesive molecules and coreceptors roughly of the same short dimensions (such as CD4 or CD8, CD2, CD28, and their respective ligands) or moderately larger (such as LFA-1 and its ligand ICAM-1), but also by much larger sterically repulsive molecules such as CD45, CD43, and CD148 (29, 30). The interaction takes place in a context of mechanical forces: The T lymphocyte crawling on the APC surface while TCRs probe their ligands creates a mechanical shear force in the order of 1,000 pN at the cell scale (31). Motion in the axis perpendicular to membrane plane due to membrane fluctuations exists as in other cell types (32), but the T lymphocyte also probes the APC by extending and retracting microvilli that are enriched in TCRs (33). Forces exerted by a T lymphocyte upon TCR engagement have been measured with BFP, showing initial pushing and pulling forces around 25 pN (34), by traction force microscopy, showing forces between 50 and 200 pN after initial spreading (35), and by DNA sensors showing forces between 12 and 18 pN s after binding (15). The 6- to 45-pN range chosen is well suited to mimic these observations.

In a laminar flow chamber, as well as in other methods, a first important limitation is due to the use of TCR or pMHC grafted on artificial surfaces. Adhesive or repulsive molecular environments are usually absent on one surface at least, as well as membrane reorganization that allows clustering of adhesive molecules and expelling of larger antiadhesive molecules. A second limitation is due to the kinetics of force application, which is necessary to bond detection and may modify protein–protein binding. Many ligand–receptor pairs involving biomolecules display multiple binding states, of which the most stable may not be reached instantaneously. Properties of a ligand–receptor bond depend thus on its history (36). Experimental evidence obtained on antigen–antibody bonds supports the general view that bond formation is a time- and force-dependent process involving a continual strengthening that may require milliseconds to seconds or more (28, 37). A third point is that, rather than unidimensional paths, energy landscapes should be represented as multidimensional surfaces allowing multiple reaction pathways [indeed proposed for catch bonds (38)]. Consequently, it is important to recall that the flow chamber method displays the behavior of bonds that are a few milliseconds old, whereas typical contact time used with atomic force microscopy or BFP is on the order of 100 ms. Thus, different experimental methods may explore different regions of the energy landscape.

Do Agonist TCR and pMHC Form Intrinsic Catch Bonds?

We did not observe catch bonds in the dissociation of our 5 agonist TCR–pMHC ligand pairs in our cell-free experimental setup, but 3 classical slip bonds found for either a very potent or poor activators (3A, 3Y, and 9L), and 2 almost “ideal” bonds (i.e., showing no force dependence) being moderately potent activators (H74 and 9V). There is no doubt that catch bonds can be detected with the flow chamber (9, 39), including by our group (40). Forming catch bonds at 10 to 15 pN has been proposed to increase ligand discrimination by strongly increasing differences in bond lifetimes between catch bond forming agonists peptides and slip bond-forming irrelevant or antagonist peptides (19–22). Using the laminar flow chamber, nonspecific TCR–pMHC interactions could not be detected here, and so presumably had lifetimes shorter than the detection threshold of 180 ms. The specificity of agonist versus irrelevant peptide detection may therefore be very good even if agonist peptides form slip bonds with the TCR. Also, previous studies on catch bond-forming TCRs found that lifetime differences between strong or weaker agonist pMHC at 10 to 15 pN were typically around 2-fold (19, 21–23). Here, differences in off-rates between strong and weaker agonists between 6 and 15 pN were also up to 2-fold (Fig. 2), illustrating that significant survival differences may also be produced by agonist pMHC without catch bonds. This different response of TCR–pMHC to force that we report here could be solely due to specificities in the TCR–pMHC interactions we studied. It is also possible that cellular (19, 20, 23) and cell-free (23) experiments that observed catch bonds may have produced misleading results, for the following 2 reasons. First, whether an increase in average survival duration when force increases suffices to define an intrinsic bond strengthening is debatable. As the laminar flow chamber allows measurement of association kinetics, we were able to show that all of the TCR–pMHC interactions studied show a very strong decrease in bond formation (2 to 3 log) when shear increases (Fig. 3). This contrasts with L-selectin/ligand interactions, arguably the prototype of catch bonds, which show the opposite: an increase in observable bond formation when shear increases (41), consistent with an increase in bond strength. In force-clamp experiments, a fraction of newly formed bonds may break before clamp force is reached. If this fraction changes when the chosen clamp force is modified, the statistics of bond lifetimes under clamp force will be measured on a different population of bonds. The observation of an increase of bond lifetime when the clamp force increases might be possible for slip bonds if several bound states coexist in a population of heterogeneous bonds formed by a same ligand–receptor pair: Increasing the clamp force could select the stronger bound states because weaker bonds would break before the clamp force is reached; observed lifetimes would be longer while the number of bonds detected would decrease. Conversely, if genuine catch bonds are formed, the number of bonds formed should increase with increased clamp force. Measurement of the number of bonds observed at different clamp forces relative to the number of contact events is therefore needed to differentiate the 2 cases, as is done with the laminar flow chamber. Second, to demonstrate single bond measurements, BFP and atomic force microscopy rely on ensuring that there is only a low proportion of binding events (classically less than 10%) relative to the total number of cell–surface or surface–surface contacts during the experiment: the proportion of double binding events is then the square of the proportion of single events, i.e., less than 1% (42). While this argument does indicate that the minimal observable binding event predominates under these conditions, it does not prove that this event corresponds to a single molecular bond: the minimal observable binding event could comprise multiple molecular interactions. The fact that a single TCR–pMHC interaction is measurable by the method is indeed an assumption in studies using low adhesion probabilities to demonstrate single molecular binding (42). Therefore, we believe that the laminar flow chamber uses currently the most stringent criteria to demonstrate measurement of single molecular bonds.

By contrast with cell-free experiments, the use of live T lymphocytes may complicate the interpretation of results in other ways. BFP or optical tweezers create cell contacts of micrometer scale lasting hundreds of milliseconds that may allow a cell reaction to modify the readout. Indeed, it has long been shown that the TCR is a mechanotransducer (12, 13) and that T cell can actively modulate the lifetime of TCR–pMHC association (10). A gathering of receptors due to a cellular response could, for example, quickly reinforce the initial bond and make the critical force for cell sensibility appear as the peak lifetime force of a catch bond (43). Indeed, recent experiments show an increase in catch bond-forming TCR–pMHC survival time up to 15-fold for CD8-expressing T lymphocytes compared with non–CD8-expressing T lymphocytes (21). This increase could be a cellular response enhanced by CD8, as such a change seems unlikely to be caused mechanically by the very low-affinity CD8–MHC interaction. Also, the change in the distribution of bond durations toward an increase in the proportion of catch bonds in ref. 19 could be interpreted as a consequence of cell activation and not as its cause. A TCR–pMHC binding-triggered increase in the apparent affinity of other TCRs microns away has been recently interpreted as a facilitating cell reaction (44). Moreover, TCR binding to pMHC can exhibit slip or catch bonds depending on the molecular context of the interaction and active cellular processes (45), strongly suggesting that catch bond formation may not be an intrinsic feature of TCR–pMHC interactions.

Ten Piconewtons Is a Critical Force for Ligand Discrimination by the T Lymphocyte.

We find a good correlation between TCR–pMHC bonds’ off-rate and their activation potency in the force range where previous studies found catch–slip transitions for activating peptides (i.e., 10 to 15 pN). Thus, bond lifetime around 10 pN might be a critical parameter linked to T lymphocyte activation, irrespective of the molecular mechanism. While it is difficult to determine the exact force exerted by the cell on individual TCR, these forces might be close to 10 pN: Experiments done at a scale smaller than the cell can show forces in the same order of magnitude (50 pN) (35), as were the initial pulling forces (25 pN) of the T lymphocyte reported by Husson et al. (34). Most importantly, DNA sensors showed that a 12- to 18-pN force is indeed applied on TCR by the T lymphocyte seconds after binding and before calcium signaling, and seems to be necessary for ligand discrimination (15).

A Minimal Encounter Duration Might Be an Important Prerequisite for Lymphocyte Activation.

A form of control of the distribution of encounter duration is needed to test association kinetics models. The laminar flow chamber is uniquely well suited to this, as the displacement of binding sites imposes a distribution of short encounters in the millisecond range, which may be estimated through relatively simple numerical simulations. The poor fit of our 2D TCR–pMHC association data by a $k_{\mathrm{on}}$ model is similar to our observations for several antigen–antibody bonds (26–28). We propose the use of another association model in which binding occurs after a minimal encounter duration varying accordingly to a characteristic duration $t_{\mathrm{on}}$. To compare models with an equal number of free parameters, we set a common value for the proportionality factor f_E, an assumption supported by trials with 2 free parameters showing little change for f_E. The $t_{\mathrm{on}}$ association model appears to describe our results better than the $k_{\mathrm{on}}$ association model.

We interpret the rough part of the energy landscape, responsible for the minimal encounter duration, as the diffusive rearrangements necessary for peptidic chains to form the bond. Among membrane dynamical properties that may control the duration of molecular encounters between TCR and pMHC, localized fluctuations of microvilli tips, with a typical amplitude of several tens of nanometers (32, 46) and a frequency of 0.2 to 30 Hz (32), could impose encounter durations suitable for bond formation by the fastest TCR–pMHC interactions. A major question is whether this feature is relevant to TCR signaling. A striking point is that any TCR/pMHC encounter below the minimal duration would fail to produce a force-resistant interaction and prevent signal transduction: The minimal encounter duration could act as a specificity threshold.

Overall, our data suggest that a complete description of the kinetics of the TCR–pMHC interaction must take into account the time of bond formation and illustrate the importance of simultaneously measuring association and dissociation.

Materials and Methods

Molecules.

As described in ref. 5, HLA A2 molecules were expressed in Escherichia coli as inclusion bodies from amino acid 1 to amino acid 278; a biotinylation sequence for BirA enzyme was added at the C-terminal end. Five different peptide and MHC molecules were used, differing by a single amino acid in either the peptide (3A, 9V, 3Y, 9L) or the HLA A2 molecules (H74). The 1G4 TCR α- and β-subunits were expressed in E. coli as inclusion bodies, refolded in vitro, and purified using size exclusion chromatography.

Microspheres.

Dynabeads M450 Tosylactivated microspheres (diameter, 4.5 µm; Invitrogen) were coated with a monoclonal mouse anti-His tag antibody (MCA485G; Serotec) according to the manufacturer’s protocol (27), and then incubated with 1G4 TCR bearing a 6-histidine tag.

Surface Preparation.

The functionalized surfaces used in the flow chamber were prepared as described before (27). Briefly, $75\times 25$-mm² glass slides (VWR) were cleaned in a “piranha” solution, a heated mix of 70% H₂SO₄ solution (95 to 98% in water; Fisher Bioblock) and 30% H₂O₂ solution (50% in water; Sigma-Aldrich), and then coated with a poly-l-lysine solution (150,000 to 300,000 Da; Sigma-Aldrich), rinsed, and then incubated with a glutaraldehyde solution (2.5% in 0.1 M borate buffer, pH 9.5; Sigma-Aldrich), rinsed, and then incubated with a solution of biotinylated BSA (100 µg/mL; Sigma-Aldrich) in PBS, rinsed, and then incubated in a blocking solution of glycine (0.2 M) and BSA (1 mg/mL) in PBS, rinsed, and then incubated in a streptavidin solution (10 µg/mL in PBS; Sigma-Aldrich), and then rinsed with PBS.

Flow Chamber Experiments.

We used a unique automatized laminar flow chamber setup (27) on an inverted microscope (Diavert; Leica) with a CCD camera (IDS) and a 10× lens. Movies were recorded at 50 images per second and compressed by the IDS U-Eye software using a M-JPEG codec. Experiments were performed at 37 °C on substrates coated with various densities of pMHC on average 6 times per density under 5 shear rates each from 5 to 45 s⁻¹. Force on bond was calculated as $F=\sqrt{a/2R}\left(T+\mathrm{\Gamma }/a\right)$ with $T=1.7005\times 6\pi \mu a^{2}G$ and $\mathrm{\Gamma }=0.9440\times 4\pi \mu a^{3}G$ (with $T$, the traction on the microsphere; $\mathrm{\Gamma }$, the torque on the microsphere; $a$, the microsphere radius [2.25 µm]; $R$, the total bond length [32 nm]; $\mu$, the medium viscosity [7 × 10⁻⁴ Pa⋅s at 37 °C]; and $G$, the shear rate) (47).

Trajectory Analysis and Arrest Statistics.

Statistics of bond formation were determined by counting the number of microsphere arrests and the total distance traveled by microspheres after sedimentation, as previously described (25, 27). Statistics of bond rupture were determined by measuring the durations of microsphere arrests defined if their position did not change by more than 0.5 μm during 0.2 s, and if its velocity before the arrest was within the velocity range of moving sedimented microspheres. The BLD under a given condition (i.e., a given shear rate and a given ligand surface density) was defined as the number of arrests divided by the total distance traveled by sedimented microspheres. The BLD of specific association was calculated by subtracting from the BLD measured with assay surface the BLD obtained with control surface. Bond rupture under a given condition was described by survival curves of the bonds, obtained by counting the fraction of arrests exceeding the duration $t$ versus $t$, and corrected by subtracting nonspecific arrests estimated from control surfaces (37).

Numerical Simulations.

The distribution of TCR and pMHC encounter durations as a function of shear rate was calculated by combining dynamics of a microsphere in laminar flow with an estimate of the diffusion volumes of TCR and pMHC reactive sites (SI Appendix, Fig. S1). A molecular encounter was defined to begin and last while the diffusion volume of a TCR binding site intersects the diffusion volume of a pMHC, calculated as follows. We assume that, in both molecules, polypeptidic linkers outside of Ig domains give some length variability and degrees of rotational freedom. TCR binding site was at the extremity of the TCR (of length L3 = 8 nm), itself bound at the extremity of the anti-His tag antibody Fab fragment (of length L2 = 8 nm) that is hinged to the Fc fragment (of length L1 = 8 nm); distance from its anchoring point is equal to L1 + L2 + L3 + ΔR_TCR, where ΔR_TCR is the length variation with 0 < ΔR_TCR < ΔR_TCRmax and solid angle φ_TCR is its rotational freedom with 0 < φ_TCR < φ_TCRmax.. pMHC binding site is on the distal parts of domains α₁ and α₂ of the HLA A2 molecule (of length L4 = 8 nm); the C-terminal end of the HLA α₃ domain is linked to the biotin; binding site is separated from its anchoring point by L4 + ΔR_pMHC, where ΔR_pMHC is the length variation and solid angle φ_pMHC is its rotational freedom with 0 < φ_pMHC < φ_pMHCmax. Both bindings diffuse rapidly in shell-shaped volumes described by their thicknesses ΔR_TCRmax and ΔR_pMHCmax and by their solid angles φ_TCRmax and φ_pMHCmax, respectively (we define ΔR_max = ΔR_TCRmax + ΔR_pMHCmax and φ_max = φ_TCRmax + φ_pMHCmax). Validity of this simulation was systematically tested in a previous work (27).