Proteomic and genomic signatures of repeat instability in cancer and adjacent normal tissues

Significance

Repeats in proteins, including short tandem repeats, interspersed repeats, and repetitive domains, are hotspots of evolution. However, their role in tumor evolution is essentially unknown, being limited to microsatellites, a small subclass. Here, we develop a computational technique to measure the repeat content in bulk samples, beyond microsatellites, directly from proteomic and genomic sequence raw data of tumors and their matched normal tissues. Our analyses suggest that variations in the repeat content of tumors (repeat instability) are a compensatory, transient, and adaptive mechanism in tumor evolution, which is most pronounced in early stages of tumorigenesis. Repeat instability is also manifested in normal tissues adjacent to tumors and seems to be the first route of escape from stress toward neoplasia.

Abstract

Repetitive sequences are hotspots of evolution at multiple levels. However, due to difficulties involved in their assembly and analysis, the role of repeats in tumor evolution is poorly understood. We developed a rigorous motif-based methodology to quantify variations in the repeat content, beyond microsatellites, in proteomes and genomes directly from proteomic and genomic raw data. This method was applied to a wide range of tumors and normal tissues. We identify high similarity between repeat instability patterns in tumors and their patient-matched adjacent normal tissues. Nonetheless, tumor-specific signatures both in protein expression and in the genome strongly correlate with cancer progression and robustly predict the tumorigenic state. In a patient, the hierarchy of genomic repeat instability signatures accurately reconstructs tumor evolution, with primary tumors differentiated from metastases. We observe an inverse relationship between repeat instability and point mutation load within and across patients independent of other somatic aberrations. Thus, repeat instability is a distinct, transient, and compensatory adaptive mechanism in tumor evolution and a potential signal for early detection.

Cancer clonal evolution (1, 2) is marked by a wide range of genomic instabilities and somatic aberrations, which lead to intratumor heterogeneity and eventually enable tumor cells to proliferate and metastasize (3–6). These aberrations include substantial complex structural variations on every scale as exemplified by the prevalence of aneuploidy (7) and chromosomal instability (8, 9), hypermutation (10, 11) and microsatellite instability (MSI) (12–14), and complex short insertions and deletions (15) as well as large complex genomic rearrangements, such as chromothripsis (16) and chromoplexy (17). Elucidating the relationship between different mutational classes is critical for inferring the exact clonal composition and phylogeny of tumors (18–20) and subsequently, determining how different aberrations affect clinical outcome (14, 21, 22) and which of these are involved in resistance to treatment and metastases formation (23–25).

Notwithstanding recent advances, identification of structural variations of short repeats in protein sequences remains elusive. This is the case because of the general difficulty of identifying diverse types of repeats in sequences, which vary in length, level of divergence, and periodicity, and because of the short length of reads obtained with next generation sequencing (NGS), which creates major difficulties for the current assembly techniques (26–28), exacerbated by various causes of sequencing errors and DNA damage (29). Consequently, variations in the compositional order of proteins (30, 31), a large class of mutations, which includes runs of amino acids, short tandem repeats, interspersed repeats, repetitive domains, and more generally, overrepresentation of motifs in low-complexity regions (hereafter, collectively denoted repeats), has not been systematically characterized in cancer. To date, microsatellites, a relatively minor subclass of repetitive sequences composed of tandem repeats of 1- to 5-bp units, represent the only well-studied case (11–14).

Repeats in proteins are hotspots of protein and species evolution that emerge through replication slippage and recombination (32–34). Repetitive domains are building blocks of key macromolecular complexes [e.g., nuclear pores (35) and proteasomes (36)] and play essential roles in a variety of biological processes, notably transcription regulation, protein–protein interaction, and immunity, as exemplified by the enormous variety of Zinc finger (37), Ankyrin (38), WD40 (39), and Leucine-rich (40) repeats in animal proteins. Variations in the number of repeat units have been associated with acquisition of new functions and rapid evolution of complex phenotypic traits in diverse life forms (41–45). This fast evolution of repeats comes at the cost of promoting genetic diseases, in particular cancer and neurodegeneration (46–48), where repeat dynamics (mostly expansion but in some cases contraction) often correlates with disease severity (49, 50). Evolution of new repeats is markedly accelerated after duplication and is largely driven by positive selection, highlighting their potential role as disease drivers in somatic evolution (51).

In light of the importance of repeats in rapid evolutionary processes and their demonstrated involvement in human pathology, we hypothesized that repeat dynamics might play a more important role in tumor evolution than presently realized, especially because repeat generation in tumors can be enhanced due to impaired DNA replication (52, 53) and repair (54). To this end, we generalized the quantification of repetitive motifs beyond microsatellites and developed a rigorous methodology to systematically quantify variations in the repeat content (repeat instability) of genomes (bypassing difficulties associated with assembly) and of repeat-containing proteins directly from genomic and proteomic sequence raw data. Applying the methodology to a collection of diverse datasets, we demonstrate its utility for identifying tissue-specific and tumor-specific repeat instability signatures (RISs) and elucidate the transient dynamics and compensatory role of repeat instability in tumor evolution.

Results

Repeat Instability in Amino Acid and Nucleotide Sequences.

The following datasets were analyzed (SI Appendix, Table S1): 1) proteomic datasets of breast and prostate cancer patients, including an original cohort of ovarian cancer patients; 2) genomic datasets of prostate cancer patients, including an original cohort of benign tissues serving as a noncancerous control; 3) genomic pancancer cohorts from The Cancer Genome Atlas (TCGA), which include a tumor sample, an adjacent matched normal sample, and a blood sample from each individual, providing for a comparison between tissues; and 4) samples from patients with metastatic spread, which allowed for analysis of repeat instability during the evolution from the primary tumor to the metastatic state.

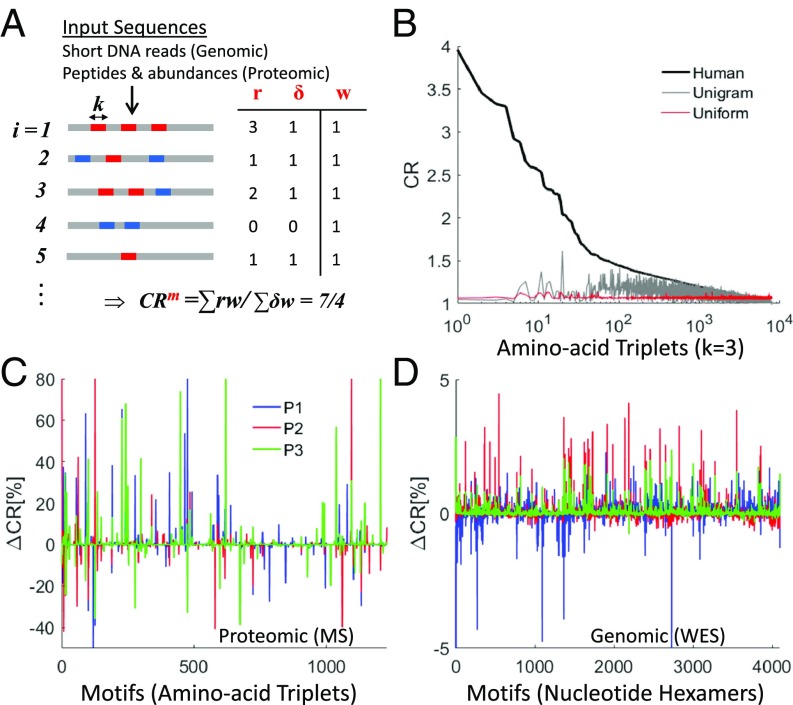
To measure the repetitiveness of motifs (k-mers) in a set of amino acid or nucleotide input raw sequences from bulk samples (i.e., peptides or short DNA reads), we define the compositional order ratio (CR) of a motif (m) as the total number of the motif recurrences (R^m) divided by the total number of sequences in which the motif appears (P^m): CR^m = R^m/P^m (Materials and Methods and Fig. 1A). The CR is high when a motif recurs multiple times in a sequence. The CR signal in the human proteome strongly departs from random expectations (Fig. 1B) and is substantially more robust for repeat identification than alternative measures of repetitiveness, such as the frequency of a motif or its fraction in the proteome (SI Appendix, Fig. S1).

Fig. 1.

Methodology for estimating repeat instability in genomic and proteomic sequence raw data. (A) Illustration of the method for estimating the CR of motifs (i.e., k-mers) using k = 3 (triplets) for proteomic data and k = 6 (hexamers) for genomic data (Materials and Methods). The distribution of 2 motifs (blue and red) is illustrated on a list of input sequences, i = 1…N. Input sequences can be either peptides (with abundances w_i) obtained from proteomic MS data or DNA short reads obtained from NGS (with equal abundances, w_i = 1). CR evaluation of the red motif (m) in the case of genomic data is shown in the table, where for each sequence i, r_i is the number of red motif recurrences, δ_i = 1 if the red motif exists, or δ_i = 0 if no red motif exists. (B) Application of CR estimation to the 8,000 amino acid triplet motifs distributed in the human proteome (black curve) shown against 2 random proteomes (uniform: with uniform probability of amino acid recurrence [red] and unigram: where the probability of amino acids recurrence is based on the human proteome [gray]). (C and D) Examples of the RISs (RIS = ∆CR) in tumors relative to their matched normal tissue of 3 patients (blue, red, and green) in the breast cancer proteomic dataset (C) and in the genomic breast cancer dataset (D) (SI Appendix, Table S1).

The CR is directly estimated from both proteomic and genomic raw sequence data (Fig. 1A). In proteomic data, CR is evaluated from a list of thousands of measured peptides (typically 10- to 30-amino acids long) and their abundances; the abundance values are used to estimate the effective number of sequences (Materials and Methods). We used triplets (k = 3, 8,000 amino acid triplets) to measure CR in proteomic data, as this is the optimal choice of motif length to characterize protein repeats (31). In whole-exome sequencing (WES) data (coverage depth 100×), CR is computed from a list of millions of short DNA reads (typically, 50- to 150-base pairs long) using hexamers (k = 6, 4,096 nucleotide hexamers) such that the proteomic and genomic motif spaces have comparable sizes. The choice of k = 6, a shorter unit length than the naïve choice of k = 9, which translates into an amino acid triplet, is also justified by the occurrence of synonymous substitutions that do not change the amino acid composition (SI Appendix, SI Text). For CR evaluation, motifs can overlap and do not need to recur in tandem such that all types of repeats, both pure and diverged, from runs to repetitive domains that are shorter than the short-read length can be identified (SI Appendix, SI Text). Several examples of repeats in proteins and their respective coding nucleotide repeats identified in our analysis are shown below, emphasizing the diversity of repeats that can be captured. Analysis of genomic data demonstrates that CR is a stable measure, which saturates at a low coverage depth (SI Appendix, Fig. S2) and is unbiased with respect to the sample size (SI Appendix, Fig. S3).

We define the RIS (RIS = ∆CR) of a sample as the vector of CR percentage changes for all motifs compared with a control sample (Materials and Methods). In a patient, the somatic signature of a tumor is computed relative to a control sample taken either from an adjacent matched normal tissue or from the blood. Fig. 1 C and D shows examples of typical tumor signatures in proteomic and genomic data. Because repeats can expand or contract in a given genome, we evaluate the overall repeat instability (ORI) by the sum over the absolute value of the signatures of all motifs (ORI = ∑|∆CR|). The repeat instability measures (RIS and ORI) can be decomposed into different classes of repeats (e.g., microsatellites vs. larger repeats) (SI Appendix, SI Text) as we later demonstrate on single patients. Importantly, proteomic signatures reflect the compound effect of somatic genome instability and differential expression of repeat-containing peptides, whereas genomic signatures reflect genome instability alone. We applied this methodology to analyze peptide sequences in the proteomic datasets and short-read nucleotide sequences in the genomic (WES) datasets (SI Appendix, Table S1). We start with the analysis of proteomic datasets and gradually move to the analysis of genomic cohorts, ending with single patients’ analysis.

Proteomic Repeat Instability Reflects Breast Cancer Tumor Progression.

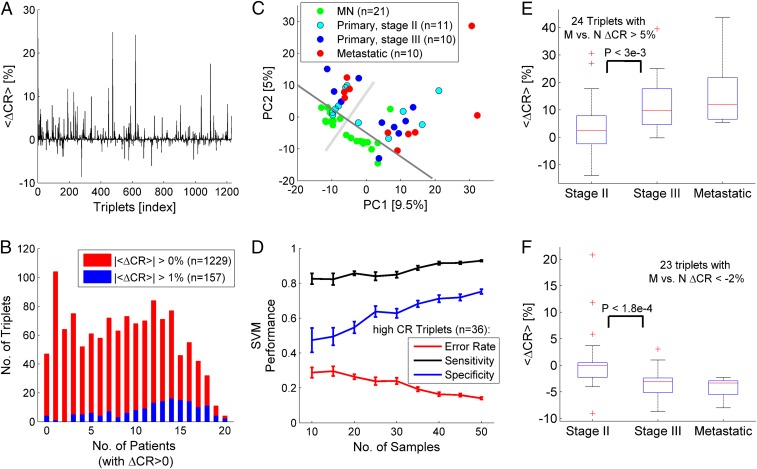
We first applied the repeat analysis methodology to a proteomic dataset from 21 breast cancer patients (55) (SI Appendix, SI Text and Table S1). We found that the CR of motifs (amino acid triplets) tends to increase in tumors relative to matched normal tissues as measured by the average signature of triplets across patients (Fig. 2A). To ensure that this trend was not a consequence of large variations of CR in a few patients, we assessed the frequency of variation in the CR among the patients. The histogram of the frequencies is bimodal, with CR consistently increasing for many triplets and consistently decreasing for a few triplets among the patients (Fig. 2B). The remarkable shift to high frequency that was observed for strongly altered (>1%) triplets confirms that CR increase is the dominant phenomenon and that CR can be used to characterize tumors. Principal component analysis (PCA) of the CR estimates (52 samples × 1,229 triplets) shows clear separation of matched normal samples from tumor samples in the first 2 principal components (PCs) (Fig. 2C). This separation was captured in 2 experimental pools (SI Appendix, SI Text and Table S1), indicating that the tumor vs. normal segregation is robust. The PCA suggests that the dimensionality of discrimination is low such that classifiers can be built using a small number of discriminative features (i.e., triplets). Examples of discriminative triplets (e.g., PVP, APV, APA, YGY, DVL, TAA) are shown in SI Appendix, Fig. S4.

Fig. 2.

Analysis of tumor signatures in proteomic data from 21 breast cancer patients. (A) The average RIS across patients <∆CR> evaluated relative to the respective matched normal (MN) tissue in each patient. When both stage III and metastatic tissues are sampled from the same patient, the average signature is used. (B) Histograms of the number of triplets vs. the number of patients in which the triplets’ CR increased (ΔCR > 0) shown for all identified triplets (|<ΔCR>| > 0%, n = 1,229; red) and for triplets with |<ΔCR>| > 1% (n = 157; blue). (C) PCA of the CR matrix (52 samples × 1,229 triplets), indicating the separability between normal and tumor samples in the first 2 PCs. A gray solid line is superimposed for visual clarity of the discrimination. Perpendicular to it, the light gray line indicates the division between the 2 experimental pools (SI Appendix, SI Text and Table S1). (D) The effect of sample size on the SVM linear classifier using the top high-CR triplets as features (n = 36). Classification performance in a leave-1-out analysis improves with sample size. Error bars are estimated from 20 trials of random choice of samples. (E) Triplets (n = 24) with increased average signature (<ΔCR> > 5%) in the metastatic samples (M) relative to matched normal (N) reveal that CR increases in the transition from stage II to stage III. (F) Triplets with decreased signatures in the metastatic signature (<ΔCR> < −2%, n = 23) tend to decrease from stage II to stage III. P values correspond to the KS test. Trends in E and F are not expected (SI Appendix, Fig. S5). Accuracy = percentage of correct classifications. Sensitivity = TP/(TP + FN). Specificity = TN/(TN + FP). FN, false negative; FP, false positive; TN, true negative; TP, true positive.

To further test the predictive signal of RISs, we built binary classifiers that discriminate between normal and tumor samples using support vector machine (SVM) with a linear kernel and examined various feature selection criteria in a standard leave-1-out analysis (SI Appendix, Table S2). Every tested selection criterion (Kolmogorov–Smirnov [KS] test, Fisher score, and CR-based criteria) achieved classification accuracy >80% with a small set of triplets (∼10 to 30). We further inspected the simplest criterion for selecting triplets with high CR (i.e., those that frequently recur in the list of peptides). This approach achieved a maximum accuracy of 89% with only 36 selected triplets (SI Appendix, Table S2) that are frequently and significantly altered among the patients (SI Appendix, Fig. S4). To ensure that the classifier performance is not sensitive to the small number of samples, we also tested its performance as a function of the number of samples and found that it improves as more samples are included, testifying to the generality and robustness of this simple approach for discriminating between tumor and normal samples (Fig. 2D).

Although good performance was achieved in discriminating tumor from normal samples, metastases do not appear to be well separated from primary tumors (Fig. 2C). Nonetheless, we noticed that several triplets displayed consistent variation from normal to primary tumor to metastases (e.g., the triplet TAA in SI Appendix, Fig. S4). Thus, to test for signatures correlated with cancer progression, we selected triplets with the strongest average signature in the metastases (relative to matched normal) and tested whether their signatures varied from stage II to stage III. This particular comparison was performed, because selection of triplets with strong signatures in the metastases statistically selects weaker signatures in stage II and stage III, but differences between stage II and stage III are not expected (SI Appendix, Fig. S5). As implied by the tendency of CR increase in tumors, we found more triplets with average signatures increased from stage II to stage III (Fig. 2E) than triplets for which the average signatures decreased (Fig. 2F). These trends were robust to the choice of the threshold used to select triplets with strong signatures in metastases (SI Appendix, Fig. S5). Notably, a weaker variation between stage III and metastases was observed, suggesting that the differential expression of repeats is especially important at early stages of tumor evolution. Mapping all discriminative triplets to proteins and identifying repeat-unstable proteins (SI Appendix, SI Text) indicated that the proteins with high repeat instability are enriched among the proteins encoded by known cancer genes (SI Appendix, Fig. S6), indicating a role of repeat instability in oncogenesis.

Last, by analyzing the distribution of intervals between consecutive triplets, we decomposed the repeat instability signal into different repeat classes (SI Appendix, SI Text). Runs of single amino acids are the most abundant repeat type, yet they made up only a fraction of all of the repeats that we analyzed. The ORI was similar between primary and metastatic tumors (relative to matched normal), and variations in the repeat content of different repeat types (i.e., runs vs. larger repeats) were uncorrelated across patients (SI Appendix, Fig. S7).

Proteomic Repeat Instability Discriminates Tumors from Normal Tissues in Ovarian and Prostate Cancers.

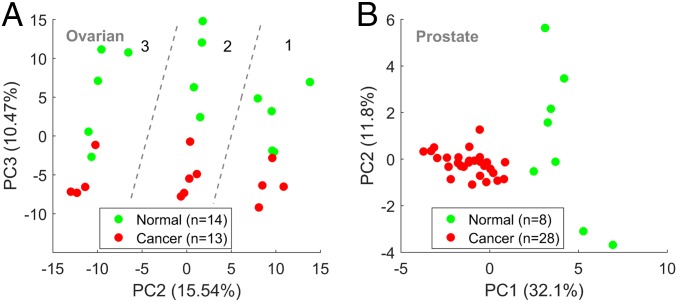
To further test the capacity of the proteomic CR signal to discriminate between tumors and normal tissues, we analyzed 2 additional datasets: an original cohort of ovarian cancer tumors (n = 13) and unmatched normal tissues (n = 14) and a published dataset (56) of prostate cancer tumors (n = 28) and matched normal tissues (n = 8) (SI Appendix, SI Text and Table S1). In the ovarian dataset, we identified 474 triplets with CR > 1. PCA of the CR matrix identified the 3 subsets of patients in this dataset as distinct clusters in the PC1–PC2 plane (SI Appendix, Fig. S8). Nonetheless, tumors were well separated from normal tissues by PC3 in each of the 3 subsets (Fig. 3A and SI Appendix, Fig. S8). SVM applied to this cohort verified that this discrimination is highly robust, achieving high accuracy (>90%) with few selected features (SI Appendix, Fig. S8). In the prostate dataset, the results were different. Unlike in the breast and ovarian datasets, PCA of the full CR matrix (36 samples by 1,330 triplets) as well as SVM analysis do not discriminate between tumors and normal tissues (SI Appendix, Fig. S9). Nonetheless, PCA based on selected features (n = 20) discriminates tumors from normal samples (Fig. 3A and SI Appendix, Fig. S9). These results demonstrate high similarity between the proteomic repeat instability of tumors and normal tissues in the prostate but also reveal tumor-specific signatures.

Fig. 3.

PCA of proteomic ovarian and prostate datasets. (A) Analysis of an original ovarian dataset, which includes 13 primary tumors and 14 unmatched normal tissues (SI Appendix, Table S1). PCA of the CR matrix (27 samples by 474 triplets) discriminates well between tumors and normal tissues in the 3 different experimental pools of patients (separated by dashed lines) as depicted in the PC2–PC3 plane. This discrimination is also captured by SVM analysis and is highly robust (SI Appendix, Fig. S8). (B) Analysis of the proteomic prostate dataset (56), which includes 28 primary tumors and 8 matched normal sampled patients (SI Appendix, SI Text and Table S1); 1,330 triplets with CR > 1 were identified. PCA only based on the top selected features discriminates well between tumors and normal tissues (SI Appendix, Fig. S9) and is demonstrated here in the PC1–PC2 plane for the top 20 triplets identified by Fisher score test. This discrimination is, however, less robust than in the breast and ovarian datasets and suggests an overall higher similarity between tumors and normal tissue in the prostate.

The proteomic CR signatures reflect changes in expression levels of repeat-containing proteins and accordingly, do not directly convey any information on genomic somatic variation in the repeat content in protein-coding DNA. Hence, to explore the role of repeat instability in somatic evolution, we turn to the analysis of genomic data. Hereafter, we analyze short reads of nucleotide sequences obtained from WES data (SI Appendix, Table S1).

Genomic Repeat Instability Discriminates between Healthy and Cancerous Prostate Tissues.

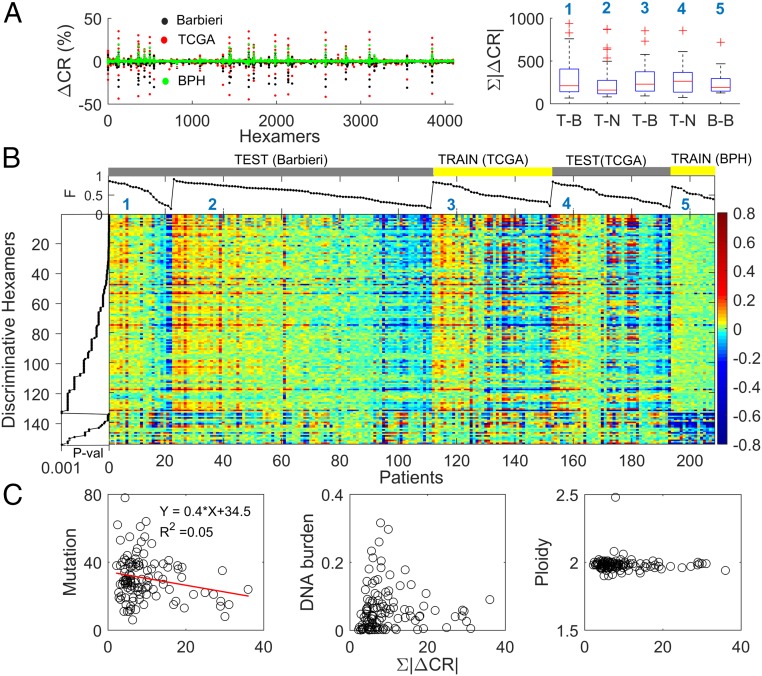
We explored genomic repeat instability in the prostate, the tissue type with the richest dataset among the ones examined, which includes samples from both healthy individuals and cancer patients (SI Appendix, Table S1). We analyzed the TCGA dataset of prostate cancer patients (57), focusing on cases for which a primary tumor sample and 2 control samples from blood and from an adjacent matched normal tissue were collected. In each patient (n = 41), we computed the CR signatures of the tumor and of the adjacent normal samples relative to blood. In most of the patients, the signatures of tumor and adjacent normal samples were strongly and positively correlated (Fig. 4A and SI Appendix, Fig. S10). This correlation was independent of the nature of the signatures (i.e., expansion dominated or contraction dominated), implying that the signatures are primarily tissue specific (SI Appendix, Fig. S10). High similarity between the signatures was also observed across patients as demonstrated by the bimodal distribution of the pairwise correlations (SI Appendix, Fig. S10). This reflects the prevalence of positive or negative correlation between the signatures from different patients, a consequence of the dominance of either repeat expansion or contraction in a given genome. The similarity between the signatures of prostate tumors and their respective adjacent tissues (relative to blood) is consistent with the similarity between tumors and matched normal tissues observed in the proteomic prostate dataset.

Fig. 4.

Repeat instability in prostate tissues. (A) RISs (RIS = ∆CR) of all prostate datasets (SI Appendix, Table S1), Barbieri et al. (58) (n = 111; black), TCGA (n = 41; red), and BPH (n = 15; green), superimposed (Left). The 10 most dominant hexamers are evident (large peaks). The ORI (ORI = ∑|∆CR|) distributions of tumor (T), adjacent normal (N), and benign (B) tissues across the datasets (Right). In the dataset of Barbieri et al. (58), tumor signatures are estimated relative to blood (T–B; n = 22) or to an adjacent tissue (T–N; n = 89), respectively (1 to 2). In TCGA, signatures of tumors (T–B) and adjacent normal tissues (N–B) are computed relative to blood (3 to 4). Benign signature (B–B) is computed relative to blood (5). (B) Heat map of the 154 discriminative hexamers (SI Appendix, Table S3) contrasting RIS of tumors in the TCGA dataset with that of benign prostates, both computed relative to blood (Train). Test sets display similar characteristics to tumors of the train set (signature numbers are the same as in A, Right). Results of training–test sets are robust (SI Appendix, Fig. S11). Colors reflect actual ∆CR values (in percent). Hexamers are ordered by their KS P values and grouped into those that have higher |∆CR| in tumors and those with higher |∆CR| in the benign tissues within the train set. Patients are ordered by the portion (F) of discriminative hexamers that increased in each signature. (C) Relationship between ORI and the number of nonsilent mutations, DNA burden of copy number alterations, and ploidy in tumors. Each point represents a patient in the dataset of Barbieri et al. (58). ORI is estimated using the set of 154 discriminative hexamers.

To determine whether these RISs include tumor-specific characteristics, we compared them with signatures of benign prostate hyperplasia (BPH) from healthy individuals (n = 15) (SI Appendix, SI Text and Table S1). Superposition of tumor, adjacent normal, and benign signatures relative to matched blood (Fig. 4 A, Left) highlights the close similarity between them, with the healthy signatures being slightly weaker. Accordingly, the distributions of the ORI values of tumor and adjacent normal signatures in cancer patients are similar, whereas for healthy signatures, lower values were observed (Fig. 4 A, Right). However, these differences had limited statistical significance, emphasizing the strong tissue specificity of prostate signatures. Thus, to identify tumor-specific features, we trained SVM classifiers as in the proteomic case, but to account for the expansion-dominated and contraction-dominated genomic signatures, we considered the absolute value (|ΔCR|) in our analysis. Tumor tissues were robustly discriminated from benign ones (SI Appendix, Table S3, task 1), with 154 discriminative motifs identified using the KS test (P value < 0.001) (Fig. 4B). The classifiers could not distinguish between tumor and adjacent normal signatures relative to blood, and no discriminative motifs were found (SI Appendix, Table S3, task 2) as expected from their close similarity. Thus, using adjacent normal tissues as a control instead of blood leads to significantly weaker signatures (Fig. 4A). Nonetheless, these signatures contain tumor-specific information: the identified discriminative motifs between these signatures and those of benign tissues largely overlap those that were identified in task 1 (SI Appendix, Table S3, task 3). Therefore, we used this signature when a blood sample was missing.

To test the predictive power of the 154 discriminative motifs, we considered an independent dataset (58) of 111 prostate cancer patients (SI Appendix, Table S1). The repeat instabilities of the test and training sets showed remarkable similarity (Fig. 4B). The similarity between the tumor and adjacent matched normal signatures, but not the healthy signatures, implies that the adjacent normal prostate tissues in cancer patients possess tumor-specific features in the absence of histological evidence. We validated this prediction using various training–test sets, demonstrating that tumors are predicted with high accuracy (>90%) based on both tumor and adjacent normal signatures (SI Appendix, Fig. S11).

To identify genes that were most strongly affected by repeat instability, we mapped the short repeat-containing reads onto the human genome and estimated repeat instability in genes (SI Appendix, SI Text). We found that the 10 most unstable (dominant) motifs (with |∆CR| > 5% in >80% of the patients) (Fig. 4A) were not discriminative and did not map to coding regions but rather, to regulatory regions (SI Appendix, Fig. S12). Because these dominant signatures appear in all tissues, including benign prostates, it seems likely that they represent repeat hotspots in noncoding regulatory regions that might exert currently unknown effects on transcription regulation (59). In contrast, discriminative motifs mapped to protein-coding regions (SI Appendix, Fig. S12).

As in the proteomic case, the set of most repeat-unstable genes was significantly enriched in known cancer genes (SI Appendix, Fig. S13). We analyzed in detail the amino acid and nucleotide compositions of the identified repeat-unstable genes. This analysis also emphasized the ability of our methodology to identify diverse types of repeats from runs of amino acids in proteins (e.g., the glutamine tracks in FOXP2 protein) (SI Appendix, Fig. S14) to repetitive domains (e.g., Cysteine-rich PAK1 inhibitor CRIPAK) (SI Appendix, Fig. S15) as determined from the recurrence of hexamers in the protein-coding DNA (SI Appendix, SI Text).

Lastly, we explored the relationship between repeat instability and other somatic aberrations in this dataset. The ORI of discriminative motifs weakly and inversely correlated with the nonsilent point mutation load but was independent of copy number alterations (i.e., DNA burden) and aneuploidy status (Fig. 4C). The apparent, even if weak, tradeoff between repeat instability and the mutation load suggests that, in tumor evolution, repeat instability could be a compensatory mechanism for point mutations. To test this hypothesis, we performed a pancancer analysis, exploring a wider distribution of mutation loads.

Genomic Repeat Instability Is Inversely Related to Somatic Point Mutation Load in the Pancancer Dataset.

In addition to the prostate adenocarcinoma analyzed above, 3 other cancer types, namely breast (60), bladder (61), and lung (62), were selected from the TCGA (SI Appendix, Table S1). The selected cancers represent different point mutation load regimes: prostate and breast cancers have relatively low numbers of point mutations per sample, whereas bladder and lung cancers have comparatively high numbers of point mutations (63). As in prostate cancer, we focused our analysis on patients with available data from all 3 types of samples (tumor tissue, adjacent matched normal tissue, blood) to measure the RISs of the primary tumor and its adjacent normal sample relative to the blood sample. Similar to the observation on prostate cancer (SI Appendix, Fig. S10), adjacent normal and tumor signatures strongly correlated in individual patients across all cancer types (SI Appendix, Fig. S16).

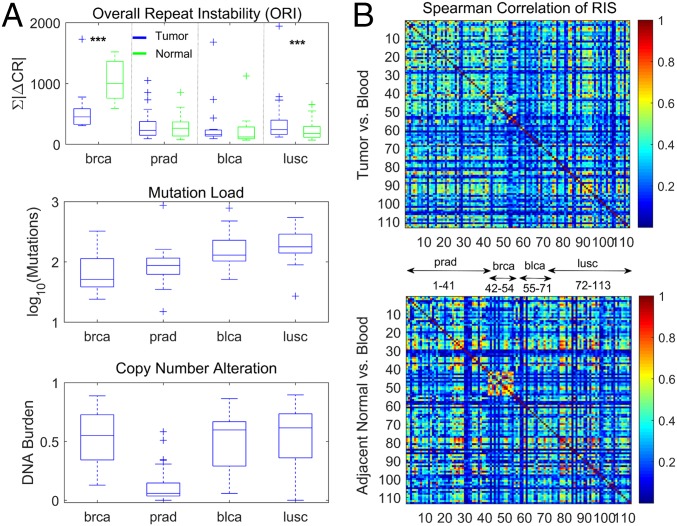
Across cancer types, we identified a consistent inverse relationship between the ORI and the number of nonsilent point mutations, which was independent of the overall genomic mutational burden (Fig. 5A). Despite the similarity between adjacent normal and tumor signatures observed in each patient (SI Appendix, Fig. S16), patients with low-mutational load cancers (i.e., breast) display higher repeat instability in normal tissues compared with the respective tumor signatures, whereas for high-mutational load cancers (bladder and lung), normal signatures were weaker than the respective tumor signatures (Fig. 5A). In prostate patients, the similarity between tumors and normal tissues was the highest, explaining the difficulty in the identification of tumor-specific features in this case and the need for a noncancerous control (compare with Fig. 4). Consistently, we observed a greater similarity between tumors and normal tissues in the prostate proteomic dataset. Thus, repeat instability is high when the mutation load is low and low when the mutation load is high in accord with previous observations on MSI (11), and this effect is stronger for the signatures of adjacent normal tissues in the vicinity of tumors than for the tumor signatures themselves. The inverse relationship between the point mutation load and the ORI holds both for gain (expansion) and loss (contraction) of repeats but is more pronounced for gain (SI Appendix, Fig. S17).

Fig. 5.

Pancancer analysis of repeat instability in the TCGA datasets. (A) The ORI (ORI = ∑|∆CR|; vs. blood) in tumors and corresponding adjacent matched normal tissues (Top; few outliers with ORI > 2,000 are omitted for clarity) (SI Appendix, Fig. S17). The mutation load estimated by number of nonsilent point mutations (Middle) and the copy number alterations (i.e., DNA burden) measured by the fraction of altered genes (gain or loss) in the proteome (Bottom). An inverse relationship exists between repeat instability and point mutation load. In low-mutational load cancer types, repeat instability is larger in the adjacent normal tissues than in tumors, but this reverses in high-mutational load cancers. ***KS test P value < 0.01. (B) Spearman correlation among patients of tumor RISs (RIS = |∆CR|; Upper) and of adjacent matched normal signatures (Lower) measured relative to the blood sample in each patient.

Furthermore, to elucidate the differences between cancer and adjacent normal genomes across tissues, we assessed the pairwise correlations among patients of both adjacent normal signatures and the respective tumor signatures (Fig. 5B). Adjacent normal tissue signatures display higher correlations across patients compared with the respective tumor signatures: that is, the normal signatures are more tissue specific. This effect was more pronounced in patients with low-mutational load cancers (breast and prostate), where the repeat instability is high. The weaker tissue specificity of tumor signatures suggests that common mechanisms, such as impaired DNA replication and repair, similarly affect the repeat content of tumors across tissues and individuals and consequently, blur the similarity between the same tissue samples across individuals, with a net effect of reduced tissue specificity. This effect conversely enhances the tumor-specific signal in tumor signatures as we demonstrated in the case of prostate cancer (Fig. 4 and SI Appendix, Table S3), leading to a more homogenous structure of the pairwise correlations between tumor signatures, across patients, and across different cancer types (Fig. 5B).

Genomic Repeat Instability Recapitulates Tumor Phylogeny within Patients and Correlates with Metastatic Spread.

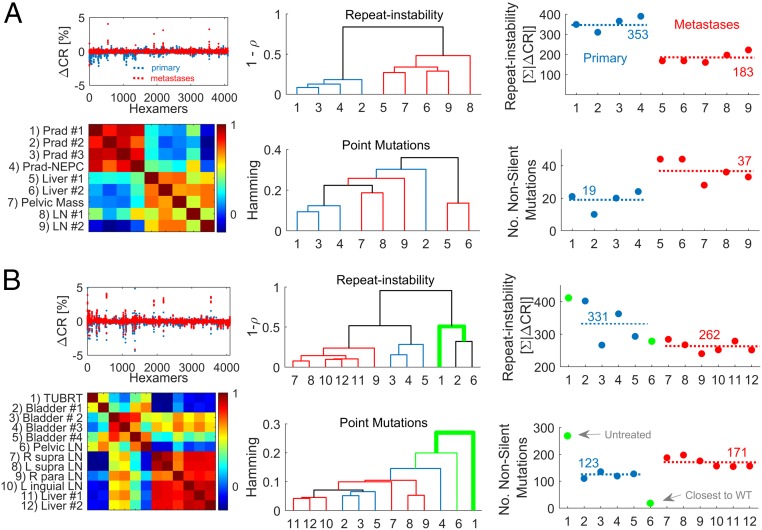
To validate the role of repeat instability as a distinct and compensatory mutation class in tumor evolution, we studied 2 patients with metastatic spread (SI Appendix, Table S1). The 2 patients with the largest number of available sequenced samples from different anatomical sites were selected from 2 recent studies of metastatic prostate cancer (WCM0) (24) and chemotherapy-resistant urothelial carcinoma (WCM117) (25). The prostate cancer patient represents a low-mutation load cancer type, whereas the bladder cancer patient represents a high-mutation load cancer type.

The analysis of the RISs from different anatomical sites of the same patient measured relative to blood highlights a clear hierarchy based on the correlation between the signatures, where primary tumors and metastases are well separated into 2 clusters both in the prostate cancer patient (Fig. 6A) and in the bladder cancer patient (Fig. 6B). Furthermore, we approximated the tumor phylogeny by similarity dendrograms that were constructed from the repeat instability pairwise correlation distances and from the Hamming distances between mutated genes using the simple unweighted pair group method with arithmetic mean (UPGMA). The repeat instability- and point mutation distance-based dendrograms were comparable (Fig. 6) and were weakly sensitive to the choice of the linkage criterion (e.g., shortest distance or UPGMA) and distance measure (Spearman or Pearson correlation) (SI Appendix, Fig. S18). Critically, however, the tumor phylogeny inferred from repeat instability was more concordant with the detailed phylogeny that we have previously obtained by rigorous analysis of the clonal compositions of samples and the tempo of somatic aberrations (24, 25). Repeat instability-based phylogeny captures some fine details of the relationship among samples: 1) the prostate primary tumor sample with neuroendocrine features (Fig. 6A) is close to the other primary tumor samples (24); 2) the metastatic pelvic lymph node in the bladder cancer patient that was surgically removed at the time of the cystectomy is close to the bladder primary tumors (Fig. 6B), in particular to the untreated primary tumor (despite marked difference in the ORI between these samples), as previously inferred using independent techniques (25); and 3) metastases from the same anatomical site cluster together, with few differences. The finding that the phylogenies derived from repeat instability are closely similar to the true phylogenies suggests that repeat instability evolves by divergence at clock-like rates.

Fig. 6.

Analysis of multiple samples from 2 individuals with metastatic spread. (A) Analysis of a prostate cancer patient with large metastatic spread and multiple available biopsies from ref. 24. (Left) The RISs (RIS = ∆CR) of primary tumor samples (blue) and metastases (red) vs. blood are superimposed (Top), and the heat map of the pairwise Spearman correlations across samples (Bottom) is shown. (Center) The dendrogram inferred by the correlations distance (1 − ρ) among the RIS of samples (Top) and the dendrogram inferred by the hamming distance between the nonsilent point mutation of samples across genes (Bottom). Dendrograms are estimated using UPGMA. Primary tumor leaves are colored in blue, metastatic leaves are in red, and connecting branches are in black. Sample numbers are as in the heat map. (Right) The inverse relationship between the ORI (ORI = ∑|∆CR|; Top) and the nonsilent point mutation load (Bottom). Average values are depicted by dashed lines. Sample numbers are as in the heat map. Prad, prostate adenocarcinoma; NEPC, neuroendocrine prostate cancer; LN, lymph node. (B) Similar analysis of a bladder cancer patient with the largest metastatic spread from ref. 25. Untreated sample (1) and a treated metastatic sample (pelvic), which is the closest to the tumor ancestor wild type (6), are colored in green and are not considered to estimate averages of repeat instability and mutation load (dashed lines in Right) of the treated samples. TUBRT, transurethral resection of bladder tumor; L, left; R, right.

To test the hypothesis that repeat instability is a compensatory, adaptive path of tumor evolution, we compared the ORI and the nonsilent point mutation load in primary tumors and metastatic sites. In both patients, repeat instability was significantly higher in primary tumors than in metastases, corroborating the inverse relationship between repeat instability and point mutation load (Fig. 6 A, Right and B, Right). In contrast, in both patients, the number of mutations as well as the number of gene copy number alterations (genomic burden) significantly increased from the primary to the metastatic states (SI Appendix, Fig. S19), further indicating that repeat instability is a distinct phenomenon. The transient dynamics of repeat instability is also captured in the bladder patient, showing a large increase in the untreated primary tumor relative to wild type followed by a gradual reduction in the treated primary and metastatic tumors inverse to the dynamics of point mutations (Fig. 6B). Importantly, the 2 patients represent 2 distinct evolutionary regimes, whereby the transition to a metastatic state in the low-mutation load cancer type (prostate) is accompanied by an apparent increase in dN/dS (i.e., positive selection), whereas in the high-mutation load cancer type (bladder), this transition is marked by a decrease in dN/dS (SI Appendix, Fig. S20) (i.e., purifying selection) in accord with theoretical predictions (64, 65). Thus, repeat instability dynamics in individual patients is robust to mutation selection status. These patients had no mutations in mismatch repair genes. Only the bladder patient had missense mutations in PLOD/POLE genes. Thus, repeat instability dynamics appears robust to DNA repair status.

Last, to assess the relative contributions of different classes of repeats, we decomposed the RISs into MSI and larger repeats instability (LRI) by analyzing the distribution of interval recurrences of consecutive hexamers (SI Appendix, SI Text). In the prostate cancer patient, MSI and LRI were highly correlated, and each component significantly decreased from the primary to the metastatic state independently (SI Appendix, Fig. S21). In contrast, in the bladder cancer patient, despite a marked overall correlation between MSI and LRI, MSI only weakly decreased from the primary to the metastatic states, whereas LRI dropped substantially (SI Appendix, Fig. S22). In both patients, MSI makes up about 20% of the repeat instability signal, emphasizing the importance of accounting for different types of repeats. Taken together, these findings imply that repeat instability is most pronounced at early stages of tumor progression and that it is a transient genome alteration that compensates for the relatively low number of driver mutations in early stages but is partially reversed as mutations accumulate and tumor cells adapt.

Discussion

The involvement of repeat instability in human pathology is supported by ample evidence (11–14, 46–50). However, the current understanding of the role of this phenomenon in somatic evolution is mostly limited to microsatellites. Here, we developed a technique to measure the repeat content of proteogenomes, accounting for a broad variety of repeats. This approach allowed us to systematically assess repeat instability across multiple studies directly from sequence raw data of bulk samples, yielding insights into its dynamics and role in tumor evolution.

Our analyses of genomic signatures show that, compared with blood, cancers and adjacent normal tissues manifest similar RISs. These signatures are, to a large extent, tissue specific in accord with analyses of repeat instability in other disorders (49, 50). However, tumor-specific signatures, which correlate with tumor evolution and allow for discriminating cancers from healthy samples, also exist. Repeat instability is inversely related to the point mutation load but is independent of other somatic aberrations. This inverse relationship was observed between low-mutational load cancers and high-mutational load primary tumors and critically, between primary tumors and metastases from the same patient. Because repeat instability includes MSI, our findings support and generalize previous results showing that MSI is prevalent across cancer types (14) but is consistently more pronounced in patients with low mutation loads compared with those with high mutation loads (11). Given that about 2/3 of the mutations in cancer can be attributed to replication errors (53), which promote repeat instability (11, 49, 50), the observed tissue specificity of repeat instability could be explained, in part, by tissue-specific cell division rates. Because blood has a relatively high rate of cell divisions (66), it is substantially diverged from other tissues and is, therefore, an optimal available choice for a control to characterize repeat instability (and other somatic aberrations). Despite this divergence, the effective population size of blood cells is likely large so that purifying selection is highly efficient (i.e., blood is largely free of deleterious mutations) and thus, can serve as an adequate control.

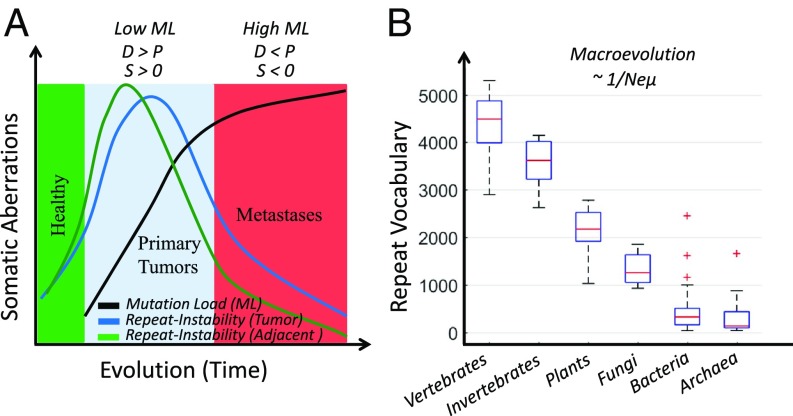
Collectively, our observations indicate that repeat instability is a distinct adaptive path in tumor evolution. We propose a model of tumor evolution (Fig. 7A) in which, at the initial phase of tumorigenesis (low-mutational load cancers at the pancancer level and primary tumors at the patient level), there are few cancer driver mutations, and repeat instability serves as an additional complementary mechanism, which increases (or maintains) the fitness of tumors. Later in tumor evolution, when metastases and/or high mutation loads accumulate, repeat instability is reduced as tumors adapt to specific niches. In high mutational loads, the number of deleterious passenger mutations is substantial, imposing selective pressure (64, 67) that could reduce repeat instability. This theoretically predicted transition in the evolutionary regimes of tumors at high mutation load is also captured as the association of point mutation load with clinical outcome (65). Thus, although most tumors evolve near neutrality (65, 68–70), excess mutation loads could lead to decreased fitness both through intracellular mechanisms and through the generation of neoantigens, which elicit immune response (71–75). The immune system then exercises purifying selection, thereby reducing repeat instability in the tumor cell population. Those repeats that have been fixed in the cell population are likely beneficial. This is consistent with recent observations on microsatellite-unstable colon carcinomas, where strong purifying selection eliminates antigen-presenting tumors (73), whereas immune-adapted tumors metastasize (76). Hence, although high mutation loads represent vulnerability to cancer, beneficial mutations eventually fix in a population of tumor cells, whereas deleterious mutations are removed such that cancer maintains its fitness. The observed sharp decrease in repeat instability at high mutation loads, as least in part, is likely to reflect the dynamic nature of repeat propagation, which is fast and reversible, unlike accumulation of point mutations. This property presents a therapeutic challenge yet opens avenues for identifying neoantigens and developing immunotherapies against immune-adapted tumors (71, 77).

Fig. 7.

Proposed evolutionary model of repeat dynamics in cancer and normal tissues. (A) In healthy tissues (e.g., benign), repeat instability is low (green zone). At the initial phase of tumor evolution (e.g., primary and low-mutation load [ML] cancer types; cyan zone), tumors harbor a small number of positively selected (S > 0) drivers (D). Repeat instability acts to increase or maintain the fitness of tumors. Normal tissues adjacent to tumors react similar to the selective pressures imposed by the microenvironment and therapy. Repeat instability in adjacent normal tissues is even higher than that of the corresponding tumors but is quickly reduced as the transition to a neoplastic state is not achieved and normal cellular function is retained. Later in evolution (i.e., metastases and high-ML cancer types; red zone), the number of driver mutations increases, tumors are more adapted, and repeat instability reduces. At least in high-ML cancers, the accumulation of passenger mutations (P) outcompetes the drivers (P > D); hence, cancers resort to purifying selection (S < 0), which reduces the repeat instability. Hence, repeat instability acts as a transient, compensatory mechanism. The faster transient effect in adjacent normal tissues explains their higher repeat instability in low-ML cancers and lower repeat instability in high-ML cancers relative to the respective tumors. (B) Repeat content, measured as the vocabulary of amino acid triplets that compose protein repeats, correlates with ordering of organisms by the product of effective population size (Ne) and mutation rate (μ). Adapted from ref. 31, which is licensed under CC BY 3.0.

According to our model, at the initial phase of tumor evolution, repeat instability can compensate for the lack of a sufficient number of driver mutations and thus, increase tumor fitness, whereas later in evolution, high repeat instability negatively affects tumor fitness and is selected against. A positive correlation between high MSI and better prognosis in cancer patients has been reported (14). In the context of our model, these findings are likely to reflect stages of tumor progression at which repeat instability already exceeded the optimal value. The existence of compensatory adaptive paths (that is, point mutations vs. repeat instability) suggests that, although the dynamic range of somatic aberrations in cancers is substantial, the fitness of tumors tends to be stable over time and can be robust to environmental pressure.

Under this view, normal tissues adjacent to tumors evolve under comparable selective pressures imposed by the microenvironment, such as fluctuations in blood flow (78), metabolic gradients (79), and therapy, so that they acquire signatures similar to those of the tumors. This view is concordant with recent reports on significant similarities between the somatic mutation signatures of cancers and normal tissues (80, 81). Accordingly, analysis of these tissue samples should allow prediction of cancer breakout before pathological evidence as we demonstrated in the case of prostate cancer. We hypothesize that repeat instability is low in healthy tissues, rapidly increases in tumors and adjacent normal tissues, and then drops as cancer progresses (Fig. 7A). This transient dynamics is partially captured by the single-patient analysis (compare with Fig. 6B) and by the (slightly) lower repeat instability in benign tissues compared with primary tumors (compare with Fig. 4). Such a transient compensatory mechanism of repeat expansion–contraction in tumors is reminiscent of chromosomal duplications in fungi (82) and gene duplications in viruses (83), which seem to represent the first rapid route of adaptation. Thus, at the initial phase of tumor evolution, both adjacent normal tissues and the tumor cells respond to the environmental stress by increased repeat instability. Tumor cells then acquire additional (driver) mutations, whereas normal cells in the respective tissues start on the path of tumorigenesis but fail to undergo neoplastic transformation, whereby repeat instability rapidly drops. This scenario implies a faster repeat dynamics in adjacent normal tissues relative to tumors (Fig. 7A), which may explain the differences between tumor and normal signatures as a function of the mutation load across cancer types (compare with Fig. 5). The link between repeat instability and cancer progression is concordant with the somatic evolution of repeat instability in some neurological disorders, where variations in the number of repeat units have been associated with disease severity (49, 50). Considering also the observed connection between proteomic repeat instability and cancer progression, we suggest that RISs can serve as important diagnostic and prognostic markers that could be sensitive enough to detect cancer in early stages.

In this work, we quantified and emphasized the importance of gain and loss of repeat units in tumor evolution. Similar to gene duplications (84, 85), selective constraints are relaxed in repeats after duplication (51) such that mutations can accumulate at higher rates and eventually lead to the acquisition of functions. However, in contrast to gene duplicates, which evolve under slightly relaxed purifying selection and mostly exhibit subfunctionalization of ancestral proteins (85, 86), repeats evolve much faster under strongly relaxed purifying selection and positive selection such that neofunctionalization is likely to be the primary route of evolution (51). Such rapid evolution of repeats has been documented in colonic carcinogenesis (87). Indeed, we observed that highly repeat-unstable genes were enriched among known cancer genes both in genomic and proteomic data. This implies involvement of repeat instability and more specifically, fast-evolving copies of repeats in oncogenesis.

The microevolutionary dynamics of repeat instability in cancer (Fig. 7A) is similar to the evolution of repeats over long spans of evolution (Fig. 7B). In diverse life forms, after the rapid evolution of repeat copies (51), some repeats become conserved as they gain function (51, 88). The conservation of mutated repeats seems to eventually translate into an increase in the diversity of the repeat content of extant species proteomes in a manner that correlates with the ordering of major clades by N_eμ (effective population size, N_e, multiplied by the mutation rate, μ): that is, by the power of purifying selection (31, 89) (Fig. 7B). These parallels with species evolution should serve as a motivation for the study of repeat instability in somatic evolution of cancer.

Additional integrated genomic–proteomic research is needed to study how somatic changes in the genome are translated into differential expression of repeat-containing peptides and how repeat copies diverge by accumulating mutations during tumor evolution. Such research could lead to the identification of new cancer drivers and the development of therapeutic strategies, in particular immunotherapies, which target this mutational class. Because the results indicate that repeat instability is an adaptive mechanism that is important at the early stages of tumor evolution, we hypothesize that RISs could be relevant for early cancer detection by cell-free DNA and liquid biopsy analysis. The roles of repeat instability in other pathologies and various evolutionary scenarios remain to be explored.

Materials and Methods

The repeat instability method consists of quantifying the repeat content of proteogenomes in the space of short motifs (i.e., k-mers) over the alphabet of sequences analyzed. The extent of repetitiveness of a motif m in a genome or proteome is measured by its CR as illustrated in Fig. 1A. The CR is defined as the number of the motif recurrences in a set of sequences (i.e., WES DNA short reads or Stable Isotope Labeling with Amino Acids in Cell Culture-Mass Spectrometry [MS] peptides) divided by the number of sequences in which it appears:

$$C{R}^m=\frac{{\displaystyle {\sum }_i^{Ns}{w}_i^m{r}_i^m}}{{\displaystyle {\sum }_i^{Ns}{w}_i^m{\delta }_i^m}}\equiv \frac{R^m}{P^m},$$ [1]

where m = 1,…, N_m, and N_m = A^k is the number of searched k-long motifs over the alphabet A (e.g., N_m = 20³ for amino acid triplets, N_m = 4⁶ for DNA hexamers). r_i^m is the number of recurrences of motif m on sequence i. δ_i^m = 1 if r_i^m > 0 and is 0 otherwise. w_i^m is a weight factor that measures the relative abundance of sequence i in a sample, which is particularly relevant for proteomic data. N_s is the number of input sequences. By definition, CR is ≥1. In this motif representation, a repeat array in the genome is represented by (a contribution to) the CR of the k-mer motifs of which it consists. Different repeat arrays can contribute to the CR of a particular motif. The variation in the repetitiveness of a motif m between 2 samples (e.g., a tumor sample and a control sample) is measured (in percentage points) by

$$\mathrm{\Delta }C{R}^m=100\times \frac{C{R}_2^m-C{R}_1^m}{C{R}_1^m},$$ [2]

where CR₁^m and CR₂^m are the CR values for the motif m in samples 1 and 2, respectively. Sample 1 serves as a reference. The RIS is expressed as the vector of ΔCR changes of all motifs, and the ORI is given by the sum over the absolute values of motif variations, ∑_m|∆CR^m|.

A detailed description of the methods, including parameterization of the motif search in amino acid (i.e., k = 3) and nucleotide sequences (i.e., k = 6), decomposition of the repeat instability signal to different repeat classes (e.g., microsatellites vs. larger repeats), effects of large structural variations on repeat instability, implementation of the methods to the genomic and proteomic datasets, estimation of statistical and systematic errors, estimation of repeat instability in genes, and machine learning tools used in the study, are provided in SI Appendix, SI Text. All datasets are described in SI Appendix, SI Text and Table S1. For the original BPH cohort, after informed consent, BPH tissue samples were collected from patients who underwent surgical resection due to symptomatic BPH. Samples were examined and annotated by expert genitourinary pathologists. Tissue cores were taken for DNA extraction followed by WES or whole-genome sequencing (>40×). Matched blood samples were used as patients’ control samples. The study of BPH was approved by the Weill Cornell Medicine Institutional Review Board. A comprehensive molecular characterization of the BPH samples is currently being finalized.