The entropic bond in colloidal crystals

Significance

Chemical bonding, in various forms, is integral to the structure of matter and the function of living systems. However, what are the minimal requirements to form a bond? We show that classical systems governed solely by entropy exhibit unconventional, entropy-mediated bonding. We also show the description of such systems in terms of bonds provides better understanding for the design of materials from nanoscale building blocks. Our results suggest well-defined analogs of chemical bonds exist in a broad range of unconventional systems.

Abstract

A vast array of natural phenomena can be understood through the long-established schema of chemical bonding. Conventional chemical bonds arise through local gradients resulting from the rearrangement of electrons; however, it is possible that the hallmark features of chemical bonding could arise through local gradients resulting from nonelectronic forms of mediation. If other forms of mediation give rise to “bonds” that act like conventional ones, recognizing them as bonds could open new forms of supramolecular descriptions of phenomena at the nano- and microscales. Here, we show via a minimal model that crowded hard-particle systems governed solely by entropy exhibit the hallmark features of bonding despite the absence of chemical interactions. We quantitatively characterize these features and compare them to those exhibited by chemical bonds to argue for the existence of entropic bonds. As an example of the utility of the entropic bond classification, we demonstrate the nearly equivalent tradeoff between chemical bonds and entropic bonds in the colloidal crystallization of hard hexagonal nanoplates.

Chemical approaches to the study of matter are based on the notion of bonding (1). Covalent and ionic bonds, metallic bonds (1), and even hydrogen bonds, whose definition continues to be refined (2, 3), rely on the reconfiguration of electron density to bind atoms and molecules. However, key characteristics of chemical bonds (4)—local energy gradients and temporal stability—could be provided by unconventional mechanisms. The “mechanical bond” (5), for instance, connects ring-like molecules by virtue of their topology. Although the rings are not covalently bonded to each other, they cannot be separated without breaking a covalent bond in one of the rings. The mechanical bond is defined primarily through what it does, rather than what it is (3).

Entropic ordering (6–9) is another unconventional mechanism that involves local (free) energy gradients (10) and temporal stability. Counterintuitively, hard particles in the range of nanometers to a few microns and with no interactions other than excluded volume can rearrange from a disordered fluid into an ordered crystal, or from one crystal structure to another, upon crowding (8–26). These colloidal crystals can be surprisingly complex and remarkably structurally diverse, and arise solely from particle shape anisotropy and the statistical thermodynamic principle of entropy maximization. Many of them are isostructural to known atomic or molecular crystals, and even crystallize along similar kinetic pathways (27), despite the absence of chemical bonds between particles. Instead, the apparent “effective” interparticle attraction in hard particle colloidal crystals is purely statistical, arising from the tendency to maximize the number of microstates available to the system (10). This phenomenon raises the question of whether the directional entropic forces associated with ordering in dense colloids imply the existence of, for all intents and purposes, bonds between particles—bonds mediated not by electrons, but by entropy.

Here, we argue for the consideration of “entropic bonds”—emergent, statistical bonds mediated, upon crowding, by entropy. To support our argument, we map the change in entropy due to local rearrangement of particles and compute bond lifetimes in a model system of hard nanoplates. We demonstrate how to manipulate the structure of bonded states, thereby controlling entropic valence. We show that this schema can be used to predict the strength of enthalpic bonds needed to assemble ligand-stabilized nanoplates, rather than relying on entropy, demonstrating how entropic and enthalpic bonds can be interchanged for self-assembly (28). Our results open up the possibility of classes of systems in which bonding can be designed (18, 26, 29) and continuously manipulated.

Model Systems and Results

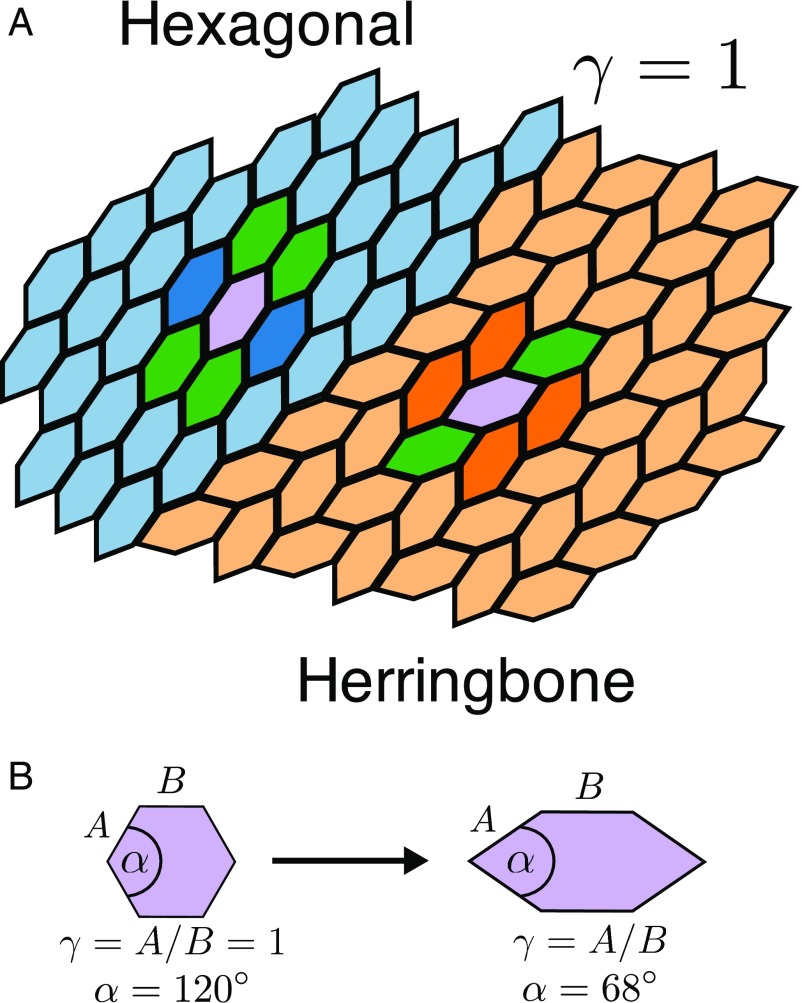
We study a model system of hard hexagonal nanoplates. In experiments (28), lanthanide-fluoride (Ln${\mathrm{F}}_3$) nanoplates are functionalized by ligands on their edges and driven to self-assemble 2D superlattices (Fig. 1A) by either/both entropy and enthalpy, depending on experimental conditions. They may be synthesized over a wide range of elongated hexagonal shapes and thus provide a tunable shape with which to explore quantitatively the notion of the entropic bond. We consider hexagonal particles defined by the angle $\alpha$ and elongation $\gamma$ (Fig. 1B). We define regular hexagons as having $\alpha =120^{○}$ and $\gamma =1$, so that analogs of the Ln${\mathrm{F}}_3$ nanoplates studied in ref. 28 have $\alpha =68^{○}$ with a variable $\gamma$. Monte Carlo (MC) simulations, in which small, local MC trial moves to translate or rotate particles approximate physical time for a Brownian colloidal particle (30), were used to equilibrate the systems of nanoplates over a range of densities. Details of the simulation methodology are described in Methods.

Fig. 1.

(A) Schematic of the two superlattices formed by ${\mathrm{L}\mathrm{N}\mathrm{F}}_3$ nanoplatelets: hexagonal (light blue) and herringbone (light orange). To highlight the difference in the local arrangement within the superlattices, a reference particle is colored purple, and the different lattice positions are highlighted: primary (green), hexagonal (blue), and herringbone (orange). Note this schematic is for an elongation value $\gamma =1$ for which both tilings fill space. (B) Transformation of a regular hexagon $\left(\alpha =120^{○},\gamma =1\right)$ into an elongated hexagon $\left(\alpha =68^{○},\gamma \right)$. $\gamma$ is the ratio of sides $B$ and $A$, a tunable shape parameter to study the influence of shape on entropic bonds

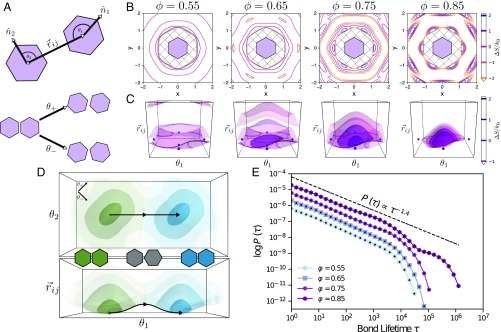
We first consider the entropy-driven self-assembly of hard nanoplates, in which all interparticle interactions other than excluded volume (steric) interactions are suppressed. In such systems, any changes in free energy $F$ are a result of changes in entropy $S$: $\beta \mathrm{\Delta }{F}_{12}=-\mathrm{\Delta }S/k_{\text{B}}$. We can directly account for the rearrangement of entropy $\left(\mathrm{\Delta }S/k_{\text{B}}\right)$ by the associated change in free energy of particle pairs $\left(\beta \mathrm{\Delta }{F}_{12}\right)$, thus increases in entropy are associated with decreases in free energy and consequently increases in the stability of the system. We calculate the entropy of particle pairs in their local coordinate system (Fig. 2A) by computing the potential of mean force and torque (PMFT) (10), yielding the change of entropy of a pair configuration relative to that of an ideal gas: $\mathrm{\Delta }S/k_{\mathrm{B}}=S/k_{\mathrm{B}}-S_{\mathrm{I}\mathrm{G}}/k_{\mathrm{B}}$. In Fig. 2 B and C, we show lines (B) and surfaces (C) of constant $\mathrm{\Delta }S/k_{\mathrm{B}}$ for hard hexagons at packing fractions of $\varphi =0.55,0.65,0.75,0.85$. These computed entropy landscapes quantify the structure of entropically driven self-assembled states (see Methods, Bond Identification and SI Appendix, Fig. S3 for the method of segmenting the PMFT into bonding regions).

Fig. 2.

(A, Top) Schematic of a pair of regular hexagons, describing the coordinate system for directional entropic forces in 2D systems: $\left(r,{\theta }_1,{\theta }_2\right)$. ${\theta }_1$ is the angle between the orientation of particle $i$ and the interparticle vector ${\overrightarrow{r}}_{ij}$ (and vice versa for ${\theta }_2$). This coordinate system distinguishes between pair orientations integrated over in the $\left(x,y\right)$ coordinate system. (A, Bottom) Schematic illustrating alternate coordinates for particle orientation associated with particle libration: ${\theta }_{+}$ and ${\theta }_{-}$. ${\theta }_{+}$ accounts for shearing motion, and ${\theta }_{-}$ accounts for twisting motion. (B) Contour plots of the entropy $\left(\mathrm{\Delta }S/k_{\text{B}}\right)$ in the $\left(x,y\right)$ coordinate system at 4 different densities: $\varphi =0.55,0.65,0.75,0.85$. At low density $\left(\varphi =0.55\right)$, there is very little attraction or repulsion between hexagons. As density increases, regions of effective attraction and repulsion begin to develop as evidenced by the dark purple “ring” around the geometrically forbidden ring that aligns with the edges of the hexagon, showing that these edges are effectively attractive, while the rings that develop further out correspond to low-entropy configurations that are not favorable and are effectively repulsive. Once in the solid phase $\left(\varphi =0.75\right)$, these regions of attraction and repulsion (high-entropy regions and low-entropy regions) are more distinct. (C) Contour plots of the entropy $\left(\mathrm{\Delta }S/k_{\text{B}}\right)$ in the $\left.\left(r,{\theta }_1,{\theta }_2\right)\right)$ coordinate systems at 4 different densities: $\varphi =0.55,0.65,0.75,0.85$. In both B and C, the color bar indicates constant $\mathrm{\Delta }S/k_{\text{B}}$ contours corresponding to isosurfaces; negative entropy indicates that such configurations are unfavorable, while positive entropy indicates favorable configurations of particle pairs. (D) Schematic of an entropic bonding transition from a view of the ${\theta }_1-{\theta }_2$ plane (Top) and the ${\overrightarrow{r}}_{ij}-{\theta }_1$ plane (Bottom) at a density of $\varphi =0.75$. Different entropic bonds are indicated by color, while the darker shade indicates a higher entropy, with the shades being at the same isosurfaces shown in C. A proposed reaction coordinate is provided, showing a possible pathway particles may take to reconfigure from one bond configuration to another. (E) Bond lifetime distribution for hard regular hexagons at 4 densities $\varphi =0.55,0.65,0.75,0.85$, corresponding to low-density fluid, high-density fluid, low-density solid, and high-density solid phases, respectively. Each data series is shifted by a decade for visual clarity. For each dataset, statistical error calculated from four independent samples is smaller than plot markers. The line added above the data shows the power-law decay behavior of entropic bonds at short times.

Analysis of the PMFT of hard hexagons explains their tendency to self-assemble into edge-aligned pairs: for example, at a packing fraction $\varphi =0.75$, the edge-aligned configuration (Fig. 2C) $\left(r=1.026,{\theta }_1=\frac{\pi }{6},{\theta }_2=\frac{\pi }{6}\right)$, shown as a dark purple sphere, results in an increase in the entropy over a similar arrangement in an ideal gas by $\mathrm{\Delta }S/k_{\text{B}}>1.36\pm 0.004$. As shown in Fig. 2E, a lifetime is associated with this alignment tendency, compelling us to refer to pairs of aligned hexagons as “bound.” These bound configurations are separated by transition state configurations of vertex-to-edge-aligned pairs (Fig. 2 C and D, shown as a light purple sphere in C and in gray in D); e.g., at $\varphi =0.75$, the transition state decreases the system entropy by $\mathrm{\Delta }S/k_{\text{B}}\ge 1.83\pm 0.003$.

We next compute for several packing fractions the probability $P$ that a pair of hexagons remains bound for MC time $\tau$ (Fig. 2E). We observe longer lived bonds at higher packing fractions. Bond-lifetime distributions over four decades of MC time indicate power-law decay followed by exponential decay. Similar lifetime distributions were reported for hydrogen bonds in simulations of liquid water (31, 32). In water, the power law decay is ascribed to relative molecular rotation, called “libration,” which causes bonds to quickly break and reform. Libration also occurs in hard particle systems, (33) where it is convenient to combine the relative nanoplate orientations as ${\theta }_{\pm }={\theta }_1\pm {\theta }_2$ (Fig. 3A). We note that the entropy landscapes in Fig. 2 C and D indicate a high entropy penalty for ${\theta }_{-}$ libration (gear-like motion, top left corner to bottom right corner in plots), but a low entropy penalty for ${\theta }_{+}$ libration (coordinated rolling motion; bottom left corner to top right corner). The low entropy penalty for ${\theta }_{+}$ libration indicates that mode of nanoplate dynamics should be fast, leading to bond-breaking and reforming on short time scales. The observed exponential decay at longer times results from the long time required for a particle pair in a configuration near the entropy maximum (free-energy minimum) to break its entropic bond. The second exponential decay observed in $\varphi =0.85$ is a result of the collective rearrangements of many particles required for bond breaking at very high densities (see SI Appendix, Fig. S1 for snapshots of simulations at $\varphi =0.55,0.65,0.75$ and 0.85).

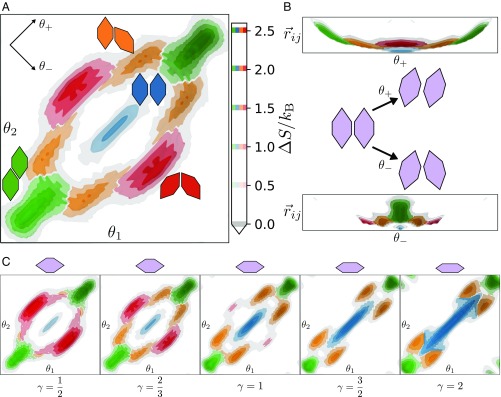
Fig. 3.

(A) Top view of the entropy landscape of elongated hexagons at $\gamma =\frac{2}{3}$, with entropic bond motifs labeled as follows: primary bonds (green), present in both hexagonal and herringbone lattices; hexagonal bonds (blue), present only in the hexagonal lattice; herringbone bonds (orange), present only in the herringbone lattice; and defect bonds (red), which are antagonistic to either crystal lattice (see Fig. 1A to see these motifs in the superlattice structure). Note that due to the symmetry of elongated hexagons, the entropy landscape is periodic, repeating every $\pi$; thus, the range of the landscapes is restricted to ${\theta }_1,{\theta }_2\in \left[0,\pi \right]$. Entropy isosurfaces indicate regions corresponding to each bond type (isosurfaces corresponding to $\mathrm{\Delta }S/k_{\text{B}}=\left[2.5,\hspace{0.17em}2,\hspace{0.17em}1.5,\hspace{0.17em}1,\hspace{0.17em}0.5\right]$ shown in lighter coloring). $\mathrm{\Delta }S/k_{\text{B}}=0$ is indicated with a gray isosurface for reference. Note that because $\beta \mathrm{\Delta }{F}_{12}=-\mathrm{\Delta }S/k_{\text{B}}$, entropy maxima, rather than minima, represent the entropically preferred (energetically preferred) local motifs. (B) Orthographic views of $\left(r,{\theta }_{+}\right)$ (Top) and $\left(r,{\theta }_{-}\right)$ (Bottom) showing the curvature of the entropy landscape in $r$. The greater elongation along the ${\theta }_{+}$ direction compared with ${\theta }_{-}$ indicates greater ability for shear libration, as opposed to twist libration. Included between them is a schematic illustrating these alternate coordinates for convenience. (C) Orthographic view of the isosurfaces of entropically favorable configurations of elongated hexagons at $\gamma =\frac{1}{2}$, $\gamma =\frac{2}{3}$, $\gamma =1$, $\gamma =\frac{3}{2}$, and $\gamma =2$ at pressures $P=\left[16.0,14.9,13.5,12.6,12.1\right]$, respectively. Changing the shape parameter $\gamma$ has a significant impact on the size, shape, and connectivity between entropic bonding regions: as $\gamma$ increases, the favorable defect regions shrink, and become unfavorable for $\gamma =\left[\frac{3}{2},2\right]$, while those for herringbone and hexagonal bonds grow. See SI Appendix, Entropic Bonding Landscapes in Elongated Hexagon Systems and Figs. S4–S6 for alternate views of these entropy landscapes.

Fig. 3 B–D indicates that hard hexagonal platelets exhibit local gradients (here, in entropy) that drive the formation of preferred spatial arrangements of particles, as in conventional chemical bonds. Also, as in conventional chemical bonds, these arrangements exhibit measurable lifetimes indicating temporal stability. In these 2 respects, entropic bonds reproduce hallmarks of conventional chemical bonds. However, the macroscopic scale (i.e., nanometers to microns) of systems that exhibit entropic bonding means that the properties of the bonded particles can be manipulated, which thereby manipulating the structure of the bonds.

To demonstrate and quantify the manipulation of entropic bonds, we examine the effect of particle-shape changes on bond structure. To see this, we compute the entropy landscape for elongated hexagons. Elongating the particle shape breaks rotational symmetry and results in four geometrically distinct edge-to-edge-aligned configurations (Fig. 3A), which we label as primary, hexagonal, herringbone, and defect, according to the crystals in which these motifs arise (Fig. 2A). Isosurfaces of constant $\mathrm{\Delta }S/k_{\text{B}}$ are shown in Fig. 3A for particles with $\gamma =\frac{2}{3}$ at pressure $P=14.9$ (the highest pressure fluid observed). The computed entropy landscape shows the distinct bonded states that correspond to each of the geometrically distinct edge-to-edge nanoplate configurations or “motifs.”

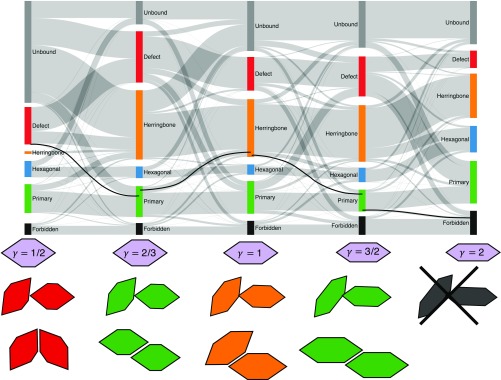
To understand how we may use the shape parameter $\gamma$ to manipulate entropic bonds, we use alluvial diagrams (Fig. 4). Originally developed (34) to visualize change in complex networks, these diagrams allow us to understand the relationship between bond size and particle shape. For each shape parameter $\gamma$ investigated, we identify geometric configurations belonging to a particular entropic bond, as defined by a voxel centered at $\left(r,{\theta }_1,{\theta }_2\right)$ in Fig. 3C and aggregate them into a colored rectangle, where the size of the rectangle increases with the number of identified configurations. The identification of each configuration is computed independently for different particle shapes. Different particle shapes lead to entropy landscapes with different topographies. Because of this topography change, a geometric configuration that is identified with a particular bonded state for one particle shape can be identified with a different bonded state for a different particle shape. Bonded-state identification changes are indicated via gray bands between the colored rectangles in Fig. 4. Analysis of the alluvial diagram reveals the ability to manipulate and control entropic bonds simply by changing the shape of a hard particle, in this case by increasing or decreasing the value of $\gamma$. As shown in Fig. 4 (black line), a configuration identified with a defect bond for $\gamma =\frac{1}{2}$ may be manipulated to belong to a herringbone bond at $\gamma =1$ or a primary bond at $\gamma =\frac{2}{3}$ or $\gamma =2$. This ability to continuously (as opposed to discretely) manipulate entropic bonds makes such bonds unique, providing a method to design and control interparticle interactions and their resulting self-assembly behavior.

Fig. 4.

Manipulation of entropic bonds, shown via an alluvial diagram, indicating particle shape modification of bonded state structure in $\left(r,{\theta }_1,{\theta }_2\right)$ space for elongated hexagons at $P=\left[16.0,14.9,13.5,12.6,12.1\right]$ for shape parameters $\gamma =\left(\frac{1}{2}.\frac{2}{3},1,\frac{3}{2},2\right)$. Bar sizes correspond to phase space volume associated with each bond type. Gray lines associate “flows” within and between bond types as particle shape changes. Additional bars indicate regions of phase space that change from being associated with bonds to nonbonded or geometrically forbidden states, keeping total phase space volume constant across all shapes. Examples below each shape indicate the same voxel in $\left(r,{\theta }_1,{\theta }_2\right)$ for each shape, and the corresponding bond, demonstrating how the bonds change as a function of particle shape. The most striking observation is the considerable increase in the voxels belonging to the herringbone bond from $\gamma =\frac{1}{2}\to \frac{2}{3}$, followed by the reduction in defect voxels from $\gamma =\frac{3}{2}\to 2$. Observation of the flow between bonding regions as $\gamma$ changes shows that particle shape has a significant impact on entropic bonding regions, suggesting the ability to strategically engineer entropic bonds via shape manipulation. See Fig. 3C and SI Appendix, Figs. S4–S6 for the entropic bonding regions used to compute the alluvial diagram.

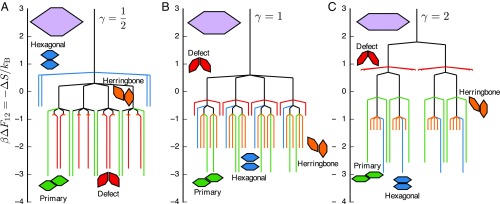
Entropic bonds can be manipulated and the alluvial diagram in Fig. 4 helps to summarize changes to the topography of the bonding landscape, however entropic bonds also allow manipulation of the topology of the bonding landscape, in terms of connectivity and transition states between bonding states. In particular, visual inspection of the entropic bonds shown in Fig. 3C indicates that the shape parameter $\gamma$ does not only have a significant effect on the size and shape of the resulting entropic bonds, but also on the maximal entropy of and connectivity between each bond. To quantify the effect that $\gamma$ has on these variables and the resulting entropic bonds, we use techniques from the study of transition states that have previously been used to study protein folding and other problems involving complex energy landscapes, via so-called disconnectivity graphs (35). Disconnectivity graphs provide insight into the stability of different conformations of a system, as well as indicate which structures or intermediate states may impede a system from reaching its most stable state (its energetic minimum) (35). We use disconnectivity graph analysis to reveal the relationship between the shape parameter $\gamma$, the emergent directional entropic forces, the entropic bonds that form, and the self-assembled structure of the hard hexagonal platelet system (Fig. 5). Disconnectivity graphs in other contexts depict the structure of (free-)energy landscapes as trees, where minima of distinct conformations are “leaves”, and transition states (saddle points) between conformations are nodes. Because we are concerned with the entropy, we represent entropy maxima as leaves and saddle points in the entropy as nodes. Also note that instead of plotting $\mathrm{\Delta }S$ directly, we plot the entropy maxima as $-\mathrm{\Delta }{S}_{12}/k_{\text{B}}=\beta \mathrm{\Delta }{F}_{12}$ to facilitate comparison with the standard approach (using free energy). We use the values of the maximal entropy associated with each entropic bond, as well as the lowest entropy value associated with the transition between two bonds to create the disconnectivity graphs (35) shown in Fig. 5. Fig. 5 shows results for three representative values of $\gamma$; see SI Appendix, Figs. S7 and S8 for disconnectivity graphs for the regular hexagons and all elongated hexagons, respectively.

Fig. 5.

Disconnectivity graphs indicating entropy landscape topology for elongated hexagons at $P=\left[16.0,13.5,12.1\right]$ for shape parameters $\gamma$: $\gamma =\frac{1}{2}$ (A), $\gamma =1$ (B), and $\gamma =2$ (C). The values of the topology are plotted as $-\mathrm{\Delta }S/k_{\text{B}}=\beta \mathrm{\Delta }{F}_{12}$ due to the convention of using disconnectivity graphs to analyze and interpret free-energy landscapes. Each leaf represents an entropic bonding motif found at entropy maxima (plotted as a minima) on the landscape, while each node is the entropy of the metabasin connecting leaves or nodes. Each line is colored by its corresponding bonding motif. Traversing the graph provides information about the relative entropy penalty required to break a bond, as well as which bonds may directly interconvert. For example, consider A, $\gamma =\frac{1}{2}$: while the relative entropy of a herringbone bond is greater than that of a hexagonal bond, the entropy penalty required to break the herringbone bond is much less than that of the hexagonal bond, indicating that the hexagonal bond is more stable than the herringbone bond, which is more likely to convert to a defect or primary bond. Analysis of these (and the other studied values of $\gamma$ in Fig. 3C and SI Appendix, Figs. S4–S6) shows that the combination of bond entropy and the relative entropy penalty required to break a bond lead to the preference for hexagonal bonds over herringbone bonds, leading to the entropy-driven self-assembly of the hexagonal lattice.

Examining Fig. 5 reveals increasing entropic penalty for pairs of particles bound in the defect configuration with increasing elongation ($\mathrm{\Delta }S/k_{\text{B}}$ changes by more than 2 from $\gamma =\frac{1}{2}$ to $\gamma =2$; Fig. 5), which occurs along with a disappearance of states within the entropy basin for defect bonding (Fig. 4). In contrast, we see an increase in the entropic preference for pairs of nanoplates bound in the hexagonal motif ($\mathrm{\Delta }S/k_{\text{B}}$ changes by nearly 2 from $\gamma =\frac{1}{2}$ to $\gamma =2$; Fig. 5), but the size of the entropy basin for hexagonal bonding shows little variation across particle shape (Fig. 4). Further analysis of disconnectivity graphs (Fig. 5 A–C) indicates little dependence of $\mathrm{\Delta }{S}_{\text{primary}}/k_{\text{B}}$ (entropy of the primary bonding motif) as a function of elongation ($\gamma$). However, defect bonds depend strongly on $\gamma$; $\mathrm{\Delta }{S}_{\text{defect}}/k_{\text{B}}$ increases with $\gamma$, leading to a stronger entropic preference for bound pairs consistent with the ordered crystal structures. $\mathrm{\Delta }S/k_{\text{B}}$ also changes as a function of $\gamma$ for hexagonal and herringbone bonds, indicating competition between these motifs in the dense fluid phase. Taken together, these effects contribute to the long range order observed in the experimental colloidal crystal assembly of (Ln${\mathrm{F}}_3$) nanoplates (28). From this we conclude that the entropy of an entropic bond, as shown in Fig. 5, and its relative depth in the entropy landscape, rather than the size of the bond as shown in the Fig. 4, determines the self-assembled structure of hard hexagonal platelets.

Discussion

Motivated by a growing body of work (8–26) showing entropy-driven self-assembly of hard, anisotropic particles into crystals comprised of local geometric motifs with temporal stability, we investigated whether these stable motifs act as “bonds” in a similar sense to familiar chemical bonds. Surprisingly, our results show that even minimal, classical, single-component systems of hard hexagons exhibit behavior that resembles conventional bonding. The purely entropic systems we report on here show behaviors that resemble hydrogen bonding (3, 36), such as directionality and the ability to be broken by thermal fluctuations. Of course, the entropic bond is not a hydrogen bond, as entropic bonds are enforced by emergent free-energy barriers that change with density. Rather than resulting from the rearrangement of local electron density, these free-energy barriers result from the rearrangement of local entropy. The emergent nature of the entropic bond shares similarities with other traditional bonds (1), especially metallic bonds, where electron density is delocalized.

Our model system of hard, elongated hexagons illustrates general features of entropic bonding, including the contrast between bond strength and size, and how bonds can be manipulated, as well as providing insight into the mechanisms driving the stabilization of nanoplate assembly. Our results show that the entropic stabilization of hexagonal crystals of elongated hexagons derives from the relative free energy of an entropic bond, as well as the relative increase in free energy required to break an entropic bond. We observe that the shape of the nanoplates may be manipulated to alter both the size and strength of these entropic bonds. It has been shown that superlattice assembly can produce alternative motifs when enthalpic interactions dominate (Fig. 2A). Ref. 28 reported experiments and simulations of the self assembly of a herringbone lattice for nanoplates with excess enthalpic attraction between different edge types. Following ref. 28, we define an interaction bias $1+ϵ$ as the ratio of attraction between edges of opposite type to the attraction between edges of like type (detailed derivation in SI Appendix, Interaction Bias):

$$\left(1+ϵ\right)=\frac{\left(2\mathrm{\Delta }{S}_{\text{primary}}+2\mathrm{\Delta }{S}_{\text{hexagonal}}\right)}{4\mathrm{\Delta }{S}_{\text{herringbone}}}.$$

We can estimate the threshold value of $ϵ$ required to bias formation of the enthalpically driven, herringbone lattice over the entropically preferred hexagonal lattice by comparing the free-energy minima associated with the entropic bonds. Despite the fact this estimate ignores the collective nature of the entropic bond, we find reasonable agreement between $ϵ$ estimated from our purely entropic systems and the results from systems with enthalpic interactions reported in ref. 28 (see Fig. 6). This result agrees with what one would expect from an approximation of interparticle interactions in which the entropic and enthalpic effects were independent. While such a first-order approximation is indeed simplistic, the agreement in the required interaction bias between the 2 systems indicates that such analysis provides a starting point for assembly pathway engineering. Indeed, the success of this prediction supports our contention that entropic bonds are as useful a schema as traditional bonds, as does recent work showing that 2-body approximations are sufficient to capture relevant physical behavior (33). This comparison also provides a powerful approach for designing patchy colloids (37) with considerably less computational effort.

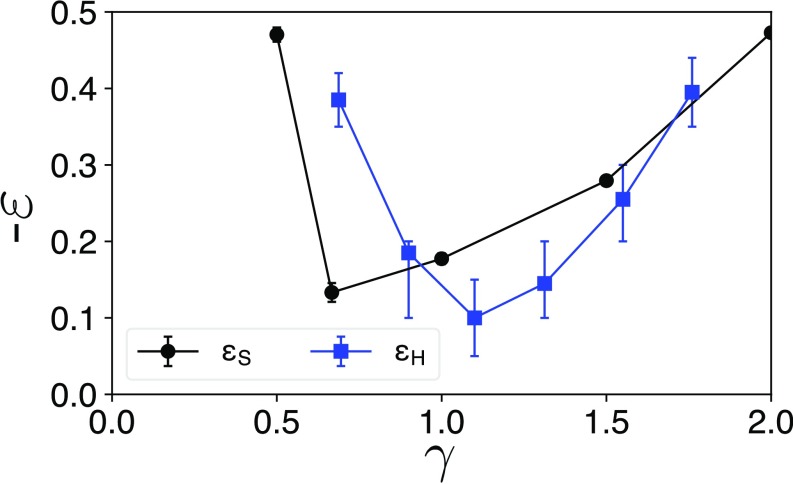
Fig. 6.

Comparison of the enthalpic interaction bias (28) ${\epsilon }_H$ and entropic interaction bias ${\epsilon }_S$ required to self-assemble an alternating/herringbone lattice. Because the simulations used to compute ${\epsilon }_H$ account for nanoplate shape, $\epsilon$ implicitly contains both entropic and enthalpic contributions. Thus, the difference in the biases results from the addition of enthalpic interactions as shown in ref. 28. The fact that $-\epsilon >0$ for all $\gamma$ indicates that the hexagonal lattice should self assemble for all $\gamma$, as observed in both this study and in ref. 28. The similarity in functional form and magnitude for both ${\epsilon }_H$ and ${\epsilon }_S$ indicate that manipulation of nanoplate shape alters entropic bonds, resulting in similar changes to the interaction bias as manipulation of the bias via chemical functionalization.

The systems we studied here were two dimensional, but previous demonstrations of the role of directional entropic forces in self-assembling 3D systems of hard polyhedra (10, 18, 21, 25, 26, 29, 38) provides further support to interpreting these forces in the language of bonds. Moreover, the existence of different classes of ordered structures (crystals, rotator crystals, liquid crystals, and quasicrystals) in hard particle systems suggests that entropic bond behavior and properties can vary widely by particle shape (14, 39). We hypothesize that further investigation to quantify, both spatially and temporally, bonding between neighboring polyhedra of varying shape will reveal entropic bonds with properties that mimic, albeit classically, the ionic, covalent, metallic (1), hydrogen (2), or mechanical (5) bond types that exist in other chemical systems.

Finally, supramolecular chemical descriptions have been previously applied to Janus (40) and depletion-mediated lock-and-key colloid interactions (41–44). The systems we studied here, and those studied in refs. 40–44, would—like most colloidal systems—typically be categorized as “nonbonded” interactions. Nevertheless, we found that the, ostensibly, nonbonded platelet systems we studied exhibit a form of bonding that could be extracted from considering effective interactions arising between platelets. We consider the form of bonding discussed here different not only from chemical bonds but also from nonbonded interactions considered in, e.g., proteins and clusters (37, 45–51). There, supramolecular objects reconfigure among different conformations via transition states that can also be described with disconnectivity graphs. However, such conformational changes are intramolecular. In the hard particle systems we studied here, bonding is defined intermolecularly. In this sense, the bonds we consider in our systems are much more aligned with chemical bonds.

If weak, entropic mediation can lead to unconventional forms of bonding under appropriate thermodynamic conditions, then there may exist thermodynamic conditions under which a much broader class of objects with other forms of mediation, including, e.g., depletion and van der Waals interactions, might also exhibit unconventional forms of bonding and, if so, may profit from supramolecular bonding descriptions like those used here and in related work (40–44).

Methods

We used the HOOMD-Blue (52–55) simulation package with the Hard Particle Monte Carlo (HPMC) (56) plugin to simulate systems of $N=\mathrm{4,096}$ hard nanoplatelets (see SI Appendix, Figs. S1 and S2 for example simulation trajectory snapshots). Hard, regular hexagons $\left(\alpha =120^{○};\gamma =1\right)$ (example simulation trajectory frames shown in SI Appendix, Figs. S1 and S2) were initialized on a lattice at the desired density $\varphi$ and were run in the NVT (canonical) ensemble. Hard elongated hexagons $\left(\alpha =68^{○};\gamma \right)$ were initialized on a lattice at $\varphi =0.2$, thermalized for $10^5$ MC sweeps at constant volume into a low-density fluid phase, and then run in the NPT (isothermal-isobaric) thermodynamic ensemble at the desired pressure. NPT moves allow the simulation box to shear as well as expand or contract. All systems of particles were equilibrated and then run for an additional $3\times 10^7$ MC sweeps for the purposes of computing the required quantities. To best capture the entropic forces that lead to the self assembly of the nanoplatelets, the PMFTs are computed in the highest pressure fluid observed. Reduced pressures decrease bonding strength, while increased pressures increase bonding strength.

Bond Identification.

We used automated image segmentation reliably identify the different entropic bonding states. Watershed image segmentation (57) is well-suited to this application because it assigns each pixel/voxel of an image to a region associated with an entropy maximum/free-energy minimum by “flooding” the entropy landscape starting at free-energy minima until these flooded regions meet, giving each pixel/voxel a unique label associated with a given minimum (see SI Appendix, Fig. S3 for an illustration of the watershed cut process on PMFTs of hard regular hexagons). Watershed image segmentation has the added benefit of providing information about the boundaries between bonds, allowing for identification of transition states between minima via network analysis techniques.

Bond Lifetime Distribution.

We calculated bond lifetime distributions from MC simulations. Bonded particle pairs were identified as above, and we tested every MC sweep for changes in bonding. MC moves were local and limited to $10\%$ of the move required to break a bond to approximate particle dynamics (30) and to prevent artificial bond breaking by unphysical moves. Four independent replicates were computed at each density. To appropriately account for both short timescale behavior and long timescale behavior, we use logarithmic histogram binning in Fig. 1.

Disconnectivity Graphs.

Topological analysis of the entropy landscape facilitates deeper understanding of the entropic bonds that form as a result of the emergent directional entropic forces present in the system. Disconnectivity graphs (58–61) are one way to analyze such landscapes, showing the connections between entropy maxima/free-energy minima and the associated transitions between metabasins.

Scientific Software

Figures in this work (main text and SI Appendix) were produced with Matplotlib, (62), Mayavi (63), and d3.js (64, 65). Data analysis was performed using Freud (66), NumPy, SciPy, SciKit-Image, and IPython (67–72).