How drag sharpens a T cell’s view on antigen

How about a Gedankenexperiment (German for thought experiment)? Let us consider a surface which is sticky, yet to an unknown degree. To determine stickiness we may do the following (experimental strategy 1): We place an object onto the surface, turn the surface upside down, and measure the time until the object detaches under its own weight. While strategy 1 has its merits, it also comes with 2 major drawbacks: First, the rupture process cannot be accelerated. If the bonds happen to be rather stable, detachment may take some time. Second, the information revealed by a single experiment is rather limited: By chance, rupture may happen immediately or may take considerable time. To arrive at a robust estimate of the mean time required for detachment, we would have to record the duration of many rupture processes.

Experimental strategy 2, a refined version of the first strategy, will certainly improve the situation: If we pull at constant velocity on the fixed surface, the pulling force increases with time, which narrows down the distribution of rupture times and neutralizes the 2 shortcomings inherent to strategy 1. First, experiments can be conducted in rapid succession, even when assaying strong bonds, since every bond will rupture as soon as force exceeds a certain threshold. Second, information gathered from a single pulling experiment is much increased in content, as this regimen renders the width of the rupture time distribution rather small. Strategy 2 is furthermore amenable to further refinements, such as implementing pulling speeds which increase over time or modulating the pulling velocity guided by the output of the previous attempt.

Of note, our Gedankenexperiment can be regarded as a macroscopic metaphor to molecular recognition processes taking place in the context of cell–cell contacts, as they occur for example during T cell antigen recognition (Fig. 1A). In fact, multiple experimental studies have indicated the presence of forces acting on the bond between the T cell antigen receptor (TCR) on the T cell surface and the major histocompatibility complex (MHC) molecule, which displays antigenic peptides for T cell recognition on the surface of antigen-presenting cells (APCs) (1–9). In analogy to our Gedankenexperiment, mechanical forces are considered to improve the fidelity of the T cell search for such peptides. At present it is quite a matter of heated debate, how such tensile forces affect bond lifetimes. Two rupture models are discussed in this context: Slip bonds, which dissociate preferentially under force, and catch bonds, which become more stable under force (10).

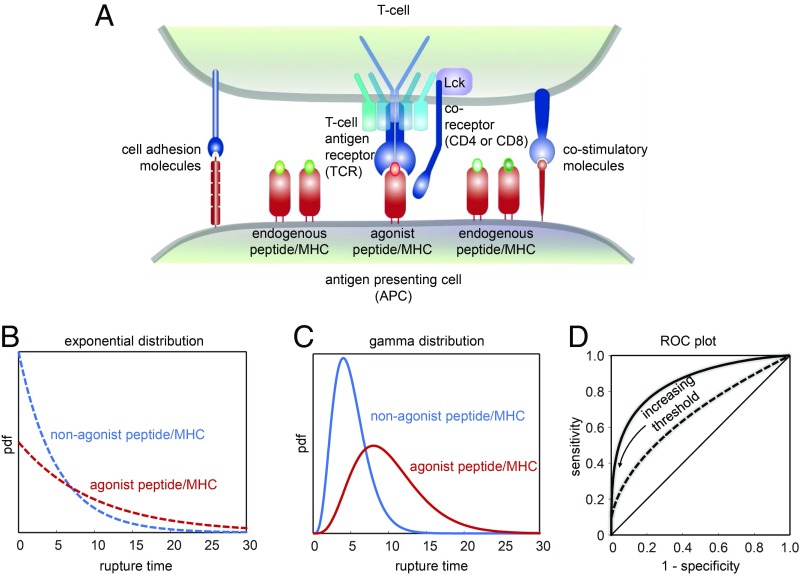
Fig. 1.

(A) Scheme outlining T cell antigen recognition in the context of the immunological synapse, the area of contact between a T cell and an APC. T cells manage to detect the presence of even a single agonist pMHC complex among highly abundant nonstimulatory but structurally similar endogenous pMHC complexes. Forces acting on TCR–pMHC bonds may help in discriminating between activating and nonactivating pMHC. Previously proposed catch bonds between TCR and activating ligands were not observed in the recent study by Limozin et al. (13), highlighting the importance of slip bonds for effective and sensitive detection of rare agonist ligands. Note the presence of coreceptors (tethered to Lck, an intracellular kinase interacting with the TCR upon ligand engagement), adhesion molecules, and costimulatory molecules within the immunological synapses with possible implications for TCR–pMHC engagement. (B–D) Classification according to rupture times. (B) Comparison of 2 exponential rupture time distributions with a mean of 5 (blue) and 10 (red). (C) Comparison of 2 gamma-distributed rupture time distributions with the same mean values as in B. (D) ROC plot for the exponential (dashed line) and the gamma-distributed (solid line) rupture time distribution under variation of the discrimination threshold. With increasing threshold, specificity increases at the expense of a decreasing sensitivity.

In previous studies, catch bonds were reported to characterize the nature of interactions between the TCR and the agonistic peptide carried by the MHC (pMHC), while non-agonistic pMHCs were described to feature slip-bond behavior (2, 11). Such results are compelling as they elegantly explain why TCR–pMHC bond lifetimes determined via surface plasmon resonance hardly correlate with the peptide’s stimulatory potency (12); after all, bond rupture times measured without force are generally different from those determined under load within the T cell–APC interface.

To this date, evidence for catch bonds has been primarily obtained from experiments employing biomembrane force probes, where T cells are brought in contact with pMHC-decorated beads for several hundred milliseconds (2, 3). It is, however, conceivable that T cells elicit an intracellular response to TCR engagement already during this contact time. It is therefore unclear whether the observed catch bonds caused T cell activation or had merely been the result of it. In a study published in PNAS (13), Limozin et al. develop an elegant cell-free assay to describe the behavior of single TCR–pMHC bonds under load: Beads decorated with TCR were moved over a pMHC-coated surface in a laminar flow chamber, giving thereby rise to a well-defined constant shear force on single-molecule bonds. The design of the flow chamber allowed for applying shear forces amounting to a few piconewtons. Surprisingly, of the 5 chosen agonistic pMHC combinations there was not a single one showing catch-bond behavior. These results can be taken as an indication that 1) catch bonds are not as universal for agonist pMHC–TCR interactions as proposed earlier and 2) previously observed catch bonds may be the consequence of cellular reorganization processes downstream of the actual TCR–pMHC binding event. Indeed, recent experiments suggested contributions of coreceptors and intracellular kinases to TCR–pMHC rupture kinetics by forming a trimolecular catch bond (14).

Limozin et al. (13) further juxtaposed the measured rupture times to EC₅₀ values measured in T cell activation assays. While they found only a weak correlation under force-free conditions, high correlation was observed under shear forces in the low piconewton regime. Correlations got worse at higher force regimes. It hence appears as if drags on the TCR between 5 and 10 pN promote the T cell’s capacity to specifically recognize antigen.

A striking feature of T cells is their ability to rapidly screen APCs for agonist pMHCs with exquisite sensitivity and selectivity. Only as few as 1 to 5 single MHC molecules on the APC surface may actually contain peptides of pathogenic origin; the vast majority of presented peptides stem in most cases from endogenous “self” proteins which have been processed by APCs along with foreign ones. Combining high sensitivity with high selectivity is, however, an exceedingly difficult task because high specificity typically comes with the trade-off of low sensitivity and vice versa.

Let us describe T cell antigen recognition in generic terms by a binary classifier system, which is based on an input variable, in our case the bond rupture time: An input surmounting a given threshold produces an activating response. Otherwise the binding is ignored. Important figures of merit for such classifiers are so-termed true and false positives, which arise when the rupture time for the agonistic or nonagonistic peptide happens to be larger than the threshold, respectively. The fidelity of such a binary classifier can be depicted with receiver operating characteristic (ROC) curves: In an ROC plot, the true-positive rate—also called sensitivity—is plotted versus the false-positive rate, which is 1 minus the specificity. If the classification lacks discriminative power, the curve follows the diagonal. With increasing discriminatory power, the curve shifts to the upper half of the plot. An ideal ROC plot consists of points in the top left corner only, i.e., indicating both high sensitivity and high specificity.

It turns out that an exponential distribution of rupture times, as is typically observed without force (Fig. 1B), performs rather poorly in an ROC plot (Fig. 1D, dashed line): In Fig. 1B we plotted as an example the attempt to discriminate via a threshold classifier 2 TCR–pMHC bonds with mean lifetimes differing by a factor of 2. While the specificity improves with increasing threshold in the ROC plot, sensitivity decreases dramatically.

There are, however, other statistical distributions, which show a substantially improved performance. A prominent example is featured by a gamma distribution (Fig. 1C). Indeed, the ROC plot shows now a pronounced bending toward the top left corner, indicative of a higher discriminative power (Fig. 1D, solid line). Of note, gamma-distributed activation kinetics of a T cell signaling protein were recently observed in a reconstituted signaling system (15). In general, gamma-distributed values constitute a good approximation of the sum of multiple exponentially distributed stochastic parameters, for example several rate-limiting steps in a signaling network, and could hence be regarded a consequence of kinetic proofreading in T cell activation (16).

Would tensile forces acting on the TCR–pMHC bond produce similar outcomes in the ROC plot? The answer depends on how the forces are exerted. Let us return to our Gedankenexperiment from the beginning. In experimental strategy 1 we considered the application of constant forces. At the molecular level, this approach would be analogous to a force clamp experiment. Under such conditions, the Bell model describes the unbinding kinetics well, which lead to exponentially distributed rupture forces (17): Hence there would be no major advantage over an experiment performed without force. In contrast, following experimental strategy 2., i.e., applying forces under constant velocity, affects the shape of the rupture time distribution (18), which resembles that of a gamma distribution (19). In other words, pulling or dragging at constant speed substantially improves the discriminative power of the antigen recognition process without any major penalty for sensitivity.

By placing slip bonds back into the spotlight, the study by Limozin et al. (13) adds important arguments to the ongoing discussion regarding the role of forces in T cell antigen recognition. Interestingly, experimental outcomes suggested a relevant force range between 5 pN and 10 pN, which is somewhat lower than was previously measured for the peak of typical TCR–pMHC catch bonds.

What now remains is a lot of work ahead of us: 1) How T cells and also APCs exert forces on single TCR–pMHC bonds, 2) whether (and how) such forces affect the signaling mechanisms underlying T cell recognition, and 3) whether (and how) coreceptors contribute to force-based antigen discrimination are truly relevant questions for future studies. Even partial answers will be invaluable for in-depth understanding of the T cell compartment in health and disease and thus hold many promises for the rational development of T cell-based therapies to combat cancer and autoimmunity. Yet also from a purely academic point of view, shedding light on these issues appears intellectually highly rewarding especially when comparing diverse physiological T cell scenarios ranging from T cell selection in the thymus to T cell effector phases executed by terminally differentiated T cells in the periphery. After all, context matters in biology more than in any other scientific discipline, from the level of the whole organism down to the level of individual molecules.