Disentangling the role of photosynthesis and stomatal conductance on rising forest water-use efficiency

Significance

Forests remove about 30% of anthropogenic CO₂ emissions through photosynthesis and return almost 40% of incident precipitation back to the atmosphere via transpiration. The trade-off between photosynthesis and transpiration through stomata, the water-use efficiency (WUE), is an important driver of plant evolution and ecosystem functioning, and has profound effects on climate. Using stable carbon and oxygen isotope ratios in tree rings, we found that WUE has increased by a magnitude consistent with estimates from atmospheric measurements and model predictions. Enhanced photosynthesis was widespread, while reductions in stomatal conductance were modest and restricted to moisture-limited forests. This result points to smaller reductions in transpiration in response to increasing atmospheric CO₂, with important implications for forest–climate interactions, which remain to be explored.

Abstract

Multiple lines of evidence suggest that plant water-use efficiency (WUE)—the ratio of carbon assimilation to water loss—has increased in recent decades. Although rising atmospheric CO₂ has been proposed as the principal cause, the underlying physiological mechanisms are still being debated, and implications for the global water cycle remain uncertain. Here, we addressed this gap using 30-y tree ring records of carbon and oxygen isotope measurements and basal area increment from 12 species in 8 North American mature temperate forests. Our goal was to separate the contributions of enhanced photosynthesis and reduced stomatal conductance to WUE trends and to assess consistency between multiple commonly used methods for estimating WUE. Our results show that tree ring-derived estimates of increases in WUE are consistent with estimates from atmospheric measurements and predictions based on an optimal balancing of carbon gains and water costs, but are lower than those based on ecosystem-scale flux observations. Although both physiological mechanisms contributed to rising WUE, enhanced photosynthesis was widespread, while reductions in stomatal conductance were modest and restricted to species that experienced moisture limitations. This finding challenges the hypothesis that rising WUE in forests is primarily the result of widespread, CO₂-induced reductions in stomatal conductance.

Plants assimilate carbon dioxide (CO₂) that moves through stomatal openings in foliage. This leads to unavoidable losses of water via transpiration and results in costs associated with accessing water, maintaining the transpiration stream, and repairing damage caused by drought (1–3). The trade-off between photosynthesis (A) and transpiration, reflected by water-use efficiency (WUE), is at the core of ecosystem functioning, underlying global-scale vegetation–climate interactions and the terrestrial water cycle.

Methods for estimating WUE differ in scale (individual leaf, plant, ecosystem) and in whether the abiotic influence of atmospheric evaporative demand is considered. Leaf WUE is defined as the ratio of A and transpiration. Transpiration is the product of stomatal conductance, g_s, and the difference in intercellular and atmospheric water-vapor pressure divided by the total atmospheric pressure, which is often presented as vapor pressure deficit (VPD) (4). Multiplying WUE by VPD yields the intrinsic WUE (iWUE = A/g_s), which is not sensitive to increased transpiration driven by abiotic changes in VPD, and thus is more closely coupled with plant ecophysiological function (4). The iWUE can be derived independently from the carbon isotope composition (δ¹³C) of plant material and that of atmospheric CO₂, whose difference reflects discrimination against ¹³C (Δ¹³C) occurring during diffusion of CO₂ through stomata and assimilation by photosynthesis. Intrinsic WUE is directly linked to the ratio of intercellular (c_i) to atmospheric (c_a) CO₂ (c_i/c_a) (4, 5). Ecosystem WUE is calculated as the ratio between gross primary production (GPP) and evapotranspiration (ET), both derived from eddy covariance (EC) flux measurements. An ecosystem-scale analog of iWUE, called the inherent WUE (WUEei), can be readily calculated as WUEei = GPP × VPD/ET (6). Others (7) have calculated the underlying WUE (uWUE = WUEei/√VPD = (GPP × √VPD)/ET), which incorporates information about stomatal closure at high VPD (typically assumed to be a function of 1/√VPD), and thus should be more closely coupled to changes in A.

Both global-scale atmospheric δ¹³C values (8) and tree ring δ¹³C chronologies (9–11) have revealed a trend of increasing iWUE in recent decades and suggest that c_i has increased in proportion with c_a, leading to a near-constant c_i/c_a ratio. This is indicative of an active plant response to increasing c_a, involving proportional changes in A and g_s (12). In contrast, ecosystem-scale EC data from 21 temperate forests suggest an even larger increase in WUEei and that c_i has remained constant (6). This result implies that g_s decreases strongly in response to rising c_a, and implementing this physiological response in a land surface model leads to larger reduction in ET and increase in runoff than large-scale observations show (13). Resolving these discrepancies in quantitative changes in WUE and explaining the underlying mechanisms is key to understanding and projecting vegetation responses and changes in the terrestrial water cycle under future c_a and climatic conditions.

Here, we used tree-ring α-cellulose δ¹³C and δ¹⁸O to document 30-y trends in iWUE, c_i, and g_s measured for 12 tree species (6 conifers and 6 broadleaves) at 8 forests within the AmeriFlux network, including 5 mesic and 3 xeric sites (Methods and SI Appendix, Fig. S1 and Table S1). We estimated changes in iWUE from δ¹³C and used δ¹⁸O to estimate the ¹⁸O enrichment in leaf water above the source water, Δ¹⁸O_LW. The latter reflects variability in transpiration and g_s only (14), as opposed to δ¹³C, which reflects changes in both A and g_s. We assessed trends in radial growth as a surrogate of photosynthetic carbon gain by computing the basal area increment (BAI) from tree-ring widths at all sites. Finally, we compared tree-ring isotope estimates of WUE (iWUE) with those obtained from EC data (WUEei) and with predictions of iWUE changes derived from a model that predicts an optimal c_i/c_a ratio, balancing carbon gain and water costs as a function of changing environmental conditions (2, 15).

Results

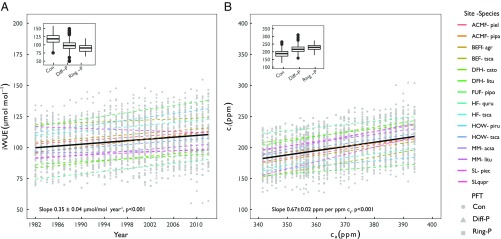
Tree-ring δ¹³C-derived iWUE significantly increased over the last 30 y, with a slope for the combined data set of 0.35 ± 0.04 μmol⋅mol⁻¹⋅y⁻¹ (P < 0.001) (Fig. 1A). Conifers showed higher iWUE values than broadleaf species (SI Appendix, Table S2), and within broadleaf species, ring porous species had lower iWUE than diffuse porous species (Fig. 1A). The trends in iWUE were positively associated with c_a, temperature, and VPD, and negatively associated with precipitation and soil moisture. One-half of the variance in the linear mixed-effects model, however, was explained by the variation in iWUE among species, and individual trees within each species (SI Appendix, Table S2). At the species level, iWUE increased through time for most species, except Pinus echinata at SL where iWUE decreased, and Acer saccharum at MM and Tsuga canadensis at BEF where no trend was detected (SI Appendix, Fig. S2 and Table S3). Relative changes in iWUE (2012 relative to 1982) ranged between −11.5% and 26.9% with an average of 13.8% (±8.6%) across all sites and species (SI Appendix, Fig. S3A).

Fig. 1.

Changes in intrinsic water-use efficiency and intercellular CO₂. Trend in intrinsic water-use efficiency (iWUE) (A) and in the intercellular CO₂ (c_i) in relation to changes in atmospheric CO₂ (c_a) (B) across the 12 species (n = 5 replicates per species) at 8 AmeriFlux sites in the United States. Insets show changes in iWUE and c_i for the different species grouped by plant functional type (PFT): coniferous (Con), diffuse porous (Diff-P), and ring porous (Ring-P) broadleaf species. The full name of each species is provided in SI Appendix, Table S1.

We observed a consistent increase in the relationship between c_i and c_a (slope, 0.67 ± 0.022 ppm⋅ppm⁻¹; P < 0.001; Fig. 1B and SI Appendix, Fig. S4 and Table S4) and in the c_i/c_a ratio over time across all 12 species, with conifers showing lower c_i/c_a ratios than broadleaf species (SI Appendix, Fig. S5 and Table S5). Similarly, carbon isotope discrimination (Δ¹³C_c) increased with increasing c_a by 0.008 ± 0.002‰ ppm⁻¹ of c_a (SI Appendix, Fig. S6 and Table S6), with higher sensitivity for conifers (slope, 0.009 ± 0.002 ppm⁻¹ of c_a) compared with ring porous broadleaves (slope, 0.002 ± 0.003‰ ppm⁻¹ of c_a).

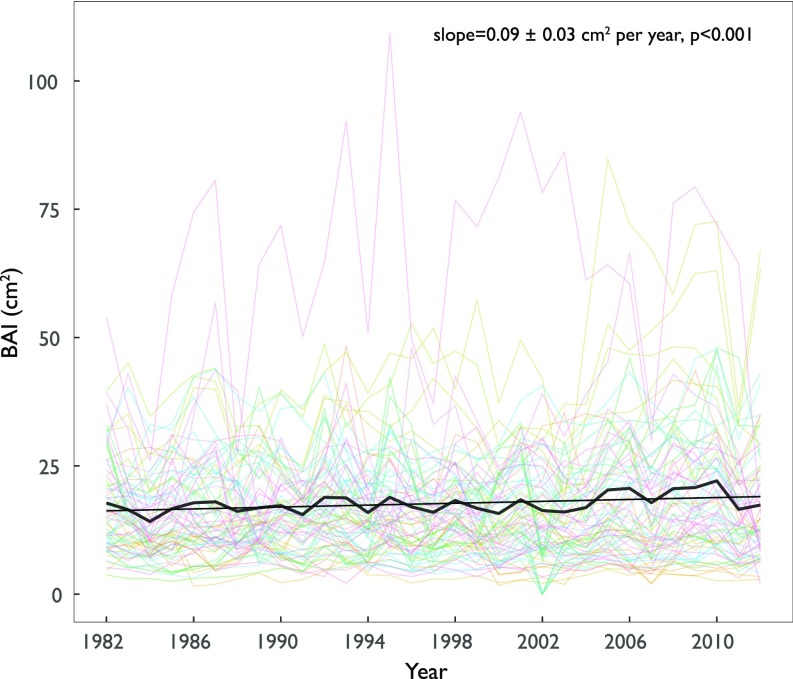
The trends in BAI and Δ¹⁸O_LW were used to constrain the contribution of A and g_s, respectively, in driving the observed changes in iWUE. On average, BAI increased over the last 30 y, with a slope for the combined dataset of 0.09 ± 0.03 cm²⋅y⁻¹ (P < 0.001) (Fig. 2), although the trend was not consistent over site–species combinations (Fig. 3A and SI Appendix, Figs. S7 and S8). Directionality of changes in Δ¹⁸O_LW obtained from measured tree-ring δ¹⁸O (Methods and SI Appendix, Supplementary Text and Fig. S9) revealed that the mechanisms responsible for increasing iWUE were influenced by differences across sites in moisture conditions (SI Appendix, Figs. S10–S12 and Table S1). For mesic sites, we observed no changes or a reduction in Δ¹⁸O_LW (Fig. 3B), indicative of constant or increasing g_s (Fig. 3C). BAI, however, increased or remained constant for the majority of the species, with the exception of Picea rubens and Acer saccharum, where it decreased (Fig. 3A). In contrast, at xeric sites, the Δ¹⁸O_LW showed a significant upward trend indicative of reduction in g_s (Fig. 3 B and C), which, however, negatively impacted tree growth only in the case of conifers (Fig. 3A).

Fig. 2.

Changes in basal area increment (BAI). Trend in BAI across the 12 species (n = 5 replicates per species) at 8 AmeriFlux sites in the United States.

Fig. 3.

Changes in BAI and Δ¹⁸O_LW, and physiological link between Δ¹⁸O_LW and g_s. Slopes (±SE) of the temporal changes in BAI (A) and Δ¹⁸O_LW (B) for the investigated species. Slopes significantly different from zero (SI Appendix, Table S7) are denoted with different colors, according to the P values. The black circle denotes sites where VPD increased. The vertical blue line separates mesic from xeric sites. C summarizes the physiological link between the Δ¹⁸O_LW and changes in transpiration (T) and g_s. The arrows indicate when the slope of Δ¹⁸O_LW was either greater than or less than zero.

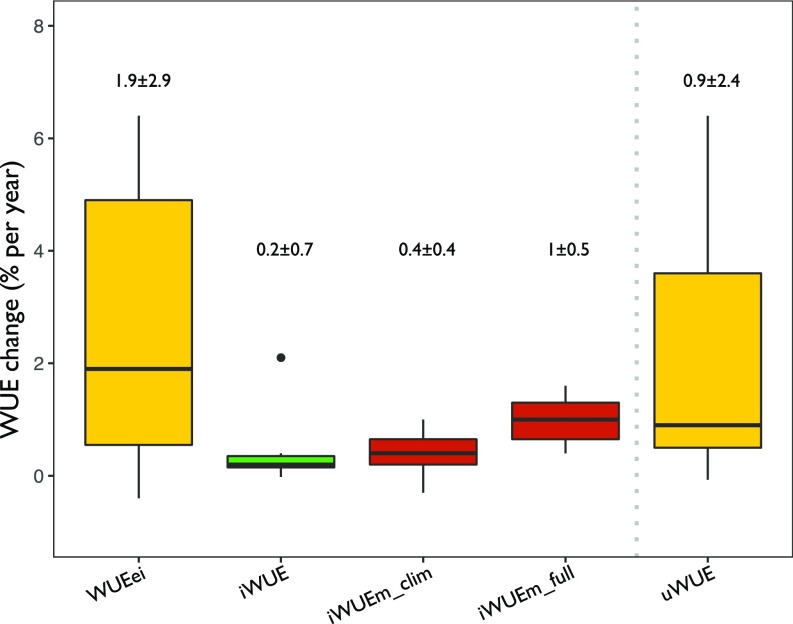
For the period of 1992–2012 (concurrent with EC measurements), tree-ring and model-derived estimates of iWUE agreed well, but EC-derived WUEei had steeper temporal trends. We observed a median Sen’s slope of 0.2 (±0.7)% y⁻¹ for the tree-ring derived iWUE, 0.4 (±0.4)% y⁻¹ for model prediction including only climate, and 1.0 (±0.5)% y⁻¹ including climate and CO₂ interactions. In contrast, WUEei from EC showed a significantly higher slope (P < 0.05) and higher variability among sites than the other 2 approaches, with a median Sen’s slope that was 9.5 times higher (1.9 ± 2.7% y⁻¹) than that obtained for iWUE (Fig. 4). Nonetheless, the EC-derived WUE trend fell within the range of model predictions, which included both climate and CO₂ effects (Fig. 4).

Fig. 4.

Comparing tree-ring δ¹³C and EC-based estimates of WUE and prediction from the carbon–water optimality model. Distribution of Sen’s slopes of year-by-year percentage changes in WUE (percentage per year) relative to the first year flux data were available at each site and obtained by considering 3 different methods: ecosystem fluxes (WUEei and uWUE), tree-ring δ¹³C (iWUE), and prediction from the carbon–water optimality model (16). In this latter case, we show predictions when only climate (iWUEm_Clim) and both climate and CO₂ effects were included (iWUEm_full). Numbers above each boxplot indicate the median ± SD.

Discussion

Tree-ring isotope chronologies presented in this study fill the knowledge gap for underrepresented species (SI Appendix, Fig. S1 and ref. 16) in the highly productive forests of the Eastern United States. Changes in iWUE observed in our study are similar in magnitude to those reported for other temperate forests in the northern hemisphere (9–11) (SI Appendix, Fig. S3) and to those derived from the global estimate of a 20% increase over the 20th century inferred from atmospheric δ¹³C-CO₂ observations (8). An increase in iWUE has been mostly associated with a proportional adjustment of A and g_s to the increase in c_a, which leads to an increase in c_i (but at a slower rate than c_a), and a constant c_i/c_a ratio (12). Our results show that, for every ppm of c_a over the last 30 y, c_i increased by 0.67 ± 0.022 ppm, consistent with rates reported for a large scale study in Europe (11), however inconsistent with EC observations (6) showing a constant c_i for the 1992–2010 period (SI Appendix, Fig. S13). Moreover, we also found that the increase in iWUE was not achieved—at least not for all of the species—by a proportional adjustment of A and g_s (12). Instead, it reflects a dynamic leaf gas exchange response to c_a and climate (17), with increase in A, and small changes in g_s modulated by differences in moisture conditions among sites.

The increase in c_i across all of the species could partially indicate a CO₂ fertilization effect on A. This is consistent with the dependence of A on c_i as described by the model for C3 plant photosynthesis (18). Moreover, results from free-air CO₂ experiments (FACEs) (19) and independent global measurements (8) based on atmospheric δ¹³C-CO₂ supported an increase in A with rising c_a. Lower c_i values observed for conifers compared with broadleaves could be related to either differences in g_s and mesophyll conductance (20) or in foliar nitrogen concentration (SI Appendix, Fig. S14), the latter being an important determinant of photosynthetic capacity (19). Nevertheless, enhanced A and iWUE in response to c_a contribute to maintaining or increasing tree growth for the majority of the species.

Exposing trees to almost 700 ppm of c_a increased iWUE (FACEs, SI Appendix, Fig. S3B) by enhancing A but also reducing g_s. However, this latter result was not consistent across all of the experiments and studied species (19, 21), and still “the mechanism by which the stomata sense [CO₂], and where in the leaf [CO₂] is sensed, is unclear” (22). If a reduction in g_s under increasing c_a occurs across all of the investigated species, this should be reflected in a reduction in leaf transpiration, which in turn leads to less dilution of the enriched (in the heavy isotope ¹⁸O) water at the evaporative site by the unenriched water coming from the soil via xylem, thus increasing the Δ¹⁸O_LW (14, 23) (Fig. 3C). However, Δ¹⁸O_LW trends show differences among species, which are mostly related to differences among sites in moisture conditions. For all of the species in mesic forests, g_s remained constant or increased over the last 30 y (as indicated by the reduction in Δ¹⁸O_LW), even when VPD increased (at HF and SL). This finding suggests that favorable soil moisture conditions can reduce the value of water lost so that g_s remains high and that, for species that do not routinely experience water stress, increasing A to maintain and/or increase tree growth is a more beneficial response to rising c_a than conserving water. A reduction in g_s (as inferred by the significant increase in Δ¹⁸O_LW) was observed only for species experiencing more xeric condition since the 1990s and an increase in VPD. Interestingly, in this latter case, we only observed a reduction in BAI for conifers, while tree growth for broadleaf species increased. Conifers in general show a more sensitive response of g_s and A to VPD than broadleaf species, likely due to a narrower hydraulic safety margin (24, 25). The difference between mesic and xeric sites for changes in g_s was not captured by the carbon–water optimality model, as it predicted a reduction of g_s at all sites (SI Appendix, Fig. S15), while observations show reduction only at the xeric sites. Other factors could have affected g_s in the studied species, such as reduced sensitivity of g_s to the increase in c_a in older trees (26), and structural changes of plant hydraulic architecture allowing the water to move through the soil–atmosphere continuum (27). It is often overlooked when working at the ecosystem scale, but known since pioneering studies from Francis Darwin (28), that stomata aperture is ultimately a mechanical process associated with changes in turgor and osmotic pressure in the guard and the epidermal cells (29, 30), supported by the efficiency of the hydraulic system in transporting water (3, 31). Indeed, results from a FACE experiment at one of our sites (DFH) showed that the reduction in g_s was not a direct response to c_a, but to the whole-plant hydraulic conductance (27). Changes in leaf area index (LAI) can also play a role, although none of the sites in our study showed evidence of temporal trends in LAI (SI Appendix, Fig. S16).

Both tree and ecosystem WUE increased over the investigated years, although with different magnitudes. Our tree-ring results, on one hand, suggest a more modest increase in iWUE compared with a previous EC-based synthesis (6) and the EC analyses in this study. Some of the explanations for the discrepancies between the two approaches could be related to the different timescales they represent (32, 33), or to uncertainties in estimating canopy ET (i.e., nontranspirational water fluxes and/or contribution from understory vegetation ET) (34) and GPP and respiration from ecosystem CO₂ fluxes. Two recent studies showed that current methods used for partitioning CO₂ fluxes do not account for the light-dependent reduction in respiration, leading to an overestimation of GPP (35, 36), and consequently WUE. Our results based on Δ¹⁸O_LW, on the other hand, do not support a general reduction of g_s in recent decades, except when low moisture limits forest productivity. This finding calls into question the notion that rising c_a reduces g_s and hence transpiration, at least for mesic ecosystems in the northeastern United States, where, indeed, no significant changes in ET were observed (SI Appendix, Fig. S17). FACE experiments reported reduced transpiration (as assessed through sapflow measurements) under increasing c_a (37), but no significant changes in sap flux were also observed (38, 39). This points to smaller reductions in transpiration in response to climate change than previously thought, with important implications for forest–climate interactions (40), which will require additional research to resolve. Moreover, the assumption that different tree species follow the same physiological strategy in response to increasing c_a, regardless of the moisture conditions they experience, and that this strategy remains static over time, is probably too simplistic. Whether it is A and/or g_s driving increasing WUE depends on a dynamic coordination of functional traits (1–3) and their adjustment to environmental changes. Implementing such a dynamic response challenges the ability of large-scale vegetation models to predict how g_s will continue to optimize water loss relative to carbon gain under future CO₂ emission scenarios.

Methods

Sites and Environmental Parameters.

Eight forested sites within the AmeriFlux network were selected to represent major temperate forest types for the United States and to span a range of biological properties (32, 41) and climate conditions (SI Appendix, Fig. S1 and Table S1). Mesic and xeric sites were identified based on the long-term changes in precipitation (P), i.e., 1991–2012 compared with 1901–1960 average. Wetter conditions were reported since the 1990s for the sites in the Northeast and the Midwest, whereas precipitation decreased in the case of the three sites in the Southeast and Southwest (42). For the long-term temperature and P data, we referred to available data at meteorological stations near the study sites, obtained from the Global Historical Climatology Network. Growing season (May to September) and annual mean for both temperature and P were calculated from monthly values and indicated along the text as T_grs and P_grs and T_a and P_a. VPD was calculated from actual vapor pressure and T (43) from CRU TS 3.23, with data extracted at site locations. Finally, we obtained the standardized precipitation–evaporation index (SPEI), relative to August, with 3-mo lag from the global database (http://sac.csic.es/spei/).

Measure of Carbon and Oxygen Isotope Ratios in Tree Rings.

Wood cores were collected from 10 to 15 trees for each of the dominant and codominant tree species at each site and constructed stable isotope chronologies for the last 30 y (1982–2012). All of the wood cores were dated from the bark to the pith. Ring width measurements were carried out with a sliding scale micrometer (Velmex Measuring System) using MeasureJ2X software (VoorTech Consulting). Ring width series were cross-dated from 1960 to 2012 first within each tree, then among trees, and finally between species within a site by using the COFECHA software (44). For stable isotope analyses, only the 5 trees showing the highest correlation with the mean chronology were selected. BAI was calculated for each tree by following the “outside-in” function to convert raw ring-width measurements to BAI based on the diameter of the tree and the width of each ring moving toward the pith. The method assumes a circular growth pattern. A mean BAI value was computed for each tree species at an annual resolution averaged over 2–3 wood cores sampled per tree. For HF, we used BAI used in ref. 45, and updated to 2012. From each of the 5 trees (n = 2 wood cores per tree), each annual ring from 1982 to 2012 was separated and then shredded by using a razor blade. For the two Quercus species only the latewood was separated, as it better reflects the contribution of sugars from the current year’s photosynthetic activity (45, 46). Wood from each ring was subjected to α-cellulose extraction (47, 48), and then homogenized by using an ultrasonic bath. About 0.3 ± 0.1 mg of each ring sample was weighed in tin capsules and converted to CO₂ with an elemental analyzer (ECS 4010; Costech Analytical) coupled to a continuous flow isotope ratio mass spectrometer (Delta PlusXP; ThermoFinnigan) to determine δ¹³C. An additional 0.3 ± 0.1 mg of each sample was weighed in silver capsules, converted to CO with a pyrolysis elemental analyzer (TC/EA; ThermoFinnigan), and analyzed for δ¹⁸O with a continuous flow isotope ratio mass spectrometer (Delta PlusXP; ThermoFinnigan). Carbon and oxygen isotope ratios were expressed in per mil (‰) relative to the Vienna PDB and Vienna SMOW international standards, respectively. Isotope analyses were carried out at the Stable Isotope Core Laboratory (Washington State University). The SDs for internal standards were less than 0.2‰ and 0.4‰ for δ¹³C and δ¹⁸O values, respectively, whereas SDs for Sigma-Aldrich α-cellulose (item C8002, lot 031M0133V) were less than 0.2‰ and 0.6‰ for δ¹³C and δ¹⁸O values, respectively. Finally, mean SDs across replicates on given years and assessed for each species were 0.2‰ and 0.3‰ for δ¹³C and δ¹⁸O values, respectively.

Calculation of Tree WUE.

We derived iWUE from δ¹³C measured in tree ring α-cellulose (49) based on the well-established theory linking leaf c_i/c_a with isotopic carbon discrimination, Δ¹³C_c (5):

$${\mathrm{\Delta }}^{13}{\mathrm{C}}_{\mathrm{c}}=a+\left(b-a\right)\hspace{0.17em}\frac{c_{\mathrm{i}}}{c_{\mathrm{a}}}=\hspace{0.17em}\frac{\left({\mathrm{\delta }}^{13}{\mathrm{C}}_{\mathrm{a}}-\hspace{0.17em}{\mathrm{\delta }}^{13}{\mathrm{C}}_{\mathrm{c}}\right)}{\left(1+\frac{{\mathrm{\delta }}^{13}{\mathrm{C}}_{\mathrm{c}}}{\mathrm{1,000}}\right)}.$$ [1]

δ¹³C_c and δ¹³C_a are the carbon isotope compositions of tree ring α-cellulose and c_a, a is the isotope fractionation during CO₂ diffusion through stomata (4.4‰), and b is the isotope fractionation during fixation by Rubisco (27‰). Note that Eq. 1 is the “simple” form of isotopic discrimination that does not include effects due to mesophyll conductance and photorespiration, which were not available for the species here. We derived c_i from the following equation:

$$c_{\mathrm{i}}=c_{\mathrm{a}}\hspace{0.17em}\frac{{\mathrm{\delta }}^{13}{\mathrm{C}}_{\mathrm{a}}-\hspace{0.17em}{\mathrm{\delta }}^{13}{\mathrm{C}}_{\mathrm{c}}-a}{b-a}.$$ [2]

c_a and δ¹³C were obtained from Mauna Loa records (50) from 1990 to 2012, while from 1990 back to 1982 we used data published in ref. 51. iWUE (in micromoles of CO₂ per mole of H₂O) was then calculated using the following equation:

$$iWUE=\frac{A}{g_{\mathrm{s}}}=\frac{c_{\mathrm{a}}-c_{\mathrm{i}}}{1.6}=\frac{c_{\mathrm{a}}}{1.6}\left(\frac{b-{\mathrm{\Delta }}^{13}{\mathrm{C}}_{\mathrm{c}}}{b-a}\right),$$ [3]

where 1.6 is the molar diffusivity ratio of CO₂ to H₂O (i.e., g_CO2 = g_H2O/1.6). The iWUE as derived from Eq. 4 is normalized by a constant VPD of 1 mol⋅mol⁻¹. Intrinsic WUE was converted from micromoles of CO₂ per mole of H₂O at VPD of 1 mol mol⁻¹ to grams of C/kilogram of H₂O normalized at VPD of 1 kPa to better compare the leaf and ecosystem WUE. The conversion factor from micromole/mole at VPD of 1 mol mol⁻¹ to grams of C/kilogram of H₂O at 1 kPa is 12/18*100/1,000.

Calculation of Δ¹⁸O_c and Δ¹⁸O in Leaf Water (Δ¹⁸O_LW).

We calculated the ¹⁸O enrichment in tree-ring α-cellulose above the source water, Δ¹⁸O_c, according to the following equation (52):

$${\mathrm{\Delta }}^{18}{\mathrm{O}}_{\mathrm{c}}=\frac{\left({\mathrm{\delta }}^{18}{\mathrm{O}}_{\mathrm{c}}-{\mathrm{\delta }}^{18}{\mathrm{O}}_{\mathrm{P}}\right)}{1+\left(\frac{{\mathrm{\delta }}^{18}{\mathrm{O}}_{\mathrm{P}}}{\mathrm{1,000}}\right)},$$ [4]

where δ¹⁸O_c is the oxygen isotope composition measured in α-cellulose extracted from each ring, while δ¹⁸O_P is the δ¹⁸O of precipitation, which we estimated as described in SI Appendix (SI Appendix, Supplementary Text and Fig. S18). We assume δ¹⁸O_P to be reflected in the oxygen isotope composition of the soil water (i.e., source water), modified by evaporation (53). We also assume that the tree species at each site had access to water at similar soil depth, so that there are no differences in the δ¹⁸O of the source water over the long term. From Δ¹⁸O_c, we then estimated Δ¹⁸O_LW, which is directly linked to transpiration and g_s. Notably, less enriched (in ¹⁸O) water from the soil and more enriched (in ¹⁸O) water at the leaf evaporative sites continuously mix, as a function of transpiration rates and the pathway of water movement through foliar tissues (54, 55) so that lower Δ¹⁸O_LW results from an increase in transpiration and g_s (56). The Δ¹⁸O_c can be described by the following equation (57):

$${\mathrm{\Delta }}^{18}{\mathrm{O}}_{\mathrm{c}}={\mathrm{\Delta }}^{18}{\mathrm{O}}_{\mathrm{LW}}\left(1-p_{\mathrm{x}}{p}_{\mathrm{ex}}\right)+{\epsilon }_{\mathrm{wc}},$$ [5]

where p_ex is the proportion of oxygen exchanging with local water in the stem during cellulose synthesis, p_x is the proportional amount of stem water relative to both leaf and stem water in the tissue where cellulose is synthesized, and finally ε_wc is the isotope fractionation occurring during cellulose synthesis in the stem. Eq. 5 can be rearranged so to derive Δ¹⁸O_LW as follows:

$${\mathrm{\Delta }}^{18}{\mathrm{O}}_{\mathrm{LW}}=\left(\frac{{\mathrm{\Delta }}^{18}{\mathrm{O}}_{\mathrm{c}}-{\epsilon }_{\mathrm{wc}}}{1-p_{\mathrm{x}}{p}_{\mathrm{ex}}}\right).$$ [6]

Generally, a fixed value of 27‰ and 0.4 are considered for ε_wc and p_xp_ex, respectively. We estimated dampening factors diluting the signal of leaf water δ¹⁸O when sugars are translocated to the stem and used for synthesis of cellulose. Specifically, we derived p_xp_ex from P_a and P_grs (52). Moreover, we also assume a variable ε_wc, which was derived from T_grs, based on the equation in ref. 57, showing the dependence of the fractionation factor on temperature.

Flux Data.

We compiled flux and micrometeorological observations from 7 out of the 8 AmeriFlux sites where we sampled wood cores from the dominant species (SI Appendix, Tables S1 and S8). Duke forest was not included because data were not available. Data were acquired from the AmeriFlux data archive, the Fluxnet database, or site PI. In this latter case, gap-filling and partitioning of carbon fluxes were performed by the site PIs. Net carbon fluxes were partitioned into GPP and total ecosystem respiration (R_eco) by using the temperature sensitivity of respiration to then extrapolate night to daytime R_eco (58). We calculated ET from the latent heat flux. Half-hourly data were aggregated to daily values for the calculation of the growing season (grs) (May to September) GPP (grams of C⋅meter⁻²⋅grs⁻¹) and ET (kilograms of H₂O⋅meter⁻²⋅grs⁻¹). We only considered GPP and ET obtained during dry canopy conditions (i.e., with no precipitation event) to avoid error introduced from canopy evaporation after precipitation events (6). We calculated inherent (6, 59) and underlying WUE (7) as described in the main text and by using mean of VPD over the grs months.

Estimates of iWUE from the Water–Carbon Optimality Model.

The model predicts an optimal c_i/c_a ratio that balances carbon gains and water costs and maximizes leaf-level A minus costs. The water–carbon trade-off is governed by the costs arising from the maintenance of carboxylation capacity (V_cmax) and the transpiration stream as a function of g_s. The model is based on the Farquhar–von Caemmerer–Berry model for C3 photosynthesis (18), the coordination hypothesis assuming that A operates at the intersection of the light and Rubisco-limited assimilation rates during typical daytime conditions (60), and the least-cost hypothesis assuming an optimal balance of carbon costs as functions of V_cmax and g_s (1, 2). Thus, it simulates how photosynthetic parameters (c_i, g_s, V_cmax, and J_max) and rates (A, light use efficiency) acclimate to environmental conditions (CO₂, T, radiation, VPD, and atmospheric pressure). A complete derivation and description of the model is given in ref. 16. Forcing data used for simulations presented here are annually varying c_a, daily mean T, and specific humidity (WATCH-WFDEI) (61), converted to VPD as a function of T and elevation.

Statistical Analyses.

We used R Studio (62) and specific packages for statistical analyses. Linear regressions were employed to explore trends in iWUE, c_i, c_i/c_a, Δ¹³C, and BAI. Linear mixed models (63) were employed to explain temporal changes in iWUE, c_i, c_i/c_a, and Δ¹³C as a function of environmental factor and c_a (fixed factors). Multiple species (and replicates per species) nested in the sites were included as the random factor. Each of the numerical fixed factors was centered to the mean to remove multicollinearity. An autocorrelation structure of order 1 was included in the model for each site per species combination to allow for the temporal dependency of measurements carried out in subsequent years. Quality of fit was assessed using residual distribution plots, qqnorm plots of standardized residuals against quantiles of standard normals for both individual points and for the random effects. Marginal (only fixed factors) and conditional (fixed plus random factors) proportions of the explained variance (R²_m and R²_c, respectively) were calculated (64). For the comparison among EC-derived, tree-ring isotope, and predicted WUE, we first calculated the year-by-year percentage changes in WUE relative to the beginning of the EC data record. Then we used the Mann–Kendall Tau nonparametric trend test with Sen’s method to obtain slopes of trend in WUE for the different sites (6). Finally, differences in the slope for WUE among the different methods were assessed by the nonparametric Kruskal–Wallis and post hoc Dunn tests.