Abstract
This paper proposes an effective method for accurately recovering vessel structures and intensity information from the X-ray coronary angiography (XCA) images of moving organs or tissues. Specifically, a global logarithm transformation of XCA images is implemented to fit the X-ray attenuation sum model of vessel/background layers into a low-rank, sparse decomposition model for vessel/background separation. The contrast-filled vessel structures are extracted by distinguishing the vessels from the low-rank backgrounds by using a robust principal component analysis and by constructing a vessel mask via Radon-like feature filtering plus spatially adaptive thresholding. Subsequently, the low-rankness and inter-frame spatio-temporal connectivity in the complex and noisy backgrounds are used to recover the vessel-masked background regions using tensor completion of all other background regions, while the twist tensor nuclear norm is minimized to complete the background layers. Finally, the method is able to accurately extract vessels’ intensities from the noisy XCA data by subtracting the completed background layers from the overall XCA images. We evaluated the vessel visibility of resulting images on real X-ray angiography data and evaluated the accuracy of vessel intensity recovery on synthetic data. Experiment results show the superiority of the proposed method over the state-of-the-art methods.
Keywords: X-ray coronary angiography, Tensor completion, Robust principal component analysis, Vessel segmentation, Layer separation, Vessel enhancement, Vessel recovery
1. Introduction
1.1. Motivation
Cardiovascular diseases are the leading cause of death in the world [1]. Minimally invasive vascular interventions, such as percutaneous coronary intervention and robot-assisted coronary intervention [2], have been routinely applied into the clinic. During these interventions, contrast-filled vessels are imaged by X-ray coronary angiography (XCA) to help surgeons navigate the catheters. Apart from interventional guidance, XCA images are also important references for coronary disease diagnosis and therapeutic evaluation [3–5]. It is important to extract contrast-filled vessels from X-ray coronary angiography (XCA) data for the diagnosis and intervention of cardiovascular diseases [6,7].
Robust subspace learning via decomposition into low-rank plus additive matrices, an important topic in machine learning and computer vision, has been applied to medical imaging application [8]. Based on the fact that an image sequence is often modeled as a sum of low-rank and sparse components in some transform domains, robust principal component analysis (RPCA) has been widely exploited to recover low-rank data (or separate sparse outlier) from the corrupted or undersampled noisy data in biomedical imaging [9–11].
However, the visibility of vessels in XCA images is poor even though the contrast agents in X-ray imaging significantly enhance the angiography images. This is because that the XCA image is a display of the X-ray attenuation sum along the projection path, the projection image contains various anatomical structures, including not only vessels but also bones, diaphragms, and lungs. These structures represent complex background structures, motion disturbances, and noises in XCA images. Because the contrast-filled vessels have different motion patterns for the contrast-filled vessels and background structures, they include the vessel layer or foreground layer, whereas all other structures are called background layer. Due to the complex dynamic structures, the background layer seriously disturbs the observation and measurement of vessels. To facilitate the diagnosis and treatment of cardiovascular diseases, automatical extraction of the vessel layer and effective removal of the nonvascular background layer has become a prerequisite to improve the visibility and detection of vessels for various clinical applications, such as 3D reconstruction of coronary arteries [12], 3D/2D image coronary registration [13], coronary artery labeling [14], heart’s dynamic information extraction [15], and myocardial perfusion measurement [4,5,16]. In addition, vessel extraction is usually used as a preprocessing step to remove noises and complex backgrounds from XCA images while emphasizing vessel-like structures for most sophisticated pipeline algorithms including vessel segmentation and vessel centerline extraction.
Currently, most vessel extraction methods mainly focus on removing background noises and improving the saliency of vessels. While vessel structures can be highlighted, the vessel intensity information in the images is neglected and lost after the processing steps with previous methods. A more accurate vessel layer extraction with structure and intensity recovery will definitely facilitate further quantitative analysis of XCA images. Therefore, the purpose of this work is to accurately extract vessel layers with reliable recovery of the structure and intensity information from the original XCA sequences.
1.2. Related works
Most vessel analysis techniques can be classified into three categories: vessel segmentation, vessel centerline extraction and vessel enhancement (or vessel extraction). Vessel segmentation is a fundamental step of many biomedical applications. A vessel/non-vessel pixel classifier or the vessel outline is defined by vessel segmentation. Various segmentation approaches have been developed in the past years, including filter-based methods, tracking-based methods, active contour methods, graph-based methods [17], convolutional neural networks [18], and etc. The surveys in [19,20] give the detailed description and summary. The extraction of vascular networks based on vessel centerlines is also essential for many applications. The centerline extraction methods include direct tracking methods, model-based methods, minimal-path techniques, artificial neural networks (ANN) and etc [21]. Vessel enhancement aims at emphasizing the vessel intensities while suppressing the background intensities, and usually serves as a preprocessing step of vessel segmentation and centerline extraction. This work mainly falls into the vessel enhancement category.
Currently, there are generally two classes of vessel enhancement methods for XCA images: filter-based methods and layer separation methods. The filter-based method convolves different kernels with images and presents vessels with the filter responses. For example, the matched filter detection method was first proposed by Chaudhuri et al. [22]. In this method, the authors construct 12 different Gaussian shaped templates to search the vessel segments along different directions. Generally, vesselness filters widely use image derivatives to encode border (first order) and shape (second order) information about vessel structures. For example, a large class of filters [23,24] utilize the Hessian matrix at various scales, which is based on second derivative. Being different from the Hessian-based filters, a filter based on Radon-like features (RLF) is proposed by aggregating the desired information derived from an image within structural units (e.g. edges) [25]. This RLF filter has been applied to the vessel segmentation in coronary angiograms and achieved satisfying performances [26,27]. Though these filter-based methods highlight vascular structures and suppress noises, they can distort the intensities of vessels.
Layer separation is another class of vessel enhancement methods. The approach considers the image as the sum of several layers, and thus tries to separate these layers. Because the final aim of layer separation for XCA images is to extract the vessel layer, we also call the layer separation processing as vessel layer extraction in this paper. Generally, layer separation methods process a sequence of similar images, e.g. a video. These separation methods can be further categorized into two groups: motion-based and motion-free [7]. Motion-based methods separate different layers by estimating the motions of every layer according to various motion assumptions. For example, Zhang et al. separated different transparent layers in XCA sequences by constructing a dense motion field [28]. Zhu et al. have proposed a dynamic layer separation method under a Bayesian framework that combines dense motion estimation, uncertainty propagation and statistical fusion [29]. Preston et al. jointly estimated different layers and their corresponding deformations for image decomposition [30].
Unlike motion based methods, motion-free methods separate the different layers under certain hypotheses without motion estimation. For example, Tang et al. [31] separated vessel and background signals from XCA images by implementing independent component analysis. This vessel extraction method needs to subtract a pre-contrast mask image from later contrast images. Therefore, the registration of the mask and contrast images is required to reduce the motion artifact before subtraction. However, due to the complex and dynamic backgrounds producing outliers [32,33] in the two images, the efficiency of this registration-based vessel extraction method is largely limited by the structure matching accuracy in the challenging image registration with outliers [34–36]. Recently, various low-dimensional representation learning techniques have been developed for the feature analysis of video data [37,38]. Specifically, assuming that the complex background layer is a low-rank matrix whereas the moving foreground layer is sparse, RPCA with low-rank and sparse decomposition [39] has been widely exploited to separate the moving foregrounds from the backgrounds. For example, Ma et al. have combined RPCA with morphological filtering to significantly increase the visibility of contrast-filled vessels [40] and have also developed a fast online layer separation approach for real-time surgical guidance [7]. Jin et al. [6] have proposed a motion coherency regularized RPCA (MCR-RPCA) for contrast-filled vessel extraction by incorporating the spatio-temporal contiguity of vessels based on the total variation (TV) norm [41]. In recent work [42], the MCR-RPCA method [6] was compared with the state-of-the-art methods and proven to perform best with the clearest vessel detection and almost no background information. However, these RPCA-based methods via image vectorization for 2D matrix-based image sequence computation cannot naturally preserve high-dimensional imaging sensor’s spatial and time information simultaneously.
Being similar to RPCA, another two classes of low-rank based algorithms called matrix and tensor completion, which aim to recover a low-rank matrix and tensor from noisy partial observations of its entries, have much progress in recent years [8]. Different from RPCA, these data completion methods can be interpreted as a data-driven learning problem since the unknown missing pixels are inferred from the known pixels in the spatial and/or temporal contexts. Though the optimization models for matrix completion are quite clear, data completion for tensors is complicated. Tensors refer to multi-dimensional arrays, which can naturally reserve more spatio-temporal information than do matrices [43]. Based on different definitions of tensor ranks, e.g. CP rank [44,45] and Tucker rank [46], many different tensor completion models have been proposed. Typically, tensor nuclear norm (TNN) [47], which is designed for 3D tensors based on tensor Singular Value Decomposition (t-SVD) [48,49], has been verified effective for 3D tensor completion [50,51]. Hu et al. have further optimized the TNN model for the video completion task by integrating a twist operation [52].
1.3. Overview and contributions
Existing layer separation works share a similar global strategy for layer modeling, i.e., these methods treat an XCA image as a whole, and aim to directly separate layers from all the pixels. Under this strategy, the intensity of every pixel in an XCA image has a potential to be split up into several parts. As a result, local interaction of different layers will affect the global separation. Specifically, popular RPCA methods have the following three main limitations for foreground/background separation in XCA images. First, vectorizing the XCA video sequence into a matrix makes the RPCA model ignore the 3D spatio-temporal information between the consecutive frames of the XCA sequence. For example, X-ray imaging produces a lot of dense noisy artifacts, whose positions change in a gradually moving pattern in the XCA frames. The RPCA methods often recognize these moving artifacts as foreground objects.
The second limitation is that most RPCA-based image decomposition imposes the foreground component being pixel-wisely sparse (e.g., L1-norm for the sparsity) and the background component being globally low-rank without locally considering the complex spatially varying noise in observation data. However, an observation of low dose X-ray imaging is not only badly corrupted by spatially varying signal-dependent Poisson noise [53,54], but also of low contrast and low SNR between the noise and the signal. This serious signal-dependent noise locally affects every entry of the data matrix and results in unsatisfying foreground vessel images containing many artifact residuals. Though Bayesian RPCA modeling data noise as a mixture of Gaussians is developed [55] to fit a wide range of noises such as Laplacian, Gaussian, sparse noise and any combinations of them, or GoDec+ [56] introduces a robust local similarity measure called correntropy to describe the data corruptions including Gaussian noise, Laplacian noise, and salt & pepper noise on real vision data, these methods cannot tackle the challenging problem of spatially varying noise in low-rank and sparse decomposition. To further remove these spatially varying noisy artifacts from the low contrast foreground vessel, the importance of vessel details in the foreground image sequences should be highlighted. Recently, reducing noise while preserving the visually important image details have attracted increasing attention in noisy image enhancement [53,57] and vessel image segmentation [58]. Specifically, by exploiting joint enhancement and denoising strategy, the desirable vessel extraction method can preserve the feature detail of foreground vessels to accurately recover the vessel structures with the noisy artifacts being removed simultaneously.
Third, there exist some parts of vessels with low-rank properties due to the periodically moving pattern of hearts and the contrast agents’ adhesion along the vessel wall. Therefore, current RPCA methods always keep tiny amounts of vessel residue as parts of the low rank background layer such that the extracted foreground vessels suffer severe distortion or loss of vessels’ intensities. This intensity loss results in incomplete recovery of vessel intensity and makes it impossible for accurate analysis of the contrast agent concentration and the corresponding blood flow perfusion conditions [5,16], such that the extracted vessels can only be used for vessel shape definition and morphological analysis.
While layer separation works mainly focus on solving the ill-posed multi-layer overlapping problem, we have noticed two important features of XCA images: First, contrast-filled vessel pixels only occupy a small fraction of the whole image data. In other words, the overlap between vessels and the background layer only exists in the vessel regions, and the pixels outside the vessel regions entirely belong to the background layer. Therefore, once the structures of contrast-filled vessel regions are determined by a vessel segmentation algorithm with high detection rate, all the other pixels in the remaining regions can be regarded as a background layer, whereby the layer separation problem is much more simplified by limiting the layer separation only in these vessel regions. By further exploiting the spatio-temporal consistency and low-rankness embedded in the whole data of the background layers, the small missing parts of the background layers overlapped with the foreground vessels can be fully completed using the state-of-the-art tensor completion methods. Then, the challenging problem of foreground vessel extraction can be tackled by subtracting the completed background layers from the overall XCA data.
Second, according to Beer-Lambert Law, a given X-ray image reflects the X-ray exponential attenuation composition (or sum) of material linear attenuation coefficients for the foreground contrast-filled vessels and background layers along the X-ray projection paths. Therefore, the additive property of X-ray exponential attenuation composition along the vessel and background layers in X-ray imaging can be directly exploited to exactly decompose the whole XCA image into the vessel and background layers. This X-ray attenuation sum model is then perfectly fitted into the low-rank and sparse decomposition model and justify the above-mentioned foreground vessel extraction strategy via completion and subtraction of the background layers from the whole XCA images. There are some X-ray image segmentation [27,59] and denoising [53] applications for the X-ray attenuation decomposition in computer-aided diagnosis and intervention. To the best of our knowledge, the proposed method is the first work to precisely fit such X-ray attenuation decomposition into the low-rank and sparse decomposition for accurately extracting vessels’ shapes and intensities from the complex and noisy backgrounds in XCA images.
Based on the above-mentioned strategies, this paper proposes a foreground/background layer separation framework in a logarithmic domain, where the raw XCA image is first mapped. We then extract the vessel mask regions and subsequently recover vessel intensities in these regions. The vessel region extraction is done by combining the RPCA algorithm with a vessel feature filtering based image segmentation method. The vessel intensity recovery problem is solved by a tensor completion method called t-TNN (twist tensor nuclear norm) [52]. By focusing on the vessel intensity recovery problem only in the small parts of vessel regions, the proposed vessel extration (or vessel recovery) method called VRBC-t-TNN (vessel region background completion with t-TNN) can extract vessel layers with accurate recovery of vessel structures and intensities. The contributions of this paper are summarized as follows:
(1) By taking the sparse outlier of vessel layers and the low rankness of background layers into the vessel/background separation for accurate vessel extraction, we map the raw XCA images into a logarithmic domain in order to fit the X-ray attenuation sum model of vessel/background layers into a decomposition framework of low-rank backgrounds plus sparse foreground vessels. This intensity mapping lays the foundation for not only satisfactorily segmenting the vessel shapes but also accurately recovering vessel intensities from backgrounds.
(2) Because an XCA image often consists of some large, non-overlapped background regions and some small, background-overlapped vessel regions, the accurate vessel extraction problem is divided into three steps: (1) Masking (or segmenting) out all the background-overlapped vessel regions by using RPCA plus adaptive vessel feature filtering, (2) Completing the background information in the masked vessel regions, and (3) Subtraction of the completed background layers from the overall XCA images.
(3) By exploiting the spatio-temporal consistency and low-rankness of background layers in the background data completion, the proposed method introduces an effective tensor completion to complete the low-rank background layers that are then subtracted from the overall XCA images. Therefore, both the structures and the intensities of vessels are well recovered with the proposed method.
2. Methods
2.1. Overview
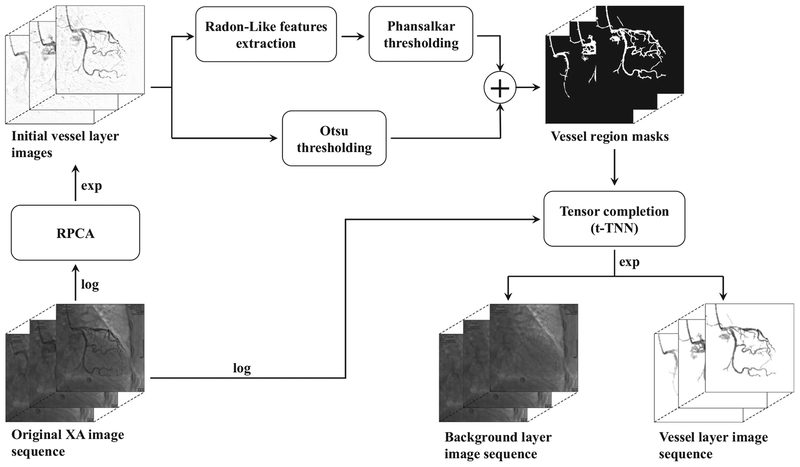
The proposed vessel layer extraction method called VRBC-t-TNN contains three main procedures. First, the vessel mask regions are extracted by combining the RPCA algorithm [60] with a vessel feature filtering based segmentation method [27]. As a preprocessing step of RPCA, a global logarithm transformation is performed on the input XCA sequence to create the X-ray attenuation sum model for the subsequent vessel/background decomposition. By exploiting the sparse outlier property of moving contrast in vessel regions and eliminating the disturbance of background structures, the initial contrast-filled vessel layer is extracted from the X-ray attenuation data by RPCA algorithm [60]. The vessel regions are then segmented out from the initial vessel layers via joint enhancement and denoising strategy that is implemented by RLF filtering and spatially adaptive thresholding. Secondly, the whole background layers are completed by completing the vessel-overlapped background regions based on neighboring background pixel information via a tensor completion algorithm called t-TNN [52]. Finally, the vessel layers are accurately extracted via subtraction of all the background layers from the whole attenuation data. Fig. 1 provides an overview of the whole procedure. Details are described in the remaining part of Section 2.
Fig. 1.
Overview of VRBC-t-TNN for an XCA image sequence.
2.2. Global intensity mapping
A global logarithm mapping is carried out on the whole XCA image data to perfectly fit the X-ray attenuation sum model of angiograms. In X-ray imaging, photons coming through human body are attenuated by contrast agents and various human tissues. The intensity of rays is reduced exponentially by the sum of attenuation coefficients, as the following equation:
| (1) |
where Xin and Xout represent the intensities of X-rays that come into and out of human body, respectively, μ denotes the attenuation coefficient, d denotes the path of rays.
By applying the log operator on both sides, we get:
| (2) |
The XCA image intensity normalized to the range [0, 1] can be regarded as the normalization of the ray intensity, i.e. the ratio of Xout to Xin. Then we get the following equation:
| (3) |
where AF and AB represent the attenuation sums caused by foreground vessels and complex backgrounds, respectively. Eq. (3) demonstrates that the XCA image is a sum of vessel/background layers in the logarithm domain, accordingly the multiplication of the two layers in the original image domain.
After this logarithm mapping, the linear sum model of Eq. (3) is ready for vessel/background separation via low-rank plus sparse matrix decomposition in RPCA (Illustrated in Section 2.3), as well as low-rank background plus foreground vessel extraction in tensor completion (Illustrated in Section 2.5). Therefore, we use the logarithm operation as a preprocessing of image data and perform exponentiation operation afterwards for the whole experiments in this work.
2.3. Preliminary vessel layer extraction
Though vessels can be segmented directly from original XCA images, the complex background structures and spatially varying noises may bring too many noisy artifacts into the segmentation results. Therefore, in this step an initial vessel layer with reduced background structures is preliminarily extracted from the XCA attenuation data sequence for better vessel segmentation. The XCA attenuation sequence is formed as a matrix D with each frame vectorized as a column. By exploiting the sparse outlier of moving contrast in the vessel layers, the RPCA algorithm is performed on the XCA attenuation data to extract the contrast-filled vessel layer.
The RPCA model [39] minimizes the sum of matrix nuclear norm of background and L1 norm of foreground component:
| (4) |
where denotes the data matrix, and denote the low-rank component (background layer) and the sparse component (foreground layer), respectively, λ is a positive weighting parameter, ||S||1 = ∑i, j |Si,j| is the L1 norm, ||L||* denotes the nuclear norm of L, which is an approximation to the matrix rank. The nuclear norm in Eq. (4) tightly couples all samples in the image sequence. This RPCA model has been proven efficient in moving object detection, including vessel layer extraction for XCA data [6,40]. Generally, the contrast-filled vessels move quickly with a high frequency while other tissues have a moving patterns at a lower frequency in XCA sequences. Therefore, the dynamic vessels can be captured by the sparse component S and the relatively static background structures are mainly recognized as the low-rank component L.
Being different from the RPCA-based method in [27], an effective optimization approach [60] based on inexact augmented Lagrange multipliers (IALM) is adopted to solve the minimization problem in Eq. (4). Eq. (4) is equivalent to its augmented Lagrangian function , which is given by:
| (5) |
where X is the Lagrangian multiplier, μ is a positive penalty scalar, is the Frobenius norm, 〈A, B〉 = Tr(A*B) is the inner product of two matrices, where A* denotes the conjugate transpose of A and Tr (·) denotes the matrix trace.
Variables (L, S, X) in Eq. (5) can be optimized alternately. We summarize the solution in Algorithm 1. The detailed deduction can be found in [60].
| Algorithm 1 IALM-RPCA [60]. | |
|---|---|
| Input: XCA data matrix D, λ. | |
| 1: | Initialize: L, S, X. |
| 2: | while not converged do |
| 3: | L sub-problem: |
| solved by: | |
| (U, Σ, V) = SVD(Dk – Sk + Xk/μ); | |
| 4: | S sub-problem: |
| solved by: | |
| Sk+1 = Sλ/μ(D − Lk+1 + Xk/μ); | |
| 5: | Xk+1 = Xk+μ(D − Lk+1 + Sk+1); |
| 6: | k = k + 1; |
| 7: | end while |
| Output: Initial background layer L, initial vessel layer S. | |
2.4. Feature-preserving vessel segmentation
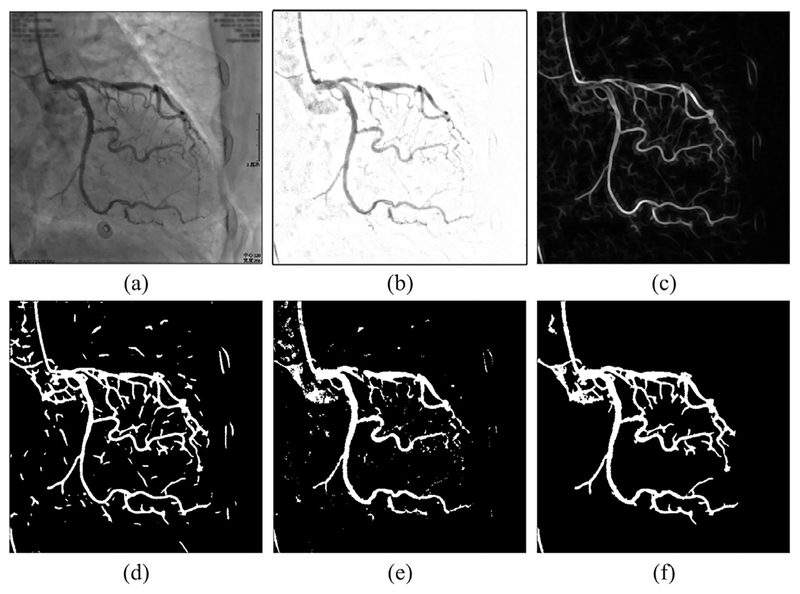
In this step, the initial vessel layer sequence is further processed to compute the vessel mask regions via vessel segmentation. Part of this vessel segmentation step uses a similar strategy with the works in [26,27]. Since most vessels have similar ridge shapes, we can highlight vessel structures using ridge detection filters. By achieving anisotropic sampling of neighborhoods based on edge sensing along different orientations, the Radon-like features (RLF) filtering [25] is implemented to completely highlight all vessels including minor segments. This RLF filtering can preserve vessel structure details while suppressing spatially varying noises. The RLF filtering is performed on each frame of the initial vessel sequence S obtained by Algorithm 1. An example image of RLF features is shown in Fig. 2(c).
Fig. 2.
Vessel segmentation illustration. (a) Original XCA image. (b) Initial vessel layer image. (c) RLF image of (b). (d) Locally adaptive thresholding result of (c). (e) Otsu’s global thresholding result of (b). (f) Vessel mask resulting from the combination of (d) and (e).
A locally adaptive thresholding method [61] is further performed on the RLF-filtered images to get binary images representing the vessel trees. This locally adaptive threshold tlocal for each pixel is calculated using the mean m and standard deviation s of the center pixel’s surrounding pixels, by the following equation:
| (6) |
where f, g, h are parameters, R is the dynamic range of s. A binary image is obtained by thresholding every pixel with the calculated tlocal of each pixel. The local thresholding result is displayed in Fig 2(d). Then too small regions are regarded as noises and thus removed from this binary image to obtain a vessel tree mask image.
Since RLF filtering thins vessels, this vessel tree cannot cover all the vessel pixels. Therefore, the initial vessel layer images are also segmented with the Otsu’s global thresholding [62], which separates the pixels of an image into two classes by minimizing the intra-class variance. We calculate one global thresholding value for the whole XCA images to avoid over-segmentation. An example of the resulted images is shown in Fig. 2(e).
Subsequently, these two binary images of local/global thresholding are combined together by conditional morphological dilation to construct the final vessel mask images, as shown in Fig. 2(f). The vessel segmentation algorithm is detailed in Algorithm 2.
2.5. Background completion using t-TNN
Regarding the vessel mask regions as missing entries of the background layer, we can construct the background layers by recovering the intensities of these entries via tensor completion methods. After testing several algorithms, we adopt the t-TNN algorithm [52] that can exploit the temporal redundancy and low-rank prior between the neighboring frames more efficiently than other tensor completion algorithms. The original XCA sequence is formed as a tensor with each slice being a matrix representation of each frame. All areas except the vessel mask regions, denoted as Ω, are presumed to be the known background layer pixels. To make sure that Ω does not contain edge pixels of the vessels, each vessel region mask image is first dilated by a 5 × 5 mask, then the background regions of all the frames constitute Ω. By performing t-TNN tensor completion to recover the unknown pixel values in vessel areas, we can extract the whole background layer sequence.
| Algorithm 2 Vessel segmentation. | |
|---|---|
| Input: Initial vessel layer image Iiv (a frame of S from Algorithm 1). | |
| 1: | Otsu threshold all Iivs to get binary mask MOs; |
| 2: | Calculate the Radon-Like features of Iiv, the resulted RLF image is denoted by Riv; |
| 3: | Phansalkar threshold Riv to get mask MP; |
| 4: | Remove regions smaller than a fixed size ts, from MP; |
| 5: | Take the foreground pixels in MP as seeds, do conditional dilation in MO, the result mask image is denoted by Mc; |
| 6: | Merge the foreground regions in MP and Mc, together to get the final mask image MV. |
| Output: Binary vessel mask image, MV. | |
The t-TNN model is based upon a tensor decomposition scheme called t-SVD [49,63] (see details in Section 2.5.1). Having a similar structure to the matrix SVD, t-SVD models a tensor in the matrix space through a defined t-product operation [49]. The TNN (represented by Eq. (13)) can simultaneously characterize the low-rankness of a tensor along various modes by transforming into the nuclear norm of block circulant representation. In the t-TNN model, a three-way tensor representation named twist tensor is designed to laterally store 2-D data frames in order; the twist tensor can then be used to exploit the low-rank structures of video data sequence based on the t-SVD framework. By equalizing the nuclear norm of the block circulant matricization of the twist tensor, t-TNN can not only exploit the correlations between all the modes simultaneously but also take advantage of the low-rank prior along a certain mode, e.g., X-ray image sequence over the time dimension.
2.5.1. Notations and preliminaries
An N−way (or N−mode) tensor is a multi-linear structure in . In this paper we mainly discuss 3-way tensors. Matlab notations are adopted for convenience. For instance, the (i, j, k)th entry of tensor is denoted by or . A slice of a tensor is a 2-D section defined by fixing all but two indices, and a fiber is 1-D section defined by fixing all indices but one. For a 3-way tensor , the notation , and denote the kth horizontal, lateral, and frontal slices, respectively. Particularly, denotes .
denotes the Fourier transform of along the third dimension. Accordingly, . The Frobenius norm of is , and the L1 norm of is . The inner product of two tensors of size n1 × n2 × n3 is defined asThe [64].
The block-based operators, i.e., bcirc, bvec, bvfold, bdiag and bdfold, are used to construct the TNN based on t-SVD. For , the values can be used to form the block circulant matrix
| (7) |
The block vectorizing and its opposite operation are defined as:
| (8) |
The block diag matrix and its opposite operation are defined as:
| (9) |
Then the t-product is defined as follows [49]:
| (10) |
The t-product is analogous to the matrix product except that the circular convolution replaces the product operation between the elements. The t-product in the original domain corresponds to the matrix multiplication of the frontal slices in the Fourier domain as follows:
| (11) |
The transpose tensor of is a tensor , obtained by transposing each frontal slice of and then reversing the frontal slice order along the third dimension [49]. The identity tensor is a tensor whose first frontal slice is an identity matrix while other slices are zero matrices. A tensor is orthogonal if . A tensor is f-diagonal if all of its frontal slices are diagonal matrices.
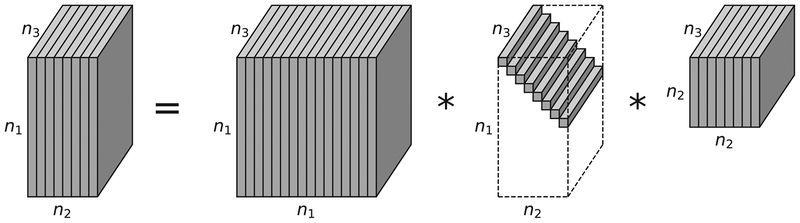
Based on the concepts introduced above, the tensor-SVD (t-SVD) of is given by
| (12) |
where and are orthogonal tensors of size n1 × n1 × n3 and n2 × n2 × n3, respectively. is a rectangular f-diagonal tensor of size n1 × n2 × n3, and the entries in are called the singular values of . * denotes the t-product here. Fig. 3 shows the t-SVD decomposition.
Fig. 3.
The t-SVD of an n1 × n2 × n3 tensor.
Based on the Fourier domain property of t-product as Eq. (11), t-SVD can be efficiently computed in the Fourier domain [49,63]. Each frontal slice of , and can be obtained via the matrix SVD, i.e., . Then the t-SVD of can be obtained by , , .
The tensor nuclear norm (TNN) of is defined as the average of the nuclear norms of all the frontal slices of [51,63], i.e.,
| (13) |
Though the factor 1/n3 in the TNN definition would not affect the results of the relevant optimization problems, this is important in theory. This factor makes TNN consistent with the matrix nuclear norm. It also guarantees that the dual norm of TNN is the spectral norm of a tensor [51,63].
Using the definition of TNN in Eq. (13), the tensor completion problem [52] can be represented by
| (14) |
where is the corrupted tensor, refers to the projection of on the observed entries Ω. Accordingly, is the complementary projection, i.e., . Eq. (14) can be solved using the t-SVD mentioned above.
2.5.2. Vessel layer extraction using t-TNN tensor completion
TNN of Eq. (14) is a general model for 3D data completion problems. Based on this model, Hu et al. extended TNN into t-TNN for video processing [52]. Their work has demonstrated that the t-TNN model is able to process panning videos better, by exploiting the horizontal translation relationship between frames [52]. As for XCA data, there also exists global displacements in image sequences due to patient’s breath and movement. Through experiments, we have found that the t-TNN model is more suitable than TNN for this background completion work. Therefore, t-TNN is adopted as the tensor completion model in this method.
In t-TNN, a twist operation is defined for a three dimensional tensor , which is a dimension shift, as the following equation shows:
| (15) |
Though this twist operation is simply a dimension shift of tensors, it emphasizes the temporal connections between frames [47]. Based on TNN, the t-TNN norm of tensor is defined as follows:
| (16) |
where the twist operation is a dimension shift of , and shifts it back [52].
By minimizing the t-TNN norm-based rank of the input tensor subject to certain constraints, the tensor completion work can be addressed by solving the following convex model [52]:
| (17) |
where and refer to the original corrupted data tensor (original XCA sequence) and the reconstructed tensor (background layer), respectively.
In general, Eq. (17) is solved by the alternating direction method of multipliers (ADMM) algorithm [65]. First, by introducing a new variable , Eq. (17) can be solved by the following minimization model [52]:
| (18) |
where denotes the indicator function indicating whether the elements of and on the support of Ω are equal, is the Lagrangian multiplier, and μ is a positive penalty scalar.
Variables , and in Eq. (18) can be optimized alternately with the other variable being treated as a fixed parameter, similar to Algorithm 1. Since the detailed deduction of Algorithm 3 is too long and out of the scope of this paper, we refer the interested reader to the work in [52].
| Algorithm 3 t-TNN based background completion [52]. | |
|---|---|
| Input: Original XCA data , non-vessel mask region Ω (acquired from M in Algorithm 2). | |
| 1: | Initialize: ρ0 > 0, η > 1, k = 0, , . |
| 2: | while and k < K do |
| 3: | sub-problem: |
| solved by: | |
| 4: | sub-problem: |
| solved by: | |
| for do | |
| end for | |
| for do | |
| end for | |
| 5: | |
| 6: | ρk+1 = ηρk, k = k + 1 |
| 7: | end while |
| 8: | Vessel layer |
| Output: Background layer tensor , vessel layer tensor . | |
After constructing the background layer data by t-TNN, the final vessel layer can be obtained by subtracting from the original data . Note that this subtraction is done in the logarithm domain, the corresponding operation for original image data would be division.
The whole procedure of the t-TNN background completion step is shown in Algorithm 3.
3. Experimental results
3.1. Real and synthetic XCA data
In this work, we used two types of experimental data for the evaluation of VRBC-t-TNN: real clinical XCA data and synthetic XCA data. All the 12 sequences of real XCA images are obtained from Ren Ji Hospital of Shanghai Jiao Tong University. Each sequence contains 80 frames whose image resolution is 512 × 512 pixels with 8 bits per pixel. All the experiments in this paper were approved by our institutional review board.
To accurately evaluate the vessel region and intensity recovery, we constructed 10 sequences of synthetic XCA images with ground truth background layer images (GTBL) and vessel layer images (GTVL). To get GTVLs, we perform vessel extraction similar to Algorithms 1 and 2 described in Section 2 with slightly different parameters on the real XCA data. Then we remove some artifacts manually from the extracted rough vessel images to obtain the GTVLs. The GTBLs are the consecutive frames selected from the real XCA data. Because a XCA image is the product of the vessel layer and the background layer according to the X-ray imaging mechanism (see Section 2.2), we multiply a sequence of GTVLs to the clean regions of GTBLs from a different sequence to obtain the synthetic XCA data. An example synthetic image with GTBL and GTVL is shown in Fig. 7(a).
Fig. 7.
Examples of vessel layer extraction results from synthetic data. Each group of results contains a background layer image labeled 1 and a vessel layer image labeled 2. (a–0) Synthetic XCA image. (a–1,2) Ground truth background layer and vessel layer image. (b)-(l) Layer separation results: (b) MedSubtract. (c) PRMF. (d) MoG-RPCA. (e) IALM-RPCA. (f) MCR-RPCA. (g) VRBC-PG-RMC. (h) VRBC-MC-NMF. (i) VRBC-ScGrassMC. (j) VRBC-LRTC. (k) VRBC-tSVD. (l) VRBC-t-TNN.
3.2. Experiment demonstration
For Algorithm 1, the codes of IALM-RPCA [60] are from the author’s website1, and the parameter λ is set to be 1/imagewidth = 1/512. For Algorithm 2, the codes of RLF [25] are also from the author’s website2. And we set the local window size as 16 × 16, f = 3, g = 10, h = 1 for locally adaptive thresholding. The region threshold ts in Algorithm 2 is set to be 300 pixel size. For Algorithm 3, codes of t-TNN are obtained from an online library called mctc4bmi3 [66].
Apart from VRBC-t-TNN, we also tested other layer separation methods for the comparison purpose. The median subtraction method (MedSubtract) used by Baka et al. constructs a static background layer image as the median of the first 10 frames of a sequence and substract it from all the frames [67]. Several open source RPCA algorithms, including PRMF4 [68], MoG-RPCA5 [55], IALM-RPCA and our previously proposed MCR-RPCA6 [6] were tested. The proposed framework VRBC can use other matrix completion and tensor completion methods to replace t-TNN. We tested some open source data completion methods including PG-RMC [69], MC-NMF [70], ScGrassMC [71], LRTC [72] and tSVD [50] as comparison, whose codes are obtained from Sobral’s library lrslibrary7 [73] and mctc4bmi [66].
To evaluate the performance of our vessel segmentation strategy in the proposed vessel extraction framework, we compare the vessel segmentation results with six other vessel segmentation algorithms including two deep learning methods: the Hessian based Frangi vesselness filter (Frangi’s)8 [24], Coye’s method (Coye’s)9 [74], Felfelian’s method [75], the MSRG (multiscale region growing) algorithm [76], CNN-Xray method designed for real-time fully-automatic catheter segmentation10 [77], and the U-net based retinal blood vessels segmentation method11 [78]. These six algorithms are all performed on the original XCA images without performing RPCA. The CNN-Xray method treats some vessels images from XCA vessel sequences and their manually labelled vessel masks as training sets. The Retinal-unet method adopts annotated retinal blood vessels as training sets to generate shapes similar to those in the XCA vessels. Since the vessel segmentation in the proposed framework is performed on the whole image sequence, it is impractical to finely tune the parameters of segmentation algorithms for each frame. Therefore, the parameters of these seven vessel segmentation methods are tuned to get the generally best results for all the sequences.
3.3. Visual evaluation of experimental results
The vessel segmentation results of real XCA data are shown in Fig. 4. The layer separation results of the real XCA data are shown in Figs. 5 and 6. The layer separation results of the synthetic data are shown in Fig. 7. One thing to notice is that the GTBL images like Fig. 7(a–1) were selected from the original XCA images and may also contain some small vessel structures. Though the areas where we added the GTVLs (Fig. 7(a–2)) are vacant of vessels, there may exist vessels in other areas. Thus, it is normal that the extracted vessel layer images (b–2)–(l–2) contain more vessels than the ground truth (a–2) in Fig. 7. Therefore, all the quantitative experiments in Sectionss 3.4–3.6 are carefully designed to avoid the influence of these vessel artifacts.
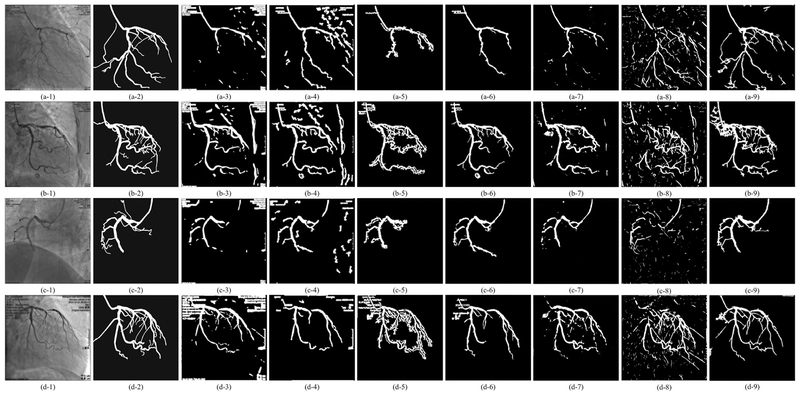
Fig. 4.
Vessel mask images by different vessel segmentation methods. Segmentation results of four XCA images are shown in four rows. From left to right, each row displays the original XCA image, the manually outlined ground truth vessel mask, the images processed by Frangi’s, Coye’s, Felfelian’s method, MSRG, CNN-Xray, Retina-unet, and the proposed method, respectively.
Fig. 5.
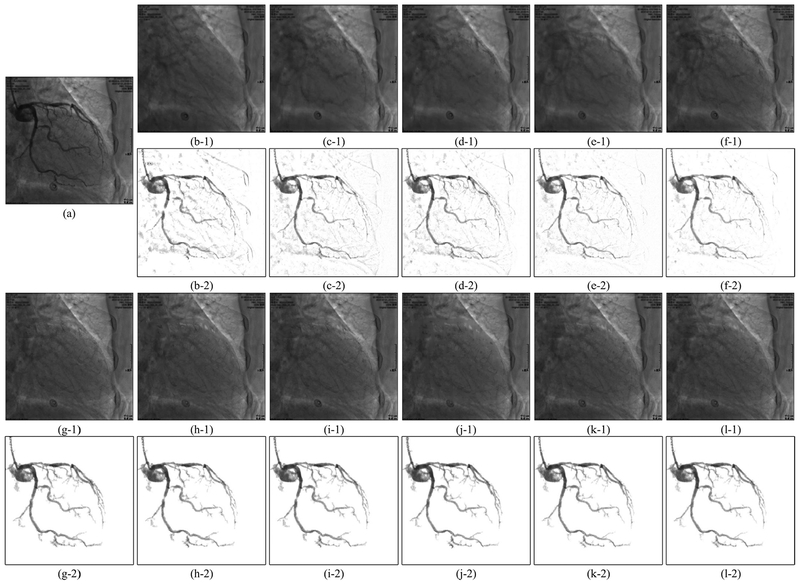
Example 1 of vessel layer extraction results from real data. Each group of results contains a background layer image labeled 1 and a vessel layer image labeled 2. (a) Original XCA image. (b)–(l) Layer separation results: (b) MedSubtract. (c) PRMF. (d) MoG-RPCA. (e) IALM-RPCA. (f) MCR-RPCA. (g) VRBC-PG-RMC. (h) VRBC-MC-NMF. (i) VRBC-ScGrassMC. (j) VRBC-LRTC. (k) VRBC-tSVD. (l) VRBC-t-TNN.
Fig. 6.
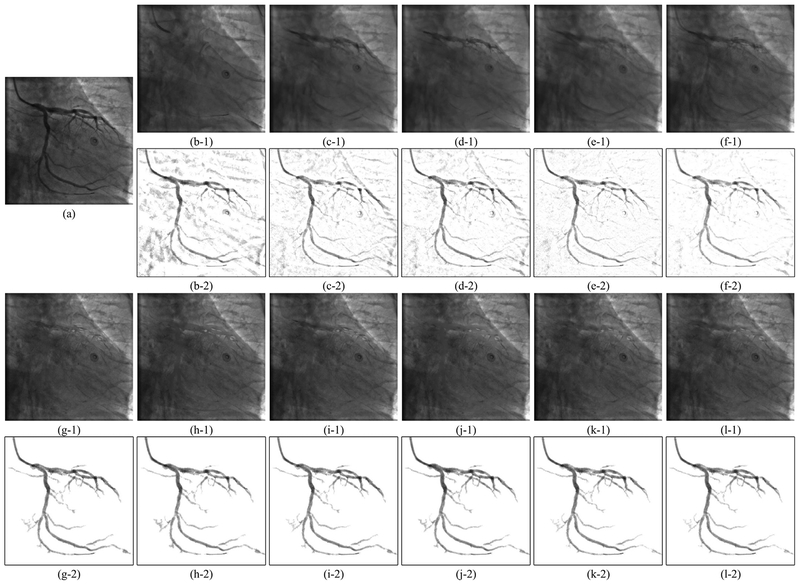
Example 2 of vessel layer extraction results from real data. Each group of results contains a background layer image labeled 1 and a vessel layer image labeled 2. (a) Original XCA image. (b)–(l) Layer separation results: (b) MedSubtract. (c) PRMF. (d) MoG-RPCA. (e) IALM-RPCA. (f) MCR-RPCA. (g) VRBC-PG-RMC. (h) VRBC-MC-NMF. (i) VRBC-ScGrassMC. (j) VRBC-LRTC. (k) VRBC-tSVD. (l) VRBC-t-TNN.
As can be seen in Fig. 4, because of the complex background noises, the four traditional filters detect either too few vessels or too many noises. Though for many frames these four filters are capable to detect the main structures of vessels, their performances on recognizing tiny vessels are unsatisfactory. Similarly, the two deep learning based segmentation methods can only approximately detect the vessel contours with too many noisy residuals in the vessel layer. This poor performance is due to the 2D convolutional neural networks being unable to distinguish the spatial-temporally continuous vessels from the complex and noisy backgrounds only by their 2D convolutional features. Due to the denoising effect of RPCA and the ability of RLF in detecting tiny vessels, the proposed strategy results in the most accurate vessel masks which can cover the vast majority of vessels. From Figs. 5–7, we could see that all these layer separation methods can remove noises and increase the vessel visibility to some extent. Among these algorithms, because MedSubtract constructs a static background layer image which does not change over time, the extracted vessel layer image with lots of noise remaining is the worst among these extracted results. The four RPCA methods achieve much better vessel extraction results with more noises being removed. Among these four RPCA methods, our previously proposed MCR-RPCA method [6] achieves the best vessel extraction results with the least residual background noises. However, though RPCA methods can nicely capture the vessel structures in the vessel layer images, the vessel intensities are not fully extracted since obvious vessel residuals can be observed in their resulting background layer images.
In contrast, the proposed VRBC framework embedded within all the completion methods greatly improves the vessel extraction performances. The vessel intensities are further extracted compared to RPCA algorithms. Among all these algorithms, the result images of VRBC-t-TNN achieve the best visual performances. Both the background layer images and the vessel layer images are visually appealing and seem to be well recovered in terms of structure and intensity preserving ability.
3.4. Quantitative evaluation of vessel segmentation
To quantitatively evaluate the performances of vessel segmentation, we calculate the detection rate (DR), precision (P) and F-measure (F) using ground truth vessel masks. These three indicators are calculated as follows:
| (19) |
where TP (true positives) is the total number of correctly classified foreground pixels, FP (false positives) is the total number of background pixels that are wrongly marked as foreground, and FN (false negatives) is the total number of foreground pixels that are wrongly marked as backgrounds. For a certain method, detection rate indicates its power to detect more foreground pixels, precision measures correct ratio of detection, and F-measure combines detection rate and precision to indicate the overall performance of certain extractor.
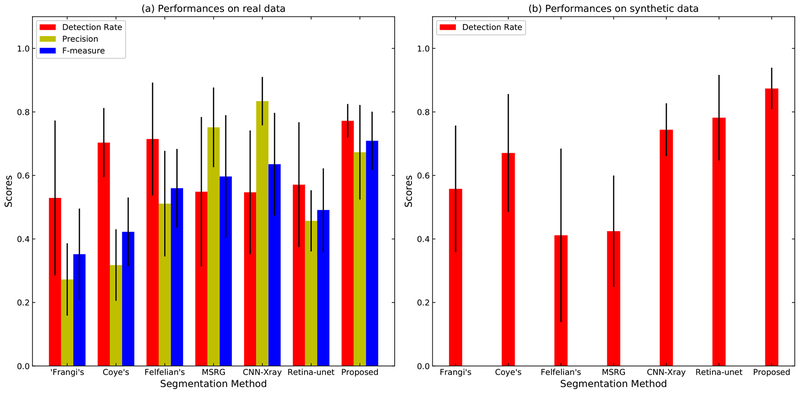
In the real XCA experiments, we manually outlined the vessels of 12 images from 12 different sequences as the ground truth masks. Then we measured the detection rate, precision and F-measure of these 12 images, as shown in Fig. 8(a). For the synthetic data, the ground truths of all frames are acquired during the synthetic process of GTVLs. However, because the GTBLs also contain some vessels, the extracted vessel masks would inevitably contain more vessels than do the GTVLs. Therefore, we cannot correctly measure the precision and F-measure using the ground truth images. Thus, we only measured the detection rates of the 10 synthetic sequences, as shown in Fig. 8(b) and Table 1.
Fig. 8.
Performance of vessel segmentation methods. (a) The general detection rate, precision and F-measure of twelve real XCA images. (b) The general detection rate of ten synthetic sequences.
Table 1.
The average detection rate, precision, F-measure (mean value ± standard deviation) for all methods using the real and synthetic data.
| Real | Synthetic | |||
|---|---|---|---|---|
| Method | DR | P | F | DR |
| Frangi’s | 0.529 ± 0.244 | 0.272 ± 0.114 | 0.352 ± 0.144 | 0.558 ± 0.199 |
| Coye’s | 0.703 ± 0.109 | 0.318 ± 0.113 | 0.422 ± 0.108 | 0.671 ± 0.186 |
| Felfelian’s | 0.715 ± 0.178 | 0.511 ± 0.166 | 0.560 ± 0.124 | 0.412 ± 0.273 |
| MSRG | 0.549 ± 0.235 | 0.752 ± 0.125 | 0.597 ± 0.193 | 0.425 ± 0.175 |
| CNN-Xray | 0.547 ± 0.195 | 0.834 ± 0.076 | 0.636 ± 0.162 | 0.744 ± 0.083 |
| Retina-Unet | 0.571 ± 0.196 | 0.457 ± 0.096 | 0.491 ± 0.131 | 0.782 ± 0.135 |
| Proposed | 0.773 ± 0.050 | 0.704 ± 0.126 | 0.729 ± 0.067 | 0.888 ± 0.048 |
For real XCA data, the proposed method generally obtains the highest scores in the indicators measured. For synthetic data, the detection rates of the proposed method is both the highest and the most stable. The quantitative measurements verify the accuracy and robustness of the proposed vessel segmentation method. Compared to traditional static segmentation strategies and deep learning based methods, this proposed method can robustly detect the vast majority of the vessel areas.
3.5. Quantitative evaluation on vessel visibility using real data
We quantitatively evaluated the vessel visibility using the contrast-to-noise ratio (CNR) [40] of vessel layer images. CNR is defined as:
| (20) |
where μV and μB are the pixel intensity means in the vessel and background regions, respectively, σB is the standard deviation of the pixel intensity values in the background regions.
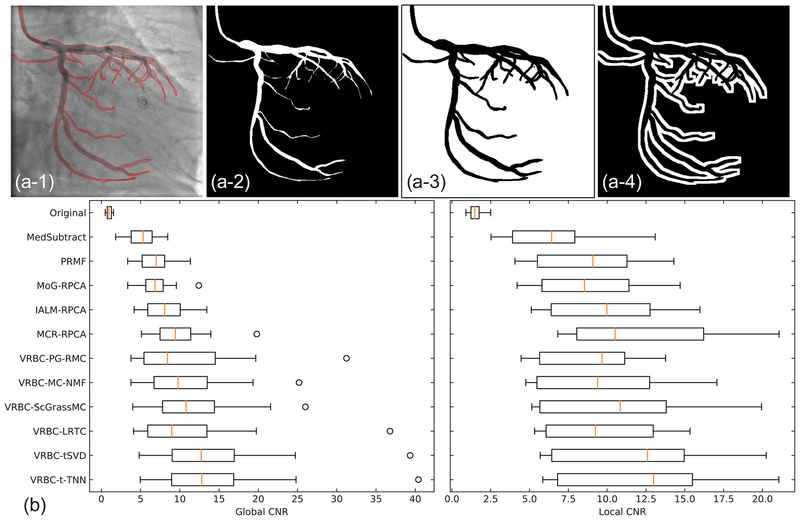
To get ground truth vessel mask regions and background regions, we used the manually outlined vessel masks in Section 3.4. Two types of background regions are then defined. The global background regions cover the whole area except the vessel regions, while the local background regions are the 7 pixel wide neighborhood area surrounding the vessel regions. Fig. 9(a) shows the examples of these regions. Twelve frames from different sequences are tested to compute the global and local CNR values. The general performances are shown in Fig. 9(b) and Table 2.
Fig. 9.
CNR values on real data. (a–1)–(a–4) Original image with manually drawn vessel edges, the vessel regions, the global background regions, and the local background regions. (b) Global and local CNR values of twelve images from different image sequences of real data.
Table 2.
The average CNR values (mean value ± standard deviation) for all methods using the real data.
| Method | Global CNR | Local CNR |
|---|---|---|
| Original | 1.026 ± 0.345 | 1.558 ± 0.500 |
| MedSubtract | 5.074 ± 2.035 | 6.475 ± 3.109 |
| PRMF | 6.869 ± 2.461 | 8.955 ± 3.690 |
| MoG-RPCA | 6.941 ± 2.518 | 8.959 ± 3.644 |
| IALM-RPCA | 8.323 ± 2.974 | 9.909 ± 3.485 |
| MCR-RPCA | 9.898 ± 4.016 | 12.252 ± 5.094 |
| VRBC-PG-RMC | 11.266 ± 8.214 | 9.078 ± 3.245 |
| VRBC-MC-NMF | 11.098 ± 6.367 | 9.710 ± 4.149 |
| VRBC-ScGrassMc | 12.197 ± 6.848 | 10.700 ± 4.879 |
| VRBC-LRTC | 11.846 ± 9.199 | 9.717 ± 3.649 |
| VRBC-tSVD | 14.842 ± 9.887 | 11.722 ± 4.643 |
| VRBC-t-TNN | 14.976 ± 9.961 | 12.083 ± 4.789 |
CNR measures the contrast between the vessels and backgrounds. A larger CNR value implies a better vessel visibility. We can find that all methods can greatly increase the vessel visibility compared to the original images. Generally, VRBC-t-TNN achieves the highest global CNR, and the second highest local CNR, slightly lower than MCR-RPCA. This CNR evaluation indicates that VRBC-t-TNN greatly improves the vessel visibility and suppresses much noises simultaneously.
3.6. Quantitative evaluation on vessel intensity recovery using synthetic data
To measure the accuracy of vessel intensity recovery, we directly calculated the differences between the extracted vessel layers and the ground truths. The reconstruction error of vessels is defined as follow:
| (21) |
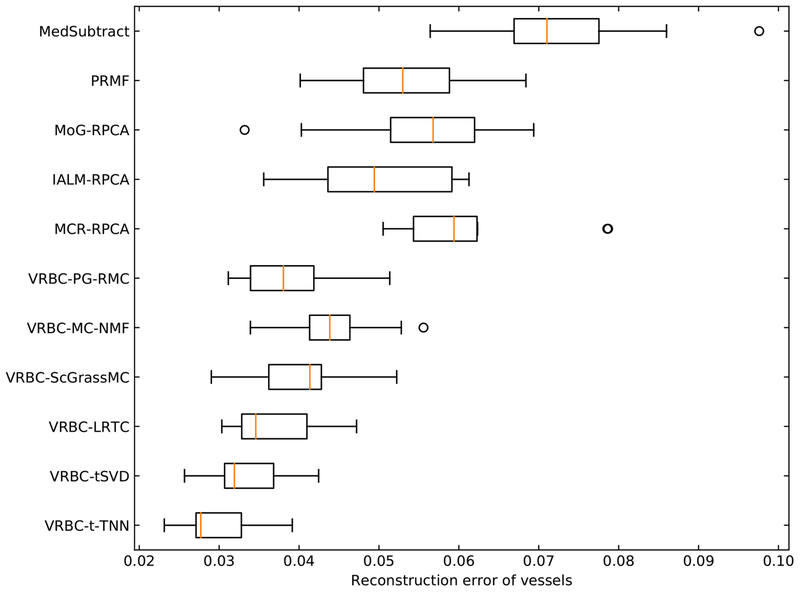
where V denotes the vessel regions, Iresult and Igroundtruth denote the intensities of the resulting vessel layer images and the ground truth vessel layer images, respectively. For each synthetic XCA sequence, the Erecon of the whole sequence is calculated. Fig. 10 and Table 3 show the general performances of different algorithms on the 10 synthetic sequences.
Fig. 10.
Erecon values in vessel regions on synthetic data.
Table 3.
The average Erecon values (mean value ± standard deviation) for all methods using the 10 synthetic sequences.
| Method | Erecon |
|---|---|
| MedSubtract | 0.073 ± 0.012 |
| PRMF | 0.053 ± 0.009 |
| MoG-RPCA | 0.055 ± 0.012 |
| IALM-RPCA | 0.050 ± 0.009 |
| MCR-RPCA | 0.061 ± 0.010 |
| VRBC-PG-RMC | 0.039 ± 0.006 |
| VRBC-MC-NMF | 0.045 ± 0.006 |
| VRBC-ScGrassMc | 0.041 ± 0.007 |
| VRBC-LRTC | 0.037 ± 0.006 |
| VRBC-tSVD | 0.033 ± 0.005 |
| VRBC-t-TNN | 0.030 ± 0.005 |
Erecon measures the vessel intensity difference between the separation result and the ground truth. A small Erecon indicates an accurate vessel layer extraction. We can see that VRBC achieves smaller Erecon values than other existing methods. Among them, VRBC-t-TNN achieves the best performance. This Erecon evaluation indicates that VRBC-t-TNN can accurately recover the contrast-filled vessel intensities from XCA images.
3.7. Computation times
Finally, we report on the computation costs incurred by our VRBC-t-TNN algorithm on a Lenovo PC equipped with an Intel Core i5–4460 Quad-Core 3.2 GHz CPU and 8 GB of RAM executing Matlab codes. The average processing time of a 512 × 512 × 80 real XCA sequence is approximately 970 s. The RPCA step, vessel filtering step and t-TNN step take approximately 28 s, 740 s and 200 s, respectively.
4. Discussion and conclusion
We have presented a new low-rankness based decomposition framework for accurate vessel layer extraction from XCA image sequences. By constructing the background layer via tensor completion of the vessel regions from original XCA images, the proposed method can overcome limitations in current vessel extraction methods and has significantly improved the accuracy of vessel intensity recovery with enhanced vessel visibility. In this method, the raw XCA image sequences are first mapped into a logarithmic domain to perfectly fit the X-ray attenuation sum model along the vessel and background layers into the subsequent vessel/background decomposition modeling. We subsequently use the low-rank and sparse decomposition via RPCA algorithm to extract the contrast-filled vessel regions. RLF filtering and spatially adaptive thresholding are performed on the vessel layer images to segment out vessel masks. An accurate background layer image sequence is then constructed by t-TNN tensor completion by exploiting the spatio-temporal consistency and low-rankness of background tensor from the consecutive background layers. Finally, the vessel layer images are acquired by subtracting the background layer from original XCA images. Experiments have been done to demonstrate the vessel visibility and accuracy of the results.
The efficacy of the proposed vessel and background layer decomposition framework is based on the exact X-ray attenuation sum model via logarithmic mapping of raw XCA images. This mapping gives sense to the gray levels that are linearly dependent on the matter thickness and density in the vessel and background layers. The linear attenuation sum model is then perfectly fitted into the additive model of low-rank background plus sparse foreground decomposition for the vessel/background separation.
Since RPCA is able to detect moving contrast and to weaken the background noise with the further denoising effect of adaptive vessel feature filtering, RPCA coupled with adaptive vessel feature filtering improved the vessel segmentation that is robust to the complex background noise. There is a general concern that RPCA as a preprocessing step might fail to recognize a portion of vessels and thus lead to segmentation leaks in XCA images. In most cases, the RPCA-based vessel enhancement hardly eliminates any vessel parts in the extracted vessel layer images and is actually able to detect more vessel pixels in the subsequent segmentation step. Especially, some vessel pixels that are faded in background noises are highlighted due to the RPCA’s effect in detecting moving pattern from backgrounds.
Furthermore, integrating the t-TNN tensor completion into layer separation reconstructs the background layer with more reliable intensity recovery. As can be seen from Figs. 5–7, obvious vessel residuals can be observed in the background layer images resulting from the RPCA methods, which indicates that vessels and backgrounds cannot be fully separated if solely based on the low-rank and sparsity decomposition. The reason may be that the low-rank and sparsity difference between the vessel layer and the background layer is not big enough to separate the two layers. The background completion via t-TNN tensor completion is different from RPCA methods. To recover unknown background pixels in the vessel-overlapped mask regions, the t-TNN based background completion uses the low-rankness and the inter-frame spatio-temporal connectivity of complex backgrounds and uses all other background pixels. By subtracting the completed background layers from overall XCA images, the completion process bypasses the interaction of the vessels and the backgrounds in the overlapped areas for accurate vessel intensity recovery. As can be seen in Figs. 5 and 6, the missing background pixel intensities in the vessel mask regions of the background layer images seem to be well recovered with seldom vessel residual effects after implementing VRBC-t-TNN. This implies that tackling vessel extraction problem via background completion overcomes the challenge and incompleteness of vessel intensity recovery. Observing the result images of synthetic data in Fig. 7, result images from VRBC-t-TNN are the most approximate to the ground truths. The Erecon evaluation on synthetic data also supports this observation. These experiments demonstrate that VRBC-t-TNN can well recover the pixel values of the background layers and vessel layers.
Though all layer separation problems are ill-posed, the proposed data completion approach is much more effective than present layer separation works. From the information theory viewpoint, the traditional layer separation models, including RPCA and motion based methods, try to get two outputs (the vessel and the background layers) with one input (original image sequence). In this way, there is an uncertainty for every pixel of the XCA data. In contrast, the tensor completion infers background intensities in the vessel-overlapped regions with the known information from all the other background pixels, such that only a small number of missing pixels in the masked regions have uncertainties. Since the amount of unknowns to be solved is much reduced, it is not strange that the proposed method can recover vessel intensity more accurately. Besides, thanks to exploiting the low-rank and sparse decomposition modeling and the sparse outlier of moving contrast in RPCA-based method, we can completely extract the vessel regions, whose remaining noisy artifacts are further removed with fine vessel feature detail being simultaneously preserved by RLF-filtering and spatially adaptive thresholding.
It should be noted that a small missing vessel in the vessel segmentation step may cause wrong “labeling” in the VRBC-t-TNN framework. A slightly larger vessel mask including all possible vessels will help fix the small missing vessel problem. Furthermore, we can tentatively sample small vessel mask regions for tensor completion and then subtract the completed backgrounds from XCA image for small vessel extraction. The small vessel segmentation deficiency can be well compensated by an iterative scheme of trial-and-completion. Therefore, the principal of the segmentation step is to prefer over-segmentation over under-segmentation. In this work, the proposed layer separation framework generally achieves satisfactory vessel extraction results for all the sequences. However, it should be pointed out that there are still some cases where the method misses some small vessel segments if they disconnect with the main vessels in the XCA images. Therefore, more elaborate and robust small vessel imaging and segmentation [79] methods would further improve the performances.
In the low-rank and sparse decomposition framework, the successful low-rank background modeling does guarantee the accuracy of foreground vessel extraction. On the one hand, the proposed background modeling with t-TNN-based video tensor completion after segmenting foreground vessel mask regions works better in background modeling than do the other tensor completion algorithms we have tried for this vessel extraction application. We believe that the performance of vessel extraction may be further improved with the development of new tensor completion algorithms. On the other hand, considering that the dynamic real-world background sequences may span one or more linear or nonlinear manifolds [80], we will incorporate the nonlinear structures [81] and multi-view subspace clustering [82] of XCA data into background modeling for accurate vessel extraction in our future research.
The computation time of the proposed algorithm also needs to be reduced for real-time applications so that our future work will implement deep vessel extraction via low-rank constrained convolutional neural networks [83,84], which can capture sophisticated hierarchical feature representations of contrast-filled vessels from the complex and noisy backgrounds. Besides, most video-based RPCA and matrix (or tensor) completion methods require computing the large SVD (or t-SVD) that is increasingly costly as matrix (or tensor) sizes and ranks increase. Therefore, by factorizing a matrix (or tensor) into a product of two small matrices (or tensors) to reduce the dimension of the matrix (or tensor) for which the SVD must be computed, parallel matrix (or tensor) factorization framework [85,86] with foreground/background clustering regularization [80,87] can be explored to greatly boost the overall performance in terms of vessel recovery accuracy and computational speed. Furthermore, being different from the most batch learning methods that require heavy memory cost to process a large number of video frames, the efficient online optimization algorithms [86,88,89] implemented in a sequential way rather than in a batch way would be more useful to quickly extract the contrast-filled vessels from the complex and noisy backgrounds.
One of the potential direct clinical applications of this work is to bring perfusion concentration analysis into quantitative coronary analysis (QCA). Traditional QCA measures lesions by calculating the minimum luminal area, percentage area stenosis, etc., to analyze the stenosis degree of coronary diseases. Since vessels are overlapped by various structures in the original XCA images, these measurements are mainly shape-based. However, the proposed VRBC-t-TNN can well construct a clean vessel layer image with accurate contrast intensity. Therefore, it is expected that quantitative analysis on the blood flow and perfusion concentration could be done with the help of VRBC-t-TNN. This concentration analysis will give more clinical information compared to traditional QCA.
Another potential application of this work is to improve the performances of 3D/4D (3D+time) vessel reconstruction. In recent years, the reconstruction of 3D/4D coronary vessels using 2D X-ray angiography has been developed a lot [12]. This reconstruction can provide clinicians with 3D/4D information, which will improve the clinical judgement. The 3D/4D reconstruction could also contribute to the quantitative analysis and computer diagnosis of coronary diseases. One of the factors that severely influence this vessel reconstruction is the overlap of different structures [12]. Since the proposed method removes other background structures and extract clean vessel layer images with more reliable intensities, it will promote the 3D/4D vessel reconstruction work.
Acknowledgments
This work was partially supported by the National Natural Science Foundation of China (61271320, 61362001, 81371634, 81370 041, 8140 0261 and 61503176), National Key Research and Development Program of China (2016YFC1301203 and 2016YFC0104608), and Shanghai Jiao Tong University Medical Engineering Cross Research Funds (YG2017ZD10, YG2016MS45, YG2015ZD04, YG2014MS29 and YG2014ZD05). Qiegen Liu was partially supported by the young scientist training plan of Jiangxi province (20162BCB23019). Yueqi Zhu was partially supported by three-year plan program by Shanghai Shen Kang Hospital Development Center (16CR3043A). BF was partially supported by NIH Grants R01CA156775, R21CA176684, and R01CA204254, and R01HL140325. The authors would like to thank all authors for opening source codes used in the experimental comparison in this work. The authors would also like to thank the anonymous reviewers whose contributions considerably improved the quality of this paper.
Footnotes
References
- [1].Townsend N, Wilson L, Bhatnagar P, Wickramasinghe K, Rayner M, Nichols M, Cardiovascular disease in europe: epidemiological update 2016, Eur. Heart J 37 (42) (2016) 3232–3245. [DOI] [PubMed] [Google Scholar]
- [2].Rafii-Tari H, Payne CJ, Yang GZ, Current and emerging robot-assisted endovascular catheterization technologies: a review, Ann. Biomed. Eng 42 (4) (2014) 697–715. [DOI] [PubMed] [Google Scholar]
- [3].Toth D, Panayiotou M, Brost A, Behar JM, Rinaldi CA, Rhode KS, Mountney P, 3D/2D Registration with superabundant vessel reconstruction for cardiac resynchronization therapy, Med. Image Anal 42 (2017) 160–172. [DOI] [PubMed] [Google Scholar]
- [4].Ge H, Ding S, An D, Li Z, Ding H, Yang F, Kong L, Xu J, Pu J, He B, Frame counting improves the assessment of post-reperfusion microvascular patency by TIMI myocardial perfusion grade: evidence from cardiac magnetic resonance imaging, Int. J. Cardiol 203 (2016) 360–366. [DOI] [PubMed] [Google Scholar]
- [5].Ding S, Pu J, Qiao ZQ, Shan P, Song W, Du Y, Shen JY, Jin SX, Sun Y, Shen L, Lim YL, He B, TIMI Myocardial perfusion frame count: a new method to assess myocardial perfusion and its predictive value for short-term prognosis, Catheter. Cardiovasc. Interv 75 (5) (2010) 722–732. [DOI] [PubMed] [Google Scholar]
- [6].Jin M, Li R, Jiang J, Qin B, Extracting contrast-filled vessels in X-ray angiography by graduated RPCA with motion coherency constraint, Pattern Recogn 63 (2017) 653–666. [Google Scholar]
- [7].Ma H, Hoogendoorn A, Regar E, Niessen WJ, van Walsum T, Automatic online layer separation for vessel enhancement in X-ray angiograms for percutaneous coronary interventions, Med. Image Anal 39 (2017) 145–161. [DOI] [PubMed] [Google Scholar]
- [8].Bouwmans T, Sobral A, Javed S, Jung SK, Zahzah EH, Decomposition into low-rank plus additive matrices for background/foreground separation: a review for a comparative evaluation with a large-scale dataset, Comput. Sci. Rev 23 (2017) 1–71. [Google Scholar]
- [9].Roohi SF, Zonoobi D, Kassim AA, Jaremko JL, Multi-dimensional low rank plus sparse decomposition for reconstruction of under-sampled dynamic MRI, Pattern Recogn 63 (1) (2017) 667–679. [Google Scholar]
- [10].Ravishankar S, Moore BE, Nadakuditi RR, Fessler JA, Low-Rank and adaptive sparse signal (LASSI) models for highly accelerated dynamic imaging, IEEE Trans. Med. Image 36 (5) (2017) 1116–1128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Shi C, Cheng Y, Wang J, Wang Y, Mori K, Tamura S, Low-rank and sparse decomposition based shape model and probabilistic atlas for automatic pathological organ segmentation, Med. Image Anal 38 (2017) 30–49. [DOI] [PubMed] [Google Scholar]
- [12].Çimen S, Gooya A, Grass M, Frangi AF, Reconstruction of coronary arteries from X-ray angiography: a review, Med. Image Anal 32 (2016) 46–68. [DOI] [PubMed] [Google Scholar]
- [13].Miao S, Wang JZ, Liao R, Convolutional neural networks for robust and real–time 2-D/3-D registration, in: Deep Learning for Medical Image Analysis, Elsevier, 2017, pp. 271–296. [Google Scholar]
- [14].Liu X, Hou F, Qin H, Hao A, Robust optimization-Based coronary artery labeling from X-Ray angiograms, IEEE J. Biomed. Health Inf 20 (6) (2016) 1608–1620. [DOI] [PubMed] [Google Scholar]
- [15].Zhang T, Huang Z, Huang Y, Wang G, Sun X, Sang NS, Chen W, A novel structural features-based approach to automatically extract multiple motion parameters from single-arm X-ray angiography, Biomed. Signal Proc. Control 32 (2017) 29–43. [Google Scholar]
- [16].Sakaguchi T, Ichihara T, Natsume T, Yao J, Yousuf O, Trost JC, Lima JAC, George RT, Development of a method for automated and stable myocardial perfusion measurement using coronary X-ray angiography images, Int. J. Cardiovasc. Imag 31 (2015) 905–914. [DOI] [PubMed] [Google Scholar]
- [17].Kitamura Y, Li W, Li Y, Ito W, Ishikawa H, Data-Dependent higher-Order clique selection for Artery–Vein segmentation by energy minimization, Int. J. Comput. Vis 117 (2) (2016) 142–158. [Google Scholar]
- [18].Nasr-Esfahani E, Karimi N, Jafari MH, Soroushmehr SM, Samavi S, Nallamothu BK, Najarian K, Segmentation of vessels in angiograms using convolutional neural networks, Biomed. Signal Proc. Control 40 (2018) 240–251. [Google Scholar]
- [19].Kirbas C, Quek F, A review of vessel extraction techniques and algorithms, Comput. Surv 36 (2) (2004) 81–121. [Google Scholar]
- [20].Lesage D, Angelini ED, Bloch I, Funka-Lea G, A review of 3D vessel lumen segmentation techniques: models, features and extraction schemes, Med. Image Anal 13 (6) (2009) 819–845. [DOI] [PubMed] [Google Scholar]
- [21].Schneider M, Hirsch S, Weber B, Székely G, Menze BH, Joint 3-D vessel segmentation and centerline extraction using oblique hough forests with steerable filters, Med. Image Anal 19 (1) (2015) 220–249. [DOI] [PubMed] [Google Scholar]
- [22].Chaudhuri S, Chatterjee S, Katz N, Nelson M, Goldbaum M, Detection of blood vessels in retinal images using two-dimensional matched filters, IEEE Trans. Med. Imag 8 (3) (1989) 263–269. [DOI] [PubMed] [Google Scholar]
- [23].Sato Y, Nakajima S, Shiraga N, Atsumi H, Yoshida S, Koller T, Gerig G, Kikinis R, Three-dimensional multi-scale line filter for segmentation and visualization of curvilinear structures in medical images, Med. Image Anal 2 (2) (1998) 143–168. [DOI] [PubMed] [Google Scholar]
- [24].Frangi AF, Niessen WJ, Vincken KL, Viergever MA, Multiscale vessel enhancement filtering, in: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, 1998, pp. 130–137. [Google Scholar]
- [25].Kumar R, Vázquez-Reina A, Pfister H, Radon-like features and their application to connectomics, in: Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), IEEE, 2010, pp. 186–193. [Google Scholar]
- [26].Syeda-Mahmood T, Wang F, Kumar R, Beymer D, Zhang Y, Lundstrom R, McNulty E, Finding similar 2d x-ray coronary angiograms, Med. Image Comput. Comput. Assist. Interv. MICCAI (2012) 501–508. [DOI] [PubMed] [Google Scholar]
- [27].Jin M, Hao D, Ding S, Qin B, Low-rank and sparse decomposition with spatially adaptive filtering for sequential segmentation of 2D+t vessels, Phys. Med. Biol 63 (17) (2018) 17LT01. [DOI] [PubMed] [Google Scholar]
- [28].Zhang W, Ling H, Prummer S, Zhou KS, Ostermeier M, Comaniciu D, Coronary tree extraction using motion layer separation, in: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Springer, 2009, pp. 116–123. [DOI] [PubMed] [Google Scholar]
- [29].Zhu Y, Prummer S, Wang P, Chen T, Comaniciu D, Ostermeier M, Dynamic layer separation for coronary DSA and enhancement in fluoroscopic sequences, in: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Springer, 2009, pp. 877–884. [DOI] [PubMed] [Google Scholar]
- [30].Preston JS, Rottman C, Cheryauka A, Anderton L, Whitaker RT, Joshi S, Multi-layer deformation estimation for fluoroscopic imaging, in: Proceedings of the International Conference on Information Processing in Medical Imaging, Springer, 2013, pp. 123–134. [DOI] [PubMed] [Google Scholar]
- [31].Tang S, Wang Y, Chen YW, Application of ICA to X-ray coronary digital subtraction angiography, Neurocomputing 79 (2012) 168–172. [Google Scholar]
- [32].Qin B, Gu Z, Sun X, Lv Y, Registration of images with outliers using joint saliency map, IEEE Signal Process Lett 17 (1) (2010) 91–94. [Google Scholar]
- [33].Wang G, Chen Y, Zheng X, Gaussian field consensus: a robust nonparametric matching method for outlier rejection, Pattern Recognit 74 (2018) 305–316. [Google Scholar]
- [34].Qin B, Shen Z, Zhou Z, Zhou J, Lv Y, Structure matching driven by joint-saliency-structure adaptive kernel regression, Appl. Soft Comput 46 (2016) 851–867. [Google Scholar]
- [35].Zhang S, Yang K, Yang Y, Luo Y, Wei Z, Non-rigid point set registration using dual-feature finite mixture model and global-local structural preservation, Pattern Recognit 80 (2018) 183–195. [Google Scholar]
- [36].Qin B, Shen Z, Fu Z, Zhou Z, Lv Y, Bao J, Joint-saliency structure adaptive kernel regression with adaptive-scale kernels for deformable registration of challenging images, IEEE Access 6 (2018) 330–343. [Google Scholar]
- [37].Chang X, Ma Z, Lin M, Yang Y, Hauptmann AG, Feature interaction augmented sparse learning for fast kinect motion detection, IEEE Trans. Image Proc 26 (8) (2017) 3911–3920. [DOI] [PubMed] [Google Scholar]
- [38].Li Z, Nie F, Chang X, Yang Y, Beyond trace ratio: weighted harmonic mean of trace ratios for multiclass discriminant analysis, IEEE Trans. Knowled. Data Eng 29 (10) (2017) 2100–2110. [Google Scholar]
- [39].Candès EJ, Recht B, Exact matrix completion via convex optimization, Found. Comput. Math 9 (6) (2009) 717–772. [Google Scholar]
- [40].Ma H, Dibildox G, Banerjee J, Niessen W, Schultz C, Regar E, van Walsum T, Layer separation for vessel enhancement in interventional x-ray angiograms using morphological filtering and robust PCA, in: Proceedings of the Workshop on Augmented Environments for Computer-Assisted Interventions, Springer, 2015, pp. 104–113. [Google Scholar]
- [41].Rudin LI, Osher S, Fatemi E, Nonlinear total variation noise removal algorithm, Phys. D 60 (1–4) (1992) 259–268. [Google Scholar]
- [42].Wang S, Wang Y, Chen Y, Pan P, Sun Z, He G, Robust PCA using matrix factorization for background/foreground separation, IEEE Access 6 (2018) 18945–18953. [Google Scholar]
- [43].Madathil B, George SN, Twist tensor total variation regularized-reweighted nuclear norm based tensor completion for video missing area recovery, Inf. Sci 423 (2018) 376–397. [Google Scholar]
- [44].Carroll JD, Chang J-J, Analysis of individual differences in multidimensional scaling via an N-way generalization of “Eckart–Young” decomposition, Psychometrika 35 (3) (1970) 283–319. [Google Scholar]
- [45].Harshman RA, Foundations of the PARAFAC procedure: models and conditions for an “explanatory” multi-modal factor analysis, UCLA Work. Pap. Phon 16 (1970) 84. [Google Scholar]
- [46].Tucker LR, Some mathematical notes on three-mode factor analysis, Psychometrika 31 (3) (1966) 279–311. [DOI] [PubMed] [Google Scholar]
- [47].Ely G, Aeron S, Hao N, Kilmer ME, 5D and 4D pre-stack seismic data completion using tensor nuclear norm (TNN), in: SEG Technical Program Expanded Abstracts 2013, Society of Exploration Geophysicists, 2013, pp. 3639–3644. [Google Scholar]
- [48].Braman K, Third-order tensors as linear operators on a space of matrices, Linear Alg. Appl 433 (7) (2010) 1241–1253. [Google Scholar]
- [49].Kilmer ME, Braman K, Hao N, Hoover RC, Third-order tensors as operators on matrices: a theoretical and computational framework with applications in imaging, SIAM J. Matrix Anal. Appl 34 (1) (2013) 148–172. [Google Scholar]
- [50].Zhang Z, Ely G, Aeron S, Hao N, Kilmer M, Novel methods for multilinear data completion and de-noising based on tensor-SVD, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2014, pp. 3842–3849. [Google Scholar]
- [51].Lu C, Feng J, Chen Y, Liu W, Lin Z, Yan S, Tensor robust principal component analysis: Exact recovery of corrupted low-rank tensors via convex optimization, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, pp. 5249–5257. [Google Scholar]
- [52].Hu W, Tao D, Zhang W, Xie Y, Yang Y, The twist tensor nuclear norm for video completion, IEEE Trans. Neural Netw. Learn. Syst 28 (12) (2017) 2961–2973. [DOI] [PubMed] [Google Scholar]
- [53].Irrera Paolo IB, Delplanque M, A flexible patch based approach for combined denoising and contrast enhancement of digital X-ray images, Med. Image Anal 28 (2016) 33–45. [DOI] [PubMed] [Google Scholar]
- [54].Zhu F, Qin B, Fen W, Wang H, Huang S, Lv Y, Chen Y, Reducing poisson noise and baseline drift in X-ray spectral images with bootstrap poisson regression, Phys. Med. Biol 58 (6) (2013) 1739–1758. [DOI] [PubMed] [Google Scholar]
- [55].Zhao Q, Meng D, Xu Z, Zuo W, Zhang L, Robust principal component analysis with complex noise, in: Proceedings of the International Conference on Machine Learning, 2014, pp. 55–63. [Google Scholar]
- [56].Guo K, Liu L, Xu X, Xu D, Tao D, GoDec+: fast and robust low-Rank matrix decomposition based on maximum correntropy, IEEE Trans. Neural Netw. Learn. Syst 29 (6) (2018) 2323–2336. [DOI] [PubMed] [Google Scholar]
- [57].Zhao W, Lv Y, Liu Q, Qin B, Detail-preserving image denoising via adaptive clustering and progressive PCA thresholding, IEEE Access 6 (2018) 6303–6315. [Google Scholar]
- [58].Pandey D, Yin X, Wang H, Zhang Y, Accurate vessel segmentation using maximum entropy incorporating line detection and phase-preserving denoising, Comput. Vis. Image Und 155 (2017) 162–172. [Google Scholar]
- [59].Albarqouni S, Javad F, Nassir N, X-ray in-depth decomposition: revealing the latent structures, in: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Springer, 2017, pp. 444–452. [Google Scholar]
- [60].Lin Z, Chen M, Ma Y, The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices, arXiv preprint arXiv: 1009.5055 (2010). [Google Scholar]
- [61].Phansalkar N, More S, Sabale A, Joshi M, Adaptive local thresholding for detection of nuclei in diversity stained cytology images, Proceedings of the ICCSP International Conference on Communications and Signal Processing (2011) 218–220. [Google Scholar]
- [62].Otsu N, A threshold selection method from gray-level histograms, IEEE Trans. Syst. Man, Cybern 9 (1) (1979) 62–66. [Google Scholar]
- [63].Lu C, Feng J, Chen Y, Liu W, Lin Z, Yan S, Tensor robust principal component analysis with a new tensor nuclear norm, arXiv preprint arXiv: 1804.03728 (2018). [DOI] [PubMed] [Google Scholar]
- [64].Kolda TG, Bader BW, Tensor decompositions and applications, SIAM Rev 51 (3) (2009) 455–500. [Google Scholar]
- [65].Boyd S, Parikh N, Chu E, Peleato B, Eckstein J, Distributed optimization and statistical learning via the alternating direction method of multipliers, Found. Trends. Mach. Learn 3 (1) (2011) 1–122. [Google Scholar]
- [66].Sobral A, hadi Zahzah E, Matrix and tensor completion algorithms for background model initialization: a comparative evaluation, Pattern Recognit. Lett 96 (2017) 22–33. [Google Scholar]
- [67].Baka N, Metz CT, Schultz CJ, van Geuns R-J, Niessen WJ, van Walsum T, Oriented gaussian mixture models for nonrigid 2D/3D coronary artery registration, IEEE Trans. Med. Image 33 (5) (2014) 1023–1034. [DOI] [PubMed] [Google Scholar]
- [68].Wang N, Yao T, Wang J, Yeung D-Y, A probabilistic approach to robust matrix factorization, in: Proceedings of the European Conference on Computer Vision, Springer, 2012, pp. 126–139. [Google Scholar]
- [69].Cherapanamjeri Y, Gupta K, Jain P, Nearly-optimal robust matrix completion, arXiv preprint arXiv: 1606.07315 (2016). [Google Scholar]
- [70].Xu Y, Yin W, Wen Z, Zhang Y, An alternating direction algorithm for matrix completion with nonnegative factors, Front. Math. China 7 (2) (2012) 365–384. [Google Scholar]
- [71].Ngo T, Saad Y, Scaled gradients on Grassmann manifolds for matrix completion, in: Proceedings of the Advances in Neural Information Processing Systems, 2012, pp. 1412–1420. [Google Scholar]
- [72].Liu J, Musialski P, Wonka P, Ye J, Tensor completion for estimating missing values in visual data, IEEE Trans. Pattern Anal. Mach. Intell 35 (1) (2013) 208–220. [DOI] [PubMed] [Google Scholar]
- [73].Sobral A, Bouwmans T, Zahzah E.-h., LRSLibrary: low-rank and sparse tools for background modeling and subtraction in videos, Robust Low-Rank and Sparse Matrix Decomposition: Applications in Image and Video Processing, CRC Press, Taylor and Francis Group, 2016. [Google Scholar]
- [74].Tyler C, A Novel Retinal Blood Vessel Segmentation algorithm for Fundus Images, MATLAB Central File Exchange, 2016. [Google Scholar]
- [75].Felfelian B, Fazlali HR, Karimi N, Soroushmehr SM, Samavi S, Nallamothu B, Najarian K, Vessel segmentation in low contrast X-ray angiogram images, Proceedings of the International Conference on Image Processing, ICIP (2016) 375–379. [Google Scholar]
- [76].Kerkeni A, Benabdallah A, Manzanera A, Bedoui MH, A coronary artery segmentation method based on multiscale analysis and region growing, Comput. Med. Image Gr 48 (2016) 49–61. [DOI] [PubMed] [Google Scholar]
- [77].Ambrosini P, Ruijters D, Niessen WJ, Moelker A, Walsum T.v., Fully automatic and real-time catheter segmentation in X-Ray fluoroscopy, in: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, 10434, Springer, 2017, pp. 577–585. [Google Scholar]
- [78].Liskowski P, Krawiec K, Segmenting retinal blood vessels with deep neural networks, IEEE Trans. Med. Image 35 (11) (2016) 2369–2380. [DOI] [PubMed] [Google Scholar]
- [79].Almasi S, Ben-Zvi A, Lacoste B, Gu C, Miller EL, Xu X, Joint volumetric extraction and enhancement of vasculature from low-SNR 3D fluorescence microscopy images, Pattern Recognit 63 (2017) 710–718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [80].Javed S, Mahmood A, Bouwmans T, Jung SK, Background–foreground modeling based on spatiotemporal sparse subspace clustering, IEEE Trans. Image Proc 26 (12) (2017) 5840–5854. [DOI] [PubMed] [Google Scholar]
- [81].Fan J, Chow TW, Non-linear matrix completion, Pattern Recognit 77 (2018) 378–394. [Google Scholar]
- [82].Brbić M, Kopriva I, Multi-view low-rank sparse subspace clustering, Pattern Recognit 73 (2018) 247–258. [Google Scholar]
- [83].Gu J, Wang Z, Kuen J, Ma L, Shahroudy A, Shuai B, Liu T, Wang X, Wang G, Cai J, Chen T, Recent advances in convolutional neural networks, Pattern Recognit 77 (2018) 354–377. [Google Scholar]
- [84].Babaee M, Dinh DT, Rigoll G, A deep convolutional neural network for video sequence background subtraction, Pattern Recognit 76 (2018) 635–649. [Google Scholar]
- [85].Mackey L, Talwalkar A, Jordan MI, Distributed matrix completion and robust factorization, J. Mach. Learn. Res 16 (1) (2015) 913–960. [Google Scholar]
- [86].Li P, Feng J, Jin X, Zhang L, Xu X, Yan S, Online robust low-rank tensor modeling for streaming data analysis, IEEE Trans. Neural Netw. Learn. Syst (99) (2018) 1–15, doi: 10.1109/TNNLS.2018.2860964. [DOI] [PubMed] [Google Scholar]
- [87].Qin B, Hu C, Huang S, Target/background classification regularized nonnegative matrix factorization for fluorescence unmixing, IEEE Trans. Inst. Meas 65 (4) (2016) 874–889. [Google Scholar]
- [88].Vaswani N, Bouwmans T, Javed S, Narayanamurthy P, Robust subspace learning: robust PCA, robust subspace tracking, and robust subspace recovery, IEEE Signal Process. Mag 35 (4) (2018) 32–55. [Google Scholar]
- [89].Ma S, Aybat NS, Efficient optimization algorithms for robust principal component analysis and its variants, Proc. IEEE 106 (8) (2018) 1411–1426. [Google Scholar]