Ultimate MRI

Abstract

The basic principles of Magnetic Resonance have been understood for over 70 years and a mainstay of medical imaging for over 40. At this point, it’s no longer about simply porting these principles to medical imaging. But we are by no means confined to simply polishing either. Significant innovation and even revolution can come to old technologies. The recent revolution in optical microscopy shattered the resolution constraint imposed by a seemingly fundamental physical law (the diffraction limit) and reinvigorated a 500-year-old modality. Progress comes from re-examining old-ways and sidestepping underlying assumptions. This is already underway for MRI; and is fueled by advances in image reconstruction. Reconstruction increasingly employs sophisticated general models often using subtle and hopefully innocuous prior knowledge about the object. This allows a careful re-examination of some basic prerequisites for MRI such as uniform static fields, linear encoding fields, full Nyquist sampling, or even a stationary object. These powerful reconstruction tools are driving changes in acquisition strategy and basic hardware. The scanner of the future will know more about itself and its patient and his/her biology than ever before. This strategy emboldens relaxed hardware constraints and more specialized scanners, hopefully expanding the reach and value offered by MR imaging.

Introduction

The future of MRI technology appears to rest on a number of evolving directions that have moved us away from a slavish devotion to Fourier encoding to a more general model. In a modern accelerated parallel imaging acquisition the Nyquist sampling “limit” is merely a suggestion which is now rarely followed. The vast minority of the kspace samples are actually encoded by the RF reception system not the gradients. The immediate benefit is a substantial increase in acquisition speed, quality and information extraction. These benefits have opened of the flood-gates to sophisticated image reconstruction methods that manipulate the data to a degree that would have been found discomforting a generation ago. Prior knowledge can creep into image generation in subtle ways, but with such remarkable benefits that it’s impossible to argue against that path, although a wary eye on unwanted side effects is needed.

Simultaneous with the advance of the signal processers, increasingly sophisticated hardware optimization strategies are being developed to increase performance. Perhaps more importantly, the optimization targets are changed. As the ability of image reconstruction improves, acquisition and hardware targets shift to maximally exploit the algorithm’s ability, and old constraints are relaxed. The latter provides elbow-room for the hardware designer to contemplate either expanding in the faster/ stronger/ see-more direction, or the cheaper more portable path. But, as engineering challenges fall, new biological challenges rise, from the static, switched field and RF field issues as well as from patient motion. Fortunately, biological effects can also be brought under the lens of model-based optimized design and influenced by image reconstruction improvements. MR system engineering considerations are expanding from traditional engineering of B field generation/shaping to intimately incorporating biological models and constraints. As biology becomes firmly entrenched in the engineering, the creation and exploitation of new degrees of freedom is needed to navigate these biological constraints.

This article briefly reviews three broad areas seen in the (somewhat murky) “crystal ball” as the start of a lengthy path toward the “ultimate MRI.” The first is entitled “Scanner, know thyself”, which describes the liberating effect of an improved forward model for image reconstruction. This includes a coordinated acquisition and reconstruction strategy; an idea of seemingly obvious benefit but underappreciated for years. The second section is entitled “Know your patient” which touches on some of the well-known benefits of incorporating prior knowledge about the image and/or imaging subject for accelerating the acquisition, or extracting. The Machine Learning (ML) tidal wave appears well poised to maximally exploit these “priors”, perhaps without even telling us what they are. Finally, the article briefly addresses the potential of these two paths to expand the concept of what a scanner looks like and does, with an eye toward extending the reach of MR.

Scanner, know thyself

An old physics proverb states: “if you can measure a systematic error, you can fix the systematic error.” Often, the “error” is calculated from a measurable property of the instrument. E.g. image distortion is predictable from a measured B₀ field deviation map and knowledge of the acquisition bandwidths. The effect on the recorded data is easily modeled, suggesting that the image reconstruction also be based on this model. A “forward-model” describing how to generate the data given the image is intrinsic to even the earliest MR image reconstructions. Lauterbur’s original reconstruction assumed the data consisted of projections formed from linear gradients (1) and the Aberdeen group’s elegant spin-warp model (2) and the latter kspace picture (3) included a similarly idealized model of the acquisition. Currently, the term “model-based reconstruction” usually implies a more general forward model describing how to estimate the raw data based on the object followed by some form of iterative search to invert that relationship to find the object giving; the “best fit” to the data, possibly subject to constraints.(4) (5, 6) This approach has gradually replaced attempts to “fix” the data to adhere to the standard discrete Fourier transform (DFT) model, for example by re-gridding (7, 8) or “correct” the image after simple reconstruction for things like B₀ off-resonance (9, 10) or (B₁⁻) receive coil shading (11).

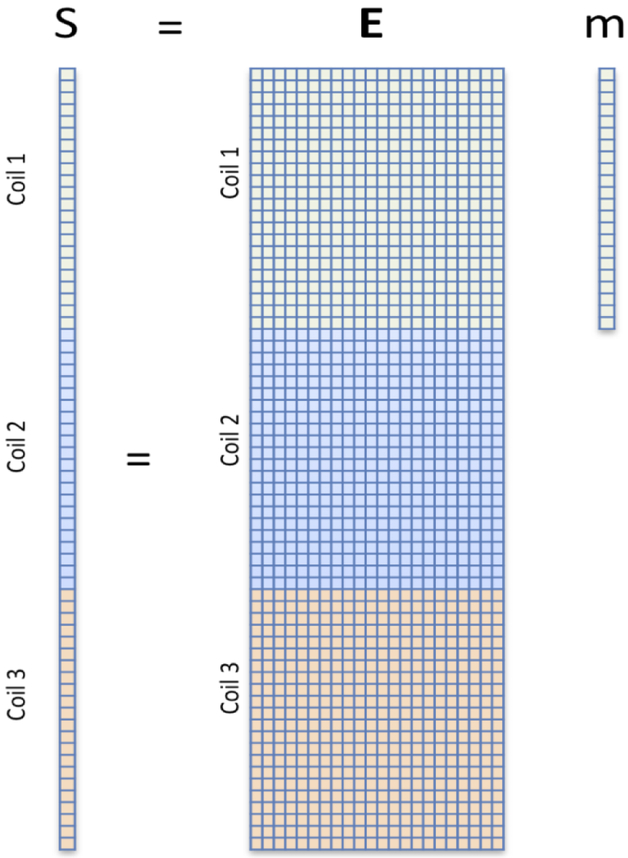
The basic formalism of the forward model is show in Figure 1. Each digitized data point is a weighted sum of the pixel values, with complex weights imposed by the encoding fields. On a pixel by pixel basis, the encoding phase factors are easy to calculate as are spin relaxation and coil reception profile magnitude factors. The summation implicit in the matrix multiplication is provided by the receive coil. Thus, the forward model is a simple linear matrix equation with vectorized sampled (raw) data and image pixels. In a uniformly sampled spin-warp framework, the encoding matrix is the discrete Fourier transform (DFT) and the image would be solved one coil at a time by applying its well-known inverse. For anything more complicated, the encoding matrix is no longer the DFT or even guaranteed to have an inverse and good luck finding an inverse matrix given E’s size (almost 10¹⁶ elements for a 256-cube image with 32 receive channels.) But the image vector can be iteratively estimated as a least-squares optimization problem minimizing the “data consistency”, i.e. the difference between the measured and expected data points using methods such as the conjugate gradient method (12) or the LSQR solver (13). Other approaches have been explored such as Minimum Likelihood formalisms useful when more difficult noise models must be accomodated. (4, 14)

Fig. 1: Linear forward model approach to MR image encoding and reconstruction.

For a raw-data signal sampled at time t, an applied magnetic field modulates the proton spin phase with a simple e^{−iγΔB(x,y,z,t)t} phase factor where ΔB(x,y,z) is the deviation from a uniform field due to any source, e.g. an applied encoding field, magnet inhomogeneity, eddy current, or truck passing by. Other modulations such as relaxation effects and detection coil sensitivity profiles also appear as multiplicative factors in front of each pixel’s value. The detection process simply sums the weighted values from all pixels, allowing the entire process to be described as a matrix multiplication. In most MRI scanners, a good deal of work ensures that E is very nearly the discrete Fourier matrix, with its well-behaved properties and a known inverse, where as the “inverse problem” of estimating the image based on the data and forward model is more burdensome, requiring an iterative search.

Extracting information from the coil profiles

The power of the method lies in its ability to generalize and take into account any imperfection that can be described in the forward model; it is extendible in virtually any direction imaginable. A second advantage, discussed in the next section, is the ability to regularize the optimization, imposing prior knowledge constraints or penalties such as scarcity in some domain. One of the first glimpses of the power of the forward model arises from simply adding the multiplicative B₁⁻ receive coil profile to the model and stacking the sampled “kspace” data vectors and encoding matrices from the individual coils in a phased array (as in Fig. 1). Note, at some point we should probably stop referring to the data-vector as “kspace” since E now deviates from the DFT matrix. The “tall, skinny” E matrix immediately screams “over-determined” and suggests that samples could be omitted. The B₁⁻ receive coil profiles, previously viewed as a nuisance shading of the final image, are recast as valuable spatial encoding fields. They modulate the signal similar to the gradient field’s role (although with non-orthogonal patterns). If the under-sampling pattern is regular (e.g. every other kspace line), then we immediately recognize the SENSE method (15).

Fixing acquisition imperfections

The complete flexibility and general nature of the model-based approach positions it well for future innovation. Any sort of spatial modulated can be applied to the spins and we now know how to reconstruct the image as long as E is well conditioned. Extensions have included non-rectilinear kspace trajectories (5, 16), non-linear encoding fields (17, 18), gradient nonlinearity, (19) pre-characterized eddy current and measured gradient imperfections(20), quadratic encoding from RF excitations patterns (21, 22), and temperature related permanent magnet field drift (23). The scanner of the future will have an extensive pre-characterization and even dynamic selfassessment of its fields and utilize this information within a generalized image reconstruction framework. Additionally, even if a pre-characterization of a gradient is not known, it is possible to try to describe the miscalibration (nuisance parameters) in the model by including them in the forward model as a small number of unknowns and jointly estimate them with the image. (24)

Patient Motion is defeated

Mitigating patient motion, the mother of all nuisance parameters, is an important, although not fully realized extension of the formalism. Motion corruption of MRI is currently estimated to cost $1.4B USD yearly in the US alone (25). For the case of rigid-body head motion, the image is rendered artifact free if forward model is successfully placed in the coordinate system of the object, ideally including a model of spin-history effects. Non-rigid body motion is more difficult but has been approached through an image entropy cost function. (26, 27) The rigid body forward model contains rotation and translation matrices in front of E, allowing a different object position for each sample point. Artifact-free images follow from the inversion of this custom, motion-inclusive, E matrix. Inverting the model is straight-forward when the position information at each sample time is known, e.g. from a navigator acquisition or external tracking system.(28, 29) The problem becomes harder, but perhaps not intractable, if the position information is not known but is left for the iterative reconstruction to estimate. Estimation of the position parameters is plausible given that a multielement coil array, in effect, encodes head position. I.e. the signals from the elements are modulated in a predictable way as the head moves closer to some elements and farther from others.(30)

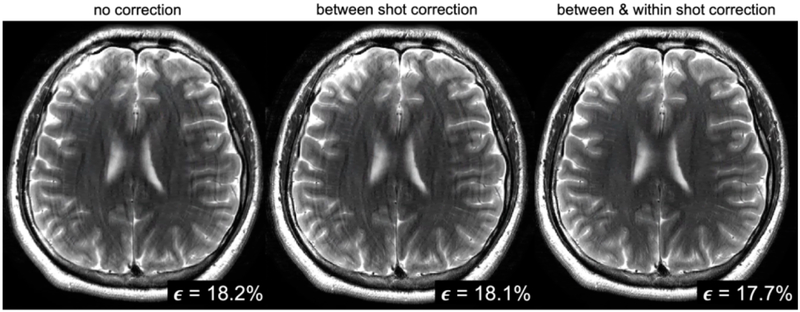
Thus the motion information has been embedded in our data all along, waiting for a smart search algorithm to find it. Considerable progress has been made toward stabilizing this non-convex search using a data-consistency cost function (31-33) and also an image entropy cost function.(26, 27) But the result is a difficult non-convex optimization problem and more needs to be done to ensure speedy convergence to a high-quality image. Additional book-keeping is needed to help mitigate spin history effects and convergence could be aided by perhaps regularizing the motion (i.e. imposing smooth motion, or piece-wise continuous position parameters). In such a non-convex joint-optimization (image + motion parameters), aiding the optimization is about more than just speeding up the search; it often leads to a better solution (removes more artifact). To this end, neural-net based machine learning appears well-poised to assist in the difficult non-convex search problem, either by directly relying on a CNN trained to identify motion artifact(34), or indirectly using this training to facilitate the search process in the forward model formalism(35). Figure 2 shows results from a CNN supported data-consistency driven reconstruction of a moving head using only data from a conventional multi-shot RARE T₂ acquisition, perhaps the most common clinical brain sequence. The CNN improved convergence speed, provided more artifact mitigation, and allowed extension of the model to include motion within the shot. (35)

Fig. 2: Jointly solving for motion.

In this reconstruction of a RARE style clinical T₂ brain acquisition, the forward model included head rotation and translation unknowns, both between shots of the RARE sequence and within the shot. No tracking or navigator information was used, instead a joint search was performed for the head position parameters and the image based on only the kspace data from the array. A machine learning method was employed within the search to improve the non-convex optimization, but the final image derives only from the forward model inversion (using the best estimate of the motion parameters). From Haskell et al. (35)

This and other promising results suggest that motion can be mitigated without the added complexity of trackers or navigators. But why stop with motion? A host of other biological nuisances corrupt our images, such as respiration and pulsatile flow, both of which are parameterized with relatively few (unknown) parameters. As more physiological sensors are built into the patient bed, incorporating their information into the reconstruction is likely beneficial.

Finally, the vast success of model-based reconstructions has implications for the choice of acquisition protocol. This started with parallel imaging driving the proliferation of multichannel arrays; today, virtually all clinical images are detected with phased array coils. The next step was tailoring the sampling patterns to improve accelerated imaging by controlling aliasing patterns (36-38) or random sampling (39). Other studies have optimized flip angle schemes, for example to optimize performance of MR fingerprinting parameter mapping. (40)

Know your patient

The flexibility outlined above provides a strong push toward the adaptation of generalized reconstruction methods. But, additional benefits arise from adding prior knowledge about the object, for example as a simple regularization term in the cost function. Of course, if you already know what the object looks like, why bother imaging it? A valid question, but impressive results can be obtained from innocuous seeming assumptions about the object. Compressive sensing assumes that the object is sparse in a chosen domain and achieves impressive ability to de-noise or further increase undersampling (which speeds up the acquisition). (39) Other popular regularizers include Tikhonov regularization toward a reference image or simply a uniform image, quadratic roughness, and total variation (TV). (4)

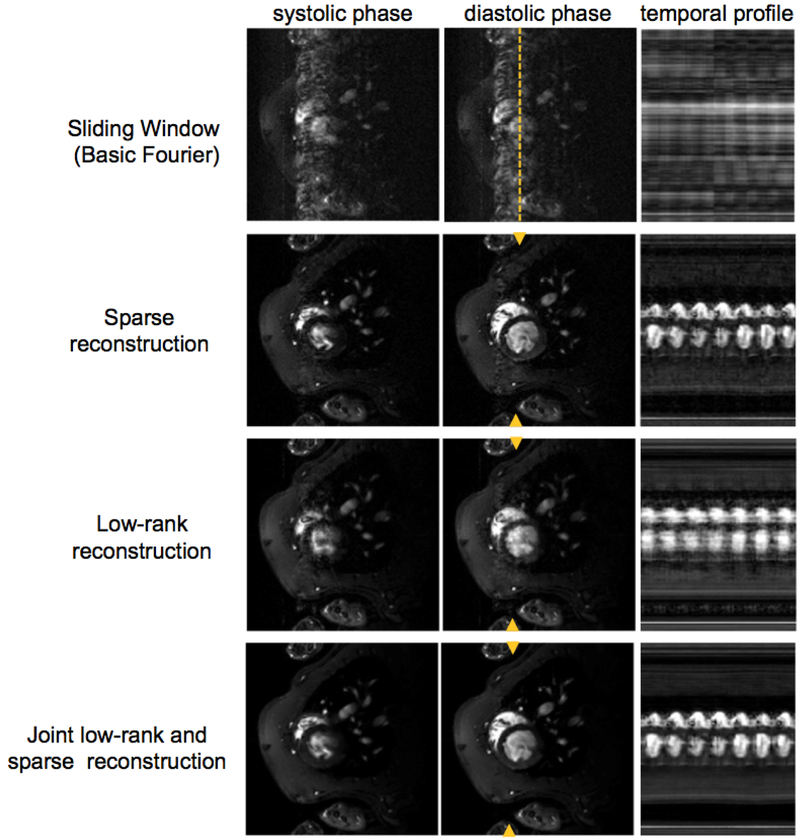
Of course, the real benefit of the regularization occurs when you have a pretty good idea what you are looking for. This occurs most naturally when performing time-series imaging or stepping through image contrast parameters (for T₁ or T₂ mapping). In this case, the previous image makes a good regularizer and allows exploitation of the high degree of mutual information in the series. Namely, an image series with only small temporal changes is naturally very sparse in time domain. Figure 3 shows the incredible improvements achieved in reconstructing a sparsely sampled, un-gated cardiac time-series using a combined low-rank and sparse model.(41) Contrast mapping exams are another area where good priors can easily be found. Two images with slightly different TEs acquired in the same patient have considerable joint information, thus reconstructing this data jointly has benefits. (42, 43) MR scanners have traditionally reconstructed, a patient’s scan as if it did not know anything about the scan of the same anatomy completed 5 minutes earlier. Joint reconstruction of all the images from an exam makes a good deal of sense and the generalized framework (perhaps with small patient position changes explicitly modeled) appears both doable and desirable. Maximum benefit will be derived when the acquisition scheme is also fully coordinated to take advantage of the joint reconstruction.

Fig. 3: Prior knowledge in the reconstruction.

In this example, data from a highly undersampled non-gated cardiac time-series in a rat was reconstructed using a combined Sparse + low rank model of the spatial temporal data. From Zhao et al. (41)

Finally, its impossible to talk about the revolution in image reconstruction without addressing the newly born 900 lb gorilla in the room; Machine Learning (ML). The term ML itself is poorly defined, but the main flavor in use by the MRI community is supervised learning based on a Convolutional Neuronal Networks (CNN) trained on example data. The application of the trained network to a new (unknown) data set is computationally fast, and evidence suggests that the CNN can generalize sufficiently to reconstruct data not in the training set. (44-47) This approach, in effect, throws out the detailed physics used in the forward models discussed above and replaces it with a completely generic model; the convolutional neural net. By finding the weights for the net in the training process, the network is “learns” all it needs to know to produce reconstructions similar to the training data. In most MR work with CNNs, a “physics-based” forward model is used to generate the training data, implying that the CNN “model” will only be as good as the original forward model. This does not feel like an advance, although applying the CNN is computationally faster and perhaps achieves a more optimum regularizer against noise. But some control is lost, both in knowledge about what it is happening to the data, especially in terms of blurring and the strength of the regularization applied.

The limited methods for understanding and controlling what the network is doing has generated some skeptics.(48) Nonetheless, the CNN has many nice features such as built in image translational invariance (49) and commonalities with well known methods like spline interpolation.(50) If Compressed Sensing is occasionally derided as “intelligent smoothing”, then it is fair to describe ML reconstructions as “intelligent interpolation.” Viewing it as a fancy interpolation tool, it is safest if the unknown data is well represented by the training data (limiting interpolation and avoiding extrapolation.) Nonetheless, the successes of the ML approach speak for themselves, and it appears to be a powerful tool, perhaps best employed where we do not have a good model to guide us, as is the case for removal of complex artifacts such as from motion or for use within a more traditional model; i.e. employ the CNN within a forward model framework (35, 46, 51, 52).

Breath and reach of MR expands

The hardware designer of the future should feel liberated by the reconstruction revolution. First and foremost, the system designer can rest assured that there is a path to image reconstruction for any crazy idea s/he comes up with. The ability to reconstruct images with relaxed acquisition hardware constraints (for example B₀ uniformity or gradient linearity) provides two possible paths. One path is toward increased performance capabilities. Stronger/faster gradients are possible if you relax the linearity constraint (a primary determinant of the Peripheral Nerve Stimulation (PNS) ceiling). Similarly, improved ability to handle eddy currents during reconstruction could boost gradient efficiency. Another path is toward scanners that are cheaper and easier to site and operate, significantly increasing the impact of MRI.

Relaxing engineering constraints is paramount for reducing costs, and the improved reconstructions allow every aspect of the system to be re-evaluated. First and foremost, successful denoising strategies enable lower field systems with concomitant benefits in cost and siting. Gradient efficiency and thus amplifier and water cooling costs can be impacted when changes to the encoding fields can be managed. Magnets become cheaper, lighter and shorter when the field homogeneity constraint is relaxed. (53) Even in high-income countries the cost of MRI shapes when and how it is used. In countries with limited scanner access the impact could be still greater.(54) The introduction of low-cost, and/or truly portable scanners could also enable new point-of-care and monitoring applications which are not feasible for today’s scanners in centralized settings. As lower fields become practical, unconventional designs including extremely portable and single-sided designs can be contemplated. (23, 55-57)

In conclusion, the image reconstruction revolution is significantly changing the look and feel of MRI scanners. The scanner seen in the crystal ball knows more about itself and its patient and has elegant ways to utilize this information which hopefully will translate into new benefits.

Highlights.

• As MRI is moving toward a more generalized approach with added degrees of freedom in the RF reception, transmission and encoding fields, and generalized model based reconstructions that can reconstruct from just about anything.

• Model-based reconstructions, together with their streamlined approach to adding prior knowledge will increase opportunities for faster imaging and imaging with relaxed hardware constraints, ultimately extending the performance and reach of MRI.