Abstract
DNA has been recognized as a promising natural medium for information storage. The expensive DNA synthesis process makes it an important challenge to utilize DNA nucleotides optimally and increase the storage density. Thus, a novel scheme is proposed for the storage of digital information in synthetic DNA with high storage density and perfect error correction capability. The proposed strategy introduces quaternary Huffman coding to compress the binary stream of an original file before it is converted into a DNA sequence. The proposed quaternary Huffman coding is based on the statistical properties of the source and can gain a very high compression ratio for files with a non-uniform probability distribution of the source. Consequently, the amount of information that each base can store increases, and the storage density is also improved. In addition, quaternary Hamming code with low redundancy is proposed to correct errors occurring in the synthesis and sequencing. We have successfully converted a total of 5.2 KB of files into 3934 bits in DNA bases. The results of biological experiment indicate that the storage density of the proposed scheme is higher than that of state-of-the-art schemes.
Keywords: DNA information storage, Quaternary Huffman code, Synthetic DNA, Storage density
Introduction
Global data are increasing explosively with the rapid development of the digital society, which is raising great challenges for information storage. Current technologies mainly rely on optical and semiconductor media to store data (Goda and Kitsuregawa 2012), which cannot satisfy current practical needs (Panda et al. 2018). Moreover, the production of monocrystalline silicon leads to serious environmental pollution and energy consumption. Therefore, there is an urgent need for an alternative storage medium. DNA has high information storage density and has attracted extensive attention. The binary storage capacity of a DNA molecule is about 4.2 × 1021 bits per gram, which is 420 billion times that of traditional storage media. DNA is also one of the most stable biomolecules, and thus can preserve information over extremely long periods.
The idea of storing information in DNA nucleotides has been proposed for decades, and the substantial progress achieved has been promising (Panda et al. 2018; Yazdi et al. 2015; Shipman et al. 2017; Akram et al. 2018). Joe Davis and a collaborator from MIT precisely encoded icons into DNA, which they called Microvenus (Davis 1996). Bancroft et al. (2001) successfully stored encoded words into DNA segments and utilized the four bases (A, T, C, and G) to encrypt information. Church and Kosuri made a remarkable breakthrough when they encoded images, an HTML draft, and a Java script (5.27 MB of files in total) into DNA molecules with higher efficiency and lower cost using the next generation of DNA synthesis and sequencing technology (Church and Kosuri 2012). A theoretical storage density of 1 bit/nt was achieved with one binary digit encoded per base. Goldman and his team exploited Huffman code to convert the binary digits of information into base-3 digits, which were then mapped to DNA bases according to the rotating code (Goldman et al. 2013). About 739 KB of data were stored in DNA, and the storage density was 0.33 bits/nt. Grass et al. (2015) proposed a special error correction scheme to cope with the errors in synthesis and sequencing. Bornholt et al. (2016) achieved a storage density of 0.88 bits/nt by taking the exclusive-or of two strands to form a third one. Blawat et al. (2016) developed a robust and efficient forward error correction scheme, which can deal with all types of errors in DNA synthesis, amplification, and sequencing. Notably, Erlich and Zielinski creatively developed a storage strategy called DNA Fountain, which applied fountain code to DNA information storage (Erlich and Zielinski 2017). They made one base corresponding to two binary digits and improved the coding potential and reliability of DNA nucleotides.
A high storage density can effectively reduce the cost and time of DNA synthesis and sequencing. Nevertheless, previous methods mainly tried to convert binary streams directly into DNA sequences without considering the characteristics of the original input data. Thus, the information storage densities were not greater than 2 bits/nt. Recently, Dimopoulou et al. (2019) applied a coding algorithm to the quantized wavelet coefficients of an image and conducted simulations on a Lena image with a size of 512 by 512 pixels . They achieved a nearly lossless compression and a coding potential of 2.14 bits/nt. They achieved a higher compression ratio using discrete wavelet decomposition (DWT) to take advantage of the spatial redundancies of the image, but they did not consider the statistical distribution of the input data.
This work presents a novel strategy for information storage in DNA that takes advantage of non-uniform data distributions to compress data through entropy-based coding, which results in higher coding density. We propose compressing the input binary streams with fully lossless quaternary Huffman coding before converting them into DNA bases. The quaternary Huffman coding is a type of entropy coding that can take full advantage of the statistical redundancy of the source and reduce the number of bits required to represent data. The compression allows us to make full use of the DNA bases and improve the storage density for files with a non-uniform probability distribution of the source, such as text, image, and audio. We also introduce an improved quaternary Hamming code based on the actual requirements for errors arising in the synthesis or sequencing process. Experimental results show that the improved quaternary Hamming code can robustly correct errors with low redundancy. Lastly, we design the carrier DNA strands while considering the difficulties in synthesizing long DNA sequences and the objective requirement of biological experiment. The results of biological experiment show that the original input files are synthesized and recovered perfectly by sequencing and decoding.
Methods
The framework of the proposed DNA information storage strategy
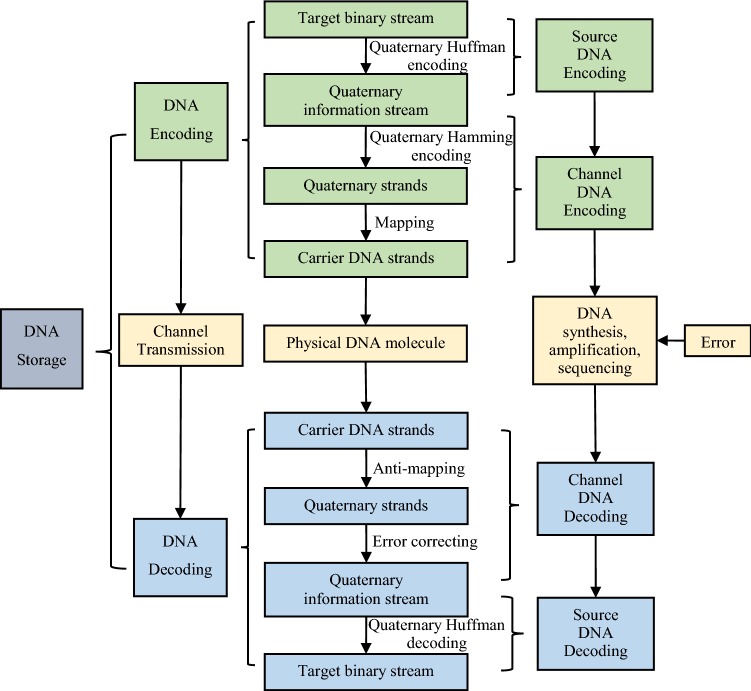
Similar to a communication system, the proposed DNA information storage framework includes DNA encoding, channel transmission, and DNA decoding, as shown in Fig. 1.
Fig. 1.
The framework of the proposed DNA information storage strategy
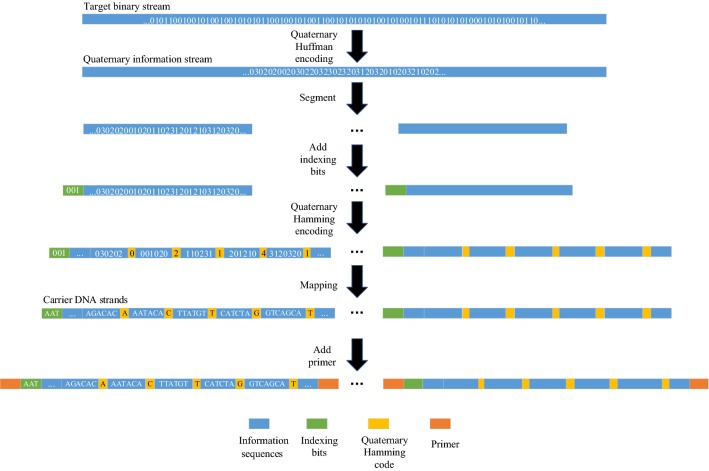
DNA encoding realizes the conversion from a target binary stream to carrier DNA strands, which can be further divided into source DNA encoding and channel DNA encoding. The encoding process is illustrated in Fig. 2. The source DNA encoding constructs the quaternary information stream with quaternary Huffman coding to compress the input binary stream. In channel DNA encoding, the quaternary information stream is segmented into several strings with a certain length, and then indexing and quaternary Hamming code are sequentially attached to these strings to obtain the quaternary strands. Next, the quaternary digits are mapped to DNA bases (0–A, 1–T, 2–C, and 3–G). The carrier DNA strands are synthesized, stored, and later retrieved.
Fig. 2.
The proposed DNA encoding process
Channel transmission corresponds to several biological processes based on DNA molecules, including synthesis, amplification, and sequencing. We use polymerase chain reaction (PCR) to amplify the strands and sequence the DNA library to recover the original information. All of these procedures are important for DNA information storage, but several errors may be introduced (Hughes and Ellington 2017; Mardis 2017).
DNA decoding is just the reverse of encoding, and completing the original information restoration. Similar to DNA encoding, DNA decoding contains channel DNA decoding and source DNA decoding. The reads acquired from DNA sequencing are scanned to obtain the carrier DNA strands. During channel DNA decoding, the quaternary strands are obtained according to the mapping rule between four bases and the quaternary digits. Strings with errors are corrected through the quaternary Hamming code, and then all fragments are connected to the full-length quaternary information stream based on the order inferred by the indexing bases. The source DNA decoding retrieves the binary stream by quaternary Huffman decoding.
Quaternary Huffman coding
As lossless coding methods with variable length, Huffman coding can produce the shortest codes as it represents more frequently appeared symbols by fewer bits. Huffman coding has a good compression capability and is the optimal method for multiple independent information sources.
DNA is a natural quaternary storage model with four bases: A, T, C, and G. Therefore, a coding method that can generate multi-ary code is required to make full use of the four bases. However, Huffman coding is mostly used for binary coding, which does not directly satisfy this requirement.
There are two works on Huffman code for DNA information storage to the best of our knowledge. Ailenberg used the principles of the Huffman code to define DNA codons for unambiguous information coding (Ailenberg and Rotstein 2009). They did not directly use the Huffman code to compress the original file. The second work adopted the Huffman code to convert the binary digits of information into base-3 digits. However, due to the not full consideration for the four bases of DNA, the storage density achieved by this ternary Huffman coding was very low, with 0.33 bits/nt (Goldman et al. 2013).
Considering the natural characteristic of DNA and the shortcomings of the above works, the proposed method keeps the tree construction idea of Huffman coding, while the output code revised to quaternary, and the output quaternary digits are mapped to the four bases of DNA. As a result, DNA nucleotides can be taken full advantages of, and the information storage density increases.
According to the Huffman coding process, it is necessary to build a complete Huffman tree to make the average length of the output codes the shortest. For D-variants Huffman coding, of order leaves is divided from one order node, and the number of increased leaf nodes by one split is . Therefore, the total number of leaves is:
| 1 |
where is a non-negative integer that represents the number of times the node splits from the first order of -ary tree. That is, the total number of symbols in a system with bases is:
| 2 |
where represents the number of combinations during the coding process. If this equivalence cannot be satisfied, additional symbols with a probability of zero should be added to obtain:
| 3 |
An example of quaternary Huffman coding with eight source symbols is shown in Fig. 3. The original number of source symbols is eight, and the number of bases is four. Two (i.e., ) additional symbols with a probability of zero are added since there is no positive integer that can satisfy Eq. (2), and thus the value of is two.
Fig. 3.
An example of quaternary Huffman coding with eight source symbols
The binary stream converted from the source file is divided into segments with length called scanning bits. A larger value of can lead to more efficient coding. However, the value of cannot be increased indefinitely due to its high influence on the complexity of the algorithm. The upper bound of (i.e., ) in this work is set to 52 to guarantee reasonable algorithm complexity. The process of quaternary Huffman coding is shown in Fig. 4, and the detailed steps are listed in Algorithm 1.
Fig. 4.
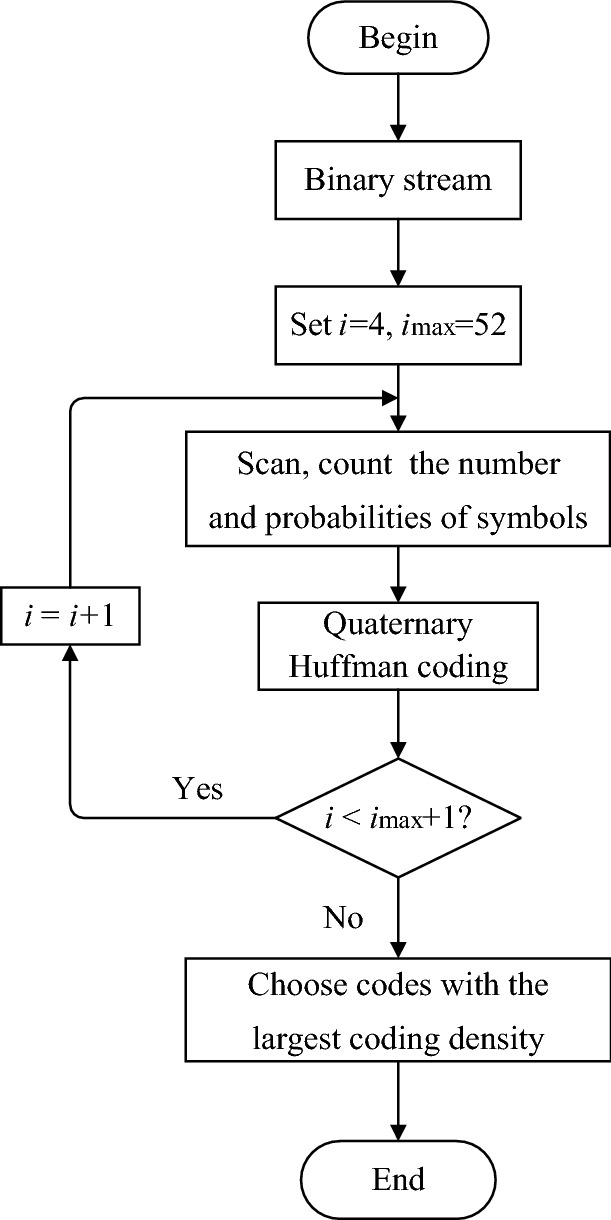
The process of quaternary Huffman coding
Quaternary Hamming code
Hamming code is one of the most widely used channel codes. The relevant theories and techniques have matured after years of research and applications since the concept was put forward in 1950. It is widely used in communication, data storage (Borchert et al. 2013), image encoding, and digital circuit (Rajaei et al. 2017). Hamming code is the most efficient single error correcting complete block code and is an optimal alternative with low redundancy when the channel environment is appropriate (Babu et al. 2017). Therefore, we use Hamming code to correct errors while considering the situation of specific errors arising in DNA synthesis and sequencing. Although Hamming code was chosen in this study, other error correction codes such as RS code can also be compatible with the proposed quaternary Huffman coding strategy.
The information is divided into several groups based on a certain rule when correcting errors. Parity check bits are arranged in each group, and then tests are done to determine the location of errors. The codes with errors can be corrected by reversing the wrong bits.
The Hamming code is generally represented by , which satisfies the inequality function as follows:
| 4 |
where is the number of transmission bits, is the number of information bits, and is the number of check bits.
According to Eq. (4), the relationship between and can be derived as shown in Table 1.
Table 1.
The relationship between the number of information bits and check bits
| The number of information bit (bits) | 1 | 2–4 | 5–11 | 12–26 | 27–57 | 58–120 | … |
| The number of check bit (bits) | 2 | 3 | 4 | 5 | 6 | 7 | … |
However, Hamming code cannot be directly used in our scheme because parity check is not applicable to quaternary code. Therefore, we make modifications to define a new value of the check bits in this study. Taking quaternary Hamming (7, 4) code as an example, we set the check bits matrix to:
| 5 |
where is a matrix indicating the relationship between check bits and information bits, and is a matrix of the information bits.
If errors occur, the location of errors is determined first. Non-zero values of the syndrome are subtracted from the error bits in quaternary (allowing borrowing) to obtain the correct bits. That is, error correction is completed by the quaternary Hamming code.
Results and discussion
We validate the performance of the proposed DNA information storage framework by performing three sets of experiments. First, coding experiments are conducted with text, image, audio, and compressed file. Second, experiments are performed with different lengths of quaternary Hamming code to compare their correction capabilities. Third, a biological experiment based on synthesis DNA is carried out.
Coding performance of quaternary Huffman coding
We perform coding experiments to assess the coding performance of the proposed quaternary Huffman code, and introduce the compression ratio as a measurement. The experimental results are given for the case of even scanning bits since results for odd bits are relatively poor. The coding environment comprises Windows 10 64 bit as the operating system, an i7-7500u processor, 8 GB of running memory, and MATLAB R2017a.
To validate the generality of the proposed quaternary Huffman coding, different formats of files are provided as the input data, including texts, images, compressed files, etc., as shown in Table 2. The formats of the compressed files are .rar and .zip, which are used to package the first three text files and an image file called kids.tif.
Table 2.
Input data for encoding, size, and type
| Size | Type | Name |
|---|---|---|
| 6.24 KB | Text | medicalcase.txt |
| 26.6 KB | Text | writtenjudgment.txt |
| 796 B | Text | SongofMulan.txt |
| 392 B | Text | LittleStar.txt |
| 1.37 MB | Text | PilgrimagetotheWest.txt |
| 4.02 KB | Monochrome image | circbw.tif |
| 43.5 KB | Gray image | rice.png |
| 94.7 KB | Color picture | kids.tif |
| 44 KB | Audio | sp01.wav |
| 67.7 KB | Zipped file | file.rar |
| 69.2 KB | Zipped file | file.zip |
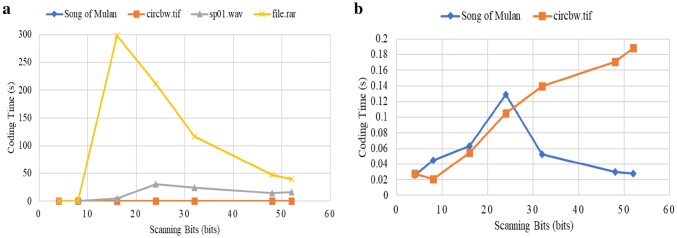
Figure 5 shows the compression ratios of Song of Mulan, circbw.tif, sp01.wav, and file.rar with different scanning bits. The highest compression ratios for these files are 10.81, 12.48, 7.9, and 7.62, respectively. Thus, our encoding scheme achieves high performance on text, image, audio, and compressed file. In addition, the compression ratio increases with the number of scanning bits. This occurs because the types of source symbols increase and the probabilities of each symbols become more diverse as the scanning bits increase, leading to better performance of the Huffman coding.
Fig. 5.
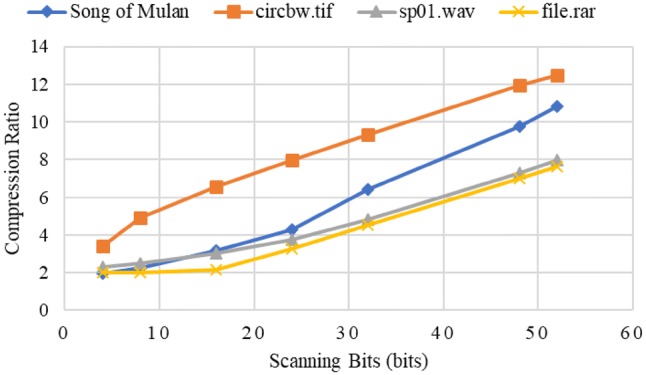
Compression ratios of Song of Mulan, circbw.tif, sp01.wav, and file.rar with different scanning bits
Figure 6 shows the relationship between the scanning bits and coding time. There are very different patterns for the four files. The coding time is proportionally related to the number of source symbols since the coding object is the probability of source symbols. Theoretically, the number of source symbols is when the scanning bits are . However, there are usually not that many symbols in each file in practice, which will lead to reduced coding time. The number of source symbols of each type of file shows different trends when the scanning bits increase due to the files’ unique binary stream characteristics. Consequently, the patterns of the coding time differ for different types of files.
Fig. 6.
a Coding time of Song of Mulan, circbw.tif, sp01.wav, and file.rar with different scanning bits. b Coding time of Song of Mulan and circbw.tif with different scanning bits
In particular, for file.rar, the number of source symbols is before is 16, so the coding time increases steadily. But after that, the number of source symbols decreases, and so does the coding time.
Error correction performance of quaternary Hamming code
The error correction capability is compared between different quaternary Hamming codes: Hamming (15, 11) code, Hamming (31, 26) code, and Hamming (63, 57) code. The codes are applied to the same file, circbw.tif. Random errors with probabilities of 1/10,000, 1/5000, 1/2500, and 1/1000 are introduced to simulate different situations of practical errors. The corrected DNA sequences are compared with the actual one to evaluate the number of bits unable to be rectified and corresponding frequencies. Trials with the same error probability are all carried out 100 times, and the average values are presented as the results in Table 3.
Table 3.
Experimental results of quaternary Hamming code
| Code | Transmission redundancy (%) | Probability of errors | Error frequency after correcting |
|---|---|---|---|
| Hamming (15, 11) | 26.67 | 1/10,000 | 0 |
| 1/5000 | 0 | ||
| 1/2500 | 0 | ||
| 1/1000 | 0.013‰ | ||
| Hamming (31, 26) | 16.13 | 1/10,000 | 0 |
| 1/5000 | 0.003‰ | ||
| 1/2500 | 0.002‰ | ||
| 1/1000 | 0.012‰ | ||
| Hamming (63, 57) | 9.52 | 1/10,000 | 0 |
| 1/5000 | 0.003‰ | ||
| 1/2500 | 0.002‰ | ||
| 1/1000 | 0.037‰ |
As shown in Table 3, the redundancy of Hamming code gradually decreases as the number of bits increases. The error rate in biological experiments is generally less than 1/10,000 if the operation is rigorous and advanced DNA synthesis and sequencing techniques are used. Therefore, all three codes provide reasonably good error correction performance. However, longer Hamming code bits result in, a greater probability of errors occurring since errors in DNA sequences are random. Consequently, the error frequency after correcting increases correspondingly.
We eventually select quaternary Hamming (31, 26) code after considering the trade-off between redundancy and error correction performance of the Hamming code and the specific errors arising in DNA synthesis and sequencing. The quaternary Hamming (31, 26) code performs well in error correction without introducing too much redundancy. Therefore, the channel bandwidth is relatively narrow in this case.
Real oligonucleotide synthesis and sequencing
We carry out a biological experiment to verify the feasibility of the proposed scheme. Files of Song of Mulan, Twinkle Twinkle Little Star, and circbw.tif (Fig. 7), are chosen as input data for the experiment (5.2 KB in total). Specifically, the length of carrier DNA strands is 465 nt due to difficulties in synthesizing long DNA sequences. The information stream encoded by quaternary Huffman code with 32 scanning bits is segmented into eight fragments of 380 bits (although the last one can be less than 380 bits). Next, 10 bits for indexing and 75 bits of quaternary Hamming (31, 26) code are added to each fragment in order. The obtained quaternary fragments are converted into carrier DNA strands, and two 25 nt primers are attached to both ends of them during DNA synthesis. Consequently, a total of 3934 DNA bases are obtained.
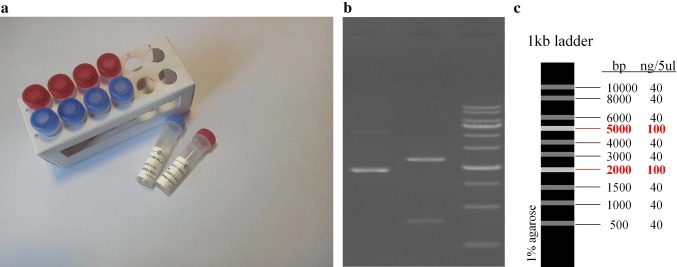
Fig. 7.
Input data for the biological experiment: a Song of Mulan, b Twinkle Twinkle Little Star, and c circbw.tif
The biological experiment includes three steps: synthesis of the carrier DNA strands, PCR amplification and sequencing of the short strands, and the recovery of information by decoding DNA strings. The carrier DNA strands in the stored pool (Fig. 8a) are amplified using PCR. Primers are first designed and amplified, and then target sequences could be obtained by colony PCR. After the preparation, the amplification results are detected by enzyme identification. The electrophoretograms of the enzyme samples show that the acquired sequences are consistent with the expected one (Fig. 8b, c). We use Sanger method to sequence DNA library, and eight carrier DNA strands are acquired after reading a group of backup sequences. The decoder corrects errors based on quaternary Hamming (31, 26) code and then retrieves the original information through quaternary Huffman decoding.
Fig. 8.
Biological experiment: a DNA pool, b the electrophoretogram of enzyme samples, and c marker
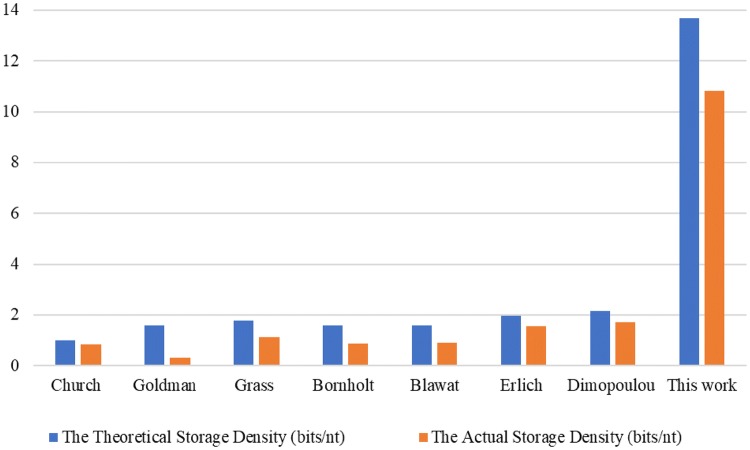
Table 4 shows the experimental results of comparing the previous schemes for information storage in DNA and the proposed method. A more intuitive comparison of the storage density is shown in Fig. 9. The theoretical storage density and the actual density of the proposed scheme are both significantly greater than those of the other methods. The theoretical storage density is the information content per base without considering indexing, error correction bits, and primers; while, the actual storage density is the information content per base in consideration these conditions. Notably, our storage density does not include video files (Table 4). The quaternary Huffman coding is less effective for video files. This is because arithmetic coding that makes full use of the statistical properties of the source, such as CABAC, has already been used when obtaining the binary video streams, which makes the advantages of entropy-based coding less obvious. Error correction represents the presence of error correction code to deal with synthesis and sequencing errors. Full recovery denotes whether all information is restored without any error. Random access refers to whether the scheme supports the writing and reading of specific content. Redundancy represents the excess oligonucleotides that do not store original information. Cost indicates the amount of money required to store 1 MB of information with the assumption that the price of DNA synthesis is 1.5 yuan per base.
Table 4.
Comparison of experimental results of different storage schemes
| Parameter | Input data (MB) | Theoretical storage density (bits/nt) | Actual storage density (bits/nt) | Error correction | Full recovery | Random access | Redundancy (%) | Cost (yuan/bit) |
|---|---|---|---|---|---|---|---|---|
| Church and Kosuri (2012) | 0.65 | 1 | 0.83 | No | No | No | 17.00 | 1.81 |
| Goldman et al. (2013) | 0.63 | 1.58 | 0.33 | Yes | No | No | 79.11 | 4.55 |
| Grass et al. (2015) | 0.08 | 1.78 | 1.14 | Yes | Yes | No | 35.96 | 1.32 |
| Bornholt et al. (2016) | 0.15 | 1.58 | 0.88 | No | No | Yes | 44.30 | 1.70 |
| Blawat et al. (2016) | 22 | 1.6 | 0.92 | Yes | Yes | No | 42.50 | 1.63 |
| Erlich and Zielinski (2017) | 2.11 | 1.98 | 1.57 | Yes | Yes | No | 20.71 | 0.96 |
| Dimopoulou et al. (2019) | 0.26 | 2.14 | 1.71 | Yes | Yes | No | 19.36 | – |
| Proposed method | 0.005 | 13.68 | 10.83 | Yes | Yes | No | 20.00 | 0.27 |
Fig. 9.
Theoretical and actual storage densities of previous storage schemes and the proposed scheme
Conclusions
This study proposes a novel DNA information storage scheme that can effectively improve the storage density and correct errors with low redundancy. The digits encoded per base dramatically increase using quaternary Huffman code to compress the input binary streams for files with a non-uniform probability distribution of the source. The challenges of expensive DNA synthesis and low utilization of DNA molecules are addressed. The Hamming code is improved to meet the needs of quaternary sequence error correction and can correct errors occurring in the synthesis and sequencing with low redundancy. The biological experiment shows that texts and images stored in synthetic DNA molecules can be successfully recovered through DNA sequencing and decoding. The actual storage density obtained in the biological experiment is 10.83 bits/nt, which is better than that of the state-of-the-art schemes. Nevertheless, it should be noted that although the information storage density has been greatly improved in our scheme, it is not applicable to files with evenly probability distributed source, such as video. This issue shall be addressed in future work. In addition, the proposed scheme does not support random access. Even if only a part of the information is requested, all information must be sequenced. Further studies are required to enable random access of the information.
Compliance with ethical standards
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
References
- Ailenberg M, Rotstein O. An improved Huffman coding method for archiving text, images, and music characters in DNA. Biotechniques. 2009;47:747–754. doi: 10.2144/000113218. [DOI] [PubMed] [Google Scholar]
- Akram F, Haq IU, Ali H, Laghari AT. Trends to store digital data in DNA: an overview. Mol Biol Rep. 2018;45:1479–1490. doi: 10.1007/s11033-018-4280-y. [DOI] [PubMed] [Google Scholar]
- Babu HMH, Mia MS, Biswas AK. Efficient techniques for fault detection and correction of reversible circuits. J Electron Test. 2017;33:591. doi: 10.1007/s10836-017-5679-4. [DOI] [Google Scholar]
- Bancroft C, Bowler T, Bloom B, Clelland CT. Long-term storage of information in DNA. Science. 2001;5536:1763–1765. doi: 10.1126/science.293.5536.1763c. [DOI] [PubMed] [Google Scholar]
- Blawat M, Gaedkea K, Hütter I, Chen XM, Turczyk B, Inverso S, Pruitt BW, Church GM. Forward error correction for DNA data storage. Procedia Comput Sci. 2016;80:1011–1022. doi: 10.1016/j.procs.2016.05.398. [DOI] [Google Scholar]
- Borchert C, Schirmeier H, Spinczyk O (2013) Generative software-based memory error detection and correction for operating system data structures. In: Proceedings of the 2013 43rd annual IEEE/IFIP international conference on dependable systems and networks (DSN), pp 1–12
- Bornholt J, Lopez R, Carmean DM. A DNA-based archival storage system. IEEE Micro. 2016;99:637–649. [Google Scholar]
- Church GM, Kosuri S. Next-generation digital information storage in DNA. Science. 2012;6102:1628. doi: 10.1126/science.1226355. [DOI] [PubMed] [Google Scholar]
- Davis J. Microvenus. Art J. 1996;55:70–74. doi: 10.1080/00043249.1996.10791743. [DOI] [Google Scholar]
- Dimopoulou M, Antonini M, Barbry P, Appuswamy R (2019) A biologically constrained encoding solution for long-term storage of images onto synthetic DNA. arXiv:1904:03024
- Erlich Y, Zielinski D. DNA fountain enables a robust and efficient storage architecture. Science. 2017;6328:950–954. doi: 10.1126/science.aaj2038. [DOI] [PubMed] [Google Scholar]
- Goda K, Kitsuregawa M. The history of storage systems. Proc IEEE. 2012;2012:1433–1440. doi: 10.1109/JPROC.2012.2189787. [DOI] [Google Scholar]
- Goldman N, Bertone P, Chen SY, Dessimoz C, LeProust ME, Sipos B, Birney E. Towards practical, high-capacity, low-maintenance information storage in synthesized DNA. Nature. 2013;7435:77–80. doi: 10.1038/nature11875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grass RN, Heckel R, Puddu M, Paunescu D, Stark WJ. Robust chemical preservation of digital information on DNA in silica with error-correcting codes. Angew Chem Int Ed. 2015;8:2552–2555. doi: 10.1002/anie.201411378. [DOI] [PubMed] [Google Scholar]
- Hughes A, Ellington D. Synthetic DNA synthesis and assembly: putting the synthetic in synthetic biology. Cold Spring Harbor Perspect Biol. 2017;1:a023812. doi: 10.1101/cshperspect.a023812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mardis R. DNA sequencing technologies: 2006–2016. Nat Protoc. 2017;2:213–218. doi: 10.1038/nprot.2016.182. [DOI] [PubMed] [Google Scholar]
- Panda D, Molla KA, Baig MJ, Swain A, Behera D, Dash M. DNA as a digital information storage device: hope or hype? 3 Biotech. 2018;8:239. doi: 10.1007/s13205-018-1246-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajaei N, Rajaei R, Tabandeh M. A soft error tolerant register file for highly reliable microprocessor design. Int J High Perform Syst Archit. 2017;7:113–119. doi: 10.1504/IJHPSA.2017.091479. [DOI] [Google Scholar]
- Shipman SL, Nivala J, Macklis JD, Church GM. CRISPR-Cas encoding of a digital movie into the genomes of a population of living bacteria. Nature. 2017;7663:345–349. doi: 10.1038/nature23017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yazdi SMHT, Kiah HM, Ruiz EG, Ma J, Zhao H, Milenkovic O. DNA-based storage: trends and methods. IEEE Trans Mol Biol Multi-Scale Commun. 2015;1:230–248. doi: 10.1109/TMBMC.2016.2537305. [DOI] [Google Scholar]