Abstract
In recent years, great strides have been made for causal structure learning in the high-dimensional setting and in the mixed data-type setting when there are both discrete and continuous variables. However, due to the complications involved with modeling continuous-discrete variable interactions, the intersection of these two settings has been relatively understudied. The current paper explores the problem of efficiently extending causal structure learning algorithms to high-dimensional data with mixed data-types. First, we characterize a model over continuous and discrete variables. Second, we derive a degenerate Gaussian (DG) score for mixed data-types and discuss its asymptotic properties. Lastly, we demonstrate the practicality of the DG score on learning causal structures from simulated data sets.
Keywords: High-dimensional Data, Causal Structure Learning, Directed Acyclic Graphs, Mixed Data-types
1. Introduction
Identifying the causal structure underlying a system of variables embodies a large portion of modern-day scientific research. Algorithms have been developed over the past few decades to learn causal structures from observational data (Spirtes et al., 2000). These algorithms output graphs that use vertices to represent random variables and edges to represent the various types of causal relationships occurring between those variables. The canonical vertex-edge graph used for causal modeling is a directed acyclic graph (DAG). In a causal DAG, directed edges express the existence and direction of direct causal relationships. More importantly, the edges of a causal DAG provide researchers with a means to calculate the effects of manipulating one or more variables within the graph (Pearl, 2009). These properties, among others, are at the root of a growing interest in learning causal graphs under various assumptions and in different settings—such as in the high-dimensional and mixed data-type settings.
By and large, algorithms for learning causal graphs fall into one of two main categories: score-based or constraint-based. Score-based algorithms use a score function as a guide to the best causal graph by evaluating the “goodness” of each graph encountered during the search process. Constraint-based algorithms use tests of conditional independence to learn constraints that restrict the set of possible causal graphs. In this paper, we focus on the score-based approach. Score-based algorithms have already been scaled to thousands of variables (Nandy et al., 2018; Ramsey et al., 2017) and scores for mixed data-types have also been successfully applied (Andrews et al., 2018; Raghu et al., 2018). However, if a score fails to scale with respect to sample size or the number of measured random variables, then an algorithm using that score will fail to scale as well. Since it is not uncommon for high-dimensional data sets to contain a mixture of continuous and discrete variables—such as in biological and clinical data sets—it is important to develop highly scalable scores for mixed data-types.
1.1. Related Work
Recently, (Raghu et al., 2018) provided an in-depth overview comparing several state of the art algorithms for learning DAGs from data sets with mixed data-types. Their paper contains an extensive simulation study on methods that scale to hundreds of variables (Andrews et al., 2018; Cui et al., 2016; Sedgewick et al., 2018). Unfortunately, these methods become impractical for one reason or another as the number of samples or measured random variables grows large.
The conditional Gaussian (CG) and mixed variable polynomial (MVP) scores were introduced for causal structure learning in the mixed data-type setting by (Andrews et al., 2018). Both of these scores partition the instances of the data with respect to the values of the discrete variables and then analyze the continuous variables within each partition. Due to their need to repeatedly partition the data, as the number of samples or measured random variables grows large, both of these scores become inefficient.
Copula PC is a modification to the constraint-based PC algorithm (Spirtes et al., 2000) introduced by (Cui et al., 2016). The Copula PC algorithm extends the ideas of Rank PC (Harris and Drton, 2013) to include ordinal and binary data-types. The method has two main steps: estimate a correlation matrix, and run a causal search algorithm on the estimated correlation matrix. In their paper, they use Gibbs sampling to estimate the correlation matrix and run the result using the PC-Stable algorithm (Colombo and Maathuis, 2014). The scalability of their procedure largely depends on the method of estimation for the correlation matrix. Unfortunately, sampling procedures, such as Gibbs sampling, are known to suffer from slow convergence in high-dimensions (Bishop, 2006).
Mixed graphical models (MGM), originally introduced for learning undirected graphs (Lee and Hastie, 2013), was adapted by (Sedgewick et al., 2018) for the purpose of learning causal DAGs. Their approach involves post-processing the undirected output of MGM using a variant of the PC algorithm (Spirtes et al., 2000). The MGM procedure searches over undirected graphs by maximizing a pseudo-likelihood function with gradient-based optimization. Afterwards, the PC variant removes and directs edges in the graph using tests of conditional independence. In their paper, tests based on multinomial logistic regression are used to determine conditional independence. Both the MGM procedure and logistic regression involve iteratively updating parameters which can be impractical in high-dimensions.
Other works capable of learning causal structures from mixed data-types include (Bøttcher, 2004) which does not allow discrete variables to have continuous parents and (Borboudakis and Tsamardinos, 2016; Hyttinen et al., 2014) which use answer set programming. The latter of these two approaches provides a powerful and flexible framework for learning causal structures, but often fails to scale past tens of random variables.
1.2. Outline
The remainder of this paper is organized as follows. In Section 2 we review several graphical preliminaries and basic concepts for scoring graphs. In Section 3 we derive the degenerate Gaussian (DG) score for mixed data-types. In Section 4 we demonstrate the practicality of the DG score in high-dimensions on simulated data. Section 5 states our conclusions.
2. Preliminaries
Throughout this paper, we use the following notation: An upper case letter denotes a random variable (e.g., Xj) and a lower case letter denotes the state or value of a random variable (e.g., Xj = xij). The subscript i distinguishes between different instances of the data and the subscript j distinguishes between different variables. Sets are denoted with bold-face letters. For a set of p random variables X = (X1,…,Xp) where Xj may be either continuous or discrete, we define an index set V := {1,…,p}. We further define V = C ∪ D where C ∩ D = ∅ and the partitions C and D are index sets for the continuous and discrete variables, respectively.
2.1. Graphical Concepts and Notation
A directed acyclic graph (DAG) for the set of random variables X contains a set vertices V that index the members of X and a set of directed edges E that connect the members of V (at most one edge between any two vertices). For vertices j1, j2 ∈ V, we say that j1 is a parent of j2 and that j2 is a child of j1 if j1 → j2 ∈ E. We denote the set of parents of j2 as and the set of children of j1 as . If there is an edge in either orientation between j1 and j2, we say that j1 and j2 are adjacent.
A path is a sequence of distinct vertices j1,…,jm such there is an edge between ik and ik+1 for all k = 1,…,m – 1. Furthermore, that path is directed if every edge on the path is oriented ik → ik+1. A directed cycle occurs when there is a path from j1 to j2 and j2 → j1. As suggested by the name, a DAG does not contain any directed cycles. A collider occurs on a path if jk–1 → jk ← jk+1 and the collider is unshielded if jk–1 and jk+1 are not adjacent.
The connectivity of a DAG may be characterized using a graphical criterion called d-separation; for in-depth details, see (Koller et al., 2009). At a high level, d-separation is of interest when learning causal DAGs because given a few assumptions d-separation in the true causal graph has a one-to-one correspondence with conditional independence in the data. Unfortunately, multiple DAGs often encode the same d-separations–this means the true causal DAG is only identifiable up to a (Markov) equivalence class. Fortunately, Markov equivalence may be completely characterized using two simple graphical concepts: two DAGs containing the same adjacencies and unshielded colliders are Markov equivalent (Pearl, 2009).
2.2. Scoring DAGs
Two fundamental assumptions of causal algorithms are the causal Markov condition and the causal faithfulness condition. The causal Markov condition states that d-separation in the data-generating graph implies conditional independence in the data. Conversely, the causal faithfulness condition states that conditional independence in the data implies d-separation in the data-generating graph. These conditions imply that the distribution over a set of random variables will factorize according to the true graph and that a more parsimonious factorization does not exist. By factorization, we mean that given a set of p random variables X = (X1,…,Xp) generated according to a DAG , the joint distribution can be written as,
| (1) |
or equivalently
| (2) |
Equation 2 leads to a useful property of scoring criteria, namely, decomposability. A score is decomposable if it decomposes according to the graph. That is, if a score S is decomposable, then
| (3) |
where s is a local evaluation of S. In a local search over causal graphs, a decomposable score may be efficiently updated after transitioning from one graph to another using only the local differences. A second useful property of scoring criteria is score equivalence. A score S is score equivalent if S gives the same score to any two Markov equivalent DAGs. Score equivalence is used in algorithms such as Greedy Equivalent Search (GES) (Chickering, 2002) which searches over Markov equivalence classes directly. A third useful property of scoring criteria is consistency. A score is consistent if it ranks a model whose parameter space contains the true distribution better than a model whose parameter space does not. Additionally, a consistent score will rank the simpler of two models whose parameter spaces both contain the true distribution. Consistency is usually required by algorithms for asymptotic proofs of correctness.
We score our proposed model using the Bayesian Information Criterion (BIC). BIC was first introduced by (Schwarz et al., 1978) as a approximation for the marginal likelihood
| (4) |
where θ are the parameters of the distribution, is the maximum likelihood estimate of the parameters, and n is the number instances in the data. Later it was extended to a more general class of models (including linear Gaussian DAGs) by (Haughton, 1988). BIC is used by (Chickering, 2002) in GES because it is decomposable, score equivalent, and consistent.
3. Method
In this section, we introduce the DG score and showed that it is score equivalent and consistent. Additionally, we note that it is efficient to compute.
Let X = (X1,…,Xp) be a set of p random variables with n instances. Our method relies on a standard transformation of the variables:
| (5) |
where is the indicator function such that if Xj = k and otherwise and ∣Xj∣ = k for Xj ∈ D. We use superscripts to index the indicator random variables for each discrete variable (i.e., ).
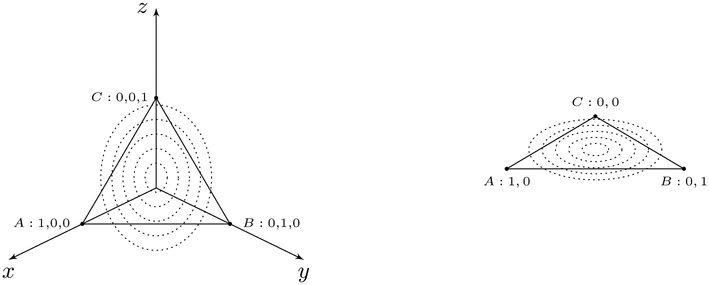
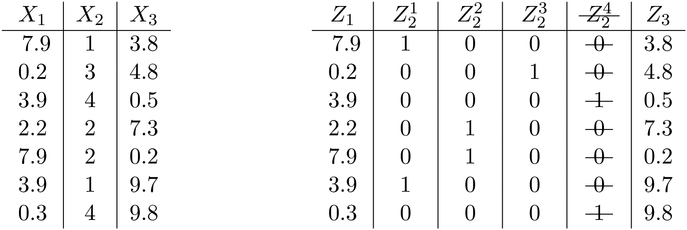
Equation 5 embeds the discrete variables into a continuous space using their one-hot vector representations. However, the naïve embedding results in a degenerate distribution1, depicted on the left of Figure 1. Thus, the last indicator variable of each one-hot vector is dropped; this may be thought of as a projection of each one-hot vector into a lower dimensional space, depicted on the right of Figure 1. Figure 2 illustrates an example of applying the transformation to a data set. After a data set has been transformed, the data are treated as jointly Gaussian. Consequently, we call our score the degenerate Gaussian (DG) score.
Figure 1:
An example embedding before and after removing the last indicator variable. The figure on the left illustrates an embedded random variable pre-removal of degeneracy (3-dimensions) and the figure on the right illustrates an embedded random variable post-removal of degeneracy (2-dimensions).
Figure 2:
An example data set with mixed data-types before and after embedding. The table on the left illustrates a data set with mixed data-types pre-embedding and the table on the right illustrates a data set with mixed data-types post-embedding; the redundant indicator column has been removed.
Since BIC is decomposable, we write the DG score as the sum of local components
| (6) |
where
| (7) |
and c is a penalty discount parameter used to tune the density of the resulting graph. The log likelihood for a subset Q of the variables in Equation 7 is computed with the Gaussian log likelihood function
| (8) |
Since the only non-constant in Equation 8 is , we may compute the full covariance matrix as a preprocessing step, then during search local scores may be calculated simply by retrieving the relative rows and columns of the full covariance matrix. Thus, score calculations will be constant time.
Interestingly, the embedded values of a discrete variable do not affect how the scores of different graphs compare relative to each other. This means that the actual values of the embedding are irrelevant to search and the transformation described in Equation 5 will give the same result as any other embedding. We show this by proving that the DG score is order invariant (the preferential ordering of graphs does not change) under an affine transformation of the embedded values of a discrete variable.
Lemma 1 The DG score is order invariant under an affine transformation of the embedded values of a discrete variable.
Proof Consider the affine transformation Z′ = AZ + b where
and Aj is any full rank linear transformation of Zj for j ∈ D. Using Z′ rather than Z in Equation 6 results in an additional term
But n log ∣Aj∣ is constant with respect to . Accordingly, an affine transformation of the embedded values of a discrete variable amounts to adding a constant to the score. Thus, the embedded values of a discrete variable do not affect how the scores of different graphs compare relative to each other. ∎
The DG score is score equivalent due to the fact that BIC is score equivalent; however, it is not necessarily consistent. For consistency, we introduce two assumptions.
Assumption 1 The continuous random variables are Gaussian. Each k-category discrete random variable represents a latent (k – 1) dimensional Gaussian random variable.
Note that a latent Gaussian random variable with less than k – 1 dimension can be represented in k – 1 dimensions as a degenerate Gaussian. Define Øj : Lj → Zj as the mapping from the latent continuous variable Lj to the embedding of the measured discrete variable Zj. Then the maximum likelihood estimate of covariance for the true underlying Gaussian distribution is given by , where
| (9) |
and accounts for the variation in the data lost due to discretization.
Assumption 2 The discretization defined by the mapping Øj loses no information:
If we interpret the unique values of as cluster centers, then will be the distance of to its corresponding cluster center–the cluster residuals. Accordingly, Assumption 2 states that the cluster residuals are uncorrelated with the other random variables in the data. This assumption will often be violated, however, in practice most violations are subtle and performance is relatively unaffected. To support this statement, we refer to the simulation results in Section 4 and Appendix A.
Proposition 2 The DG score is consistent.
Proof Under Assumptions 1 and 2, the maximum likelihood estimate of covariance for the true underlying Gaussian distribution is given by Equation 9. Accordingly, since BIC is consistent for Gaussian DAG models (Haughton, 1988; Spirtes et al., 1997), the estimate from Equation 9 is consistent. By Lemma 1, the choice of Øj does not affect how the scores of different graphs compare relative to each other. Therefore, any choice of Øj, including the transformation described in Equation 5 gives a consistent result. Thus, the DG score is consistent. ∎
4. Evaluation
In this section, we evaluate the practicality of the DG score in high-dimensions on simulated data. In the simulation study we compare our introduced method to several other state of the art methods.
4.1. Simulation Study
In order to evaluate the practicality of our method in comparison to other state of the art algorithms, we simulated data using two models: the conditional Gaussian model and the Lee and Hastie model; these are the models used for comparison in (Raghu et al., 2018), but were originally introduced as simulator in (Andrews et al., 2018) and (Sedgewick et al., 2018), respectively. In our experiments, we varied the number of measured variables, the average vertex degree of the graphs, and the sample size.
Bayesian networks were randomly generated to simulate data. For each network, first a DAG over a set of continuous and discrete random variables was generated. The random variables were uniformly, randomly assigned to be either continuous or discrete with probability 0.5. Edges were added between the vertices in the graph according to a randomly defined causal ordering and added until the average vertex degree of the graph reached a pre-specified amount. In causal order, the distribution of each random variable given it’s parents was parameterized. For more details on the methods used for simulation, see Appendix B.
We compare the DG score against the same structure learning methods studied in (Raghu et al., 2018): the conditional Gaussian (CG) score, causal mixed graphical models (MGM), and copula PC (Copula). For the CG and DG scores, we used the fast Greedy Equivalent Search (fGES) (Ramsey et al., 2017), which is an optimized version of Greedy Equivalent Search (Chickering, 2002). We apply the structure prior introduced in (Ramsey et al., 2017; Andrews et al., 2018) to both scores and set it to 1.0 (as suggested in those papers). Finally, we use a penalty discount of 1.0, 2.0, 4.0, and 8.0. For causal MGM (Sedgewick et al., 2018), we used a value of 0.2 for all three parameter penalties. In their paper, the authors use a data driven method to choose these parameters, so our naïve choice could result in weaker performance for MGM. That being said, we chose these values at the suggestion of the authors and did so to reduce search times. We used CPC-Stable (Ramsey et al., 2006; Colombo and Maathuis, 2014) as the second step with a logistic-regression-based test of conditional independence with alpha levels of 1e-2, 1e-3, 1e-4, and 1e-5. For copula PC (Cui et al., 2016), we used Gibbs sampling (1000 samples) to estimate the correlation matrix. We then used PC-Stable (Colombo and Maathuis, 2014) with alpha levels of 1e-2, 1e-3, 1e-4, and 1e-5. Note that copula PC is intended to be used on mixed data-types when the discrete variables are either binary or ordinal; however, in our simulations we used 2-4 category categorical data.
The following performance measures were used to evaluate correctness and computational efficiency:
We varied the simulation parameters over the number of measured random variables (100, 500, or 1000), the average vertex degree of the graph (2, 4, or 6), and the number of samples (200, 1000, or 5000) and report the mean statistics over 10 repetitions along with 95% confidence intervals. All simulations and comparisons took place within the Tetrad system’s algorithm comparison tool (Ramsey and Malinsky, 2016) on a laptop with an Intel(R) Core I5 @ 2.2 GHz with 8GB of RAM. For readability, the tables below report selected results; however, the full tables of all simulation results are in Appendix A.
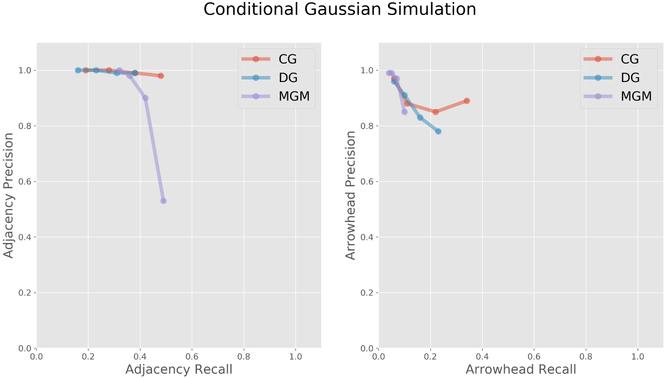
First we performed a comparison using data generated from a conditional Gaussian model. Figure 3 illustrates how the various methods perform on the conditional Gaussian simulated data with 500 measured random variables, average vertex degree 4, and 1000 samples. Copula PC was excluded from this comparison because it failed to return a result in under two hours. CG performed the best (as to be expected on conditional Gaussian simulated data); however, both DG and MGM have good precision in adjacency and arrowhead statistics.
Figure 3:
Conditional Gaussian simulated data with 500 measured random variables, average vertex degree 4, and 1000 samples.
Table 1 tabulates how the various methods performed on the conditional Gaussian simulated data while varying the number of measured random variables, the average vertex degree of the graph, and the number of samples. The two score-based methods (CG and DG) performed the best on low samples (arrowhead statistic reported as “-” imply that no edges were oriented). However, as the sample size increases, DG and MGM perform similarly on adjacencies. In general, the score-based methods performed better on the arrowhead statistics. Copula PC never performed very well, but that is likely because it was not intended to run on 2-4 category categorical data. Overall, CG arguably performed the best on the reported statistics and DG performed the best on computation time.
Table 1:
Conditional Gaussian simulation.
| Simulation | Algorithm | Statistics | Time | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Measured | Degree | Samples | Method | Parameter | Adj Precision | Adj Recall | Arrhd Precision | Arrhd Recall | Seconds |
| 100 | 2 | 200 | CG | 1.0 | 0.94 ± 0.03 | 0.41 ± 0.04 | 0.74 ± 0.15 | 0.11 ± 0.05 | 1.52 |
| DG | 1.0 | 0.96 ± 0.02 | 0.33 ± 0.04 | 0.65 ± 0.21 | 0.10 ± 0.06 | 0.06 | |||
| MGM | 1e-4 | 0.98 ± 0.02 | 0.25 ± 0.04 | - | - | 7.52 | |||
| Copula | 1e-5 | 0.70 ± 0.12 | 0.07 ± 0.01 | - | - | 307.38 | |||
| 1000 | CG | 1.0 | 0.99 ± 0.01 | 0.70 ± 0.05 | 0.93 ± 0.06 | 0.45 ± 0.08 | 8.46 | ||
| DG | 1.0 | 0.99 ± 0.01 | 0.56 ± 0.04 | 0.74 ± 0.13 | 0.30 ± 0.06 | 0.05 | |||
| MGM | 1e-4 | 0.99 ± 0.01 | 0.52 ± 0.05 | 1.00 ± 0.00 | 0.05 ± 0.04 | 41.63 | |||
| Copula | 1e-5 | 0.45 ± 0.06 | 0.29 ± 0.04 | 0.06 ± 0.03 | 0.01 ± 0.01 | 390.63 | |||
| 4 | 1000 | CG | 1.0 | 0.97 ± 0.01 | 0.54 ± 0.04 | 0.86 ± 0.05 | 0.41 ± 0.05 | 16.50 | |
| DG | 1.0 | 0.98 ± 0.01 | 0.40 ± 0.02 | 0.76 ± 0.06 | 0.25 ± 0.04 | 0.06 | |||
| MGM | 1e-4 | 0.99 ± 0.01 | 0.36 ± 0.03 | 0.95 ± 0.11 | 0.04 ± 0.01 | 35.67 | |||
| Copula | 1e-5 | 0.61 ± 0.02 | 0.18 ± 0.03 | 0.26 ± 0.15 | 0.02 ± 0.01 | 417.53 | |||
| 500 | 4 | 1000 | CG | 1.0 | 0.98 ± 0.01 | 0.48 ± 0.03 | 0.89 ± 0.02 | 0.34 ± 0.03 | 453.97 |
| DG | 1.0 | 0.99 ± 0.01 | 0.38 ± 0.01 | 0.78 ± 0.01 | 0.23 ± 0.01 | 0.81 | |||
| MGM | 1e-4 | 0.98 ± 0.01 | 0.36 ± 0.01 | 0.99 ± 0.01 | 0.05 ± 0.01 | 941.90 | |||
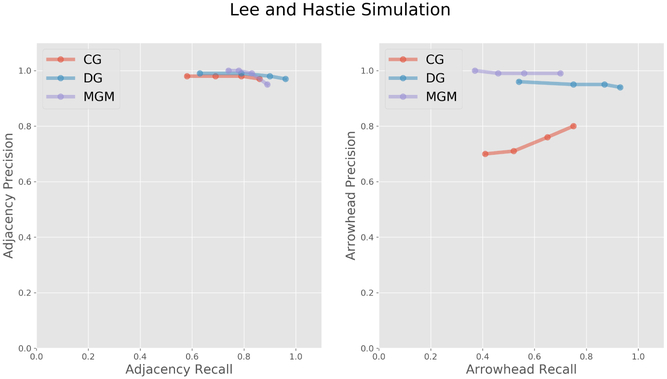
Second we performed a comparison using the Lee and Hastie model. Figure 4 illustrates how the various method perform on the Lee and Hastie simulated data with 500 measured random variables, average vertex degree 4, and 1000 samples. Copula PC was excluded from this comparison because it failed to return a result in under two hours. DG perform the best, however, all methods have good adjacency statistics. MGM also has good arrowhead precision. CG performs poorly on the arrowhead statistics relative to the other methods.
Figure 4:
Lee and Hastie simulated data with 500 measured random variables, average vertex degree 4, and 1000 samples.
Table 2 tabulates how the various methods performed on the Lee and Hastie simulated data while varying the number of measured random variables, the average vertex degree of the graph, and the number of samples. The two score-based methods (CG and DG) performed the best on low samples (arrowhead statistic reported as “-” imply that no edges were oriented). However, as the sample size increases, CG, DG, and MGM perform similarly on adjacencies. CG performs poorly on the arrowhead statistics relative to the other methods, but this is likely because it is attempting to fit a far more complex model class. Copula PC never performed well, which may be because it was not intended to run on 2-4 category categorical data. Overall, DG arguably performed the best on the reported statistics and performed the best on computation time.
Table 2:
Lee and Hastie simulations.
| Simulation | Algorithm | Statistics | Time | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Measured | Degree | Samples | Method | Parameter | Adj Precision | Adj Recall | Arrhd Precision | Arrhd Recall | Seconds |
| 100 | 2 | 200 | CG | 1.0 | 0.98 ± 0.01 | 0.80 ± 0.01 | 0.67 ± 0.06 | 0.45 ± 0.06 | 3.23 |
| DG | 1.0 | 0.99 ± 0.01 | 0.82 ± 0.02 | 0.89 ± 0.05 | 0.65 ± 0.03 | 0.12 | |||
| MGM | 1e-2 | 0.94 ± 0.02 | 0.80 ± 0.02 | 0.96 ± 0.04 | 0.27 ± 0.03 | 5.15 | |||
| Copula | 1e-5 | 0.90 ± 0.05 | 0.28 ± 0.06 | - | - | 307.66 | |||
| 1000 | CG | 1.0 | 0.99 ± 0.01 | 0.96 ± 0.01 | 0.74 ± 0.04 | 0.80 ± 0.04 | 16.53 | ||
| DG | 1.0 | 0.99 ± 0.01 | 0.98 ± 0.01 | 0.96 ± 0.04 | 0.96 ± 0.02 | 0.08 | |||
| MGM | 1e-2 | 0.90 ± 0.02 | 0.97 ± 0.01 | 1.00 ± 0.01 | 0.80 ± 0.04 | 37.76 | |||
| Copula | 1e-5 | 0.77 ± 0.03 | 0.61 ± 0.03 | 0.08 ± 0.06 | 0.02 ± 0.02 | 395.25 | |||
| 4 | 1000 | CG | 1.0 | 0.95 ± 0.01 | 0.86 ± 0.01 | 0.79 ± 0.03 | 0.76 ± 0.02 | 51.91 | |
| DG | 1.0 | 0.95 ± 0.02 | 0.97 ± 0.01 | 0.90 ± 0.04 | 0.93 ± 0.01 | 0.27 | |||
| MGM | 1e-2 | 0.98 ± 0.01 | 0.88 ± 0.02 | 0.97 ± 0.02 | 0.67 ± 0.04 | 176.07 | |||
| Copula | 1e-5 | 0.73 ± 0.04 | 0.47 ± 0.01 | 0.10 ± 0.06 | 0.02 ± 0.01 | 414.41 | |||
| 500 | 4 | 1000 | CG | 1.0 | 0.97 ± 0.01 | 0.86 ± 0.01 | 0.80 ± 0.01 | 0.75 ± 0.01 | 2082.13 |
| DG | 1.0 | 0.97 ± 0.01 | 0.96 ± 0.01 | 0.94 ± 0.02 | 0.93 ± 0.01 | 1.94 | |||
| MGM | 1e-2 | 0.95 ± 0.01 | 0.89 ± 0.01 | 0.99 ± 0.01 | 0.70 ± 0.02 | 1888.53 | |||
Table 3 tabulates how DG with a penalty discount of 1 performs on high-dimensional data from both the conditional Gaussian model and from the Lee and Hastie model. All other method were excluded from this table because they failed to return a result in under two hours. For DG, performance on high-dimensional data is similar to performance on low-dimensional data and DG remains very efficient.
Table 3:
DG with a penalty discount of 1 on high-dimensional data.
| Simulation | Statistics | Time | ||||||
|---|---|---|---|---|---|---|---|---|
| Method | Measured | Degree | Samples | Adj Precision | Adj Recall | Arrhd Precision | Arrhd Recall | Seconds |
| CG | 500 | 4 | 1000 | 0.99 ± 0.01 | 0.38 ± 0.01 | 0.78 ± 0.01 | 0.23 ± 0.01 | 0.24 |
| 500 | 4 | 5000 | 0.98 ± 0.01 | 0.61 ± 0.01 | 0.80 ± 0.02 | 0.48 ± 0.01 | 0.58 | |
| 500 | 6 | 1000 | 0.99 ± 0.01 | 0.26 ± 0.01 | 0.78 ± 0.02 | 0.17 ± 0.01 | 0.30 | |
| 1000 | 4 | 1000 | 0.99 ± 0.01 | 0.37 ± 0.01 | 0.82 ± 0.02 | 0.23 ± 0.01 | 0.44 | |
| LH | 500 | 4 | 1000 | 0.97 ± 0.01 | 0.96 ± 0.01 | 0.94 ± 0.02 | 0.93 ± 0.01 | 0.33 |
| 500 | 4 | 5000 | 0.96 ± 0.01 | 1.00 ± 0.01 | 0.94 ± 0.02 | 0.99 ± 0.01 | 0.74 | |
| 500 | 6 | 1000 | 0.94 ± 0.01 | 0.94 ± 0.01 | 0.90 ± 0.02 | 0.91 ± 0.01 | 2.09 | |
| 1000 | 4 | 1000 | 0.98 ± 0.01 | 0.94 ± 0.01 | 0.95 ± 0.01 | 0.92 ± 0.01 | 1.25 | |
5. Conclusions
In this paper, we introduced the degenerate Gaussian (DG) score for learning directed acyclic graphs (DAGs) from high-dimensional data with mixed data-types. The DG score is score equivalent, consistent, and efficient to compute. It performs competitively when learning causal models generated outside of its assumed model class (conditional Gaussian model) when compared to methods assuming the correct model, but is orders of magnitude faster. Additionally, when DG is able to correctly model the underlying causal relationships (Lee and Hastie model), it has near perfect performance. Scaling up the DG score to high-dimensions has little effect on overall performance and the score continues to be very efficient. The methods presented are available on GitHub2.
Acknowledgments
We thank Vineet Raghu for sharing the code from his comparison and for insightful discussions. Research reported in this publication was supported by grant U54HG008540 awarded by the National Human Genome Research Institute through funds provided by the trans-NIH Big Data to Knowledge (BD2K) initiative. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. This work was also supported by the CURE grant #4100070287 from the Pennsylvania Department of Health (PA DOH). The content of this paper is solely the responsibility of the authors and does not necessarily represent the official views of the funding agencies. The Pennsylvania Department of Health specifically disclaims responsibility for any analyses, interpretations or conclusions.
Appendix
Appendix A.
In this appendix, we report the means for the full experiments. Omitted rows represent algorithms that failed to return a result in under two hours. Arrowhead statistic reported as “-” imply that no edges were oriented.
Table 4:
Conditional Gaussian simulation.
| Simulation | Algorithm | Statistics | Time | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Measured | Degree | Samples | Method | Parameter | Adj Precision | Adj Recall | Arrhd Precision | Arrhd Recall | Seconds |
| 100 | 2 | 200 | CG | 1.0 | 0.94 | 0.41 | 0.74 | 0.11 | 1.52 |
| 2.0 | 0.99 | 0.29 | 0.97 | 0.05 | 1.32 | ||||
| 4.0 | 1.00 | 0.16 | 0.94 | 0.02 | 1.27 | ||||
| 8.0 | 1.00 | 0.08 | 1.00 | 0.01 | 1.26 | ||||
| DG | 1.0 | 0.96 | 0.33 | 0.65 | 0.10 | 0.06 | |||
| 2.0 | 0.99 | 0.25 | 0.74 | 0.05 | 0.04 | ||||
| 4.0 | 1.00 | 0.15 | 0.73 | 0.02 | 0.04 | ||||
| 8.0 | 1.00 | 0.07 | 1.00 | 0.01 | 0.03 | ||||
| MGM | 1e-4 | 0.98 | 0.25 | - | - | 7.52 | |||
| 1e-5 | 0.99 | 0.19 | - | - | 6.66 | ||||
| Copula | 1e-4 | 0.53 | 0.09 | - | - | 307.38 | |||
| 1e-5 | 0.70 | 0.07 | - | - | 307.38 | ||||
| 100 | 2 | 1000 | CG | 1.0 | 0.99 | 0.70 | 0.93 | 0.45 | 8.46 |
| 2.0 | 1.00 | 0.61 | 0.92 | 0.29 | 7.45 | ||||
| 4.0 | 1.00 | 0.48 | 0.95 | 0.15 | 6.94 | ||||
| 8.0 | 1.00 | 0.33 | 0.97 | 0.08 | 6.38 | ||||
| DG | 1.0 | 0.99 | 0.56 | 0.74 | 0.30 | 0.05 | |||
| 2.0 | 1.00 | 0.47 | 0.81 | 0.21 | 0.05 | ||||
| 4.0 | 1.00 | 0.37 | 0.85 | 0.13 | 0.05 | ||||
| 8.0 | 1.00 | 0.26 | 0.93 | 0.07 | 0.05 | ||||
| MGM | 1e-4 | 0.99 | 0.52 | 1.00 | 0.05 | 41.63 | |||
| 1e-5 | 1.00 | 0.47 | 1.00 | 0.04 | 41.44 | ||||
| Copula | 1e-4 | 0.4 | 0.33 | 0.09 | 0.03 | 409.87 | |||
| 1e-5 | 0.45 | 0.29 | 0.06 | 0.01 | 390.63 | ||||
| 100 | 4 | 1000 | CG | 1.0 | 0.97 | 0.54 | 0.86 | 0.41 | 16.50 |
| 2.0 | 0.99 | 0.43 | 0.83 | 0.28 | 12.47 | ||||
| 4.0 | 0.99 | 0.31 | 0.88 | 0.14 | 8.15 | ||||
| 8.0 | 0.99 | 0.19 | 0.95 | 0.05 | 6.33 | ||||
| DG | 1.0 | 0.98 | 0.40 | 0.76 | 0.25 | 0.06 | |||
| 2.0 | 0.99 | 0.32 | 0.84 | 0.18 | 0.05 | ||||
| 4.0 | 1.00 | 0.25 | 0.90 | 0.11 | 0.05 | ||||
| 8.0 | 0.99 | 0.16 | 0.96 | 0.05 | 0.05 | ||||
| MGM | 1e-4 | 0.99 | 0.36 | 0.95 | 0.04 | 35.67 | |||
| 1e-5 | 1.00 | 0.32 | 0.95 | 0.03 | 35.04 | ||||
| Copula | 1e-4 | 0.54 | 0.21 | 0.16 | 0.02 | 436.74 | |||
| 1e-5 | 0.61 | 0.18 | 0.26 | 0.02 | 417.53 | ||||
Table 5:
Conditional Gaussian simulation continued.
| Simulation | Algorithm | Statistics | Time | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Measured | Degree | Samples | Method | Parameter | Adj Precision | Adj Recall | Arrhd Precision | Arrhd Recall | Seconds |
| 500 | 4 | 1000 | CG | 1.0 | 0.98 | 0.48 | 0.89 | 0.34 | 453.97 |
| 2.0 | 0.99 | 0.38 | 0.85 | 0.22 | 350.87 | ||||
| 4.0 | 1.00 | 0.28 | 0.88 | 0.11 | 301.60 | ||||
| 8.0 | 1.00 | 0.19 | 0.97 | 0.06 | 297.51 | ||||
| DG | 1.0 | 0.99 | 0.38 | 0.78 | 0.23 | 0.81 | |||
| 2.0 | 0.99 | 0.31 | 0.83 | 0.16 | 0.56 | ||||
| 4.0 | 1.00 | 0.23 | 0.91 | 0.10 | 0.56 | ||||
| 8.0 | 1.00 | 0.16 | 0.96 | 0.06 | 0.53 | ||||
| MGM | 1e-2 | 0.53 | 0.49 | 0.85 | 0.10 | 2326.04 | |||
| 1e-3 | 0.90 | 0.42 | 0.97 | 0.07 | 961.96 | ||||
| 1e-4 | 0.98 | 0.36 | 0.99 | 0.05 | 941.90 | ||||
| 1e-5 | 1.00 | 0.32 | 0.99 | 0.04 | 937.30 | ||||
Table 6:
Lee and Hastie simulation.
| Simulation | Algorithm | Statistics | Time | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Measured | Degree | Samples | Method | Parameter | Adj Precision | Adj Recall | Arrhd Precision | Arrhd Recall | Seconds |
| 100 | 2 | 200 | CG | 1.0 | 0.98 | 0.80 | 0.67 | 0.45 | 3.23 |
| 2.0 | 1.00 | 0.70 | 0.76 | 0.26 | 2.35 | ||||
| 4.0 | 1.00 | 0.53 | 0.93 | 0.13 | 1.55 | ||||
| 8.0 | 1.00 | 0.32 | 1.00 | 0.07 | 1.35 | ||||
| DG | 1.0 | 0.99 | 0.82 | 0.89 | 0.65 | 0.12 | |||
| 2.0 | 1.00 | 0.71 | 0.92 | 0.48 | 0.06 | ||||
| 4.0 | 1.00 | 0.55 | 0.93 | 0.25 | 0.05 | ||||
| 8.0 | 1.00 | 0.34 | 1.00 | 0.07 | 0.04 | ||||
| MGM | 1e-2 | 0.94 | 0.80 | 0.96 | 0.27 | 5.15 | |||
| 1e-3 | 1.00 | 0.68 | 0.98 | 0.15 | 3.67 | ||||
| 1e-4 | 1.00 | 0.59 | 0.98 | 0.08 | 3.47 | ||||
| 1e-5 | 1.00 | 0.49 | 1.00 | 0.05 | 3.40 | ||||
| Copula | 1e-2 | 0.63 | 0.43 | 0.17 | 0.01 | 307.86 | |||
| 1e-3 | 0.81 | 0.36 | 0.28 | 0.01 | 307.70 | ||||
| 1e-4 | 0.86 | 0.30 | - | - | 307.68 | ||||
| 1e-5 | 0.90 | 0.28 | - | - | 307.66 | ||||
| 100 | 2 | 1000 | CG | 1.0 | 0.99 | 0.96 | 0.74 | 0.80 | 16.53 |
| 2.0 | 0.99 | 0.91 | 0.65 | 0.65 | 17.02 | ||||
| 4.0 | 1.00 | 0.85 | 0.60 | 0.40 | 19.96 | ||||
| 8.0 | 0.99 | 0.72 | 0.74 | 0.22 | 11.50 | ||||
| DG | 1.0 | 0.99 | 0.98 | 0.96 | 0.96 | 0.08 | |||
| 2.0 | 1.00 | 0.96 | 0.96 | 0.91 | 0.07 | ||||
| 4.0 | 1.00 | 0.89 | 0.96 | 0.79 | 0.06 | ||||
| 8.0 | 1.00 | 0.76 | 0.96 | 0.58 | 0.06 | ||||
| MGM | 1e-2 | 0.90 | 0.97 | 1.00 | 0.80 | 37.76 | |||
| 1e-3 | 0.99 | 0.96 | 1.00 | 0.70 | 32.98 | ||||
| 1e-4 | 1.00 | 0.92 | 1.00 | 0.56 | 31.27 | ||||
| 1e-5 | 1.00 | 0.89 | 1.00 | 0.44 | 29.77 | ||||
| Copula | 1e-2 | 0.48 | 0.71 | 0.09 | 0.06 | 403.25 | |||
| 1e-3 | 0.66 | 0.68 | 0.10 | 0.04 | 396.65 | ||||
| 1e-4 | 0.73 | 0.63 | 0.10 | 0.03 | 395.57 | ||||
| 1e-5 | 0.77 | 0.61 | 0.08 | 0.02 | 395.25 | ||||
| 100 | 4 | 1000 | CG | 1.0 | 0.95 | 0.86 | 0.79 | 0.76 | 51.91 |
| 2.0 | 0.96 | 0.78 | 0.76 | 0.65 | 43.66 | ||||
| 4.0 | 0.96 | 0.69 | 0.72 | 0.52 | 38.67 | ||||
| 8.0 | 0.97 | 0.59 | 0.73 | 0.41 | 32.60 | ||||
| DG | 1.0 | 0.95 | 0.97 | 0.90 | 0.93 | 0.27 | |||
| 2.0 | 0.96 | 0.94 | 0.90 | 0.89 | 0.21 | ||||
| 4.0 | 0.97 | 0.83 | 0.91 | 0.77 | 0.16 | ||||
| 8.0 | 0.98 | 0.68 | 0.93 | 0.60 | 0.11 | ||||
| MGM | 1e-2 | 0.98 | 0.88 | 0.97 | 0.67 | 176.07 | |||
| 1e-3 | 1.00 | 0.84 | 0.97 | 0.56 | 135.72 | ||||
| 1e-4 | 1.00 | 0.79 | 0.96 | 0.45 | 106.78 | ||||
| 1e-5 | 1.00 | 0.74 | 0.95 | 0.37 | 82.00 | ||||
| Copula | 1e-2 | 0.55 | 0.50 | 0.10 | 0.05 | 531.39 | |||
| 1e-3 | 0.63 | 0.53 | 0.12 | 0.04 | 432.96 | ||||
| 1e-4 | 0.68 | 0.50 | 0.15 | 0.03 | 417.76 | ||||
| 1e-5 | 0.73 | 0.47 | 0.10 | 0.02 | 414.41 | ||||
Table 7:
Lee and Hastie simulation continued.
| Simulation | Algorithm | Statistics | Time | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Measured | Degree | Samples | Method | Parameter | Adj Precision | Adj Recall | Arrhd Precision | Arrhd Recall | Seconds |
| 500 | 4 | 1000 | CG | 1.0 | 0.97 | 0.86 | 0.80 | 0.75 | 2082.13 |
| 2.0 | 0.98 | 0.79 | 0.76 | 0.65 | 1875.14 | ||||
| 4.0 | 0.98 | 0.69 | 0.71 | 0.52 | 1638.23 | ||||
| 8.0 | 0.98 | 0.58 | 0.70 | 0.41 | 1275.42 | ||||
| DG | 1.0 | 0.97 | 0.96 | 0.94 | 0.93 | 1.94 | |||
| 2.0 | 0.98 | 0.90 | 0.95 | 0.87 | 1.54 | ||||
| 4.0 | 0.99 | 0.79 | 0.95 | 0.75 | 1.15 | ||||
| 8.0 | 0.99 | 0.63 | 0.96 | 0.54 | 0.79 | ||||
| MGM | 1e-2 | 0.95 | 0.89 | 0.99 | 0.70 | 1888.53 | |||
| 1e-3 | 0.99 | 0.83 | 0.99 | 0.56 | 1304.90 | ||||
| 1e-4 | 1.00 | 0.78 | 0.99 | 0.46 | 1062.12 | ||||
| 1e-5 | 1.00 | 0.74 | 1.00 | 0.37 | 968.14 | ||||
Appendix B.
In this appendix, we detail the parameters used for simulation of the data. Each parameter will be followed by the values we used in simulation and a short description. We split the parameters into 3 groups: general parameters used across all simulations, parameters specific to the conditional Gaussian simulation, and parameters specific to the Lee and Hastie simulation.
General Parameters
numRuns: 10 - number of runs
numMeasures: 100, 500, 1000 - number of measured variables
avgDegree: 2, 4, 6 - average degree of graph
sampleSize: 200, 1000, 5000 - sample size
percentDiscrete: 50 - percentage of discrete variables (0 - 100) for mixed data
differentGraphs: true - true if a different graph should be used for each run
coefSymmetric: true - true if negative coefficient values should be considered
Conditional Gaussian Parameters
minCategories: 2 - minimum number of categories
maxCategories: 4 - maximum number of categories
varLow: 1.0 - low end of variance range
varHigh: 3.0 - high end of variance range
coefLow: 0.2 - low end of coefficient range
coefHigh: 0.7 - high end of coefficient range
meanLow: 0.5 - low end of mean range
meanHigh: 1.5 - high end of mean range
Lee and Hastie Parameters
numCategories: 3 - maximum number of categories
varLow: 1.0 - low end of variance range
varHigh: 2.0 - high end of variance range
coefLow: 0.5 - low end of coefficient range
coefHigh: 1.5 - high end of coefficient range
Footnotes
A degenerate distribution is a distribution with support only on a lower dimension space; on the left of Figure 1 we see that there is only support on the plane x + y + z = 1.
Contributor Information
Bryan Andrews, Intelligent Systems Program, University of Pittsburgh, Pittsburgh, PA 15260, USA.
Joseph Ramsey, Department of Philosophy, Carnegie Mellon University, Pittsburgh, PA 15213, USA.
Gregory F. Cooper, Department of Biomedical Informatics, University of Pittsburgh, Pittsburgh, PA 15260, USA
References
- Andrews Bryan, Ramsey Joseph, and Cooper Gregory F. Scoring Bayesian networks of mixed variables. International journal of data science and analytics, 6:3–18, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop Christopher M. Pattern recognition and machine learning. springer, 2006. [Google Scholar]
- Borboudakis Giorgos and Tsamardinos Ioannis. Towards robust and versatile causal discovery for business applications. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pages 1435–1444. ACM, 2016. [Google Scholar]
- Bøttcher Susanne Gammelgaard. Learning Bayesian Networks with Mixed Variables. PhD thesis, Aalborg University, 2004. [Google Scholar]
- Chickering David Maxwell. Optimal structure identification with greedy search. Journal of machine learning research, 3:507–554, 2002. [Google Scholar]
- Colombo Diego and Maathuis Marloes H. Order-independent constraint-based causal structure learning. The Journal of Machine Learning Research, 15:3741–3782, 2014. [Google Scholar]
- Cui Ruifei, Groot Perry, and Heskes Tom. Copula PC algorithm for causal discovery from mixed data. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases, pages 377–392. Springer, 2016. [Google Scholar]
- Harris Naftali and Drton Mathias. PC algorithm for nonparanormal graphical models. The Journal of Machine Learning Research, 14(1):3365–3383, 2013. [Google Scholar]
- Haughton Dominique. On the choice of a model to fit data from an exponential family. The Annals of Statistics, 16:342–355, 1988. [Google Scholar]
- Hyttinen Antti, Eberhardt Frederick, and Järvisalo Matti. Constraint-based causal discovery: Conflict resolution with answer set programming. In UAI, pages 340–349, 2014. [Google Scholar]
- Koller Daphne, Friedman Nir, and Bach Francis. Probabilistic graphical models: principles and techniques. MIT press, 2009. [Google Scholar]
- Lee Jason and Hastie Trevor. Structure learning of mixed graphical models. In Artificial Intelligence and Statistics, pages 388–396, 2013. [Google Scholar]
- Nandy Preetam, Hauser Alain, and Maathuis Marloes H. High-dimensional consistency in score-based and hybrid structure learning. The Annals of Statistics, 46:3151–3183, 2018. [Google Scholar]
- Pearl Judea. Causality. Cambridge university press, 2009. [Google Scholar]
- Raghu Vineet K, Poon Allen, and Benos Panayiotis V. Evaluation of causal structure learning methods on mixed data types. In Proceedings of 2018 ACM SIGKDD Workshop on Causal Discovery, pages 48–65, 2018. [PMC free article] [PubMed] [Google Scholar]
- Ramsey Joseph, Zhang Jiji, and Spirtes Peter. Adjacency-faithfulness and conservative causal inference. In Proceedings of the 22th Conference on Uncertainty in Artificial Intelligence, pages 401–408, 2006. [Google Scholar]
- Ramsey Joseph, Glymour Madelyn, Sanchez-Romero Ruben, and Glymour Clark. A million variables and more: the fast greedy equivalence search algorithm for learning high-dimensional graphical causal models, with an application to functional magnetic resonance images. International journal of data science and analytics, 3:121–129, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsey Joseph D and Malinsky Daniel. Comparing the performance of graphical structure learning algorithms with Tetrad. arXiv preprint arXiv:1607.08110, 2016. [Google Scholar]
- Schwarz Gideon et al. Estimating the dimension of a model. The annals of statistics, 6: 461–464, 1978. [Google Scholar]
- Sedgewick Andrew J, Buschur Kristina, Shi Ivy, Ramsey Joseph D, Raghu Vineet K, Manatakis Dimitris V, Zhang Yingze, Bon Jessica, Chandra Divay, Karoleski Chad, et al. Mixed graphical models for integrative causal analysis with application to chronic lung disease diagnosis and prognosis. Bioinformatics, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spirtes Peter, Richardson Thomas, and Meek Chris. The dimensionality of mixed ancestral graphs Technical report, Technical Report CMU-PHIL-83, Philosophy Department, Carnegie Mellon University, 1997. [Google Scholar]
- Spirtes Peter, Clark N Glymour Richard Scheines, Heckerman David, Meek Christopher, Cooper Gregory, and Richardson Thomas. Causation, prediction, and search. MIT press, 2000. [Google Scholar]