Platelet packing density is an independent regulator of the hemostatic response to injury

Abstract

Background:

Hemostasis studies performed in vivo have shown that hemostatic plugs formed after penetrating injuries are characterized by a core of highly activated, densely packed platelets near the injury site, covered by a shell of less activated and loosely packed platelets. Thrombin production occurs near the injury site, further activating platelets and starting the process of platelet mass retraction. Tightening of interplatelet gaps may then prevent the escape and exchange of solutes.

Objectives:

To reconstruct the hemostatic plug macro- and micro-architecture and examine how platelet mass contraction regulates solute transport and solute concentration in the gaps between platelets.

Methods:

Our approach consisted of three parts. First, platelet aggregates formed in vitro under flow were analyzed using scanning electron microscopy to extract data on porosity and gap size distribution. Second, a three-dimensional (3-D) model was constructed with features matching the platelet aggregates formed in vitro. Finally, the 3-D model was integrated with volume and morphology measurements of hemostatic plugs formed in vivo to determine how solutes move within the platelet plug microenvironment.

Results:

The results show that the hemostatic mass is characterized by extremely narrow gaps, porosity values even smaller than previously estimated and stagnant plasma velocity. Importantly, the concentration of a chemical species released within the platelet mass increases as the gaps between platelets shrink.

Conclusions:

Platelet mass retraction provides a physical mechanism to establish steep chemical concentration gradients that determine the extent of platelet activation and account for the core-and-shell architecture observed in vivo.

Introduction

The formation of a hemostatic plug in vivo has been explored previously using fluorescent probes to detect platelet activation status, fibrin formation, thrombin activity and solute transport rates [1–8]. The results showed that following injury a gradient of platelet activation is formed that is characterized by a core of highly activated, densely packed platelets near the injury site, covered by a shell of less activated, more loosely packed platelets. Thrombin activity and fibrin co-localize with the platelet core. Notably, this core-and-shell architecture develops in the microcirculation following either laser or puncture injury causing blood extravasation [2], in the femoral artery following laser injury [9], and in the jugular vein following puncture injury [10]. What is responsible for the formation of this characteristic architecture remains yet to be determined. One hypothesis is that the core-and-shell architecture forms in response to gradients of soluble platelet agonists. Thrombin production occurs primarily at the injury site, enhancing platelet activation and drawing them closer to one another through the process of platelet mass retraction, more commonly referred to as ‘clot retraction’, the process in which thrombi contract in a platelet-dependent manner. Although this process is usually viewed as helping to stabilize hemostatic plugs, here we have tested the idea that the shrinking of the gaps between platelets during retraction has additional consequences, reducing diffusive and convective transport rates and increasing the local concentration of soluble agonists such as thrombin.

Previous studies support the idea that mass transport and the hemostatic process are intimately coupled [3,4,6]. For example, evidence obtained in vitro suggests that the movement of coagulation factors is hindered in the gaps between platelets [11,12]. Similarly, observations in vivo show that plasma leakage from the hemostatic mass decreases during the retraction phase [5]. Taken together these observations suggest that platelet mass retraction limits the influx into the mass of plasma components such as coagulation factors and fibrinogen [13], and concentrates locally produced thrombin and the products of platelet secretion by limiting their escape. If so, then retraction could also represent a mechanism evolved to limit the growth of the hemostatic mass.

Testing this hypothesis requires a detailed understanding of the structure of hemostatic plugs. Previous studies have used electron microscopy to examine the cellular composition of pathological thrombi that were formed in vivo in the venous and arterial circulation using whole specimens [14] or histological sections [15–20]. Yet, two-dimensional images alone, however detailed, do not provide an optimal route for examining transport, which is inherently three-dimensional. Here, we describe a novel approach to address this challenge by constructing a three-dimensional model of the inter-platelet environment.

Our approach consisted of three parts. In the first, gap size distribution and porosity were determined by analyzing scanning electron microscope images of platelet aggregates formed under flow in a microfluidic chamber coated with collagen and tissue factor. In the second part, an algorithm that packs ellipsoids using molecular dynamics was used to reproduce the in vitro structural measurements. Finally, these elements were combined to produce 3-D reconstructions of hemostatic plugs formed in vivo. Blood flow and mass transport were simulated within the resulting 3-D constructs.

To our knowledge, this is the first study to examine the nature of the platelet aggregate microenvironment and how platelet mass retraction affects mass transport. The results show that the accumulation of tightly packed platelets at a site of injury establishes a local environment that is characterized by narrow gaps and tortuous spaces in which the movement of plasma stagnates. This allows thrombin and other platelet agonists to reach higher local concentrations than would otherwise occur. It is in this complex environment that platelet mass retraction creates steep agonist concentration gradients, producing corresponding gradients in the extent of platelet activation that account for the core-and-shell architecture observed in vivo.

Methods

Mice

C57Bl/6J mice (Jackson Laboratories, Bar Harbor, ME, USA) were used for all studies examining wild-type mice. The University of Pennsylvania Institutional Animal Care and Use Committee approved all procedures.

Laser-induced injury in mouse cremaster arteriole

The laser-induced thrombosis model was performed as previously described [2].

Microfluidic assay

Whole blood was drawn from healthy volunteers who self-reported being free of oral medications for at least 10 days. Mouse blood was drawn via cardiac puncture. Blood was anticoagulated with citrate. All studies were approved by the University of Pennsylvania’s Internal Review Board and Institutional Animal Care and Use Committee.

Microfluidic device fabrication [21], design and experimental settings are as previously described [22]. Citrated whole blood was recalcified to 15 mM using a calcium chloride solution immediately prior to each experiment. Flow rates were controlled using a syringe pump (Harvard Apparatus, Holliston, MA, USA). After allowing clots to form for 10 min, samples were fixed by washing out the remaining whole blood with HEPES-buffered saline for 2 min, peeling the device from the glass slide, dispensing 2% glutaraldehyde solution in sodium cacodylate onto the clots, and fixing overnight at 4 °C.

Computational fluid dynamics (CFD)

Computational fluid dynamics based on the Stokes equation was used to resolve the flow in the narrow gaps between platelets as well as in the lumen surrounding the platelet plug. Fluid density (1025 kg m⁻³) and viscosity (1.2 mPa) of plasma was used. The computational mesh was generated using Abaqus (Dassault Systèmes Simulia Corp., Providence, RI, USA). A sufficiently small mesh element size was used to discretize the narrow gaps between the platelets in order to resolve the flow behavior in these small regions. The overall size of the mesh for different clots varies between 2 to 8 million tetrahedral elements depending on the size of each clot and how small the gaps were. A custom-stabilized finite element flow solver was developed in Python using the FEniCS package [23] to solve the Stokes equation. No-slip boundary conditions were imposed on each platelet ellipsoid and the vessel wall.

Thrombin generation model

Thrombin transport was studied by solving the advection-diffusion equation:

$$\partial c/\partial t=D{\nabla }^{2}c-u\nabla c$$

where c denotes the concentration of a chemical species (thrombin), D is the species diffusion coefficient, and u is the velocity vector field obtained by CFD described above. Thrombin transport was considered for a series of consolidation stages. In all thrombin transport simulations, a group of 10 neighboring platelets at the bottom of the hemostatic plug was chosen to release thrombin. The thrombin flux was normalized with respect to the total surface area of the ‘procoagulant’ ellipsoids to ensure that the total thrombin released per unit time was equivalent across simulations. Our modeling choice was motivated by in vivo evidence showing that thrombin generation is localized over a small area at the bottom of the hemostatic plug [1,24]. Using time-dependent simulations we determined that equilibrium in the thrombin concentration gradient was reached within a few seconds, whereas hemostatic plug consolidation occurs over minutes [5]. Based on these results we used time-independent steady-state solutions to resolve the thrombin concentration in the small gaps between the platelets; thus, the results of our simulations offer a snapshot of the thrombin gradient for a platelet mass along a series of consolidation stages. Parameter values are listed in Table 1.

Table 1.

Parameter values

Name	Value	Unit	Description
Dirichlet Boundary Condition	Parabolic inflow with centerline velocity of 2	mm s−1	Velocity at the inlet
Neumann Boundary Condition	0	Pa	Pressure at outlet
D	80	μm2 s−1	FII diffusion coefficient

Statistics

One-way anova was used with Tukey’s honest significant difference post hoc comparisons.

Results

Overall strategy

We employed a combined empirical-theoretical approach to computationally reconstruct a hemostatic plug and quantify plasma velocity and mass transport in its internal gaps (Figure S1). Intravital microscopy was utilized in the cremaster muscle laser injury model to obtain overall 3-D morphology of the hemostatic plug. Because intravital fluorescence microscopy cannot resolve platelet-level detail, SEM images of platelet aggregates formed under flow over a surface of collagen and tissue factor were analyzed to estimate clot porosity and determine the interplatelet gap size distribution. A previously published algorithm [25] was then utilized to generate jammed packings of hard ellipsoids to match the porosity and gap size distribution estimated from the SEM images. Finally, a computationally reconstructed hemostatic plug was obtained by filling the 3-D volume obtained from the intravital studies with the ellipsoid packings matching the physical features of the SEM images. Computational fluid dynamics was then used to compute flow in and around the platelet mass and a simple thrombin generation model was employed to examine soluble species transport between the platelets. Further details on each aspect of our approach are described in more detail below.

Characterization of the platelet aggregate microenvironment

Hemostatic plugs formed in vivo after penetrating injuries have a heterogeneous architecture comprised of platelets and fibrin. The pore space, which is the volume occupied by fluid, is highly tortuous and interconnected, making it difficult to describe simply. However, as with transport through most porous media, it is the overall porosity and the gap size distribution that may be considered as the dominant features. Overall porosity is the ratio of total pore space volume to total clot volume and ranges between 0 and 1, whereas the gap size distribution characterizes the statistical variation of pore size over space. Overall porosity and mean gap size were estimated using SEM images of platelet aggregates that formed when human or mouse blood was flowed over a collagen and tissue factor surface in microfluidic devices at venous (100 s⁻¹) and arterial (1000 s⁻¹) shear rates. Platelet accumulation was observed for up to 10 min, by which time peak accumulation had occurred. Representative images are shown in Fig. 1(A–C). In each case we observed densely packed structures composed mainly of platelets. Fibrin was not abundant and was usually detected primarily at the bottom of an aggregate, near the junction with collagen and tissue factor.

Fig. 1.

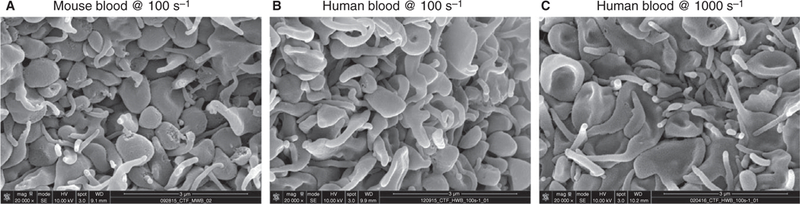
Defining the microenvironment of a platelet aggregate under flow. Scanning electron microscope images of top-down view of whole blood clotting under flow over a surface of collagen and tissue factor. Aggregates are composed almost exclusively of densely packed platelets. (A) Wild-type mouse blood perfused at venous shear rate (100 s⁻¹). Human whole blood perfused at venous shear rate of 100 s⁻¹ (B), and at arterial shear rate of 1000 s⁻¹ (C).

The SEM images were binarized using the gray value of each pixel (Fig. 2A,B). The threshold value was chosen by an investigator who compared binarized and corresponding SEM images without knowing the conditions of the experiment. The resulting images were then processed to extract overall porosity and gap size distributions (Fig. 2C); see supplementary materials for MATLAB code. Single parameter sensitivity analysis was implemented to ensure that the binarization method was robust to the choice of threshold value (Figure S1). The gap size distributions (Fig. 2D) and overall porosities (Fig. 2E) of the three types of aggregates shown in Fig. 1 were found to be statistically equivalent. Different platelet aggregate microenvironments, however, exist and can be detected by the procedures that we used. This can be seen by comparing the 2-D porosities extracted from aggregates obtained flowing mouse blood on a surface of collagen in the presence or absence of tissue factor (Figure S2).

Fig. 2.

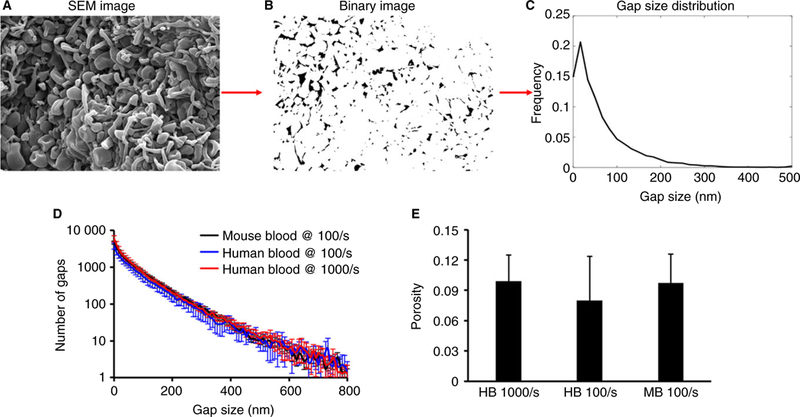
Analysis of SEM images of platelet aggregates. (A) An example of a scanning electron image of a platelet aggregate obtained from flowing whole blood over collagen and tissue factor. (B) Binary image version of image A obtained after thresholding. (C) Using a custom-written code in MATLAB (Supplementary Material) a binary image is scanned to obtain the gap size distribution. In all three types of platelet aggregates the gap size distribution (D) and overall surface porosity (E) are statistically equivalent.

Computational reconstruction of the platelet aggregate microenvironment

As an initial approximation, a molecular dynamics algorithm was used to generate jammed disordered packings of non-intersecting ellipsoids (Fig. 3A) [25]. In this algorithm, hard ellipsoids with a semi-axis ratio of 1 : 1 : 0.4 were initialized with random positions and velocities, and an infinitesimally small volume. The ellipsoid population was then evolved in time through collisions and size expansions until a jammed state corresponding to maximal density was achieved. However, neither the mean overall porosity (0.33, Figure S3) nor the gap size distribution (Fig. 3C) obtained in this manner corresponded to the values that we had measured (Fig. 2).

Fig. 3.

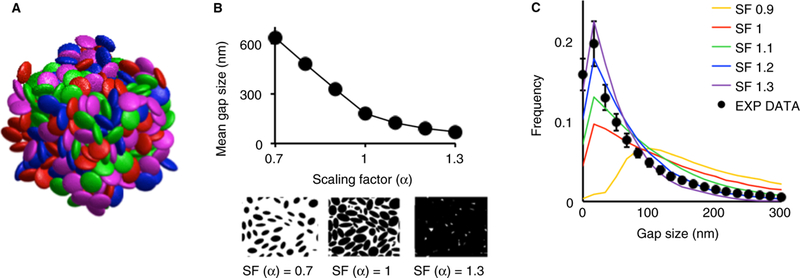
Computational reconstruction of the platelet aggregate microenvironment. (A) An example of a randomly jammed ellipsoid packing. Each ellipsoid semi-axis measures 1, 1 and 0.4 μm, respectively. Colors are for illustration purpose only. (B) Once a jammed ellipsoid packing is achieved, the volume of each ellipsoid can be expanded, or contracted, by multiplying each semi-axis by a scaling factor. This process is illustrated by the two images below the horizontal axis showing how a cross-section of the 3-D packing changes with different values of the scaling factor. As the scaling factor increases, the volume of each ellipsoid also increases, causing intersection between ellipsoids, thus reducing the porous fraction (not shown) and the mean gap size. (C) Gap size frequency distributions computed from ellipsoid packings with different scaling factors and compared with the gap size distribution of the mouse wild-type data. Values of the scaling factor between 1.1 and 1.3 result in gap size distributions that approximate the distribution measured from experimental data.

Therefore, to better match experimental characteristics, a scaling factor, α, was introduced to scale the size of all ellipsoids. Values for α were selected to match the gap size distribution of the ellipsoidal packings to those obtained from image analysis of the experimental platelet aggregates (Fig. 3B and C). The comparisons show that α values between 1.1 and 1.3 best reproduced the experimentally measured gap size distribution. Note that although resting and activated platelets are not ellipsoids (Fig. 1), porosity and gap size distribution, rather than platelet shape, are the most important considerations for obtaining representative interplatelet plasma velocity and transport dynamics. To confirm this idea, we varied the shape of the ellipsoids from highly oblong to spherical. These changes had little effect on porosity, mean gap size or interplatelet velocity (Table S1).

Three-dimensional reconstruction and interplatelet plasma velocity of in vivo hemostatic plugs

We reconstructed a total of eight hemostatic plugs formed in the mouse microcirculation following laser injury. Previous studies have shown that hemostatic plugs formed in vivo have a core of fully activated, P-selectin-positive, densely packed platelets overlaid with a shell of less activated, relatively loosely packed platelets [2]. In the in vivo study shown in Fig. 4(A), platelets were fluorescently labeled with CD41 and P-selectin conjugated antibodies. Using the confocal z-stack, the 3-D volume of the hemostatic platelet plug was visualized. The core (red) and shell (blue) portions of the hemostatic platelet plug volume were then digitally ‘filled’ with ellipsoids (α = 1.3 and 1.1, respectively) as described in the previous section (Fig. 4B). This selection recapitulates the heterogeneous packing observed in hemostatic plugs formed in vivo, producing regions with different porosities and mean gap sizes.

Fig. 4.

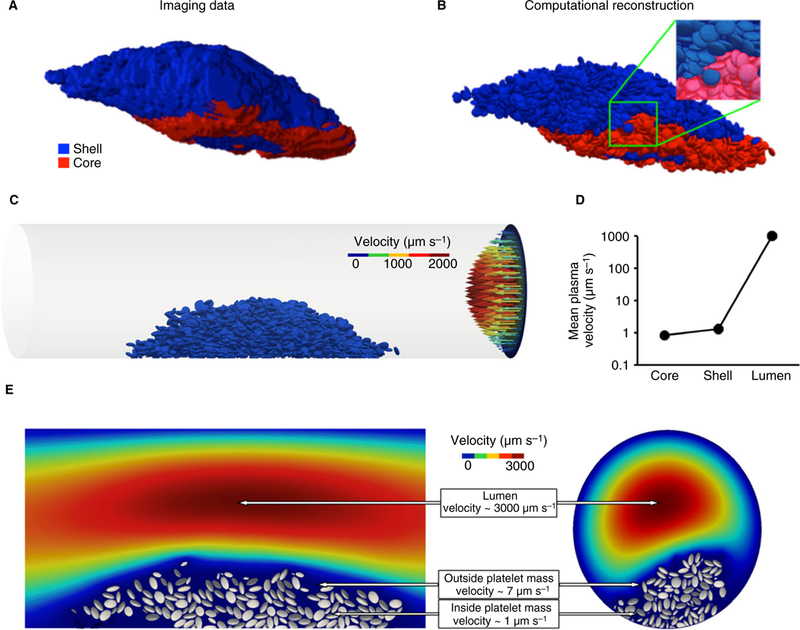
From in vivo to in silico. (A) The volume of a hemostatic plug formed within a cremaster muscle arteriole determined from a 3-D image stack taken 20 mins post-injury. Blue represents the fluorescence coming from the CD41 channel (shell); red is the fluorescence associated with the P-selectin channel (core). (B) Reconstruction of the in vivo hemostatic plug. The hemostatic plug volume is filled with a jammed ellipsoid packing as in Fig. 3(A). (C) A cylinder having the same dimensions as the vessel from the experiment is used to model the blood vessel. The hemostatic plug is positioned in the modeled vessel using experimental images as a visual guide. Blood flow is simulated solving the Navier-Stokes equations; the parabolic flow is illustrated by the arrows on the right end of the cylinder. The hemostatic plug and the arrows are color-coded according to the velocity they represent. (D) Mean interplatelet velocity in the core and the shell, compared with the plasma velocity in the rest of the vessel. (E) Plasma velocity decreases sharply inside of the platelet mass. Sections parallel (left) and perpendicular (right) to the direction of the flow illustrate how the microenvironment between the platelets is sheltered from the flow.

This computationally reconstructed hemostatic platelet plug was then placed in a cylinder having the same dimensions as the vessel injured during the experiment and blood flow was simulated. The extravascular portion of the hemostatic platelet plug was not considered in this study. Computational fluid dynamics simulations were run with a centerline velocity of 2 mm s⁻¹ in a vessel with diameter 35 μm. The results show that the plasma velocity between the platelets is in the order of microns-per-second, which is approximately three orders-of-magnitude slower than blood flow within the vessel lumen (Fig. 4C). Differences between the core and the shell were small compared with the much greater mean plasma velocity of 1000 μm s⁻¹ in the vessel lumen (Fig. 4D). The sudden reduction in plasma velocity between the vessel lumen and the platelet mass is especially clear in the 2-D cross-sections shown in Figs 4(E) and S4.

Determinants of interplatelet plasma velocity

The reconstructed hemostatic plug shown in Fig. 4(B) was used to analyze the effects of mean gap size on interplatelet plasma velocity. The mean gap size and overall porosity were varied by changing the scaling factor, α. The smallest scaling factor (α = 0.7) corresponded to a mean gap size of 650 nm, whereas the largest scaling factor (α = 1.2) corresponded to a mean gap size of 91 nm (Fig. 5A). The results indicate that across this range large variations in gap size produce small variations in the mean interplatelet velocity (Fig. 5A, filled circles, left vertical axis).

Fig. 5.

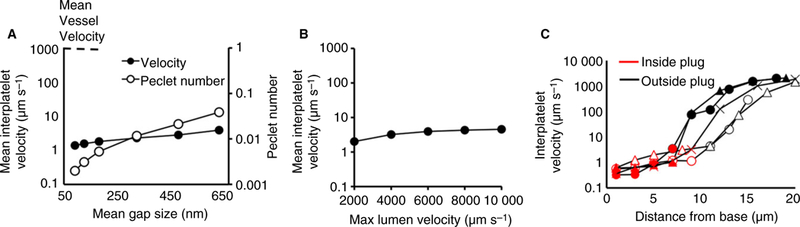
Determinants of interplatelet plasma velocity. (A) Over a biologically relevant range of gap sizes (60 to 600 nm), gap size has little effect on the interplatelet plasma velocity (filled circles, left vertical axis), and diffusion is the main driver of transport inside a hemostatic plug (empty circles, right vertical axis). (B) Increasing the maximum velocity in the vessel has little effect on the mean interplatelet velocity. (C) Interplatelet velocity measured at different points from the reconstruction of five actual hemostatic plug volumes. Each plug is indicated by a different symbol (empty triangles, empty circles, filled triangles, filled circles and crosses). On the outside of the plug (black points) plasma velocity is about 1 mm s⁻¹, whereas in the inside of the plug (red points) the plasma velocity drops by three orders of magnitude.

We also considered whether interplatelet plasma velocity changes over time as the hemostatic mass accumulates, contracts and stabilizes. The results indicate the interplatelet plasma velocity remains slow throughout (Figure S5). It was also negligibly affected when ellipsoids of different aspect ratios were used for the reconstruction (Table S1).

The relative contributions of convective and diffusive transport of thrombin in the interplatelet environment were investigated by computing the Peclet number, P_e = LU/D, where D is the thrombin diffusion coefficient [26], L the mean gap size and U the mean interplatelet velocity. A value of the Peclet number much smaller than 1 indicates that diffusion dominates molecular movement, whereas a value much bigger than 1 indicates that convection dominates. As shown in Fig. 5(A) (open circles, right vertical axis), over a range spanning an order-of-magnitude in mean gap size, the value of the Peclet number remains well below 1, pointing to the dominant nature of diffusion in the hemostatic plug microenvironment. A similarly weak effect is observed for lumen velocity on interplatelet plasma velocity (Fig. 5B).

Finally, the interplatelet velocity spatial distribution across a hemostatic plug was estimated by evaluating the velocity at distinct points along a line running perpendicular to the vessel length. The calculations were performed in the reconstructions of five actual hemostatic plugs (Fig. 5C). The plasma velocity, which was typically about 1 mm s⁻¹ outside a plug, decreases by three orders-of-magnitude within 10 microns into the plug.

The impact of mass retraction on thrombin distribution

Here we address mass transport as a function of platelet mass retraction using a simple model of constant thrombin generation in a reconstructed hemostatic plug. Thrombin generation was simulated by a flux at the boundary of a small group of ‘procoagulant’ ellipsoids at the bottom of the reconstructed platelet plug, a choice supported by in vivo evidence showing that thrombin generation is localized over a small area at the bottom of the hemostatic plug [1,24]. Different extents of platelet mass retraction were simulated using scaling factors, α = 1, 1.1, 1.2. The steady-state thrombin concentration gradient across the platelet mass for each case is shown in Fig. 6. The results show that by decreasing gap size, mass retraction causes an increase in the local thrombin concentration. Given that the total thrombin released per unit time was equal in each case, the increase in thrombin concentration is the result of increased retention. Additionally, in each simulated case the interplatelet plasma velocity (Table S2) and the thrombin concentration gradient (Fig. 6, Table S3) are symmetric, which indicates the absence of any flow-dependent bias within a platelet mass.

Fig. 6.

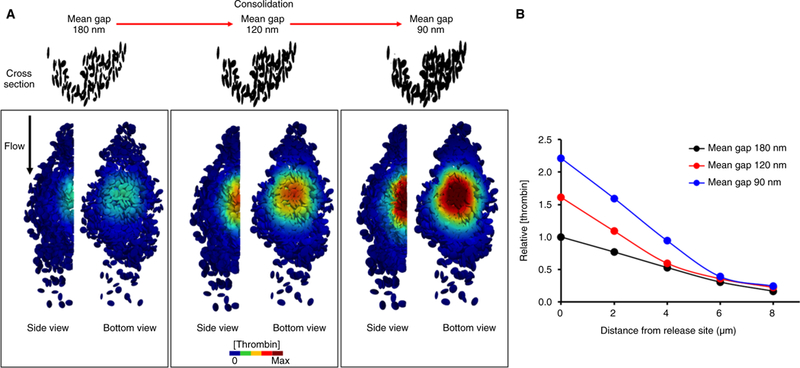
The thrombin concentration increases as gap size decreases. Simulation of constant thrombin generation from a small group of procoagulant platelets placed at the bottom of the platelet pile. Visual representation (A) and quantitative analysis (B) show that as the gap sizes become narrower the concentration of thrombin increases.

Hemostatic plug architecture alters the thrombin concentration gradient

Finally, we examined the plasma velocity and thrombin concentration gradient during different developmental stages of the platelet plug in the presence or absence of ADP P2Y₁₂ receptor signaling. We have shown previously that blocking the contribution of ADP using the P2Y₁₂ receptor antagonist, cangrelor, results in a hemostatic platelet plug that retains its core, but loses its shell [2]. For each platelet plug (vehicle and cangrelor), two distinct stages were analyzed, the maximum volume stage (Fig. 7Ai–Bi) and the final stable configuration (Fig. 7Aii–Bii). The volume of each plug was reconstructed as described in the previous sections, with the shell region (P-selectin negative platelets) and core region (P-selectin positive platelets) modeled as having distinct packing configurations (α = 1.1 and 1.3, respectively).

Fig. 7.

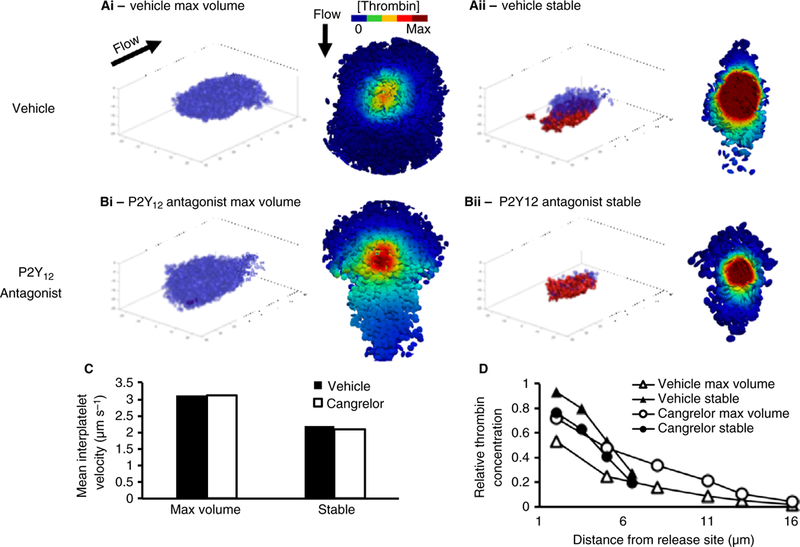
The thrombin concentration gradient is affected by the hemostatic plug architecture. Simulation of constant thrombin generation during the development of a hemostatic plug in a vehicle (Ai–Aii) and a cangrelor-treated (Bi–Bii) mouse. Successive stages of a hemostatic plug development were acquired via confocal microscopy and two distinct stages were identified: maximum volume (Ai–Bi) and final stable configuration (Aii–Bii). Blue transparent ellipsoids represent the shell, whereas red ellipsoids represent the core. To the right of each image is the bottom-up view of the corresponding thrombin concentration gradient. (C). The mean interplatelet velocity in both vehicle and cangrelor cases is slow and weakly affected by the size and the architecture of the hemostatic plug (D) The thrombin gradient at the maximum volume stage is shallow (empty symbols), with the appearance of the core thrombin retention increasing and the gradient becoming steeper.

The results show that, despite large variations in the hemostatic plug volume and core–shell ratio between vehicle and cangrelor, interplatelet plasma velocity was relatively constant (Fig. 7C). Because the maximum volume stage is reached prior to maximal platelet retraction and formation of a core region, the mean gap size is large, leading to a shallow concentration gradient that extends from the thrombin generation flux towards the edge of the platelet plug (Fig. 7Ai, Bi and D, empty symbols). When the core emerges, tight spaces between platelets hinder thrombin diffusion, resulting in a steeper concentration gradient as thrombin is retained close to its source: the thrombin concentration falls 4-fold in 4 microns (Fig. 7Aii, Bii and D, filled symbols). Interestingly, the vehicle and P2Y12 antagonist-treated cases do not differ (compare triangle and circle symbols in Fig. 7D), suggesting that once the core is formed the shell does not influence thrombin transport originating in the core.

Discussion

Hemostatic plugs formed in response to penetrating injuries in the mouse vasculature are characterized by a core of highly activated, densely packed platelets near the injury site, covered by a shell of less activated and loosely packed platelets. How the core-and-shell architecture comes about is unclear. One hypothesis is that it forms in response to gradients of soluble agonists: thrombin production near the injury site enhances platelet activation, driving platelet accumulation followed by mass retraction, which increases platelet packing density and reduces transport. To understand exactly how platelet packing density regulates transport, an explicit representation of the 3-D pore network in a platelet mass is needed.

Mass transport within a hemostatic plug has been studied previously using computational approaches in 2-D models [4,27–30]. Although informative, these approaches have limitations. Homogeneous porous media models require specification of effective transport properties, whereas in 2-D explicit models, platelet contact points prevent interplatelet fluid flow. To overcome these limitations, 3-D models are best suited to predict the transport properties of complex three-dimensional geometries. One prior study has utilized 3-D reconstruction of a platelet plug from fluorescence data; however, that study did not consider platelet mass retraction and was based on a single hemostatic plug at a single time-point [31].

Our goal was to study how platelet mass retraction creates conditions that favor thrombin accumulation. We computationally reconstructed hemostatic plugs combining data from confocal fluorescence and electron microscopy with computer-optimized ellipsoid packings. Our study is the first to examine the impact of gap size on plasma velocity and mass transport adopting a computational approach that is systematic, single-platelet based, data-driven, 3-D and robust. The analysis reveals that mass transport in the platelet mass is diffusion dominated and that platelet mass retraction promotes the retention of chemical species released in the mass. Both of these findings are general and robust over a wide range of gap sizes.

We find that the hemostatic plug is characterized by extremely narrow gaps and porosity values that are even smaller than previously estimated [2,31]. These properties provide a basis for regulating chemical reactions by purely physical means. In all experiments, the gap size distribution of the platelet aggregate surface takes the shape of a negative exponential distribution with a mean gap size of 80 nm, which could serve as a means to reproduce a barrier function as effective as that of healthy endothelium [32]. If this gap size distribution is representative of hemostatic plugs formed in vivo it would explain how platelet packing density could be a physical mechanism for regulating hemostatic plug growth by reducing solute exchange and increasing the local concentration of agonists [4,13].

Our results suggest that interplatelet plasma velocity is slow and minimally affected by variations in hemostatic plug size, architecture, mean gap size, packing density, outside blood velocity, or the specific location within a hemostatic plug. This suggests that slowing plasma velocity to shift mass transport into the diffusion-controlled regime could be a necessary condition for hemostasis. A sheltered environment increases the residence time of individual molecules and, therefore, their potential bioactivity. These results suggest a mechanism for how platelet mass retraction acts to increase the local concentration of thrombin, and how the core formation acts to retain thrombin. Our findings are consistent with observations from in vivo studies showing that thrombin activity is confined to the core region of the hemostatic plug [1].

This study has potential shortcomings as well as strengths. Experimentally, samples for electron microscopy must be fixed and dehydrated, which can introduce potential artifacts. To minimize this possibility, we followed rigorous sample preparation methods [33] and used hexamethyldisilazane for drying, which has been demonstrated to minimize artifacts in drying biological samples [34]. Computationally, rigid ellipsoids were employed to model deformable platelets. However, the analysis suggests that it is the properties of the pore size distribution that define the transport rates in a porous medium, not the shape of the particles forming the medium. A second computational limitation is the relatively small size of the hemostatic plugs modeled. The approach presented worked well with hemostatic plugs 40 to 50 microns in length (~10 000 ellipsoids). This size was a practical choice: currently it would be computationally prohibitive to model larger hemostatic masses. However, the results that were obtained suggest that the transport inside a larger mass should not be very different as only a few thousand platelets are needed to create an internal microenvironment dominated by diffusion. Finally, we chose to model thrombin generation as a constant flux from the boundaries of a subset of ellipsoids rather than simulating the actual chemical reactions. During platelet mass retraction, for instance, the delivery of prothrombin could be hindered and ‘starve’ the thrombin generation reaction. The effects of substrate delivery and anticoagulant dynamics are important and will be investigated in future studies. Still, thrombin is generated and our analysis shows that platelet mass retraction acts to retain thrombin and to shape its local concentration gradient. Notably, despite these limitations, this study provides useful insights into the role of platelets in determining the plasma movement and thrombin retention within an aggregate. The results are consistent with several observations obtained using in vivo [1,3,5,6], in vitro [11,12,35] and computational approaches [4,13,27,30,31,36].

In conclusion, in addition to other factors limiting the size of the hemostatic plug (inhibitors, agonists’ half-life, etc.), the results presented here showed that clot retraction provides a mechanism capable of regulating the movement and the concentration of important soluble agonists, and thus the resulting platelet response.

Supplementary Material

1

Fig. S1. Overall approach flow chart.

Fig. S2. Sensitivity analysis of SEM image analysis method.

Fig. S3. Platelet aggregate microenvironment on different procoagulant surfaces.

Fig. S4. Reproducibility of the packing algorithm.

Fig. S5. Interplatelet plasma velocity.

Fig. S6. Interplatelet plasma velocity during hemostatic plug evolution.

Table S1. Effect of ellipsoids aspect ratio.

Table S2. Interplatelet plasma velocity sampled along the flow direction.

Table S3. Relative thrombin concentration sampled along the flow direction.

Essentials.

• Platelet packing density in a hemostatic plug limits molecular movement to diffusion.

• A diffusion-dependent steep thrombin gradient forms radiating outwards from the injury site.

• Clot retraction affects the steepness of the gradient by increasing platelet packing density.

• Together, these effects promote hemostatic plug core formation and inhibit unnecessary growth.

Addendum

M. Mirramezani designed and conducted the computational studies, and edited and revised the manuscript. B. A Herbig designed and conducted the experimental studies. T. J. Stalker designed and conducted the experimental studies, and analyzed data. L. Nettey conducted the computational studies. M. Cooper analyzed data. J. W. Weisel, S. L. Diamond, T. Sinno and L. F. Brass analyzed and interpreted data. S. C. Shadden designed computational studies, analyzed and interpreted data and revised the manuscript. M. Tomaiuolo designed and conducted the computational studies, analyzed and interpreted data, and drafted the manuscript.