Nonparametric Bootstrap of Sample Means of Positive-Definite Matrices with an Application to Diffusion-Tensor-Imaging Data Analysis

Abstract

This paper presents nonparametric two-sample bootstrap tests formeans of randomsymmetric positivedefinite (SPD) matrices according to two differentmetrics: the Frobenius (or Euclidean)metric, inherited from the embedding of the set of SPD metrics in the Euclidean set of symmetric matrices, and the canonical metric, which is defined without an embedding and suggests an intrinsic analysis. A fast algorithm is used to compute the bootstrap intrinsic means in the case of the latter. The methods are illustrated in a simulation study and applied to a two-group comparison of means of diffusion tensors (DTs) obtained from a single voxel of registered DT images of children in a dyslexia study.

1. Introduction

Statistical inference for distributions on manifolds is a broad discipline with wide-ranging applications. Its study has gained momentum, due to its applications in biosciences and medicine, geosciences, astronomy, computer vision and image analysis, electrical engineering, and other fields.

A general framework for nonparametric inference for location on manifolds was introduced in Patrangenaru (1998) and Bhattacharya and Patrangenaru (2003, 2002, 2005). There, properties were derived for two types of Fréchet means on finite-dimensional manifolds: (1) the (embedding-dependent) extrinsic mean, associated with the Euclidean distance induced on the manifold by an embedding in Euclidean space, and (2) the (Riemannian-structure-dependent) intrinsic mean, associated with the geodesic distance derived from a Riemannian metric on the manifold. Furthermore, the consistency of extrinsic sample means as an estimator of extrinsic means, under one set of conditions, and of intrinsic means, under another set of conditions, was established. Derivations of the asymptotic distributions of intrinsic and extrinsic sample means, and of confidence regions for the population means based on them, were also provided.

Extrinsic means are appealing for their simplicity. When an explicit embedding is available, the extrinsic mean of a set of data points can be computed by taking the mean in the embedding Euclidean space and projecting the result onto the manifold (assuming there is a unique closest point on the embedded manifold, which is the case for almost all data-sets). In contrast, the intrinsic mean is computed directly on the manifold as the point that minimizes the sum of squared geodesic distances from the data points to it. Intrinsic means (also called centers of mass in the literature) are mathematically elegant and do not require an embedding, but require a Riemannian geometric structure instead. One type of manifold on which intrinsic means are guaranteed to exist, and is particularly relevant to this paper, is a Cartan-Hadamard manifold: a complete, simply-connected Riemannian manifold of nonpositive curvature.

Computational speed is of particular importance in a nonparametric analysis when applying computationally intensive resampling methods like the bootstrap, as each resample requires a new computation of the intrinsic or extrinsic sample mean. Computing both extrinsic and intrinsic sample means is trivial if the manifold is flat in a sufficiently small neighborhood that contains the sample, in the Euclidean sense in the case of the former and in the Riemannian sense in the case of the latter (Patrangenaru, 2001).

In more general situations, extrinsic means sometimes have closed-form expressions while intrinsic means, when they exist, typically require iterative methods to compute. Therefore it is not surprising that in several applications, computations of extrinsic means have been found to be considerably faster than computation of intrinsic means by some commonly-used methods (Bhattacharya et al., 2012). However, there are other iterative algorithms that, when applied to compute intrinsic means of samples of small enough diameter in an arbitrary Riemannian manifold, require very few iterations. Among these is what Groisser (2004, 2005) called the “Riemannian averaging algorithm”, a gradient-descent algorithm that has been suggested independently by several authors (Pennec, 1999; Le, 2001; Groisser, 2004; Fletcher et al., 2004). See also Smith (1994) and Edelman et al. (1998). This algorithm has been tested numerically for some special manifolds by several authors (Pennec et al., 2006; Fletcher and Joshi, 2007). For a Riemannian manifold possessing a lot of symmetry, such as a Riemannian homogeneous space (see the Appendix for a definition), the gradient-descent algorithm is fast in the sense of computation-time as well, because there are simple closed-form expressions for geodesics. For a wide class of algorithms that includes Newton’s method as well as the gradient-descent algorithm, Groisser (2004) established quantitative sufficient conditions for convergence, and convergence-rate bounds.

As a specific manifold, in this paper we study the space Sym⁺(p) of p × p symmetric positive-definite (SPD) matrices, a convex open subset of the space M(p,ℝ) of all real p × p matrices. When endowed with the Frobenius (Euclidean) metric inherited from $M(p,ℝ)\cong {ℝ}^{p^2}$, the space Sym⁺(p) is flat, and therefore provides an example in which the extrinsic sample mean has a simple closed-form expression and coincides with the intrinsic mean according to that metric. As an alternative, it has been suggested to analyze data on this manifold using a canonical metric g_can (Lenglet et al., 2006; Pennec et al., 2006; Schwartzman, 2006; Fletcher and Joshi, 2007), with respect to which Sym⁺(p) is a Cartan-Hadamard symmetric space (see the Appendix for a definition of symmetric space). The space Sym⁺(p) with this metric is complete but curved, suggesting an intrinsic analysis. In statistics literature, covariance matrices are perhaps the most visible occurrence of SPD matrices. In such instances, p may be any positive integer and is limited only be the number of variables considered in a given study. As such, it may be quite large. However, SPD matrices also arise as observations in cosmic background radiation (CBR), where p = 2, and in diffusion tensor imaging (DTI), where p = 3. While the theory we consider holds true for arbitrary p, we will focus our attention for computations on p = 3 to motivate an application to DTI analysis.

A useful methodology in estimating the variability of sample means is Efron’s nonparametric bootstrap (Efron, 1982). It is documented that the coverage error of confidence intervals produced by pivotal nonparametric bootstrap has faster convergence than that of standard confidence intervals (Babu and Singh, 1984; Bhattacharya and Ghosh, 1978; Hall, 1997). Data analysis on manifolds has often been performed via nonparametric bootstrap, with the first examples in directional and axial data analysis (Ducharme et al., 1985; Fisher and Hall, 1989). In this paper, we compare the bootstrap-based analysis under the flat Euclidean metric with an intrinsic bootstrap analysis under the canonical metric. For each bootstrap resample, we compute the canonical intrinsic sample mean using the gradient-descent algorithm. To be precise about the metric used, we hereafter refer to these two types of analysis as Frobenius (or Euclidean) and canonical, rather than extrinsic and intrinsic.

In this paper we design nonparametric two-sample bootstrap tests for means of random positive definite matrices, according to both the Frobenius and canonical metrics. We present a simulation study to show the effectiveness of these methods. Then, as an application, we apply these procedures to compare means of populations of diffusion tensor images.

The rest of the paper is organized as follows. Section 2 introduces basic properties of the set of SPD matrices. Section 3 presents the Frobenius analysis, including the statistical theory behind our tests and the methods for and results of our simulation study. Section 4 presents the corresponding canonical-metric analysis, as well as a discussion of the algorithm used to compute intrinsic means, including its convergencebehavior. Section 5 presents a simulation study to compare coverage probabilities for confidence regions for the Frobenius and canonical methodologies. Section 6 contains our application of the methodology to DTI analysis. Section 7 concludes. For completeness, the necessary theoretical background for SPD matrices and the Riemannian geometry of the canonical metric is provided in Appendix A.

2. SPD matrices

Let Sym(p) ⊂ M(p,ℝ) denote the set of symmetric matrices, and let Sym⁺(p) ⊂ Sym(p) denote the set of positive-definite symmetric matrices:

$$Sy{m}^{+}(p)=\left\{M\in Sym(p):v^{T}Mv>0\forall \text{nonzero}v\in {ℝ}^p\right\}.$$ (2.1)

Sym⁺(p) is an open subset of Sym(p), and it is easily seen from (2.1) that it is also a convex subset: if M₁,M₂ ∈ Sym⁺(p), then (1 − t)M₁ + tM₂ ∈ Sym⁺(p) for all t ∈ [0,1]. Sym⁺(p) is also an open cone: if M ∈ Sym⁺(p), then tM ∈ Sym⁺(p) for all t > 0.

The Euclidean metric on ${ℝ}^{p^2}$, when transferred to M(p,ℝ) by the natural identification $M(p,ℝ)\cong {ℝ}^{p^2}$, is often called the Frobenius metric on M(p,ℝ). The same terminology is used for the Riemannian metric on M(p,ℝ) obtained by transferring the standard Riemannian metric on ${ℝ}^{p^2}$, and also for the induced Riemannian metric on any vector subspace of M(p,ℝ). All of these Riemannian metrics are flat (the curvature is identically zero). Thus Sym(p), with the Frobenius Riemannian metric, is flat. The open subset Sym⁺(p) ⊂ Sym(p) therefore inherits the structure of a flat, but incomplete, Riemannian manifold: the geodesics are open segments of straight lines constrained by the boundary of Sym⁺(p) as a subset of Sym(p) (see Schwartzman (2006)). We refer to this Riemannian structure on the Sym⁺(p) as the Frobenius metric structure on this space.

Another Riemannian metric considered in analysis of DTI data is the “canonical metric” mentioned in the Introduction (Arsigny et al., 2006; Schwartzman, 2006). This metric is complete on Sym⁺(p), but it is not flat. However, the curvature of this metric is non-positive, an extremely convenient geometric feature, as we will see in Section 4.1. Details on this canonical metric are given in the Appendix.

Geodesic convexity—a generalization to Riemannian manifolds of the notion of convexity in vector spaces—suffices for meaningful intrinsic data-analysis on a Riemannian manifold. The convexity of Sym⁺(p) in M(p,ℝ) trivially makes the entire open manifold Sym⁺(p) geodesically convex with respect to the Frobenius metric, so one may think of this metric, rather than the vector-space structure, as what facilitates a statistical analysis on Sym⁺(p). Moreover, the intrinsic and extrinsic means for the Frobenius metric coincide, so it is enough to refer to both as the Frobenius mean. The manifold Sym⁺(p) is also geodesically convex with respect to the canonical Riemannian metric as well, allowing the definition of an intrinsic mean. Furthermore, Sym⁺(p) with this metric is also a homogeneous space (in fact, a symmetric space), which facilitates the rapid computation of the intrinsic mean using an algorithm from Groisser (2004)¹. We describe the analysis using these two different metrics in the next two sections.

3. Nonparametric estimation of Frobenius means

3.1. Nonparametric inference for Frobenius means

Suppose we are given an i.i.d. sample of n SPD matrices Y₁, …, Y_n ∈ Sym⁺(p). Let vecd(·) be a vectorization operator that extracts the entries of its symmetric matrix argument of size p × p into a vector in a Euclidean vector space of dimension p(p + 1)/2. The exact form of this operator is not crucial; for ease of interpretation, here we extract the diagonal entries first and then the off-diagonal entries above the diagonal (see Table 6). The Frobenius sample mean of the vectorizations X_i = vecd(Y_i), i = 1, …, n, is simply the entry-by-entry average $\overline{X}={\sum }_{i=1}^n{X}_i/n$. Similarly, we can compute their sample covariance matrix $S={\sum }_{i=1}^n\left(X_i-\overline{X}\right){\left(X_i-\overline{X}\right)}^T/n.$

Table 6:

DTI data in a group of control (columns 1 – 6) and dyslexia (columns 7 – 12)

	1	2	3	4	5	6
d11	0.8847	0.6516	0.4768	0.6396	0.5684	0.6519
d22	0.9510	0.9037	1.1563	0.9032	1.0677	0.9804
d33	0.8491	0.7838	0.6799	0.8265	0.7918	0.7922
d12	0.0448	−0.0392	0.0217	0.0229	−0.0427	0.0269
d13	−0.1168	−0.0631	−0.0091	−0.1961	−0.0879	−0.1043
d23	0.0162	−0.0454	−0.1890	−0.1337	−0.1139	−0.0607
	7	8	9	10	11	12
d11	0.5661	0.6383	0.6418	0.6823	0.6159	0.5643
d22	0.7316	0.8381	0.8776	0.8376	0.7296	0.8940
d33	0.8232	1.0378	1.0137	0.9541	0.9683	0.9605
d12	0.0358	−0.0044	−0.0643	0.0309	−0.0929	−0.0635
d13	−0.2289	−0.2229	−0.1675	−0.2217	−0.1713	−0.1307
d23	−0.1106	−0.0449	−0.0192	−0.0925	−0.0965	−0.1791

REMARK 3.1 (Estimation of the Euclidean mean for SPD matrices)

Due to convexity, the Central Limit Theorem (CLT) can be applied to any distribution of SPD matrices. The Euclidean mean of such a probability distribution can be estimated using the studentized version of the CLT if a large random sample is available, or by using nonparametric bootstrap if only a small random sample is available.

Now suppose we are given two independent such samples of sizes n₁ and n₂, where the vectors X_a,i, i = 1, …, n_a i.i.d.r.vec.’s with the mean μ_a,a = 1,2. For testing H₀ : μ₁ − μ₂ = δ₀, Hotelling’s T² statistic is

$$T^2=T^2\left({\delta }_0\right)={\left({\overline{X}}_1-{\overline{X}}_2-{\delta }_0\right)}^T{\left(\frac{1}{n_1}{S}_1+\frac{1}{n_2}{S}_2\right)}^{-1}\left({\overline{X}}_1-{\overline{X}}_2-{\delta }_0\right)$$ (3.1)

where ${\overline{x}}_j$, j = 1,2 are the Frobenius means of the two samples and S_j, j = 1,2 are their sample covariance matrices.

If the samples are i.i.d. with $X_{a,j_a}~{\mu }_a$, ∑_a, j_a = 1, …, n_a, a = 1,2 from two independent multivariate populations, and the total sample size n = n₁ + n₂, is such that $\frac{n_1}{n}\to q\in (0,1)$ as n →∞, and $\frac{1}{q}{\sum }_1+\frac{1}{1-q}{\sum }_2>0$, then by the CLT, we have that under the null hypothesis H₀ : μ₁ − μ₂ = δ₀, $T^2\to {\chi }_{p(p+1)/2}^2$ in distribution, as n → ∞. Therefore, a parametric test based on this asymptotic limit would reject H₀ at level α if $T^2>{\chi }_{p(p+1)/2}^2(\alpha )$. A parametric approximation for finite samples is the Fdistribution with p(p + 1)/2 degrees of freedom for the numerator and Yao’s approximation for the degrees of freedom of the denominator (Yao (1965)). If the distributions are unknown and the samples are small, as in our data example, the parametric asymptotic distribution may not provide an accurate approximation to the distribution of the test statistic. Here, instead, we use a nonparametric approach based on the bootstrap. We compute a bootstrap distribution of

$$T^{2*}={\left({\overline{X}}_1^{*}-{\overline{X}}_2^{*}-{\overline{X}}_1+{\overline{X}}_2\right)}^T{\left(\frac{1}{n_1}{S}_1^{*}+\frac{1}{n_2}{S}_2^{*}\right)}^{-1}\left({\overline{X}}_1^{*}-{\overline{X}}_2^{*}-{\overline{X}}_1+{\overline{X}}_2\right)$$ (3.2)

and we take $T_{\alpha }^{2*}$, the 100(1 − α) percentile of T^2*, where the ${\overline{X}}_i^{*}$ and $S_i^{*}$ are, respectively, bootstrap replicates of the sample mean and covariance, for i = 1, 2. The 100(1 − α)% confidence region ${\mathcal{C}}_{\alpha }^1$ for δ = μ₁ − μ₂ based on this bootstrap distribution is given by

$${\mathcal{C}}_{\alpha }^1=\{\delta |T^2(\delta )\le T_{\alpha }^{2*}\}.$$ (3.3)

In each bootstrap resample, two samples of sizes n₁ and n₂ are sampled with replacement from the original data and the test statistic (3.2) is recomputed.

REMARK 3.2

All of the above apply to two random samples from a pair of independent random vectors in general. In particular they apply to any marginals of a pair of random symmetric matrices, with the number of degrees of freedom of the chi-square asymptotic distribution of T² being equal to the number of marginals under consideration.

In cases where n₁ and n₂ are small, however, (3.1) and (3.2) may not be usable due to the covariance term being non-invertible. For such cases, confidence regions may instead be based upon the nonpivotal statistic

$$W^2=W^2\left({\delta }_0\right)={\left({\overline{X}}_1-{\overline{X}}_2-{\delta }_0\right)}^T\left({\overline{X}}_1-{\overline{X}}_2-{\delta }_0\right)$$ (3.4)

and the bootstrap distribution of

$$W^{2*}={\left({\overline{X}}_1^{*}-{\overline{X}}_2^{*}-{\overline{X}}_1+{\overline{X}}_2\right)}^T({\overline{X}}_1^{*}-{\overline{X}}_2^{*}-{\overline{X}}_1+{\overline{X}}_2)$$ (3.5)

Denoting the 100(1 − α) percentile of W^2∗ by $W_{\alpha }^{2*}$, a second 100(1 − α)% confidence region ${\mathcal{C}}_{\alpha }^2$ for δ = μ₁ − μ₂ is given by

$${\mathcal{C}}_{\alpha }^2=\{\delta |W^2(\delta )\le W_{\alpha }^{2*}\}.$$ (3.6)

Alternatively, the p-value for a bootstrap test of the null hypothesis H₀ : μ₁ − 𝜇₂ = δ₀ against the two-sided hypothesis can be calculated using T² as follows:

$${\text{Pvalue}}_T=\frac{\#\left(T^2\left({\delta }_0\right)>T^{2*}\right)}{B}$$ (3.7)

where # (T²(δ0) > T^2* denotes the number of bootstrap replicates of T^2∗ that T²(δ₀) is larger than and B is the number of bootstrap replicates. Similarly, a test can be performed using W² by calculating the following p-value:

$${\text{Pvalue}}_W=\frac{\#\left(W^2\left({\delta }_0\right)>W^{2*}\right)}{B}.$$ (3.8)

3.2. Simulation Study

In order to explore how the above hypothesis tests perform, we performed a simulation study for data in Sym⁺(3). We consider three cases for the relationships between the Frobenius means. For the first case, the Frobenius means for both populations are equal. For the second case, the means are not equal, but the angles between the corresponding principal directions of the matrices are small. For the final case, these angles are somewhat larger. The exact angles will be provided as each case is explored.

We simulated n SPD matrices from a population with a given mean 𝜇 as follows. We generated each SPD matrix as the sample covariance matrix for a sample of m vectors from a trivariate normal distribution with a population covariance matrix of 𝜇. As such, m controls the variability of the population via consistency of the sample covariance matrix.

For each case, we performed both hypothesis tests (when applicable) at a variety of values of n₁ = n₂ = n and m. For each set of data, in addition to recording the p-values, we recorded the Fréchet sample variance (FSV) for each sample to show the effect of changing m. 10,000 bootstrap replicates were used to perform the tests.

The results of the simulations are shown in Table 1. Note that the T² test could not be performed for n = 6 due to lack of invertibility and that FSV decreases as mincreases. For Case 1, all p-values were large, indicating that both tests would correctly fail to reject H₀.

Table 1:

Results of the simulation study using the Frobenius metric. FSV is the Fréchet sample variance, where each “a/b” entry represents the quantity for group a and b, respectively. Pvalue_T is the p-value for the T² bootstrap test. Pvalue_W is the p-value for the nonpivotal bootstrap test.

n	m	Case 1			Case 2			Case 3
		FSV	PvalueT	PvalueW	FSV	PvalueT	PvalueW	FSV	PvalueT	PvalueW
6	6	2.6656/0.6292	N/A	0.2909	1.02/.2047	N/A	0.0396	.5563/.5883	N/A	0.04
6	24	.0729/.2940	N/A	0.6601	.2388/.0876	N/A	0.0585	.1296/.1013	N/A	0.1396
6	96	.0472/.0490	N/A	0.1295	.0511/.0314	N/A	0.0441	.0408/.0571	N/A	0
6	192	.0291/.0334	N/A	0.3765	.0372/.0191	N/A	0.089	.0310/.0245	N/A	0
6	288	.0134/.0107	N/A	0.4991	.0149/.0125	N/A	0.0132	.0200/.0133	N/A	0
18	6	.9662/1.0111	0.2823	0.3006	.6573/.7830	0.9518	0.9117	1.0722/1.0990	0.0891	0.2323
18	24	.1953/.1231	0.9279	0.8591	.2290/.1905	0.3456	0.2928	.0978/.1833	0.0032	0.0027
18	96	.0477/.0536	0.5307	0.5894	.0636/.0403	0.1121	0.1777	.0496/.0604	0	0
18	192	.0205/.0316	0.9198	0.6084	.0195/.0328	0.0689	0.0169	.0249/.0194	0	0
18	288	.0189/.0211	0.2832	0.3141	.0114/.0134	0.0293	0.0023	.0165/.0143	0	0
36	6	1.2569/.6997	0.4837	0.4616	.7014/.7015	0.1854	0.1748	1.1635/.5277	0.0431	0.0094
36	24	.1718/.1813	0.1783	0.253	.1591/.1883	0.0177	0.0538	.1567/.2164	0.0001	0
36	96	.0516/.0491	0.6765	0.8858	.0500/.0466	0.0002	0.0018	.0418/.0410	0	0
36	192	.0222/.0216	0.5149	0.3523	.0301/.0242	0.0118	0.0032	.0200/.0248	0	0
36	288	.0175/.0165	0.6665	0.6189	.0148/.0140	0	0	.0162/.0136	0	0

For Case 2, the angles between the corresponding principal directions of the population means are 9.6217 degrees, 5.1220 degrees, and 9.0139 degrees. For n = 6, the W² test showed significant differences between the means at the 0.10 level at all values of m, but not at the 0.05 level. However, for the other sample sizes, the W² test failed to find significant differences between the means except for the cases in which the variability is quite low. The T² test was also not able to find significant differences for higher levels of variability for n = 18. It did, however, find significant differences for n = 36 except when m = 6, when the variability was rather large.

For Case 3, the angles between the corresponding principal directions of the population means are 79.1643 degrees, 37.6759 degrees, and 73.7522 degrees. Both tests performed quite well for all sample sizes considered. The T² test only once failed to find a significant difference between the means at the 0.05 level, with this occurring when there was a large amount of variability present and the difference was still significant at the 0.10 level. For the smaller sample sizes, the W² test also performed very well, except for those cases where there was a large amount of variability.

Based upon these results, it appears that both tests tend to perform better when there is lower amounts of variability present in the data. The tests also appear to be better at finding significant differences between the means when the angles between the corresponding principal directions are large since they produce very low p-values even for moderate levels of variability.

4. Computation and Nonparametric estimation of canonical intrinsic means

4.1. Intrinsic means

Let Q be a probability measure on a metric space $(\mathcal{M},d)$. The Fréchet mean set of Q is the set of all global minimizers of the Fréchet function F_Q on $\mathcal{M}$ defined by

$$F_Q(q)={\displaystyle \int d^2}(q,x)Q(dx),q\in \mathcal{M}.$$ (4.1)

If $(\mathcal{M},g)$ is a Riemannian manifold, and d = d_g is the geodesic distance function, we call the Fre´chet mean set of Q the intrinsic mean set of Q. The points of the intrinsic mean set are also called (global) Riemannian centers of mass in the literature (see Afsari (2011) and the references therein).

When F_Q has a unique minimizer, we call that point the intrinsic mean 𝜇_I(Q). If the Riemannian manifold $(\mathcal{M},g)$ is complete, then the intrinsic mean set of any probability measure Q is non-empty; at least one minimizer of F_Q exists. For complete manifolds, the sharpest uniqueness result to date is due to Afsari (2011): if Q is supported in a ball of radius less than the convexity radius of $(\mathcal{M},g)$, then the minimizer of F_Q is unique. Whether or not $(\mathcal{M},g)$ is complete or has positive convexity radius, a sufficient condition for existence and uniqueness of a minimizer is that Q be sufficiently concentrated.

For probability measures supported in a geodesically convex set, Groisser (2004) makes the following definition (up to notational changes)²:

DEFINITION 4.1

Let $U\subset \mathcal{M}$ be geodesically convex. Let Q be a probability measure on U, and define a vector field Y_Q on U by

$$Y_Q(q)={\displaystyle {\int }_U{\mathrm{Exp}}_q^{-1}}(x)Q(dx)\in T_q\mathcal{M},\text{for}\text{each}q\in U.$$ (4.2)

If Y_Q(q_Q) = 0 at a unique point q_Q ∈ U, we call q_Q the (Riemannian) center of mass of Q relative to U. When Q is a finitely-supported distribution of the form $\frac{1}{n}{\sum }_{i=1}^n{\delta }_{x_i}$ associated with points x₁, …, x_n ∈ U, we call q_Q the Riemannian average of Q relative to U. In this case (4.2) reduces to

$$Y_Q(q)=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\mathrm{Exp}}_q^{-1}}\left(x_i\right)\in T_q\mathcal{M}.$$ (4.3)

Above (and below), $\mathrm{E}\mathrm{x}{\mathrm{p}}_q:T_q\mathcal{M}\to \mathcal{M}$ is the Riemannian exponential map based at q, and “$\mathrm{E}\mathrm{x}{\mathrm{p}}_q^{-1}(x)$” means the unique vector $v\in T_q\mathcal{M}$ of minimal norm such that Exp_q(v) = x; uniqueness is guaranteed by the assumed geodesic convexity of U. In this paper we reserve the lower-case notation “exp” for the exponential of matrices.

In the setting of (4.3), note that ${\sum }_{i=1}^n(\mathrm{E}\mathrm{x}{\mathrm{p}}_q^{-1}(x_i)-Y_Q(q))=0$. Heuristically, Y_Q(q) represents a “balancing” average of the points x_i as seen from q.

In addition to ensuring that “$\mathrm{E}\mathrm{x}{\mathrm{p}}_q^{-1}(x)$” makes sense, the geodesic convexity of U in Definition 4.1 implies that F_Q is smooth and that

$$Y_Q=-\mathrm{grad}{F}_Q;$$ (4.4)

hence the zeroes of Y_Q are exactly the critical points of F_Q. Groisser (2004) uses a geometric criterion, rather than the global- minimization property, to single out a “best” critical point (and to get rid of the “relative to U”): in the setting of Definition 4.1, if Y_Q has a unique zero q_Q in a (suitably defined) convex hull of the support of Q, Groisser calls q_Q the primary center of mass (or simply the center of mass) of Q. In (Groisser, 2004) the question is raised whether the intrinsic mean, when it exists, of a probability measure Q supported in a convex set, lies in the convex hull of its support (equivalently, thanks to Afsari (2011), whether the primary center of mass q_Q coincides with the intrinsic mean 𝜇_I(Q) when both exist.) A partial answer is provided in Afsari (2011): for a discrete probability measure Q supported in a ball of radius less than the convexity radius of $(\mathcal{M},g)$, the intrinsic mean 𝜇_I(Q) exists (by the result mentioned previously) and lies in the closure of the convex hull of the support of Q.

In the example of greatest interest to us in this paper, the Riemannian manifold (Sym⁺(p),g_can), the convexity restriction on U in Definition 4.1 is no restriction at all. The reason is that (Sym⁺(p),g_can) is a Cartan-Hadamard manifold: a simply-connected complete Riemannian manifold with non-positive sectional curvature (see Section A.2). It is a classical result that any two points in a Cartan-Hadamard manifold $(\mathcal{M},g)$ can be joined by a unique geodesic arc; hence the entire manifold is convex, and we can take $U=\mathcal{M}$ in Definition 4.1, omit the phrase “relative to U”, and omit U from the notation. If $(\mathcal{M},g)$ is a Cartan-Hadamard manifold, then for any Q the function F_Q is strictly convex and achieves a minimum at some (necessarily unique) point q_Q, which is also necessarily the unique zero of Y_Q. Thus on a Cartan-Hadamard manifold, every distribution Q has a (unique) center of mass q_Q, and this center of mass coincides with the intrinsic mean 𝜇_I(Q). The existence/uniqueness proof in the case of the empirical distribution goes back to É. Cartan in the 1920s (Cartan, 1928). Indeed, an intrinsic sample mean on such a manifold may be thought of as a Cartan mean.

4.2. Intrinsic sample means on a Cartan-Hadamard manifold

To simplify certain definitions, we restrict attention to Cartan-Hadamard manifolds $(\mathcal{M},g)$. Our first definition simply provides a name and notation for an important special case of Definition 4.1.

DEFINITION 4.2

Let $(\mathcal{M},g)$ be a Cartan-Hadamard manifold. Let X₁, …, X_n be $\mathcal{M}$-valued i.i.d. random variables with common distribution Q, and let ${\widehat{Q}}_n=\frac{1}{n}{\sum }_{i=1}^n{\delta }_{X_i}$ be their empirical distribution. The intrinsic sample mean ${\overline{X}}_I$ of X₁, …, X_n is the intrinsic mean of ${\widehat{Q}}_n$:

$${\overline{X}}_I={\mu }_I\left({\widehat{Q}}_n\right)={\mu }_I\left(\frac{1}{n}{\displaystyle \sum _{i=1}^n{\delta }_{X_i}}\right).$$ (4.5)

For particular values x₁, …, x_n of the random variables X₁, … X_n, Definition 4.2 corresponds to the Riemannian average of the points x₁, …, x_n in the terminology of Definition 4.1. Groisser (2004) presents an iterative procedure for finding zeroes of vector fields on a general Riemannian manifold, and establishes sufficient conditions for convergence as well as convergence-rate bounds.³ Applied to the negative-gradient vector field Y_Q, this procedure becomes the “Riemannian averaging algorithm”, which is simply unit-stepsize gradient-descent for the function F_Q. It is proven in Groisser (2004) that if Q is contained in a geodesic ball B_D(q₀) whose radius D is smaller than a certain number ${\tilde{D}}_{\text{crit}}^{\prime }$, and the algorithm is initialized at any point in a larger, concentric ball B_ρ(q₀) with ρ less than a certain number ρ₃(D) that increases as D decreases, then the algorithm converges to the intrinsic mean of Q. (In Groisser (2004), specific lower bounds on ${\tilde{D}}_{\text{crit}}^{\prime }$ and ρ₃(D) are given in terms of local geometric invariants; these radii are not tiny in general. We will see this for the case of (Sym⁺(3),g_can) in Section 4.3.) When applied to the distribution $\frac{1}{n}{\sum }_{i=1}^n{\delta }_{x_i}$, this algorithm computes the Riemannian average of x₁, …, x_n.

REMARK 4.3

Some common variants of this algorithm are obtained by replacing “unit step-size” with a more general constant step-size τ (replacing Y_Q with τY_Q) or with variable step-size that is updated at each iteration; cf. (Fletcher and Joshi, 2007; Afsari et al., 2011) (and, in a more general context, Smith (1994)). When the data are not too spread out, as is typically the case for biological samples, the unit-stepsize algorithm generally works well. When the data are more spread out, convergence may be slower (and is not guaranteed if the data are too spread out). For an explanation of this in terms of the “eigenvalues” of the Hessian of F_Q, and some instructive examples, see Afsari et al. (2011).

For a general distribution $\tilde{Q}$, the Riemannian averaging algorithm It ${\text{It}}_{\tilde{Q}}$ consists simply of iterating the map ${\mathrm{\Psi }}_{\tilde{Q}}:\mathcal{M}\to \mathcal{M}$ defined by

$${\mathrm{\Psi }}_{\tilde{Q}}(q)=\mathrm{E}\mathrm{x}{\mathrm{p}}_q\left(Y_{\tilde{Q}}(q)\right).$$ (4.6)

The upper-bound restriction on D mentioned above is merely sufficient for the algorithm to converge; the algorithm can converge without this condition being satisfied. Note that if ${\text{It}}_{\tilde{Q}}$ converges, the point it converges to must be a fixed-point of ${\mathrm{\Psi }}_{\tilde{Q}}$, and therefore a zero of $Y_{\tilde{Q}}$ (because Exp_q is one-to-one on a Cartan-Hadamard manifold, and Exp_q(0) = q).

We now focus attention on $(\mathcal{M},g)=\left(Sy{m}^{+}(p),g_{\text{can}}\right)$ and distributions ${\widehat{Q}}_n=\frac{1}{n}{\sum }_{i=1}^n{\delta }_{V_i}$, where V₁, … V_n ∈ Sym⁺(p). In practice, the algorithm ${\text{It}}_{{\widehat{Q}}_n}$ is computable on a (small enough) convex subset of a general Riemannian manifold if we can efficiently invert the exponential map. For the Cartan-Hadamard manifold (Sym⁺(p),g_can), we can do this easily and explicitly because (Sym⁺(p), g_can) is also a symmetric space (see Section A.2).

Furthermore, as noted at the end of Section 4.1, for any probability measure $\tilde{Q}$ on a Cartan-Hadamard manifold, we know a priori both that $Y_{\tilde{Q}}$ has exactly one zero, and that this zero is the intrinsic mean of $\tilde{Q}$. In particular, for (Sym⁺(p),g_can), any time ${\text{It}}_{{\widehat{Q}}_n}$ converges, it converges to the intrinsic sample mean ${\overline{V}}_I$ of V₁, …,V_n. In our application to DTI data, the algorithm ${\text{It}}_{{\widehat{Q}}_n}$ was found to converge quite rapidly (see Table 4), and therefore was an efficient method for computing intrinsic sample means ${\overline{V}}_I$.

Table 4:

Convergence behavior of the averaging algorithm on (Sym⁺(3),g_can), initialized at the Frobenius mean, for the simulated data and actual DTI data. n = 6 for the DTI control group and dyslexia group, as described in Section 6. D is the radius of the smallest ball, centered at the Frobenius mean, containing all the data, and κ = κ(D) is as defined in Section 4.3. “Actual iterations needed” is the number of iterations that were needed for convergence with a canonical-distance threshold of 10⁻⁶. N_it(κ) is the smallest integer N for which κ^ND ≤ 10⁻⁶; see inequality (4.9).

n	m	D	κ	Actual Iterations Needed	Nit(κ)
6	6	2.1868	1.3965	8	N/A
6	24	0.8116	1.2106	4	N/A
6	48	0.5906	0.3481	4	13
6	96	0.3449	0.0854	3	5
6	192	0.3103	0.0680	3	5
6	288	0.2496	0.0431	3	4
18	6	3.1204	1.4751	8	N/A
18	24	1.1137	1.2628	5	N/A
18	48	0.6343	1.1751	5	N/A
18	96	0.4836	0.1866	4	8
18	192	0.3804	0.1060	4	6
18	288	0.3788	0.1049	4	6
36	6	3.7187	1.5147	9	N/A
36	24	1.2048	1.2769	5	N/A
36	48	0.8856	1.2242	4	N/A
36	96	0.5403	0.2529	3	10
36	192	0.4632	0.1676	3	7
36	288	0.2646	0.0486	3	4
Control Group		0.4346	0.1437	3	7
Dyslexia Group		0.3063	0.0662	3	5

To write an explicit formula for ${\mathrm{\Psi }}_{{\widehat{Q}}_n}$ on (Sym⁺(p),g_can), we first make one more definition. In any Cartan-Hadamard manifold $\mathcal{M}$, the exponential map $\mathrm{E}\mathrm{x}{\mathrm{p}}_M:T_M\mathcal{M}\to \mathcal{M}$ is a diffeomorphism for all $M\in \mathcal{M}$; thus ${\left(\mathrm{E}\mathrm{x}{\mathrm{p}}_M\right)}^{-1}:\mathcal{M}\to T_M\mathcal{M}$ is well-defined globally. We will use a name for this inverse that is common in the statistics literature, though not in the differential geometry literature:

DEFINITION 4.4

Let $(\mathcal{M},g)$ be a Cartan-Hadamard manifold and let $M\in \mathcal{M}$. The Riemannian logarithm map based at M is the map ${\mathrm{Log}}_M≔{\left(\mathrm{E}\mathrm{x}{\mathrm{p}}_M\right)}^{-1}:\mathcal{M}\to T_M\mathcal{M}$.

In the Appendix, we use the characterization of (Sym⁺(p),g_can) as a symmetric space to compute explicit formulas for Exp_M and Log_M for all M ∈ Sym⁺(p); these are given in (A.17)–(A.18). Substituting these into (4.3) and (4.6), for a sample V₁,...V_n of matrices V_i ∈ Sym⁺(p), the map ${\mathrm{\Psi }}_{{\widehat{Q}}_n}$ iterated in the Riemannian averaging algorithm is given by

$${\mathrm{\Psi }}_{{\widehat{Q}}_n}(M)=M^{1/2}\exp (\frac{1}{n}{\displaystyle \sum _{i=1}^n\log }(M^{-1/2}{V}_i{M}^{-1/2}))M^{1/2},$$ (4.7)

where “log” is the logarithm function on SPD matrices (see the proof of Proposition A.11).

4.3. Convergence of the averaging algorithm on Sym⁺(3)

The literature on the Riemannian averaging algorithm and its variants (see Remark 4.3) contains quite a bit of misinformation, especially concerning convergence of the algorithm. Afsari et al. (2011) is a good reference for correct statements of what has been proven to date. Many other papers make implicit assumptions in their proofs, while some make assertions that have not been proven (and may be mathematically incorrect), citing sources that do not prove what it is said they prove. At least one reference suggests that theorems about Newton’s method apply to this gradient-descent algorithm for averaging, and therefore that the latter should be quadratically convergent. To our knowledge, though, this has never been proven.

While the non-positive curvature of a Cartan-Hadamard manifold helps existence and uniqueness of the intrinsic mean of any probability distribution $\tilde{Q}$, the combination of negative curvature and large diameter of supp$(\tilde{Q})$ (large compared to a length-scale determined by curvature) seems to interfere with convergence of the unit-step-size gradient-descent averaging algorithm. Some evidence for this is reported in Rentmeesters and Absil (2011), whose authors found that in numerical experiments with points uniformly distributed in a ball of radius D in (Sym⁺(3),g_can), the algorithm failed to converge for D ≥ 4. The mathematical basis for expecting such a problem is discussed in Afsari et al. (2011).

Nonetheless, Groisser (2004) shows that the unit-step-size averaging algorithm on any Riemannian manifold $(\mathcal{M},g)$ always does converge if supp$(\tilde{Q})$ is contained in a ball of radius no larger than a certain (nonsharp!) number $D_{\text{crit}}^{\prime }$ that is explicitly computable in terms of curvature-bounds and the convexity radius of $(\mathcal{M},g)$ For Cartan-Hadamard manifolds, the convexity radius is infinite, so $D_{\text{crit}}^{\prime }$ is computable from curvature-bounds alone. In Section 6 of Groisser (2004), the general results earlier in the paper are used to compute $D_{\text{crit}}^{\prime }$ for complete, locally symmetric manifolds $(\mathcal{M},g)$ of non-negative curvature. The same general results and method can be used to compute $D_{\text{crit}}^{\prime }$ for manifolds of bounded non-positive curvature and infinite convexity radius (in particular, for any Cartan-Hadamard symmetric space); one simply has to replace “ψ(1, x)” in equation (6.1) with “ψ(−1, x)”, defined in Table 1 (p. 104) of Groisser (2004); specifically, ψ(−1, x) := ψ₋(x) := x coth x − 1.

Theorem 4.8 and 5.3 of Groisser (2004) give additional information, including convergence-rate estimates. For simplicity, we will state the results that we wish to use here only for a Cartan-Hadamard manifold with curvature bounded below by the negative number δ, and combine these with results from the non-positive curvature analog of the computations in Groisser (2004, Section 6).

1. There is a unique solution $\left({\overline{\rho }}_{\text{crit}},{\overline{D}}_{\text{crit}}\right)\in [0,\infty )\times [0,\infty )$ of the pair of equations $s(\overline{\rho },\overline{D})=\overline{D},\frac{\partial \overline{s}}{\partial \rho }(\overline{\rho },\overline{D})=0,$ where $s(\overline{\rho },\overline{D})≔\left(1-{\psi }_{-}(\overline{\rho },\overline{D})\right)\overline{\rho }$. Approximate values of ${\overline{\rho }}_{\text{crit}}$ and ${\overline{D}}_{\text{crit}}$ are

   $${\rho }_{\text{crit}}\underset{˜}{>}0.7948,D_{\text{crit}}\underset{˜}{>}\mathrm{0.4314.}$$ (4.8)

2. Let ${\rho }_{\text{crit}}^{\prime }={\overline{\rho }}_{\text{crit}}|\delta {|}^{-1/2},D_{\text{crit}}^{\prime }={\overline{D}}_{\text{crit}}|\delta {|}^{-1/2}$. For $0\le D<D_{\text{crit}}^{\prime }$ let p₁(D) = inf {p | s(p,D) > D} and p₃(D) = sup {p | s(p,D) > D}. Then $D\le {\rho }_1(D)<{\rho }_{\text{crit}}^{\prime }<{\rho }_3(D).$

3. Assume that $\tilde{Q}$ is a probability distribution supported in a closed ball $\overline{B_D\left(q_0\right)}$, where $D<D_{\text{crit}}^{\prime }$, and that ρ₁(D) < ρ < ρ₃(D). Then:

   • (a)
     The map ${\mathrm{\Psi }}_{\tilde{Q}}$ defined in (4.6) maps B_ρ(q₀) into itself.
   • (b)
     For every q ∈ B_ρ3(q₀), the sequence of iterates ${\left\{q_k≔{\mathrm{\Psi }}_{\tilde{Q}}^k(q)\right\}}_{k=1}^{\infty }$ converges to the intrinsic mean ${\mu }_I(\tilde{Q})$. These iterates satisfy

     $$d\left(q_{k+1},q_k\right)\le \kappa (D)d\left(q_k,q_{k-1}\right)\le \kappa {(D)}^{k}D,$$ (4.9)

     where κ(D) = ψ₋((D + ρ₁(D))|δ|^1/2).

We will use these results in Section 4.5 (where $\tilde{Q}$ will be a discrete distribution ${\widehat{Q}}_n$ as in Definition 4.2).

REMARK 4.5

The main focus of Afsari et al. (2011) is on computing Riemannian means using constantstep-size gradient-descent with step-size not required to be 1, since this added flexibility can improve convergence. However, Theorem 4.1 of Afsari et al. (2011) can be used to derive a statement about the unitstep-size algorithm that is relevant here: the value of the largest radius D for which the convergence is guaranteed for the unit-step-size gradient-descent algorithm on a Cartan-Hadamard manifold (for a distribution $\tilde{Q}$ supported in a ball $\overline{B_D\left(q_0\right)}$ can be improved by about 11% over the number $D_{\text{crit}}^{\prime }$ above. (This theorem in Afsari et al. (2011) is stated only for distributions with finite support, but that assumption does not seem essential to the proof, and is satisfied anyway for the applications in the present paper.) This theorem guarantees convergence of the unit-step-size algorithm if $D\le D_{\text{crit}}^{\prime \prime }$, where $D_{\text{crit}}^{\prime \prime }$ is the unique positive number $\tilde{D}$ for which $x\coth {(x)|}_{x=4\sqrt{|\delta |}\tilde{D}}=2$ (equivalently, ${\psi }_{-}\left(4|\delta {|}^{1/2}\tilde{D}\right)=1$) —which works out to $D_{\text{crit}}^{\prime \prime }\underset{˜}{>}0.4788|\delta {|}^{-1/2}$, or 0.6771 in the case of Sym⁺(3). However, the convergence-rate bound (4.9) does not apply for $D_{\text{crit}}^{\prime }\le D\le D_{\text{crit}}^{\prime \prime }$.

4.4. Nonparametric inference for canonical intrinsic means

Due to the nature of the canonical metric, tests of equality of canonical means cannot be performed using the statistics (3.1) and (3.4). Instead, alternative test statistics can be formulated in a tangent space, as in Huckemann (2012). In particular, suppose we are given two independent samples of sizes n₁ and n₂, where the observations V_{a, i},i = 1, …, n_a, a = 1, 2, are i.i.d. SPD matrices with canonical means μ_a,I, a = 1,2. We are interested in testing H₀ : 𝜇_{1, I} = 𝜇_{2, I} = 𝜇.

Let Y_a,i = Log_𝜇(V_a,i), for i = 1, …, n_a, a = 1,2, be projections of the observations to the tangent space at 𝜇, where Log_𝜇 is as defined in (A.18). To form the statistic, let X_a,i = vecd(Y_a,i), for i = 1, …,n_a,a = 1,2. Define S_a to be the sample covariance matrix of the X_1,i. Define the quantity B as

$$\begin{gathered} B=\mathrm{vecd}\left({\mathrm{Log}}_{\mu }\left({\overline{V}}_1\right)\right)-\mathrm{vecd}\left({\mathrm{Log}}_{\mu }\left({\overline{V}}_2\right)\right)-\mathrm{vecd}\left({\mathrm{Log}}_{\mu }\left({\mu }_{1,I}\right)\right)+\mathrm{vecd}\left({\mathrm{Log}}_{\mu }\left({\mu }_{2,I}\right)\right) \\ =\mathrm{vecd}\left({\mathrm{Log}}_{\mu }\left({\overline{V}}_1\right)\right)-\mathrm{vecd}\left({\mathrm{Log}}_{\mu }\left({\overline{V}}_2\right)\right), \end{gathered}$$ (4.10)

where ${\overline{V}}_a$, a = 1,2 are the canonical sample means. Then a T² statistic can be defined as

$$T^2=B^T{\left(\frac{1}{n_1}{S}_1+\frac{1}{n_2}{S}_2\right)}^{-1}B.$$ (4.11)

However, since 𝜇 is unknown, we instead perform inference at the tangent space of ${\overline{V}}_p$, the pooled canonical sample mean of all n₁ + n₂ observations, redefining the Y_a,i,X_a,i,S_a, and B accordingly, and plug these into (4.11).

To perform inference, we compute a bootstrap distribution of

$$T^{2*}=B^{*T}{\left(\frac{1}{n_1}{S}_1^{*}+\frac{1}{n_2}{S}_2^{*}\right)}^{-1}{B}^{*},$$ (4.12)

where

$$B^{*}=\mathrm{vecd}({\mathrm{Log}}_{{\overline{V}}_p}({\overline{V}}_1^{*}))-\mathrm{vecd}({\mathrm{Log}}_{{\overline{V}}_p}({\overline{V}}_2^{*}))-\mathrm{vecd}({\mathrm{Log}}_{{\overline{V}}_p}({\overline{V}}_1))+\mathrm{vecd}({\mathrm{Log}}_{{\overline{V}}_p}({\overline{V}}_2))$$ (4.13)

and the ${\overline{V}}_a^{*}$ and $S_a^{*}$ are bootstrap replicates of, respectively, the canonical sample mean and sample covariance, for a = 1, 2. Bootstrap p-values for this test can be calculated as in (3.7).

Alternatively, especially for those cases when n₁ and n₂ are small, a nonpivotal test statistic can be defined as

$$W^2=B^{T}B.$$ (4.14)

We can then compute a bootstrap distribution of

$$W^{2*}=B^{*T}{B}^{*},$$ (4.15)

where B^∗ is as defined in (4.13). Bootstrap p-values can then be calculated as in (3.8).

4.5. Simulation Study

To explore the performance of the hypothesis test procedures presented above, we conducted a simulation study, just as in Section 3.2. The results of this study are shown in Table 2. Both test procedures for the canonical means perform very similarly to their corresponding tests for the Frobenius means, as the p-values are nearly the same.

Table 2:

Results of the simulation study using the canonical metric. n and m are as in Section 3.2. FSV is the Fréchet sample variance, where each “a/b” entry represents the quantity for group a and b, respectively. PvalueT is the p-value for the T² bootstrap test. PvalueW is the p-value for the nonpivotal bootstrap test.

n	m	Case 1			Case 2			Case 3
		FSV	PvalueT	PvalueW	FSV	PvalueT	PvalueW	FSV	PvalueT	PvalueW
6	6	5.2433/4.3517	N/A	0.2059	2.215/1.642	N/A	0.1073	2.5667/2.6636	N/A	0.0821
6	24	.2252/.3796	N/A	0.7497	.3671/.3279	N/A	0.0389	.3184/.5010	N/A	0.1136
6	96	.1049/.1505	N/A	0.1494	.0932/.1096	N/A	0.0412	.1186/.1345	N/A	0
6	192	.0924/.0645	N/A	0.3497	.0658/.0457	N/A	0.0947	.0739/.0644	N/A	0
6	288	.0340/.0210	N/A	0.4947	.0361/.0283	N/A	0.0126	.0465/.0386	N/A	0
18	6	4.3803/4.1406	0.4019	0.3956	2.5019/4.7915	0.6683	0.3786	4.0874/3.1783	0.0496	0.1167
18	24	.5325/.3980	0.8601	0.8402	.5511/.4719	0.3268	0.2049	.4642/.7620	0.0024	0.0006
18	96	.1164/.1413	0.4955	0.5422	.1234/.1127	0.1137	0.1877	.1175/.1416	0	0
18	192	.0536/.0668	0.8909	0.5922	.0474/.0762	0.0601	0.015	.0758/.0676	0	0
18	288	.0382/.0544	0.307	0.3762	.0375/.0391	0.033	0.002	.0460/.0467	0	0
36	6	3.6592/3.6854	0.6359	0.5911	3.7022/4.1293	0.0498	0.0637	4.8348/4.7676	0.0339	0.0169
36	24	.6213/.5235	0.2355	0.2587	.5224/.5685	0.0208	0.0228	.5454/.6272	0.0001	0.0001
36	96	.1137/.1144	0.6779	0.8799	.1378/.1174	0.0005	0.0026	.1396/.1426	0	0
36	192	.0548/.0585	0.4863	0.3311	.0746/.0679	0.0143	0.0058	.0626/.0695	0	0
36	288	.0429/.0418	0.6715	0.6275	.0353/.0413	0.0001	0	.0404/.0466	0	0

For this study, we also recorded the amount of time, in seconds, needed to calculate all 20,000 canonical means (10,000 for each group) in the bootstrap replications. These results are shown in Table 3. We additionally recorded the number of iterations needed for the original canonical sample means to converge for both groups. To initialize the algorithm for computing the canonical means, we used the Frobenius sample means.

Table 3:

Timing information for the simulation study using the canonical metric. Time refers to the amount of time required to perform all 20,000 mean calculations needed for the bootstrap test. Iterations refers to the number of iterations needed for the averaging algorithm to converge for the original sample, where each “a/b” entry represents the quantity for group a and b, respectively.

n	m	Case 1		Case 2		Case 3
		Time (sec)	Iterations	Time (sec)	Iterations	Time (sec)	Iterations
6	6	772.7	12/10	477.6	8/6	543.6	8/7
6	24	261.4	4/4	287.3	4/4	308.8	4/4
6	96	226.1	3/3	227.8	3/3	225.2	3/3
6	192	224.0	3/3	229.8	3/3	240.5	3/3
6	288	208.0	2/3	232.2	3/3	234.2	3/3
18	6	1811.4	9/8	1622.5	7/9	1697.9	8/7
18	24	806.5	4/4	826.3	4/4	877.8	4/5
18	96	627.5	3/3	638.3	3/3	634.3	3/3
18	192	650.7	3/3	663.3	3/3	641.9	3/3
18	288	650.6	3/3	715.1	3/3	642.1	3/3
36	6	2923.9	6/7	3132.0	8/8	3380.2	8/9
36	24	1541.8	4/4	1569.3	4/4	1575.4	4/4
36	96	1300.9	3/3	1212.4	3/3	1248.3	3/3
36	192	1347.4	3/3	1289.6	3/3	1286.0	3/3
36	288	1383.1	3/3	1311.4	3/3	1360.6	3/3

It is interesting to compare the convergence behavior in the canonical-mean computations to what can be predicted from the general results stated in Section 4.3. For (Sym⁺(3),g_can), it can be shown that a sharp lower bound on sectional curvature is $\delta =-\frac{1}{2}$ (this is essentially done in (Rentmeesters and Absil, 2011)). Thus, from (4.8), we have $D_{\text{crit}}^{\prime }\underset{˜}{>}0.4314\sqrt{2}\approx 0.6101$. Since we initialized the algorithm at the Frobenius mean q₀, the distance from q₀ to the furthest data-point is the radius D of a closed ball $\overline{B_D\left(q_0\right)}$ containing all the data-points. The algorithm always converged in our simulations, even though for about half of the (n,m) pairs we used, D was greater than $D_{\text{crit}}^{\prime }$. For the cases in which $D<D_{\text{cit}}^{\prime }$, we can compare the number of iterations needed for convergence to within the threshold we used (d(q_k+1,q_k) < 10⁻⁶) to the “worst case” number determined by (4.9), N_it(κ). Table 6 lists our findings for simulated data in an experiment separate from our bootstrap experiments, as well as for the actual DTI data used in Section 6.2.⁴

Note that since sectional curvature has dimensions of (length)⁻², and the range of the sectional-curvature function at each point of (Sym⁺(3),g_can) is [δ₀,0], where ${\delta }_0=-\frac{1}{2}$, and the injectivity radius is infinite, a natural length-scale for this Riemannian manifold is ${\delta }_0^{-1/2}=\sqrt{2}\approx 1.4142$. Thus the “normalized” radii obtained by dividing the values of D in Table 4 by $\sqrt{2}$ give a meaningful measure of how localized the data were. We note that for the actual DTI data we used, D was less than $\sqrt{2}$ for both groups. However, we do not have a suggestion at this time for what multiples of $\sqrt{2}$ should be used to make quantitative definitions of notions like “very localized data”. The largest value of D seen in our simulated data was approximately 3.7, which occurred for (n,m) = (36, 6), and came from a sample for which the algorithm converged in 9 iterations. We note that in the numerical experiments mentioned in Rentmeesters and Absil (2011), Rentmeester and Absil found this gradient-descent algorithm not to converge for their data with D ≥ 4. It seems likely that the reason we observed convergence for a value of D close to which Rentmeesters and Absil (2011) observed non-convergence is, again, a reflection of difference between the distributions from which Rentmeesters and Absil (2011) and we simulated data. As mentioned earlier, Rentmeesters and Absil (2011) used data that were uniformly distributed over a ball. The probability density function for our simulated data is related to a Wishart distribution. As such, the data is concentrated around the mode. Thus for our (n,m) = (36, 6) sample, the large value of D may have been due to a single outlier, whose influence on convergence-behavior would be limited, whereas the uniform distribution used in Rentmeesters and Absil (2011) on a given ball would have led to a larger number of data-points near the boundary of the ball, more greatly influencing convergence-behavior.

The fact that the algorithm converged in all our simulations, and that it converged faster (often much faster) than “predicted” by N_it(κ), is interesting, and highlights the nature of the bounds given in Section 4.3. First, the radius $D_{\text{crit}}^{\prime }$ is a very coarse bound, and is “critical” only for the proof of convergence in Groisser (2004). (Similarly, the somewhat larger $D_{\text{crit}}^{\prime \prime }$ in Remark 4.5 is a coarse bound that is simply what Afsari et al. (2011, Theorem 4.1) happens to imply for the unit-step-size algorithm.) Second, for $D<D_{\text{crit}}^{\prime }$, the convergence-rate κ(D) is a bound on the slowest convergence we can ever see. Our simulated data were chosen from a probability distribution concentrated about the mode, but slowest convergence is expected for data-clouds that have relatively large diameter and whose distribution with respect to direction in the tangent space at the mean is much farther from being uniform, for theoretical reasons discussed in Afsari et al. (2011). This expectation is supported by the fact that the number of iterations needed for convergence in our simulations was less than N_it(κ), with the difference increasing as D increased.

5. Coverage Probabilities for Confidence Regions

In the preceding simulation studies, we illustrated that the Frobenius and canonical methodologies perform similarly for hypothesis tests of equality of means. In each case, regardless of whether the T² or W² procedures were used, the p-values that were produced were very similar for each distance. Since the same data was used for both methods, this indicates that, for a given data set, the inference procedures will perform similarly. However, it is also important to examine how these procedures perform in the long term.

To examine this, we performed an additional simulation study to compare coverage probabilities for nominal 95% confidence regions for the difference between the means of two populations. A summary of the results of this study are displayed in Table 5. Cases 1, 2, and 3 refer to the same scenarios considered in the previous studies. In this context, the probabilities for Case 1 reflect probabilities of true coverage. That is, the means are, in fact, equal. Since the means are not equal for Cases 2 and 3, though, these probabilities reflect probabilities of false coverage.

Table 5:

Coverage probabilities for confidence regions for the difference between means of two populations. Probabilities for Case 1 are probabilities of true coverage. Those for Cases 2 and 3 are probabilities of false coverage.

n	m	Case 1				Case 2				Case 3
		T2		W2		T2		W2		T2		W2
		Fro	Can	Fro	Can	Fro	Can	Fro	Can	Fro	Can	Fro	Can
6	24	N/A	N/A	0.918	0.926	N/A	N/A	0.890	0.900	N/A	N/A	0.566	0.580
6	96	N/A	N/A	0.890	0.894	N/A	N/A	0.782	0.780	N/A	N/A	0.012	0.012
6	192	N/A	N/A	0.924	0.924	N/A	N/A	0.676	0.684	N/A	N/A	0.000	0.000
18	24	0.962	0.964	0.930	0.928	0.932	0.918	0.860	0.862	0.146	0.140	0.070	0.000
18	96	0.974	0.976	0.958	0.950	0.772	0.770	0.584	0.592	0.000	0.000	0.000	0.000
18	192	0.962	0.960	0.920	0.908	0.434	0.438	0.246	0.248	0.000	0.000	0.000	0.000
36	24	0.952	0.960	0.940	0.942	0.834	0.834	0.788	0.808	0.000	0.000	0.000	0.000
36	96	0.958	0.952	0.932	0.926	0.350	0.348	0.278	0.296	0.000	0.000	0.000	0.000
36	192	0.942	0.948	0.950	0.944	0.048	0.046	0.030	0.032	0.000	0.000	0.000	0.000

In all but one scenario (Case 1, n = 36,m = 192, Frobenius) the T² region has a higher coverage probability than the associated W² statistic, as expected due to the pivotal nature of the T² statistic. Despite this, the W² statistic has the advantage that it can be used even when n is small relative to p, as illustrated by the fact that the T² statistic cannot be used with p = 3 for n = 6 because the sample covariances are frequently not invertible in the bootstrap resamples. If one were to consider larger values of p, this deficiency of the T² statistic would present a larger problem since the dimension of the data is p(p + 1)/2, thus requiring increasingly large sample sizes as p increases. However, for Case 1, both procedures work reasonably well for both metrics in all cases. This is also the case for all but one instance of Case 3 in which the sample size is small (n = 6) and the amount of variability is large (m = 24). This is to be expected due to the sizeable differences between these means. On the other hand, because the means differ only somewhat in Case 2, the procedures for both metrics only perform particularly well when the sample size is reasonably large and the variability is low (n = 36,m = 192). Finally, for both the T² and W² confidence regions, neither the Frobenius nor canonical procedures perform uniformly better than the other. In fact, the coverage probabilities are typically quite close to each other.

6. DTI Application

In recent years, there has been a rapid development in the application of nonparametric statistical analysis on manifolds to medical imaging. In particular, data taking values in the space Sym⁺(3) appear in diffusion tensor imaging (DTI), a modality of magnetic resonance imaging (MRI) that allows visualization of the internal anatomical structure of the brain’s white matter (Basser and Pierpaoli, 1996; LeBihan et al., 2001). At each point in the brain, the local pattern of diffusion of the water molecules at that point is described by a diffusion tensor (DT), a 3 × 3 SPD matrix. A DTI image is a 3D rectangular array that contains at every voxel (volume pixel) a 3 × 3 SPD matrix that is an estimate of the true DT at the center of that voxel. (Thus DTI differs from most medical-imaging techniques in that, at each point, what the collected data are used to estimate is a matrix rather than a scalar quantity.) At each voxel, the estimated DT is constructed from measurements of the diffusion coefficient in at least six directions in three-dimensional space. The eigenvalues of the DT measure diffusivity, an indicator of the type of tissue and its health, while the eigenvectors relate to the spatial orientation of the underlying neural fibers.

A common statistical problem in DTI group studies is to find regions of the brain whose anatomical characteristics differ between two groups of subjects. The analysis typically consists of registering the images to a common template so that each voxel corresponds to the same anatomical structure in all the images, and then applying two-sample tests at each voxel. To our knowledge, existing statistics literature on DTI group comparisons is based on certain parametric assumptions, such as multivariate normality (Whitcher et al., 2007; Schwartzman et al., 2008b). But testing for multivariate normality requires large data-sets (Székely and Rizzo, 2005; Alva and Estrada, 2009; Hanusz and Tarasin’ska, 2008), so such testing could not be done in those studies because the number of subjects was simply too small. Furthermore, while the individual DT estimates at each voxel could be modeled by a multivariate normal distribution under some measurement conditions (Basser and Pajevic, 2003), there is no evidence that the distribution across subjects is multivariate normal. We therefore prefer not to assume a specific probability model for the distribution of DTs across subjects and utilize the nonparametric methods described previously in this paper to analyze the data.

6.1. Description of Data

For this application, our primary goal is to use nonparametric methodology to detect a significant difference between the means of the clinically normal and dyslexia groups. To illustrate these methods, we apply the methodology presented in Section 3.1 and Section 6.2 to a DTI data set previously analyzed in Schwartzman et al. (2008a), for which we compare means of populations of DT images as overall markers for dyslexic children when compared with clinically normal counterparts. This data-set consists of 12 spatially registered DT images belonging to two groups of children, a group of 6 children with normal reading abilities and a group of 6 children with a diagnosis of dyslexia. Here we present the analysis of a single voxel at the intersection of the corpus callosum and corona radiata in the frontal left hemisphere that was found in Schwartzman et al. (2008a) to exhibit the strongest difference between the two groups.

Table 6 shows the data at this voxel for all 12 subjects. The d_ij in the table are the entries of the DT on and above the diagonal (the below-diagonal entries would be superfluous since the DTs are symmetric).

The Frobenius sample means, ${\overline{X}}_1$ and ${\overline{X}}_2$ and the canonical sample means ${\overline{V}}_1$ and ${\overline{V}}_2$ for the clinically normal and dyslexia groups, respectively, are as follows:

$$\begin{gathered} {\overline{X}}_1={\left(0.6455,0.9937,0.7872,0.0057,-0.0962,-0.0877\right)}^T \\ {\overline{X}}_2={\left(0.6181,0.8181,0.9596,-0.0264,-0.1905,-0.0905\right)}^T \end{gathered}$$

and

$$\begin{gathered} {\overline{V}}_1={\left(0.6318,0.9863,0.7803,0.0046,-0.0924,-0.0873\right)}^T \\ {\overline{V}}_2={\left(0.6146,0.8118,0.9537,-0.0261,-0.1910,-0.0901\right)}^T \end{gathered}$$

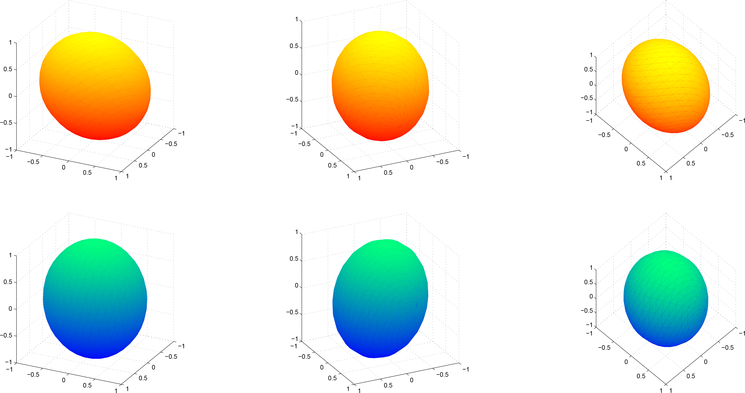
Diffusion tensors are commonly visualized as ellipsoids constructed from their spectral decompositions. Ellipsoids representing the two sample Frobenius means are provided in Figure 1and those for the sample canonical means are shown in Figure 2. In both figures, the ellipsoids are shown from three views for both groups to better display the differences between the mean tensors.

Figure 1:

Three views of the ellipsoids for the sample Frobenius means of the clinically normal (top, red) and dyslexia (bottom, blue) groups

Figure 2:

Three views of the ellipsoids for the sample canonical means of the clinically normal (top, red) and dyslexia (bottom, blue) groups

6.2. Nonparametric Inference

We can perform the hypothesis tests presented in Sections 3.1 and 6.2 by repeatedly resampling observations from the original data. As in the simulation studies in the previous sections, we used 10,000 bootstrap resamples to perform the tests. However, since n₁ = n₂ = 6, the T²tests cannot be used, so we can only consider the nonpivotal W² bootstrap tests. For the Frobenius W² test, the p-value is 0.0004, indicating a highly significant difference between the Frobenius means of the two groups. The p-value for the canonical W² test is 0.0006, which indicates that there is also a highly significant difference between the canonical means.

Because both of the tests were able to detect significant differences between the means, it is of interest to further examine the data to see which entries of the matrices appear to differ. Table 7 displays the ranges of the marginal bootstrap distributions of both types of means for the clinically normal and dyslexia groups. The marginal bootstrap distributions for the Frobenius means are plotted in Figure 3 by iteration. As suggested by the ranges in Table 7, the marginal bootstrap distributions of the canonical means are nearly identical to those of the Frobenius means.

Table 7:

Ranges of the marginal bootstrap distributions for the Frobenius and canonical sample means in the space of SPD matrices for the clinically normal and dyslexia groups.

Marginal	Frobenius				Canonical
	Clinically Normal		Dyslexia		Clinically Normal		Dyslexia
	Min	Max	Min	Max	Min	Max	Min	Max
d11	0.4921	0.8459	0.5643	0.6755	0.4902	0.8408	0.5626	0.6746
d22	0.9033	1.1415	0.7299	0.8940	0.9018	1.1402	0.7269	0.8894
d33	0.6986	0.8453	0.8232	1.0338	0.6942	0.8429	0.8425	1.0378
d12	−0.0421	0.0418	−0.0880	0.0358	−0.0422	0.0413	−0.0887	0.0350
d13	−0.1829	−0.0222	−0.2289	−0.1307	−0.1852	−0.0159	−0.2283	−0.1365
d23	−0.1798	0.0059	−0.1791	−0.0192	−0.1788	0.0032	−0.1645	−0.0273

Figure 3:

Marginals of the bootstrap distribution for the Frobenius mean for d₁₁, d₂₂, d₃₃, d₁₂, d₁₃, and d₂₃; clinically normal (red) vs dyslexia (blue)

As shown in Table 7 and Figure 3, it appears likely that the Frobenius means of the clinically normal and dyslexia groups differ in the d₂₂ and d₃₃ marginals. The minimum value of the d₂₂ marginal for the clinically normal group is greater than the maximum value for that of the dyslexia group, indicating that the ranges of this marginal differ. For the d₃₃ marginal, while there is a slight overlap in the ranges, closer inspection reveals that this is due to just two particular resamples out of the 10,000 considered. From examining the original data, it appears that these outlying occurrences are due to a heavy prevalence of observation 1 from the dyslexia group in these particular resamples.

Histograms of the bootstrap distributions for these two marginals are displayed in Figure 4 and show that there is a distinct separation in the bootstrap distributions for both the d₂₂ and the d₃₃ marginals of the Frobenius sample means. The marginal bootstrap distributions for the canonical sample means are nearly identical to those of the Frobenius sample means, suggesting a difference between the canonical means of the clinically normal and dyslexia groups in the same two marginals.

Figure 4:

Histogram of the marginal bootstrap distributions of the Frobenius Mean for d₂₂ and d₃₃; clinically normal (red) vs dyslexia (blue).

To put these results in context of the simulation study, we will now consider the amount of variability present in the data and the differences in angles between corresponding principal directions of the sample means. For the Frobenius means, the FSV for the control group is 0.0265 and it is 0.0106 for the dyslexia group. The angles between the principal directions of these means are 50.5974 degrees, 50.2119 degrees, and 7.2442 degrees. The FSV with respect to the canonical metric for the control group is 0.0739 and it is 0.0423 for the dyslexia group. The angles between the principal directions of the canonical means are 51.1738 degrees, 50.9964 degrees, and 7.0153 degrees.

As shown throughout this section, the sample means and the associated marginal bootstrap distributions are numerically close for the different metrics. This is not surprising since the data being averaged lay in a ball of relatively small radius with respect to either metric. Overall, both methods detect that there is a significant difference between the means of the dyslexia and clinically normal groups using the nonpivotal bootstrap tests. Furthermore, the methods for both metrics detect differences in the bootstrap distributions of the d₂₂ and d₃₃ marginals. It should be kept in mind, however, that this particular voxel was chosen precisely for having shown a significant difference between the groups in a previous parametric analysis (Schwartzman et al., 2008a).

7. Discussion

In this paper, we have considered nonparametric methodologies based upon nonparametric bootstrapping for comparing means of distributions of SPD matrices. The idea of using Fréchet-mean analysis for such data is motivated by previous literature on DTI analysis, including Chefd’hotel et al. (2004), Fletcher (2004), Arsigny et al. (2006), Schwartzman (2006), Zhu et al. (2007, 2009), and Dryden et al. (2009), which considered various non-Euclidean distances on the space of SPD matrices. We applied our nonparametric methodologies for the Frobenius and canonical metrics on this space. While extending these methods to more general spaces, such as the spaces of p×p positive definite matrices or p×p symmetric matrices, may be desirable in some applications, doing so is highly non-trivial due to the differing natural geometries of these spaces. For instance, while the Frobenius metric may be applicable for such data, these spaces do not have an analogous canonical metric. As such, extensions of this methodology to such spaces remain for future work.

To illustrate the effectiveness of the statistical methodology, we performed simulation studies for both metrics, showing that both the pivotal and nonpivotal procedures perform as desired. We also included an application of this methodology to analyzing the mean diffusion tensor at a voxel location in MRI images for dyslexic vs. clinically normal children. The voxel we used is the one that was found in Schwartzman et al. (2008a) to exhibit the strongest difference between the two groups. As illustrated in Section 6, the nonpivotal methodologies developed for both metrics were able successfully able to find a statistically significant difference between the means of these groups. In both the simulation study and the DTI application, the p-values obtained from the tests for both metrics, suggesting that the procedure for both perform well for comparing population means.

To compare computational cost, the data analysis procedures described in Sections 3.3 and 4.3 were each performed a number of times using MATLAB on a machine running Macintosh OS 10.8.5 on an Intel Core i5 processor running at 2.53 GHz. For the canonical metric, the computation times for various sample sizes were presented in Section 4.5. An algorithm must be used to compute the Fréchet sample means, since there is no closed-form expression for them. We found the gradient-descent algorithm we used for these computations to be fast, as was also observed in Pennec (1999), Le (2001), Groisser (2004), Fletcher et al. (2004), Smith (1994), Edelman et al. (1998), Pennec et al. (2006), and Fletcher and Joshi (2007). For the calculations using the Frobenius metric, the computational time required to compute sample means was fairly constant regardless of sample size and variability. Computing 20,000 sample means required a total of 1.02 seconds, on average. The MATLAB code for performing the tests for both metrics is available from the authors upon request.

For the DTI application, our methods, when applied to a single voxel, are fast. However, because bootstrapping requires repeated computation of the sample mean for each resample, application of the methods to the hundreds of thousands of voxels typically present in a DTI image remains computationally challenging. This is particularly true for the methods involving the canonical mean. As such, this problem is left for future work.

A Appendix: A symmetric-space structure for Sym⁺(p)

A (Riemannian) symmetric space is a Riemannian manifold $\mathcal{M}$ with the property that for each $M\in \mathcal{M}$, there exists an isometry $F:\mathcal{M}\to \mathcal{M}$ (a metric-preserving diffeomorphism) such that F(q) = q and whose derivative at q (a linear map $T_q\mathcal{M}\to T_q\mathcal{M}$) is minus the identity. It can be shown that, for each q, there is never more than one such isometry. This isometry is often called the geodesic symmetry at q because, loosely speaking, it corresponds to “reflecting”, about q, every geodesic through q. We will see later that Sym⁺(p), endowed with the canonical metric (to be defined in Section A.2) is a symmetric space.

The group of isometries of any Riemannian manifold is a Lie group⁵, and the study of symmetric spaces is carried out most efficiently when recast in terms of Lie groups. That is the approach we will take here. First, we review some terminology and features of group actions and exhibit the group action on Sym⁺(p) that will be of importance to us.

A.1. Group actions, homogeneous spaces, and Sym⁺(p)

We recall some standard group-action terminology and features. Let $\mathcal{K}$ be an arbitrary group, let $e\in \mathcal{K}$ be the identity element, and $\mathcal{M}$ an arbitrary nonempty set. Let $\tilde{\alpha }$ be a map $\mathcal{K}\times \mathcal{M}\to \mathcal{M}$, and for all $k\in \mathcal{K}$, define ${\tilde{\alpha }}_k≔\tilde{\alpha }(k,\cdot ):\mathcal{M}\to \mathcal{M}$. The map $\tilde{\alpha }$ is called a (left) action of $\mathcal{K}$ on $\mathcal{M}$ if the following two properties are satisfied:

$${\tilde{\alpha }}_{kh}={\tilde{\alpha }}_k°{\tilde{\alpha }}_h\forall k,h\in \mathcal{K},$$ (A.1)

$$\text{and}{\tilde{\alpha }}_e=\text{identity}\text{map}\mathcal{M}\to \mathcal{M}.$$ (A.2)

(If the order of composition on the right-hand side of (A.1) is reversed, $\tilde{\alpha }$ is called a right action.) Observe that (A.1)–(A.2) imply that for all $k\in \mathcal{K},{\tilde{\alpha }}_{k^{-1}}°{\tilde{\alpha }}_k$ is the identity map $\mathcal{M}\to \mathcal{M}$. Hence each map ${\tilde{\alpha }}_k:\mathcal{M}\to \mathcal{M}$ is invertible, and ${\left({\tilde{\alpha }}_k\right)}^{-1}={\tilde{\alpha }}_{k^{-1}}$.

To apply this abstract idea concretely, we fix some notation. Let GL(p,ℝ) ⊂ M(p,ℝ) be the set of invertible p × p matrices. Let O(p) ⊂ GL(p,ℝ) denote the set of orthogonal p × p matrices (G ∈ O(p) ⇐⇒ G^T = G⁻¹). Recall that GL(p,ℝ) and O(p) are Lie groups, with identity element I_p, the p×p identity matrix. We denote the Lie algebras of these Lie groups by gl(p,ℝ) and so(p) respectively. These Lie algebras can be canonically identified with spaces of matrices:

$$\begin{gathered} \mathfrak{g}\mathfrak{l}(p,ℝ)=M(p,ℝ) \\ \mathfrak{s}\mathfrak{o}(p)=\{A\in M(p,ℝ):A^T=-A\},\mathrm{the}\mathrm{space}\mathrm{of}\mathrm{antisymmetric}\mathrm{matrices}. \end{gathered}$$

The example of a group-action that is of greatest importance to us in this paper is the following.

EXAMPLE A.1

For any G ∈ GL(p,ℝ) and any M ∈ Sym⁺(p), the matrix GMG^T also lies in Sym⁺(p). For such G and M, let us define

$$\alpha (G,M)≔{\alpha }_G(M)=GM{G}^T.$$ (A.3)

Then the map α: GL(p,ℝ) × Sym⁺(p) → Sym⁺(p) is smooth (i.e. continuously differentiable) and is a left-action of GL(p,ℝ) on Sym⁺(p).

Let ${\tilde{\alpha }}_k:\mathcal{M}\to \mathcal{M}$ be a (general) left-action of a group $\mathcal{K}$ on a set $\mathcal{M}$. Given an action as above, for $q\in \mathcal{M}$, the isotropy group at q, or stabilizer of q, is the subgroup $\left\{k\in \mathcal{K}:{\tilde{\alpha }}_k(q)=q\right\}\subset \mathcal{K}$. The action $\tilde{\alpha }$ is called transitive if for all q₁, $q_2\in \mathcal{M}$, there exists $k\in \mathcal{K}$ such that ${\tilde{\alpha }}_k\left(q_1\right)=q_2$. Because of (A.1), if we are given any “basepoint” $q_0\in \mathcal{M}$, a necessary and sufficient condition for transitivity is that for all $q\in \mathcal{M}$, there exists $k\in \mathcal{K}$ such that ${\tilde{\alpha }}_k\left(q_0\right)=q$.

Assume now that the action $\tilde{\alpha }$ above is transitive. Fix a point $q_0\in \mathcal{M}$, and let $\mathcal{H}$ be the isotropy group at q₀. For each $q\in \mathcal{M}$, let ${\mathcal{C}}_q=\left\{k\in \mathcal{K}:{\tilde{\alpha }}_k\left(q_0\right)=q\right\}$, the set of group-elements that carry q₀ to q. Note that Cq₀ is just the isotropy group $\mathcal{H}$. For each $q\in \mathcal{M}$, transitivity guarantees that Cq is nonempty, and if k₁,k₂ ∈ Cq, then ${\tilde{\alpha }}_{k_1^{-1}{k}_2}\left(q_0\right)={\tilde{\alpha }}_{k_1^{-1}}\left({\tilde{\alpha }}_{k_2}\left(q_0\right)\right)={\left({\tilde{\alpha }}_{k_1}\right)}^{-1}(q)=q_0,$ so $k_1^{-1}{k}_2\in \mathcal{H}$. Thus, k₂ lies in the left $\mathcal{H}-coset{k}_1\mathcal{H}≔\left\{k_{1}h:h\in \mathcal{H}\right\}$. It is easy to check that, conversely, if $k\in k_1\mathcal{H}$, then k ∈ Cq. Thus the set Cq is precisely the coset $k_1\mathcal{H}$, where k₁ is any element of Cq. For later use, we record this fact in the following form:

$$\text{If}q\in \mathcal{M},k_1\in {\mathcal{C}}_{q,}\mathrm{and}k\in \mathcal{K},\text{then}k\in {\mathcal{C}}_q\iff k=k_{1}h\text{for}\text{some}h\in \mathcal{H}.$$ (A.4)

The set of all left $\mathcal{H}$-cosets in $\mathcal{K}$ is denoted $\mathcal{K}/\mathcal{H}$. The analysis above shows that the assignment q ↦ Cq is a 1–1 correspondence

$$\mathcal{M}\leftrightarrow \mathcal{K}/\mathcal{H}.$$ (A.5)

A homogeneous space for a Lie group $\mathcal{K}$ is a manifold $\mathcal{M}$ together with a smooth, transitive left-action of $\mathcal{K}$ on $\mathcal{M}$.

REMARK A.2

For any Lie-group action on a manifold, the isotropy group of any point is always a (topologically) closed subgroup. An important theorem in Lie theory ((Helgason, 1978), Theorem II.4.2, p. 123) is that if $\mathcal{K}$ is a Lie group and $\mathcal{H}$ is a closed subgroup, then $\mathcal{K}/\mathcal{H}$ inherits the structure of a smooth manifold; furthermore, if $\mathcal{M}$ is a homogeneous space for $\mathcal{K}$ with isotropy group $\mathcal{H}$ at some point q₀, then the map q ↦ Cq giving the correspondence (A.5) is a diffeomorphism.

Returning to our fundamental Example A.1, and taking the element I_p ∈ Sym⁺(p) as the basepoint of this space, we have the following:

PROPOSITION A.3

The action α of GL(p,ℝ) on Sym⁺(p) is transitive, and the isotropy group at I_p is O(p).

Proof. Let M ∈ Sym⁺(p) be arbitrary and let G be any square root of M (e.g. the unique symmetric positive-definite square root). Then α_G(I_p) = GG^T = G² = M. Hence α is transitive. By definition of “isotropy group” and the map α, the isotropy group at I_p is {G ∈ GL(p,ℝ) : GG^T = I_p}, which is exactly O(p).

Hence the assignment M ↦ CM, M ∈ Sym⁺(p), sets up a 1–1 correspondence

$$Sy{m}^{+}(p)\leftrightarrow GL(p,ℝ)/O(p).$$ (A.6)

The proof of Proposition A.3 showed more than was stated: if we restrict α, in its first argument, to the subgroup GL⁺(p,ℝ) ⊂ GL(p,ℝ) consisting of positive-determinant matrices, the restricted action is still transitive. For this restricted action, the isotropy group at I_p is SO(p), the orthogonal matrices of determinant 1. Thus, in addition to (A.6), we also have a 1–1 correspondence

$$Sy{m}^{+}(p)\leftrightarrow G{L}^{+}(p,ℝ)/SO(p).$$ (A.7)

A.2 Riemannian homogeneous spaces, symmetric spaces, and the canonical metric on Sym⁺(p).

Let $\tilde{\alpha }$ be a smooth action of a Lie group $\mathcal{K}$ on a manifold $\mathcal{M}$. For k ∈ $\mathcal{K}$ and q ∈ $\mathcal{M}$, let ${\left(d{\tilde{\alpha }}_k\right)}_q:T_q\mathcal{M}\to T_{{\tilde{\alpha }}_k(q)}\mathcal{M}$ be the derivative of the map ${\tilde{\alpha }}_k:\mathcal{M}\to \mathcal{M}$. A Riemannian metric g on $\mathcal{M}$ is called K-invariant if ${\tilde{\alpha }}_k$ is an isometry for all k ∈ $\mathcal{K}$; i.e. if

$$g_{{\tilde{\alpha }}_k(q)}({(d{\tilde{\alpha }}_k)}_q(u),{(d{\tilde{\alpha }}_k)}_q(v))=g_q(u,v),\forall q\in \mathcal{M},u,v\in T_q\mathcal{M}.$$ (A.8)

(In other words, for all k, q as above, ${(d{\tilde{\alpha }}_k)}_q$ is a linear isometry from the inner-product space $(T_q\mathcal{M},g_q)$ to the inner-product space $(T_{{\tilde{\alpha }}_k(q)}\mathcal{M},g_{{\tilde{\alpha }}_k(q)}).)$ A Riemannian homogeneous space for a Lie group $\mathcal{K}$ is a Riemannian manifold $(\mathcal{M},g)$, where $\mathcal{M}$ is a homogeneous space for $\mathcal{K}$, and the Riemannian metric g is $\mathcal{K}$-invariant. The following is a standard result from the theory of Riemannian homogeneous spaces.

LEMMA A.4

Let $\tilde{\alpha }$ be a smooth, transitive action of a Lie group $\mathcal{K}$ on a manifold $\mathcal{M}$, let $q_0\in \mathcal{M}$, and let $\mathcal{H}$ be the isotropy group at q₀. A scalar product g_q0 on T_q0 $\mathcal{M}$ can be extended to a $\mathcal{K}$-invariant Riemannian metric on $\mathcal{M}$ if and only if the inner product g_q0 is $\mathcal{H}$-invariant, in which case there is a unique $\mathcal{K}$-invariant extension.

Partial proof. Necessity is obvious. To prove sufficiency, assume that for each $q\in \mathcal{M}$, choose an arbitrary $k_1=k_1(q)\in {\mathcal{C}}_q(\text{so}{\tilde{\alpha }}_{k_1}(q_0)=q)$ and define an inner product g_q on $T_q\mathcal{M}$ by $g_q\text{(}u,v)=g_{q_0}({({(d{\tilde{\alpha }}_{k_1})}_{q_0})}^{-1}(u),{({(d{\tilde{\alpha }}_{k_1})}_{q_0})}^{-1}(v))$. Then clearly (A.8) is satisfied with q = q₀ and k = k₁. Furthermore g_q0 is the only inner product on $T_q\mathcal{M}$ for which this is true, establishing uniqueness. Then for any k ∈ Cq, we have k = k₁h for some $h\in \mathcal{H}$ (see (A.4)), and using the group-action properties and the Chain Rule for maps of manifolds, we have

$${(d{\tilde{\alpha }}_k)}_{q0}={(d{\tilde{\alpha }}_{k_1})}_{q0}°{(d{\tilde{\alpha }}_h)}_{q0}.$$

A straightforward computation then shows that for u,v ∈ T_q0M we have

$$g_{{\tilde{\alpha }}_k(q0)}(({(d{\tilde{\alpha }}_k)}_{q0})(u),({(d{\tilde{\alpha }}_k)}_{q0})(v))=g_{q0}(u,v).$$

Hence for all k ∈ C_q, ${(d{\tilde{\alpha }}_k)}_{q0}$ is a linear isometry from $(T_{q0}\mathcal{M},g_{q0})$ to $(T_q\mathcal{M},g_q)$ and ${(d{\tilde{\alpha }}_{k^{-1}})}_q={({(d{\tilde{\alpha }}_k)}_{q0})}^{-1}$ is a linear isometry in the other direction. Now let $q_1,q_2\in \mathcal{M}$ be arbitrary, and let $k\in \mathcal{K}$ be such that $\tilde{\alpha }(q_1)=q_2$. Transitivity implies that there exist k_i ∈ Cq_i, i = 1,2, such that $k=k_2{k}_1^{-1}.$ Then ${(d{\tilde{\alpha }}_k)}_{q_1}={({(d{\tilde{\alpha }}_{k_2})}_{q0})}^{-1}°{(d{\tilde{\alpha }}_{k_1})}_{q0}$, a composition of linear isometries, hence a linear isometry.

It remains only to establish that the assignment q ↦ g_q is smooth. This requires a technical result from Lie theory whose statement would require additional definitions and a significant digression from the main path of this paper. We refer the reader to (Cheeger and Ebin, 1975, Chapter 3) for these details.

Returning to the example that concerns us, $\mathcal{M}=Sy{m}^{+}(p)$ is an open subset of the vector space Sym(p), so for each M ∈ Sym⁺(p) there is a canonical isomorphism

$${\iota }_M:T_{M}Sy{m}^{+}(p)\to Sym(p).$$ (A.9)

We make use of the isomorphisms ι_M to express various formulas in terms of the fixed, concrete vector space Sym(p), rather than the M-dependent, abstract vector space T_MSym⁺(p).

Convention. We will write tangent vectors of Sym⁺(p) using capital letters A,B, etc., and elements of Sym(p) (viewed as the image of ${\iota }_M$ for some M) as $\check{A},\check{B}$, etc. When working at a point M ∈ Sym⁺(p) that is unambiguous from context, if we are given an element A ∈ T_MSym⁺(p), then “$\check{A}$ “ means ${\iota }_M$ (A); if we are given an element $\check{A}$ of Sym(p), then “A” means ${\iota }_M^{-1}(\check{A})$. Similarly, given an inner product g_M on T_MSym⁺(p), we use ${\check{g}}_M$ to denote the inner product defined by ${\check{g}}_M(\check{A},\check{B})=g_M(A,B)$; given an inner product ${\check{g}}_M$ on Sym(p), we use g_M to denote the inner product defined by this same equation.

Also, for M ∈ Sym⁺(p), G ∈ GL(p,ℝ), we write

$${(\check{d}{\alpha }_G)}_M≔{\iota }_{{\alpha }_G(M)}°{(d{\alpha }_G)}_M°{\iota }_M^{-1}:Sym(p)\to Sym(p).$$

With these conventions, we have

$${(\check{d}{\alpha }_G)}_M(\check{A})=G\check{A}{G}^T,\forall M\in Sy{m}^{+}(p),A\in T_{M}Sy{m}^{+}(p).$$ (A.10)

The Frobenius (Euclidean) inner product on $T_{I_p}Sy{m}^{+}\left(p\right)$ is given by $g_{I_p}(A,B)={\check{g}}_{I_p}(\check{A},\check{B})=\mathrm{t}\mathrm{r}({\check{A}}^T\check{B})=\mathrm{tr}(\check{A}\check{B})$, where $\check{A},\check{B}\in Sym(p)$. From Proposition A.3, the isotropy subgroup of the action (A.3) at I_p is the orthogonal group O(p). Using equation (A.10) we see that for H ∈ O(p),

$$\begin{gathered} g_{I_p}({(d{\alpha }_H)}_{I_p}(A),{(d{\alpha }_H)}_{I_p}(B))={\check{g}}_{I_p}{(\check{d}{\alpha }_H)}_{I_p}(\check{A}),{(\check{d}{\alpha }_H)}_{I_p}(\check{B})) \\ =\mathrm{tr}(H\check{A}{H}^{T}H\check{B}{H}^T)=\mathrm{tr}(H^{T}H\check{A}{H}^{T}H\check{B})=\mathrm{tr}(\check{A}\check{B})=g_{I_p}(A,B). \end{gathered}$$

Therefore, by Lemma A.4, we can make the following definition:

DEFINITION A.5

The canonical metric g_can on Sym⁺(p) is the unique GL(p,ℝ)-invariant extension of the Frobenius inner product on T_IpSym⁺(p).

As shown in the (partial) proof of Lemma A.4, the canonical metric is obtained from g_Ip as follows. (For simplicity, we write g for g_can in this discussion.) Given M ∈ Sym⁺(p), let G ∈ GL(p,ℝ) be such that α_G(I_p) = M (see Proposition A.3). The canonical inner product is given at M by $g_M(A,B)={\check{g}}_{I_p}({({(\check{d}{\alpha }_G)}_{I_p})}^{-1}(\check{A}),{({(\check{d}{\alpha }_G)}_{I_p})}^{-1}(\check{B}))$, for all A,B ∈ T_MSym⁺(p). Explicitly, we have GG^T = M, and therefore, using (A.10),

$$g_M(A,B)=\mathrm{tr}(G^{-1}\check{A}{(G^T)}^{-1}{G}^{-1}\check{B}{(G^T)}^{-1})=\mathrm{tr}(M^{-1}\check{A}{M}^{-1}\check{B}).$$ (A.11)

REMARK A.6

Schwartzman (2006) gives an alternate proof of the GL(p,ℝ)-invariance, by noting that conceptually, the point M ∈ Sym⁺(p) is a translation of the identity I_p by the group action, M = GI_pG^T, and this result does not depend on the specific choice of G.

As mentioned early in this section, the criteria for a Riemannian manifold to be a symmetric space can be expressed purely in terms of Lie groups. The reason for this is that it can be shown that the isometry group of a symmetric space $(\mathcal{M},g)$ always acts transitively (and smoothly) on $\mathcal{M}$. Thus a symmetric space is always a homogeneous space for its isometry group.

While every Riemannian symmetric space is a Riemannian homogeneous space, the converse is not true. Rather than give the most general Lie-theoretic characterization of symmetric spaces, we will simply state a proposition giving sufficient conditions for a homogeneous space to be a symmetric space. The reader may consult Helgason (1978) or Kobayashi and Nomizu (1969) for proofs.

Before stating the proposition, we recall that an involution of a group 𝒢 is an isomorphism $\sigma :\mathcal{G}\to \mathcal{G}$ such that σ ○ σ is the identity map $\mathcal{G}\to \mathcal{G}$.

PROPOSITION A.7

Let $(\mathcal{M},g)$ be a Riemannian homogeneous space for a connected Lie group $\mathcal{K}$, and let $\mathcal{H}$ be the isotropy group, at some point $q0\in \mathcal{M}$, for the $\mathcal{K}$-action. Suppose there exists a smooth involution σ of $\mathcal{K}$ whose fixed-point set is $\mathcal{H}$. Then $(\mathcal{M},g)$ is a symmetric space.

To apply Proposition A.7 to our space (Sym⁺(p),g_can), we use the characterization (A.7) of Sym⁺(p) (because the group GL⁺(p,ℝ) is connected, while GL(p,ℝ) is not). Define σ : GL⁺(p,ℝ) → GL⁺(p,ℝ) by σ(G) = (G^T )⁻¹. Then σ is a smooth involution whose fixed-point set is exactly the subgroup SO(p). This yields the following corollary, well-known to differential geometers (cf. Helgason (1978, Section VI.2) or Freed and Groisser (1989)).

COROLLARY A.8

(Sym⁺(p),g_can) is a symmetric space.

The map $d\sigma {|}_{I_p}:\mathfrak{g}{\mathfrak{l}}^{(p,ℝ)}\to \mathfrak{g}\mathfrak{l}(p,ℝ)$ is given by dσ|I_p(A) = −A^T, whose 1-eigenspace h is exactly the space so(p) of antisymmetric matrices, and whose (−1)-eigenspace is m = Sym(p). Define π : GL⁺(p,ℝ) → Sym⁺(p) by π(G) = GG^T. The derivative dπ|I_p is given by dπ|I_p(A) = A + A^T (here we are slightly abusing notation, by not writing explicitly the appropriate analogs of the maps ι_(·) defined earlier), which annihilates h and carries m isomorphically to T_IpSym⁺(p) = Sym(p). Theorem IV.4.2 in Helgason (1978) yields a formula for the curvature of a symmetric space in terms of the Lie-bracket operation (in our case, just the commutator of matrices) on the (−1)-eigenspace of dσ_e (in our case, e = I_p). In our case, the formula for sectional curvature of the two-plane spanned by {dπ|I_p(A),dπ|I_p(B)}, where A,B ∈ m are orthonormal, is $\frac{1}{4}\mathrm{tr}({[A,B]}^2)$; cf. Freed and Groisser (1989, p. 327), which is non-positive since the commutator of symmetric matrices is antisymmetric. Since (Sym⁺(p),g_can) is also complete and simply connected, it is therefore a Cartan-Hadamard manifold.

The characterization of symmetric spaces as (special) homogeneous spaces allows for a particularly simple characterization of geodesics (see Helgason (1978, Theorem IV.3.3(iii))), which we state here just for (Sym⁺(p),g_can): for A ∈ T_IpSym⁺(p), the geodesic γ with γ(0) = I_p,γ′(0) = A, is given by

$$\gamma (t)=\exp (t\check{A}),$$ (A.12)

where exp : M(p,ℝ) → GL⁺(p,ℝ) is the matrix exponential function.

COROLLARY A.9

The Riemannian manifold (Sym⁺(p),g_can) is complete, and Riemannian exponential map $\mathrm{E}\mathrm{x}{\mathrm{p}}_{I_p}:T_{I_p}Sy{m}^{+}(p)\to Sy{m}^{+}(p)$ is given by

$$\mathrm{E}\mathrm{x}{\mathrm{p}}_{I_p}(A)=\exp (\check{A}),\forall A\in T_{I_p}Sy{m}^{+}(p).$$ (A.13)

For general M ∈ Sym⁺(p), for all G ∈ GL(p,ℝ) that satisfy GG^T = M, the Riemannian exponential map Exp_M : T_MSym⁺(p) → Sym⁺(p) is given by

$$\mathrm{E}\mathrm{x}{\mathrm{p}}_M(A)=G\exp (G^{-1}\check{A}{(G^{-1})}^T)G^T=({\alpha }_G°\exp °{(\check{d}{\alpha }_{G^{-1}})}_M)(\check{A})$$ (A.14)

Proof. Completeness follows from (A.12) and the Hopf-Rinow Theorem (Cheeger and Ebin, 1975, Theorem 1.8). Equation (A.13) is also immediate from (A.12).

For (A.14), first consider, more generally, an arbitrary Riemannian manifold $(\mathcal{M},g)$, and suppose $\text{F}:\mathcal{M}\to \mathcal{M}$ is an isometry. It is easily seen that F carries geodesics to geodesics. Since a geodesic is determined uniquely by its basepoint and initial tangent vector, it follow that if we denote by γ₍q,v) the geodesic with basepoint q and initial tangent vector $v\in T_q\mathcal{M}$, then γ_{(F(q),(dF)q(v))} = F ○ γ_(q,v). Note that, by definition, EXP_q(v)=γ_(q,v)(1).

Now apply this to (Sym⁺(p),g_can), with F = α_G and with M,G as in the hypotheses. Using (A.10), we find that for A ∈ T_MSym⁺(p),

$$\mathrm{Ex}{\mathrm{p}}_M({\iota }_M^{-1}(G\check{A}{G}^T))=G\exp (\check{A})G^T.$$ (A.15)

Replacing $\check{A}$,with $G^{-1}\check{A}{(G^{-1})}^T$ (A.14) follows.

REMARK A.10

All symmetric spaces are complete; our formula (A.12) simply made the completeness of (Sym⁺(p),g_can) easy to see without quoting the theorem for the general case.

A.3 Riemannian Logarithm Maps

PROPOSITION A.11

The Riemannian exponential maps appearing in Corollary A.9 are diffeomorphisms.

Proof. Recall that every symmetric matrix can be diagonalized by an orthogonal matrix (in fact, a special orthogonal matrix): for every M ∈ Sym(p), there exists U ∈ SO(p) and a diagonal p × p matrix Λ such that M = UΛU⁻¹. If M ∈ Sym⁺(p) then, for any such decomposition, Λ ∈ Diag⁺(p), the set of diagonal matrices all of whose diagonal entries are positive. For Λ ∈ Diag⁺(p), we define logΛ to be the diagonal matrix obtained by replacing the diagonal entries of Λ by their logarithms. For M = UΛU⁻¹ ∈ Sym⁺(p), we then define log(M) = U(logΛ)U⁻¹. (The pair (U,Λ) is not uniquely determined by M, but it is not hard to show that U(logΛ)U⁻¹ is independent of the choice of (U,Λ).) One can easily check that for M ∈ Sym⁺(p) and $\check{A}\in Sym(p)$, we have exp(log(M)) = M and $\log (\exp (\check{A}))=\check{A}$. It is easily seen that the maps exp : Sym(p) → Sym⁺(p) and log : Sym⁺(p) → Sym(p) are smooth, hence diffeomorphisms. It follows that the map $\mathrm{E}\mathrm{x}{\mathrm{p}}_{I_p}$ in (A.13) is a diffeomorphism. For general M ∈ Sym⁺(p), from (A.16) we have $\mathrm{E}\mathrm{x}{\mathrm{p}}_M={\alpha }_G°\exp °{(\check{d}{\alpha }_{G^{-1}})}_M°{\iota }_M$, a composition of diffeomorphisms (the “exp” in this composition is really the restricted map exp|Sym_(p) : Sym(p) → Sym⁺(p)), hence a diffeomorphism.

For M ∈ Sym⁺(p) we define Log_M = (Exp_M)⁻¹ : Sym⁺(p) → Sym(p) as in Definition 4.4.

From (A.16) we can easily compute a formula for the Riemannian logarithm maps: if M ∈ Sym⁺(p), then for any G ∈ GL(p,ℝ) satisfying GG^T = M, and all M,V ∈ Sym⁺(p),

$${\mathrm{Log}}_M(V)=G\log (G^{-1}V{(G^{-1})}^T)G^T.$$ (A.16)

For specificity’s sake we may take G = M^1/2, the unique SPD square root of M, when computing Exp_M and Log_M. Thus

$$\mathrm{E}\mathrm{x}{\mathrm{p}}_M(A)=M^{1/2}\exp (M^{-1/2}{\iota }_M(A)M^{-1/2})M^{1/2}$$ (A.17)

and

$$\mathrm{L}\mathrm{o}{\mathrm{g}}_M(V)={\iota }_M^{-1}\left(M^{1/2}\log (M^{-1/2}V{M}^{-1/2})M^{1/2}\right)$$ (A.18)

(recall (A.9)), where of course M^−1/2 := (M^1/2)⁻¹ = (M⁻¹)^1/2.

A.4 Geodesic Distances in Sym⁺(p)

A geodesic $\gamma :(a,b)\to \mathcal{M}$, where $\mathcal{M}$ is a Riemannian manifold, has the property that if t₁,t₂ ∈ (a, b) are sufficiently close, then γ minimizes length among all paths from γ(t₁) to γ(t₂). However, given two points q₁, q₂ in a general Riemannian manifold, there may be geodesics of different lengths joining them (for example, for two points in the unit circle not diametrically opposite to each other, there is one geodesic of length less than π joining them, and another of length greater than π). But in a Cartan-Hadamard manifold, the unique geodesic path joining two points q₁, q₂ is always a minimal-length path, so the Riemannian distance between q₁ and q₂ is simply the length of this geodesic path. In particular, this is true of Sym⁺(p) with the canonical metric.

With the Frobenius metric, there is again a unique geodesic in Sym⁺(p) between any two points—a straight line-segment—and this path has minimal length (with respect to the Frobenius metric) among all paths joining the same two points. The squared Euclidean distance between points M,V ∈ Sym⁺(p) is simply ∥M − V ∥² = tr((M − V )²).

In any Riemannian manifold $(\mathcal{M},g)$ the length of a geodesic segment $\gamma :[0,1]\to \mathcal{M}$ is the length of its initial tangent vector. Hence in our Cartan-Hadamard manifold (Sym⁺(p),g_can), the geodesic distance between M, V ∈ Sym⁺(p) is d(M,V ) = ∥Log_M(V )∥M, where ∥A∥M = (g_can)_M(A,A)^1/2. Hence, from (A.18) and (A.11), we have the following formula (also established by Schwartzman (2006)):

$$d^2(M,V)=\mathrm{tr}\left({\log }^2(M^{-1/2}V{M}^{-1/2})\right).$$ (A.19)