Linking the Child Behavior Checklist (CBCL) with the Multidimensional Assessment Profile of Disruptive Behavior (MAP-DB): Advancing a dimensional spectrum approach to disruptive behavior

Abstract

Disruptive behavior in childhood is common. It spans from normative child misbehaviors to clinically-significant and impairing problems. While there are many rating scales evaluating such behaviors, historically, measurement has emphasized counting the number of symptoms present rather than assessing the normal-abnormal spectrum of behavioral expression. This study uses data from 644 early school age children aggregated from two data sources to statistically link a commonly used symptom count measure, the Child Behavior Checklist (CBCL), to a more developmentally-sensitive measure, the Multidimensional Assessment Profile of Disruptive Behavior (MAP-DB). Two links between conceptually similar scales on each measure were developed: CBCL Conduct Problems and MAP-DB Aggression; and CBCL Oppositional Defiant Problems and MAP-DB Temper Loss. We compared two innovative methods—Item Response Theory (IRT) and Deming regression—to determine the optimal linking relationship. Results suggest IRT methods were superior in reducing linking error compared to Deming regression. While Deming regression accurately modeled the mean scores (thus minimizing linking bias), this method could not adequately address the floor effect for scores on the CBCL. For practical purposes, this study provides a crosswalk of score conversions between the CBCL and MAP-DB, such that data aggregation and group comparisons can be made across the two measures; this enables longitudinal analyses with historically-collected CBCL data to transition to the more innovative dimensional scales of the MAP-DB without undo loss of extant data. This study furthers efforts to shift from historical symptom counts to more developmentally-sensitive measurement across the disruptive behaviors spectrum.

Disruptive behaviors (e.g., aggression, noncompliance, temper tantrums) may reflect normative responses or clinical symptoms, depending on their intensity, developmental appropriateness, context, and frequency (Wakschlag et al., 2018). Behaviors that are pervasive, dysregulated, and impairing are considered to be of clinical concern (Wakschlag, Tolan, & Leventhal, 2010). Historically, many rating scale measures have emphasized counting symptoms or extreme behaviors that mirror classification systems—such as the Diagnostic and Statistical Manual of Mental Disorders (DSM; American Psychiatric Association, 2013)—or to an empirically-derived nosology—such as the Child Behavior Checklist (CBCL; Achenbach & Ruffle, 2000). Within these schema, severity is derived from a summary score (agnostic to specific behavior) rather than a problem-weighted spectrum of severity. Scales such as the CBCL broke new ground in the latter part of the 20^th century by introducing a quantitative/empirically-derived nosology to syndrome definition in contrast to clinically defined/categorical approaches used by the traditional medical model (Achenbach, Conners, Quay, Verhulst, & Howell, 1989; Achenbach & Ruffle, 2000). The CBCL has composites for both internalizing and externalizing behavior, but it recognizes that these broadband scales may not be sufficient for tracking changes in severity. As such, it has two types of subscales: slightly narrower defined syndrome subscales (e.g., aggression; anxious/withdrawn) and diagnostic subscales (e.g., attention problems; conduct problems) that are intended to reflect DSM criteria.

However, increasing evidence suggests changes in psychopathology generally occur in much more narrowly defined processes, such that broad-band scales are incapable of detecting the change. A dimensional spectrum approach is necessary, as it has utility for identification, prediction, and mechanistic specification (Grabell et al., 2018; Wakschlag et al., 2015). Current psychometric and neuroscience-based models of psychopathology strongly support dimensional conceptualizations (ranging from normative variation to severely abnormal expression) rather than considering clinical syndromes as static and discrete discontinuous ―conditions‖ or counts (Cuthbert & Insel, 2013; Franklin, Jamieson, Glenn, & Nock, 2015; Krueger & Piasecki, 2002).

A novel instrument designed for this purpose is the Multidimensional Assessment Profile of Disruptive Behavior (MAP-DB; Wakschlag et al., 2014). The MAP-DB is theoretically and empirically derived to generate narrowly-defined dimensions conceptualizing the core latent features of disruptive behavior as developmentally expressed (Carter, Gray, Baillargeon, & Wakschlag, 2013). One novel feature of the MAP-DB is the inclusion of both normative and problem behaviors so as to capture the full behavioral spectrum from mild, normative expressions to severe pathognomonic indicators. The MAP-DB’s multidimensional framework is defined in relation to four core developmental processes: regulation of anger/frustration (Temper Loss), aggressive behavior (Aggression), internalization of rules (Noncompliance; Punishment Insensitivity) and empathic processes (Low Concern for Others) (for explication of these developmental processes and how they go awry in disruptive behavior see Bufferd, Dyson, Hernandez, & Wakschlag, 2016; Wakschlag et al., 2012; Wakschlag et al., 2010).

Unfortunately, clinicians and researchers have been hesitant to convert to this more appropriate dimensional conceptualization for fear of losing comparability with existing symptom count data, such as the CBCL. Scientific efforts are hampered by the inability to combine data from both the historically ground-breaking but now dated conceptualizations of psychopathology and the modern, narrowly-defined dimensional conceptualizations. The purpose of this study is to statistically link subscales from the CBCL to a more neurodevelopmentally-derived, dimensional conceptualization of disruptive behavior provided by the MAP-DB. Linking these measures will allow the CBCL to be treated as an alternative form to the MAP-DB and provide a comparable score as if the MAP-DB was administered, and vice versa.

There are many potential applications of linking patient-reported outcomes. Linking allows scales from different forms to be compared (Choi, Schalet, Cook, & Cella, 2014). Thus, historical data can be aggregated with new studies and relative severities can be compared across time. Linking also allows results from different studies to be directly compared without having to standardize differences and compare only effect sizes; it allows comparisons on the original scale of the one or the other forms. This also can support large-scale testing efforts, where different subsites within the larger study collect data on different measures. By linking to a common reporting metric, the various groups can be compared on an appropriate scale.

Method

Participants

To enhance the robustness of score-linking analyses, we combined MAP-DB and CBCL data from two different study sources (N=644). All children were enrolled between 2011 and 2017. The median age of the samples was 7 years (see Table 1).

Table 1:

Participant Demographics by Sample

	MAPS		LBCD		Total
	N	%	N	%	N	%
	524		120		644
Boys	242	46.2	60	50.0	302	46.9
Girls	282	53.84	60	50.0	342	53.1
Black/African-American	231	44.1	55	46.2	286	44.5
White	134	25.6	51	42.9	185	28.8
Hispanic	149	28.4	4	3.4	153	23.8
Other	10	1.9	9	7.6	19	3.0
	Mean Age/Yrs.	SD	Mean Age/Yrs.	SD	Mean Age/Yrs.	SD
Age in years, mean (sd)	6.6	(1.1)	7.4	(1.3)	6.8	(1.2)

Data Source 1: Multidimensional Assessment of Preschoolers (MAPS) Study (n=524).

The first sample was from the early school age wave of the MAPS Study, an ongoing study of early emerging disruptive behavior (Wakschlag et al., 2014; Wakschlag et al., 2015). Mothers and children were recruited from pediatric clinics in the Midwestern United States at preschool age and were oversampled for psychopathology risk. Seventy-nine percent of the MAPS Study sample (n=414) were participants in a multi-wave intensive longitudinal study that began in preschool and extended to early school age. This intensive sample was supplemented with an additional 110 families who had participated in a survey study at the time of original recruitment and were re-contacted to participate in survey completion at early school age.

Data Source 2: Laboratory for Child Brain Development (LBCD) Studies (n=120).

The second sample was derived from a set of studies focused on differentiating normal-abnormal irritability in young children conducted in the Northeastern United States. For this sample, healthy control children were recruited from the local community (n=85, 71%) with no personal or first-degree family history of psychopathology. Children with impairing irritability symptoms were also recruited from area child psychiatry clinics (n=35, 29%; Perlman et al., 2015; Perlman, Luna, Hein, & Huppert, 2014; Karim & Perlman, 2017). Table 1 provides demographic information regarding the participants, by study source sample and overall, demonstrating roughly comparable sociodemographic characteristics across the Midwestern and Northeastern studies.

Measures

The Child Behavior Checklist (CBCL) is a problem behavior checklist, which has been used extensively to assess internalizing and externalizing syndromes (Achenbach & Ruffle, 2000). The CBCL uses age- and gender-based T-scores, with higher scores indicating more frequent symptoms. It has different versions for young children (ages 1.5 to 5 years) and older children (ages 6 to 18 years), with separate normative scores within each version by age and gender. For this study, the parent-completed 6- to 18-year-old version was used. Behaviors on the CBCL are rated by parents on a 3-point subjective frequency scale (0=never; 1=sometimes; 2=often).

The Multidimensional Assessment Profile of Disruptive Behavior (MAP-DB) is a multidimensional measure of disruptive behavior (Wakschlag et al., 2014), with four dimensions (listed above) and different versions depending on the age of the child (Infant/Toddler, Preschool, School Age, and Adolescence; Biedzio & Wakschlag, in press). For this study, the School Age version was used. The MAP-DB has been extensively validated at preschool age (an age at which normal-abnormal differentiation is especially challenging; Biedzio & Wakschlag, in press; Briggs‐Gowan et al., 2014; Wakschlag et al., 2014; Wakschlag et al., 2015; White et al., 2016), and the infant/toddler, school age, and adolescence versions have been developed more recently to enable developmentally meaningful dimensional measurement across age periods (Biedzio & Wakschlag, in press). All MAP-DB versions are completed by the primary caregiver using the same 6-point rating scale based on behavior over the past month (0=never; 1=rarely [<1/x/wk.]; 2=some [1–3] days/wk.; 3=most [4–6 days/wk.]; 4=daily; and 5=many times each day). The MAP-DB dimensions were developed using Item Response Theory (IRT), a modern psychometric approach that recognizes items are neither equally ―difficult‖ nor equally related to the underlying construct; thus some items are more effective at differentiating severity than others (Reise & Waller, 2009). The IRT-based scoring process weights each item to reflect its severity and relation to the latent construct rather than a simple sum of symptom counts.

Data Analysis

There are multiple options for conducting score linking, but the strongest designs feature a single-group study where all participants complete both scales in their entirety (Dorans, 2007; Kolen & Brennan, 2014), as in the current study. We use two different statistical methods to carry out and test this linkage: IRT-based linking to a calibrated item pool and a non-IRT-based method comparison via Deming regression. The MAP-DB was originally calibrated and scored using IRT, such that rescoring the CBCL onto the MAP-DB metric can be achieved via IRT methods (Choi et al., 2014; Kolen & Brennan, 2014); for additional robustness and sensitivity check, Deming regression (Carstensen, 2010), described below, was also used because it allows for error variance in both the independent and dependent variables, thereby allowing for symmetric conversions between the scales (i.e. converting CBCL scores to the MAP-DB and MAP-DB scores to the CBCL, which is a requirement for linking; Kolen & Brennan, 2014). Given the differences in the underlying conceptual frameworks of the CBCL and MAP-DB, we further hypothesized that not all scales would meet the necessary statistical criteria, as outlined below, for linking.

Requirements for Score Linking:

In order to link two instruments, they should measure the same concept and be essentially unidimensional (Dorans, 2007). To test the concordance between the CBCL and the MAP-DB, as well as their unidimensionality, we correlated the subscales, calculated Cronbach’s alpha on the aggregated item set, and fit a unidimensional factor model to each set of potential subscales, as well as a multidimensional factor model consistent with the multidimensional structures of the CBCL and MAP-DB.

A second requirement for IRT-based linking is that the strong assumptions for IRT (e.g., local independence, lack of differential item functioning, etc.) should hold in the aggregated item set (Dorans, 2007). However, given that the goal of this study is not initial scale development, modifications to these established scales due to the strong assumptions of IRT were not considered tenable.

Analytic Procedure:

We used several methods to evaluate whether the aggregated items were sufficiently ―unidimensional‖ for linking, including statistical rules of thumb and published examples. The scales should be significantly correlated, have a high first-to-second eigenvalue, and have a small root mean square error of approximation (RMSEA) for unidimensional models of the linked scales. (Reise, Cook, & Moore, 2015).

Linking was then conducted using Deming regression (a non-IRT method), and fixed anchor co-calibration (and IRT-based method) (Choi et al., 2014). Deming regression was chosen as the non-IRT method for score conversions because it recognizes that standard regression procedures do not account for error variance in both scales (Carstensen, 2010). It requires a known ratio of error variances on the two measures, which were known in this case based on the two measures’ scoring rules: the CBCL uses a T-score with a mean of 50 and standard deviation of 10, and the MAP-DB uses an IRT-based score with a mean of 0 and standard deviation of 1, for an expected variance ratio of 100:1. We also calculated the regressions using the observed variance ratio in the sample, which was smaller than the theoretical ratio.

Next, we conducted IRT-based fixed anchor co-calibration between the MAP-DB and CBCL items. In order to set the scale of the MAP-DB, we fixed the item parameters that also occur on the well-validated MAP-DB Preschool form, freeing the sample mean and standard deviation so that MAP-DB scores are comparable across the lifespan without requiring all ages to have the same items (Wakschlag et al., 2014). Although the MAP-DB is generally administered as a full instrument, and some studies have used the multidimensional factor correlations for scoring, the standard scoring procedure treats each dimension as a unidimensional factor since the MAP-DB follows a very simple structure (i.e., each item contributes to the score of one and only one dimension). Thus, this study was conducted as a unidimensional link on the items used for this conversion as opposed to including all MAP-DB items, even those not included in the linked dimension.

The Deming regression and IRT-based fixed anchor co-calibration methods were chosen because they have unique strengths and weaknesses. Deming regression is a ―direct statistical adjustment‖ method, whereas IRT uses an ―indirect‖ procedure based on the psychometric properties of items (Dorans, 2007). Deming regression allows the conversion to happen between the scores most frequently reported, that is, between the age- and gender-based T-scores on the CBCL and the IRT scores for the MAP-DB. IRT-based co-calibration uses the raw item-level scores and, unless a separate relationship is developed for each age-by-gender cell, ignores the demographic adjustments on the CBCL.

After conducting both types of links, graphical and statistical procedures were used to determine the optimal method. Descriptive statistics were calculated for the scores on the individual measure, the differences between them, and the root mean square difference (RMSD). Finally, Bland-Altman plots were produced to examine the limits of agreement between the linked and actual scores (Bland & Altman, 1986).

Potential Links

We considered multiple links across the CBCL and MAP-DB. DSM disorders are groupings of heterogeneous behaviors, such that several of the MAP-DB narrow-band dimensions could reasonably be linked together with a single CBCL DSM-oriented scale (e.g., both MAP-DB Noncompliance and Temper Loss may be linked to CBCL Oppositional Defiant Problems). We restricted linking one CBCL DSM-oriented scale and one MAP-DB dimension at a time. We considered two potential links most meaningful: CBCL Conduct Problems to MAP-DB Aggression; and CBCL Oppositional Defiant Problems to MAP-DB Temper Loss. Other links were also considered, but were determined not to be possible for failure to meet the assumptions of linking.

Results

Unidimensionality

There are numerous indices for unidimensionality, none of which is sufficient on its own. As such, we calculated multiple of these and present them in Table 2. Both proposed links met less-stringent requirements suggesting that they were “unidimensional enough’’ to proceed with linking. Additionally, if the potential link between MAP-DB Noncompliance and CBCL Oppositional Defiant Problems would have also been considered, it would have met these minimal statistical assumptions (results not shown).

Table 2:

Unidimensionality of the Proposed Links

Proposed Linking	Mean Score Correlation	Latent Correlation	First-to-Second Eigenvalue Ratio	RMSEA
CBCL Conduct Problems => MAP-DB Aggression	0.79	0.91	4.9	0.06
CBCL Oppositional Defiant Problems => MAP-DB Temper Loss	0.76	0.91	13.6	0.06

Abbreviations: CBCL=Child Behavior Checklist; MAP-DB= Multidimensional Assessment Profile of Disruptive Behavior; RMSEA=Root mean square error of approximation

Multidimensionality

Both the CBCL and MAP-DB are multifactor scales. As such, we fit a multidimensional confirmatory factor model where items loaded onto a factor consistent with their originating scale. At this phase, linking both the MAP-DB Noncompliance and Temper Loss to CBCL Oppositional Defiant Problems became untenable. The CBCL scale no longer appeared unidimensional when both MAP-DB scales were included insofar as some Oppositional Defiant items were more closely related to Noncompliance while others were more closely related to Temper Loss. We chose to proceed only with linking it with Temper Loss, as that scale on the MAP-DB is more frequently reported in the published literature. The multidimensional model fit better when only including the four factors related to the proposed links. The latent correlations—which are similar to disattenuated correlations presented in other linking manuscripts—are also provided in Table 2. As expected, these are substantially better than the raw correlations and acceptable for linking (Choi et al., 2014).

Non-IRT Linking

First, we conducted direct linking (Dorans, 2007) between the CBCL T-scores and the MAP-DB scale scores using Deming regression. Deming regression allows for a researcher or clinician to input the score from one test into a formula, multiply it by one coefficient and add a second coefficient and get the implied score after linking on the other test. These optimal linking equations (using the CBCL T-Scores) are as follows:

CBCL Conduct Problems and MAP-DB Aggression:

• {e1a} Conduct Problems * 0.17 – 9.34 = Aggression

• {e1b} Aggression * 5.96 + 55.68 = Conduct Problems

CBCL Oppositional Defiant Problems and MAP-DB Temper Loss:

• {e2a} Oppositional Defiant Problems * 0.18 – 9.87 = Temper Loss

• {e2b} Temper Loss * 5.57 + 55.04 = Oppositional Defiant Problems.

Figure 1 graphically shows these conversions, including the ordinary least squares regression ine between the two measures, which should be considered the bounds on score conversions. The point at which all four lines intersect is the sample mean of both scales.

Figure 1: Deming Regression Score Conversions.

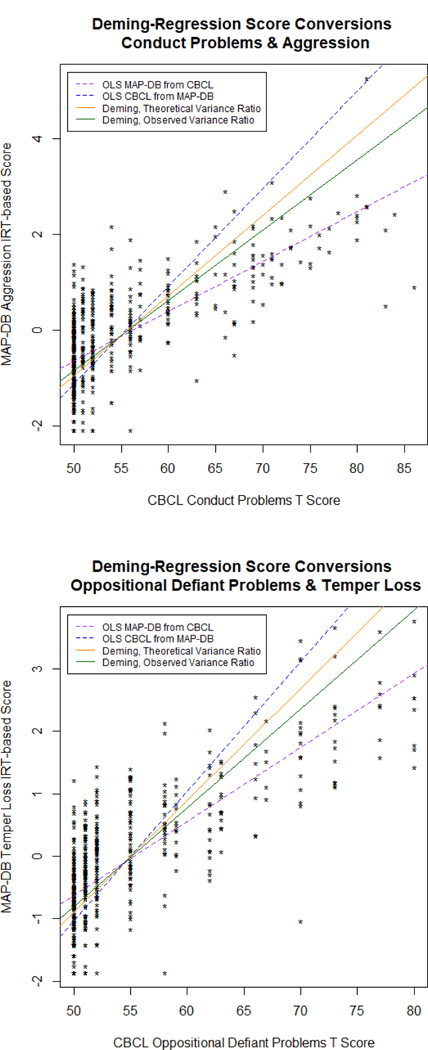
Non-IRT score conversions, using Deming regression with theoretical and sample-observed variance ratios. As is apparent, there are significant floor effects on the CBCL, while the MAP-DB makes finer distinctions among those within the average severity ranges.

IRT-based Linking

IRT-based linking is an indirect method (Dorans, 2007), insofar as it uses item-level responses to get implied scale-level scores on the other measure. This, however, meant that some items required modifications in order to proceed with IRT-based linking. Some items on the Conduct Problems subscale required collapsing frequency rates for behaviors that are quite extreme and uncommon in childhood (e.g., animal cruelty, vandalism, etc.). Most of these items are not included in the empirical CBCL subscales due to low endorsement rates, and as such, it is not surprising that the same measurement issues were exhibited in these samples. Similarly, several items on the MAP-DB Aggression dimension were rarely endorsed as ―daily‖ or ―multiple times per day‖ and as such also had to be collapsed.

After collapsing item categories as needed, the items were calibrated onto the MAP-DB metric using the graded response model and fixed-anchor calibration (Choi et al., 2014). The sample distributions were computed for MAP-DB Aggression (mean = −0.24 sd = 1.15) and Temper Loss (mean = −0.14 sd = 1.10). Unlike Deming regression, which allows a straightforward conversion formula, IRT-based linking requires item-level data and IRT scoring software for pattern-based scoring, or at least the raw sum score (i.e., not the CBCL T-score) to get sum score-based IRT scores (as in Table 3) using the Lord and Wingersky algorithm (Cai, 2015).

Table 3:

IRT-based Score Conversions

Raw Sum Score	CBCL Conduct Problems to MAP-DB Aggression		CBCL Oppositional Defiant Problems to MAP-DB Temper Loss
	Theta Score	SD	Theta Score	SD
1	−1.14	0.82	−1.17	0.75
2	−0.34	0.65	−0.44	0.60
3	0.13	0.57	0.03	0.54
4	0.50	0.49	0.42	0.50
5	1.02	0.39	0.75	0.47
6	1.22	0.36	1.06	0.46
7	1.34	0.34	1.36	0.47
8	1.55	0.33	1.68	0.48
9	1.70	0.32	2.02	0.50
10	1.84	0.31	2.37	0.53
11	1.97	0.31	2.71	0.58
12	2.10	0.30
13	2.22	0.30
14	2.34	0.30
15	2.46	0.30
16	2.58	0.30
17	2.70	0.30
18	2.82	0.30
19	2.94	0.31
20	3.07	0.31
21	3.19	0.32
22	3.32	0.32
23	3.46	0.33
24	3.60	0.34
25	3.75	0.36
26	3.91	0.37
27	4.08	0.39
28	4.27	0.42
29	4.49	0.45
30	4.70	0.47
31	4.91	0.48

Abbreviations: CBCL=Child Behavior Checklist; MAP-DB= Multidimensional Assessment Profile of Disruptive Behavior

Evaluating Linking Accuracy

Table 4 summarizes the agreement and differences between the two linking methods. The mean difference, standard deviation of differences, and RMSD should be minimized, whereas the correlation between scores should be maximized. Deming regression minimized the mean difference (bias), but the other fit statistics favored the IRT-based link. Bland-Altman plots representing the links are provided in Figures 2 and 3. The dotted red line indicates the ideal, or unbiased, difference, whereas the black line shows the obtained mean difference. The dashed grey lines are the 95% limits of agreement, which suggest a high degree of uncertainty at the individual level, with greater uncertainty for Deming regression than for IRT-based methods. Both linking methods were approximately equally good, but the IRT-based method was marginally superior. The decreased uncertainty in the IRT-based linking indicates improved linking accuracy for this method over the Deming regression linking. However, in cases where only score-level data may be available (as opposed to item-level data), the Deming regression formulas should provide a sufficient conversion method. In all cases there was a high degree of uncertainty in individual-level score conversions. For this reason, Table 4 also calculates the sample size necessary for a group-level RMSD ≤ 0.20.

Table 4:

Linking Accuracy

Linking Method	MAP-DB Mean (SD)	CBCL-Linked Mean (SD)	N	Mean Difference (SD)	Score Correlation	RMSD	Sample Size Needed for Group-RMSD ≤ 0.2
Deming Regression: CD => Agg	−0.16 (1.11)	−0.16 (1.28)	551	0 (0.92)	0.72	0.91	22
IRT Co-Calib: CD => Agg	−0.18 (1.10)	−0.30 (1.00)	638	0.12 (0.76)	0.74	0.77	16
Deming Regression: ODD => Temp Loss	−0.10 (1.10)	−0.10 (1.26)	551	0 (0.84)	0.76	0.84	19
IRT Co-Calib: ODD => Temp Loss	−0.11 (1.07)	−0.15 (1.00)	638	0.04 (0.68)	0.79	0.69	13

Abbreviations: CBCL=Child Behavior Checklist; CD=Conduct Disorder Problems; MAP-DB= Multidimensional Assessment Profile of Disruptive Behavior; ODD= Oppositional Defiant Disorder Problems; RMSD=Root mean square difference

Note: Deming regression required sufficient data to calculate CBCL T-scores, and as such, sample sizes were smaller when large missing data occurred.

Figure 2: Conduct Problems and Aggression Bland-Altman Plots.

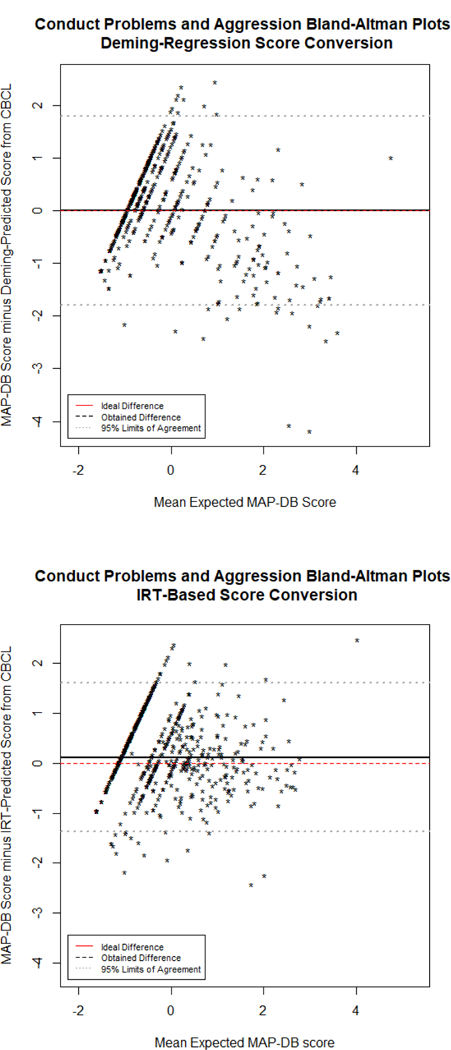
Bland-Altman plot representing the agreement between scores linked from the CBCL and obtained on the MAP-DB Early School Age Form. The mean of the linked and actual Aggression score is on the x-axis, whereas the difference (actual minus linked) is on the y-axis. A pronounced floor effect from the CBCL is apparent, regardless of method used for linking.

Figure 3: Oppositional Defiant Problems and Temper Loss Bland-Altman Plots.

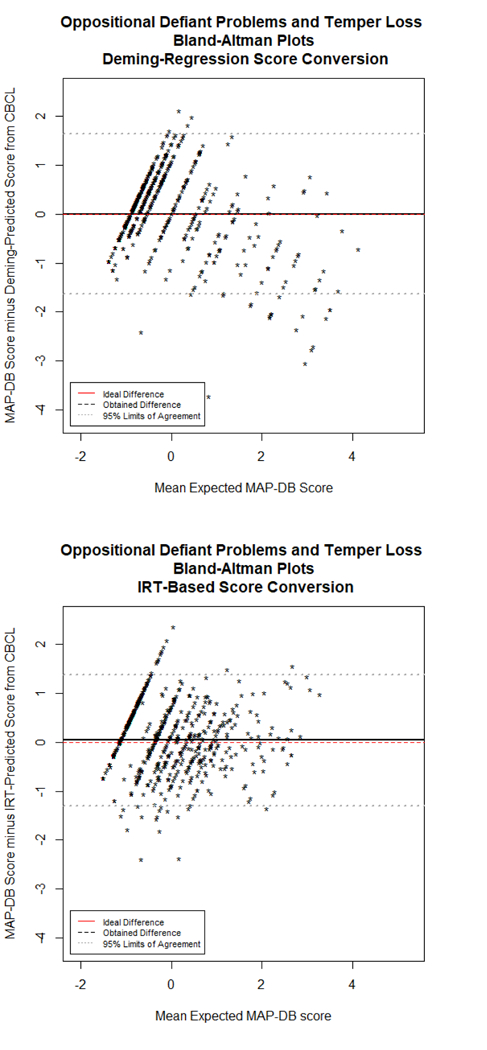
Bland-Altman plot representing the agreement between scores linked from the CBCL and obtained on the MAP-DB Early School Age Form. The mean of the linked and actual Aggression score is on the x-axis, whereas the difference (actual minus linked) is on the y-axis. A pronounced floor effect from the CBCL is apparent, regardless of method used for linking.

Discussion

This study is an essential first step towards enabling linkage of traditional problem behavior counts to more innovative measurement approaches within a neurodevelopmental framework of disruptive behaviors. The CBCL is one of the most well-known problem behavior checklists, which has a rich history of research supporting utility in screening for externalizing behavior using counts. The capacity of newer measures, such as the MAP-DB, are needed to differentiate the gradients of behavior along a continuum within narrow band, mechanistically-oriented dimensions and are key to filling critical gaps in translation of modern neurodevelopmental understandings of psychopathology to application (Garvey, Avenevoli, & Anderson, 2016; Grabell et al., 2018; Mittal & Wakschlag, 2017).

In this study, IRT-based linking methods were found to be superior to Deming regression for converting between the CBCL and the MAP-DB. While Deming regression minimized linking bias, it had much wider variability in agreement, largely due to the floor effects on the CBCL. Both methods had better agreement for individuals with problematic disruptive behavior (which is where measurement “matters’’), but the MAP-DB provided better differentiation among individuals with “normal’’ levels of disruptive behavior. While traditional measurement and clinical approaches have focused on assessing problematic behaviors, given the high frequency of normative “problem’’ behaviors in young children, the MAP-DB provided the full spectrum of normal-abnormal disruptive behavior.

Based on these results, clinicians and researchers can use the score crosswalk table provided in Table 3 to rescore CBCL raw scores as if they were MAP-DB scores. Users can add up the raw score from the relevant CBCL DSM-Oriented subscale, find that value in the raw sum score column, and move across the row to find the appropriate linked score on the MAP-DB IRT scale. Conversions between measures will allow data aggregation and reanalysis in large-scale efforts, allowing clinicians and researchers who have used the CBCL in the past to move to a more developmentally-sensitive measure of behavioral quality without losing extant data.

In further support of the developmentally-specified approach of the MAP-DB, we observed a significant floor effect for the CBCL (as indicated by the T-score of 50), with few individuals receiving high scores on it. However, there was a range of scores represented on the MAP-DB, suggesting that it was better at capturing a continuum of disruptive behavior from mild, normatively occurring forms to severe, rare forms. The linking results—particularly for the Deming regression, and to a lesser extent for the IRT-based co-calibration—may have been affected by the floor effect on the CBCL.

Regardless of the method, linking inherently includes additional error variance into an individual score. As such, linked scores should only be used for group-level comparisons. Researchers interested in individual scores on a particular measure should collect data on the target measure, using linking to compare population means across linked measures. While the IRT-based conversion had a smaller RMSD than the Deming regression approach, the 95% limits of agreement for both methods are wide, indicating that even advanced linking methods cannot account for the substantive and psychometric differences between these scales. Table 4 estimates the group sample size necessary to achieve a group-based linked RMSD less than 0.20. Linking discrepant scales can provide sample-level prediction, but cannot replace administration of a more appropriate measure of the desired construct.

Comparative Advantages of the MAP-DB and CBCL

The CBCL and MAP-DB have different advantages. The first, and greatest, for the CBCL is the richness and longevity it has experience in research and clinical care. The greatest advantage for the MAP-DB is its greater neurodevelopmental framework—a dimensional conceptualization of psychopathology, and greater differentiation of the normal-abnormal spectrum. The MAP-DB also has the advantage of being developed with IRT (Reise & Waller, 2009), as opposed to only using IRT for linking. The strengths of either of these linking approaches is that the results are symmetric—MAP-DB scores can be converted to CBCL scores, or CBCL scores can be converted to MAP-DB scores depending on the purpose of the analyses in question.

Ideally there would be matching domains on both tests, in which case links could be developed across all of them. However, the MAP-DB does not include internalizing domains and as such, the CBCL has unique content there. It also has prosocial/positive health competency subscales, for which there is no comparable content on the MAP-DB. The broadband framework of the CBCL supports its use in large scale research consortia, where there is a greater emphasis on assessing as many domains as possible in limited time. Symptom checklists are also efficient in screening for multiple disorders. The alternative is also the case—the MAP-DB uses narrow-band scales which greater differentiates disruptive behaviors. Conceptually, several MAP-DB scales could be linked with one CBCL domain. As discussed above, a prime example of this is the MAP-DB Noncompliance and Temper Loss, both of which, on their own, appear to be unidimensional with the CBCL Oppositional Defiant Problems. But they are more narrowly-defined, and as such, the CBCL ceases to look unidimensional in the presence of both types of items.

The MAP-DB has other advantages within the disruptive behavior spectrum. Atypicality on the MAP-DB is conceptualized as deviation from expectable patterns within a developmental period and operationalization of age typical expression. This neurodevelopmental framework rests on abundant evidence that psychopathological syndromes reflect unfolding processes that are tied to atypicalities in neural maturation and function, requiring a more developmentally-grounded and neuroscience-informed measurement approach (Casey, Oliveri, & Insel, 2014; Mittal & Wakschlag, 2017). Within this framework, emphasis is placed on differentiating not merely by the presence or absence of a symptom but by the quality of the behavior (e.g., duration, intensity and recovery), the contexts in which it occurs, and the frequency of such occurrences (Stringaris et al., 2012; Wakschlag et al., 2018). Preliminary evidence from the MAP-DB demonstrates the utility of this dimensional spectrum approach for identification, prediction and mechanistic specification (Grabell et al., 2018; Wakschlag et al., 2015).

Limitations

Several limitations should be noted. First, this study sought to link two established scales with existing items. While the MAP-DB has undergone extensive dimensionality testing, we did not carry out such tests on the CBCL, so conventional IRT assumptions may not hold for the CBCL. Most of the extant psychometric analyses of the CBCL have emphasized the syndrome scales as opposed to the DSM-oriented scales as well, thus preventing utilization of previous publications for addressing these IRT assumptions within the CBCL. Improved linking and dimensionality tests may have been possible through selection of a subset of existing MAP-DB and CBCL items rather than using the full scales (though the feasibility and utility of implementing links based off of item subsets is much less).

Second, data were drawn from two distinct data sources, both of which were selected for some degree of disruptive behavior as well, thus the generalization of this linking relationship to a general population sample is limited. As is evident in Figures 2 and 3, the greatest score discrepancies occurred for children with less-severe disruptive behavior; the MAP-DB distinguishes typical disruptive behavior within the ―average‖ range, whereas the CBCL results in a floor effect. Applying these linking relationships to an unselected sample likely will result in frequent floor effects on the CBCL and discrepancies in the score conversions.

Third, neither sample alone was sufficient to develop the links, thus it was not possible to test for subpopulation invariance by data source. Previous measurement testing across diverse populations suggest that bias due to sampling differences should be minimal, and that if anything, having diverse samples improves the robustness and generalizability of a linking relationship, but future research should look at linking accuracy and invariance across data sources and sociodemographic sub-groups.

Finally, the improved IRT results and improved linking in general require access to item-level data, which may not be immediately available to all researchers. While this is not a limitation of the study as conducted, it is a limitation of the potential application of these results. We urge researchers interested in linking scales to use all available data for linking and caution that linking two scales only puts those scales on comparable metrics but does not change the construct or any unwanted measurement properties from the original test.

Future Research Directions

The work presented here advances clinical research by serving a crucial integrative function, bridging a long tradition of research with current understandings of the neurodevelopmental nature of psychopathology. These data provide a valuable opportunity to model linkages between a well-established problem behavior checklist and a novel, developmentally-informed dimensional spectrum approach.

The present findings are but a first look at linkage of dimensional measures like the MAP-DB to established problem behavior checklists. Future efforts are necessary to support this work, including cross-validation of the current results. Further, the utility of the MAP-DB has been most extensively demonstrated at preschool age. More research on the utility of the MAP-DB in early school age is necessary, and linking between the MAP-DB Preschool and the CBCL 1.5–5 years would also yield additional valuable information. Efforts such as that would further expand the utility of the MAP-DB as a common reporting metric for disruptive behavior throughout childhood. Finally, a key next step will be demonstrating the incremental utility of dimensional measures like the MAP-DB in regard to neurodevelopmental processes relative to problem behavior sum counts. We have laid the groundwork for this, and in so doing, have set the stage for leveraging the strengths of diverse measurement towards an enhanced understanding and prevention of developmental psychopathology.