Genetic and Environmental Architecture of Processing Speed Across Midlife

Abstract

Objective:

Processing Speed (PS) is an important domain in cognitive aging that is characterized by multiple related but nonidentical abilities. Few studies have directly investigated the relationships among PS measures, and none have used genetically informed methods. In this study, we examined the relationship between measures of PS at up to two time points during middle age.

Method:

We examined data from 1262 middle-aged men when the sample was at a mean age of 56 and a mean age 62 years. Participants completed six measures of PS from three different cognitive tests. We used a genetically-informative, confirmatory factor analytic approach to evaluate the phenotypic and genetic relationships cross-sectionally at both single time points and across time.

Results:

A higher-order common PS factor accounted for the covariance among three test-specific factors, and each test-specific factor accounted for the covariance between two observed measures. The general PS factor was explained primarily by genetic influences at both time points (a²_age56=.75, a²_age62=.64), and all test-specific factors were heritable (a² range: .45 to .65). Factor loadings from the test-specific factors to the general PS factor varied from λ=.46 to .82. The model was stable over time, though there were differing rates of phenotypic change among latent factors (.20 SD to .44 SD). Cross-time genetic correlations were near unity for all latent factors.

Conclusion:

These results suggest that PS is highly heritable when considered at a latent variable level, and that there are different rates of change in tests of PS within this sample.

Processing speed (PS) has been extensively studied in the cognitive aging literature and a major PS theory posits that cognitive declines during aging are the result of a general slowing of perceptual and cognitive processes which limits how quickly or efficiently one can understand or react to information (Salthouse, 1996; Salthouse, 2000). PS is characterized by multiple related but nonidentical domains (e.g., psychomotor speed and perceptual speed) and many tests of PS exist (Deary, Johnson, & Starr, 2010; Salthouse, 2000; Sheppard & Vernon, 2008). Furthermore, the age-PS relationship differs across measures of PS (Deary et al., 2010; Finkel & Pedersen, 2004; Salthouse, 1994; Verhaeghen & Salthouse, 1997), complicating the assessment of age-related decline. Here we used genetically-informed multivariate analyses to investigate the relationships among six measures of processing speed at two time points in a sample of middle-aged men. Specifically, we evaluated the genetic and environmental influences on PS measures, the stability of latent factors over time, and the level of change in PS at a latent variable level.

A comparison of seven studies found that PS explains an average of 74% of variance in fluid cognition across the adult lifespan (Verhaeghen & Salthouse, 1997). Slower PS is associated with impairment in other cognitive domains as well (Earles & Salthouse, 1995; Finkel & Pedersen, 2000; Finkel, Reynolds, McArdle, & Pedersen, 2005; McDermott & Ebmeier, 2009; Salthouse, 2000; Zimprich & Martin, 2002). Several studies have found that early PS deficits mediate subsequent declines in other cognitive domains such as memory (Brown, Brockmole, Gow, & Deary, 2012; Finkel & Pedersen, 2004; Lemke & Zimprich, 2005).

Babcock et al. (1997) conducted a confirmatory factor analysis of nine PS measures in two age groups (18-24; 55-80), and modeled the relationship among domains of PS. The model included three test-specific factors (motor speed, alphanumeric speed, and geometric speed) with inter-factor correlations ranging from r=.25 to .47. The authors then loaded the test-specific factors onto a higher-order general PS latent factor which accounted for the majority of test-specific factor variance (81% in the younger cohort, 89% in the older). Thus, in this study, these measures were assessing the same construct, but each test carried additional variance and the tests were not highly correlated (Babcock et al., 1997). Differences between test-specific factors may explain why PS tasks vary in their associations with age. For example, in a meta-analysis of 50 cross-sectional studies involving many PS tasks, Verhaeghen & Salthouse (1997) reported an average age-PS correlation of r=−.52, but with substantial variability; values ranged from r= −.23 to −.72. The use of test-specific factors is uncommon when creating a latent factor for PS; studies typically load PS measures directly onto a single latent factor to represent general PS ability (Finkel et al., 2005; Tucker-Drob, Briley, Starr, & Deary, 2014). Further investigation of test-specific factors is warranted, particularly within a longitudinal model that can compare how the factors change with age.

Like phenotypic studies, twin studies suggest that PS measures assess similar, but not identical, constructs. Twin analyses provide a unique perspective on the relationship among PS measures through the estimation of genetic and environmental influences. Heritability is the proportion of total variance between individuals in a given population that is due to genetic factors (Knopik, Neiderhiser, DeFries, & Plomin, 2016). A meta-analysis of 13 quantitative genetic studies and 33 measures of PS found a sample-size-weighted average heritability of .48 (SD=.20), indicating that about half of the variance in PS performance is due to genetic influences (Sheppard & Vernon, 2008). However, it is important to note the wide range of these heritability estimates (.00 to .90). The meta-analysis was unable to determine if the measures truly vary in heritability or if differences in study characteristics (e.g., age) contributed to variation. Further research is needed to explicate how PS measures relate to one another at a genetic level.

Multivariate genetic models estimate genetic correlations that represent the shared genetic influences between measures, providing another perspective on how measures are related. A high genetic correlation suggests that the same set of genes contributes to performance on both measures, and a weak genetic correlation suggests that the measures have distinct genetic underpinnings (Carey, 1988). Improved knowledge of the shared and unique genetic influences across multiple measures of PS will help elucidate the extent to which measures of PS are influenced by the same or different underlying abilities. In a longitudinal design, cross-time genetic correlations between the same factor indicate the stability of genetic influences on that latent factor. A high cross-time genetic correlation indicates that the same set of genes are active at both time points. The calculation of cross-time genetic correlations for PS latent factors will determine if change is primarily due to genetic or environmental influences. To our knowledge, no study has investigated the genetic relationships across multiple PS measures.

In the present study we used a genetically-informative, confirmatory factor analytic approach to evaluate the phenotypic and genetic relationships among six measures of processing speed at the end of midlife, an important period where age-related cognitive changes intensify (Craik & Bialystok, 2006; Finkel et al., 2005). We investigated several hypotheses regarding the relationships across measures: First, we hypothesized that we would need higher-order PS and test-specific latent factors to capture variance among PS measures at each time point. Second, we examined the validity and stability of our model of PS across six years. We expected that the same model would fit the data at both times, but that there may be differences between some model parameters. Finally, we compared the phenotypic, genetic, and environmental estimates across time. For the best-fitting PS factor, we expected that the individual differences would demonstrate strong genetic stability, but also expected some mean-level change.

Methods

Participants

Data were from waves 1 and 2 of the Vietnam Era Twin Study of Aging (VETSA), a longitudinal study of cognitive aging with baseline at midlife (Kremen, Franz, & Lyons, 2013; Kremen et al., 2006). Briefly, all participants were recruited from the Vietnam Era Twin (VET) Registry, a sample of male-male twin pairs who served in the United States military at some time between 1965-1975 (Kremen et al., 2013). Although all are military veterans, roughly 80% of VETSA participants did not experience combat, and the sample is representative of American men in their age group in terms of health and lifestyle characteristics (Kremen et al., 2013; Schoenborn & Heyman, 2009). Zygosity was determined by 25 microsatellite markers for 92% of the sample; zygosity was determined by questionnaire and blood group for the remainder of the sample. This method had 95% agreement with DNA-based results in people with both types of measurements. At both time points, participants received a comprehensive set of psychological, cognitive, and physiological assessments; the complete protocol is described elsewhere (Kremen et al., 2013; Kremen et al., 2006). The study was approved by the Institutional Review Boards of participating institutions.

The current analyses included 1,262 individuals (347 monozygotic (MZ) pairs, 270 dizygotic (DZ) pairs, 28 unpaired) who completed the wave 1 battery (mean age=55.88, SD=2.43), and 1,151 participants (307 MZ pairs, 222 DZ pairs, 93 singletons) who completed the wave 2 battery (mean age=61.70, SD=2.44). There were 990 participants who were evaluated longitudinally, and an average of 5.74 years between assessments (SD=.70).

Measures

There were six PS measures from three tests: the Delis-Kaplan Executive Function System (DKEFS) Trail-Making Test (Delis, Kaplan, & Kramer, 2001); Simple Reaction Time (Nesselroade, 2010); and a Stroop task (Golden & Freshwater, 2002).

We used two conditions of the DKEFS Trail-Making Test: In the Number Sequencing condition participants connect a series of numbers in numerical order. In the Letter Sequencing condition participants connect a series of letters in alphabetical order. The score for each was time in seconds to complete the task.

Simple Reaction Time:

The left hand Reaction Time task requires participants to press the D key on a computer keyboard as soon as a star appears on the left side of the screen. The right hand Reaction Time task requires participants to press the L key on a computer keyboard as soon as a star appears on the right side of the screen. Scores were the average Reaction Time over 10 trials each for the left and for the right hand (Nesselroade, 2010).

Stroop:

We used two conditions from a Stroop task (Golden & Freshwater, 2002). The Word Reading condition asks participants to read the names of three colors with the words printed in black ink; the Color Naming condition requires the naming of three different colored sets of “X”s. For each condition participants name, out loud, as many stimulus items as they can in 45 seconds. The score is the number of correct items. Participants were screened for color-blindness.

Practice Effect Correction

Identical measures were administered at each time point. We adjusted wave 2 scores for practice effects and attrition effects following the method of Rönnlund et al. (2005). As described previously (Elman et al., 2018), practice effects were gauged by comparing returnees with same age participants who took the tests for the first time. Attrition effects were gauged by comparing returnee performance at wave 1 with the entire sample at wave 1. There were practice effects for all PS measures.

Statistical Analysis

For all analyses, wave 1 scores were transformed into z-scores. More positive values indicate slower PS. Wave 2 scores were z-scored on the basis of the wave 1 means and SDs.

In a twin analysis, the total variance of a trait is portioned into three components: additive genetic influences (A), shared/common environmental influences (C) that make members of a twin pair more similar to each other, and unique environmental influences (E) that make twins different from one another. E also contains any measurement error. The resulting model is referred to as an ACE model (Eaves, Last, Young, & Martin, 1978).

Twin analyses rely on a comparison of the cross-twin correlation within MZ pairs to the cross-twin correlation within DZ pairs. In a univariate ACE model, additive genetic influences are assumed to correlate perfectly between MZ pairs because they are genetically identical. DZ pairs are assumed to correlate at .50 because they share, on average, 50% of their segregating alleles. The shared environment is assumed to be correlated at 1.0 between both types of twins (the equal environment assumption). Finally, the method assumes equal means and variances within twin pairs and across zygosity (Neale & Cardon, 1992). The twin modeling assumptions of equality of variance and equality of means were tested for each observed variable through univariate model comparisons.

We evaluated the relationship among PS measures by fitting a series of common pathway models that derived latent factors from the covariance between measures (Kendler, Heath, Martin, & Eaves, 1987). All common pathway models were compared to a Cholesky decomposition which perfectly represents the genetic, environmental, and phenotypic variances (Neale & Cardon, 1992). We then examined a reduced Cholesky in which parameters estimated at zero were dropped from the model. Because the reduced Cholesky did not have a significantly worse fit than the full Cholesky (see results), we used the reduced Cholesky as the comparison model. Model fit for subsequent confirmatory models was determined to be acceptable if the common pathway model did not fit significantly worse than the reduced Cholesky (p > .05) by comparing the −2 log-likelihood (−2LL) values using chi-squared difference tests (Δχ²). Additionally, we compared models via the Akaike information criterion (AIC), which assesses the balance between goodness-of-fit and parsimony (Markon & Krueger, 2004). Lower AIC values indicate a better model fit. All analyses were conducted with the structural equation modeling program, OpenMx, a package in R that allows for missing observations using full-information maximum likelihood (Neale et al., 2016; R Development Core Team, 2014).

We fit a series of multivariate model comparisons at each timepoint separately to evaluate three competing, but not mutually exclusive, hypotheses. First, we fit a single factor common pathway model which hypothesizes that all measures assess the same latent phenotype. Second, we fit a model in which each pair of measures (Trails Number Sequencing and Letter Sequencing; Stroop Word Reading and Color Naming; Reaction Time Left hand and Right hand) load uniquely on one test-specific factor. This model hypothesizes that each pair of measures from each of the three tests represents at least partially distinct aspects of PS. Since this model allows for correlations among the resulting three latent PS factors, it is referred to as a correlated factors model. Third, we fit a multilevel (higher-order) model which hypothesizes that an overall PS domain exists and that there are also test-specific factors that each represent distinct aspect of PS.

Finally, we evaluated the best-fitting model longitudinally, allowing the residual variance of observed variables to correlate across time. To confirm that differences in parameter estimates across time were due to actual change, as opposed to an altered relationship between observed variables and factors, we conducted tests of measurement invariance. Each invariance model constrained parameters across time by setting unstandardized parameters derived from wave 2 equal to like parameters from wave 1. We compared four invariance models that iteratively increase the number of cross-time constraints to test specific hypothesis about measurement stability (Vandenberg & Lance, 2000) Parameter estimates of the longitudinal model were then evaluated for stability of genetic and environmental influences as well as any mean change in factor variance across time.

Results

Descriptive Statistics

Participants within and across twin pairs performed equally well on all phenotypic measures except for Trails Letter Sequencing at wave 1. Setting these means equal within pairs resulted in a significant change in model fit (Δχ² =8.14; p <.01; AIC=986.3) compared with a model where means were allowed to differ. The difference in model fit is likely due to a larger than expected difference between Trails Letter Sequencing means of MZ brothers (.17). Within-pair means were similar for all other measures, and it is possible that this larger than expected difference in means is due to chance. Table 1 presents sample characteristics and test descriptive statistics for each wave.

Table 1:

Sample Characteristics and Measure Means for Wave 1 and Wave 2 participants

	Wave 1	Wave 2	---
N	1262	1151	---
Age	55.9 (2.4)	61.7 (2.4)	---
Education	13.8 (2.1)	13.8 (2.1)	---
	Wave 1	Wave 2	Wave 2 Practice Effect
	Raw Scores (SD)	Raw Scores (SD)	Corrected Z scores (SD)
Trails Number (seconds)	33.57 (12.80)	34.08 (14.53)	.18 (1.0)
Trails Letter (seconds)	33.89 (14.16)	34.93 (15.70)	.24 (1.0)
Stroop Word (items completed)	93.54 (14.33)	88.84 (14.10)	.45 (.98)
Stroop Color (items completed)	69.17 (11.48)	65.66 (11.10)	.49 (.97)
Reaction Time Left (milliseconds)	291.39 (35.85)	303.89 (35.09)	.37 (.90)
Reaction Time Right (milliseconds)	279.73 (31.85)	293.28 (31.86)	.32 (.93)

Top: Means and standard deviations are presented.

Bottom: Means and standard deviations are presented. The wave 1 raw scores and wave 2 raw scores columns report data before it was transformed into Z scores. All wave 2 data include attrition replacement subjects and returnees. The wave 2 practice corrected column reports Z scored data after practice correction. Wave 2 practice corrected Z scores are scaled on the means and standard deviations of wave 1 data and the signs of some measures were reversed so that greater values indicate slower processing speed; therefore, Z scores greater than zero (mean of wave 1) indicate a slowing of processing speed as compared to wave 1.

Cholesky Results

The left side of Table 2 presents the full Cholesky results. Common environmental parameters were estimated at zero for four of the six measures. Therefore, we fixed these four parameters to zero and retained the two non-zero common environmental parameters for the Trails measures in the reduced Cholesky (right side of Table 2). The reduced Cholesky resulted in a minimal change in fit compared to the full Cholesky (Δχ² =0.89; p =1.0; AIC=3931.73). Table 3 shows the comparisons of the common pathway models to this reduced Cholesky decomposition. Heritability estimates of the reduced Cholesky ranged from .21-.63 and were significant for each measure. Unique environmental influences explained 37-71% of measure variance and were all significant.

Table 2:

Standardized variance components for wave 1 processing speed measures

	Full Cholesky			Reduced Cholesky
	a2	c2	e2	a2	c2	e2
Trails Number	.19 (.02, .37)	.10 (.00, .26)	.72 (.63, .82)	.21 (.06, .37)	.08 (.00, .22)	.72 (.63, .80)
Trails Letter	.33 (.11, .49)	.06 (.00, .26)	.61 (.53, .70)	.37 (.18, .47)	.03 (.00, .19)	.60 (.52, .69)
Stroop Word	.63 (.48, .73)	.00 (.00, .12)	.37 (.32, .43)	.63 (.57, .69)	.00	.37 (.31, .43)
Stroop Color	.56 (.38, .67)	.01 (.00, .17)	.41 (.36, .48)	.58 (.51, .64)	.00	.41 (.36, .49)
Reaction Time Left	.31 (.13, .43)	.02 (.00, .18)	.67 (.59, .77)	.33 (.24, .42)	.00	.67 (.58, .76)
Reaction Time Right	.31 (.13, .42)	.01 (.00, .15)	.68 (.59, .79)	.32 (.22, .40)	.00	.68 (.60, .78)

Reported values represent the proportion of measure variance accounted for by the genetic (a²), common environmental (c²), and unique environmental (e²) influences with 95% Confidence Intervals. The a² term is the heritability of that measure.

Table 3:

Wave 1 model comparisons

Model	−2LL	df	AlC	Δχ2	Δ df	p
Full Cholesky	18426	7247	3931.7	---	---	---
Reduced Cholesky	18427	7265	3896.7	0.89	18	1
Single Factor	19199	7290	4619.4	772.8	25	<.001
Correlated Factor	18445	7282	3880.7	18.1	17	0.38
Higher Order	18447	7284	3878.5	19.9	19	0.40

The reduced Cholesky is compared to the full Cholesky. All other models are compared to the reduced Cholesky. −2LL = Negative Log-Likelihood; df = degrees of freedom; AIC = Akaike information criterion; Δχ²= likelihood ratio test (difference in −2LL between the model and its comparison model); Δdf = difference in df between the model and its comparison model. Best fitting model is shown in bold font.

Correlations among PS measures are presented in Table 4. Although phenotypic correlations between measures were all significant, magnitudes were large (based on Cohen’s convention; Cohen, 1992) for measures from the same test (Trails r=.55; Stroop r=.62; Reaction Time r=.61), consistent with at least some test-specific variance. Correlations between measures from different tests were of much smaller magnitude (r range: .10 to .33). All genetic correlations between PS measures were significant with the exception of that between Reaction Time Right and Trails Number Sequencing. Genetic correlations were greatest for measures from the same test (Trails r=.97; Stroop r=.67; Reaction Time r=.88). Genetic correlations between measures from different tests ranged from .22 to .55. Unique environmental correlations for measures from the same test were significant (Trails r =.36; Stroop r = .53; Reaction Time r = .48). Reaction Time tasks were nonsignificantly related to all but one other PS measures. All unique environmental correlations between Stroop and Trails measures were significant.

Table 4:

Correlations among processing speed measures at wave 1

Phenotypic	Trails Number	Trails Letter	Word Reading	Color Naming	Reaction Left
Trails Letter	.55 (.51, .59)
Word Reading	.20 (.14, .26)	.28 (.23, .34)
Color Naming	.25 (.20, .31)	.33 (.27, .38)	.62 (.58, .65)
Reaction Left	.16 (.10, .21)	.19 (.13, .25)	.25 (.19, .30)	.25 (.19, .31)
Reaction Right	.10 (.04, .16)	.13 (.08, .19)	.23 (.17, .28)	.23 (.17, .28)	.61 (.58, .65)
Genetic	Trails Number	Trails Letter	Word Reading	Color Naming	Reaction Left
Trails Letter	.97 (.76, 1.0)
Word Reading	.35 (.16, .68)	.44 (.30, .65)
Color Naming	.55 (.33, .94)	.53 (.39, .77)	.67 (.60, .73)
Reaction Left	.46 (.18, .84)	.55 (.35, .82)	.48 (.34, .63)	.53 (.38, .69)
Reaction Right	.22 NS	.24 (.04, .47)	.37 (.22, .51)	.44 (.28, .59)	.88 (.76, .98)
Unique Environmental	Trails Number	Trails Letter	Word Reading	Color Naming	Reaction Left
Trails Letter	.36 (.28, .43)
Word Reading	.14 (.04, .24)	.16 (.06, .26)
Color Naming	.12 (.02, .21)	.17 (.07, .27)	.53 (.45, .60)
Reaction Left	.05 NS	.00 NS	.05 NS	.03 NS
Reaction Right	.07 NS	.08 NS	.12 (.02, .22)	.07 NS	.48 (.41, .56)

Phenotypic, genetic, and unique environmental correlations were derived from the reduced Cholesky. 95% confidence intervals are presented in the parentheses. NS=nonsignificant.

Wave 1 Model Comparisons

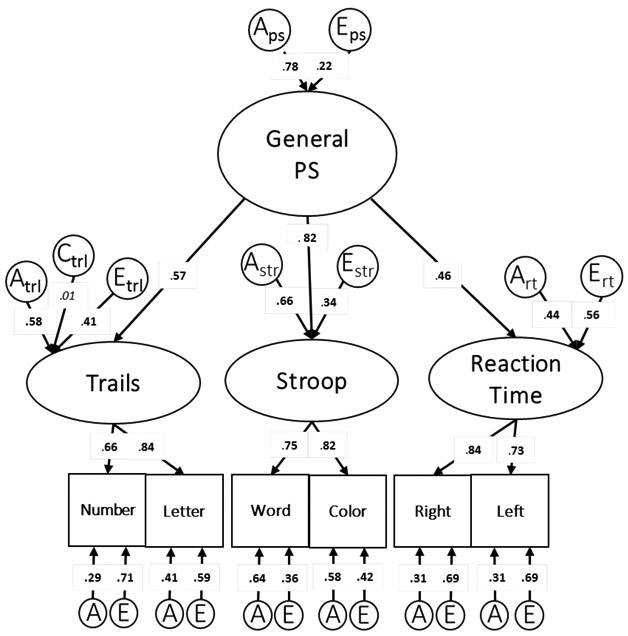
The best fitting model in wave 1 was the higher order model (Figure 1). Model comparison results are presented in Table 3. The general PS factor was highly heritable (A_ps = .78), and unique environmental influences accounted for the remainder of the variance (E_ps=.22). The general PS factor accounted for 32% (95%CI [.22, .44]) of the variance in the Trails factor, 67% (95%CI [.50, .90]) of the variance in the Stroop factor, and 21% (95%CI [.14, .30]) of the variance in the Reaction Time factor.

Figure 1:

Wave 1 Higher Order Factor model. Standardized variance components are presented; “A” indicates the heritability of the related factor, “C” indicates the common environmental influences, and “E’ indicates the unique environmental influences. As explained in the footnote above, the standardized variance components for the test-specific factors can be calculated via the hierarchal common pathways.

Standardized variance components for the wave 1 higher order model are presented in the left half of Table 5¹. Genetic influences on test-specific factors ranged from .44 to .66. Unique environmental influences accounted for the remaining variance (range: .34 to .56). The genetic and environmental variances unique to each test-specific factor were also calculated. There was significant genetic variance unique to the Reaction Time factor (a²=.28), and only nonsignificant remaining genetic variance associated with the Trails factor (a²=.33) or the Stroop factor (a²=.14). There was significant unique environmental variance associated with each test-specific factor: Reaction Time factor (e² =.51 (95%CI [.40, .63]), Trails factor (e² =.40 (95%CI [.23, .46]), Stroop factor (e² =.19 (95%CI [.08, .29]). Factor loadings indicate that test-specific factors accounted for a significant portion of variance in their respective measures (range: 44% to 70%). After accounting for the effect of the general PS factor and the test-specific factors, there were minimal residual genetic influences unique to the individual PS measures (a² range: .00 to .27); there were significant unique residual environmental influences (e² range: .18 to .53).

Table 5:

Standardized variance components of higher order models

	Higher Order Factor Models		Unrestricted Longitudinal Model
Genetic (A)	Wave 1	Wave 2	Wave 1	Wave 2
General PS Factor	.78 (.66, .89)	.64 (.50, .76)	.75 (.64, .85)	.64 (.52, .74)
Trails Factor	.58 (.25, .69)	.57 (.27, .68)	.54 (.28, .70)	.51 (.26, .66)
Stroop Factor	.66 (.58, .73)	.58 (.49, .67)	.65 (.57, .72)	.60 (.51, .68)
Reaction Time Factor	.44 (.33, .55)	.53 (.41, .63)	.49 (.34, .55)	.52 (.41, .62)
Unique Environmental (E)	Wave 1	Wave 2	Wave 1	Wave 2
General PS Factor	.22 (.11, .34)	.36 (.24, .50)	.25 (.14, .36)	.36 (.26, .48)
Trails Factor	.41 (.31, .52)	.43 (.32, .56)	.40 (.30, .50)	.45 (.40, .56)
Stroop Factor	.34 (.27, .42)	.42 (.33, .52)	.35 (.28, .43)	.40 (.32, .49)
Reaction Time Factor	.56 (.45, .67)	.47 (.37, .59)	.55 (.45, .66)	.48 (.38, .59)

Parameters and 95% confidence intervals are presented. As explained in the footnote above, the standardized variance components for the test-specific factors on the wave 1 model can be calculated via the hierarchal common pathways using the estimates in Figure 1. Variance components for the longitudinal model can be calculated via the estimates presented in Figure 2. Variance components for the wave 2 model can be calculated via the estimates presented in supplemental Figure 1

Wave 2 Model Comparisons:

In wave 2, the higher order model also had the best fit and resulted in a nonsignificant change in fit relative to the reduced Cholesky (Δχ² =23.83; p =.20; AIC=3137.56). Model comparisons are presented in the supplement (Table S2). The wave 2 higher order model was identical in structure to that presented for wave 1 data in Figure 1. Standardized variance components of the wave 2 higher order model were very similar to those of the wave 1 higher order model (Table 5).

Longitudinal analysis:

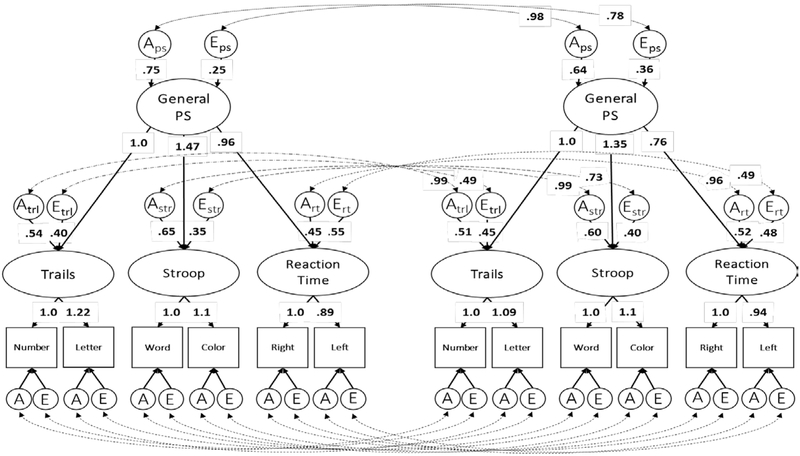
The best-fitting longitudinal model is referred to as the unrestricted longitudinal model and is presented in Figure 2. Table 6 presents the model findings for testing factorial invariance between wave 1 and wave 2. Three of the four invariance model comparisons were nonsignificant, suggesting that the overall model structure (via configural invariance), factor loadings (via weak invariance), and latent variable intercepts (via strong invariance) were comparable across time. Only the most constrained invariance model, which holds factor loadings, latent variable intercepts, and residual variances equal across time resulted in a significant change in model fit (strict invariance: Δχ² =48.80; p <.01; AIC=4971.90).

Figure 2:

Unrestricted longitudinal model. Standardized variance components are presented; “A” indicates the heritability of the related factor, ”C” indicates the common environmental influences, and “E’ indicates the unique environmental influences. As explained in the footnote above, the standardized variance components for the test-specific factors can be calculated via the hierarchal common pathways. Significant estimates are bolded. For readability, the figure does not include standardized variance components for the common environmental influences on the Trails factors (C_trl) or label the residual influences on the observed variables.

Table 6:

Tests of factorial invariance for the longitudinal model

Model	−2LL	df	AIC	Δχ2	df diff	p
Reduced Cholesky	32868	13909	5050.0	---	---	---
Unrestricted longitudinal	32950	14002	4945.8	81.7	93	0.79
Weak Invariance	32956	14011	4936.2	6.5	9	0.69
Strong Invariance	32963	14014	4935.1	6.9	3	0.07
Strict Invariance	33012	14020	4971.9	48.8	6	<.01

Each model is evaluated against the model directly above it via a Δχ2 and AIC comparison. A comparison between the unrestricted longitudinal and the reduced cholesky is a test of configural invariance. Invariance testing supports configural, weak, and strong invariance (p >.05).

Table 5 presents the standardized variance components for the unrestricted longitudinal model. The residual genetic and environmental influences on the individual PS measures were similar to those of the single timepoint model and are provided in the supplement. Factor variances were standardized at the first timepoint, and parameters were measured in standard deviations from the means at wave 1. Larger values at wave 2 indicate slower processing speed. There was a significant slowing of processing speed indicated by change in the general PS factor over time (mean change = .20 SD; 95%CI [.13, .27]). Test-specific factors also showed significant slowing of performance over time, but means did not change equally. The Trails factor changed the least (mean change = .20 SD; 95%CI [.14 .27]), followed by the Reaction Time factor (mean change = .38 SD; 95%CI [.33,.44]), then the Stroop factor (mean change = .44 SD; 95%CI [.38,.51]).

Genetic, environmental, and phenotypic cross-time correlations of the unrestricted longitudinal model are presented in Table 7. Genetic cross-time correlations were near unity for all latent factors. Unique environmental cross-time correlations were weaker than genetic cross-time correlations and varied across test-specific factors (range: .49 to .79). The phenotypic cross-time correlation for the general PS factor was .91, and test-specific cross-time phenotypic correlations ranged .70 to .89; 95% CIs for the Trails and Reaction Time factors did not overlap with the general PS factor, suggesting that these cross-time correlations were significantly smaller than that of the general PS factor.

Table 7:

Phenotypic, genetic and environmental cross-time correlations

	Genetic	Unique environmental	Phenotypic
General PS factor	.98 (.93, 1.0)	.78 (.59, .93)	.91 (.87, .94)
Trails factor	.99 (.86, 1.0)	.49 (.33, .66)	.78 (.72, .83)
Stroop factor	.99 (.95, 1.0)	.73 (.64, .81)	.89 (.86, .91)
Reaction Time factor	.96 (.82, 1.0)	.49 (.31, .59)	.70 (.64, .75)

Correlations are calculated within the longitudinal model. Parameters and 95% confidence intervals are presented.

Discussion

In the present study we used a genetically informative, confirmatory factor analytic approach to evaluate the relationship among six measures of processing speed in a sample of community-dwelling men assessed at middle- and late-middle age. The best fitting common pathway model included a higher order general PS factor that represented the covariance of the three test-specific factors, each of which represented the covariance of two observed PS measures. Over the 6 years between assessments, there was a significant change in the general PS factor and in the test-specific factors. However, the test-specific factors changed at different rates. The general PS factor was highly heritable and accounted for more than half of the common genetic variance across test-specific factors at both time points. Genetic cross-time correlations were near unity for all latent factors, suggesting that the same set of genes operates at each time point. These results support the use of a multilevel model in characterizing the PS domain and highlight the importance of considering test-specific variance.

These results suggest that forming a single composite variable from PS measures provides a relatively incomplete representation of the PS domain. Correlations across tests of PS were small to moderate based on Cohen’s convention (Cohen, 1992) and a single factor model, hypothesizing that these measures all assess the same construct, fit the data poorly. These results are consistent with the Babcock et al. (1997) model in which the common phenotypic variance across PS measures was largely captured in a higher order factor after accounting for test-specific variance. In addition to genetic analyses, we also expanded on the Babcock et al. (1997) results by investigating rates of change across six years. The change in the general PS factor (mean change = .20 SD) and Trials factor (.20 SD) were significantly different from that of the Stroop factor (.44 SD) and the Reaction Time factor (.38 SD). Thus, studies evaluating age-related decline in PS may come to different conclusions depending on which measure is examined. Studies using different PS measures can clearly be assessing somewhat different constructs. In addition, studies may be ignoring important test-specific variance when using only a single composite variable or latent factor. Similar results were found for episodic memory (Kremen et al., 2014; Panizzon et al., 2015), and similar examination of other cognitive domains is warranted.

Our data (Table 2) are consistent with a meta-analysis of PS measure heritability (Sheppard & Vernon, 2008). However, previous twin studies have not evaluated multiple PS measures within the same sample and the meta-analysis is unable to conclude if the variability in measure heritability is due to test differences or sample differences. In the present study we are able to conclude that heritability differences across these six measures are due to test differences. Cross-time genetic correlations for the general PS factor and the test-specific factors were highly stable (rs > .96) and not significantly different from 1.0, indicating that the same set of genetic influences specific to each latent factor is likely to be operating at both time points. Cross-time environmental correlations for the general PS factor (r = .77) and test-specific factors (r range: .44 to .73) were less stable overtime. This pattern of correlations suggests that change between time points for the general PS factor and test-specific factors is likely due to unique environmental factors, whereas genetic factors influence stability.

We found it somewhat surprising that the within-test phenotypic correlations only ranged from .55 to .62. For example, given the similarity between Trails Number Sequencing and Letter Sequencing, we expected a much higher correlation. The same is true for Stroop and Reaction Time. This pattern of findings suggests that unique processes are present for each measure, even those from the same test. For example, although Stroop word reading and color naming are similar in design, the word reading task may require additional verbal skills that make it less correlated with color naming. Manual-motor speed in Trails may be different from verbal-motor speed in the Stroop test, and manual reaction time is different than the manual speed required for Trails. Combining measures within each test yielded test-specific factors with phenotypic cross-time correlations of .70 to .89, which are higher than within-test correlations based on the same timepoint. Therefore, although we noted the limitations of using only a single global PS measure, it is also worth noting that our results do support the value of creating more reliable latent PS variables. The use of a latent variable may better capture a general PS ability that is not influenced by other non-PS factors, e.g., verbal skills.

We acknowledge that there are several limitations in this study. First, the sample is primarily Caucasian and entirely male. Although the sample is representative of the target population in terms of health and social factors, we cannot be certain if the results will be generalizable to women or other racial/ethnic groups. For example, a review of sex differences in PS found that men and women perform differently on tasks of PS; men perform better on reaction time tests than women, while women do better on tests that involve digits and letters than men (Roivainen, 2011). These task-specific differences may affect the relationship between the factors or tests in the present analyses. Second, it is possible that the inclusion of other measures of PS would alter the factor structure. However, similarity with the model of Babcock et al. (1997), which included different PS measures, suggests that the general structure may remain the same.

Concluding statement

In the present study we delineated common and unique variance among PS measures in a middle-aged sample over a six-year interval. The six individual PS measures were surprisingly weakly related at a genetic and phenotypic level. The results suggest that the use of a single measure of PS or the use of a single composite variable or latent factor is likely to miss important information that could lead to different conclusions about PS and how it changes with age. Instead, the results support a higher order general PS factor with additional test-specific factors to best represent PS. Test-specific factors show differential change with age, with change being primarily due to unique environmental influences and stability being primarily accounted for by genetic influences.

Public Significance: Processing speed is an important cognitive ability that declines as people age. Although individual measures of speed were weakly related, a factor capturing their commonality was highly heritable and stable across 6 years. This study is clinically relevant because it suggests that combining measures of processing speed may more accurately represent one’s cognitive ability.