Population pharmacokinetics of treosulfan in paediatric patients undergoing hematopoietic stem cell transplantation

Abstract

Aims

Treosulfan is an alkylating agent increasingly used prior to haematopoietic stem cell transplantation. The aim of this study was to develop a population pharmacokinetic (PK) model of treosulfan in paediatric haematopoietic stem cell transplantation recipients and to explore the effect of potential covariates on treosulfan PK. Also, a limited sampling model (LSM) will be developed to accurately predict treosulfan exposure suitable for a therapeutic drug monitoring setting.

Methods

In this multicentre study, 91 patients, receiving a total dose of 30, 36 or 42 g/m² treosulfan, administered over 3 consecutive days, were enrolled. A population PK model was developed and demographic factors, as well as laboratory parameters, were included as potential covariates. In addition, a LSM was developed using data from 28 patients.

Results

A 2‐compartment model with first order elimination best described the data. Bodyweight with allometric scaling and maturation function were identified as significant predictors of treosulfan clearance. Treosulfan clearance reaches 90% of adult values at 4 postnatal years. A model‐based dosing table is presented to target an exposure of 1650 mg*h/L (population median) for different weight and age groups. Samples taken at 1.5, 4 and 7 hours after start of infusion resulted in the best limited sampling strategy.

Conclusions

This study provides a treosulfan population PK model in children and captures the developmental changes in clearance. A 3‐point LSM allows for accurate and precise estimation of treosulfan exposure.

What is already known about this subject

• Various population pharmacokinetic models of treosulfan have been published, including 3 in paediatric patients. However, these were limited by a small sample size and the extent of exploration of possible covariates to explain interpatient variability.

What this study adds

• We developed a bodyweight‐based allometric model with a maturation function. Treosulfan clearance reaches 90% of adult values at 4 postnatal years. The predictive performance of the current model is superior compared to previously published models.

1. INTRODUCTION

Treosulfan is an alkylating agent with both myeloablative and immunosuppressive properties.1 In the last decade, treosulfan is increasingly being used in conditioning regimens prior to haematopoietic stem cell transplantation (HSCT) in children with both malignant and nonmalignant disorders. It has been shown to be effective and has a relatively mild toxicity profile.2, 3, 4, 5, 6, 7 The most commonly reported toxicities are skin, mucosal, gastrointestinal and hepatic toxicity.4, 6, 7, 8

Treosulfan is an analogue of busulfan, from which it differs for 2 hydroxyl groups leading to a somewhat different mechanism of action.9 Treosulfan is a prodrug and is nonenzymatically, pH‐dependently converted into monoepoxide and diepoxide derivatives ((S,S)‐EDBM and (S,S)‐DEB, respectively).10 These metabolites are thought to be responsible for DNA alkylation, interstrand DNA crosslinking, chromosomal aberration and, finally, induction of apoptosis.11

To date, only a few papers have described the clinical pharmacokinetics (PK) of treosulfan in children, often based on small sample size datasets.12, 13, 14, 15, 16, 17, 18 Three population PK models in children have been published, including 1 by our own group (see Table S1). However, the sample size of 2 of the 3 studies was limited and, besides bodyweight (BW), no significant covariates could be identified to explain interindividual variability in PK.12, 16, 17 Also, the inclusion of infants (children aged <2 years) was limited; a population particularly of interest because variability and total exposure seems especially high in this subgroup.13, 18

To perform PK‐guided dosing and to accurately establish the exposure, intensive blood sampling is required. This may be laborious for both patients and staff employing PK‐guided dosing in daily practice. In a pilot study, we reported that a limited sampling model (LSM) based on PK data from 20 paediatric patients based was capable of accurately predicting the area under the concentration–time curve from zero to infinity (AUC_0–∞), with a model‐based approach, requiring only 2 blood samples.17

The primary aim of the current study is to develop a population PK model of treosulfan in paediatric HSCT recipients with improved predictive performance compared to previously published models using a comprehensive multi‐institutional dataset. The secondary aim is to identify patient‐related factors that may explain PK variability by means of a covariate analysis. Finally, an LSM will be developed to accurately estimate treosulfan systemic exposure suitable for a therapeutic drug monitoring (TDM) setting.

2. METHODS

2.1. Patient population

All paediatric patients who had participated in a prospective, observational, multicentre study and who had received treosulfan as part of conditioning prior to HSCT between June 2011 and March 2017 in the Leiden University Medical Center, The Netherlands, and the Bambino Gesù Children's Hospital in Rome, Italy were included in this population PK analysis. Patients without permanent central venous access were excluded. The Leiden University Medical Center institutional Ethics Committee approved the study protocol (P12.267), which was subsequently approved in the Bambino Gesù Children's Hospital. Written informed consent to participate in the study was obtained from either parents or legal guardian, and patients older than 12 years were asked to give their assent, according to the Helsinki Declaration (last amended in 2013, Fortaleza, Brazil). In line with current dosing recommendations, patients older than 1 year received intravenous treosulfan in a total dose of 42 g/m², administered over 3 consecutive days (14 g/m² per day, 3‐hour infusion). Patients younger than 1 year received a total dose of 30 g/m² or 36 g/m² (10 g/m² or 12 g/m² per day, 3‐hour infusion). Patients who underwent a second transplantation (n = 7) in which treosulfan was also part of the conditioning regimen were included twice in the analysis. Samples were taken at first and second transplantation. Because the time between first and second transplantation was more than several months, these results were considered as distinct individuals.

2.2. Sampling and analysis

For treosulfan PK assessment, blood samples were collected in serum tubes (BD Vacutainer Plus plastic serum tube) on day 1. In patients who gave additional consent, blood samples were also collected on day 3 to determine intrapatient variability. Samples were collected at 1.5, 3.5, 4, 5, 7 and 9 hours after start of infusion (extensive sampling) or at 4 and 7 hours after start of infusion (limited sampling). Samples were centrifuged as soon as possible (i.e. within 5 hours), and serum stored at −20°C. A validated reversed‐phase high‐pressure liquid chromatography using ultraviolet detection was used to determine treosulfan concentration in serum, as previously reported.17 Briefly, treosulfan and the internal standard busulfan were made detectable through derivatization with sodium diethyldithiocarbamate. Linearity was established up to 500 mg/L with a lower limit of quantification of 6.8 mg/L. Accuracy of quality control samples was within the 90–110% limit. The intraday imprecision, expressed as coefficient of variation (CV%), ranged from 2.0 to 3.3% and interday imprecision ranged from 2.1 to 2.8%.

2.3. Pharmacokinetic modelling

Nonlinear mixed effect modelling was used to estimate PK parameters as implemented in the NONMEM software package (version 7.3.0; Icon Development Solutions, Ellicott City, MD, USA), using PsN toolkit 4.7.0 and Piraña version 2.9.7 as modelling environment. Plotting of the results was performed using statistical software package R (v3.4.4) and R studio Version 1.0.456.

2.4. Base model

Initially, a base model was developed without covariates. Plots of observed concentration–time data of treosulfan were examined. One‐, 2‐ and 3‐compartmental PK models with first‐order elimination were compared to find the optimal fit for the concentration–time data. Interindividual variability (IIV) was assumed to follow a log‐normal distribution and was implemented in the model as follows (Equation 1):

$$P_i=P_{\mathit{POP}}\times {\mathit{exp}}^{{\eta }_i}$$ (1)

where P_i is the PK parameter of i^th individual, P_pop is the population mean value of the parameters and η_i is a normally distributed random value with mean zero and variance ω². In 24 patients, interoccasion variability could be evaluated and implemented similarly (Equation 2) with each dose and subsequent sampling defined as a separate occasion.

$$P_i=P_{\mathit{POP}}\times \mathit{exp}\left({}^{{\eta }_{1x1+}{\eta }_{2x2+}\dots \dots {\eta }_{\mathit{ixi}+}}\right)$$ (2)

A proportional error model and a combined proportional and additive error model were examined to describe the residual error. Eventually, a proportional error model was implemented as follows (Equation 3):

$$Y_{\mathit{ij}}=Y_{\mathit{\text{PREDij}}}\times \left(1+{\mathit{\epsilon xp}}_{\mathit{\text{proportional}}}\right)$$ (3)

where Y_ij is the j^th measured concentration in the i^th subject, Y_PREDij is the predicted concentration based on the model and εxp_proportional is the proportional error component.

Four of 410 (1%) serum concentration time points were below the lower limit of quantification. These measurements (actual values) were included in the dataset as proposed by Hecht et al.19

2.5. Covariate analysis

The parameter values were standardised for a BW of 70 kg and allometrically scaled (Equation 4):

$$F_{\mathit{\text{size}}}={\left(\frac{\mathit{BW}}{70\mathit{kg}}\right)}^a$$ (4)

where F_size is the fractional difference in allometrically scaled size compared with a 70 kg individual. When scaling clearance (Cl) and intercompartmental clearance (Q) α is fixed to 0.75 and for volume of distribution of the central (V1) and peripheral compartment (V2) α is fixed to 1.20

Furthermore, a sigmoid E _max model was used to describe the maturation of treosulfan Cl on postmenstrual age (PMA) as follows (Equation 5):

$$F_{\mathit{mat}}=\left(\frac{1}{1+{\left(\frac{\mathit{PMA}}{{\mathit{TM}}_{50}}\right)}^{-\mathit{\text{Hill}}}}\right)$$ (5)

where F_mat is the fraction of adult treosulfan clearance value, TM₅₀ is the PMA at which maturation is 50% of the adult value, and the Hill coefficient is associated with the slope of the developmental profile.21 PMA was estimated by adding a gestational age of 40 weeks to postnatal age.

Total clearance (Cl_tot) could then be described as follows (Equation 6):

$${\mathit{Cl}}_{\mathit{tot}}={\mathit{Cl}}_{\mathit{pop}}\times F_{\mathit{\text{size}}}\times F_{\mathit{mat}}$$ (6)

where Cl_pop is the overall population value of parameter. A similar model was used for Q.

Other potential covariates were chosen based on biological or physiological plausibility and clinical relevance. Assessed covariates included: sex, underlying disease, conditioning regimen, haemoglobin, haematocrit, serum albumin and estimated glomerular filtration rate (eGFR) as a measure of renal function. This was calculated using the revised Schwartz formula (see Data S1) and, to avoid implausibly high eGFR values, was capped at 120 mL/min/1.73 m^2. 22 There were no missing covariate values. All preselected covariate relationships were used for a systematic stepwise covariate modelling, with stepwise forward inclusion and backward deletion.23 In the forward inclusion and backward deletion, the levels of statistical significance were set at P < .05 and P < .01, respectively, corresponding to differences in the NONMEM objective function value (OFV) of 3.84 and 6.64, respectively (1 degree of freedom). A covariate effect was only maintained in the model if the inclusion resulted in reduction of random variability of the PK parameter and improved model fit.

2.6. Final model evaluation

Model selection was based on physiological plausibility, visual inspection of goodness‐of‐fit plots (e.g. observed concentrations vs individual and population‐predicted concentrations) and statistical significance. Throughout the model building process, an adjusted model was chosen over the original model if the drop in the OFV [−2 log likelihood] was >6.63 (P < .01, with 1 degree of freedom, assuming χ² distribution). Shrinkage in interindividual variability and residual error were automatically calculated by NONMEM. Values below 30% were deemed acceptable.24 Evaluation of the precision of the PK parameters was performed with 1000 bootstrap replicates. The stability and performance of the final model were assessed using a prediction‐corrected visual predictive check (VPC), since different dosages were used. Prediction‐corrected VPC was performed with 1000 replicates by simulating concentrations from the final model with the use of the original dataset. The median and the 10th and 90th percentiles of the simulated concentrations at each time point were calculated and plotted together with the median and the 10th and 90th percentiles of the observed concentrations. The distribution of the observed concentrations was visually compared to the simulated distribution. Differences and overlap of the simulated and original distributions indicated the adequacy of the identified model. In addition, the previously published models of Ten Brink et al.,17 Danielak et al.12 and Mohanan et al.16 were compared with the final model to show their ability to describe the current extensive treosulfan PK dataset. The difference in predictive performance was shown by means of comparing the prediction‐corrected VPCs of the different models.

2.7. Simulations to individualize dosing

Based on our final model, individual treosulfan doses were estimated to target an AUC_0–∞ of 1650 mg*h/L, the daily median of treosulfan AUC_0–∞ in patients receiving the most common dose of 14 g/m². Bayesian PK parameter estimates were obtained by posthoc estimation in NONMEM. AUC_0–∞ was then calculated as:

$${\mathit{AUC}}_{0-\infty }=\frac{\mathit{\text{Dose}}*F}{\mathit{Cl}}$$ (7)

where F is equal to 1.

Clinical covariates were based on the 5^th, 50^th and 95^th percentile estimates of weight per age for boys as provided by the CDC standard growth charts for infants and children.25

2.8. LSM

2.8.1. Patients and data collection

Thirty‐five full PK profiles from 28 different patients were used to find the optimal LSM for treosulfan. These full PK profiles consisted of 6 blood samples collected over 9 hours (1.5, 3.5, 4, 5, 7 and 9 hours after start of a 3‐hour infusion).

2.9. PK and statistical analysis

True exposure (AUC_full0–∞) was calculated from all measured concentration–time points using posthoc estimation in NONMEM with the final model ((DOSE *F1)/Cl). LSM‐predicted AUC (AUC_pred0–∞) was calculated by selecting several concentration–time points and combinations of time points. Bias and imprecision were calculated to assess the performance of the different LSMs according to the guidelines proposed by Sheiner and Beal.26 Formulas can be found in Data S1. A Pearson correlation coefficient test was performed to determine the correlation between AUC_full0–∞ and AUC_pred0–∞.

2.10. Nomenclature of targets and ligands

Key protein targets and ligands in this article are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY,27 and are permanently achieved in the Concise Guide to PHARMACOLOGY 2017/2018.

3. RESULTS

3.1. Patients

A total of 91 paediatric patients were included in this study; 58 were male and 33 female. Patient characteristics are summarized in Table 1. Median age was 4.3 years (range 0.1–18.2) and median BW was 15.6 kg (range 3.8–75.0). Seven patients underwent a second transplantation in which treosulfan was also part of the conditioning regimen. The median time between the first and second transplantation was 8.5 months. The dataset consisted of 410 samples. The concentration–time data were reviewed for completeness and consistency of sampling and dosing times. For distribution of samples, see Table S2. Full concentration–time profiles of treosulfan are shown in Figure 1.

Table 1.

Patient characteristics (n = 91)

Characteristic
Age (y)	4.3 (0.1–18.2)
No. of infants (age ≤2 y)	33 (36%)
Bodyweight (kg)	15.6 (3.8–75.0)
BSA (m2)	0.7 (0.3–1.9)
Sex (% male)	63.7
Creatinine (μmol/L)	26 (8–166)
Albumin (g/L)	38 (20–52)
Haematocrit (L/L)	0.291 (0.199–0.384)
Haemoglobin (mmol/L)	6.6 (4.6–10.5)
eGFR (mL/min/1.73 m2)	111 (16–120)
Underlying disease (n)
Haemoglobinopathy	35 (38.5%)
Haematological malignancy	17 (18.7%)
Primary immune deficiency	26 (28.6%)
Bone marrow failure	11 (12.1%)
Other	2 (2.2%)
No. of transplants (n)
1	84 (92.3%)
>1	7 (7.7%)
Donor (n)a
MSD	29 (31.9%)
MUD (≥ 9/10)	41 (45.1%)
MMFD (haplo)	20 (22.0%)
Stem cell source (n)1
BM	56 (61.5%)
PBSC	23 (25.3%)
CB	10 (11.1%)
BM + CB	1 (1.1%)
Conditioning regimen (n)
Treosulfan+ fludarabine+thiotepa	59 (64.8%)
Treosulfan+fludarabine	29 (31.9%)
Treosulfan+other (e.g. melphalan)	3 (3.3%)
Treosulfan dose (n)
10 g/m2	16 (17.6%)
12 g/m2	2 (2.2%)
14 g/m2	73 (80.2%)
Transplant Centre (Leiden/Rome)	63/28
Exposure
Treosulfan AUC0–∞ (mg*h/L)	1658 (643–3371)

Data are presented as median (range) unless stated otherwise.

^a1 patient died before transplantation, but after completing conditioning.

AUC_0–∞: area under the curve from zero to infinity; BM: bone marrow; BSA: body surface area; CB: cord blood; eGFR: estimated glomerular filtration rate; MMFD: mismatched family donor; MSD: matched sibling donor; MUD: matched unrelated donor; PBSC: peripheral blood stem cells.

Figure 1.

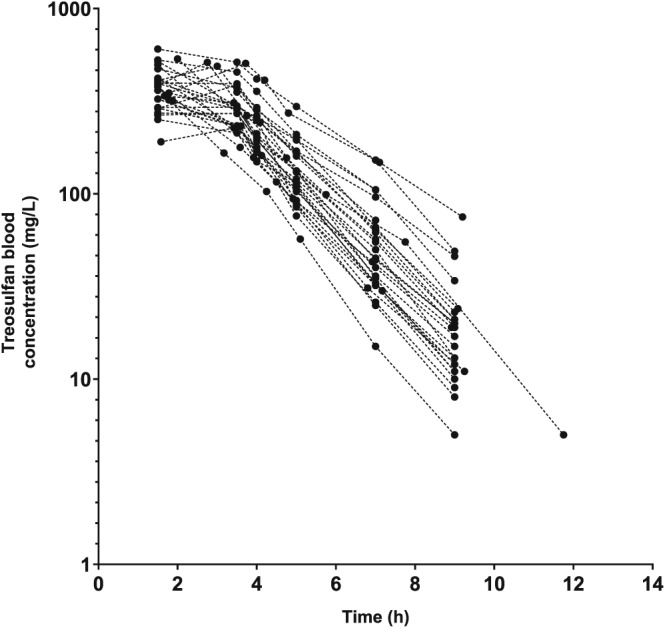
Full concentration–time profiles of treosulfan in 27 paediatric patients undergoing haematopoietic stem cell transplantation, receiving 14 g/m²

3.2. Structural model development

Treosulfan PK was best described by a 2‐compartment model with first‐order elimination from the central compartment. Adding the second compartment showed a significant improvement compared to the 1‐compartment model (ΔOFV = −127.78). The 2‐compartment model was parameterized in terms of volume of distribution of the central (V1) and peripheral (V2) compartment, and clearance from the central compartment (Cl) and intercompartmental clearance between V1 and V2 (Q). The base model showed the following PK parameters: average clearance (Cl) of 5.94 L/h (CV: 79.9%), average central distribution volume (V1) of 0.77 L (CV: 141.4%), average peripheral distribution volume (V2) of 8.73 L (CV: 90.5%) and average Q of 24.6 L/h (CV: 128.5%).

3.3. Covariate model

A BW‐based allometric model was added to all clearance and volume of distribution parameters and significantly improved the model (ΔOFV = −90.22). The addition of maturation of treosulfan Cl based on PMA on Cl and Q improved the model even further (ΔOFV = −39.63). The maturation of treosulfan clearance reaches 50% of adult values at 38 weeks PMA, that is 2 weeks prior to birth assuming a full‐term gestational age of 40 weeks. Clearance reaches 90% of adult values at age approximately 4 years (Figure 2). In the stepwise covariate modelling process, eGFR was found to be a significant covariate on Cl (ΔOFV = −16.72), but the VPC worsened when eGFR was incorporated in the model and interindividual variability of the PK parameters increased. Therefore, we decided not to include eGFR to the model and only incorporate BW and maturation of clearance in the final model.

Figure 2.

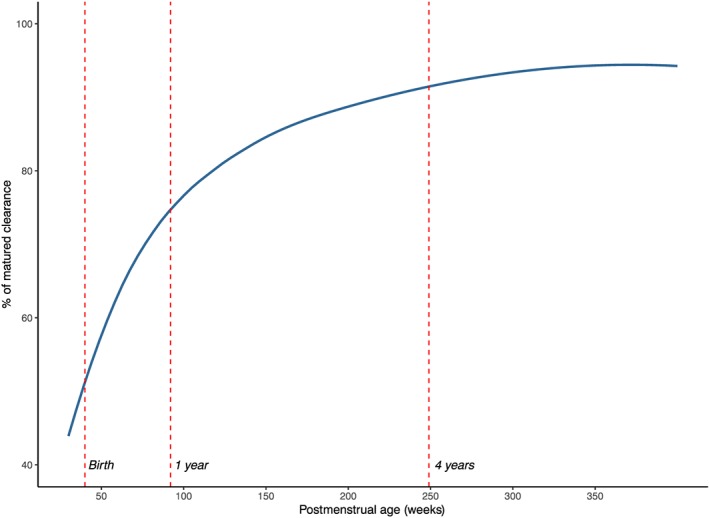
Maturation of treosulfan clearance as percentage of adult values

3.4. Model evaluation

Parameter estimates of the base model, the model with only allometric scaling and the final model are presented in Table 2. Diagnostic plots of the final model are shown in Figure 3. The final model file code is provided in Data S2. The relative standard error (RSE) for the estimated V2 and Q IIV was over 100%, 201% and 153% respectively. Interestingly, this was not seen when parameters were normalized to the median weight (15.6 kg; RSE 53% and 46% for V2 and Q respectively, data not shown). However, evaluation with a bootstrap procedure with 1000 bootstrap replicates showed estimates that are in line with the estimates of the PK parameters and their random variability of the final model. The prediction‐corrected VPC confirmed an acceptable agreement between the observed data and model‐based simulated values (Figure 4A). The median PK parameter estimates and 95% confidence intervals (CIs) from the bootstrap analysis are presented in Table 2.

Table 2.

Summary of model parameter estimates

Parameter	Base model			Model with allometric scaling			Final model			1000 bootstrap runs
	Estimate	RSE (%)	Shr. (%)	Estimate	RSE (%)	Shr. (%)	Estimate	RSE (%)	Shr. (%)	Median value	95% CI
Cl (L/h)	5.94	6		15.9a	5		18.8a	7		19.4a	16.6–26.2
V1 (L/)	0.77	17		18.8a	17		20.2a	18		19.8a	5.1–29.6
Q (L/h)	24.6	26		17.3a	28		21.3a	31		22.0a	9.7–68.9
V2 (L)	8.73	10		16.8a	14		16.8a	16		16.8a	10.9–29.6
Hill							1.2	34		1.1	0.3–3.2
TM50							38	19		43	22.2–74.4
Interindividual variability
Cl (CV%)	79.9	11	1	36.9	11	11	31.8	13	15	31.4	22.8–40.2
V1 (CV%)	141.4	16	4	45.5	42	20	45.9	42	26	48.4	24.9–87.1
V2 (CV%)	90.5	14	2	15.7	208	19	17.3	201	19	20.7	9.1–46.0
Q (CV%)	128.5	22	17	45.5	103	21	41.4	153	24	43.3	15.7–77.4
Interoccasion variability
Cl (CV%)	13.1	21	32	13.3	22	38	13.9	23	27	13.0	9.8–17.1
Residual variability
σ (proportional error)	11.8	7	30	12.4	7	27	12.3	4	27	12.0	9.4–14.6

Cl = clearance; CV = coefficient of variation; Hill = Hill coefficient for maturation, Q = intercompartmental clearance; RSE = relative standard error; Shr. = shrinkage; TM₅₀ = postmenstrual age at 50% maturation; V1 = volume of distribution of central compartment; V2 = volume of distribution of peripheral compartment.

^anormalised to a bodyweight of 70 kg.

Figure 3.

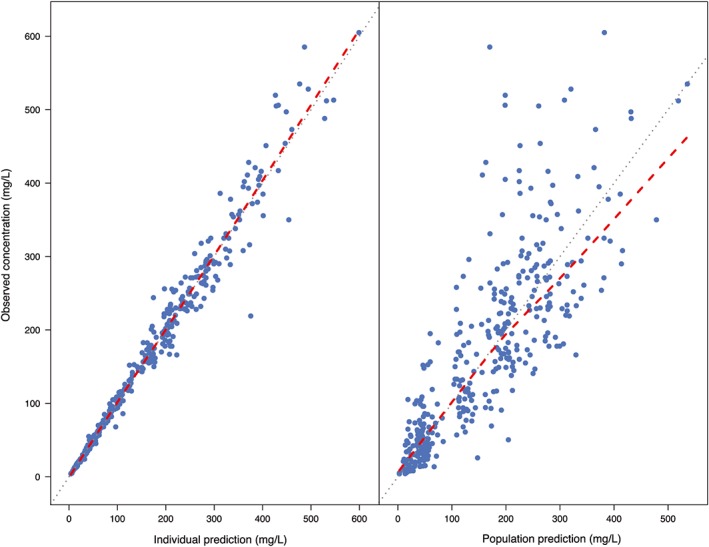
Goodness‐of‐fit plots for the final pharmacokinetic model. Left: individual‐predicted concentrations vs observed concentrations. Right: population‐predicted concentrations vs observed concentrations. Blue dots represent the observations and the red dashed line is a local regression fit of these values. Grey dashed line is the line of unity

Figure 4.

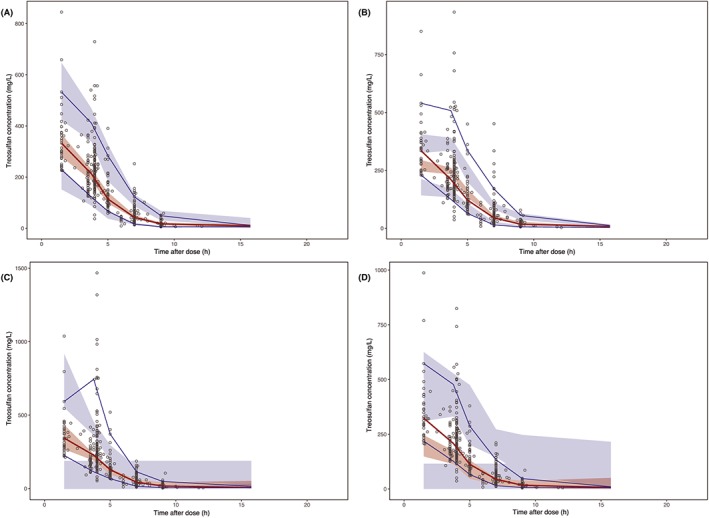
Prediction‐corrected visual predictive check with median, 10^th and 90^th observation percentile. The observed treosulfan serum concentrations are shown as open circles. The red and blue lines represent the observed median and 10^th and 90^th percentile. The shaded areas represent the 95% confidence interval around each of the prediction percentiles. A, Present study, B, Ten Brink et al.17, C, Danielak et al.12, D, Mohanan et al.16

3.5. Comparison with previously published population PK models

Our model accounted for age and size differences over a wide age range in children (1 month–18 years). To evaluate the prediction accuracy in children, we performed prediction‐corrected VPCs with the previously published treosulfan PK models (Figure 4B, C and D) build on paediatric data.12, 16, 17 The prediction‐corrected VPCs show that all 3 models show poor predictions and are not able to properly describe the current dataset.

3.6. Simulations to individualize dosing

The derived population PK parameters from our model were used to calculate the required treosulfan dose to reach an AUC_0–∞ of 1650 mg*h/L (median estimated AUC_0–∞ in our cohort) for a set of virtual patients (normal weight and age range). In Table 3, the treosulfan dose per day required to target an AUC_0–∞ of 1650 mg*h/L can be found for each age category for the 3 different corresponding normal weight percentiles (5^th, 50^th, 95^th). Figure 5 shows that the amount of treosulfan required varies per age, indicated as the area between the dotted lines. The recommended treosulfan dose per kg is lower in early years of life and reaches a maximum at approximately 4 years accounting for maturation of clearance and because dose per kg is higher in younger children based on allometric theory (Figure 5A). Figure 5B shows the absolute treosulfan dose, increasing with age and weight, but with a steeper slope in the beginning accounting for maturation.

Table 3.

Recommended treosulfan dose for different age and weight categories (5^th, 50^th and 95^th percentile)

Age	Weight (kg)	Treosulfan dose (mg) per day
0 mo	2.6	1350
	3.3	1600
	4.2	1950
3 mo	5.2	2650
	6.4	3100
	7.7	3550
6 mo	6.6	3500
	7.9	4000
	9.5	4600
9 mo	7.4	4100
	8.9	4700
	10.6	5300
1 y	8.1	4600
	9.6	5200
	11.5	6000
2 y	10.1	6100
	12.2	7000
	14.7	8000
3 y	12.0	7300
	14.3	8300
	17.3	9600
4 y	13.6	8250
	16.3	9450
	20.3	11 100
5 y	15.2	9100
	18.5	10 500
	23.5	12 700
6 y	16.9	10 000
	20.8	11 700
	27.0	14 250
7 y	18.7	11 000
	23.2	12 800
	30.9	16 000
8 y	20.7	11 900
	25.8	14 000
	35.3	17 700
9 y	22.7	12 800
	28.7	15 250
	40.4	19 700
10 y	24.9	13 800
	32.1	16 700
	46.2	21 900
11 y	27.5	14 900
	36.1	18 300
	52.6	24 200
12 y	30.6	16 200
	40.7	20 000
	59.3	26 600
13 y	34.2	17 600
	45.8	22 000
	66.1	28 900
14 y	38.5	19 300
	51.2	24 000
	72.7	31 100
15 y	43.0	21 000
	56.5	25 800
	78.8	33 100
16 y	47.3	22 600
	61.1	27 400
	84.3	34 900
17 y	50.8	23 900
	64.7	28 700
	88.8	36 300
18 y	53.2	24 800
	67.3	29 500
	92.0	37 400

Figure 5.

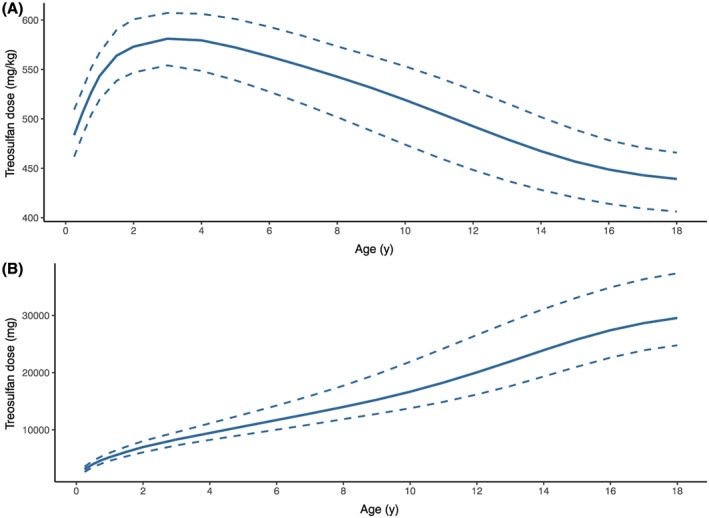
Required treosulfan daily dose in order to obtain a median AUC_0–∞ of 1650 mg*h/L against age A, in mg/kg and B, absolute dose (mg). The solid line represents the 50^th weight percentile for that age, the upper dashed line represents the 5^th weight percentile and the lower dashed line represents the 95^th weight percentile

3.7. LSM

The results of the LSM are shown in Table 4 and Figure 6. Predictive performance measurements used are: correlation, percentages of predicted AUCs within 10, 15 and 20% range of the true AUC_0–∞ and different ways of describing bias (mean prediction error, MPE; mean percentage prediction error, MPPE) and precision (root mean squared prediction error, RSME; mean absolute percentage predictive error, MAPE). Figure 6 shows results of 4 LSMs, including both regression lines with 95% confidence intervals as measurements of predictive performance. The best 2‐point markers were T = 4 and 7 hours (R² = 0.97, MAPE = 5.06%, MPPE = 0.59%), with 97% of AUC_pred0–∞ falling within 15% range of AUC_full0–∞. The best 3‐point marker was T = 1.5, 4 and 7 hours (R² = 0.99, MAPE = 2.84%, MPPE = −0.05%), with 100% of AUC_pred0–∞ falling within 15% and even within 10% range of AUC_full0–∞. With the tested single‐point marker (T = 1.5), prediction performance is far less compared to the 2‐ and 3‐point markers. The percentage of AUC_pred0–∞ that lies within 15% range of AUC_full0–∞ is 69%. Population prediction without sampling has a very poor predictive performance and <35% of AUC_pred0–∞ lies within the 15% range of AUC_full0–∞.

Table 4.

Limited sampling schemes based on 1 or multiple time points

Time points blood sampling	R2 Pearson	Percentage of AUCpred within 10% range of AUCfull	Percentage of AUCpred within 15% range of AUCfull	Percentage of AUCpred within 20% range of AUCfull	MPE (mg*h/L)	MPPE (%)	RMSE (mg*h/L)	MAPE (%)
No sampling (population prediction)	0.01	22.86	31.43	40.00	−52.60	4.23	543.45	23.83
T = 1.5	0.67	54.29	68.57	82.86	−29.17	0.41	291.71	11.65
T = 4/7	0.97	91.43	97.14	100	11.01	0.59	101.79	5.06
T = 1.5/3.5	0.93	77.14	94.29	97.14	−26.76	−0.66	138.88	5.62
T = 5/7/9	0.96	82.86	94.29	100	−6.23	−0.49	112.20	5.86
T = 3.5/4/7	0.96	82.86	97.14	100	−0.81	−0.06	103.74	5.07
T = 1.5/3.5/4	0.97	91.43	97.14	100	−2.86	0.53	100.09	3.92
T = 4/5/7	0.97	91.43	100	100	2.54	0.13	89.83	4.82
T = 1.5/4/5	0.98	97.14	100	100	−9.00	0.01	77.84	3.28
T = 1.5/4/7	0.99	100	100	100	0.61	−0.05	61.62	2.84
T = 1.5/3.5/4/5	0.99	100	100	100	−7.91	0.01	61.93	2.41
T = 1.5/4/5/7/9	0.99	100	100	100	−0.67	−0.07	45.98	1.91
T = 1.5/3.5/4/7/9	1.00	100	100	100	1.43	0.06	18.72	0.82

AUC_pred: predicted area under the curve; AUC_full: full or true area under the curve; MPE: mean prediction error; MPPE: mean percentage prediction error; RMSE: root mean squared prediction error; MAPE: mean absolute percentage predictive error.

Figure 6.

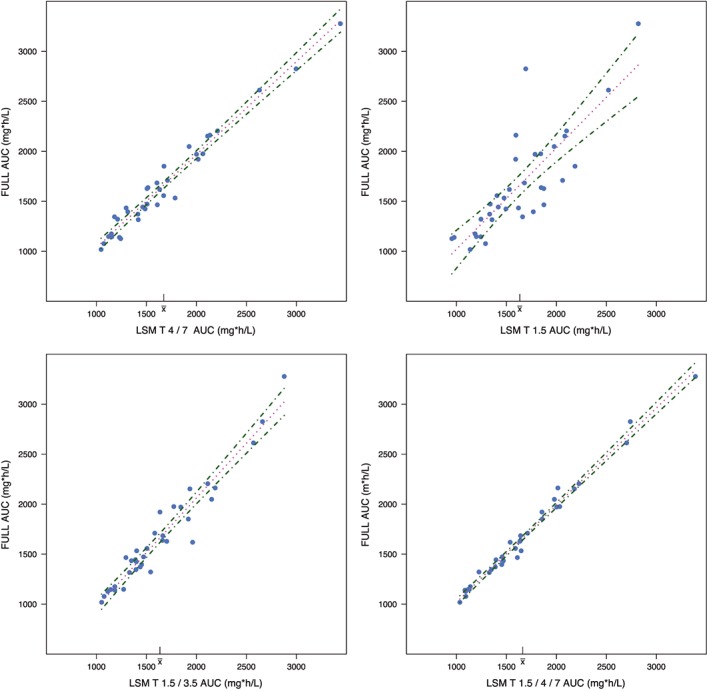
Regression line (dotted lines) plots of different limited sampling methods with 95% confidence intervals (dot–dashed lines). Upper left: Predictive performance of T = 4 and 7 hours as limited sampling model; upper right: predictive performance of T = 1.5 hours as limited sampling model; lower left: predictive performance of T = 1.5 and 3.5 hours as limited sampling model; lower right: predictive performance of T = 1.5, 4 and 7 hours as limited sampling model

4. DISCUSSION

In this study, the population PK of treosulfan in paediatric HSCT recipients was best described by a 2‐compartment model. Allometric scaling of all parameters using BW and the addition of a maturation function using PMA was found to best account for differences in size and age. Other covariates such as sex, underlying disease, conditioning regimen, haematocrit and serum albumin did not significantly influence treosulfan PK. eGFR seems to influence treosulfan PK, because it is known from literature that up to 39% of treosulfan is excreted via the kidneys in unchanged form.28, 29, 30 However, addition of this covariate led to an increased IIV and the prediction‐corrected VPC worsened compared to the model with BW and maturation of clearance only. Therefore, we ultimately chose not to include this covariate in the final model. In our dataset, only a few patients had an eGFR below 60 mL/min/1.73 m² (n = 5). It is likely that this number might be insufficient to establish this potential relationship accurately.

Danielak et al. also studied covariates, but only weight and sex were examined with weight being a significant covariate.12 Mohanan et al. considered more covariates such as age, BW, body surface area, sex, liver size, liver fibrosis and biochemical parameters.16 Interestingly, none of these variables explained the wide IIV in their cohort. Our model was based on a larger PK dataset, accounting for a wide age range in children (1 month–18 years), which allows us to incorporate a maturation component in the model and account for maturation of clearance in the first years of life. Treosulfan clearance reaches 90% of adult values at 4 postnatal years.

The parameter estimations obtained in this study are somewhat comparable to the other published models in terms of clearance, but differ in terms of intercompartmental clearance, and the volume of distribution parameters. However, comparison is rather difficult when the values are not reported in a standardized fashion. Standardizing to a BW of 70 kg increased the RSE of IIV of V2 and Q in our model. However, evaluation with a bootstrap procedure with 1000 bootstrap replicates showed estimates that are in line with the estimates of the PK parameters and their random variability of the final model. Standardizing to the median weight might be more appropriate, because standardizing to a weight outside the observed weight range can increase uncertainty of parameter estimates.31 By contrast, comparison with other models is more difficult when standardizing to the median weight, so in the final model the PK parameters were standardized to 70 kg. As we compared the prediction‐corrected VPCs of the current model vs the models of Ten Brink et al..,17 Danielak et al.12 and Mohanan et al.,16 it is clear that the current model has superior predictive performance both in the high and low concentration range.

The present study shows a model‐based individualized dosing table of treosulfan, aiming for an AUC_0–∞ of 1650 mg*h/L, which was the median exposure of our population. The recommended treosulfan dose is dependent on age and weight. An increase in treosulfan daily dose per kg until the age of 4 years can be seen, reflecting the maturation of clearance and allometry. Recently we showed that there is a relationship between treosulfan exposure and early toxicity.18 Patients with an exposure >1650 mg*h/L have an increased risk of developing grade 2 or higher mucositis and skin toxicity. Our model could be used to establish the initial dose, prior to or during treosulfan administration to facilitate therapeutic drug monitoring and thereby prevent toxicity. Little is known about the relationship between treosulfan exposure and transplant outcome parameters yet; however, the study of Mohanan et al. reported an association between treosulfan clearance <7.97 L/h/m² and poor overall survival (hazard risk 2.7; CI 1.09–6.76, P = .032) and event‐free survival (hazard risk 2.4; CI 0.98–5.73, P = .055) in 87 paediatric patients with thalassemia major undergoing HSCT.16 More studies conducted in different disease settings are needed to establish how systemic exposure to treosulfan can influence patient outcome. Subsequently, the optimal target exposure can then be established.

We also studied a limited sampling strategy, which potentially minimizes the burden of sampling and is convenient for performing TDM in the future. Ten Brink et al. chose 2 time points at 4 and 7 hours after start of infusion, although MPE and MAPE values of the T = 1.5 and 5 hours strategy were slightly better.17 This was done because of practical reasons to avoid sampling during infusion. In the current study, with the addition of new samples, a preference for sampling at T = 1.5 hours besides a sample after infusion was shown. This results in 100% of predicted AUC_0–∞ falling within 15% and even within 10% radius of full AUC_0–∞. We recommend adding a sample at T = 1.5 hours to the 2‐sample strategy of 4 and 7 hours after infusion, not only to increase predictive performance, but also to make to TDM protocol more robust. For instance, if in clinical practice 1 of the samples needs to be discarded due to unforeseen sampling or storage errors, one would still be able to accurately estimate the AUC_0–∞.

Our study has some limitations. Our dataset consisted of rich (full curves) and sparse (2‐point curves) data combined together, which is less useful for noncompartmental analysis. However, the current approach of population PK, using nonlinear mixed effects modelling, allows data from a variety of unbalanced sparse and rich data to be analysed. Moreover, drug levels of concomitantly given drugs (such as fludarabine and thiotepa), which might influence treosulfan PK, were not available. In addition, because treosulfan is a prodrug, the active metabolites could be of interest to incorporate in the population PK model. Danielak et al. found a weak correlation between exposure to treosulfan and the metabolite S,S‐EBDM (r = 0.1681, p < 0.0001). Also, patients with treosulfan exposure above 1650 mg*h/L were most likely to have a high S,S‐EBDM exposure.32 These issues should be addressed in future studies. We have capped the eGFR values at 120 mL/min/1.73 m², which could introduce a bias. However, renal function was not a significant predictor for treosulfan clearance and therefore was not of influence in our analysis.

In conclusion, a 2‐compartment population PK model to describe the serum concentration–time profiles of intravenously administered treosulfan was developed. BW and age (as PMA) have been identified as significant and clinically relevant covariates influencing treosulfan PK. Treosulfan serum concentrations at 1.5, 4 and 7 hours after start of infusion can be used to accurately estimate treosulfan exposure, particularly in a TDM setting.

CONTRIBUTORS

M.Y.E.C.v.d.S., J.Z., A.B., F.L., H.J.G., A.C.L. and D.J.A.R.M. wrote the manuscript, M.Y.E.C.v.d.S., J.Z., H.J.G., A.C.L. and D.J.A.R.M. designed the research, M.Y.E.C.v.d.S., A.B., F.L., A.C.L. and D.J.A.R.M. performed the research and M.Y.E.C.v.d.S. and D.J.A.R.M. analysed the data.

COMPETING INTERESTS

An unrestricted research grant by Medac GmbH was provided to A.L. All other authors declare no conflict of interest.

Supporting information

Table S1 Existing population pharmacokinetic models

Data S1 Supporting information

Table S2 Distribution of collected samples

Data S2 Supporting information

van der Stoep MYEC, Zwaveling J, Bertaina A, et al. Population pharmacokinetics of treosulfan in paediatric patients undergoing hematopoietic stem cell transplantation. Br J Clin Pharmacol. 2019;85:2033–2044. 10.1111/bcp.13995

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.