From individual movement behaviour to landscape-scale invasion dynamics and management: a case study of lionfish metapopulations

Abstract

Modelling the dynamics of small, interconnected populations, or metapopulations, can help pinpoint habitat patches that are critical for population persistence in patchy habitats. For conservation purposes, these patches are typically earmarked for protection, but for invasive species management, these patches could be targeted to hasten the populations' demise. Here, we show how metapopulation modelling, coupled with an understanding of size-dependent dispersal behaviour, can be used to help optimize the distribution of limited resources for culling specific populations of invasive Indo-Pacific lionfish (Pterois volitans) in the western Atlantic. Through simulation using fitted model parameters, we derive three insights that can inform management. First, culling lionfish from target patches reduces the probability of lionfish occupancy at surrounding patches. Second, this effect depends on patch size and connectivity, but is strongest at the local scale and decays with distance. Finally, size-dependent dispersal in lionfish means that size-selective culling can change both a population's size distribution and dispersal potential, with cascading effects on network connectivity, population dynamics and management outcomes. By explicitly considering seascape structure and movement behaviour when allocating effort to the management of invasive species, managers can optimize resource use to improve management outcomes.

This article is part of the theme issue ‘Linking behaviour to dynamics of populations and communities: application of novel approaches in behavioural ecology to conservation’.

1. Introduction

The relationships among landscape patterns, animal movement behaviour and emergent connectivity can yield important insights into the forces structuring populations and communities [1,2]. As ongoing human developments repeatedly redraw the layout of natural landscapes, the ability of animals to move among fragmented patches has become one of the most important factors determining how animals will respond to accelerating global change [3,4]. Perhaps most importantly, a more cohesive understanding of these spatial relationships is a necessary prerequisite for strategic spatial planning to restore degraded natural landscapes, promote the persistence of threatened species and restrict the spread of invasive species in a rapidly changing world [5,6].

An increasing number of studies consider how the dynamics of new invasions are affected by spatial landscape patterns, which can alternatively help or hinder invasive spread by influencing dispersal behaviour, adaptive potential, species interactions and resource availability [7–10]. However, relatively little consideration has been given to how similar spatial processes can influence the management of well-established invaders, particularly in the marine environment, which can limit the success of spatially uniform regional management plans [11,12].

One promising approach for exploring the spatial aspects of invasive species management is through a metapopulation framework. Metapopulations are defined as a collection of spatially restricted local populations connected by some degree of migration (i.e. a patch network) [13], and their dynamics can be described by mathematically rigorous models using biological and landscape data from real metapopulations [14]. Metapopulation models are most commonly used in conservation planning to help identify habitat patches critical for the persistence of threatened populations, earmark these critical areas for protection and study the effects of habitat loss at the network level [15]. However, populations of invasive species inhabiting and moving across fragmented habitat often fulfil the criteria of a metapopulation [16–19], and are in fact more often likely to satisfy the metapopulation modelling assumptions of dynamic population equilibrium and low detection error than are populations of threatened species that are rare and in decline [20]. It follows that the traditional metapopulation approach could be used ‘in reverse’ to identify habitat patches important to invaders, prioritize those patches for management and study how localized management efforts might influence broader invasive population dynamics across the network of patches [17,21].

Among the existing metapopulation modelling approaches (e.g. [22–24]), the incidence function model (IFM) might be the most useful to examine invasive populations. The IFM is relatively simple to parametrize using field data on adult dispersal, patch occupancy, patch size and location, which are relatively straightforward to collect in many systems [20,25,26]. The resulting parameter estimates can be used to characterize the existing metapopulation and for simulation modelling to determine how different management scenarios might influence metapopulation dynamics at the network scale [14,20,27,28]. The IFM has been widely used to answer such questions for a diverse set of threatened species including mammals [25,29], birds [30], amphibians [31], invertebrates [32] and plants [33,34]. A similar approach has been proposed [17], but not to our knowledge applied, to invasive species.

One shortcoming of the IFM is that it does not explicitly consider differences in dispersal behaviour between individuals. Yet, individual behaviour can have large implications for population dynamics [35]. Some metapopulation modelling approaches do consider individual behaviour (e.g. [36]); they generally adopt an individual-based model (IBM) approach, which can be more difficult to parametrize and interpret. Instead of the more complicated IBM approach, we used a size-structured modification to the IFM approach. This method was adopted because size is an important factor that influences individual differences in dispersal, size data are relatively easy to collect for most organisms compared to other potentially important factors like sex [37], and this approach is relatively easy to parametrize with field data.

In an invasion management context, the IFM can be used to study the effects of removal programmes at specific patches or to explore the influence of size-selective removal strategies on population dynamics [38]. Although the quantitative predictions of such a simple model should be treated with caution, the IFM is well suited for making qualitative comparisons between alternative management scenarios that are easier to interpret and test than the predictions of more complex models [20]. This approach represents a useful tool for the spatial optimization of invasion management resources when the spatial processes underpinning invasion dynamics are still poorly understood.

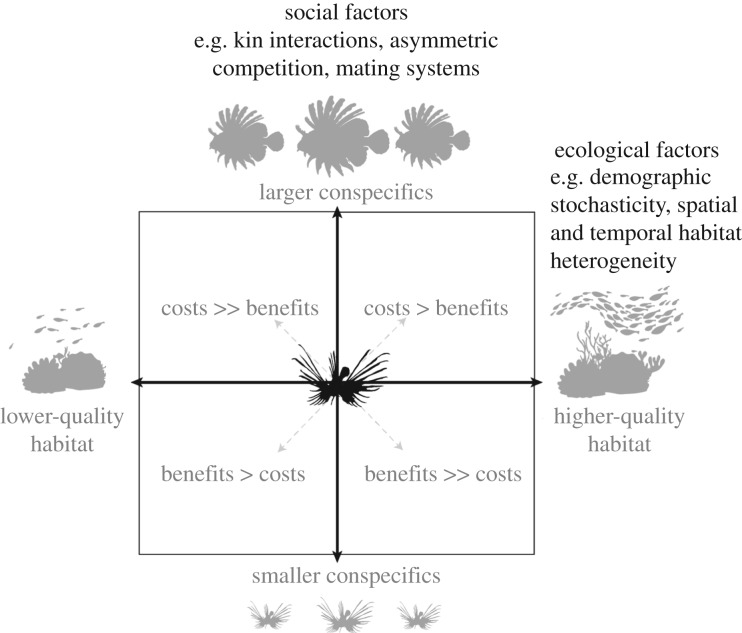
The invasion of the western Atlantic by Indo-Pacific lionfish (Pterois volitans and Pterois miles) is a prime example of a system where management planning could benefit from a better understanding of spatial population dynamics. This unprecedented invasion by a mobile marine predator has had negative consequences on many coral reefs, with potential economic repercussions for the communities that rely on them [39]. Although eradication is unlikely, there is a clear need for management to mitigate these impacts. Regional-scale connectivity of lionfish populations is realized through larval dispersal, which is difficult to measure and impossible to manage. Instead, lionfish populations are currently managed primarily through periodic, labour-intensive culling or competitive harvesting derbies at local scales, which target mainly juvenile and adult lionfish. However, the distribution of culling efforts is still haphazard in space and time, with little systematic understanding of how patches should be prioritized or of how culling at the patch scale affects population dynamics at the landscape scale ([40,41]; but see [42]). Current regional guidance for lionfish management suggests at least two removal strategies based on population dynamics: (i) prioritizing removal at sites of high lionfish colonization to reduce the intensity of predation experienced by native fish at that site, or (ii) prioritizing removal at sites of low lionfish colonization that are more likely to remain clear for longer periods of time and might require less frequent culling [43]. However, these strategies provide no guidance on how such sites should be selected across a landscape. Moreover, current guidance does not take into account the internal (i.e. body size, body condition) and external (i.e. social and environmental) factors that influence individual movement, which collectively drive overall spatial population dynamics [44–46] (figure 1). Past work has shown that lionfish movement behaviour in patchy landscapes varies among individuals and is strongly influenced by conspecific density and body size ([47]; figure 2). Culling that is intentionally or unintentionally size-selective can drive changes in overall population size structure, which can fundamentally alter movement patterns, network connectivity and population dynamics. In the absence of empirical studies, metapopulation models can provide a useful first approximation of these spatial processes to help inform management.

Figure 1.

Individual dispersal decisions are influenced by multiple drivers, including both social factors and ecological factors. These drivers are context- and condition-dependent; thus, different individuals placed at the centre of this figure may experience different costs and benefits of dispersal, depending on whether surrounding patches have larger or smaller conspecifics and higher or lower habitat quality, which give rise to variation in movement behaviour. Adapted from [44].

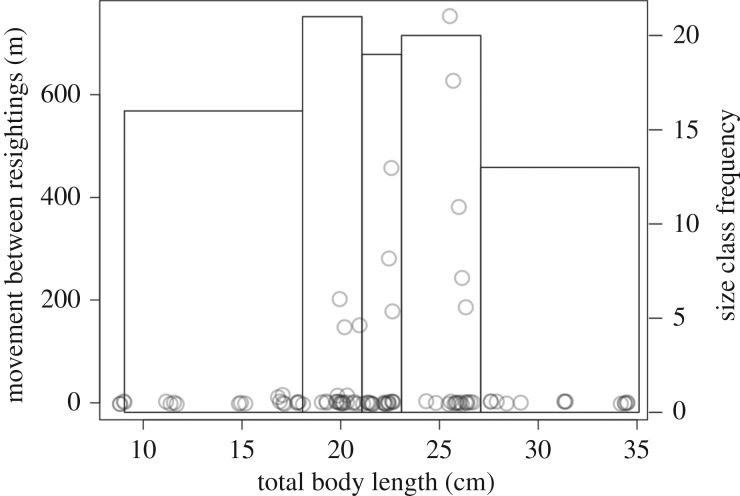
Figure 2.

Frequency distribution of individual movement events (dots, jittered to improve visibility) observed across lionfish body sizes in patch reef habitat in Eleuthera, The Bahamas, showing a trend towards greater maximum movements between resightings at intermediate body sizes. The superimposed histogram (grey lines) represents the frequency distribution of fish sizes across all trips divided into five quintiles, and corresponding to size classes used in the size-selective culling scenarios. Size classes are uneven because size class quintiles were defined based on size class bins containing equal numbers of individual movement events, and there was a greater concentration of movement events for some size classes than others.

In this study, we demonstrate the usefulness of metapopulation modelling using the IFM as a conceptual tool for exploring how spatial and behavioural processes can influence management outcomes for invasive lionfish on Caribbean coral reefs. Lionfish provide a particularly convenient model system for applying the IFM as many lionfish populations satisfy the model's assumptions that (i) they fit the criteria of a metapopulation, (ii) the metapopulation is in colonization–extinction equilibrium, and (iii) species detection error is low [20]. Roughly one-third of invasive lionfish are estimated to occupy patch reef habitat [48], and these patchy populations are expected to meet the criteria of a metapopulation. Patch reefs are generally small with well-defined boundaries and surrounded by large expanses of unsuitable sandy matrix [49]. Tracking studies have shown that lionfish inhabiting patches are largely sedentary but undertake occasional inter-patch movements, and that dispersal is size-dependent [47]. Extinction–colonization equilibrium is also a reasonable assumption for well-established and minimally managed populations, in contrast with growing populations of recent invaders or declining populations of threatened species [50]. Finally, lionfish are diurnally active and relatively conspicuous on unmanaged reefs [51], and are easily detected in targeted searches [52], minimizing detection error which often complicates metapopulation models of threatened species that are rare or difficult to detect [26]. In addition, the focus on presence–absence data in the IFM is justified by studies showing that the ecological impacts of lionfish are significant at low population densities of the invader and can be substantial for even a single lionfish [53].

We fit the IFM using data on the number and movement of adult lionfish over multiple surveys across a network of 34 unmanaged reef patches in The Bahamas, where this invader is well established. Parameter estimates from the fitted model were then used to carry out simulations in real and hypothetical patch networks to answer three key questions about the influence of spatial processes on management: (i) can metapopulation modelling be used to identify priority patches for invasive species management?, (ii) how effective are removals at a high-colonization patch relative to a low-colonization patch for overall population control?, and (iii) how might size-selective control strategies applied across the broader population (e.g. derbies, food fisheries) affect underlying population dynamics and influence management outcomes for targeted removals?

Our results demonstrate how a metapopulation modelling approach can be used to provide a novel perspective on the relationship between dispersal behaviour, emergent population dynamics and invasive control measures that could contribute to better management outcomes.

2. Material and methods

(a). Field data collection

This study used field data on the presence, absence, number and movement of externally tagged lionfish across a network of 34 unmanaged, natural coral reef patches in Eleuthera, The Bahamas, collected as part of a previous lionfish movement study (see [47]). Reef patches were distributed over a 2 km² area in Rock Sound (76°49.000 W, 22°22.500 N), east of Cape Eleuthera, within a matrix of sand with occasional seagrass and sparse gorgonians and sponges. This patch network was bounded by large expanses of unsuitable sandy habitat on three sides and only a few isolated patches on the fourth side, such that the study network can be considered semi-independent [54]. Patches were at an average depth of 3 m, and ranged in area from approximately 17 to 570 m² (mean ± s.d.: 128 ± 110 m²) with inter-patch distances varying between 57 and 2322 m (830 ± 443 m). Surveys were carried out on all patches in the network approximately every 3–4 days for seven weeks (n = 8 surveys) and recorded the presence and total length (TL, cm) of all tagged and untagged juvenile and adult lionfish detected through detailed lionfish-specific searches, as well as patch rugosity and relief [52]. We omitted recruits during occupancy surveys because (i) colonization by recruits is expected to be negligible over short time-frames (e.g. in another study, only 14 recruits were seen over three months in a network of 52 experimental patch reefs with 0–12 adults per reef, [55]), (ii) recruits are expected to contribute little to ecosystem impacts owing to their small size and consumption rates [56], and (iii) management actions target adults [43,51]. This is consistent with the original formulation of the IFM, which was parametrized with data on adult butterflies without considering the distributions of eggs or larvae [20].

(b). Parametrizing the incidence function model

Our field data provided the necessary input parameters for the IFM: a species-specific dispersal parameter (α, defined as 1/mean dispersal distance of the population), occupancy of each patch i (p_i, 0 if empty, 1 if occupied), patch location (x and y coordinates) and patch area (A_i). Because extinction risk is typically a function of population size, and population size is generally related to patch area, the IFM assumes that extinction probability is a function of A_i. However, this relationship may not hold when patch quality is variable. In this patch network, the number of lionfish was not strongly related to patch area, suggesting that lionfish population size varies with some unmeasured aspect of habitat quality. To account for variation in habitat quality, we calculated ‘effective area’ A_Ei as: A_Ei = Q_iA_i/Q*, where Q_i is the mean number of lionfish observed on a patch across all surveys, and Q* is the maximum observed number of lionfish on any patch in the network [20,57]. Effective area was linearly related to the mean patch occupancy across surveys (electronic supplementary material, figure S1), and thus to ‘extinction’, thus satisfying the original model assumption. Where more information on patch quality is available, Q_i could be replaced by another variable. Patch locations and effective areas were in turn used to calculate pairwise distances between patches i and j (d_ij) and the connectivity of each patch i (S_i), defined as [20]

$$S_i=\sum _{i\ne j}{p}_j{\mathrm{e}}^{(-\alpha d_{ij})A_{Ej}}.$$

We used these data to fit the IFM in R, v. 3.4.2 [58], using a special case of generalized linear models with binomial error and logistic link function to model the log-odds of incidence at each patch, as reviewed in detail elsewhere [20,25,59]. The full model was specified as

$$\log \left(\frac{J_i}{1-J_i}\right)=-\log (ey)+2\log (S_i)+x\hspace{0.17em}\log (A_{Ei}).$$

For the purposes of fitting, the model is expressed in the equivalent logit form

$$\mathrm{logit}(J_i)=\hspace{0.17em}{\beta }_0+2\log S_i+\hspace{0.17em}{\beta }_1\ast \log A_{Ei}.$$

Here, J_i represents the equilibrium fraction of time that patch i will be occupied, henceforth referred to as the ‘incidence’; e describes the dependence of extinction risk on patch size and can be interpreted as the probability of extinction on a patch of one unit area (here 1 m²) over one unit time (i.e. the time step between surveys, here approx. 3–4 days); y describes species colonization ability, where smaller y are associated with greater colonization ability that is more independent of patch isolation [20,60]; S_i is the connectivity of patch i; and A_Ei is the effective area of patch i. Fitting these models to known occupancy data p_i instead of the unknown J_i yields β₀, corresponding to the estimated intercept $-\log \hspace{0.17em}(\widehat{ey})$, and β_1, corresponding to the estimated slope $\hat{x}$, which describes how strongly the relationship between patch area and extinction risk is influenced by environmental stochasticity. When x < 1, environmental stochasticity has a great influence, such that even large patches are at risk of extinction. We fit the model over two consecutive surveys to obtain more accurate parameter estimates. In this case, the response variable becomes the proportional occupancy, defined as the number of times a patch is occupied divided by the number of surveys, and the connectivity of each patch is also weighted by its proportional occupancy [59].

The combined parameter estimate $\widehat{ey}$ can be separated into $\hat{e}$ and $\hat{y}$ by solving an iterative fitting function using data on the number of occupancy transitions (i.e. new colonizations or extinctions) from the same two consecutive surveys [20,59]. The final fitted model yields J_i across the original patch network, and the individual parameter estimates can be used to define extinction and colonization functions when simulating metapopulation dynamics in any real or hypothetical patch network. It should be noted that the model becomes unreliable when the mean dispersal distance exceeds the typical inter-patch distance, beyond which the metapopulation would coalesce into a single, fully mixing population that is no longer dispersal-limited. Prior to simulation, the fitted model was validated using procedures outlined in the electronic supplementary material.

(c). Exploring the metapopulation effects of single-patch management

We evaluated the impacts of managing single patches on the overall metapopulation by simulating population dynamics across the patch network before and after management actions at each patch.

To carry out metapopulation simulations, we first specified patch areas and pairwise distances, the known dispersal parameter α, the estimated IFM parameters x, e and y, and the initial configuration of occupancy values p_i across all patches. In simulations, the extinction rate remained fixed at $E_i=\hspace{0.17em}e/A_i^x$, but the connectivity $S_i={\mathrm{\Sigma }}_{i\ne j}\hspace{0.17em}{p}_{\hspace{0.17em}j(t)}{\mathrm{e}}^{(-\alpha d_{ij})A_{Ej}}$ and colonization rate $C_i=\hspace{0.17em}{S}_i^2/(S_i^2+y)$ were allowed to vary stochastically such that, in each time step t, an empty patch was colonized with probability C_i(t) and an occupied patch went extinct with probability E_i(1 − C_i(t)) [20,59]. This procedure yields a matrix of occupancies across all patches, where occupancies vary from one time step to the next. For each time step, we recorded the instantaneous number of occupied patches in the network. The mean proportion of occupied patches across all time steps yields the estimated equilibrium proportion of occupied patches (approx. equivalent to p*), and the mean of occupancies at one patch i across all time steps yields the estimated equilibrium incidence J_i (approx. equivalent to $p_i^{\ast }$) at that patch [59]. To compensate for extreme values of J_i that may arise by chance in some iterations, a more robust estimate was obtained as the mean of simulated J_i for each patch across all iterations [20].

Using this approach, we carried out 34 simulations in each of which a single, different patch (the ‘target’ patch) was removed from the network of 34 patches, and we simulated metapopulation dynamics in the modified networks over 100 iterations of 100 time steps to yield new equilibrium J_i across all other patches [61]. For lionfish, 100 time steps correspond to approximately 1 year, and culled lionfish populations have been shown to return to pre-culling levels much faster than this [62,63]. The resulting change in lionfish incidence at each patch i was defined as ΔJ_i = J_{i removal} − J_{i original}, where J_{i removal} is the incidence after removal and J_{i original} is the incidence of patch i before lionfish removal. Across the entire patch network, the reduction in incidence following the removal of a target patch was characterized in two ways: the mean ΔJ_i across patches and the cumulative ΔJ_i across all patches. The cumulative ΔJ_i was calculated as the area under the curve (AUC) of the plot of ΔJ_i as a function of distance from the target patch, where the AUC was determined using the trapz function in the pracma package in R [64]. This measure of change in incidence captures the overall cumulative magnitude of change across the network in the visually intuitive form of a polygon. AUC is negative, as it is measuring cumulative reductions in incidence, so that larger negative values of AUC correspond to a greater reduction in overall incidence across all network patches. The shape of the AUC polygon also illustrates how quickly network change drops off with distance from the target patch, and wider shapes suggest a broader halo effect while narrower shapes indicate more localized effects.

(d). Understanding population-level effects of size-selective harvesting

Because body size is known to influence dispersal in many species, including lionfish [47], removal of specific size classes may change the connectivity of the network. We evaluated the effects of changing body size distributions on network connectivity and broader population dynamics by fitting and simulating the IFM over a range of dispersal parameters (α), reflecting different population size distributions, which can arise from size-selective culling, and corresponding mean dispersal distances.

First, we investigated how changing the population size distribution influenced connectivity and incidence across the network prior to individual patch management. To do so, we first subset the distribution of all individual dispersal events between resightings of tagged fish into quintiles based on total body length to obtain five size classes (figure 2). We next removed one or more size class quintiles from our dispersal dataset and calculated a new α using the remaining dispersal data to reflect a range of size-selective management scenarios. We tested the removal (e.g. selective culling) of (i) size class quintile 5 (the largest fish, which may be the easiest to target), (ii) quintile 4 (moderately sized fish, which represent the most dispersive sizes; [47]), and (iii) both quintiles 4 and 5. We then re-fit the IFM using these new α values to obtain fitted model parameters and incidences for each selective culling scenario.

Next, we evaluated how the new connectivity profile under each selective culling scenario influenced the network-level benefits of managing target patches. More specifically, we compared the effects on mean and cumulative incidence of the complete removal of lionfish from a single, well-connected patch (patch 15 in figure 3a) under two network-culling contexts: when all size classes of lionfish are targeted (i.e. the original analysis) and when the largest size classes are broadly targeted across the network (i.e. the three size-selective culling scenarios described above).

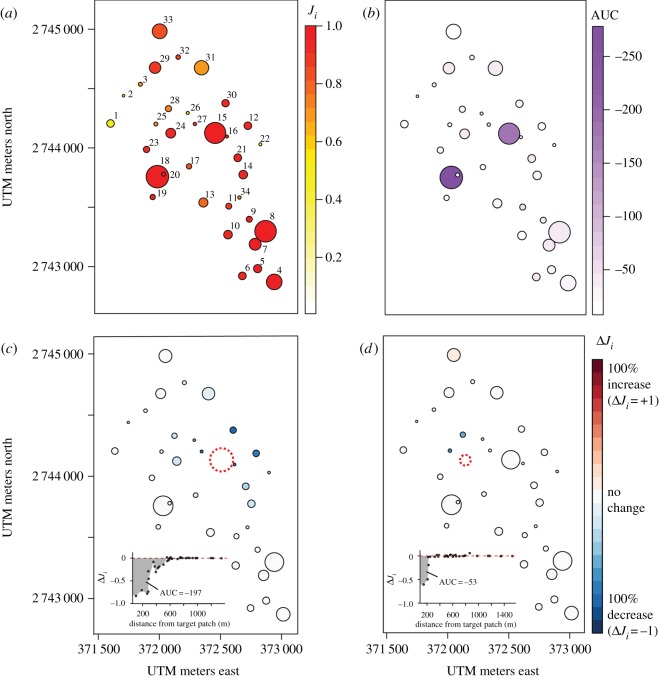
Figure 3.

(a) Fitted patch-specific lionfish incidences J_i (i.e. the fraction of time a reef patch was occupied by lionfish) plotted across a map of the study patch reef network, where warmer colours indicate higher incidence than cooler colours. (b) Relative network-wide benefits, in terms of reduced lionfish incidence, gained from the removal of lionfish from each individual patch, as measured by the AUC of ΔJ_i over distance from the target patch. As examples, change in the mean patch-specific incidences following removal of lionfish from (c) patch 15, a large well-connected patch, and (d) from patch 24, a small, less well-connected patch. Patches (circles) are numbered for easy reference in the text. Circle sizes are proportional to patch size, but are not drawn to scale, and patches that appear to overlap on these plots do not in reality. x and y axes represent Universal Transverse Mercator (UTM) coordinates (in m).

3. Results

(a). Fitting the incidence function model for lionfish on patch reefs

Our network contained 34 reef patches (figure 3a). Across the eight surveys, the mean proportion (±s.e.) of occupied patches was 0.68 (±0.05), and the overall population size in this network ranged from 49 to 75 lionfish, with a mean population density on patches (±s.e., range) of 0.022 lionfish m⁻² (±0.003, 0.003–0.073).

We parametrized the IFM using patch locations, occupancies across the two consecutive surveys with the greatest number of occupancy transitions (n = 16 between surveys 5 and 6), effective area scaled to the number of lionfish per patch, and α = 1/39, where the average distance moved between resightings of tagged lionfish (±s.e.) was 39 m (±13, range 0–753 m), when including zeros, in Tamburello and Côté [47].

Fitting the IFM using these inputs yielded parameter estimates (±1 s.e.) for $\hat{x}=2.91\pm 0.43$ and $\widehat{ey}=-4.45\pm 1.24$. Using data on the number of occupancy transitions from two consecutive surveys to disaggregate $\widehat{ey}$ yielded the estimates $\hat{e}=327.30$ and $\hat{y}=0.26$ (table 1); however, there is no way to directly determine the margin of error on these separate estimates. Fitted and simulated incidences in the original patch network were comparable (paired t-test, t₃₃ = 0.51, p = 0.61; generalized linear model: b ± s.e. = 0.65 ± 0.09, p < 0.0001, R² = 0.57; electronic supplementary material, figure S2), validating the use of obtained parameter estimates for further simulation modelling.

Table 1.

Body size, dispersal distance and IFM parameters corresponding to different size classes of a lionfish population inhabiting the study reef patches. (The size classes correspond to the quintiles shown in figure 2. The last three rows provide demographic information and fitted parameters for three hypothetical populations with one or more size classes of lionfish removed (indicated by a minus sign) in selective culling scenarios, where x describes the dependence of extinction risk on patch size, e describes the influence of environmental stochasticity on population dynamics and y describes species colonization ability.)

size class	proportion of population (n = 37)	mean total length (cm) (range)	mean dispersal distance (m)	x	e	y
all	1.00	22.76 (9–35)	39.45	2.91	327.30	0.26260
1	0.21	14 (10–18)	1.31	n.a.	n.a.	n.a.
2	0.21	20 (18–21)	20.19	5.29	5682.59	0.00028
3	0.13	22 (21–23)	49.52	2.40	169.76	1.57116
4	0.21	25 (23–27)	114.80	2.02	103.62	6.77456
5	0.23	30 (27–35)	10.39	11.38	319.71	0.00009
−4	n.a.	22 (9–35)	20.10	5.29	5682.60	0.00028
−5	n.a.	20 (9–26)	46.42	2.53	199.82	0.99624
−4 and 5	n.a.	18 (9–20.5)	23.22	4.61	2766.04	0.00151

(b). Metapopulation effects of lionfish culling on single patches

The removal of lionfish from one target patch generally reduced the incidence of lionfish in surrounding patches. The magnitude of this reduction depended most strongly on the size of the target patch and its distance to other patches (figure 3b–d). In some cases, lionfish incidence declined by as much as 98% on immediately neighbouring patches.

At the network scale, complete removal of lionfish from one patch changed the mean incidence across the network (mean ΔJ_i) by −1.5% (±2.9%, range: −12%–0%), but this metric of impact masks the potentially strong localized effects of removal. The wide variation in the importance of individual patches was better captured by the cumulative change in incidence across all patches (mean AUC = −17.32, range: −196–0). Surprisingly, the removal of target patches sometimes led to an increase in lionfish incidence on a small proportion of surrounding patches (e.g. on the northernmost patches in figure 3d). Although the mean increase in incidence at these patches was negligible (1.0% ± 1.3%) and probably a result of noise in the simulation, a few individual patches saw increases as high as 8%. Increases in lionfish incidence were most common when removing a patch that was usually unoccupied.

(c). Metapopulation effects of size-selective lionfish culling

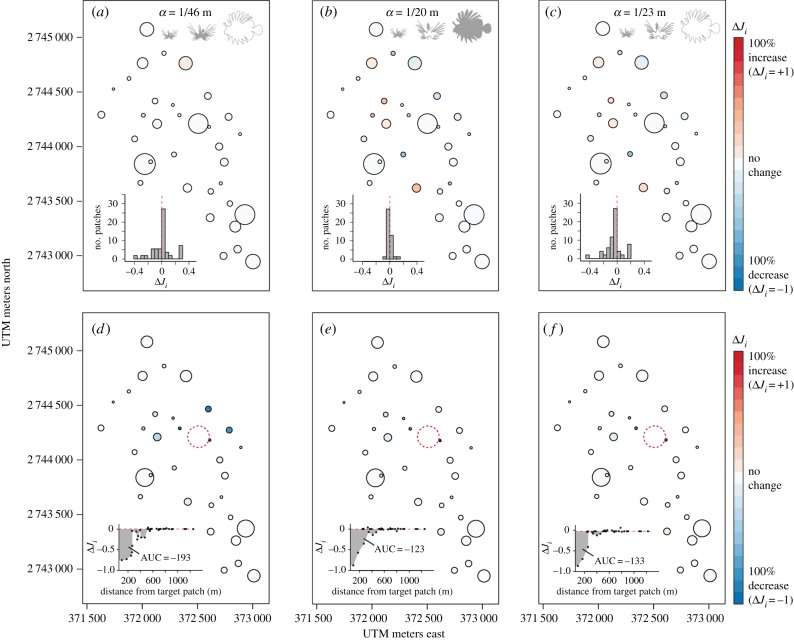
As expected, removing specific size classes from the lionfish population in selective culling scenarios reduced the mean lionfish body size. These management actions also produced a range of new mean dispersal distances used to calculate new α and network connectivity, obtain new fitted incidences and obtain new fitted IFM parameters that were used in subsequent simulations of patch removal (table 1).

When compared with the baseline incidence with all size classes present (shown in figure 3a), removal of the largest but highly sedentary size class across the population yielded a negligible change in incidences across most patches in the intact network, reflecting the low contribution of this size class to connectivity, but produced a small increase in incidence at one of the most isolated patches (figure 4a, top row). The mechanism for this increase is not understood. It may simply be an artefact of the greater likelihood of stochastic population fluctuations at poorly connected patches in the simulation (see the electronic supplementary material, figure S2). Compared to the new baseline incidence with the largest size class removed, further culling at a highly connected patch still provided strong benefits beyond the target patch that were similar to benefits of culling when all size classes were present (figure 4d versus 3c). By contrast, removal of the second largest but most mobile size class of lionfish across the population reduced incidences at more isolated patches, reflecting the disproportionate contribution of this size class to connectivity, but also increased incidence at some of the more connected patches (figure 4b), reflecting a shift in the relative importance of patches under lower population dispersal capacity. Overall, there was, therefore, little net effect on cumulative incidence at the network scale. Compared to the new baseline incidences with the most mobile size class removed, further culling at a highly connected patch has far lower benefit reflected by a narrower and less negative AUC polygon and the smaller ‘halo effect’ observed on neighbouring patches (figure 4e versus 3c). In other words, when the network is less connected because of the loss of mobile individuals, culling on a specific patch has less of an effect on outcomes at surrounding patches. Finally, removal of both of the largest size classes of lionfish yielded incidences and AUC similar to those of removing the most mobile size class alone (figure 4c,f).

Figure 4.

Change in fitted incidences before and after patch removal for three different management scenarios where (a,d) the largest size class of lionfish, (b,e) the second largest and most mobile size class and (c,f) the two largest size classes have been removed from the metapopulation by network-scale, size-selective culling. The top row shows the change in fitted incidences (ΔJ_i) prior to patch removal when compared with the baseline scenario where all size classes are present (i.e. figure 3a), with the insets showing a frequency histogram of ΔJ_i across patches. The bottom row shows ΔJ_i after removal of highly connected patch number 15 when compared with the original fitted incidences prior to patch removal within that scenario (as in figure 3c, although J_i itself is not shown), with the insets showing the change in lionfish incidence with distance from the removed patch as well as cumulative change in incidence (AUC).

4. Discussion

Limited resources for invasion management have to be distributed as effectively as possible in space and time to get the best return on investment [65]. Achieving this feat requires identifying sites that are critical for the persistence of invasive populations as well as understanding how invasive populations are connected across sites. We show here how a metapopulation approach can be used with relatively limited information on invaders to provide useful insights into spatially explicit management strategies that take into account an invader's movement behaviour, population dynamics and landscape structure. Using this approach, we found substantial heterogeneity in lionfish incidence across patches, which is likely to impede the success of spatially uniform management strategies. We also demonstrated how connectivity between patches, arising from lionfish dispersal, allows the benefits of management (i.e. culling) to extend beyond the managed patch. Finally, we explored how size-related variation in lionfish dispersal ability combined with size-selective culling can fundamentally change connectivity of a network and the effectiveness of removal strategies. By explicitly considering these insights when allocating management effort, managers can optimize the allocation of limited management resources and improve outcomes.

(a). Characterizing invasive metapopulations

Fitting the IFM to relatively little data can yield simple yet informative insights into the spatial ecology of invaders that are otherwise poorly characterized. In the case of lionfish, the IFM roughly quantifies the underlying magnitude of factors influencing colonization and extinction (discussed further in the electronic supplementary material) and illustrates wide variation in colonization and resulting incidence of lionfish across patches. This result is consistent with field records of substantial variation in lionfish recolonization rates across managed patches in other parts of Rock Sound [63]. This spatio-temporal variation in the incidence of invaders renders spatially uniform removal strategies less effective, and the IFM provides insights to help optimize the spatial and temporal distribution of management efforts.

It is important to note that although the quantitative relationships we report here apply only to our specific study site, the qualitative trends produced by the models are likely to be true in other similar patch networks colonized by lionfish. Because the IFM was designed to generate fitted parameter estimates that could be used for modelling in new patch networks [20], managers could use these parameters for modelling predicted incidences in a similar patch network using their own values for patch location, area and density (to calculate effective area), without needing to conduct more laborious, repeated surveys to obtain transition data or mark–resighting studies to obtain dispersal data.

Ultimately, the implications of the model output for any particular system will depend on the relative importance of recruitment and the temporal scale over which management typically occurs. While we did not consider larval recruitment in this study owing to the small spatial and temporal scales examined, there is a precedent in plant studies for incorporating this kind of ‘propagule rain’ from sources outside the network into metapopulation models, including the IFM [66,67]. However, managers must be careful that all of the model's assumptions are met to ensure the validity of the resulting predictions. This method is not suitable for systems where invaders are establishing and populations have not yet reached equilibrium, where individuals move between patches very easily and often, or where individuals are much more likely or capable of dispersing to some patches relative to others [20]. The latter case limits the use of such a model at larger geographical and temporal scales where larval dispersal may be strongly skewed by prevailing ocean currents.

(b). Metapopulation effects of managing single patches in a network

Considering connectivity among sites is essential for predicting management outcomes. Although populations of invaders occupying separate sites are often treated as having independent management outcomes, the benefits of management can extend far beyond the targeted area when sites are connected [17]. This is because removing invaders from a patch in a connected network reduces the pool of potential immigrants available to colonize or enhance invasive populations in surrounding patches.

Our study predicts that removing invasive lionfish from one target patch can also reduce their incidence at surrounding patches, a phenomenon often described as a ‘halo effect’ [17]. Not surprisingly, the magnitude of this beneficial halo effect (i.e. ΔJ_i) is greater when the managed patch is large, because a large source of dispersing lionfish is removed from the network, and when it is close to other patches, because compensatory migration from nearby unculled patches to the culled patch (i.e. from high- to low-density patches, [47]) depletes the population at their point of departure. These results have direct implications for the design of effective lionfish control strategies and suggest that culling lionfish on large patches that are surrounded by many other patches might result in the most far-reaching reductions in patch occupancy by lionfish. It should be noted that managing for occupancy is essentially managing for presence/absence of lionfish at individual sites, where keeping key patches of conservation concern free of lionfish may represent both a more beneficial (given the impacts of individual fish; [53]) and achievable management goal than striving for low densities or complete eradication across an entire patch network.

The fact that management at a single patch can substantially reduce incidence at a local scale (i.e. by up to 98%) but often yields only small reductions in incidence when averaged over the entire patch network (i.e. mean ΔJ_i, approx. 1.5%) implies that the network-level effects of management might be best assessed by a measure of cumulative impact, such as the AUC. The magnitude of network-level benefit reflected by AUC is, just like the mean ΔJ_i, generally proportional to the size of the managed patch. However, benefits decrease when this patch is surrounded by other large patches capable of compensating for the loss of the managed patch.

The ability to predict which patches are most important for population persistence at surrounding patches could allow managers to prioritize removals at the most influential patches and achieve greater overall reductions at a lower overall cost than management targeting other patches [17]. However, we also show that removals at some of the patches can sometimes increase incidence at distant patches (e.g. patch 33 in figure 3d). As invasive species are continually cleared from influential sites, the broader population may redistribute itself such that previously underused patches become more important and thus more vulnerable to the negative impacts of invaders. Managers should therefore consider how their management strategies may shift invasion pressure to other sensitive areas over time and monitor for such shifts as a part of adaptive management.

(c). Metapopulation effects of size-selective harvesting

Size-selective harvesting is well known to alter population traits such as size structure [38]. Given that larger individuals are usually the targets of harvesting because they are generally easier to find and sometimes easier to capture [68] and that dispersal ability is tightly linked to body size across a wide range of taxa [69], size-selective harvesting will generally remove those individuals that potentially make the greatest contribution to population connectivity in fragmented habitats [70]. Moreover, because of the tendency for ongoing compensatory immigration by mobile individuals onto recently culled patches, even localized removals may be capable of influencing size distributions at population and landscape scales [71]. The resulting changes in body size distributions and connectivity may have strong implications for population dynamics and management outcomes.

These generalizations about dispersal do not hold for lionfish because larger individuals are not the most dispersive, and thus the expectation that culling the largest individuals might reduce population connectivity is unlikely to be met. In lionfish, the interplay between the ecological and social costs and benefits of movement (figure 1) results in larger, more competitive lionfish remaining sedentary at high-quality patches, while intermediate-sized individuals account for the majority of inter-patch dispersal and connectivity [47]. Lionfish culling programmes do select for larger individuals, either because they are easier to detect and spear or because of incentives such as derby prizes or higher market value as a food fish [39]. Indeed, lionfish derbies significantly reduce the mean lionfish body sizes across the population [42]. Our simulation shows that a general targeting of the largest lionfish in the metapopulation had little effect on patch-specific incidence of lionfish or on the network-level reduction in incidence observed when localized culling occurred at a well-connected patch. However, when intermediate-sized lionfish were culled across the metapopulation, the relative importance of different patches shifts without any significant decline in net incidence across the network, and the network-level benefit of culling at a well-connected patch also declined. In other words, against a lower background level of connectivity resulting from the selective culling of the most mobile individuals, management at a local patch will have muted network-wide effects because patches are more independent from each other. Therefore, intentional or inadvertent, large-scale, size-selective harvesting could lead to increased impacts at some patches of conservation concern owing to the redistribution of invasion-related pressures across the network and may also make management at specific patches less effective. Our findings thus support prior studies that stress the importance of balancing culling efforts across a broad size spectrum at the network-wide scale, to avoid unintended consequences of size-selective harvesting [72,73]. Alternatively, the modelling approach outlined here could be used to predict, prepare for and potentially even leverage redistributions in invasion-related pressures to meet conservation goals.

5. Conclusion

We have shown how the IFM serves as a useful tool for predicting the impact of internal (e.g. body size) and external (e.g. habitat size and patch network) factors on invasive species management using limited ecological information that is obtained easily, quickly and at relatively little cost. The estimated incidences generated by the model, which incorporate information on both size-dependent movement behaviour and colonization and extinction rates, can help managers develop the most effective management strategies. This could include identifying critical size classes or individual patches as priority management targets, gauging which patches in the network are most prone to compensatory recolonization, and understanding the potential effects of size-selective culling.

This approach also has great potential for broader applications. The IFM can be used in environmental impact assessment to evaluate the cumulative effects of infrastructure development projects that can change landscape connectivity by adding or removing habitat [74]. This is particularly relevant for marine invasive species such as lionfish that thrive on artificial structures in an ecosystem where structural habitat is often limiting [75–77]. It can also be used for optimizing multispecies management in networks where invasive species coexist with and may alter the behaviour of threatened species through direct competition with species of the same trophic level or trait-mediated indirect interactions (e.g. by creating landscapes of fear for potential prey) [78,79]. By modelling population dynamics of multiple species, managers could identify patches with both the greatest benefit of invasive control removal and the greatest conservation need to determine the best way of managing invaders (e.g. via culling) and the landscape (e.g. by manipulating habitat quality and connectivity) to promote threatened species persistence [17].

Perhaps most importantly, the IFM can also be used as part of an adaptive management framework to generate testable predictions about the outcomes of alternative management strategies that account for behaviour, which can be validated through field experiments designed to accelerate learning [62,80]. Such use is facilitated by the relative ease of collecting data to parametrize the IFM, which can lead to relatively rapid prediction generation. This kind of practical research on evidence-based management alternatives is becoming increasingly important as more invasive populations become fully established across new landscapes and management interventions shift from preventing invasive spread towards long-term population control [71,81]. In the context of this work, the IFM could also be used as an annual planning tool that is updated with the latest information on body size distributions from visual surveys or other sources to adjust the spatial prioritization of culling locations to those sites where it is likely to have the most influence, as these may change over time.

The population dynamics of invasive species are ultimately an emergent property of individual dispersal events, which are themselves influenced by population demographics, community composition and landscape structure [35]. Explicitly considering the effects of these underlying factors during invasive species management planning can help to optimize benefits and costs, both within and beyond targeted areas [7,9,17], and in doing so, make the most of limited management resources to enhance overall ecosystem recovery.

Data accessibility

R code: https://figshare.com/articles/Lionfish_metapopulation_paper_-_R_code/7290152, patch survey data: https://figshare.com/articles/Lionfish_metapopulation_paper_-_Patch_survey_data/7290149, lionfish body size data: https://figshare.com/articles/Lionfish_metapopulation_paper_-_Body_size_data/7290131, lionfish dispersal distances: https://figshare.com/articles/Lionfish_metapopulation_paper_-_Dispersal_distances/7290125.

Authors' contributions

N.T. and I.M.C. designed the study. N.T. and B.O.M. performed the data analysis. N.T., B.O.M. and I.M.C. interpreted the results. N.T. wrote the manuscript, with input from all authors.

Competing interests

We declare we have no competing interests.

Funding

This study was funded by Natural Sciences and Engineering Research Council of Canada.