Establishment of maternal blood supply to the placenta: insights into plugging, unplugging and trophoblast behaviour from an agent-based model

Abstract

The ability of the baby to receive nutrients and oxygen in utero depends on the healthy development of the placenta. For maternal blood to adequately perfuse the placenta, it dramatically alters the arteries in the uterus that supply it with nutrient-rich blood right from the start of pregnancy. Placental cells (trophoblasts) invade both into the tissue of the uterus and into the maternal blood vessels nearest to the site of implantation (the spiral arteries (SAs)) and transform these allowing a relatively high and steady flow of nutrient-rich blood to perfuse the placenta. Trophoblasts also form plugs that occlude SAs, preventing maternal blood flow to the placenta until the late first trimester, at which point these plugs dislodge or disintegrate. Here we present an agent-based model of trophoblast migration within plugged SAs to tease apart the impact of chemical signals and mechanical factors on trophoblast behaviour. The model supports our previous in vitro hypothesis that plugging of the maternal arteries in early pregnancy can act to promote trophoblast invasion by providing a ‘low flow’ environment and extends our understanding by suggesting ‘weak spots’ in plug structure can lead to plug degeneration, allowing increased blood flow through the materno-fetal circulation.

1. Introduction

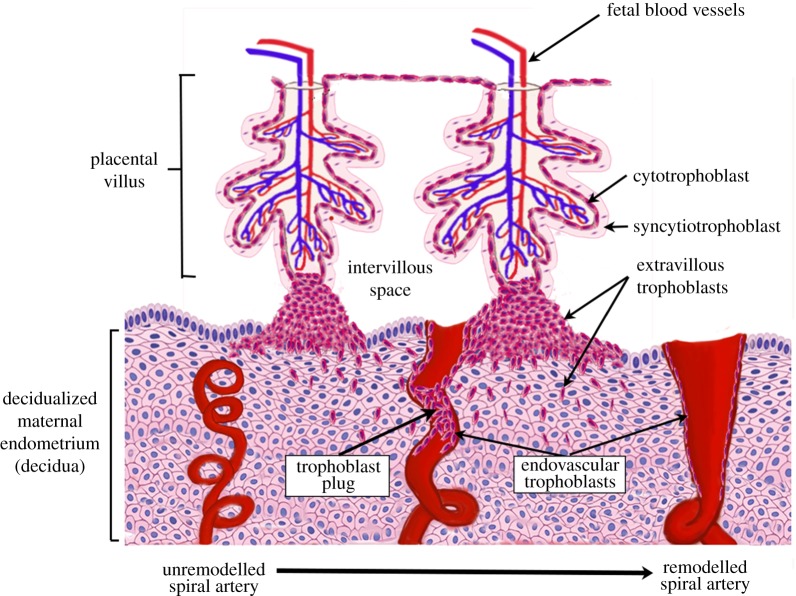
For a successful pregnancy, the fetus must establish a nutrient supply from its mother via the placenta. The placenta is formed of complex branching structures, termed villous trees, which consist of an outer bilayer of trophoblast (specialized placental epithelial cells) surrounding a stromal core containing fetal blood vessels (figure 1). Cytotrophoblasts, on the inner aspect of the trophoblast bilayer, fuse to form the overlying syncytiotrophoblast, a single multinucleated cell forming a continuous layer covering the surface of the villous trees, which is in direct contact with maternal blood for the majority of gestation [1]. Cytotrophoblasts in the tips of placental villi differentiate into a further trophoblast population—extravillous trophoblasts (EVTs), which exit the cell cycle and invade into the uterine tissue nearest to the placenta (decidualized maternal endometrium (decidua)) and its arteries (the spiral arteries (SAs), figure 1) [2].

Figure 1.

A schematic of the process of spiral artery remodelling. Prior to trophoblast mediated remodelling the spiral arteries are small tortuous vessels. Invasive extravillous trophoblasts invade both into the maternal decidua and the lumen of the spiral arteries in the first trimester of pregnancy. The endovascular trophoblast initially plugs the lumen of the spiral arteries, preventing high-velocity blood flow to the placental surface in the first trimester. Ultimately, the spiral arteries are remodelled into large ‘funnel-like’ openings and can accommodate a high flow volume of maternal blood without excessive velocity. (Online version in colour.)

Like any other systemic artery, the SAs outside of pregnancy have elastic and muscular walls and are therefore highly responsive to changes in haemodynamic status, with smooth muscle cells in the arterial wall contracting actively to modulate uterine haemodynamics. This all changes in pregnancy, as the EVTs surround the SAs, breach their walls and migrate along the vessel lumen. In combination with maternal immune cells that surround the SAs in early pregnancy, EVTs disrupt the smooth muscle layer of the vessels and degrade their basement membrane, dramatically changing their shape from tight spirals to wide bore conduits with limited vasoreactivity (figure 1) [3,4]. EVTs within the SAs (termed endovascular trophoblasts) interdigitate into the endothelial cell layer and completely replace this layer by inducing endothelial cell apoptosis. This process is critical for pregnancy success as it balances out the significant increase in maternal volumetric blood flow as gestation progresses by ensuring that this blood is delivered at relatively low flow velocities and pressures, preventing damage to the placental villi and ensuring maximal exchange [5]. Inadequacies in trophoblast invasion and SA remodelling are implicated in pregnancy complications including pre-eclampsia and fetal growth restriction [6–9]. However, despite their clinical importance, these processes are difficult to study in vivo as they occur very early in pregnancy and are highly dynamic.

During the first trimester, endovascular trophoblasts also form plugs in the SAs impeding significant maternal blood flow into the intervillous space surrounding the placental villi (figure 1) [10–14]. This creates a physiologically normal low oxygen environment that is beneficial for trophoblast differentiation and placental development [3,14–16]. Trophoblast plugs also have important upstream haemodynamic consequences that are likely to influence SA remodelling. We have previously used a porous medium model to demonstrate that the morphological structure of trophoblast plugs impacts on blood flow within them [10]. The model demonstrated that trophoblast plugs at physiological porosities are not only sufficient to impede flow to the placenta in early gestation but create a low shear stress environment upstream of the plug that facilitates endovascular trophoblast migration against the direction of flow and promotes trophoblast-induced endothelial cell apoptosis [10,17,18]. Thus, the nature of trophoblast plugs (their ability to impede flow) and the resulting impact on SA remodelling have the potential to influence pregnancy success across gestation.

The mechanisms by which trophoblast plugs dislodge/disintegrate in the late first trimester, marking the onset of significant maternal blood flow to the placenta, are not well understood. In part, this is because it is impossible to study this process in vivo as it is limited to humans and some higher primates and is beyond the resolution of current imaging technologies that are safe for use in pregnancy [16]. However, the importance of this process is highlighted by the observation that premature onset of significant maternal blood flow to the placenta, presumably as a result of premature disintegration of trophoblast plugs, has been associated with poor pregnancy outcomes [14]. There is evidence both of formation of channels in plugs and trophoblast necrosis near to these channels as the pregnancy progresses [19]; thus the assumption of a homogeneous plug structure employed by porous medium models [10] is unlikely to hold as plugs begin to disintegrate. Here, we propose a simple agent-based modelling framework to provide a basis to begin to investigate the relative influence of mechanisms driving endovascular trophoblast invasion within the SA lumen and use this modelling framework to investigate how mechanical influences (due to blood flow over and between trophoblast) may impact on plugging of the SAs in the first trimester.

2. What do we know about spiral arteries and trophoblast in the first trimester?

2.1. Spiral artery structure in the first trimester

In a previous study [10], we surveyed the literature and conducted novel measurements to determine the structure of SAs in the first trimester, and the typical dimensions and porosity of trophoblast plugs. The critical period of gestation during which the SAs are plugged and transformed is from 6 to 12 weeks. Harris & Ramsey [12] estimated an SA diameter underlying the implantation site to be 100–250 µm at 6–10 weeks gestation, increasing to 200–350 µm by 12 weeks, and this is consistent with our own measurements of SA diameter at this gestation (196 µm (±17 s.e.)) [10]. Prior to pregnancy, the SAs have smaller diameters of 20–50 µm [10–12], meaning that they are highly resistive to maternal blood flow. However, their openings ultimately remodel extensively, resulting in a diameter at the placental interface of approximately 3 mm by the end of the first trimester (after plugs have dispersed) [12]. Too much blood flow, too early in gestation, could potentially impede this remodelling process and expose the delicate placental tissue lying beneath the SAs to excessive flow velocities and pressure, which could damage the tissue structure [5]. It could also expose the placenta to pathologically high levels of oxygen at a time that the placenta is physiologically hypoxic [20].

As the evolution of SA plugging cannot be observed in vivo (their size is beyond the resolution of in vivo imaging), their structure can only be observed in snapshots from histology. Analysis of serial sections of decidual tissue has shown that plugs are formed of loosely cohesive trophoblasts [19,21–23]. Blood can permeate through the spaces between trophoblasts, and/or through channels that form in the plug structure [19]. We estimate the average diameter of an EVT to be 21.4 µm [15]. The ratio of free space to cell volume in the plug, termed porosity, varies from 0.20 to 0.60 (0.47 mean ± 0.06 s.e.) [10], with no apparent relationship between plug porosity and gestational age. As few three-dimensional reconstructions of the SAs have been conducted in the first trimester, the length of the SA lumen that is occluded by plugs is not well determined. However, it is likely that plugs are between 120 µm (0.12 mm) and 750 µm (0.75 mm) in length [10,13,23,24].

2.2. Trophoblast behaviour in vivo and in vitro

The evolution of trophoblast plugging is difficult to assess in vivo. Thus, the relationship between trophoblasts in the plug and trophoblasts that migrate along the vessel lumen is not well understood, and no study, to our knowledge, has investigated whether there is any difference in phenotype (e.g. invasive/non-invasive) between the trophoblasts in the plug or in the vessel wall [16]. A number of theories regarding this can be considered. First, trophoblasts may not be fixed inside the plug but rather may act as a transient pool of cells from which EVTs migrate towards the myometrium. Or second, the centre of the plug may remain fixed, modulating blood flow, while trophoblasts at the wall migrate toward the myometrium. The third possibility is that all cells in the plug remain fixed as a cohesive mass and colonization primarily occurs prior to plugging and via invasion of interstitial trophoblasts into the vessel wall [17].

Trophoblast behaviour in response to fluid flow (and thus cell exposure to shear stress) has been analysed in vitro and influences both trophoblast-induced endothelial cell apoptosis [25–27] and trophoblast migration [17,28]. Trophoblasts must migrate along the SAs in the opposite direction to flow to colonize these vessels, and the historical dogma (in part based on studies using trophoblasts from primates with shallower SA remodelling, and much less extensive trophoblast plugging) was that endovascular trophoblasts actively migrated retrograde to flow. However, in vitro studies using co-cultures of human trophoblasts and endothelial cells have demonstrated that increasing the shear stress to which trophoblasts are exposed increases their likelihood of migration in the direction of flow. However, under shear stresses predicted in plugged SAs (less than 2 dyn cm⁻²), trophoblasts did not demonstrate net migration in any direction, and thus such conditions would permit endovascular trophoblast migration in response to other signals such as chemotactic factors [17,28].

Chemotaxis is known to be a major contributor to cell movement across a range of biological processes. Decidual natural killer cells accumulate in high densities around the SAs during early pregnancy [29–31] and are known to secrete chemokines such as interleukin IL-8, and LIF that act as chemoattractants for EVTs [29]. Other chemokines such as MCP-1 and CCl5 (RANTES) that attract EVTs in vitro may also be produced by the upstream SA endothelium in response to low shear stress [17,32,33]. However, it is not yet known which exact combination of chemokines drive trophoblast migration in vivo, how the concentration of these chemokines varies within and around the SA, nor how far away from their source these chemoattractants could be sensed.

3. Material and methods

3.1. Experimental data

Here we employ previously generated in vitro timelapse imaging data of SGHPL-4 (an extravillous trophoblast cell line) migration across human umbilical vein endothelial cell monolayers under shear stresses of 0.5–6 dyn cm⁻² (0.05–0.6 Pa), equivalent to flow velocities of 1.5–17 cm min⁻¹ [17]. For comparison, we have previously predicted that shear stress less than 2 dyn cm⁻² is reflective of the conditions in the SAs when plugged (for the representative plug of length 0.5 mm and porosity less than 0.53) [10]. A full description of the experimental set-up for these in vitro experiments is provided in [17]. The data were previously analysed using an optical flow technique [17]; however, to provide the stochastic information compatible with agent-based modelling, the data were reanalysed by manually tracking cells through timelapse image sets (for more details, see [34]).

3.2. Model geometry

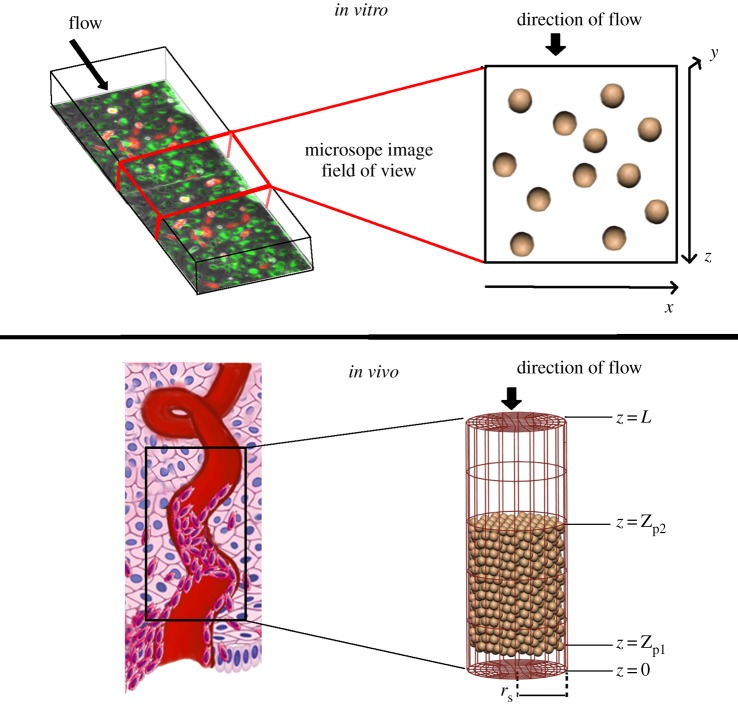
We model two cases: (1) trophoblast migration in two-dimensional space to simulate available experimental data and (2) trophoblast migration in three-dimensional space to simulate a scenario that reflects the environment of the trophoblast plug in vivo. In both models, a typical trophoblast cell radius of 20 µm was assumed [10]. Schematics of each case are shown in figure 2.

Figure 2.

Schematics of how in vivo and in vitro scenarios are modelled, with an illustration of how they relate to the physical structures modelled and flow through them. In vitro, we simulate a micro-channel, of which a subsection is imaged using timelapse microscopy. The base of the micro-channel is the x–z plane, and cells can break free of the base of the micro-channel in the y-direction and be carried with the flow. However, this does not happen commonly in the model or the in vitro data. In vivo, we simulate a portion of the plugged spiral artery as a cylindrical tube, with cells initially placed within the tube in a configuration that produces similar cell densities to those observed in anatomical imaging. (Online version in colour.)

3.2.1. Modelling the in vitro scenario

The experimental data comprise images of a monolayer of cells adhered to the wall of a micro-fluidic channel. A model of such in vitro behaviours is created by modelling one layer of cells moving in two dimensions on a plate (or wall). Here the x- and z-axes are defined in the plane as a wall with the z-axis reflecting the direction of flow. The y-axis is perpendicular to the wall, and so the cross-section of the micro-channel is defined by the x- and y-axes. Flow velocity is constant in the z-direction. Cells were seeded randomly on the plane with an initial centre–centre spacing of approximately 80 µm, similar to typical cell–cell spacing in experiments. The x–z plane is treated as a repeated unit, and cells that leave one end re-enter at the opposite end.

3.2.2. Modelling the in vivo scenario

In vivo, the distal part of the SA is modelled as a cylindrical tube with length L and radius r_S whose centreline is defined as the z-axis [10]. The model extends from the interface of the SA and the placenta (at z = 0) up to 1 mm into the decidual layer (z = L). The radius of the SA r_S is set as 0.2 mm based on literature estimates [5]. A plug extending from z = Z_p1 to z = Z_p2 is assumed to reside at the distal end of the SA, closest to the site of the placenta. Cells are seeded in the plug region to match estimates of the mean porosity of trophoblast plugs in vivo (0.47) using a hexagonal close packing algorithm [10].

3.3. Agent-based model

The agent-based model employed aims to provide a simple representation of the biological system while allowing the investigation into postulated drivers of trophoblast migration. As the contributors to this migration are many and complex, this model aims to provide a simple representation of trophoblast, while capturing the most important physical and biological features driving this motion. To do this, cells are initially seeded into a geometry in a configuration representing either the experimental set-up or an in vivo scenario. We use an off-lattice, cell-centre agent-based model, representing each cell as a point mass, and assuming that cell motion is damped [35,36]. The model then evolves over time increments, dt. The extent and direction of cell movement, for each cell, over a timestep dx is defined as

$$\mathrm{d}\mathit{x}=\mathrm{d}t\frac{\mathit{F}}{k_{\mathrm{d}}},$$ 3.1

where k_d is the damping constant and F is a force acting on the cell. We assume k_d to be the same for each cell. An estimate for k_d is made following the assumption that trophoblasts are small spherical objects, moving slowly through a fluid, flow is laminar, and the fluid is viscous, then k_d is estimated by

$$k_{\mathrm{d}}=6\hspace{0.17em}\pi \mu r,$$ 3.2

where μ is the dynamic viscosity of the surrounding fluid and r is cell radius [37]. We assume that the forces acting on a cell can be decomposed into a force driving random cell diffusion, F_random, the physical interaction of agents, F_physical, and interaction with the environment, F_environment. The net force on a cell at any given time is then defined as

$$\mathit{F}={\mathit{F}}_{\mathrm{random}}+{\mathit{F}}_{\mathrm{physical}}+{\mathit{F}}_{\mathrm{environment}}.$$

The timestep, dt, must be defined such that cells do not ‘jump over’ or get too close to one another within a single timestep. Here, dt is iteratively updated to prevent these issues.

3.3.1. Random movement of trophoblasts

The force, F_random, is implemented by assuming, in the absence of stimuli, cells move at a fixed speed and movement in any given direction is equally likely. A unit random direction vector, ${\hat{\mathit{d}}}_r$, is generated, and

$${\mathit{F}}_{\mathrm{random}}=D\hspace{0.17em}{\hat{\mathit{d}}}_r,$$ 3.3

where D controls the contribution of the random movement of cells to their overall motion. While no data are available on the movement of trophoblasts in the complete absence of stimuli (culturing cells in micro-channel systems with no flow over them negatively impacts their viability), the evidence from 0.5 dyn cm⁻² data (which includes a very low flow of 0.25 mm s⁻¹ over the cells) is that this motion is diffusive. Therefore, experimental data under this shear level are used to parametrize F_random.

3.3.2. Physical interactions between trophoblasts

Each cell interacts physically when they are in close proximity to one another due to mechanical cell–cell (CC) interactions, so F_physical = F_cc. We assume a simple function to describe the interaction between cells, reflective of trophoblast binding to one another via adhesion molecules expressed on the cell surface [38–41]. In general, when cells come in proximity to one another, they exert an attractive force on one another, until they are very close to one another and this force becomes repulsive (figure 3a) [42]. Here, we define F_cc as

$${\mathit{F}}_{\mathrm{cc}}={\mathrm{F}}_{\mathrm{cc}}\frac{({\mathit{x}}_1-{\mathit{x}}_2)}{|{\mathit{x}}_1-{\mathit{x}}_2|},$$ 3.4

where x₁ and x₂ are the locations of the centres of the two cells that are interacting. As the strengths of cell–cell interactions between trophoblasts have never been measured, we assume a simple functional form with similar properties to empirical relationships between cell separation and force

$${\mathit{F}}_{\mathrm{cc}}=\{\begin{array}{ll}\frac{a_{\mathrm{cc}}}{(r-r_0)(r_1-\mathrm{r})}-\frac{4a_{\mathrm{cc}}}{{(r_1-r_0)}^2}-b_{\mathrm{cc}},& \mathrm{for}\hspace{0.17em}r<r\\ 0,& \mathrm{otherwise},\end{array}\hspace{0.17em}\hspace{0.17em}$$ 3.5

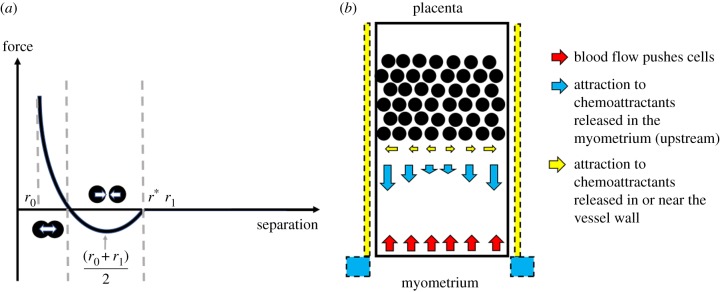
where a_cc, b_cc, r₀ and r₁ are constant parameters, and r is the distance between the centres of the two cells (normalized by radius, $r=|{\mathit{x}}_1-{\mathit{x}}_2|/R1+R2$ where R1 is the radius of cell 1 and R2 is the radius of cell 2). Physically, r₀ represents a minimum separation. Using the parameters listed in table 1 (nominal parameters), the radii over which cells influence one another are 12–68 µm. The maximum radius of influence was chosen based on the assessment of in vitro images, which showed no evidence of cell interactions but was seeded more sparsely than cells would be distributed in vivo. The parameters representing this radius of influence are, however, variable, as to date we have no direct measurements of cell–cell interactions in trophoblast cultures.

Figure 3.

(a) A schematic of the cell–cell and cell–wall interaction forces. When cells are far from one another, they are assumed to have a negligible impact on each other's motion; as they move closer they exert an attractive force on one another, until their centres are very close and this force becomes repulsive. (b) A schematic of environmental forces in the system. Blood flow acts along the negative z-axis in this model and is opposed by a chemoattractive force along the main axis of the vessel due to the production of chemoattractants upstream of the plug (e.g. in the myometrium). Chemoattractants may also be released by cells in or near to the vessel wall, and thus a radial force due to these (potentially different) chemoattractants is also modelled. (Online version in colour.)

Table 1.

Model parameters, ranges and descriptions.

parameter	description	range	value	references
geometric parameters
$r_{\mathrm{s}}^{}$	spiral artery radius (µm)	—	200	[5]
$D_{\mathrm{p}}^{}$	trophoblast diameter (µm)	30–40	40	[15,23]
L	length of decidual spiral artery modelled (mm)	—	1	see text
Zp2 − Zp1	plug length (mm)	>0.115	0.5	[23,24]
Zp1	plug distance from IVS (mm)	—	0.1	—
blood flow parameters
μ	blood viscosity (Pa s)	0.003	0.003	[10,43]
ΔP	pressure drop along segment of spiral artery (mmHg)	—	55	from [10]
drag force
kd	drag constant (N s m−1)	—	1.13 × 10−6	see text
random force, Frandom
D	diffusion constant (N)	—	2.83 × 10−13	fit to data
flow force, Fflow
a	constant of proportionality (N s m−1)	—	1.13 × 10−8	fit to data
cell–wall interaction, Fcw
acw	scaling factor of the basic Fcw force function (N)	—	1.88 × 10−14	see text
bcw	maximum attractive Fcw force (N)	—	1.04 × 10−14	fit to data
r0	location of lower asymptote of force (fraction of cell diameter)	—	0.3	see text
r1	location of upper asymptote of force (fraction of cell diameter)	—	1.7	see text
cell–cell interaction, Fcc
acc	scaling factor of the basic Fcc force function (N)	—	1.88 × 10−14	see text
bcc	maximum attractive Fcc force (N)	—	7.54 × 10−16	unknown
r0	location of lower asymptote of force (fraction of cell diameter)	—	0.3	see text
r1	location of upper asymptote of force (fraction of cell diameter)	—	1.7	see text
chemotaxis, Fchem
fax	magnitude of chemoattractant force in axial direction (N)	—	1.88 × 10−16	unknown
cax	coefficient controlling the penetration depth of axial chemoattractant force into the SA lumen (no units)	—	1	unknown
frad	magnitude of chemoattractant force in radial direction (N m−1)	—	1.88 × 10−11	unknown
crad	coefficient controlling the penetration depth of radial chemoattractant force into the SA lumen (no units)	—	1	unknown

3.3.3. Environmental influences on trophoblast

We consider three environmental stimuli with which agents can interact: (1) walls (the wall of a micro-fluidic device or the wall of the SA), (2) chemical attractants (chemotaxis) and (3) a background flow. Thus, environmental influences are decomposed into three forces

$${\mathit{F}}_{\mathrm{environment}}={\mathit{F}}_{\mathrm{cw}}+{\mathit{F}}_{\mathrm{chem}}+{\mathit{F}}_{\mathrm{flow}},$$

where F_cw is the force exerted on the cell due to interactions with walls, F_chem is the force due to chemotaxis and F_flow is the force due to flow in the neighbourhood of the cell.

Cell–wall interactions: In the same way as trophoblasts bind to one another, they can also bind to endothelial cells that form the walls of blood vessels via adhesion molecules [39]. The cell–wall force acts on a cell in the direction of the line joining the centre of the cell to the wall at the location of the cell in the axis parallel to the wall, $\hat{\mathit{l}}$. The force is defined as

$${\mathit{F}}_{\mathrm{cw}}={\mathrm{F}}_{\mathrm{cw}}\hspace{0.17em}\hat{\mathit{l}}\hspace{0.17em},$$

where

$${\mathrm{F}}_{\mathrm{cw}}=\{\begin{array}{ll}\frac{a_{\mathrm{cw}}}{(r-r_0)(r-r_1)}-\frac{4a_{\mathrm{cw}}}{{(r_1-r_0)}^2}-b_{\mathrm{cw}},& \mathrm{for}\hspace{0.17em}r<r^{\ast }\\ 0,& \mathrm{otherwise}.\end{array}\hspace{0.17em}$$

Chemotaxis: Our in vitro cell culture occurs in the absence of any chemical stimuli. In vivo, we expect two potential major sites of the release of chemoattractants: the immune cells near the SA wall, and the upstream portion of the SA (near or in the myometrium) that signals trophoblasts to invade deep into the SA. The distance at which chemoattractants could be sensed would depend on the size and diffusivity of the chemokine in question. We do not know exactly where chemokines are released to attract trophoblasts to migrate within the SAs (see §2.2), and so to define a continuum model of chemokine transport is problematic. We do know that likely sources of chemoattractant are (1) the decidua and cells in the vessel wall itself and (2) the myometrium, which is the uterine tissue that lies upstream of the spiral arteries. As data that could be used to directly model chemoattractant release or transport within the SA are so scarce, here we assume simple functional forms for chemoattractant gradient due to chemoattractant released either in the decidua or the myometrium that can be manipulated to produce a dominance of one chemoattractive force over another. The release of chemoattractants in the decidua, near the vessel wall, is assumed to act predominantly radially (perpendicular to the major axis of the blood vessel). The release of chemoattractants near the myometrium is assumed to act axially along the vessel wall and be released into the vessel lumen, so will ‘pull’ trophoblasts along the major axis of the vessel and outward toward the vessel wall. We consider one force that acts predominantly radially, F_rad, and one that acts predominantly axially F_ax (figure 3b). F_rad is defined as

$${\mathit{F}}_{\mathrm{rad}}=f_{\mathrm{rad}}\exp \hspace{0.17em}\left(\frac{c_{\mathrm{rad}}r}{r_{\mathrm{SA}}}\right)\hspace{0.17em}\widehat{\mathit{r},}$$

where f_rad is the magnitude of the force, c_rad is a constant parameter that determines the penetration of chemoattractant into the vessel lumen, $\hat{r}$ is a unit vector in the direction of the line between the centre of the SA and the cell toward the vessel wall, r is the distance from the centre of the SA to the cell in direction $\hat{r}$, and r_SA is distance from the centre of the SA to the cell in direction $\hat{\mathit{r}}$. F_ax is defined as

$${\mathit{F}}_{\mathrm{ax}}=f_{\mathrm{ax}}\exp \left(\frac{c_{\mathrm{ax}}r}{r_{\mathrm{SA}}}\right)\hspace{0.17em}\hat{\mathit{z}},$$

where f_ax is the magnitude of the force, c_ax is a constant parameter that determines penetration of chemoattractant into the vessel lumen, z is the distance of the cell along the centre-axis of the blood vessel, L is the length of the vessel and $\hat{\mathit{z}}$ is the unit vector in the direction of the SA centreline. The chemoattractants released in the decidua and in the myometrium are not necessarily the same, and thus it is not necessarily the case that the parameters defining F_rad and F_ax are the same.

Interaction of trophoblasts with a background flow: To model the interaction of a background blood flow (i.e. blood flow through the SA or in an in vitro micro-channel) with cells, we assume that the force due to background flow, F_flow, is a function of local flow velocity v. That is

$${\mathit{F}}_{\mathrm{flow}}=f(|\mathit{v}|)\hat{\mathit{v}},$$

where $\hat{\mathit{v}}$ is a unit vector in the direction of the flow velocity and f(|v|) is a function of the magnitude of the velocity vector. This function, for simplicity, is assumed to be linearly dependent on flow velocity as f(|v|) = a|v| (with a fitted to timelapse imaging data). Note that flow shear in the in vitro system is a linear function of velocity [44], so in this context, F_flow would also be a linear function of shear. Local flow velocity was chosen over shear in this model to drive force as local cell shear is a function of location on the cell surface, whereas cells and haemodynamics are described as simply as possible in this study.

3.3.4. A continuum model of spiral artery blood flow

The SA including the trophoblast plug is modelled as a porous medium with spatially varying hydraulic conductivity (K(x,y,z)) calculated from the position of the cells and the volume of the SA occupied by cells at each timestep. For numerical simplicity, blood flow through the whole artery as well as the plug is modelled using Darcy's law

$$\begin{array}{rl}\mathrm{\nabla }.\mathit{v}& =0,\\ \mathit{v}& =-\frac{K}{\mu \hspace{0.17em}}\mathrm{\nabla }p,\end{array}$$

where μ is the blood viscosity and p is local blood pressure. The Darcy flow model was solved using the mixed finite-element method [45]. The hydraulic conductivity is computed using the Kozeny–Carman equation [46]

$$K=\frac{D_p^2{ϵ}^3}{180{(1-ϵ)}^2},$$

where D_p is average trophoblast cell diameter and ε is local porosity. We follow a previous method to estimate regional K from cell locations [47]. A regular sampling grid is considered with elements large enough to contain at least 10 closely packed cells and ε of each sampling grid element is computed as the total volume occupied by cells divided by the total volume of the sampling grid element, assuming isotropic ɛ (and so K) at each element. A threshold value of K is prescribed for elements with no cells. The distribution of K in the sampling grid is transferred to the computational mesh via linear interpolation of sampling grid K onto element midpoints. Pressure boundary conditions are prescribed at the inlet and outlet of the model geometry. Driving pressure across the in vivo model geometry is estimated using our previously published haemodynamic model of the plugged SA with plug porosity of 0.5 (as our agent-based model is seeded) [10] as 55 mmHg. This driving pressure is variable, as it depends on the resistance of both the upstream and downstream components of the system [43]. Regional K is updated every timestep, and the blood flow model re-solved. It was noted that the timescale for significant changes in K is a longer timescale (5–10 min) than applied timesteps, and thus the solution of the continuum model at each model timestep may not be necessary for future implementations of similar models.

3.3.5. Simulations conducted

First, the model was simulated to reflect the in vitro experiments, and to parametrize the forces present in these experiments (F_random and F_cw and F_flow). The parameter D in equation (3.1) was fitted by holding all other parameters fixed and minimizing the difference between the average experimental speed of cell migration and the model predicted speed of cell migration in the 0.5 dyn cm⁻² dataset. To fit all other parameters, the model was simulated over a wide range for each parameter and model predictions were assessed against the distribution of cell directionality in 10° bins (figure 4a–d). The root-mean-squared error between model predicted and actual percentage of cells per bin was minimized. Then the in vivo scenario was simulated with the aim of addressing three questions: How do plugs stay together? What promotes trophoblast migration? How could plugs break up? We assume that trophoblast movement when cultured under a shear stress of 0.5 dyn cm⁻² reflects random movement, as no bias was apparent in the data. We thus used these data to parametrize F_random and F_cw by assuming that the two forces must be balanced to minimize a non-physiological cell ‘escape’ from the micro-channel wall. We then used the experimental data under higher flow conditions to parametrize F_flow. No data were available to parametrize cell–cell interactions or chemotactic forces, and thus the impact of the parametrization of these forces was assessed one-by-one. Assumed (default) and fitted model parameters are given in table 1. The model was implemented using a custom-written Fortran codebase (https://github.com/gibbogle/trophocell3D-abm). For in vitro simulations, 10 replicate simulations were conducted, and following analysis of the mean values and variability in these preliminary simulations, five replicate simulations were conducted for each parametrization assessed.

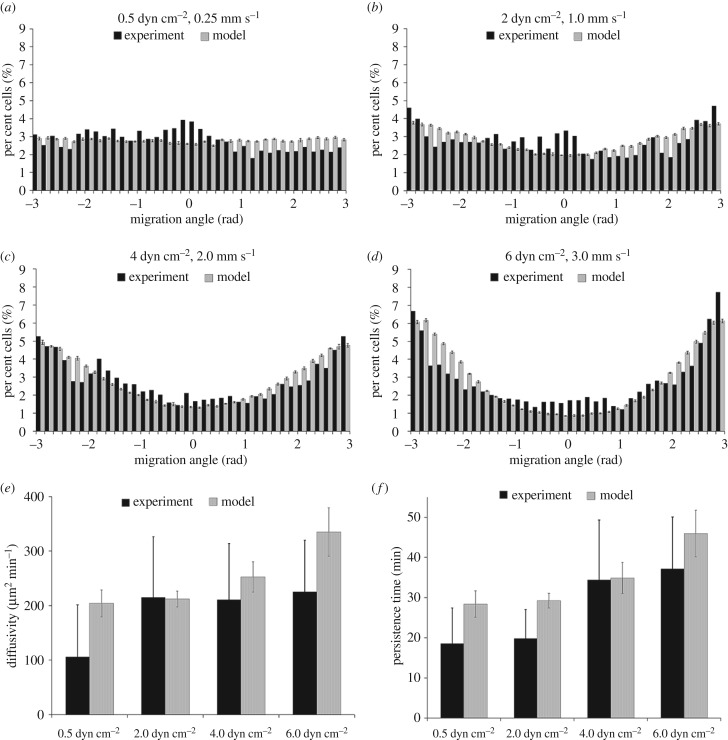
Figure 4.

Comparison of model trophoblast migration behaviours with experimentally determined behaviours. (a–d) In experimental culture, trophoblast migrates preferentially in the direction of an induced blood flow, and the model fit to reproduce these behaviours across all culture conditions. Estimates of (e) diffusivity and (f) persistence time predicted by the model are consistent with experimental data.

4. Results

4.1. Comparison to experimental data

The distribution of cell migration angle and the speed of cells relative to their direction of travel compared well with the experimental data. The average speed of trophoblast migration was 3.38, 4.66, 3.50 and 3.48 µm min⁻¹ (0.5, 2.0, 4.0 and 6.0 dyne cm⁻², respectively). As in the experimental culture system there is only a small influence on average speed in the model when flow is applied over the cells, to assess more subtle cell movement parameters, we assessed cell diffusivity and persistence time and found no statistically significant differences between the model and the experimental data (p > 0.5 and p > 0.6 for diffusivity and persistence time, respectively) [48] (figure 4).

4.2. In vivo simulations

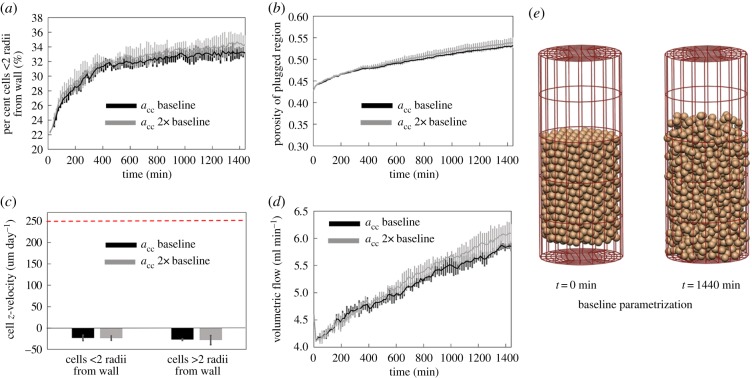
For each in vivo simulation conducted, time courses of cell movement within the SA are provided in the electronic supplementary material. With baseline parametrization (table 1) and a range of cell–cell forces, the model can be parametrized such that the plug stays intact over a long period (figure 5). As the magnitude of cell–cell interaction forces increases, cells are drawn closer together. In simulations conducted with background flow assumed to be negligible, this means that cells tend to cluster in a single group within the artery. In the presence of a background flow cells are pushed into small clusters, and so the plug appears in general as a coherent mass, but within this mass, there are regions with high cell density, and regions in which cells are sparse, akin to channels through the plug. This is reflected in higher variability in metrics of cell migration observed as the magnitude of the cell–cell interaction force is increased. In general, with baseline parametrization, the percentage of cells within two cell radii is stable over time. If the number of cells within two cell radii from the wall increases over time then the model suggests migration of cells from the plug to the vessel wall. If the distribution of cells (or) two cell radii from the vessel wall stays constant over time, then the cells originally in the plug primarily remain in the plug and those on the wall migrate independently of the plug. As the distribution of cells within the vessel lumen remains stable over time, and migration rates are low, only limited blood flow can pass through the SA and although there are changes in cell configuration from initial seeding, the plug remains relatively intact.

Figure 5.

With baseline parametrization and a range of cell–cell force strengths the model can be parametrized such that the plug stays intact over a long period. Grey black lines show model results with parameters as in table 1, and grey lines show predictions with a_cc at 2× baseline values. (a) The percentage of cells within two cell radii of the vessel wall is low and stable over time, except for an initial transient, (b) while porosity increases over time, changes are small and within the expected physiological range, (c) average z-velocity of cells is small and in the direction of flow (horizontal dashed line shows expected migration rate along the vessel wall), and (d) increases in predicted blood flow within the artery for a fixed pressure drop are small. (e) There are some changes in cell configuration from initial seeding; however, the plug remains relatively intact. (Online version in colour.)

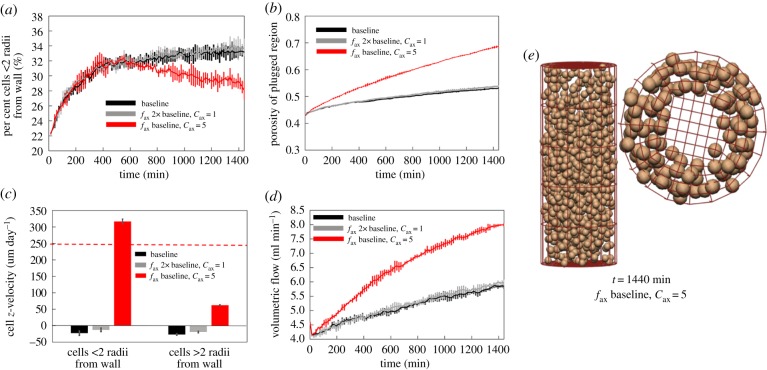
While the plug remains relatively intact with the baseline parametrization, migration rates are low. To investigate whether axial chemotactic forces can be parametrized to maintain an intact plug and to encourage trophoblast migration along the vessel wall, we considered two scenarios: an increased axial force which is evenly applied across the radius of the vessel (high f_ax and c_ax), and an increased axial force which acts predominantly near the vessel wall (low c_ax), as shown in figure 6. If chemotactic forces are not localized to near the vessel wall, the trophoblasts migrate slowly, en masse, and the plug remains intact. However, when the axial force is localized to near the vessel wall, the model predicts a rapid migration of cells along the wall of the vessel and a much slower migration of cells within the plug structure itself. Thus, the physiologically plausible scenario of a rapid migration of cells along the vessel wall, with an intact plug can be realized with the model.

Figure 6.

When increasing the axial chemotaxis force alone (f_ax at 2× baseline, c_ax = 1), the plug generally stays intact, but moves as a whole either with or against the flow. By localizing the axial chemotaxis force at the wall (f_ax at 2× baseline, c_ax = 5), the model can predict physiological migration rates near the wall, and much lower migration rates for cells in the plug. However, plug break-up occurs more rapidly. (a) The percentage of cells within two cell radii of the vessel wall, (b) changes in plug porosity over time, (c) average z-velocity of cells (horizontal dashed line shows expected migration rate along the vessel wall) and (d) increases in predicted blood flow within the artery for a fixed pressure drop. (e) When axial chemotaxis is restricted to near the vessel wall, cells migrate primarily along the vessel wall. (Online version in colour.)

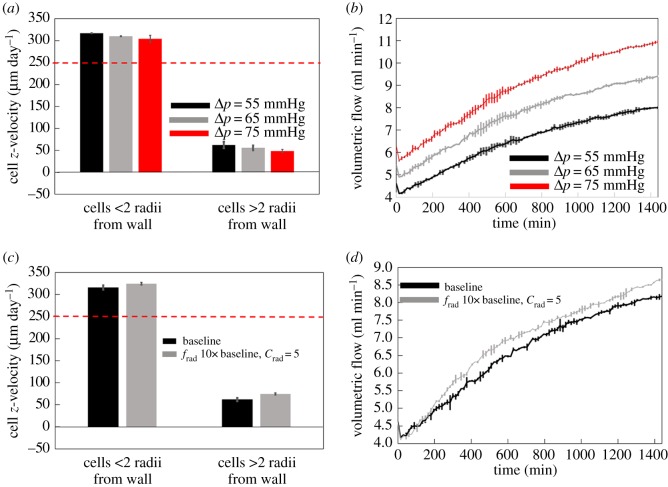
While driving pressure in the model was parametrized from previous studies, it is not completely known [10]. Increasing the driving pressure in the model increases the flow through the system and has only a small effect on net migration rates (figure 7a,b). However, increased flows push cells into clusters and thus can have the effect of forming channels in the plug more rapidly than under low flow conditions and thus promoting plug break-up.

Figure 7.

(a,b) Increasing the driving pressure across the system has a small impact on cell migration velocities (a), but increases volumetric flow through the spiral artery (b). (c,d) A strengthening radial chemotactic force draws cells away from the plugged region of the artery, resulting in a small increase in cell migration rates (c), increasing the porosity of the plugged region and so increasing blood flow through the spiral artery (d). (Online version in colour.)

By increasing the magnitude of the radial chemotactic force f_rad, we increase the likelihood that cells can be recruited from the plug to migrate along the lumen of the SA. In simulations with increased f_rad this occurs, and cells are observed to have an increased net migration rate (figure 7c,d). However, this increase is small, and the increased radial chemoattractive forces have the negative effect of removing cells from the plug, increasing local plug porosity and effectively forming a large cell-free channel through the centre of the plug. Therefore, although a significant radial pull of cells to the vessel wall due to chemotaxis could be considered to promote cell migration in the short term by recruiting cells to the vessel wall, it has a negative effect of a rapid loss of plug integrity, which in turn increases local blood flow velocities and thus slowing the net rate of migration in the longer term.

5. Discussion

When trophoblasts migrate into the SA, their movement is modulated by several competing factors. Chemotactic factors secreted by decidual immune cells and endothelial cells under low shear attract trophoblasts towards the myometrium, while any significant blood flow along the artery (generating shear stresses greater than 2 dyn cm⁻²) induces trophoblast migration in the direction of flow towards the intervillous space [17,29–31]. Recreating these competing mechanisms in vitro is problematic; for example, to seed a chemoattractant source into a micro-fluidic device at the opposing end to induced fluid flow is not practically feasible. An agent-based model of the system, as presented here, allows the opportunity to analyse the impact of these competing factors on trophoblast behaviour and to propose mechanisms that could influence trophoblast migration in vivo. The model presented here provides the first key steps toward integrated modelling of the plugging and unplugging of SAs and provides insight into the mechanisms of trophoblast migration as well as revealing gaps in our current knowledge.

5.1. How do plugs stay together?

When cell–cell interaction forces are sufficiently high, trophoblasts in the plug stay close together and no considerable cell movement out of the plug is seen. These simulations suggest that for trophoblast plugs to remain intact within the SAs for as long as they do in vivo, cell–cell adhesion must be moderately high. The model predicts that under these conditions the plug remains as a cohesive mass provided cells are not recruited radially from the plug. As cell to cell attraction force is increased, cells show an increasing tendency to cluster in small groups. This type of clustering (ranging from a few cells to groups of cells) has been reported in trophoblast plugs in baboons [49].

As our knowledge of trophoblast plugs is largely based on histological snapshots, it is impossible to determine whether trophoblasts in seemingly stable plugs remain within the plug for the entire duration of plugging, or whether trophoblasts transit through the plug en route to colonizing the SAs. When both the radial chemoattractive force and cell–cell interaction force are relatively low, cells near the wall are able to migrate more rapidly toward the myometrium. However, they must be replenished with a source of cells near the wall, potentially those from EVT columns downstream of the plug, for migration to continue. These conditions are physiologically feasible and could explain how plugs remain intact in vivo for several weeks.

5.2. How could plugs break up?

The mechanisms driving plug break-up are unknown, but hypothetical scenarios proposed for plug disintegration are that (1) the whole plug breaks up rapidly or is pushed into the intervillous space by an increasing uterine blood flow, (2) channels form in the plug, which expand progressively and ultimately result in increased flow and progressive plug disintegration and (3) cells in the middle of the plug undergo apoptotic/necrotic cell death that initiates plug disintegration. Only hypotheses (1) and (2) could be investigated by this model, as cell death was not included. Our model shows that a set of conditions exist in which it is possible for the entire plug to move intact towards the intervillous space, which could result in the scenario where plugs dislodge rapidly as a whole. In figure 4, there is net migration of cells toward the intervillous space, and although the structure of the plug evolves over time, it remains a single mass of cells (as in hypothesis 1). Increasing driving pressures in the model increases the rate of movement of this mass of cells toward the intervillous space. Under the same conditions that promote the plug remaining as a cohesive mass (high cell–cell integration and low radial chemotaxis), plugs are predicted to persist for longer and are more likely to be pushed into the intervillous space under the influence of blood flow in the SA. This would suggest a long-lasting, stable plug, which is simply swept away by a high blood flow as the delivery of blood to the uterus increases through pregnancy. In this case, break-up is initiated by an increase in volumetric blood flow rather than a loss of integrity of the plug.

The presence of blood flow in the SA acts to accentuate any asymmetries, or weak spots in the system (i.e. promotes large gaps between cells to form into channels). If cells are able to be recruited easily from the plug to migrate along the SA wall, our model indicates that increasing flow through the SA may increase this recruitment, which leads to channel formation near the centre of the plug. Even if cell–cell attraction forces are high, the presence of increasing flow may still lead to the formation of channels in the plug structure, leading to loss of plug integrity. Blood flow either acts to push more cells to the wall and depending on the symmetry of the problem and the axial chemotaxis force, promotes the remaining cells to migrate into the SA along its wall or pushes cells through the edges of channels in the plug. Figure 6e shows a clear movement of cells toward the vessel wall, in an almost symmetrical fashion as a large pathway for flow. In this, and other simulations, smaller pathways for flow first emerged as cells clustered together and became larger as time evolved. The existence of channels within the plug from six to seven weeks of gestation has been confirmed histologically [19], and regardless of the nature of cell–cell interactions or chemotaxis, the average flow velocity at the mouth of the SA (feeding the intervillous space) increases progressively (for a fixed driving pressure of 55 mmHg) as the plug disperses (either via recruitment of cells to the vessel wall, or cells being ‘pushed’ back into the intervillous space). Simultaneous trophoblast-independent remodelling events in the larger arcuate and radial arteries may provide a stimulus to induce plug dispersal in the late first trimester by increasing the pressure and blood flow in the SAs [43]. Indeed, increasing the driving pressure in the model decreases the net migration of cells with the direction of flow and rapidly increases blood flow speed within the plug as channels formed and the cycle of plug dispersal began.

The third hypothesis regarding plug break-up is more difficult to investigate, as a recent study has indicated that formation of channels in plugs is associated with trophoblast necrosis in the centre of plugs, and near to these channels as the pregnancy progresses [19]. There has been little speculation in the literature regarding probable causes of cell death within trophoblast plugs. Potentially, the damage could arise due to nutrient depletion in the centre of plugs, or in response to high shear forces exerted on cells adjacent to channels that begin to form within the plug from six weeks of gestation. However, both of these stressors may be expected to result in apoptotic rather than necrotic cell death, and together with the lack of quantification of the rates of trophoblast death within plugs (complicated by a lack of histological markers of necrotic cell death), we considered that our biological understanding of this hypothesis was insufficient to model it accurately. However, the future collection of anatomical data of trophoblast distribution, a deeper understanding of the type and rate of cell death within plugs and their susceptibility to death under high shear conditions predicted within plug channels would enable a model-based investigation to better assess how cell death may contribute to plug break up in the future.

5.3. What conditions promote trophoblast colonization of the spiral arteries?

EVTs and endovascular trophoblasts do not proliferate and thus must colonize the SA entirely by migrating into and along the vessels [50]. Endovascular trophoblasts upstream of trophoblast plugs could colonize the vessel either as a result of trophoblasts transiting though the trophoblast plug, or via interstitial trophoblasts deeper in the endometrium independently breaching the vessel wall. In the absence of any evidence supporting either of these scenarios, it is sensible to assume that both pools of cells contribute to vessel colonization and SA remodelling. Here, our model allows us to evaluate the conditions under which trophoblast migration out of the plug down the SAs may be feasible. The conditions that the model predicts provide the greatest rate of migration of trophoblasts out of the plug and towards the myometrium are when there is a high axial chemotaxis force (relative to flow forces), along with a permissive environment for cells to be recruited to migrate along the SA wall. This typically occurs when cell–cell attraction forces are low, and if one assumes that trophoblast that resides in the plug can be recruited to migrate along the vessel wall, also when radial chemotaxis is high enough compared to axial chemotaxis to promote cell migration from the plug. Strong cell–cell interaction forces result in cells clustering together, and so although cells are attracted by chemotaxis toward the myometrium, they move in clusters that migrate en masse relatively slowly compared to cells that are less attracted to one another. Similarly, if there is a high radial chemoattractive force, cells are recruited from the plug and the model predicts rapid migration. In some cases, even with low radial chemoattractive force the presence of blood flow in the SA can ‘push’ cells from the plug to the vessel wall promoting migration, but this results in channel formation within the plug and thus accelerates plug break-up. Therefore, the model predicts that each of the parameter combinations that promote migration in the short term also potentially promotes plug break-up. This suggests that cell–cell adhesion in the plug is critical to allow time for adequate trophoblast migration along the vessel walls.

5.4. Limitations

The migration of, and interaction between, trophoblasts is a complex process, and there are currently several unknowns. For this reason, the model presented here provides a simplified representation of the biological system. While the damping constant, k_d, may be reasonably approximated as a drag coefficient (equation (3.2)) when cells are moving freely in a fluid, in the absence of fluid flow, it likely underestimates the drag on cells when they are closely packed in the plug. Following previous models, we have chosen a single value of k_d for each cell [35,36] and used a physically derived estimate for its magnitude.

In this study, we employed an off-lattice, cell-centre agent-based model, which assumes that trophoblasts are near spherical cells that interact when in close proximity via a cell–cell adhesion force. This type of model has been employed in a number of studies of cell morphogenesis and migration [35,36,51]. There are a number of mechanically derived models that may be employed to simulate the cell–cell interactions when using a cell-centre approach to agent-based modelling [52]. However, at present, no data are available to determine the level of cell–cell interaction that trophoblasts exhibit when in close proximity to one another. Therefore, the modelling choice to represent cell–cell interactions using a simple functional form that represents trends in empirical data across cell types was made. An alternative approach to this problem may have been to consider the cells in a plug using a vertex dynamics model, which is often used to model epithelia, where cells are organized into tightly bound layers by adhesion molecules. In these models, cell structures are connected by networks of vertices and cells influence one another's morphology and movement strongly [53]. By contrast, trophoblast plugs are generally loosely connected, with gaps and channels in their structure, and data describing the strength of bonds between trophoblasts were not available. The cell-centred approach is limited in its ability to capture the dynamics of cells in very close proximity, even with modifications to account for close cell–cell interactions [51]; therefore, although a cell-centred approach was employed in this case, other modelling strategies such as vertex dynamics models may be applicable in investigating trophoblast plugging and migration within the endothelial layer in the future.

It is not yet clear which chemoattractants are key contributors to trophoblast migration, nor how they are distributed in and around the SA. Model predictions show that the chemotaxis effect plays an important role in cell migration depth, in agreement with a previous continuum model of trophoblast invasion through decidual stroma [54]. The chemoattractants that act on trophoblasts are many [55], and there may be multiple relevant sources of different chemoattractants that will have different diffusivities and impacts on trophoblast migration. In the future, experimental studies that could quantify stochastic trophoblast migration in response to chemotactic gradients would be useful to better parametrize a model of this type. Ideally, the release and transport of chemoattractants would be modelled using advection–diffusion equations within the model geometry. Here we follow a greatly simplified approach of assuming a functional form for chemoattractant gradients, which limits the biological interpretation of the model. However, it allows us to assess how the balance of potential attractive forces could impact on trophoblast migration. In vitro studies are beginning to elucidate the impact of chemoattractants on trophoblast migration [17,29–33], and this provides an important avenue for improving agent-based models of the process in the future.

We employed a simple Darcy flow model to describe the flow of fluid through the artery section, which necessitates a number of simplifying assumptions. Darcy flow (without a Brinkman correction) is limited, as no-slip conditions cannot be satisfied at walls. To solve the Darcy flow problem within areas devoid of cells, it was also necessary to assume a (high) permeability in these regions, whereas the governing equations for flows in these regions (or other regions with low cell densities) would more correctly be modelled as a Stokes flow. Indeed, the dynamics of blood flow around trophoblasts could be explicitly simulated as a Stokes flow, taking into account the associated computational cost of such a simulation at regular time intervals. The intention of this study was to analyse possible behaviours of trophoblast cells as simply as possible, while incorporating key postulated modulators of this behaviour. As this model is relatively simple, it allowed the assessment of qualitative cell behaviours by manipulation of a relatively small number of unknown parameters, which has allowed us to suggest possible mechanisms for plug stability, and eventual dislodgement/dissolvement. With this new knowledge, more focused experimental and computational studies can be derived to improve model accuracy.

We simulated trophoblast migration over the period of one day, which is a much shorter time period than the duration of plugging. Considering a straight SA, an average depth of 7 mm for trophoblast invasion is estimated after four weeks (decidual thickness is between 5 and 11 mm [56–58]) which gives an average migration speed (towards the myometrium) of 250 µm day⁻¹, which in general is comparable in magnitude to the predicted rate of trophoblast migration along the walls of the SAs in our model. Some simulated scenarios reflect a faster than expected migration of trophoblasts, and in particular, a faster than expected plug disintegration; however, given the unknowns in the system, we expect model predictions to describe likely mechanisms rather than quantitative timecourses of migration at this stage. To fully understand cell behaviour in the context of SA remodelling, all significant environmental factors and/or stimuli that may affect cell migration should be considered and modelled as accurately as possible. The model presented here can very well be improved by adding more factors, and by improving parametrization of unknown parameters, when more experimental data become available. In this study, we have focused on describing, qualitatively, how the balance between interacting forces may impact on trophoblast migration. Unknown parameters were varied, but as the nature of plug structural evolution was the primary focus, a formal model sensitivity analysis was not conducted.

Despite simplifications made in describing the mechanisms that drive trophoblast migration, this model, for the first time, enabled us to simulate trophoblast behaviour and visualize potential scenarios leading to plug dispersal. These data provide a suggestion for a physiological mechanism by which the channels observed in trophoblast plugs in vivo may contribute to their dispersal in the late first trimester.

Data accessibility

This article has no additional data.

Authors' contributions

A.R.C., J.L.J. and R.S. conceived and designed the study. G.B. designed the model codebase, and R.S. and G.B. implemented the model. R.S. conducted simulations and analysed data and model outputs. A.R.C. and R.S. produced figures. All authors contributed to writing and editing the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by a Gravida (National Centre for Growth and Development PhD stipend a Royal Society of New Zealand Marsden Faststart (13-UOA-032, Clark/James), and a Royal Society of New Zealand Rutherford Discovery Fellowship.