On the Upper Bounds of the Real-Valued Predictions

Abstract

Predictions are fundamental in science as they allow to test and falsify theories. Predictions are ubiquitous in bioinformatics and also help when no first principles are available. Predictions can be distinguished between classifications (when we associate a label to a given input) or regression (when a real value is assigned). Different scores are used to assess the performance of regression predictors; the most widely adopted include the mean square error, the Pearson correlation (ρ), and the coefficient of determination (or $R^2$). The common conception related to the last 2 indices is that the theoretical upper bound is 1; however, their upper bounds depend both on the experimental uncertainty and the distribution of target variables. A narrow distribution of the target variable may induce a low upper bound. The knowledge of the theoretical upper bounds also has 2 practical applications: (1) comparing different predictors tested on different data sets may lead to wrong ranking and (2) performances higher than the theoretical upper bounds indicate overtraining and improper usage of the learning data sets. Here, we derive the upper bound for the coefficient of determination showing that it is lower than that of the square of the Pearson correlation. We provide analytical equations for both indices that can be used to evaluate the upper bound of the predictions when the experimental uncertainty and the target distribution are available. Our considerations are general and applicable to all regression predictors.

Short Commentary

Background

Predictions of real-valued dependent variables from independent ones (or regression) is a widespread problem in biology. This is also true for bioinformatics applications, where statistical and machine learning methods have been extensively applied. Some examples of applications in bioinformatics (more information can be found in the reference therein) include the prediction of residue solvent accessibility,¹ protein folding kinetics,² protein stability changes on residue mutations,^3,4 protein affinity changes on residue mutations,^5,6 and binding affinity between RNA and protein molecules.⁷ Given that all prediction methods exploit data that may contain a broad range of experimental variability, an estimate of the theoretical upper bound for the prediction is crucial for the understanding and interpretation of the results.

The basic idea we worked on can be explained as follows. We start with a set of $N$ dependent variables $\left\{y_i\right\}$ we want to predict using some input features. The $\left\{y_i\right\}$ can be, as an example, the folding free energy variation on residue mutations $(\mathrm{\Delta }\mathrm{\Delta }{G}_{folding})$ or any other set of relevant quantities we would like to predict. These different variables $\left\{y_i\right\}$ represent different measures (such as the values of relative solvent accessibility in all positions of a group of proteins and the biding affinities of a set of pairs of proteins and DNA molecules) that our model should be able to predict. Each variable $y_i$ has an associated experimental uncertainty ${\sigma }_i$, which can be different for each experiment $i$. The concept of experimental measure tells us that if we repeat the experiment $i$ a very large number of times (ideally infinite), the mean value of all experiments converges to the “real measure” ${\mathrm{\mu }}_i$. This collection has a distribution that we refer to as the data set distribution (or database distribution), with a corresponding variance ${\sigma }_{DB}^2$. Formally, we indicate that a measure $y_i$ is drawn from a probability distribution $p(y_i)=p(y_i|{\mathrm{\mu }}_i,{\sigma }_i)$, to which we do not require to possess any particular form (can be normal, exponential, Poisson, for example). Following this representation, we want to compute an upper bound to the prediction accuracy of different score measures, as a function of the data uncertainty and the data set variance. The idea is that if we have a very narrow data set distribution with a variance that has the same order of magnitude of the experimental uncertainty, the theoretical upper bounds can be lower than expected. Finally, to derive the theoretical upper bounds, we use the fact that given a set of experiments of different variables, the best predictor (of those variables) is another set of experiments taken in the same conditions. No computational method can be better than a set of similar experiments.

Exploiting this idea, recently, we estimated a lower bound of the mean square error $mse$ and an upper bound of Pearson correlation $\rho$.³ Although the derivation was worked out in the context of the prediction of the free energy variation on single point mutation in proteins, the final equation is general, and it is independent of the type of data used. The lower bound of the mean square error is

$$ms{e}_{lb}\approx 2{\overline{\sigma }}^2$$ (1)

where $ms{e}_{lb}$ depends on the average uncertainty of the measures (the mean variance ${\overline{\sigma }}^2$), which reads as

$${\overline{\sigma }}^2=\frac{1}{N}\sum _1^N{\sigma }_i^2$$ (2)

whereas the upper bound for the Pearson correlation is more interesting as it depends on 2 quantities

$$\rho ub\approx \frac{1}{1+\frac{{\overline{\sigma }}^2}{\sigma {^}_{DB}^2}}$$ (3)

where we define the theoretical variance of the distributions of the experiments

$${\sigma }_{DB}^2=\frac{1}{N}\sum _1^N{\left({\mathrm{\mu }}_i-\overline{\mathrm{\mu }}\right)}^2$$ (4)

It worth remembering that, by the weak law of large numbers, when the number of samples $N$ is sufficiently large, the mean value of an empirical data distribution $\overline{y}$ converges in probability to the mean value of the theoretical distribution $\overline{\mathrm{\mu }}$ .The upper bound in equation (3) indicates that when the experimental errors are negligible with respect to the variance for the sets of the experimental values, the upper bound of the Pearson correlation is 1, as everybody expects. However, when we have a very narrow distribution of the experimental values, and at the same time the data uncertainty is not negligible, the upper bound $up$ can be significantly lower than 1.

An upper bound for the coefficient of determination $R^2$

The coefficient of determination $(R^2)$ is probably the most extensively used index to score the quality of a linear fit, in our case between predicted and observed values. Here, for the first time, we derive an upper bound for $R^2$, similar to what we did for the Pearson correlation.³ To compute $R^2$ upper bound, we use a set of observed experimental values $\left\{y_i\right\}$ as predictors for another set of observed values $\left\{t_i\right\}$. We assume that no computational method can predict better than another set of experiments conducted in similar conditions; this $R^2$ represents an upper bound for the coefficient of determination that any model trying to predict $\left\{t_i\right\}$ can achieve. Furthermore, in what follows, we consider a sufficiently large number of samples to compute the expectations. The coefficient of determination in its general form is defined as

$$R^2=1-\frac{S_e}{S_t}$$ (5)

where $S_e$ is the residual sum square that scores the difference between the predicted $\left\{y_i\right\}$ and the observed $\left\{t_i\right\}$ values, as

$$S_e=\sum _{i=1}^N{\left(y_i-t_i\right)}^2$$ (6)

and $S_t$ is total sum of squares (proportional to the variance)

$$S_t=\sum _{i=1}^N{\left(t_i-\overline{t}\right)}^2$$ (7)

Here, we assume that the sets of $\left\{y_i\right\}$ and $\left\{t_i\right\}$ are experiments conducted in the same conditions, by which we mean that we assume that $y_i$ and $t_i$ are independent and identically distributed with first and second moment finite and defined as follows

$$〈y_i〉=〈t_i〉=\underset{-\infty }{\overset{\infty }{\int }}p\left(t_i\right)t_{i}d{t}_i=\mathrm{\mu }i$$ (8)

$$\begin{array}{l}〈{\left(y_i-{\mathrm{\mu }}_i\right)}^2〉=〈{\left(t_i-{\mathrm{\mu }}_i\right)}^2〉=\\ \underset{-\infty }{\overset{\infty }{\int }}p\left(t_i\right){\left(t_i-{\mathrm{\mu }}_i\right)}^{2}d{t}_i={\sigma }_i^2\end{array}$$ (9)

Here, we use the symbol $〈f〉$ to indicate the expectation of $f$, which is equivalent to the $\mathbb{E}[f]$ notation.

Estimating $R^2$ directly is very difficult, as it is the expectation of the ratio $〈R^2〉=1-〈S_e/S_t〉$, which in general is different from (the easier computation of) the ratio of the expectations $(1-〈S_e〉/〈S_t〉)$. However, when the ratio is uncorrelated to its denominator (the covariance is 0), the 2 forms are equivalent.⁸ In our case, $S_e/S_t$ is uncorrelated of $S_t$, and we can see this by generating an infinite set of different $S_t$ values by scaling the original variables $y_{i^{\prime }}=k\cdot y_i$ and $t_{i^{\prime }}=k\cdot t_i$ while maintaining the same value for the ratio $S_e/S_t$.

Thus, we can estimate the 2 parts of the fraction independently. For $S_e$, we have

$$\begin{array}{l}〈S_e〉=\sum _{i=1}^N〈{\left(y_i-t_i\right)}^2〉\\ =\sum _{i=1}^N〈{\left(\left(y_i-{\mathrm{\mu }}_i\right)+\left({\mathrm{\mu }}_i-t_i\right)\right)}^2〉\end{array}$$ (10)

where we use the trick of adding and subtracting the term ${\mathrm{\mu }}_i$. Then, taking the square, we obtain

$$\begin{array}{l}〈S_e〉=\sum _{i=1}^N〈{\left(y_i-{\mathrm{\mu }}_i\right)}^2〉+\sum _{i=1}^N〈{\left({\mathrm{\mu }}_i-t_i\right)}^2〉\\ =2\sum _{i=1}^N{\sigma }_i^2=2N{\overline{\sigma }}^2\end{array}$$ (11)

The double product does not appear because ${\sum }_{i=1}^N〈2\left(y_i-{\mathrm{\mu }}_i\right)\left({\mathrm{\mu }}_i-t_i\right)〉=2{\sum }_{i=1}^N〈\left(y_i-{\mathrm{\mu }}_i\right)〉〈\left({\mathrm{\mu }}_i-t_i\right)〉=0$. This is due to the independence of $t_i$ and $y_i$ and the definition of the mean (equation (8)). The last equality of equation (11) comes from the definition of ${\overline{\sigma }}^2$ reported in equation (2).

The expectation of the denominator $S_t$ can be computed in a similar way

$$\begin{array}{c}〈S_t〉=\sum _{i=1}^N〈{(t_i-\overline{t})}^2〉\\ =\sum _{i=1}^N〈{\left(\left(t_i-\mathrm{\mu }i\right)+\left({\mathrm{\mu }}_i-\overline{t}\right)\right)}^2〉\\ =N{\overline{\sigma }}^2+\sum _{i=1}^N{({\mathrm{\mu }}_i-\overline{t})}^2\approxeq N{\overline{\sigma }}^2+N{\sigma }_{DB}^2\end{array}$$ (12)

The last passage becomes true for large $N$ when the mean of the experimental values $\overline{t}$ converges to the mean of the expected values $\overline{\mathrm{\mu }}$, and the last term is $N$ times data set variance.

Putting every piece together, for the expected upper bound for the coefficient of determination $R^2$, we have

$$\begin{array}{l}{R}_{ub}^2=〈R^2〉=1-\frac{〈S_e〉}{〈St〉}\\ \approx \frac{{\sigma }_{DB}^2-{\overline{\sigma }}^2}{{\sigma }_{DB}^2+{\overline{\sigma }}^2}=\frac{1-\frac{{\overline{\sigma }}^2}{{\sigma }_{DB}^2}}{1+\frac{{\overline{\sigma }}^2}{{\sigma }_{DB}^2}}\end{array}$$ (13)

As expected from statistics, the $R^2$ upper bound is lower than those obtained for the Pearson correlation (equation (3)). When the distribution of the data and the uncertainty of the data take place, the theoretical upper bound for a predictor measured using $R^2$ can be significantly lower than 1. Furthermore, given the fact that the ratio ${\overline{\sigma }}^2/{\sigma }_{DB}^2$ is bounded between 0 and 1, in general, the upper bound of ${\sigma }^2$ is also larger than that of $R^2$. However, when the value $x={\sigma }^2/{\overline{\sigma }}_{DB}^2$ is negligible (tends to zero), the upper bounds of $R^2$ and $\sigma 2$ are the same. Actually, at the first order, we have

$$R_{ub}^2\approx 1-2x\approx {\rho }_{ub}^2$$ (14)

This is what we know about the relation between $R^2$ and correlation $\mathrm{\rho }$ in standard statistical cases.

Discussion and conclusions

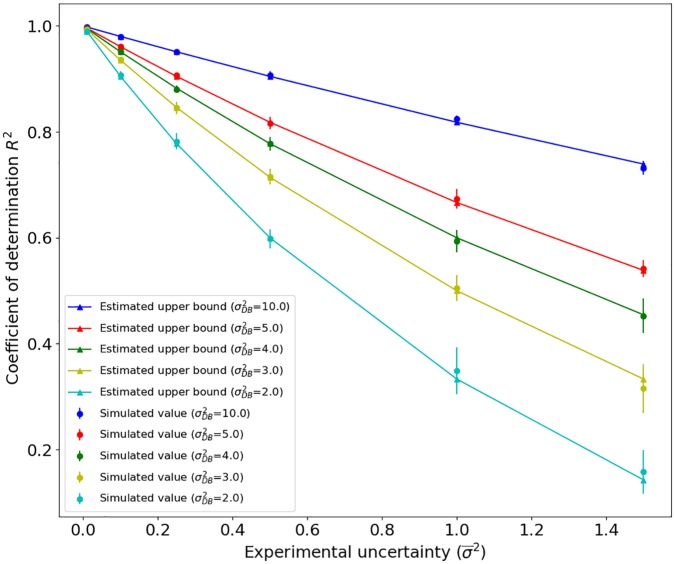
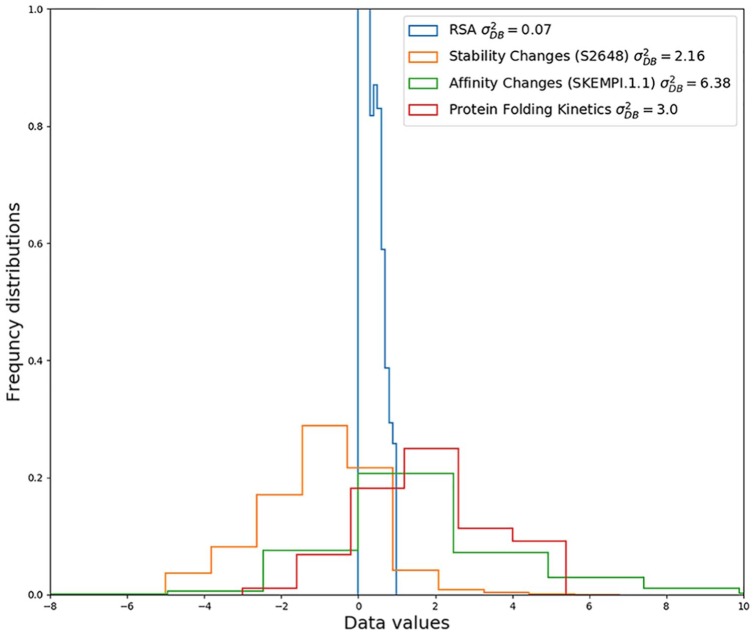
Equations (3) and (13) state that it is possible that a method performance has an upper bound lower than 1. To better appreciate the meaning of these upper bounds, we simulated different cases and graphically visualized the limits. We generated several datasets with different distributions (variance) and with variable uncertainties. Each dataset consists of 1000 random number pairs, and each pair was derived from the same distribution $(p(y_i))$, which is different for every ith pair. One set of 1000 numbers has been used as the target, and the other as the predictor. This is to simulate 2 sets of equivalent experiments. Each pair of 1000 numbers has been sampled 10 times to acquire standard deviations of the simulations. We computed the empirical $R^2$ for each run using the definition reported in equation (5). Then, we compared the values obtained with the simulated data with those computed using the upper bound equation, equation (13). The results reported in Figure 1 show an excellent agreement between the upper bound closed form and the simulation. Furthermore, from that figure, we may have an idea of the upper bounds of current datasets. For instance, in Figure 2, we report some available data set distributions. In the case of prediction of protein stability variation on residue mutation, the ${\sigma }_{DB}^2$ ranges from 2 to 9, with a data uncertainty that it is estimated in the range of 0.25 to 1.0.³ This means that the corresponding $R^2$ upper bound, in the worst case, can be only 0.5. In the case of residue solvent accessibility,¹ the average data variance is very low ($(\approx 0.01)$). However, the data variance is very low too ($(\approx 0.74)$), leading to an upper bound of $R^2$ lower than 0.90. These are just a few examples that show how relevant is knowing the distribution and data uncertainty to prevent misleading comparison between predictors tested on data with different quality or data with different variance. Of course, in practical cases, the performances achieved after correct training and testing the predictors can be significantly lower than their theoretical upper bounds. Nonetheless, knowing the upper bounds can help to identify improper training and testing procedures, when method performances greater than those obtainable using equations (3) and (13) are reported.

Figure 1.

The upper bound value of the coefficient of determination $R^2$ as a function of the average experimental uncertainty for different dataset variance.

The figure reports the values obtained using equation (13) and simulated data with empirically computed $R^2$.

Figure 2.

Examples of data set distributions with their computed variance: residue solvent accessibility (RSA),¹ protein stability changes on single point mutation (S2648 set),³ protein affinity changes on residue mutation (SKEMPI 1.1 data set),⁵ and protein folding kinetics.²