Dose–response and transmission: the nexus between reservoir hosts, environment and recipient hosts

Abstract

Dose is the nexus between exposure and all upstream processes that determine pathogen pressure, and is thereby an important element underlying disease dynamics. Understanding the relationship between dose and disease is particularly important in the context of spillover, where nonlinearities in the dose–response could determine the likelihood of transmission. There is a need to explore dose–response models for directly transmitted and zoonotic pathogens, and how these interactions integrate within-host factors to consider, for example, heterogeneity in host susceptibility and dose-dependent antagonism. Here, we review the dose–response literature and discuss the unique role dose–response models have to play in understanding and predicting spillover events. We present a re-analysis of dose–response experiments for two important zoonotic pathogens (Middle East respiratory syndrome coronavirus and Nipah virus), to exemplify potential difficulties in differentiating between appropriate models with small exposure experiment datasets. We also discuss the data requirements needed for robust selection between dose–response models. We then suggest how these processes could be modelled to gain more realistic predictions of zoonotic transmission outcomes and highlight the exciting opportunities that could arise with increased collaboration between the virology and epidemiology disciplines.

This article is part of the theme issue ‘Dynamic and integrative approaches to understanding pathogen spillover’.

1. Introduction

As a key component of transmission, dose–response relationships are expected to underlie the dynamic nature of infection and spread of disease, and are therefore an important consideration in modelling and predicting spillover risk. In the first instance, dose–response experiments characterize the relationship between exposure to a certain dose of a pathogen and the probability of developing an infection, where dose is the number of pathogen particles entering the host through a given route [1]. The dose–response data can then be interpreted through fitting mathematical models, which provide a probabilistic link between the infectivity of a pathogen, the within-host processes that determine the success of pathogen establishment into host cells, and the shape of the observed dose–response curve (e.g. [2–4]). These experiments are routinely used to derive a single value of the minimum infectious dose for an infectious agent [5], or the dose required to infect 50% of individuals (ID₅₀) which, together with the dose–response curve, commonly form the basis of microbial risk assessments (e.g. [6–8]) and experimental inoculation studies that investigate the infectivity and pathogenesis of diseases.

Despite these roots in experimental disease, there have been fewer discussions of dose–response relationships in epidemiological literature, or its influence in determining disease spillover of novel pathogens. For example, the relative contributions of frequent low-dose exposures versus rare high-dose exposures towards successful zoonotic transmission are currently unclear. Distinguishing between these two possibilities is important for managing spillover—if rare, high-dose exposures drive spillover dynamics, then identifying times, places or host characteristics that lead to high-dose exposure may lead to the development of targeted mitigation strategies. Alternatively, if exposure of many individuals to low doses leads to spillover, then mitigation must be delivered over the entire population of potential spillover hosts. The answer to this question will depend on the functional relationship between dose and infection [9]. While considerable attention has been paid to dose–response relationships, and several dose–response model structures have been proposed in the literature (e.g. [2,6,10]), there remains a paucity of studies that seek to differentiate between alternative model structures and elucidate this functional relationship (although see [11–13]). Moreover, as spillover is typically a rare event, in which only a small proportion of exposed hosts will progress to develop an infection [14], it is important to understand how low exposure doses may lead to low probabilities of infection. Here, we discuss the translation of these issues from the quantitative microbial risk assessment literature into the zoonotic spillover context. We consider the importance of the dose–response relationship to epidemiological and spillover modelling, and argue that due consideration of the dose–response relationship within transmission models will be important for the parametrization of models that are more reflective of natural transmission patterns. We then evaluate the results of existing dose–response models and discuss what additional information would be required to fully elucidate these relationships and integrate dose into transmission models.

2. Dose–response models

The standard way to consider dose–response in experimental settings is with a binary response variable, such as the occurrence of clinical infection, death, shedding or onward transmission within a given time period after exposure (e.g. [4,15]). Modelling the response of interest as a binary stochastic variable, the probability of occurrence can be expressed as a function of the exposure dose d: P(d). This probability can be estimated experimentally by measuring the proportion of exposed animals with a successful infection, shedding or mortality outcome for a given dose. Classically, the null hypothesis is that of independent action: this assumes that each particle in the inoculum has a low ‘single-hit’ probability r of causing the desired response, which is the same for every particle, and that they all act independently of each other (reviewed in [16]). If r ≪ 1, the number of successful particles follows a Poisson distribution. If the response is observed when at least one particle succeeds, it follows that the probability of observing a response can be modelled as

$$P(d,r)=1-\exp (-rd).$$ 2.1

A common empirical test of the independent action model is based on measuring the slope of the dose–response curve at half-height, i.e. at the point where the response occurs with a 50% chance, often referred to as the ID₅₀. On a log₁₀-dose scale, using basic algebra, the model predicts a slope of around 0.8 [1]. Deviations from this value indicate that at least one assumption of the model is violated: for example, particles may not cause the response independently [17,18]. First, it may take at least k successful particles to cause the response (a cooperative action or threshold model), in which case the dose–response can be modelled by summing the first k terms of the Poisson distribution, leading to a slope at half height steeper than 0.8 [1]. Biologically, this could be the result of a nonlinear immune response [19,20]. Another variant allows the single-hit rate to vary among particles or hosts, following a given distribution f(r). In general, this leads to a half-height slope of less than 0.8 [1]. A common choice for f(r) is a beta distribution, leading to a hypergeometric dose–response model. For any given host–virus pair, these alternative models can be tested statistically using experimental data (e.g. [6,12,13]). The appropriateness of alternative models, and their underlying assumptions on host–virus interactions, should be further evaluated with robust model selection approaches, sensitivity analyses and identifiability analyses (e.g. [9,12]).

Evaluating the fit of these models will be particularly important in the context of spillover, and will underpin the predicted likelihood of transmission following exposure. By definition, the ID₅₀ is the dose that has a 50% chance of infecting any one exposed individual. Under the hypothesis of independent action, if that same dose was spread across n hosts, each receiving exactly one virion and where n = ID₅₀, then there would be a 50% chance of at least one host getting infected. In general, the probability of at least one infection occurring when a given number of infective stages encounters many hosts, will be independent of the distribution of those infective stages among the hosts, provided the independent action hypothesis holds [14]. On the other hand, if the probability of infection increases more rapidly with dose than expected under the independent action hypothesis, spillover will be more likely to occur when the distribution of infective stages among hosts is highly aggregated. In this situation, spillover following infrequent but high-intensity exposures may be much more likely than would be expected from a frequent trickle of low-intensity exposures [14].

For zoonotic viruses important in spillover, the practical considerations involved in holding large numbers of animals in high containment make it essentially impossible to design an experiment capable of estimating the probability of any one individual being infected by a single virion. Furthermore, unlike situations with bacteria and other eukaryotic parasites, ensuring that a host has been exposed to a single virion is not possible. However, if the ID₅₀ can be estimated with some precision and the independent action model can be verified, then it may be reasonable to extrapolate the relationship to estimate the probability of infection with a very low infective dose. Later in this paper, we discuss how the independent action model can be fitted to empirical data, but we note previous work highlighting the uncertainty within dose–response models at low doses [16,21]. Whether these relationships should be extrapolated to extremely low infective doses, or even a single virion, is a question that should be approached with due consideration of variability in the dose–response relationship, however [9]. We would also note that there are limitations of dose–response models that should be considered when integrating within an epidemiological structure. For example, dose–response model data are derived from laboratory experiments on study populations that typically differ from study populations in an applied setting (e.g. laboratory bred animals from a specific cohort versus wild animals), and which are exposed to higher doses than might be expected in natural systems. Additional sources of variation (e.g. route of inoculation) are also likely to influence the form of the dose–response relationship in applied settings. Limitations in dose–response experiments have been discussed previously [9,16].

3. From dose–response to transmission

While the integration of dose–response relationships with epidemiological data has been previously achieved in a small number of bacterial and parasite studies (e.g. [9,22–24], dose–response relationships remain largely overlooked within epidemiological literature, particularly in the context of virus spillover. This is probably owing, in part, to a lack of data relevant to epidemiological contexts, because it is not possible to measure transmitted doses in natural studies (although see [1]). Conversely, dose–response data are at the heart of microbial risk assessment literature [16], and modelling dose–response curves in this context has strong parallels with inference of epidemiological dose–response relationships. Approaches to dose–response investigation in both research fields require a number of extrapolations and assumptions, including those underlying the single hit and the independent action theories described above [25]. Moreover, both systems are subject to sources of variation that will influence dose–response relationships, for example, specific characteristics of the pathogen or strain and heterogeneous susceptibility of exposed individuals [25]. Despite these challenges, evaluation of risks associated with bacterial foodborne disease, and more recently, water-borne parasites, has progressed rapidly over the last decades from qualitative descriptions of hazard, route and consequences of exposure, to a quantitative risk assessment framework to support more effective management and intervention strategies [26].

Currently, analogous complexities of within- and between-host processes associated with infectious disease transmission in the epidemiological context are usually combined into a single parameter: the transmission coefficient (β) [27]. Most ordinary differential equation epidemiological models [28,29] represent transmission as βSI, which implicitly assumes an independent action model. This can be made clear by including the dynamics of the transmission stages as a separate equation. Representing susceptible hosts as S, infected hosts as I and infected stages as W, the following equations, modified from [30], describe the transmission process:

$$\begin{array}{rl}{\displaystyle \frac{\mathrm{d}S}{\mathrm{d}t}=}& -\varphi WS,\\ {\displaystyle \frac{\mathrm{d}\mathit{I}}{\mathrm{d}t}=}& \hspace{0.17em}\varphi WS-I(a+b+\gamma )\\ \mathrm{and}{\displaystyle \frac{\mathrm{d}W}{\mathrm{d}t}=}& \hspace{0.17em}\mathrm{\lambda }I-(\mu +\nu N)W.\end{array}\}$$ 3.1

Here, is the rate at which individual infective stages infect susceptible hosts (which assumes an independent action model), a is the disease-induced host death rate, γ is the recovery rate of infected hosts, λ is the rate at which infective stages are released from infected hosts, μ is the death rate of infectious stages in the environment, and ν is the rate at which infective stages are removed by encountering hosts, N. In many cases, it is reasonable to assume that infective stages are short lived relative to the dynamics of the rest of the system, in which case W will be at equilibrium with the current numbers of infected and susceptible hosts, yielding

$$W=\hspace{0.17em}{\displaystyle \frac{\mathrm{\lambda }I}{\mu +\hspace{0.17em}\nu N},}$$ 3.2

and substituting into the first equation

$${\displaystyle \frac{\mathrm{d}I}{\mathrm{d}t}=\hspace{0.17em}{\displaystyle \frac{\mathrm{\varphi }\mathrm{\lambda }SI}{(\mu +\hspace{0.17em}\nu N)}-I(a+b+\hspace{0.17em}\gamma ).}}$$ 3.3

It is usually reasonable to further assume that most infective stages die before they encounter a host, so that μ ≫ νN. Thus,

$$\beta =\hspace{0.17em}{\displaystyle \frac{\mathrm{\varphi }\mathrm{\lambda }}{\mu }.}$$ 3.4

The conventional βSI transmission rate therefore assumes both independent action and that each infected individual sheds at the same rate. Hence, heterogeneities either in shedding rate or the dose–response relationship have the potential to introduce nonlinearities [14,31]. More complete consideration of dose–response relationships in models of disease transmission could enable the parametrization of models that are more reflective of transmission patterns in populations, and allow for more accurate predictions of pathogen invasion and spillover of infectious disease. Thereby, understanding the dose–response relationship could be a critical advancement for our understanding of spillover of emerging diseases from wildlife.

4. Empirical relationships

Here, we analyse previously reported results of dose–response experiments for two important zoonotic pathogens, Nipah virus (NiV) and Middle East respiratory syndrome coronavirus (MERS-CoV). Details of the experiments are given in [32] for MERS-CoV and [15] for NiV. Note that tissue culture infectious doses (TCID₅₀) are reported.

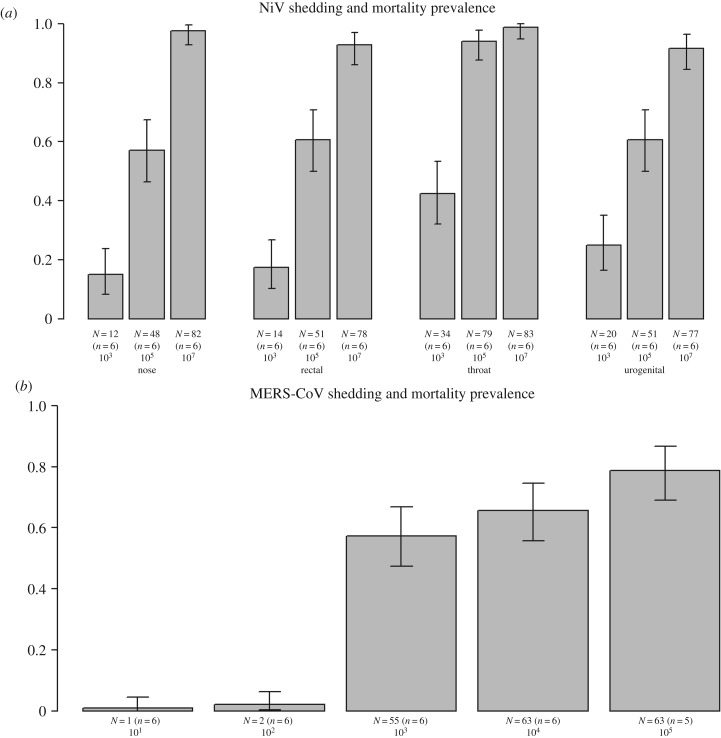
Occurrence of shedding of MERS-CoV by inoculated mice increased predictably with increasing levels of virus inoculation and showed pronounced differences between low and high doses of virus (figures 1 and 2). However, it is difficult to determine whether data of this type are consistent with the independent action model (equation (2.1)), and if so, to estimate the value of r. As can be seen from figure 1, the 95% profile confidence interval for r is very broad, with only one dose level, 10 TCID₅₀. With six mice only per dose, the confidence intervals for the true proportion shedding are also wide. Unfortunately, therefore, these data (with low sample sizes and few dose groups separated by at least an order of magnitude), are not sufficient to determine whether the independent action model is valid, or to estimate the value of the probability of infection from a single virus particle with any precision. This experimental set-up, and number of animals per dose is typical of such dose–response experiments, and the collection of the additional data required to perform discriminatory model selection is relatively rare, but has been previously achieved (e.g. [11–13,33]). Data requirements for successful model selection are discussed further in the section below.

Figure 1.

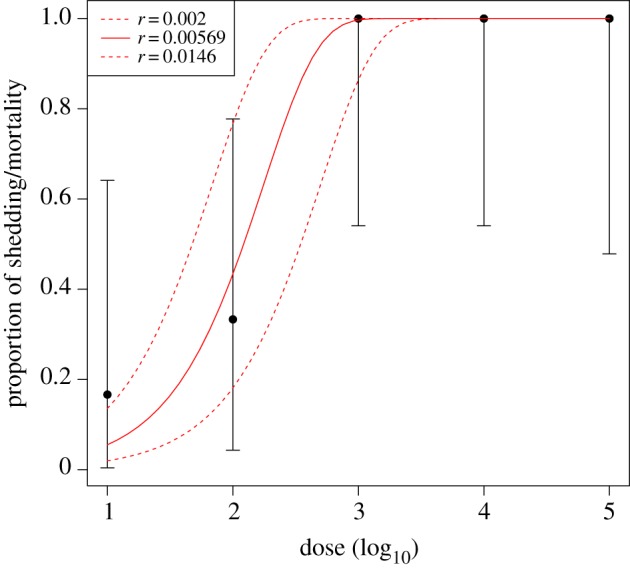
Prevalence of shedding or mortality in mice experimentally inoculated with MERS-CoV. Groups of six mice were inoculated intranasally with doses of 10¹, 10², 10³ 10⁴ or 10⁵ TCID₅₀ of MERS-CoV in a total volume of 50 µl. Data are available for only five of the mice infected at the highest dose. Viral shedding was quantified by quantitative reverse transcription-polymerase chain reaction (qRT-PCR) performed on oropharyncheal swabs. Points show prevalence of shedding or mortality in each group, and error bars are exact binomial 95% confidence intervals for the predicted probability of infection given the dose. The different coloured lines are the independent action model, for different values of r, the probability of infection from an individual virus particle. The maximum-likelihood estimate of r is 0.00571, shown as a red line. The lower and upper 95% confidence intervals based on profile likelihood for r are 0.002 and 0.0146. Dashed red lines show the corresponding dose–response curves. (Online version in colour.)

Figure 2.

Prevalence of (a) NiV and (b) MERS-CoV shedding or mortality in experimentally inoculated hamsters and mice, respectively. Groups represent intranasal inoculations with doses of 10³,10⁵ or 10⁷ TCID₅₀ of NiV in a total volume of 100 µl, and 10¹, 10², 10³, 10⁴ or 10⁵ TCID₅₀ of MERS-CoV in a total volume of 50 µl. Shedding was quantified by qRT-PCR performed on nasal, rectal, throat or urogenital (NiV) and oropharyncheal (MERS-CoV) swabs. Estimates of shedding prevalence and corresponding 95% confidence intervals were calculated using maximum-likelihood estimation, following a binomial distribution for each combination of dose and shedding route.

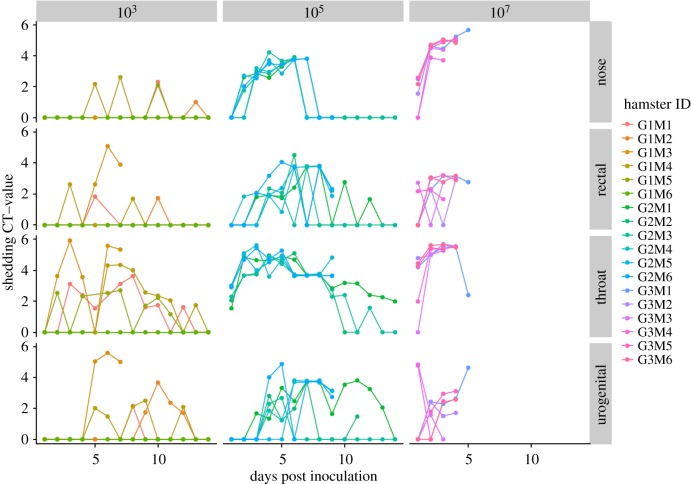
As previously presented in De Wit et al. [15], shedding of NiV increased with inoculation dose, as would be expected (figure 2). However, the data illustrate a further issue that needs to be considered when estimating dose–response relationships. Although high levels of shedding from all routes were achieved at the highest dose of 10⁷ TCID₅₀, lower doses lead to variability in the timing (figure 3) and proportion (figure 2) of hamsters shedding from different routes. At all doses, shedding was first detected in the throat. At low doses (10³ TCID₅₀), this was followed by shedding from rectal (2 dpi), then nasal and urogenital routes (4 dpi) [15]. At this dosage, shedding was more frequently observed in swabs of the throat and urogenital tract. At higher doses (10⁵ and 10⁷ TCID₅₀), shedding was detected in the nasal route earlier, alongside shedding from the throat and rectum (detection from all named routes starting from 1 dpi) [15]. Prevalence was more consistent across shedding routes: at 10⁷ TCID₅₀ all six hamsters had positive nasal, oropharyngeal, urogenital and rectal swabs by the conclusion of the experiment [15]. Moreover, shedding intensity increased with dose for some routes, including through the nasal passage and throat, but not others (i.e. rectal and urogenital routes) [15]. Heterogeneity between individuals also varied with dose and sample type—timing of shedding was more consistent among individuals via nasal and throat routes than the other sampled routes, and timing and intensity of shedding responses were more consistent across individuals exposed to higher doses (figure 3). As the precise route of infection is not known for many pathogens that spillover (for example, Hendra virus in Australian Pteropodid bats [34]), this is an important issue requiring further research, and demonstrates the need to consider shedding patterns as a potential source of variation in per-contact transmission risks, and upstream variation in pathogen exposure and transmission.

Figure 3.

Intensity (shedding in TCID₅₀ equivalents ml⁻¹) and timing (days post infection) of NiV shedding across inoculated hamsters (individuals shown by colour), separated by exposure dose and shedding route. Dose groups represent intranasal inoculations with doses of 10³, 10⁵ or 10⁷ TCID₅₀ of NiV in a total volume of 100 µl. Viral shedding titre was quantified by qRT-PCR performed on nasal, rectal, throat or urogenital swabs, evaluated daily for 14 days post inoculation. (Online version in colour.)

5. Designing experiments to test the independent action model

The empirical results described in the previous section show how difficult it is to verify or test the independent action model where experiments are undertaken using stepped doses that increase by at least an order of magnitude. This means that, in the independent action model, the response will go from close to zero to close to one within one or two dose steps, and as a result there is effectively very little information available to test the fit to the independent action model. In our previous experiment, for example, substantial individual variation in response to exposure was only observed for the 10² dose of MERS-CoV, which is close to the ID₅₀ (figure 1). So, although our datasets comprised multiple dose levels, the remaining higher and lower dose levels provided almost no additional information to determine whether the independent action model fitted the data, or to estimate the probability of infection at low doses with any precision.

To gain more information about the dose–response function, it would be necessary to undertake two-stage experiments to (i) identify the order of magnitude of dose at which infection occurs, and the variability of individual responses at that dose and then (ii) use closer increments around that dose to fit an appropriate dose–response model. Non-trivial variation among individuals would also require larger sample sizes to meaningfully discriminate between alternative models—i.e. greater than six mice/hamsters per dose group, with exact numbers to be determined by the variability observed in the first stage of experiments. Inoculation of doses close to this critical level, with higher levels of replication per dose, should provide the ability to meaningfully distinguish between different model shapes and, if the independent action model is appropriate, to estimate r. Such pilot experiments have been applied previously in many model systems.

Beyond testing the specific aims outlined above, routinely quantifying shedding in these experiments would provide valuable data in the context of zoonotic transmission or for evaluating the potential for onward transmission of pathogens. This would further facilitate the integration of dose experiment information in transmission and spillover modelling. However, the decision to undertake such experiments should depend on the relative costs and benefits associated with additional data collection. For example, the proposed experiments would require an additional number of samples (and so an additional burden on animal subjects), and so should be suitably justified. There may also be additional practical restrictions to be considered, particularly for zoonotic viruses important in spillover (e.g. biosafety considerations). Regardless, prior discussion of specific modelling and virologic goals in the design phase of dose–response experiments could facilitate the design of more comprehensive experiments, such as those suggested in this manuscript, and generate data that is useful in broader disease contexts. Deepened cross-collaboration between experimental virologists and disease ecologists investigating spillover would provide an exciting opportunity to enable researchers to use these types of experimental data to their full potential.

6. Future models

Beyond the experiment described above, the dose-dependent heterogeneity in shedding patterns shown in our datasets illustrates an important source of variability that should be considered when estimating dose–response relationships and transmission. While models describing dose–response curves can be extended to account for potential sources of heterogeneities, they have two essential limitations: they are static and they produce a binary response (‘success’ of the virus, defined as a stochastic variable). To characterize the nature of heterogeneities in these systems, and thereby enable more realistic predictions of zoonotic transmission outcomes, there is a need for novel approaches to calibrate dose–response relationships for different combinations of pathogen, host and dead-end species and individual traits.

A compartmental model, where transmission is modelled as a spatial process within and between hosts, could provide a more flexible modelling framework for the integration of such heterogeneities [35,36]. As a first approximation, hosts could be modelled as a network of tissues (e.g. organs, cell populations, bodily fluids) that lead to the external environment (and the next host) following invasion of successive compartments. Each compartment could represent a succession of basic dose–response models, followed by expansion of the successful particles in the birth–death process, as a stochastic process that can lead to successful invasion (enabling transfer to the next compartment), clearance (meaning the end of infection) or possibly death of the host (which may prevent further replication and transmission, depending on the pathogen). It would then be possible to explore the emerging patterns of transmission dose response, using a combination of analytical calculations and numerical simulations.

To include alternative dose–response models into the compartmental transmission model, we can rewrite equation (3.1) in the case of a simple dose–response experiment. Starting with a number S₀ of susceptible individuals exposed to a fixed dose W₀ for a short period T, we can solve equation (3.1) in the absence of transmission to obtain

$$S(t)=S_0{\mathrm{e}}^{-\varphi W_{0}t}.$$ 6.1

Hence the probability of being infected at the end of the exposure period T is equal to

$$1-{\displaystyle \frac{S(T)}{S_0}=1-{\mathrm{e}}^{-\varphi W_{0}T},}$$ 6.2

which is indeed the same as equation (2.1) if we set the ‘single-hit’ probability $r=\varphi T$. We can then consider an alternative dose–response model, for example:

$$P(d,r)=1-\exp (-r\hspace{0.17em}{d}^k),$$ 6.3

where the new parameter $k\ge 1$ will produce a sigmoidal response typical of a collective action model. This dose–response function can then be plugged into the SIW transmission model by equating:

$$S(t)=S_0\hspace{0.17em}{\mathrm{e}}^{-\varphi t{W}_0^k}.$$ 6.4

From which we derive the corresponding transmission term

$${\displaystyle \frac{\mathrm{d}S}{\mathrm{d}t}=-\varphi W_0^{k}S.}$$ 6.5

The choice of assumptions and the range of models worth exploring should be guided by empirical information on diverse host–pathogen systems. For example, a compartmental model may be less relevant for respiratory viruses that do not need to leave the respiratory tract to cause onward transmission (i.e. only cells in the nasal mucosa need be infected for effective transmission) [37], but may be informative for pathogens that are shed through alternative routes, such as the urinary tract [38]. Thereby, these types of models could be particularly useful for many emerging bat pathogens, where viral shedding commonly occurs through the urinary tract (e.g. Henipaviruses in Pteropodid bats [34]). Indeed, similar integrations of dose–response relationship and epidemiological modelling have been successfully applied [11,12], but further application within the context of spillover would be valuable. Furthermore, we give examples from two simplistic scenarios only (k = 1 and k > 1), though more complicated model structures with dose-dependent antagonism or heterogeneity in host susceptibility are possible (e.g. the parasite antagonism model or heterogeneous host model described in [12]). The complexity of these models should be driven by a parsimonious attempt to reproduce empirical patterns, not by a desire to capture every single mechanism at play in a real living system. Furthermore, the nature of these kinds of heterogeneities will vary with different combinations of pathogen, host species and individual traits [14], making this a challenging but important consideration in modelling.

7. Conclusion

Experimental dose–response data are highly valuable for epidemiological modelling, but here we show how the integration of dose–response relationships can be hindered by a lack of suitable data derived from dose experiments. We demonstrate how changes in the design and accessibility of dose–response experiments would facilitate integration into epidemiological modelling, and enable more realistic predictions of zoonotic transmission outcomes. We also propose alternative transmission model structures to facilitate this integration of dose–response relationships into epidemiological models. Considered integration of dose in this context will be important in predicting the likelihood of pathogen spillover. Thus, information gained by active collaboration between virologists, modellers and disease ecologists will be an important step in moving this field forward, and promoting realistic predictions of zoonotic transmission and spillover risk.

Ethics

Approval of animal experiments was obtained from the Rocky Mountain Laboratories Institutional Animal Care and Use Committee of the Rocky Mountain Laboratories. The experiments were performed following the guidelines of the Association for Assessment and Accreditation of Laboratory Animal Care, International (AAALAC) in an AAALAC-approved facility, following the guidelines and basic principles in the United States Public Health Service Policy on Humane Care and Use of Laboratory Animals and the Guide for the Care and Use of Laboratory Animals. Work with infectious MERS-CoV and NiV strains under BSL3 and BSL4 conditions, respectively, was approved by the Institutional Biosafety Committee (IBC). Inactivation and removal of samples from high containment was performed according to IBC-approved standards.

Data accessibility

The NiV dataset has been previously published (doi:10.1371/journal.pntd.0001432). Data on MERS-CoV are available upon request.

Authors' contributions

All authors were involved in the conceptualization of the paper. N.V.D., V.M. and E.D.W. led data collection and collation, T.J.L., A.J.P. and H.M. led the formal analysis and visualization for the paper, and T.J.L., O.R. and E.D.W. drafted the paper. All authors reviewed and edited the paper.

Competing interests

We declare we have no competing interests.

Funding

T.J.L. was supported by a Research Training Program (RTP) scholarship, awarded by Griffith University on behalf of the Australian Department of Education and Training. A.J.P. was supported by a Queensland Government Accelerate Postdoctoral Research Fellowship. O.R. is funded by the ALBORADA Trust. V.J.M., E.d.W. and N.v.D. are supported by the Intramural Research Program, NIAID, NIH. The project was supported by an NSF Coupled Dynamics of Natural and Human Systems grant, DEB1716698 and by the DARPA PREEMPT program managed by Dr Jim Gimlett and administered though DARPA Cooperative Agreement no. D18AC00031 (the content of the information does not necessarily reflect the position or the policy of the US government, and no official endorsement should be inferred).