Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Jul 11;6(8):2110–2116. doi: 10.1021/acsphotonics.9b00662

Vibrational Strong Coupling with Surface Plasmons and the Presence of Surface Plasmon Stop Bands

Kishan S Menghrajani 1,*, Geoffrey R Nash 1, William L Barnes 1,*
PMCID: PMC6711361  PMID: 31475218

Abstract

graphic file with name ph-2019-006622_0009.jpg

We demonstrate strong coupling between surface plasmon resonances and molecular vibrational resonances of poly(methyl methacrylate) (PMMA) molecules in the mid-infrared range through the use of grating coupling, complimenting earlier work using microcavities and localized plasmon resonances. We choose the period of the grating so that we may observe strong coupling between the surface plasmon mode associated with a patterned gold film and the C=O vibrational resonance in an overlying polymer film. We present results from experiments and numerical simulations to show that surface plasmon modes provide convenient open cavities for vibrational strong coupling experiments. In addition to providing momentum matching between surface plasmon modes and incident light, gratings may also produce a modification of the surface plasmon properties, notably their dispersion. We further show that for the parameters used in our experiment surface plasmon stop bands are formed, and we find that both stop-band edges undergo strong coupling.

Keywords: strong coupling, vibrational resonance, Rabi splitting, hybrid polariton, surface plasmon

Strong coupling involving ensembles of molecules is an important light–matter interaction that is undergoing a dramatic increase in research activity, arising from two key phenomena associated with the strong coupling regime. First, strong coupling results in the formation of new hybrid (polariton) modes. This opens a way to alter energy levels and has sparked interest across a wide range of areas, from manipulating the emission of light by triplet states1 and altering chemical reaction processes2−5 to modifying exciton transport.6 Recent work has also highlighted the important role played by the sub-band of vibrational states in strong coupling involving excitonic resonances.7 In addition to their important role in excitonic strong coupling, vibrational resonances may themselves undergo strong coupling. This may be accomplished by placing the molecules in a confined light field that has a resonance at a suitable infrared frequency. This has already been demonstrated using planar microcavities8−10 and using surface plasmon resonances, both propagating11 and localized12 to produce confined light fields.

Here we investigate the strong coupling of vibrational molecular resonances with the infrared surface plasmon modes associated with metal surfaces. We make use of periodic grating structures to probe (momentum match to) the hybrid polariton modes that arise from such strong coupling. In addition to allowing momentum matching, the grating nature of the metallic surface also modifies the dispersion of the surface plasmon modes, introducing surface plasmon stop bands.13−16 This extra degree of freedom allows us to make a first exploration of the interaction of surface plasmon stop bands and hybrid vibropolariton states produced via strong coupling.

Most experiments on strong coupling with ensembles of molecules involve planar microcavities, the molecules being placed between two mirrors that are either metallic17 or based on distributed Bragg reflectors.18 While very effective in producing strong coupling, planar microcavities do not allow easy access to the molecules they contain. The edges of such cavities can be accessed,19 but it would be preferable to gain fuller access to the molecules involved. Surface plasmons provide an excellent alternative confined light field for strong coupling,20 one that is broad-band in nature. Although strong coupling of surface plasmon modes to excitonic molecular resonances is well explored—indeed it goes back many years21—strong coupling of vibrational resonances with the surface plasmon modes of planar metal films is much less explored.11 Here, through a combination of experiment and numerical modeling, we show how surface plasmon modes may be strongly coupled with vibrational molecular resonances; our work builds on and extends recent theoretical work.22

Figure 1(a) shows a schematic of the system we consider, a 1D gold grating on a silicon substrate, overlain with a film of the polymer poly(methyl methacrylate) (PMMA). Stripe arrays such as this are a convenient way to excite surface plasmons, allowing for propagating and localized surface plasmon modes;23 they have previously been used in strong coupling experiments at visible frequencies to great effect.24Figure 1(b) shows an infrared transmittance spectrum (FTIR) of a 2.0 μm thick PMMA film on a silicon substrate (no gold) where the C=O bond resonance is present as a strong transmission minimum at ∼1732 cm–1. The sloping background to the data shown in Figure 1(b) is a result of thin-film interference between the top of the PMMA and the surface of the silicon substrate.

Figure 1.

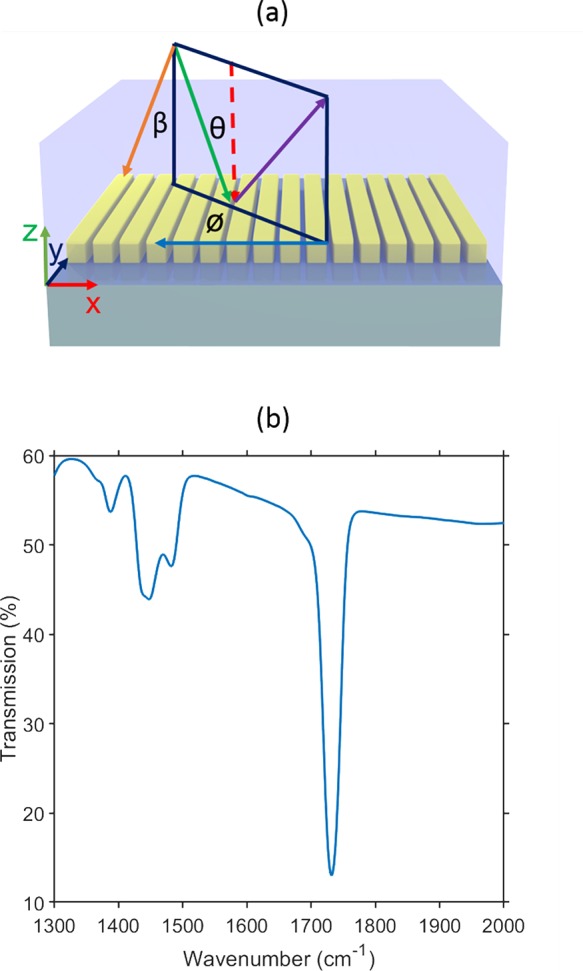
Figure 1

Open in a new tab

Schematic of sample geometry (a) and infrared absorption spectrum of PMMA (b). Top (a): Schematic of the gold grating samples used in this work. A gold grating was formed on top of a silicon substrate, upon which was deposited a layer of the polymer PMMA. Also shown is the plane of incidence; the green arrow represents the incident light direction, the black arrow the reflected direction. The polar angle θ, the azimuthal angle ϕ, and the angle of the plane of incidence β are as shown. For all measurements and calculations the incident IR light was TM polarized; that is, the electric field was in the plane of incidence. Bottom (b): Experimentally measured transmittance of a 2.0 μm thick planar layer of PMMA on a Si substrate. The strong, narrow absorption peak at 1732 cm–1 is due to the C=O bond and is the molecular resonance employed in this work. The inset shows the molecular repeat unit of PMMA.

Results and Discussion

It is useful to first look at the modes supported by the structures we investigate, and this we did through a numerical simulation performed using the commercial finite-element software COMSOL. Specifically we looked at the transmission of a planar stack comprising a silicon substrate, a 100 nm gold film (the plasmon-supporting metal), a 2 μm layer of the polymer PMMA, and finally air as the superstrate. The transmittance was calculated as a function of frequency and in-plane wavevector and is plotted on a color scale in Figure 2. The surface plasmon modes can be seen as peaks in the transmittance for p-polarized (TM) incident infrared light, since plasmon modes on planar surfaces are p-polarized.

Figure 2.

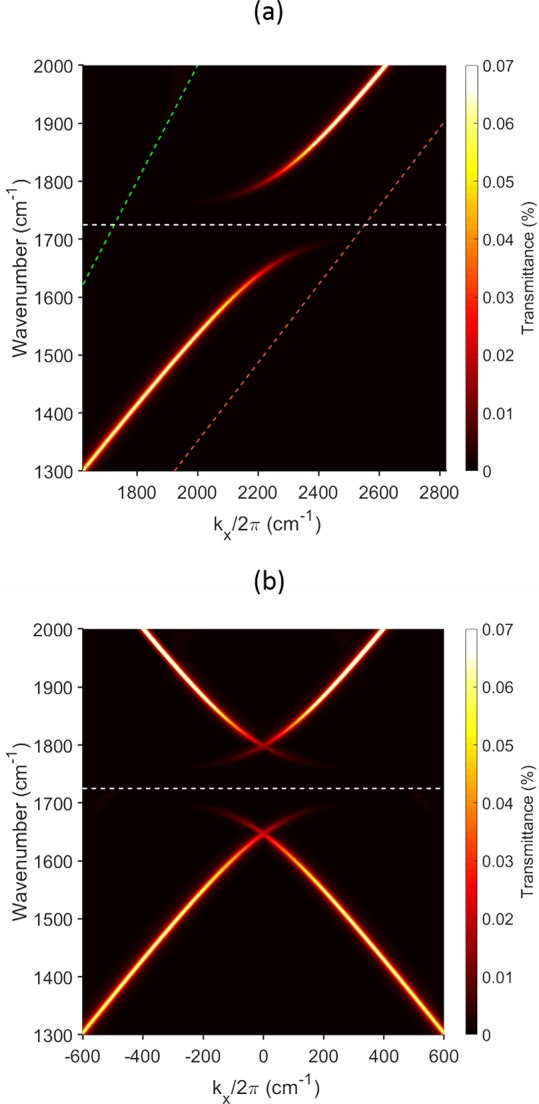
Figure 2

Open in a new tab

Surface plasmon dispersion. Calculated dispersion of the plasmon mode associated with the gold/PMMA interface. Top (a): Calculated dispersion for a planar version (no grating) of our structures; the system comprises a silicon substrate, 100 nm of gold (the plasmon-supporting metal), a 2 μm layer of the polymer PMMA and air as the superstrate. The calculated (COMSOL) transmittance is shown as a function of frequency (cm–1) and in-plane wavevector on a color scale. High transmittance indicates a mode of the system (note that here we are considering transmittance of evanescent waves because the plasmon mode is beyond the light-line). The material parameters are given at the end of the main text. The green and red dashed lines represent the air light-line and the PMMA light-line, respectively. The horizontal white dashed line at 1732 cm–1 represents the C=O vibrational mode. Notice that the plasmon mode and the anticrossing with the molecular resonance are beyond the air light-line. Bottom (b): Here we have taken the data from (a) and superimposed a shifted and folded copy so as to produce a dispersion plot to give an idea of what we expect for a grating rather than a planar structure. The grating period was taken as 4.5 μm, for which kx/2π = 1/λg = 2222 cm–1. Here β = 0° and ϕ = 0°.

The gold/PMMA plasmon mode is clearly seen in Figure 2 and lies, as expected, between the air and the PMMA light-lines. Indeed, this plasmon mode always lies beyond the air light-line, and it is for this reason that some means of momentum matching is required if this mode is to be observed in a reflection/transmission experiment. This calculation also shows the splitting of the plasmon mode at a frequency equivalent to 1732 cm–1, a direct result of the strong coupling interaction between the plasmon mode and the molecular vibrational resonance in PMMA.

Recently Memmi et al. used prism coupling to provide momentum matching and thus probe the hybridization of surface plasmons with molecular vibrational resonances.11 Here we adopt an alternative approach, that of grating coupling.25 We chose to make our grating in the form of a metal stripe array, i.e., a periodic sequence of metal strips; see Figure 1. To facilitate coupling to the surface plasmon mode at convenient angles of incidence, we chose a period of 4.5 μm.

Figure 3 shows results from calculations using COMSOL for the transmittance through a sample (where the gold film takes the form of a metallic stripe array (see Figure 1a), the stripes having a width of 3.5 μm separated by a gap of 1.0 μm, the period was thus 4.5 μm). In panel (a) the transmittance is shown for a fixed angle of incidence (12°) as a function of frequency (wavenumber). Inflections can be seen at ∼1340 and ∼1890 cm–1; these are due to second- and third-order diffraction into the silicon substrate, i.e., the silicon light-lines. The minimum-followed-by-maximum around ∼1700 cm–1 and again toward ∼2000 cm–1 are the +1 and −1 scattered surface plasmon modes. Whether transmittance maxima or minima (or both) are seen is a subtle matter, one that depends on the sample geometry and the optical setup.26 In panel (b) the transmittance is shown as a function of frequency (cm–1) and in-plane wavevector, kx (in the direction of the grating vector, i.e., normal to the grating grooves). The scattered surface plasmon modes are most clearly seen here by transmittance minima. Also shown are the relevant light-lines. For this calculation we set the oscillator strength of the vibrational resonance to zero, thereby allowing us to examine just the effect of the grating on the surface plasmon modes. We see that the scattered surface plasmon modes are now visible near normal incidence, as expected from Figure 2b.

Figure 3.

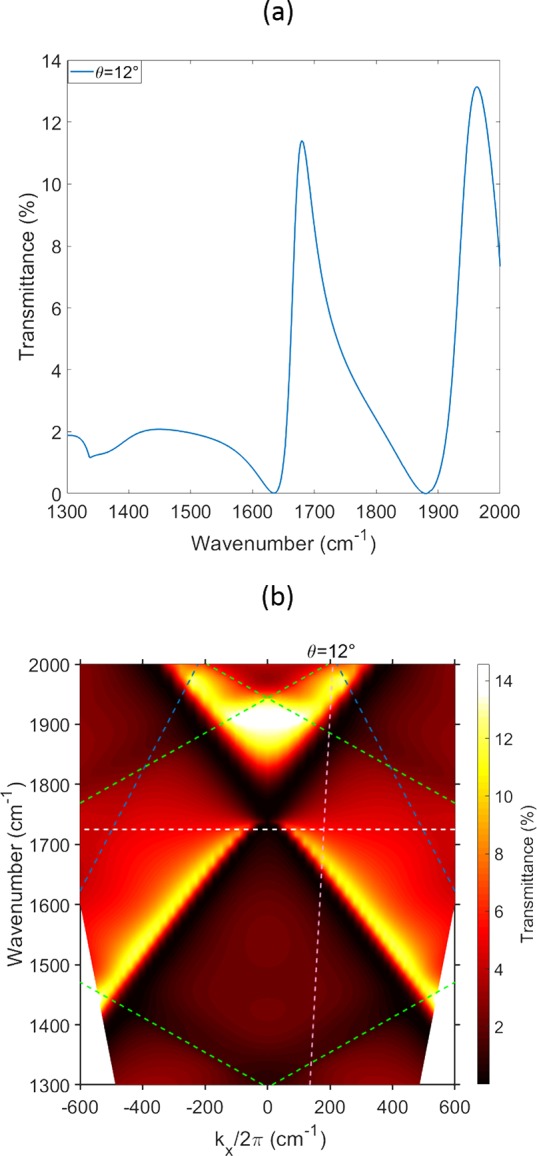
Figure 3

Open in a new tab

Numerically calculated transmission spectra (COMSOL Multiphysics) in the absence of the vibrational resonance. Top (a): Transmittance spectrum for an angle of incidence θ = 12°. Bottom (b): For dispersion plot, transmittance is shown as a function of frequency ω (in wavenumber, cm–1) and in-plane wavevector kx. The period of the grating is 4.5 μm, chosen so that the ±1 grating coupled plasmon modes are seen to cross at ∼1732 cm–1. The position of the vibrational mode is shown as a white dashed line. The oscillation strength of PMMA has been set to zero. The dashed blue and green lines are the ±1 scattered air and ±2,3 scattered silicon light-lines, respectively. The angle of incidence θ = 12° is indicated as a pink dotted line. The PMMA thickness is 1.5 μm, β = 0°, and ϕ = 0°.

Next we wished to see the effect of the vibrational resonance on the dispersion. To do this, we reintroduced the oscillator strength of the molecular (C=O) resonance into our model (see the Methods section). The results of this calculation are shown in the left-hand panel of Figure 4; hybridization between the plasmon mode and the molecular vibrational resonance can now be seen. In addition we see that the unperturbed vibrational resonance is still clearly evident; this is the horizontal dark (low-transmittance) feature at 1732 cm–1. As we will see below (Figure 8), this is because there are many regions of the PMMA film that do not couple well to the surface plasmon mode.

Figure 4.

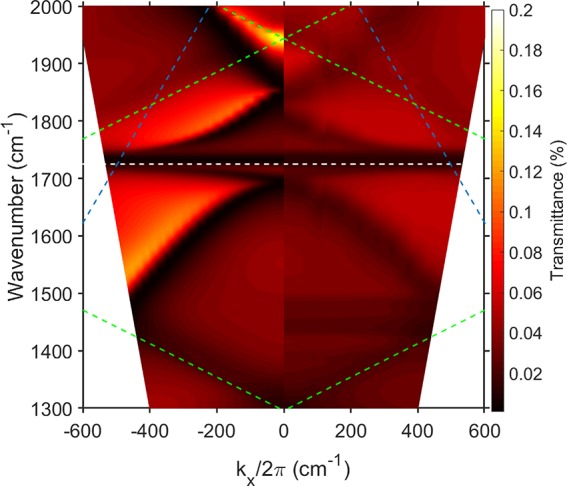
Figure 4

Open in a new tab

Surface plasmon dispersion for ϕ = 0°. On the left-hand side are numerically calculated transmittance data for TM-polarized light; on the right-hand side are experimentally measured data; both show coupling between the vibrational resonance and the plasmonic mode. The maximum polar angle for these data is 18°. The period of the grating is 4.5 μm with a 1 μm gap between metal stripes. The PMMA thickness is 1.5 μm and β = 1°. The dashed blue and green lines are the ±1 scattered air and ±2,3 scattered silicon light-lines, respectively; the white dashed line indicates the position of the C=O resonance. The calculated data have been scaled by a factor of 0.2 to allow easy comparison with the experimental data, as discussed in the text.

Figure 8.

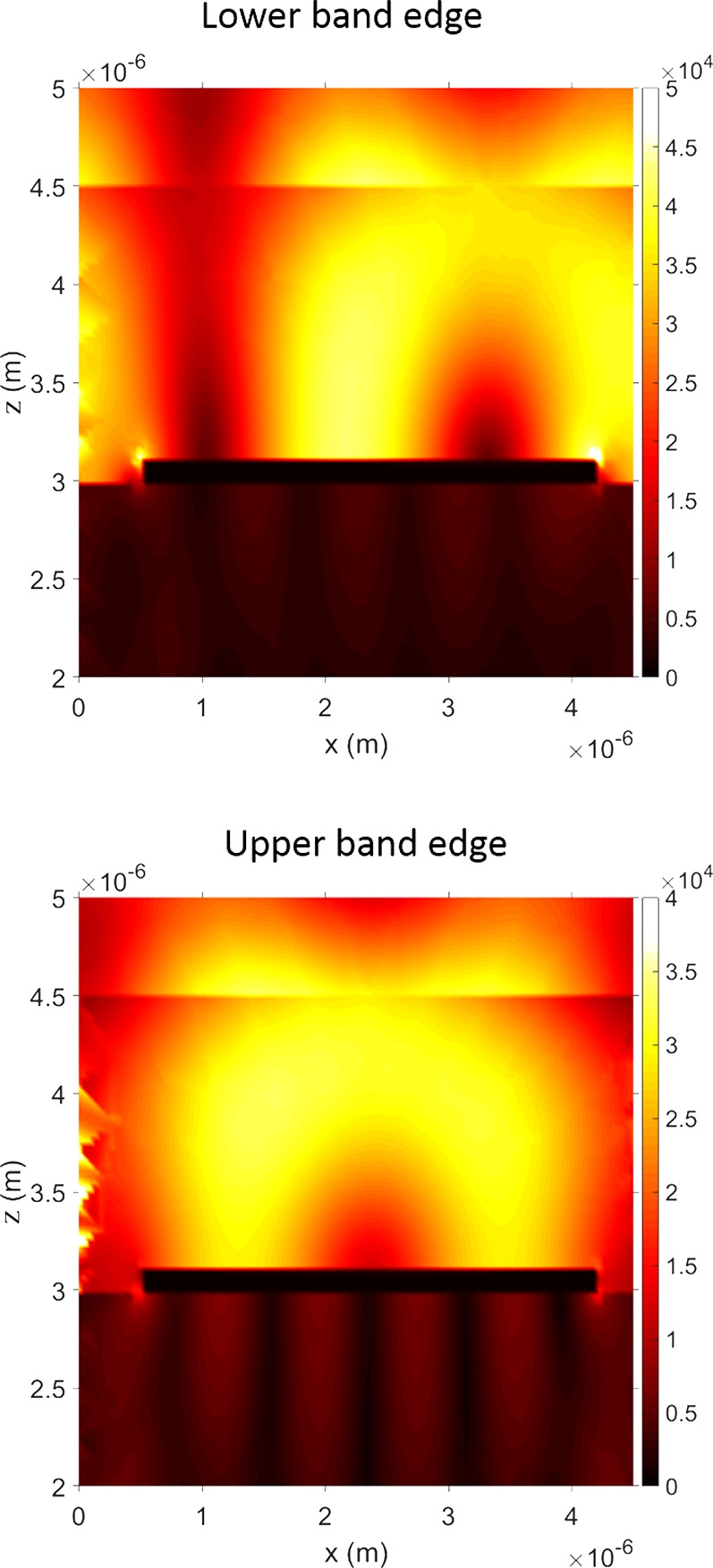
Figure 8

Open in a new tab

Electric field distributions. Calculated normalized electric field distributions for light incident at θ = 1° and ϕ = 0° for the lower band edge (1817 cm–1) and the upper band edge (1847 cm–1). The plotted values are the magnitude (norm) of the electric field, relative to the incident field (these enhancements are higher than one would expect in the visible owing to the higher Q of these IR resonances). The discontinuity in the fields for z = 4.5 μm is due to the boundary between the PMMA and the air. Here β = 0°.

Using FTIR we also acquired transmittance data from a sample nominally the same as that shown schematically in Figure 1. In our sample the PMMA thickness was 1.5 μm. The results of these measurements are shown in Figure 4 (right half), where again transmittance is shown as a function of frequency (ω) and in-plane wavevector kx. Note that in Figure 4 the calculated data have been scaled by a factor of 0.2. This has been done to facilitate comparison of experimental and calculated data; in the experiment, the scattering nature of the rear side of the Si wafer used as a substrate reduces the overall measured transmittance. The first thing to note when comparing the experimental data with the calculated data is the broad agreement about the presence and extent of the anticrossing of the plasmon mode with the C=O vibrational resonance. In addition, for kx ≈ 0, we see an additional small splitting of the surface plasmon mode, at a frequency of ∼1830 cm–1.

Where scattered surface plasmon modes cross (on a dispersion diagram) stop bands may occur, their presence depending on the details of the grating profile.13 Looking at the data in Figure 4 it appears that a surface plasmon stop band, around ∼1830 cm–1, has been produced. To further investigate this, we measured the dispersion for a plane of incidence for which ϕ = 90°; such a configuration maps out the modes for which kx = 0, thus enabling the stop-band position to be tracked as a function of ky. Figure 5 (right half) is the result of such measurements. As a comparison, numerically calculated data for the same situation, i.e., ϕ = 90°, are shown in Figure 5 (left half). Both experimental data and calculated data show surface plasmon stop bands that gradually rise in frequency, as |ky| is increased away from zero, tracking the expected dispersion for this configuration, as given by the third-order scattered Si light-line (shown as a green dashed line in the figure). Also evident in the experimental data in Figure 5 (and indeed in Figure 4) are additional vibrational resonances for frequencies around ∼1460 cm–1. These are due to CH3 and CH2 resonances that are not included in the model we have used here;27,28 see also Figure 1b.

Figure 5.

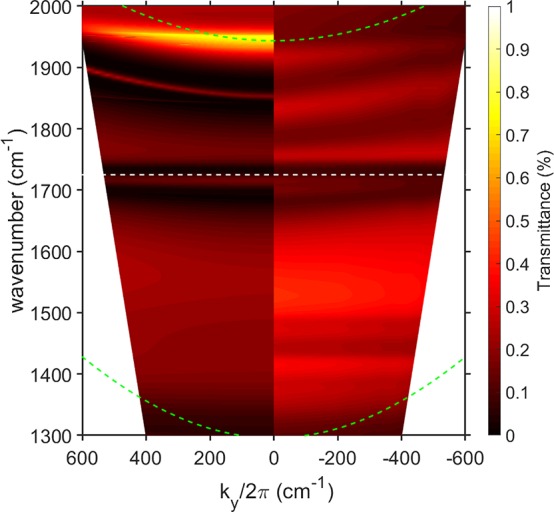
Figure 5

Open in a new tab

Dispersion for ϕ = 90°. On the left-hand side are numerically calculated transmittance data for TM-polarized light; on the right-hand side are experimentally measured data. Again, both show coupling between the vibrational resonance and the plasmonic mode. The maximum polar angle for these data is 18°. The period of the grating is 4.5 μm with a 1 μm gap between metal stripes. The PMMA thickness is 1.5 μm and β = 1°. The green dashed lines represent the ±2 and ±3 scattered Si light-lines; the white dashed line indicates the position of the C=O resonance. As for Figure 4, the calculated data have been scaled by a factor of 0.1 to allow easy comparison with the experimental data.

A feature of surface plasmon stop bands and band gaps (a band gap implies that for some range of frequencies a stop band exists for all in-plane directions) is that coupling to the band edges is sensitive to the way the sample is illuminated.13 To investigate this, we calculated the line spectra associated with the transmittance for normal incidence, i.e., θ = 0°, and near-normal incidence, β = 1°. These data are shown in Figure 6. For these data the azimuthal angle was ϕ = 90°. We see that the transmittance minimum at 1800 cm–1 and associated with the lower surface plasmon stop band is visible for off-normal incidence (red curve) but not for normal incidence (blue curve). This is consistent with the symmetry of the charge and field distributions expected in this geometry.13 Careful observation of the data in Figure 6 shows that something similar happens where the scattered plasmon modes cross at ∼1670 cm–1.

Figure 6.

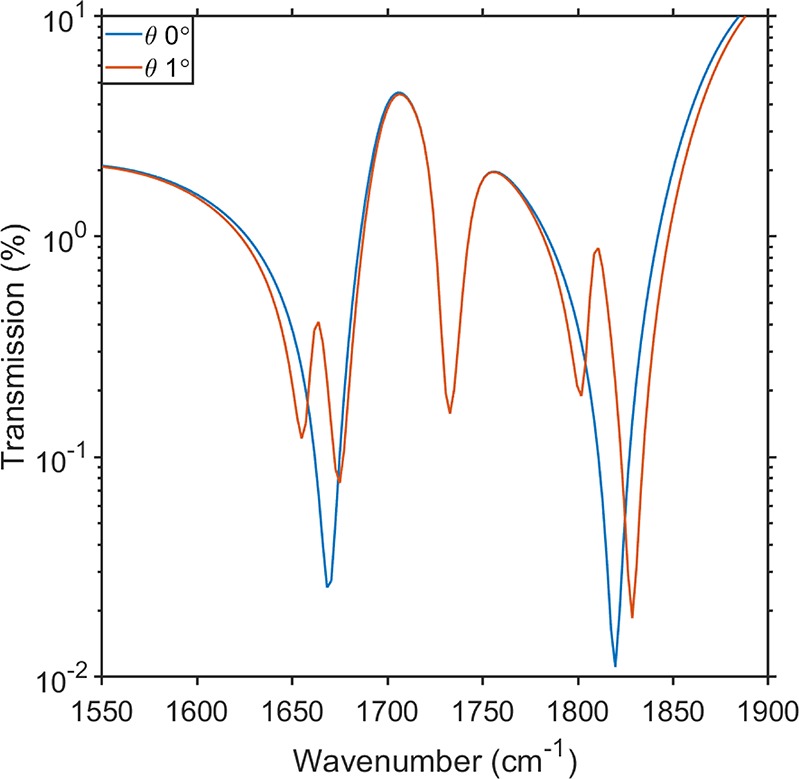
Figure 6

Open in a new tab

Coupling to band edges. Calculated transmittance for ϕ = 90° for two polar angles of incidence, θ = 0° (blue) and θ = 1° (red). The lower band edge at both ∼1670 and 1800 cm–1 is only seen for off-normal incidence illumination (red). See text for details. Here β = 0°.

To be more accurate, the data in Figures 5 and 6 both show that the polariton modes (rather than simply the plasmon modes) exhibit stop bands. Extending these results by introducing a grating structure in the second (y) direction would offer the prospect of introducing a polariton band gap and would form a bridge between studies of strong coupling between molecular resonances and surface plasmons on planar surfaces and the strong coupling of molecular resonances with the lattice resonances associated with periodic arrays of metallic nanoparticles.29−32

We also wanted to find out what happened to the two polariton stop-band edges under strong coupling. To do this, we again looked at the transmittance, for θ = 1° and ϕ = 90°, and varied the period of the grating. This approach has been used successfully before in explorations of strong coupling involving lattice resonances of periodic arrays.33 We simulated the transmittance, again using COMSOL, varying the period, but keeping the spacing between the metallic elements fixed at 1 μm. The results of such calculations are shown in Figure 7. We see that both the upper and lower band edge undergo an anticrossing. The associated field distributions, shown in Figure 8, show the expected symmetry,13 with the lower band edge having fields concentrated on the metal slab, while the upper band edge has field maxima over both metallic and gap regions. As an additional comment, we see in Figure 8 the reason that the low transmittance feature at the molecular resonance frequency (1732 cm–1) is always present (see Figures 3, 4, and 5). There are regions on these samples where the field strength is minimal, so that molecules in these regions do not couple to the plasmonic modes and do not therefore undergo strong coupling, something that has been seen before for excitonic resonances.24

Figure 7.

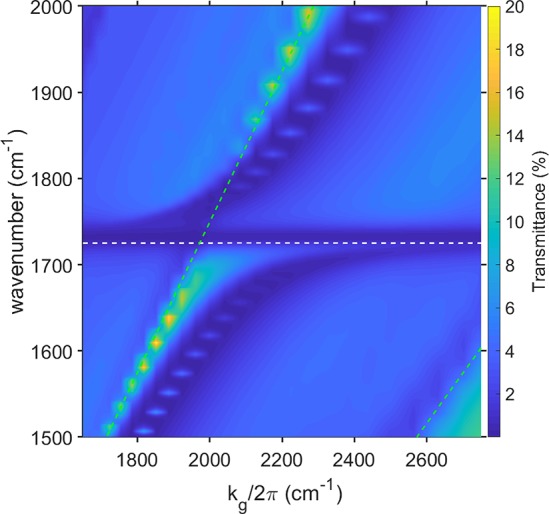
Figure 7

Open in a new tab

Effect of grating period. Calculated transmittance spectra for ϕ = 90° and for θ = 1° as a function of grating period. The PMMA thickness was 1.5 μm, and the gap between the metal stripes was kept constant at 1.0 μm. The green dashed lines are the second- and third-order grating scattered silicon light-lines. The somewhat diagonal features (transmittance minima) in the data are associated with these light-lines. The vertical feature at kg/2π ≈ 2 m–1 is an artifact of the numerical calculation. Here β = 0°.

In summary we have demonstrated strong coupling between molecular vibrational resonances and surface plasmons in the infrared by exploiting grating coupling. We showed that in addition to enabling light to be coupled to the hybrid vibroplasmon polaritons, the grating nature of the surface also leads to the formation of polariton stop bands. We further showed that both upper and lower stop bands undergo strong coupling. A future study might extend our understanding by exploring the role of 2D periodic structures, e.g., to provide a full band gap. It would for example be interesting to see what happens if such a gap was centered around the frequency of the molecular vibrational resonance: would the strong coupling be completely blocked? Finally we might add that although we have used a stripe array, a metal film with a modulated surface profile should also work,22 therefore enabling, for example, electrical access. These initial results on strong coupling involving plasmon band edges need following up with a more detailed investigation, one beyond the scope of the current report.

Methods

Sample Fabrication

One-dimensional grating structures were produced using electron beam lithography. PMMA (950k powder form) was dissolved in water at 9% concentration by weight and was subsequently spun at 4000 rpm to obtain the desired thickness. For the e-beam fabrication of the grating, an e-beam resist (PMMA: 950 K A9) was spun (4000 rpm) onto a 20 × 20 mm silicon wafer substrate so as to obtain a thickness of ∼400 nm. The substrate was then heated to 180 °C for 10 min to remove the solvent; an electron beam current of ∼20 nA was used to write the desired pattern. Following exposure the resist was developed (MEK+MIBK+IPA) for 40 s. A thin 100 nm gold film was then deposited by thermal evaporation, followed by a lift-off process to leave the desired gold stripe grating; see Figure 1a.

FTIR Measurements

The IR transmission of the samples was determined using an FTIR setup (Fourier transform infared spectroscopy, Bruker V80). To acquire dispersion curves, spectra were acquired for a range of incident angles, typically in the range −18° to +18°. All measurements were performed with a spectral resolution of 8 cm–1 and an angular resolution of 2°. To improve the signal-to-noise, averaging over 128 scans was carried out. An example of the measured transmittance spectra is shown in Figure 4 (right half).

Numerical Modeling

To model the response from our structures we employed finite-element modeling through the use of COMSOL Multiphysics. As for example in Figure 4 (left half), in the COMSOL calculations the modeling volume comprised a 3 μm layer of silicon overlain with a 100 nm gold grating, covered by a 1.5 μm layer of PMMA, and finally followed by a 3 μm air layer. Periodic boundary conditions were added in the grating (x) direction. For the meshing a minimum mesh element size of 0.22 nm was used, while the maximum mesh element size was 185 nm. A curvature factor of 0.2 was used to smooth the vertices so as to better represent the fabricated samples.

Material Parameters

For the frequency-dependent permittivity of both gold and PMMA we made use of Drude–Lorentz,

graphic file with name ph-2019-006622_m001.jpg 1

and Lorentz oscillator,

graphic file with name ph-2019-006622_m002.jpg 2

models, respectively. For gold we used parameters taken from Olmon et al.,34 specifically, ωp = 1.29 × 1016 rad s–1 and γ = 7.30 × 1013 rad s–1, with εb = 1.0. For PMMA single-oscillator parameters were taken from Shalabney et al.,8 specifically, ω0 ≡ 3.28 × 1014 rad s–1 and γ ≡ 2.45 × 1012 rad s–1, with f0 = 0.0165 and εb = 1.99. The parameters for silicon in the infrared are based on data compiled by Edwards35 and are taken to be ε = 11.76 + 0.001i, while for air we took ε = 1.0.

Acknowledgments

We acknowledge financial support from the Engineering and Physical Sciences Research Council (EPSRC) of the United Kingdom, via the EPSRC Centre for Doctoral Training in Metamaterials (Grant No. EP/L015331/1). W.L.B. acknowledges the support of the European Research Council through project Photmat (ERC-2016-AdG-742222: www.photmat.eu).

The authors declare no competing financial interest.

Notes

The research data supporting this publication are openly available from the University of Exeter’s institutional repository at: https://doi.org/10.24378/exe.1604.

References

  1. Stranius K.; Hertzog M.; Börjesson K. Selective manipulation of electronically excited states through strong light–matter interactions. Nat. Commun. 2018, 9, 2273. 10.1038/s41467-018-04736-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Hutchison J. A.; Schwartz T.; Genet C.; Devaux E.; Ebbesen T. W. Modifying Chemical Landscapes by Coupling to Vacuum Fields. Angew. Chem., Int. Ed. 2012, 51, 1592–1596. 10.1002/anie.201107033. [DOI] [PubMed] [Google Scholar]
  3. Bennett K.; Kowalewski M.; Mukamel S. Novel photochemistry of molecular polaritons in optical cavities. Faraday Discuss. 2016, 194, 259–282. 10.1039/C6FD00095A. [DOI] [PubMed] [Google Scholar]
  4. Feist J.; Galego J.; Garcia-Vidal F. J. Polaritonic Chemistry with Organic Molecules. ACS Photonics 2018, 5, 205–216. 10.1021/acsphotonics.7b00680. [DOI] [Google Scholar]
  5. Thomas A.; Lethuillier-Karl L.; Nagarajan K.; Vergauwe R. M. A.; George J.; Chervy T.; Shalabney A.; Devaux E.; Genet C.; Moran J.; Ebbesen T. W. Tilting a ground-state reactivity landscape by vibrational strong coupling. Science 2019, 363, 615. 10.1126/science.aau7742. [DOI] [PubMed] [Google Scholar]
  6. Schachenmayer J.; Genes C.; Tignone E.; Pupillo G. Cavity-Enhanced Transport of Excitons. Phys. Rev. Lett. 2015, 114, 196403. 10.1103/PhysRevLett.114.196403. [DOI] [PubMed] [Google Scholar]
  7. Plumhof J. D.; Stöferle T.; Mai L.; Scherf U.; Mahrt R. F. Room-temperature Bose–Einstein condensation of cavity exciton-polaritons in a polymer. Nat. Mater. 2014, 13, 247. 10.1038/nmat3825. [DOI] [PubMed] [Google Scholar]
  8. Shalabney A.; George J.; Hutchison J.; Pupillo G.; Genet C.; Ebbesen T. W. Coherent coupling of molecular resonators with a microcavity mode. Nat. Commun. 2015, 6, 1–6. 10.1038/ncomms6981. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Long J. P.; Simpkins B. S. Coherent coupling between a molecular vibration and Fabry-Perot optical cavity to give hybridised states in the strong coupling limit. ACS Photonics 2015, 2, 130–136. 10.1021/ph5003347. [DOI] [Google Scholar]
  10. Menghrajani K. S.; Fernandez H. A.; Nash G. R.; Barnes W. L.. Hybridization of Multiple Vibrational Modes via Strong Coupling Using Confined Light Fields. Adv. Opt. Mater. 2019, 1900403. 10.1002/adom.201900403. [DOI] [Google Scholar]
  11. Memmi H.; Benson O.; Sadofev S.; Kalusniak S. Strong coupling between surface plasmon polaritons and molecular vibrations. Phys. Rev. Lett. 2017, 118, 126802. 10.1103/PhysRevLett.118.126802. [DOI] [PubMed] [Google Scholar]
  12. Wan W.; Yang X.; Gao J. Strong coupling between mid-infrared localized plasmons and phonons. Opt. Express 2016, 24, 12367. 10.1364/OE.24.012367. [DOI] [PubMed] [Google Scholar]
  13. Barnes W. L.; Preist T. W.; Kitson S. C.; Sambles J. R. Physical origin of photonic energy gaps in the propagation of surface plasmons on gratings. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 6227–6244. 10.1103/PhysRevB.54.6227. [DOI] [PubMed] [Google Scholar]
  14. Andrew P.; Kitson S. C.; Barnes W. L. Surface-plasmon energy gaps and photoabsorption. J. Mod. Opt. 1997, 44, 395–406. 10.1080/09500349708241879. [DOI] [Google Scholar]
  15. Kitson S. C.; Barnes W. L.; Sambles J. R. Surface-plasmon energy gaps and photoluminescence. Phys. Rev. B: Condens. Matter Mater. Phys. 1995, 52, 11441–11445. 10.1103/PhysRevB.52.11441. [DOI] [PubMed] [Google Scholar]
  16. Polak D. Manipulating matter with strong coupling: harvesting triplet excitons in organic exciton microcavities. Cond-mater 2019, 1806, 09990v1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Lidzey D. G.; Bradley D. D. C.; Skolnick M. S.; Virgili T.; Walker S.; Whittaker D. M. Strong exciton-photon coupling in an organic semiconductor microcavity. Nature 1998, 395, 53. 10.1038/25692. [DOI] [Google Scholar]
  18. Muallem M.; Palatnik A.; Nessim G. D.; Tischler Y. R. Strong Light-Matter Coupling and Hybridization of Molecular Vibrations in a Low-Loss Infrared Microcavity. J. Phys. Chem. Lett. 2016, 7, 2002–2008. 10.1021/acs.jpclett.6b00617. [DOI] [PubMed] [Google Scholar]
  19. Flatten L. C.; Coles D. M.; He Z.; Lidzey D. G.; Taylor R. A.; Warner J. H.; Smith J. M. Electrically tunable organic–inorganic hybrid polaritons with monolayer WS2. Nat. Commun. 2017, 8, 14097. 10.1038/ncomms14097. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Shahbazyan T. V.Exciton–Plasmon Energy Exchange Drives the Transition to a Strong Coupling Regime. Nano Lett. 2019, 19, 3273–3279, PMID: 30973738. 10.1021/acs.nanolett.9b00827 [DOI] [PubMed] [Google Scholar]
  21. Törmä P.; Barnes W. L. Strong coupling between surface plasmon polaritons and emitters: a review. Rep. Prog. Phys. 2015, 78, 013901. 10.1088/0034-4885/78/1/013901. [DOI] [PubMed] [Google Scholar]
  22. Chang Y.; Yai J.; Wu X.; Liu X. Strong and weak coupolings in molecular vibration-plasmon hybrid structures. Opt. Express 2019, 27, 1479–1487. 10.1364/OE.27.001479. [DOI] [PubMed] [Google Scholar]
  23. García-Vidal F. J.; Martín-Moreno L. Transmission and focusing of light in one-dimensional periodically nanostructured metals. Phys. Rev. B: Condens. Matter Mater. Phys. 2002, 66, 155412. 10.1103/PhysRevB.66.155412. [DOI] [Google Scholar]
  24. Vasa P.; Wang W.; Pomraenke R.; Lammers M.; Maiuri M.; Manzoni C.; Cerullo G.; Lienau C. Real-time observation of ultrafast Rabi oscillations between excitons and plasmons in metal nanostructures with J-aggregates. Nat. Photonics 2013, 7, 128–132. 10.1038/nphoton.2012.340. [DOI] [Google Scholar]
  25. Ritchie R. H.; Arakawa E. T.; Cowan J. J.; Hamm R. N. Surface-plasmon resonance effect in grating diffraction. Phys. Rev. Lett. 1968, 21, 1530–1533. 10.1103/PhysRevLett.21.1530. [DOI] [Google Scholar]
  26. Hooper I. R.; Sambles J. R.. Surface plasmon polaritons on thin-slab metal gratings. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 67, 235404. 10.1103/PhysRevB.67.235404. [DOI] [Google Scholar]
  27. Nagai H. Infrared spectra of stereoregular plymethyl methacrylate. J. Appl. Polym. Sci. 1963, 7, 1697–1714. 10.1002/app.1963.070070512. [DOI] [Google Scholar]
  28. Luxmoore I. J.; Liu P. Q.; Li P.; Faist J.; Nash G. R. Graphene–Metamaterial Photodetectors for Integrated Infrared Sensing. ACS Photonics 2016, 3, 936–941. 10.1021/acsphotonics.6b00226. [DOI] [Google Scholar]
  29. Rodriguez S.; Rivas J. G. Surface lattice resonances strongly coupled to Rhodamine 6G excitons: tuning the plasmon-exciton-polariton mass and composition. Opt. Express 2013, 21, 27411. 10.1364/OE.21.027411. [DOI] [PubMed] [Google Scholar]
  30. Vakevainen A. I.; Moerland R. J.; Rekola H. T.; Eskelinen A. P.; Martikainen J. P.; Kim D. H.; Torma P. Plasmonic surface lattice resonances at the strong coupling regime. Nano Lett. 2014, 14, 1721–1727. 10.1021/nl4035219. [DOI] [PubMed] [Google Scholar]
  31. Wang W.; Ramezani M.; Vakevainen A. I.; Torma P.; Rivas J. G.; Odom T. W. The rich photonic world of plasmonic nanoparticle arrays. Mater. Today 2018, 21, 303–314. 10.1016/j.mattod.2017.09.002. [DOI] [Google Scholar]
  32. Kravets V. G.; Kabashin A. V.; Barnes W. L.; Grigorenko A. N. Plasmonic Surface Lattice Resonances: A Review of Properties and Applications. Chem. Rev. 2018, 118, 5912–5951. 10.1021/acs.chemrev.8b00243. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Moilanen A. J.; Hakala T. K.; Törmä P. Active Control of Surface Plasmon–Emitter Strong Coupling. ACS Photonics 2018, 5, 54–64. 10.1021/acsphotonics.7b00655. [DOI] [Google Scholar]
  34. Olmon R. L.; Slovick B.; Johnson T. W.; Shelton D.; Oh S.-H.; Boreman G. D.; Raschke M. B. Optical dielectric function of gold. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 86, 235147. 10.1103/PhysRevB.86.235147. [DOI] [Google Scholar]
  35. Edwards, In Handbook of Optical Constants of Solids; Palik E., Ed.; Academic Press Inc., 1985; Chapter Silicon (Si), pp 547–569. [Google Scholar]

Articles from ACS Photonics are provided here courtesy of American Chemical Society

RESOURCES