Two Relaxation Time Lattice Boltzmann Method Coupled to Fast Fourier Transform Poisson Solver: Application to Electroconvective Flow

Abstract

Electroconvective flow between two infinitely long parallel electrodes is investigated via a multiphysics computational model. The model solves for spatiotemporal flow properties using two-relaxation-time Lattice Boltzmann Method for fluid and charge transport coupled to Fast Fourier Transport Poisson solver for the electric potential. The segregated model agrees with the previous analytical and numerical results providing a robust approach for modeling electrohydrodynamic flows.

III. INTRODUCTION

Electro-hydrodynamics (EHD) studies the interaction of the fluid with electric field [1]. As a subset of EHD, electroconvection (EC) is a phenomenon where convective transport is induced by unipolar discharge into a dielectric fluid [2-21]. Felici first performed a stability analysis of EC using a non-linear hydraulic model [22, 23]. Linear stability analysis was investigated by Schneider & Watson [24, 25] and Atten & Moreau [26], who showed that, in the weak-injection limit, C ≪ 1, where C is the charge injection, the flow stability is determined by the criterion T_cC², where T_c is the linear stability threshold for the electric Rayleigh number (T) – a ratio between electric force to the viscous force. In the space-charge-limited (SCL) injection (C→∞), the flow stability is determined by T_c. Experimental observations of Lacroix et al. [27] and Atten et al. [28] showed that, in the SLC limit, T_c = 100 [28], while linear stability analysis suggests T_c=160.45 for the same conditions [26]. Authors suggest that the discrepancy is due to the omission of the charge diffusion term in the analysis [29]. The effect of charge diffusion was investigated by Zhang et al., who performed a linear stability analysis [12] followed by a non-linear analysis using the multiscale method [17]. Zhang et al. found that the charge diffusion has a non-negligible effect on T_c, but their analysis could not bridge the discrepancy between the experimental and theoretical values.

To gain insight into the flow-charge interaction, the EC problem has been investigated by numerical methods. Castellanos and Atten used a finite difference model, concluding that large numerical diffusivity can contaminate the model [3]. Other numerical models used to study EC phenomena include the particle-in-cell method [30], finite volume method with flux-corrected transport [31], total variation diminishing scheme [5, 8, 14-16], and the method of characteristic [4]. Recently, Luo et al. showed that a unified Lattice Boltzmann model (LBM) matches the linear and finite amplitude stability criteria of the subcritical bifurcation in EC flow [18-21] for both 2D and 3D flow scenarios. This unified LBM transforms the elliptic Poisson equation to a parabolic advection-diffusion equation and introduces artificial coefficients to control the evolution of the electric potential, which requires additional sub-iterations at each time step.

In this paper, we demonstrate an alternative approach to modeling EC flow; our segregated solver combines (i) a two-relaxation-time (TRT) LBM [32-41] for modeling fluid transport and charged species, (ii) a Fast Fourier Transform (FFT) [42-45] Poisson approach for solving for the electric field directly. The TRT model introduces two relaxation parameters aiding the numerical algorithm stability without sacrificing computational efficiency. The TRT model is parameterized with physical units without rescaling to lattice units.

IV. NUMERICAL METHOD

1. Governing Equations

The governing equations for EHD flow include the Navier-Stokes equations (NSE), with the addition of an electric forcing term F_e = ρ_c ∇ φ to the momentum equation, the charge transport equation, and the Poisson equation for electric potential.

$$\nabla •\mathbf{u}=0,$$ (1)

$$\rho \frac{D\mathbf{u}}{Dt}=-\nabla P+\mu {\nabla }^2\mathbf{u}-{\rho }_c\nabla \phi ,$$ (2)

$$\frac{\partial {\rho }_c}{\partial t}+\nabla •\left[(\mathbf{u}-{\mu }_b\nabla \phi ){\rho }_c-D_c\nabla {\rho }_c\right]=0,$$ (3)

$${\nabla }^2\phi =-\frac{{\rho }_c}{\epsilon },$$ (4)

where ρ is the density, μ - dynamic viscosity, u = (u_x, u_y) - velocity vector field, P - static pressure, μ_b - mobility, D_c - ion diffusivity, ρ_c - charge density, ε - electric permittivity, φ - electric potential. The electric force provides a source term in the momentum equation (Eq. 2). The unknown properties are velocity field u, pressure P, charge density ρ_c, and electric potential φ.

2. Lattice Boltzmann Method

The TRT-LBM is applied to NSE (Eq. 1-2) and the transport equation for charge density (Eq. 3). The mesoscopic solutions of the LBM yield a discrete distribution function of velocity f_i(x, t) and charge density g_i(x, t). The values of ρ, ρ_c, and momentum density ρu can be evaluated by weighted sums.

$$\rho (\mathbf{x},t)=\sum _i{f}_i(\mathbf{x},t),$$ (5)

$${\rho }_c(\mathbf{x},t)=\sum _i{g}_i(\mathbf{x},t),$$ (6)

$$\rho \mathbf{u}(\mathbf{x},t)=\sum _i{\mathbf{c}}_i{f}_i(\mathbf{x},t)+\frac{{\mathbf{F}}_e\Delta t}{2}=\sum _i{\mathbf{c}}_i{f}_i(\mathbf{x},t)-\frac{{\rho }_c\nabla \phi \Delta t}{2},$$ (7)

The discrete normalized velocity, c_i = (c_ix, c_iy) at position - x and time - t depends on a specific discretization scheme; here, we use the D2Q9 model (two spatial dimensions and nine discrete velocities). The spatial discretization is uniform (∆x = ∆y ), and the temporal discretization - ∆t. The c_i parameters (i=0~8) are shown in the Supplementary Material. Keeping the temporal discretization term allows for temporal accuracy control and to perform dynamic analysis. For example, in the analysis of electroconvection stability using Dynamic Mode Decomposition (DMD), it was found that the model performance is dependent on temporal discretization value [47]; thus it can be beneficial to explicitly include the ∆t in the formulation. The SI units are used for macroscopic variables and discretization, e.g., ∆x is given in meters and ∆t in seconds.

The Lattice Boltzmann Equations (LBEs) for flow field and charge density are:

$$f_i(\mathbf{x}+{\mathbf{c}}_i\Delta t,t+\Delta t)=f_i(\mathbf{x},t)\underset{\mathrm{TRT}\mathrm{collision}\mathrm{operator}}{\underbrace{-\Delta t\left[{\omega }^{+}\left(f_i^{+}-f_i^{\mathit{eq}+}\right)+{\omega }^{-}\left(f_i^{-}-f_i^{\mathit{eq}-}\right)\right]}}+\underset{\mathrm{TRT}\mathrm{source}\mathrm{operator}}{\underbrace{\Delta t\left[\left(1-\frac{{\omega }^{+}\Delta t}{2}\right)F_i^{+}(\mathbf{x},t)+\left(1-\frac{{\omega }^{-}\Delta t}{2}\right)F_i^{-}(\mathbf{x},t)\right]}},$$ (8)

$$g_i(\mathbf{x}+{\mathbf{c}}_i\Delta t,t+\Delta t)=g_i(\mathbf{x},t)\underset{\mathrm{TRT}\mathrm{collision}\mathrm{operator}}{\underbrace{-\Delta t\left[{\omega }_g^{+}\left(g_i^{+}-g_i^{\mathit{eq}+}\right)+{\omega }_g^{-}\left(g_i^{-}-g_i^{\mathit{eq}-}\right)\right]}},$$ (9)

$f_i^{\mathit{eq}}$ and $g_i^{\mathit{eq}}$ are the equilibrium distributions for flow field and charges respectively, which are given by

$$f_i^{\mathit{eq}}(\mathbf{x},t)=w_i\rho \left(1+\frac{\mathbf{u}•{\mathbf{c}}_i}{c_s^2}+\frac{(\mathbf{u}•{\mathbf{c}}_i{)}^2}{2c_s^4}-\frac{\mathbf{u}•\mathbf{u}}{2c_s^2}\right),$$ (10)

$$g_i^{\mathit{eq}}(\mathbf{x},t)=w_i{\rho }_c\left(1+\frac{(\mathbf{u}-{\mu }_b\nabla \phi )•{\mathbf{c}}_i}{c_s^2}+\frac{{\left[(\mathbf{u}-{\mu }_b\nabla \phi )•{\mathbf{c}}_i\right]}^2}{2c_s^4}-\frac{(\mathbf{u}-{\mu }_b\nabla \phi )•(\mathbf{u}-{\mu }_b\nabla \phi )}{2c_s^2}\right),$$ (11)

F_i is the forcing term accounting for the electric force

$$F_i=w_i\left(\frac{{\mathbf{c}}_i-\mathbf{u}}{c_s^2}+\frac{({\mathbf{c}}_i•\mathbf{u}){\mathbf{c}}_i}{c_s^4}\right)•{\mathbf{F}}_e’$$ (12)

where $c_s^2=P∕\rho =(1∕3)(\Delta x∕\Delta t{)}^2$ is the speed of sound [32, 33, 35, 36, 48], which is commonly set to be $c_s^2=1∕3$ in lattice units (∆x = ∆y = ∆t = 1); however, since the model is parameterized, and the ∆t is explicitly included in the formulation, $c_s^2$ has to be scaled depending on the choice of ∆x and ∆t as shown in the supplementary materials. ${\tau }^{\pm }=1∕{\omega }^{\pm }$ and ${\tau }_g^{\pm }=1∕{\omega }_g^{\pm }$ are the times at which the distribution functions relax to equilibrium, and w_i is the weight for the velocity component c_i, the values are provided in the supplementary materials. The values of c_s are tunable, especially in Eq. 11 [37, 39, 40]; they are set to be the same because of the adopted equilibrium form. The values of w_i (Eq. 11) are not restricted to the choice of w_i in Eq. 10. Since Eq.3 is isotropic and in the case of simple rectangular geometry, the reduced coordinate stencil D2Q5 can be appealing [40, 41]. The use of the coordinate stencil may be also beneficial for implementation of bounce-back Neumann condition at the walls. However, as noted by Ginzburg, the full-weight stencils are attractive because of their stability and anisotropy [41, 49]. As suggested by Luo et al., the D2Q9 model is used in the current work to model the charge transport equation [18]. Since the isotropic hydrodynamic weight is used to enable the isotropy of the high-order corrections [37, 39], D2Q9 can be reduced to D2Q5 to enhance the performance [40, 41].

The TRT approach has been previously used to model the collision operators [32-34, 37-41] and the momentum source operator [50, 51]. Alternatively, to SRT operators, TRT is more robust for EC problems, as it provides additional relaxation parameter, improving the numerical stability [48]. The terms specified in the TRT collision operators and the source operator are

$$f_i^{+}=\frac{f_i+f_{\stackrel{‒}{i}}}{2},f_i^{-}=\frac{f_i-f_{\stackrel{‒}{i}}}{2},f_i^{\mathit{eq}+}=\frac{f_i^{\mathit{eq}}+f_{\stackrel{‒}{i}}^{\mathit{eq}}}{2},f_i^{\mathit{eq}-}=\frac{f_i^{\mathit{eq}}-f_{\stackrel{‒}{i}}^{\mathit{eq}}}{2}$$ (13)

$$g_i^{+}=\frac{g_i+g_{\stackrel{‒}{i}}}{2},g_i^{-}=\frac{g_i-g_{\stackrel{‒}{i}}}{2},g_i^{\mathit{eq}+}=\frac{g_i^{\mathit{eq}}+g_{\stackrel{‒}{i}}^{\mathit{eq}}}{2},g_i^{\mathit{eq}-}=\frac{g_i^{\mathit{eq}}-g_{\stackrel{‒}{i}}^{\mathit{eq}}}{2}$$ (14)

$$F_i^{\pm }=\frac{F_i\pm F_{\stackrel{‒}{i}}}{2}$$ (15)

Subscript $\overline{i}$ denotes the velocity component opposite to i , such that ${\mathbf{c}}_i=-{\mathbf{c}}_{\overline{i}}$. Symmetric relaxation parameters ω⁺ and antisymmetric ${\omega }_g^{-}$ are determined by the viscosity and diffusivity respectively [35, 36, 52]:

$$v=c_s^2\left(\frac{1}{{\omega }^{+}}-\frac{\Delta t}{2}\right),D_c=c_s^2\left(\frac{1}{{\omega }_g^{-}}-\frac{\Delta t}{2}\right).$$ (16)

ω⁻ and ${\omega }_g^{+}$ need to satisfy

$$\Lambda ={\Lambda }^{+}{\Lambda }^{-}=\left(\frac{1}{{\omega }^{+}\Delta t}-\frac{1}{2}\right)\left(\frac{1}{{\omega }^{-}\Delta t}-\frac{1}{2}\right),{\Lambda }_g={\Lambda }_g^{+}{\Lambda }_g^{-}=\left(\frac{1}{{\omega }_g^{+}\Delta t}-\frac{1}{2}\right)\left(\frac{1}{{\omega }_g^{-}\Delta t}-\frac{1}{2}\right),$$ (17)

where Λ and Λ_g are free factors used to control the algorithm stability [48]. Here, Λ = 1/12 and Λ_g = 10⁻⁶; the large difference accounts for the mismatch between the neutral molecule and charge diffusivity. The Λ = 1/12 is chosen for the accuracy in solving the flow equation, and the choice of Λ_g = 10⁻⁶ is used for the accuracy of solving the electric properties in the domain; error analysis is included in the supplementary materials. Ginzburg and colleagues also suggested that the choice of ${\Lambda }_g^{+}={\Lambda }_g^{-}=\sqrt{1∕12}$ suppresses the third-order error in advection-diffusion equations[36, 37, 39, 49].

3. Fast Poisson Solver

The Poisson equation (Eq. 4) is directly solved by a fast Poisson solver using a 2D FFT algorithm. This solver does not use an artificial time-stepping term in solving the elliptical equation as previously proposed by the unified LBM model [18-21]. The discretized grid function can be written as:

$$[D_x^2+D_y^2]{\phi }_{x,y}=s_{x,y}$$ (18)

where $D_x^2$ and $D_y^2$ are 2^nd order derivatives operators in x - y coordinates; s_x,y - source term representing space charge effect. Fourier spectral method is used in the x-direction and 2^nd order finite difference scheme in the y-direction. In x-direction, the FFT algorithm is used to implement the standard Discrete Fourier transform (DFT).

$${\mathit{DFT}}_x[{\phi }_{x,y}]=\sum _{x=1}^{NX}{\phi }_{x,y}\text{exp}\left[-i\frac{2\pi (k_x-1)}{NX}(x-1)\right],1\le k_x\le NX.$$ (19)

where k_x is the wavenumber and NX is the number of grid points in the x-direction. The 2^nd derivative in the x-direction can be calculated in the Fourier domain

$${\mathit{DFT}}_x\left[D_x^2{\phi }_{x,y}\right]={\mathit{DFT}}_x\left[\frac{{\partial }^2{\phi }_{x,y}}{\partial x^2}\right]=-k_x^2{\mathit{DFT}}_x\left[{\phi }_{x,y}\right].$$ (20)

Fourier transform in the y-direction uses an odd extension of the domain to satisfy the Dirichlet boundary conditions.

$${\phi }_{x,y_{\mathit{ext}}}^{\mathit{ext}}=\left[0,{\phi }_{x,1},{\phi }_{x,2},\cdots ,{\phi }_{x,Ny},0,-{\phi }_{x,Ny},\cdots ,{\phi }_{x,1}\right],$$ (21)

$$s_{x,y_{\mathit{ext}}}^{\mathit{ext}}=\left[0,s_{x,1},s_{x,2},\cdots ,s_{x,Ny},0,-s_{x,Ny},\cdots ,s_{x,1}\right],$$ (22)

where NY is the number of grid points in the y-direction. The size of the extended matrices is NX×NE, where NE = 2NY + 2 ; the y_ext is the extended y indices, ranging from 1 to NE.

From the definition of DFT (Eq.19), we have:

$${\mathit{DFT}}_y\left[{\phi }_{x,y+1}^s\right]=\text{exp}({\mathit{ik}}_y\Delta y){\mathit{DFT}}_y\left[{\phi }_{x,y}\right],$$ (23)

where φ^s is a periodically shifted vector by ∆y of φ in y-direction. Applying a central differencing operator in y_ext direction gives:

$${\mathit{DFT}}_{y_{\mathit{ext}}}\left[D_{y_{\mathit{ext}}}^2{\phi }_{x,y_{\mathit{ext}}}^{\mathit{ext}}\right]=\frac{\text{exp}({\mathit{ik}}_{y_{\mathit{ext}}}\Delta y)+\text{exp}(-{\mathit{ik}}_{y_{\mathit{ext}}}\Delta y)-2}{\Delta y^2}{\mathit{DFT}}_{y_{\mathit{ext}}}\left[{\phi }_{x,y_{\mathit{ext}}}^{\mathit{ext}}\right]=\frac{-4{\sin }^2\left(k_{y_{\mathit{ext}}}\Delta y∕2\right)}{\Delta y^2}{\mathit{DFT}}_{y_{\mathit{ext}}}\left[{\phi }_{x,y_{\mathit{ext}}}^{\mathit{ext}}\right].$$ (24)

Therefore, the Fourier transform of Eq.18 is

$$-\left(k_x^2+\frac{4{\sin }^2\left(k_{y_{\mathit{ext}}}\Delta y∕2\right)}{\Delta y^2}\right){\mathit{DFT}}_{x,y_{\mathit{ext}}}\left[{\phi }_{k_x,k_{y_{\mathit{ext}}}}^{\mathit{ext}}\right]={\mathit{DFT}}_{x,y_{\mathit{ext}}}\left[s_{k_x,k_{y_{\mathit{ext}}}}^{\mathit{ext}}\right]$$ (25)

The Inverse Fast Fourier Transform (IFFT) algorithm transforms ${\mathit{DFT}}_{x,y_{\mathit{ext}}}\left[{\phi }_{k_x,k_{y_{\mathit{ext}}}}^{\mathit{ext}}\right]$ into the spatial domain. Then, the electric potential in the original domain is obtained by retaining the first half (1 ≤ y ≤ Ny) of the extended solution matrix. In principle, TRT solver can replace the Poisson solver by employing the sub-iterations within each time step [53, 54], which may be beneficial for problems with complex geometries. However, in the case with periodic boundaries, the FFT method is a more efficient choice of solving for the electric potential.

4. Boundary Conditions and Method Implementation

The numerical method is implemented in C++ using CUDA GPU computing. The number of threads in the x-direction in each GPU block is equal to NX; the number of GPU blocks in the y-direction is equal to NY. FFT and IFFT operations are performed using the cuFFT library. All variables are computed with double precision to reduce truncation errors. The numerical method was shown to be 2^nd order accurate in space. Error analysis is provided in supplementary materials. To reduce computational cost while maintaining accuracy, the grid of NX = 122, NY = 100 is used throughout this work. Macroscopic and mesoscopic boundary conditions are specified in Table I.

Table I.

Boundary conditions used in the numerical simulations.

Boundary	Macro-variables Conditions	Meso-variables Conditions
x direction boundaries	Periodic	Periodic
Upper wall	u = 0, φ = 0 and ∆ρc = 0	Bounce-back for fi [32, 38, 40, 41,48] Bounce-back for gi [32, 38, 40, 41, 48]
Lower wall	u=0, φ=φ0 and ρc = ρ0	Bounce-back for fi $\frac{\partial g_i}{\partial z}=0$

The full-way bounce-back is used for Dirichlet boundary conditions for fluid flow [18, 19, 55]. The bounce-back method for Neumann boundary conditions applied to impermeable solid walls can introduce spurious boundary layer because of the diagonal velocity-weights [40, 41]. Nevertheless, The Neumann boundary condition for g_i is an outflow boundary condition for charge density transport [18, 19, 48]. The choice of small Λ_g ⊄ can improve accuracy because of the horizontal boundaries [40, 41].

V. RESULT AND DISCUSSION

1. Non-dimensional Analysis and Solution for Hydrostatic State

Governing equations yield four non-dimensional parameters that describe the system’s state [12, 17-21].

$$M=\frac{(\epsilon ∕\rho {)}^{1∕2}}{{\mu }_b},T=\frac{\epsilon \Delta {\phi }_0}{\mu {\mu }_b},C=\frac{{\rho }_0{H}^2}{\epsilon \Delta {\phi }_0},Fe=\frac{{\mu }_b\Delta {\phi }_0}{D_e},$$ (26)

where H is the distance between the electrodes (distance between the two infinite plates), ρ₀ is the injected charge density at the anode, and ∆φ₀ is the voltage difference applied to the electrodes. The physical interpretation of these parameters are as follows: M- the ratio between hydrodynamic mobility and the ionic mobility; T- the ratio between electric force to the viscous force; C- the charge injection level; and Fe- the reciprocal of the charge diffusivity coefficient [12, 17]. For electroconvection system considered in this paper, these four non-dimensional parameters can characterize the flow. Velocity is not explicitly included; however, for the scenarios with strong advection, a different set of scaling parameters can be more attractive [46, 56].

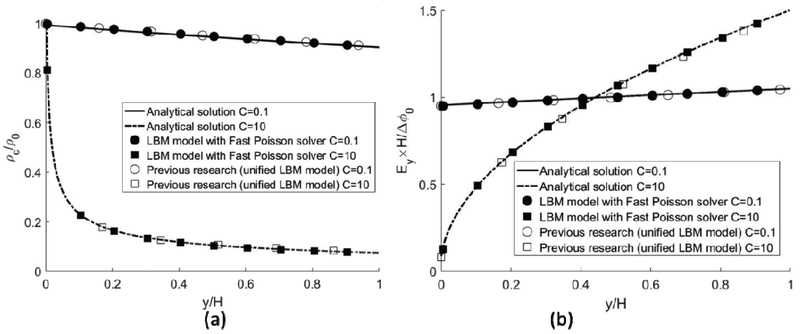
FIG. 1 shows that our hydrostatic solutions for electric field and charge density agree well with the model of Luo et al. [18, 19] and the analytical solution [30, 57]. The analytical solution is based on a reduced set of equations for the electric field in one-dimensional coordinates.

$${\rho }_c={\rho }_a(y+y_a{)}^{-1∕2},$$ (27)

$$E_y=\frac{2{\rho }_a}{\epsilon }(y+y_a{)}^{1∕2},$$ (28)

where ρ_a and y_a are parameters that depend on the boundary conditions and geometry. For the hydrostatic state, parameter C dominates the system [12, 17].

FIG. 1.

Hydrostatic solution comparison of the TRT LBM and Fast Poisson solver, unified SRT LBM [18], and the analytical solution [30, 57] for C = 0.1 and C = 10, Fe = 4000. (a) Electric field and (b) charge density;

Table II shows the dimensional parameters used for the analytical solution and the L₂ norm error between numerical results and analytical solutions. The numerical errors are lower than reported for the unified SRT LBM simulation (e_L2 =0.0076) [18].

Table II.

Dimensional parameters for the analytical model and L₂ norm errors e_L2 for weak ion injection C = 0.1 and strong ion injection C = 10.

C	0.1	10
ρa (Coulomb / m5/2)	0.218	0.75
ya (m)	4.8	0.003
eL2 of Ey	0.0031	0.0030
eL2 of ρc	0.0035	0.0031

2. Electroconvection Instability

To model electro-convective instability, the steady-state hydrostatic solution is perturbed using waveform functions that satisfy the boundary conditions and continuity equation:

$$\begin{gathered} u_x=L_x\sin (2\pi y∕L_y)\sin (2\pi x∕L_x)\times {10}^{-3} \\ {u}_y=L_y\left[\cos (2\pi y∕L_y)-1\right]\cos (2\pi x∕L_x)\times {10}^{-3}. \end{gathered}$$ (29)

The physical domain size is Lx = 1.22m and Ly = 1m limits the perturbation wavenumber to λ_x = 2π/L_x ≈ 5.15(1/m) -- the most unstable mode under the condition, where C = 10, M = 10, Fe = 4000 [19]. The electric Nusselt number Ne₀ = I₁ / I₀ acts as a criterion of flow stability, where I₁ is the cathode current at a specific condition, I₀ is the cathode current for the hydrostatic solution [5]. For cases where EC vortices exist, Ne₀ > 1. For a strong ion injection, the EC stability largely depends on T; so, in this analysis, T is varied, while other parameters are held constant: C = 10, M = 10 and Fe = 4000.

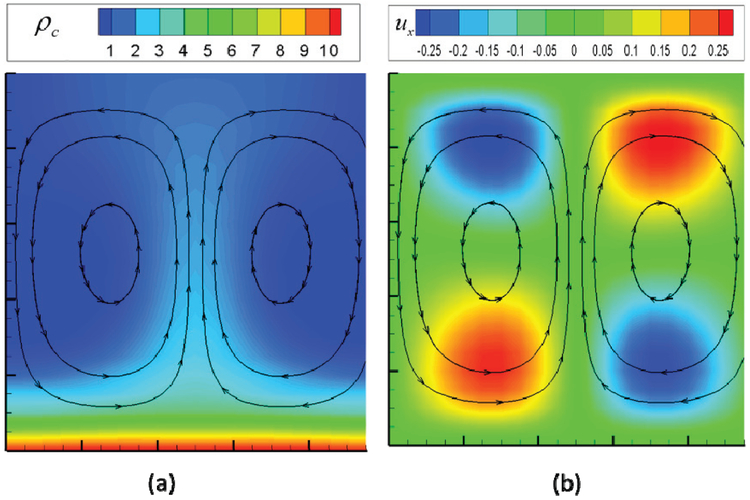
For T ≥ T_c and the perturbation is given by Eq. 29, the flow becomes unstable developing EC vortices which are maintained by an electric force acting on the ionized fluid -- a combination of applied electric field and the space charge effect. The space charge effect can alter the applied electric field in the area of high charge density [56]. FIG. 2 (a) shows the formation of counter-rotating vortices; the charge density contour plotted with streamlines. In an upward fluid motion, the local charge transport is enhanced as indicated by the higher charge density in the center of the domain. In downward flow motion, the charge transport decreases, see the darker blue in the edges of the domain. FIG. 2 (b) shows the x-directional velocity contour. High x-velocity regions are located near the top and bottom walls; the flow is symmetric, which indicates that the steady-state solution has the same wavelength in x and y directions as the perturbation equations (Eq. 29).

FIG. 2.

Charge density and u_x contours for EHD convection with vortices.

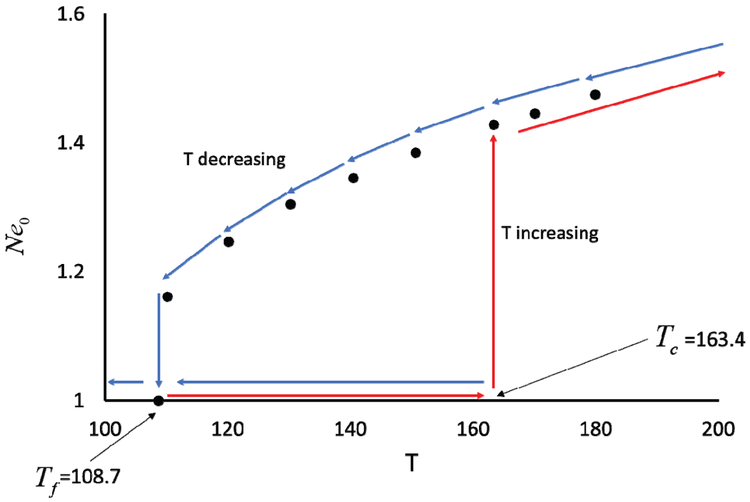
FIG. 3 (a) shows the EC flow stability analysis, demonstrated by Ne₀ as a function of T. When T < T_c the perturbation does not trigger the flow instability, the perturbed flow reverses to the hydrostatic state. If T decreases after the EC vortices are formed, they are maintained until T = T_f when the system returns to the hydrostatic state. The model predicts the bifurcation points at T_c = 163.4 and T_f = 108.7 agreeing Luo et al. [19] (T_c = 163.1, T_f = 108.7 ), the linear stability analysis [12, 19] (T_c = 163.5), and the finite volume method [16] (T_f = 108.2 ) under the same conditions. Neither numerical model or linear stability analysis agree with the experimental data. The proposed segregated TRT-LBM approach is consistent with the previous research; however, it does not modify governing equations by introducing artificial terms needed for numerical stability and yields fast convergence of the elliptical Poisson equation enabled for the FFT approach.

FIG. 3.

Electric Nusselt number Ne₀ depends on electric Rayleigh number T

VI. CONCLUSIONS

This work presents a numerical investigation of electroconvection phenomena between two parallel plates. The numerical approach combines (i) TRT-LBM for solving the transport equation of flow field and charged species, and (ii) Fast Poisson Solver. The TRT model allows for the use of two relaxation parameters, accounting for the difference between the transport properties of neutral molecules and charged species. The choice of relaxation parameters allows for both accuracy and stability over a wide variety of conditions. FFT algorithm for Poisson’s equation directly solves for electric field enabling fast overall algorithm convergence. The numerical method is 2^nd order accurate; it shows robust performance and agrees with previous results for the hydrostatic solution and for the solution where EC vortices are present.