A MR-TRUS Registration Method for Ultrasound-Guided Prostate Interventions

Abstract

In this paper, we report a MR-TRUS prostate registration method that uses a subject-specific prostate strain model to improve MR-targeted, US-guided prostate interventions (e.g., biopsy and radiotherapy). The proposed algorithm combines a subject-specific prostate biomechanical model with a B-spline transformation to register the prostate gland of the MRI to the TRUS images. The prostate biomechanical model was obtained through US elastography and a 3D strain map of the prostate was generated. The B-spline transformation was calculated by minimizing Euclidean distance between the normalized attribute vectors of landmarks on MR and TRUS prostate surfaces. This prostate tissue gradient map was used to constrain the B-spline-based transformation to predict and compensate for the internal prostate-gland deformation. This method was validated with a prostate-phantom experiment and a pilot study of 5 prostate-cancer patients. For the phantom study, the mean target registration error (TRE) was 1.3 mm. MR-TRUS registration was also successfully performed for 5 patients with a mean TRE less than 2 mm. The proposed registration method may provide an accurate and robust means of estimating internal prostate-gland deformation, and could be valuable for prostate-cancer diagnosis and treatment.

1. INTRODUCTION

Prostate cancer is a major international health problem with a large and rising incidence in many parts of the world [1–3]. Transrectal ultrasound (TRUS) is the standard imaging modality for image-guided interventions (e.g. biopsy and brachytherapy) due to its versatility and real-time capability. However, in these procedures, the cancerous regions often are not well-targeted because of the inability to reliably identify prostate cancer through TRUS [4–8]. In the past decade, MR imaging has shown promise in visualizing prostate tumors with high sensitivity and specificity for the detection of early-stage prostate cancer [9–11]. A number of researchers have reported the use of multiparametric MRI for cancer detection in prostates with high rates of success [9, 12]. Therefore, the ability to incorporate MR-targeted cancer-bearing regions into TRUS-guided prostate procedures can provide extremely important benefits in terms of more successful prostate-cancer diagnosis and treatment.

To enable a MR-targeted, TRUS-guided prostate intervention, MR-TRUS prostate registration is required to map the diagnostic MRI information onto the ultrasound images. The MR-TRUS image registration is challenging due to the intrinsic differences in grey-level intensity characteristics between the two modalities, combined with the presence of artifacts (particularly in the TRUS images). Hence, standard intensity-based approaches, such as mutual information, often perform poorly since a probabilistic relationship between MR and TRUS voxel intensities usually does not exist [13]. Recently, several non-intensity-based methods have been explored for MR-TRUS prostate registration. Bharatha et al. used an elastic finite element (FE) model to align pre- with intra-procedural images of the prostate [14]. Risholm et al. described a probabilistic method for non-rigid registration of prostate images based on a biomechanical FE model which treats the prostate as an elastic material [15]. Davatzikos et al. [16] and Mohamed et al. [17] proposed combining statistical motion modeling with FE analysis to generate 3D deformable models for MR-TRUS prostate image registration. Hu et al. used a FE-based statistical motion model trained by biomechanical simulations and registered the model to 3D TRUS images [18]. This paper introduces a MR-TRUS registration method that combines B-spline-based transformation with a subject-specific strain model. The novelty of the proposed method is the utilization of the US elastography concept to obtain detailed and subject-specific biomechanical information – 3D strain map – of the prostate. Unlike the previous biomechanical model, elastic parameters are assigned to various parts of the prostate (central zone, peripheral zone and the outer prostate gland) and surrounding structures (such as the rectal wall, bladder or bone). Our biomechanical model is able to take into account the wide variations among patients and within each prostate gland – normal prostatic tissue, cysts, cancers and calcifications all have different elastic properties. To the best of our knowledge, this is the first study to utilize US elastography to generate a subject-specific strain model to improve the volumetric deformation in MR-TRUS prostate registration.

This paper begins by introducing the prostate strain map generated from US elastography (Sec. 2.1). The B-spline-based registration is subsequently presented in Sec. 2.2. The combined deformation model is described in Sec. 2.3. The MR-TRUS registration method is validated through a prostate-phantom experiment and a clinical study of 5 prostate-cancer patients (Sec. 3). Finally, we conclude in Sec. 4 with a discussion.

2. METHODS

The proposed method employs patient-specific prostate-gland elasticity (strain) property to guide the prostate volumetric deformation in MRI and TRUS registration. As shown in Fig. 1, the MR-TRUS registration method consists of three major components: (1) to calculate a 3D prostate strain vector map obtained from the two TRUS images; (2) to use surface-based registration between the MR and TRUS prostate surfaces to capture the prostate transformation based on the B-spline model; and (3) to combine the strain vector map into the B-spline-based transformation to constrain the volumetric deformation of the prostate gland. In particular, we exploit the US elastography concept, in which a detailed 3D strain map of the prostate is generated for each patient using two sets of 3D TRUS scans acquired under different TRUS probe pressures. The B-spline transformation is calculated by minimizing the Euclidean distance between the normalized attribute vectors of surface landmarks of MR and TRUS prostate surfaces. The biomechanical mode is subsequently used to constrain the B-spline-based deformation to achieve an accurate internal volumetric deformation. The schematic flow chart of the registration method is shown in Fig. 2.

Figure 1.

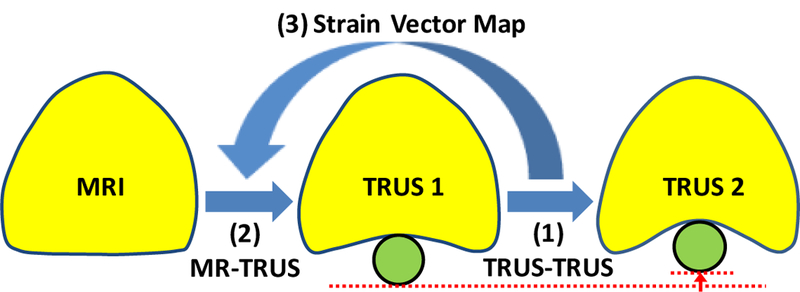
The MR-TRUS prostate registration diagram. The prostate gland is shown in yellow. The green circle represents the TRUS probe.

Figure 2.

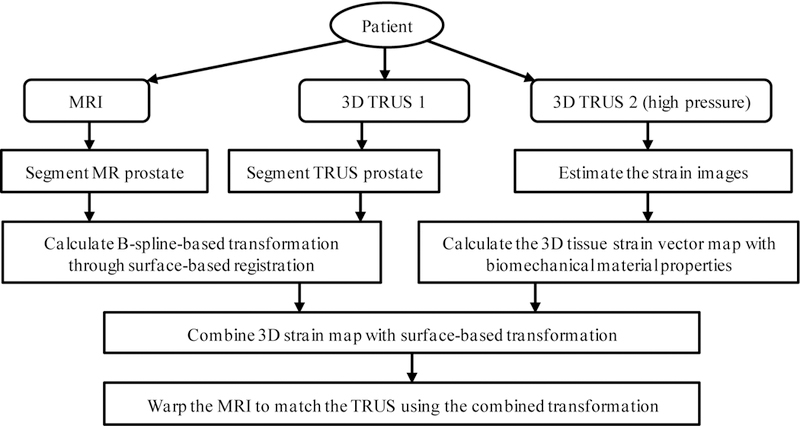
The flow chart of the MR-TRUS prostate registration.

2.1. Patient-Specific Strain Map from Elastography

Elastography, strain or elasticity imaging, is a medical imaging modality that maps the elastic properties of soft tissue. Strain is defined as the deformation of an object, normalized to its original shape, which describes the compressibility of biological tissues. In other words, a strain map displays the elastic properties of soft tissue. The essential step of generating a strain map is to accurately estimate tissue displacement between pre- and post-stress images, which is equivalent to finding the corresponding point before and after pressure for each point. As a result, the strain map reconstruction is considered as a non-rigid image registration problem [19–21]. In our study, the two 3D TRUS images were captured with a clinical ultrasound scanner under different TRUS probe-induced pressures (compression). In order to estimate the displacement of the prostate tissue deformation between two TRUS images, we mapped the first 3D TRUS image to the second 3D TRUS image with high pressure using a hybrid deformable image registration, combining normalized mutual information (NMI) metric with normalized sum-of-squared-differences (NSSD) metric. The similarity measure expresses the quality of the match between the transformed post-stress floating ultrasound image and the pre-stress reference image as a function of the transformation. Since the local intensity and contrast of the ultrasound images could change after compression, we combined a voxel-based and structure-based similarity measure. This hybrid similarity measure provides a better image alignment than using the NMI metric alone, since the NSSD-term is an edge-based alignment metric, and it is not sensitive to the local image contrast changes. Thus, the hybrid matching metric provides a better image alignment than the NSSD or NMI, because it is only sensitive to edges or local image contrast, respectively [22]. The tissue at a point undergoes an actual displacement specified by a vector, and the displacement vector contains three orthogonal components in our study. The strain tensors are obtained from the gradient of the local displacement at this point. Finally, three strain tensors in each voxel are combined into a strain vector W_Strain, which has subject-specific tissue biomechanical property.

2.2. B-Spline-based Deformation from Surface Match

We obtained the prostate tissue transformation, T_B–spline, based on the B-spline model through a surface match. To perform surface registration, the prostate capsules are segmented from the MR and TRUS images. Then, a triangular mesh surface is generated for each prostate surface, with the vertices of the surface selected as the surface landmarks. Because each surface landmark is actually a vertex of the surface, its spatial relations with vertices in the neighborhood can be used to describe the geometric properties around the surface landmark [23, 24]. Assuming x_i is a surface landmark under study, its geometric attribute is defined as the volume of the tetrahedron formed by x_i and its neighboring vertices. For each boundary landmark x_i, the volumes calculated from different neighborhood layers are stacked into an attribute vector H (x_i ), which characterizes the geometric features of x_i from a local to a global fashion. H (x_i) can be further made into an affine-invariant as Ĥ(x_i ), by normalizing it across the whole surface. By using this attribute vector, the similarity between two surface landmarks x_i and y_i, respectively, in MR and TRUS images, can be measured by a Euclidean distance between their normalized attribute vectors. The whole energy function is defined as:

$$\begin{gathered} E(T_{B-spline})=\sum _{i=1}^I\sum _{j=1}^J{p}_{ij}({\Vert \widehat{H}(y_j^{US})-\widehat{H}(T_{B-spline}(x_i^{MR}))\Vert }^2)+\delta \sum _{i=1}^I\sum _{j=1}^J{p}_{ij}\log (p_{ij})-\xi \sum _{i=1}^I\sum _{j=1}^J{p}_{ij} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\lambda {\Vert {\iiint }_{\left(x,y,z\right)\in {\Omega }_M}{(\frac{{\partial }^2{T}_{B-spline}}{\partial x^2}+\frac{{\partial }^2{T}_{B-spline}}{\partial y^2}+\frac{{\partial }^2{T}_{B-spline}}{\partial z^2})}^{2}dxdydz\Vert }^2 \end{gathered}$$ (1)

where p_ij is the fuzzy correspondence matrixes. And δ, λ and ξ are the weights for the energy terms.

2.3. Combined Deformation with Biomechanical Property

The surface-based transformation using the B-spline model does not reflect the actual prostate tissue deformation, because this model does not take into account the specific tissue elastic property. To incorporate tissue biomechanical property, the surface-based transformation T_B–spline is regulated by the strain vector map W_Strain, to constrain the B-spline-based prostate-gland transformation. The prostate elastic property is weighted into the B-spline-based tissue deformation to obtain the accurate patient-specific volumetric deformation of the prostate gland. As illustrated in Fig. 3, in contrast to the B-spline-based deformation model, our biomechanical model was able to capture accurate local deformation in heterogeneous tissue (e.g., 3 regions with various degrees of elasticity). Therefore, the transformation simultaneously estimates the surface and internal deformation.

Figure 3.

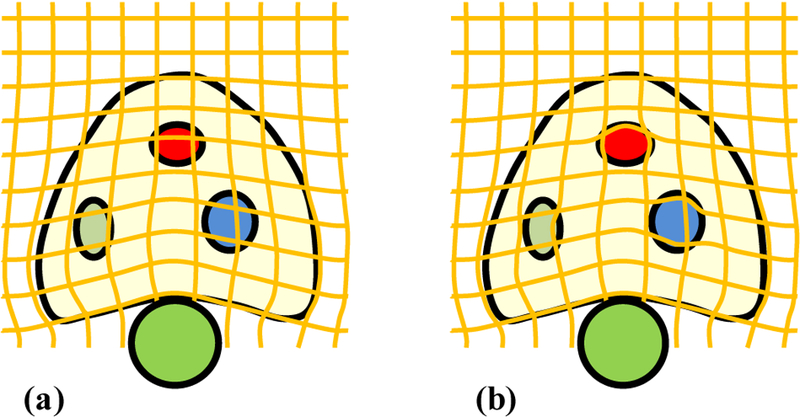
The diagrammatic drawing of deformation fields without and with the biomechanical model. (a) B-spline deformation field based on the surface match after the probe insertion, (b) Combined deformation field with B-spline model (surface deformation) and biomechanical model (volumetric deformation) after the probe insertion.

3. EXPERIMENTS AND RESULTS

3.1. Phantom Experiment

To validate the proposed registration method, we conducted an experiment with a prostate phantom (CIRS 053), in which two markers and three lesions were imbedded. The T1-and T2-weighted images of the prostate phantom were acquired using a 1.5T Philips MRI scanner. For the ultrasound scan, two sets of 3D TRUS images were acquired with an Ultrasonix ultrasound scanner under two different probe-induced pressures. Our registration results were compared with the surface-based registration (Fig. 4). In contrast to the surface-based method, [25] which resulted in large mismatch of the internal structures such as the lesions and urethra, our registration achieved a close match of the internal structures. Quantitative comparison of the two registration methods were demonstrated using the target registration error (TRE) of the two markers and the surface distance of the three lesions (Table 1).

Figure 4.

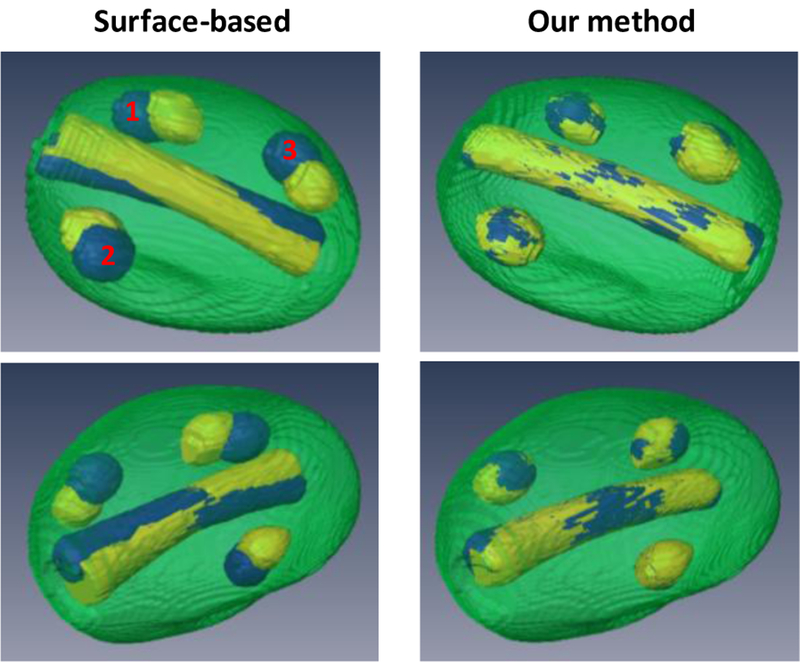
3D comparison of registration results using surface-based and our methods. Left column (surface-based method): 3D visualization images of the post-registration MRI (yellow) and TRUS (blue). Right column (our method): 3D visualization images of the post-registration MRI (yellow) and TRUS (blue).

Table 1.

TRE and surface distance comparison of two registration methods

	TRE (mm)		Surface Distance (mm)
	Maker 1	Maker 2	Lesion 1	Lesion 2	Lesion 3
Surface-based	2.76	4.31	3.01 ± 2.53	2.21 ± 1.98	2.65 ± 2.41
Our method	1.21	1.37	0.54 ± 0.31	0.57 ± 0.34	0.63 ± 0.35

3.2. Patient Study

All patients’ TRUS data were acquired using a Hitachi ultrasound machine and a 7.5MHz bi-plane probe. Each 3D TRUS data set consisted of 1024 × 768 × 75 voxels, and the voxel size was 0.10 × 0.10 × 1.00 mm³. All MR images were acquired using a Philips 1.5T MR scanner and a pelvic phase-array coil. The 3D MRI data consisted of 320 × 320 × 64 voxels, and the voxel size was 0.63 × 0.63 × 2.00 mm³. All prostate glands were contoured in T2-weighted MR and TRUS images by an experienced physician. For each patient, three to six landmarks were indentified in post-registration MR and TRUS images to facilitate quantitative comparison.

Figure 5 shows the registration results of a 65-year old prostate-cancer patient. Two cysts were identified as landmarks to evaluate the registration results (arrows) and our elastography-based registration was able to achieve a close match of these landmarks. Again, we compared our registration results with the surface-based method. Figure 6 shows the TRE comparison of all 5 patients from the two registration methods. The mean TRE is 3.13±0.61 mm for the surface-based method and 1.84±0.27 mm for our method. As a result of incorporating patient-specific biomechanical properties of the prostate gland, the proposed method significantly improved the registration accuracy of the internal prostate glands compared to the surface-based method (p-value<0.01).

Figure 5.

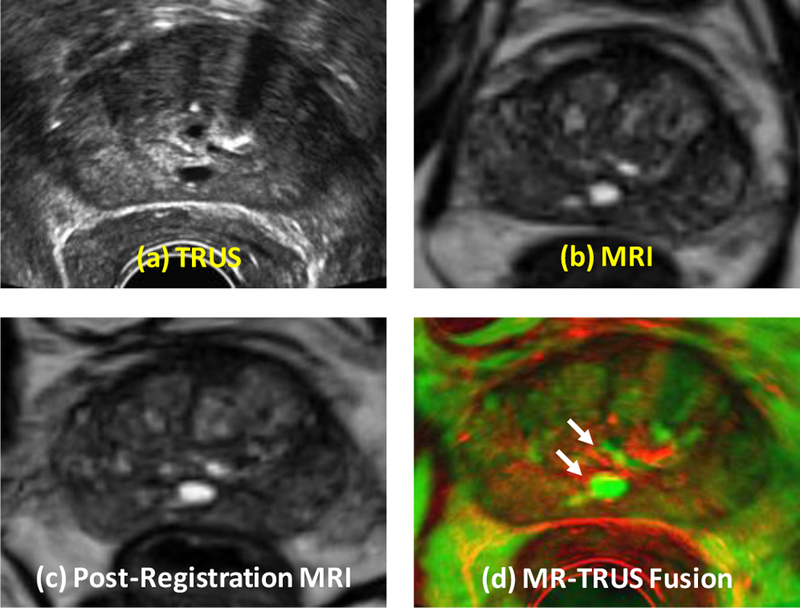
Comparison of prostate registration using the surface-based and our methods. Row 1: original TRUS (a) and MRI (b). Row 3 (our method): post-registration MRI (c) and fusion image (d). Two landmarks (white arrows) were identified to evaluate the registration accuracy.

Figure 6.

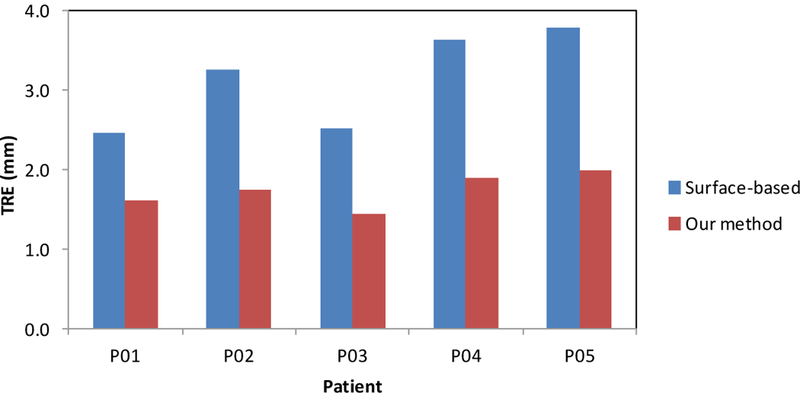
The TRE comparison of the identified land markers between the surface-based and our proposed method for 5 patients.

4. DISCUSSION AND CONCLUSION

In this report, we present a novel MR-TRUS registration method that combines the B-spline and biomechanical modeling to accurately estimate the prostate-gland deformation. Specifically, the proposed registration method combines a novel subject-specific biomechanical model with a B-spline transformation to register the prostate gland of the MR image to the TRUS volume. The subject-specific biomechanical model is obtained through US elastography in which a 3D strain map of the prostate is generated. This biomechanical model is then used to constrain the B-spline-based transformation to predict and compensate for the internal prostate-gland deformation. We have validated the accuracy of the proposed method with a prostate-phantom study and a pilot study of 5 prostate-cancer patients.

The proposed registration method may provide accurate and robust means of predicting internal prostate-gland deformation and is, therefore, well-suited to a number of interventional applications where there is a need for deformation compensation. A successful integration of multi-parametric MR and TRUS prostate images could provide extremely important benefits in terms of more successful prostate-cancer diagnosis and treatment.