Marginal Bayesian Semiparametric Modeling of Mismeasured Multivariate Interval-Censored Data

Abstract

Motivated by data gathered in an oral health study, we propose a Bayesian nonparametric approach for population-averaged modeling of correlated time-to-event data, when the responses can only be determined to lie in an interval obtained from a sequence of examination times and the determination of the occurrence of the event is subject to misclassification. The joint model for the true, unobserved time-to-event data is defined semiparametrically; proportional hazards, proportional odds, and accelerated failure time (proportional quantiles) are all fit and compared. The baseline distribution is modeled as a flexible tailfree prior. The joint model is completed by considering a parametric copula function. A general misclassification model is discussed in detail, considering the possibility that different examiners were involved in the assessment of the occurrence of the events for a given subject across time. We provide empirical evidence that the model can be used to estimate the underlying time-to-event distribution and the misclassification parameters without any external information about the latter parameters. We also illustrate the effect on the statistical inferences of neglecting the presence of misclassification.

1. Introduction

Considerable attention has been given to estimation of survival functions and of regression coefficients from a variety of standard models for univariate and multivariate censored data (see, e.g. Hougaard, 2000; Ibrahim et al., 2001). For the analysis of multivariate censored survival data, frailty and marginal models have been discussed, including versions of the proportional hazards (Cox, 1972), accelerated failure time (AFT) (e.g., Hanson & Johnson, 2004), additive hazards (AH) (e.g., Lin & Ying, 1994), and the proportional odds (PO) (e.g., Hanson & Yang, 2007) models.

These models usually assume that the determination of the event of interest is done without error which can be unrealistic. In fact, in many applications the ascertainment of the event of interest is based on a screening test which may not have perfect sensitivity and specificity. In this context, the use of standard survival models can lead to wrong inferences about the distribution of the event times (García-Zattera et al., 2016).

Compared to the rich literature on methods for correcting for misclassification in regression models for categorical data (see, e.g. García-Zattera et al., 2010, 2012, and references therein), the study of models in the context of time-to-event data has received much less attention and have been almost exclusively focused on misclassification and measurement errors in covariates (see, e.g. Gong et al., 1990). We are only aware of McKeown & Jewell (2010), where a nonparametric maximum likelihood approach is proposed in the context of misclassified univariate current status data and García-Zattera et al. (2016), where the AFT frailty modeling approach is extended to account for misclassification in the response for multivariate interval-censored data.

Frailty models are one of the most popular approaches to account for the association structure in time-to-event data. These models provide useful summary information in the absence of estimates of a baseline survival distribution and may be formulated in a parametric or semi-parametric fashion. However, under these models the regression coefficients describe changes in individual responses due to changes in covariates, they induce a particular association structure for the clustered variables, and rely heavily on the (conditional or subject-specific) assumptions in the relationship between the covariates and the event times (e.g., AFT, PH or PH), which is not always inherit in the induced marginal model. Furthermore, an often overlooked limitation of this approach is that the interpretation of regression coefficients can be highly sensitive to difficult-to-verify assumptions about the distribution of random effects, particularly its dependence on covariates. This issue is particularly relevant for interval-censored data where the degree of available information to perform diagnostic techniques is rather limited due to the censoring mechanism.

In this article, we propose a general framework for analyzing the marginal effects of predictors on the distribution of mis-measured multivariate interval-censored data. Specifically, we define the joint distribution of the multivariate time-to-event variables by combining marginal distributions arising from standard assumptions on the relationship of the predictors and time-to-event responses, and a parametric copula function, which describes the dependence structure among the event times. To avoid the potential disadvantages of adopting a fully parametric probability model, we consider a Bayesian semiparametric specification of the marginal distributions, where the baseline distribution of the event times is modeled using a Bayesian nonparametric (BNP) prior. Different misclassification models allowing for different classifiers for each subject across examinations are discussed.

The rest of the paper is organized as follows. Section 2 introduces the motivating data and research questions. The proposed model is introduced in Section 3, including the discussion of aspects associated with its computational implementation. In Section 4, the performance of the proposed model is assessed by means of simulation studies. The simulated data are also used to evaluate the effect of neglecting the presence of misclassification in the statistical analysis. The proposed model is applied to our motivating problem in Section 5. A final discussion section concludes the paper.

2. The Dental Research Questions

The Signal-Tandmobiel^® (ST) study is a longitudinal prospective oral health study conducted in Flanders, Belgium, between 1996 and 2001. This study involved a sample of 4468 Flemish primary school children (2315 boys and 2153 girls). The sample represents 7.3% of the children born in 1989 in Flanders and first examined in 1996. At the first examination the average age of the children in the sample was 7.1 years, with a standard deviation of 0.4 years. The age of the children at the first examination varied from 6.1 to 8.1 years.

The children were randomly drawn through a stratified cluster sampling design without replacement. The selection units were the schools, which were stratified by province and educational system. Thus, the target population was divided into 15 different strata, comprising the three types of the Belgian educational system (private, public, and municipal schools) for the five provinces of Flanders. Schools were selected with a probability proportional to the number of children in the first year of primary school. Whenever a school was selected, all children in the first class of the selected school were included in the sample. The children were examined on a yearly basis during their primary school time (between 7 and 12 years of age).

The children were examined annually by one of sixteen dental examiners in a mobile dental clinic on the school premises and the visit dates for each school were mainly determined by logistic reasons. Therefore, the number of visits and their timing were not related with any potential response variable or covariate gathered in the study. Clinical information was obtained based on visual and tactile observations. They included information about gingival condition, dental trauma, presence and extent of enamel developmental defects, tooth decay, presence of restorations, missing teeth, stage of tooth eruption, and orthodontic treatment need, all using established criteria, as recommended by the WHO report in 1987, and based on the diagnostic criteria for caries prevalence surveys published by the British Association for the Study of Community Dentistry (BASCD) (Pitts et al., 1997). Besides the oral health data, information on oral hygiene and dietary habits, use of fluorides, dental attendance, medical history and social demographic background of the children was also obtained from questionnaires completed by parents and school medical centers. For a more detailed description of the ST study we refer to Vanobbergen et al. (2000).

One of the main purposes of the ST study was to assess the marginal effect of covariates on the time-to-caries experience (CE). Caries lesions are typically scored at four levels of lesion severity: D₄ (dentine caries with pulpal involvement), D₃ (dentine caries with obvious cavitation), D₂ (hidden dentine caries) and D₁ (white or brown-spot initial lesions in enamel without cavitation). CE corresponds to an event indicating whether a particular tooth is decayed at least D₃ level, missing, or filled due to caries. Teeth extracted for reasons different from caries, e.g. orthodontics, were coded in a different manner and treated as missing values for CE.

CE as just defined is a monotone process. Thus, the existence of reversals in longitudinal data, that is, teeth or surfaces initially recorded as being carious and subsequently recorded as caries-free, provides evidence of the existence of classification errors. For the teeth considered here, the reversals varied from 1.3 to 3.8% across the study. Diagnosis of CE is surrounded by a number of challenges. For instance, nowadays, composite materials can imitate the natural enamel so well that it is sometimes difficult to spot a restored lesion. Another reason may be that the location of the cavity, e.g. far back in the mouth, hampers the view of the dental examiner. Hence, overlooking CE is likely to happen in practice, but the dental examiner could also classify discolorations as CE.

The selected examiners participated every year in training and calibration sessions, according to the guidelines issued by the BASCD. At the end of each calibration exercise the sensitivity and specificity of each dental examiner vis–a–vis the benchmark examiner were determined, yielding a misclassification table for each examiner for scoring of caries at tooth and surface levels. The results suggest that some examiners over– or under–score the true caries status and that the scoring behavior of the examiners was constant across the study period. It is also important to stress that children who participated in the calibration exercises were not taken at random from the main data, rather a school was selected with a presumed high prevalence for caries.

Finally, the analyses reported in Section 5 involve the four permanent first molars, that is, teeth 16, 26 on the maxilla (upper quadrants), and teeth 36 and 46 on the mandible (lower quadrants). The numbering of the teeth follows the FDI (Federation Dentaire Internationale) notation which indicates the position of the tooth in the mouth. Position 26, for instance, means that the tooth is in quadrant 2 (upper left quadrant from the viewpoint of the dental examiner) and position 6 where numbering starts from the mid–sagittal plane. The choice of these teeth for the statistical analyses is primarily based on the relatively non-negligible prevalence of the disease at this age in this population.

3. The Bayesian Semiparametric Models

Let $T_{(i,j)}\in {\mathbb{R}}_{+}$ be the continuous time-to-event (time to CE) for the jth unit (tooth) of the ith subject (child), i = 1, … , N, j = 1, … , J. Suppose that the occurrence of the event is assessed by using a sequence of subject-specific evaluations. Let 0 < v_(i,1) < v_(i,2) < ⋯ < v_(i,Ki) < +∞ be the ordered examination times for the ith subject, i = 1, … , N, where K_i is the number of examinations. In a regular interval-censored data context, the time-to-event T_(i,j) is unobserved but is known with certainty to lie in an interval T_(i,j) ∈ (v_{(i,l(i,j)–1)}, v_(i,l(i,j))] obtained from the sequence of examinations, l_(i,j) ∈ {1, … ,K_i+1}, where v_(i,0) ≡ 0 and v_(i,Ki+1) ≡ +∞. However,in our setting the determination of the event is prone to misclassification and the observed data are given by the binary variables D_(i,j,k), k = 1, … , K_i, indicating whether the (potentially) error-corrupted evaluation concludes that the event has occurred by time v_(i,k) (D_(i,j,k) = 1) or not (D_(i,j,k) = 0). An illustration of the observed data generating mechanism is given in Appendix A of the online supplementary material.

In the following, set T = (T₁, … , T_N ), where T_i = (T_(i,1), … , T_(i,J)), i = 1, … , N, is a vector of unobserved event times, and D = (D₁, … , D_N), where D_i = D_(i,1), … , D_(i,Ki)), D_(i,k) = (D_(i,1,k), … , D_(i,J,k)), i = 1, … , N, k = 1, … , K_i, is a vector of observed binary indicators of potentially misclassified event status. We assume that for each subject and unit, a p-dimensional design vector including exogenous covariates is recorded, x_(i,j), i = 1, … , N, = 1, … , J. The main aim here is to develop a method to infer on the marginal dependence of the event times T_(i,j) on covariates x_(i,j), where the event times T_(i,j) are observed only through sequences of possibly misclassified binary indicators D_(i,j,k) of the event status. To this end, we first specify marginal models for the dependence of event times on covariates in Section 3.1. Second,the link between the observable binary variables D and unobservable event times T is given by the misclassification models in Section 3.2. The event times and the misclassification models induce marginal models for the observed data D described in Section 3.3.

3.1. The Semiparametric Time-to-Event Models

Let f_{x(i,1),…,x(i,J)} be the joint density function for the unobserved time-to-event responses for the ith subject. We build on Sklar’s theorem (Sklar, 1959) and model f_{x(i,1),…,x(i,J)} by using its unique marginal-copula representation

$$f_{{\mathrm{x}}_{(i,1)},\dots ,{\mathrm{x}}_{(i,J)}}(t_1,\dots ,t_J)=c_{\rho }\left(F_{{\mathrm{x}}_{(i,1)}}(t_1),\dots ,F_{{\mathrm{x}}_{(i,J)}}(t_J)\right)\left\{\prod _{j=1}^J{f}_{{\mathrm{x}}_{(i,j)}}(t_j)\right\},$$

where $(t_1,\dots ,t_J)\in {\mathbb{R}}_{+}^J$, c_ρ is the density of the a copula function, parametrized by the finite-dimensional parameter ρ, and F_x(i,j) (t) and f_x(i,j) (t) denote the marginal cumulative distribution and density function for the jth unit of the ith subject, with covariates x_(i,j), respectively. A Gaussian copula function is assumed throughout, such that,

$$c_{\rho }(u_1,\dots ,u_J)=\mid R_{\rho }{\mid }^{-1∕2}\text{exp}\left\{-\frac{1}{2}\left({\mathrm{\Phi }}^{-1}(u_1),\dots ,{\mathrm{\Phi }}^{-1}(u_J)\right)U_{\rho }{\left({\mathrm{\Phi }}^{-1}(u_1),\dots ,{\mathrm{\Phi }}^{-1}(u_J)\right)}^{\prime }\right\},$$

where Φ⁻¹ is the inverse cumulative distribution function of a standard Normal distribution, $U_{\rho }\left(R_{\rho }^{-1}-{\mathit{I}}_J\right)$, I_J is the identity matrix of dimension J, and $R_{\rho }^{-1}$ is a correlation matrix.

The PH, AFT and PO marginal regression models are considered by expressing the covariate-dependent cumulative distribution function (CDF), F_x(t), as

$$1-F_{{\mathrm{x}}_{(i,j)}}(t)=(1-F_0(t){)}^{\text{exp}\{{\mathrm{x}}_{(i,j)}^{\prime }{\beta }_j\}},$$ (1)

$$1-F_{{\mathrm{x}}_{(i,j)}}(t)=1-F_0\left(\text{exp}\left\{{\mathrm{x}}_{(i,j)}^{\prime }{\beta }_j\right\}t\right),$$ (2)

and

$$\frac{F_{x_{(i,j)}}(t)}{1-F_{x_{(i,j)}}(t)}=\text{exp}\{x_{(i,j)}^{\prime }{\beta }_j\}\left(\frac{F_0(t)}{1-F_0(t)}\right),$$ (3)

respectively, where ${\beta }_j\in {\mathbb{R}}^p$, j = 1, … , J, is a vector of regression coefficients and F₀ is the marginal baseline CDF. Finally, we assume that, for i = 1, … , N,

$${\mathrm{T}}_i\mid \beta ,\rho ,F_0\stackrel{ind.}{\sim }{f}_{x_{(i,1)},\dots ,x_{(i,J)}}(\cdot \mid \beta ,\rho ,F_0),$$ (4)

where β = (β₁, … , β_J).

There is a rich Bayesian nonparametric (BNP) literature for robustifying the modeling of a baseline CDF F₀ (or equivalently its hazard function) in the context of univariate and multivariate frailty-based models (see, e.g. Müller et al., 2015), including the use of gamma processes (Kalbfleisch, 1978), beta processes (Hjort, 1990), piecewise exponential priors (Ibrahim et al.,2001), correlated increments priors (Sinha & Dey, 1997), Bernstein polynomials (Gelfand & Mallick, 1995) and tailfree processes (Hanson, 2006; Hanson & Yang, 2007; Zhao et al., 2009; Hanson et al., 2011). Among the BNP approaches, we opted for tailfree processes because they allow for the use of the same BNP model for F₀ under the different formulations of the model given by expressions (1), (2), and (3). By placing the three time-to-event models on common ground, potential differences in fit and/or predictive performance of the models can be attributed to the time-to-event model assumptions only, rather than to additional possible differences in quite different nonparametric models or estimation methods. Furthermore, the BNP model can be specified such that standard parametric models are special cases of the model.

We model the baseline CDF as a mixture of tailfree processes prior, centered at the Weibull family. Tailfree processes are stochastic processes that can be defined to have trajectories on the space of all probability distributions on a given space (see, e.g. Freedman, 1963; Fabius, 1964; Ferguson, 1974; Jara & Hanson, 2011). A tailfree random probability measure F₀ supported on ${\mathbb{R}}_{+}$ is defined by allocations of random probabilities to increasingly refined partitions of ${\mathbb{R}}_{+}$. Let E = {0, 1} and E^m be the m-fold Cartesian product E×⋯×E. Further, set $E^{\ast }={\bigcup }_{m=1}^{\infty }{E}^m$. Consider the sequence of partitions of $\mathbb{R}$ given by ${\pi }_0=\{{\mathbb{R}}_{+}\}$, π₁ = {B₀, B₁}, π₂ = {B₀₀, B₀₁, B₁₀, B₁₁}, …, such that ${\mathbb{R}}_{+}=B_0\cup B_1$ and B₀ ∩ B₁ = ∅, and for each $m\in \mathbb{N}$ and every ϵ = ε₁ … ϵ_m ∈ E^m, B_ϵ = B_ϵ0 ∪ B_ϵ1 and B_ϵ0 ∩ B_ϵ1 = ∅. Assume that B_ϵ0 lies below B_ϵ1 and that for all ϵ ∈ E*, B_ϵ is a left-open right-closed interval unless ϵ is a string of ones only. Throughout the paper, we use the convention that ϵ = ε₁ ⋯ ε_m–10 = 0 and ϵ = ε₁ ⋯ ϵ_m–1 1 = 1, if m = 1. Let $\mathrm{\Pi }={\cup }_{i=0}^{\infty }{\pi }_i$ and further assume that the partitions form a rich class in the sense that Π is a generator of the Borel σ-field of ${\mathbb{R}}_{+}$, $\mathcal{B}\equiv \mathcal{B}({\mathbb{R}}_{+})$.

Definition 1. Let Π be a sequence of binary partitions as before and $\mathcal{A}=\{a_{ϵ}:ϵ\in E^{\ast }\}$ be a collection of real numbers. A random probability measure F₀ on $({\mathbb{R}}_{+},\mathcal{B})$ is said to be a tailfree process with parameters ($\mathrm{\Pi },\mathcal{A}$), denoted F₀ $\mid \mathrm{\Pi },\mathcal{A}\sim \text{TFP}(\mathrm{\Pi },\mathcal{A})$, if there exist a collection $\mathcal{Y}=\{Y_{ϵ}:ϵ\in E^{\ast }\}$ of [0, 1]-valued random variables such that the following hold:

• The vectors (Y₀, Y₁), (Y₀₀, Y₀₁, Y₁₀, Y₁₁), …, are mutually independent and with probability law determined by (a₀, a₁), (a₀₀, a₀₁, a₁₀, a₁₁), …, respectively.

• For every ϵ = ε₁ ⋯ ε_m ∈ E*, Y_{ε1⋯εm–10} + Y_{ε1⋯εm–11} = 1 almost surely.

• For every ϵ = ε₁ ⋯ ε_m ∈ E*, the random probability measure F₀ is related to $\mathcal{Y}$ through the relations

$$F_0(B_{ϵ})=\prod _{j=1}^m{Y}_{{\epsilon }_1\cdots {\epsilon }_j}.$$

We consider partition sets in Π such that their limits correspond to quantiles of a parametric distribution G_θ, θ ∈ Θ, defined on $({\mathbb{R}}_{+},\mathcal{B})$ (Lavine, 1992). Specifically, we consider sets in Π of the form $B_{ϵ}^{\theta }=(l_{ϵ}^{\theta },u_{ϵ}^{\theta }]$, where $l_{ϵ}^{\theta }=G_{\theta }^{-1}(k∕2^m)$ and $u_{ϵ}^{\theta }=G_{\theta }^{-1}\{(k+1)∕2^m\}$, with $G_{\theta }^{-1}(\cdot )$ being the quantile function of G_θ, and k is the decimal representation of ϵ = ε₁ ⋯ ε_m ∈ E*. If needed, the notation Π^θ will be used to make the dependence of Π on the parameters of G_θ explicit. Without loss of generality, for the rest of the paper we assume that the sets are constructed based on the quantiles of the Weibull distribution, such that G_θ (t) = 1 – exp(−(t/η₂)^η₁) for t ≥ 0, θ = (log(η₁), log(η₂)).

Following Jara & Hanson (2011), we consider a logistic-Normal specification of the tailfree conditional probabilities, such that for every ϵ0 = ε₁ ⋯ ε_m–10 ∈ E*,

$$Y_{ϵ0}=\frac{\text{exp}\{{\lambda }_{ϵ0}\}}{1+\text{exp}\{{\lambda }_{ϵ0}\}},$$

and

$${\lambda }_{ϵ0}\mid c,\tau \stackrel{ind.}{\sim }N(0,2∕[c\tau (j)]),$$

where τ(j) is a nondecreasing known function of j. A common choice for τ(j) is j². The parameter c is a precision parameter; lower values of c allow mass of F₀ to move easily from the centering distribution G_θ. As c → 0⁺, E{F₀(·)} tends to the empirical CDF of the data (Hanson & Johnson,2002); as c → ∞, all conditional probabilities go to 0.5 and hence F₀(A) → G_θ(A) a.s. for every measurable set A. Common choices simply set c at small values, e.g. c = 1.

Under this specification Y_ϵ0 approximately follows an beta(cτ(j), cτ(j)) distribution (Jara & Hanson, 2011) and the resulting process closely matches a Polya tree prior (see, e.g. Lavine, 1992, 1994; Christensen et al., 2008). As is usually done for Polya trees priors, the tailfree model is partially specified, where the tailfree process is terminated at level L and on sets in the finest partition ${\pi }_L^{\theta }$ the random F₀ matches exactly the parametric distribution G_θ (Hanson, 2006). We typically consider L ≈ log₂(n/M), where n is the sample size and M is 5 to 10 (Hanson, 2006). The resulting process is denoted by

$$F_0\mid c,\theta \sim {\text{TFP}}^L({\mathrm{\Pi }}^{\theta },{\mathcal{A}}^c)$$ (5)

Under this prior specification, the density of a realization of the process is given by

$$\begin{array}{cc}\hfill f_0(t)& =2^J{g}_{\theta }(t)\prod _{l=1}^L{Y}_{{ϵ}_{\theta }(t,l)},\hfill \\ \hfill & =2^L{g}_{\theta }(t)\prod _{l=1}^L\frac{\text{exp}{\left\{{\lambda }_{{ϵ}_{\theta }(t,l-1)0}\right\}}^{I_{\left\{t\in B_{{ϵ}_{\theta }(t,l-1)0}^{\theta }\right\}}}}{1+\text{exp}\left\{{\lambda }_{{ϵ}_{\theta }(t,l-1)0}\right\}},\hfill \end{array}$$ (6)

where $t\in {\mathbb{R}}_{+}$, I_{A} is the indicator function for A, ϵ_θ(t, l) = ε₁ε₂ ⋯ ε_l is the set in ${\pi }_{\theta }^l$ that t is in, and g_θ(·) is the density of a Weibull distribution. This expression can be employed to derive closed form expressions for the cumulative distribution function F₀ and to construct the likelihood in different settings.

It may be difficult in practice to specify a single centering Weibull distribution with which to center the linear tailfree process; and once specified, a single centering distribution may affect inference unduly. One way to mitigate the dependence of the process on the partitioning sets is to specify a mixture of prior distributions. A mixture of tailfree processes is induced for F₀ by allowing parameters of the centering distribution G_θ and/or the precision parameter c to be random, that is,

$$F_0\mid c,\theta \sim {\text{TFP}}^L({\mathrm{\Pi }}^{\theta },{\mathcal{A}}^c)\text{and}(\theta ,c)\sim p(\theta ,c),$$

where p(θ, c) refers to the joint prior for θ and c. Smoothness properties in terms of continuity and differentiability of the densities for F₀ under the mixture of tailfree processes carry over from the results reported by Hanson (2006). One important property is posterior propriety under improper priors on the mixing parameter θ, following a simple application of Tonelli’s theorem.

3.2. The Misclassification Models

As in the case of the ST study, suppose now that the evaluation of the event status at each visit is performed by Q examiners. Denote by ξ_(i,k) ∈ {1, … , Q} the variable indexing the examiner that evaluates all four molars of subject i at examination time v_(i,k), and let ξ_i = (ξ_(i,1), … , _(i,Ki)) be the vector of indicators of the examiners that score the responses of subject i over time. We further assume that the scoring behavior of each examiner is the same across the study. Let η_q = (η_(q,1), … , η_(q,J) and α_q = (α_(q,1), … , α_(q,J)), q = 1, … , Q, be the vectors containing the unit-specific specificity and sensitivity parameters for the qth examiner, respectively. Finally, let α = (α₁, … , α_Q) and η = (η₁, … , η_Q) be the matrices containing all sensitivity and specificity parameters, respectively. In this setting, the misclassification model assumes that

$$\begin{array}{cc}\hfill \text{Pr}\left(D_{(i,j,k)}=1\mid T_{(i,j)}\in (0,v_{(i,k)}]\right)& ={\alpha }_{({\xi }_{(i,k)},j)},\hfill \\ \hfill \text{Pr}\left(D_{(i,j,k)}=0\mid T_{(i,j)}\in (v_{(i,k)},+\infty )\right)& ={\eta }_{({\xi }_{(i,k)},j)},\hfill \end{array}$$

and the process is characterized by the following conditional independence assumptions. Note that assumptions (A.1) - (A.5) represent natural extensions of the commonly used assumptions for the analysis of misclassified binary data (see, e.g. García-Zattera et al., 2010, 2012).

• (A.1)⫫_1≤i≤N D_i ∣ T₁, … , T_N, ξ₁, … , ξ_N, η, α, i.e. the observed response matrices for each subject are independent given the true unobserved event times, examiner indicators, and sensitivity and specificity parameters,
• (A.2)D_i⫫D₁, … , D_i–1, D_i+1, … , D_N ∣ T_i, ξ_i, η, α, ∀ i, i.e. the distribution of the observed response matrix for a subject only depends on his true unobserved time-to-event vector, the examiners that score his responses, and the sensitivity and specificity parameters,
• (A.3)⫫_1≤k≤Ki D_i,k ∣ T_i, ξ_i, η, α, ∀ (i, k), i.e. the observed response vectors for a subject are independent across time given his unobserved time-to-event vector, the examiners that score his responses and the sensitivity and specificity parameters,
• (A.4)⫫_1≤j≤J D_(i,j,k) ∣ T_i, ξ_(i,k), η_ξ(i,k), α_ξ(i,k), ∀ i, k, i.e. the observed responses at the kth examination are independent given the unobserved time-to-event vector, the examiner that scores his responses at the kth examination, and the examiner-specific sensitivity and specificity parameters,
• (A.5)D_(i,j,k)⫫T_(i,1), … , T_(i,j–1), T_(i,j+1), … , T_(i,J) ∣ T_(i,j), ξ_(i,k), η_(ξ(i,k),j), α_(ξ(i,k),j), i.e. the distribution of the jth observed variable at the kth examination only depends on the true unobserved time-to-event for the same variable, the examiner that scores his responses at examination k, and the sensitivity and specificity parameters of this examiner for the jth variable.

A simplified version of the above defined general misclassification model, which assumes unstructured examiner-unit specific sensitivity and specificity parameters, is to assume the same misclassification parameters across units for each examiner: for q = 1, … , Q, η_(q,j) = η_(q) and α_(q,j) = α_(q), ∀j. Extensions of the general misclassification model can also be considered. For instance, the model could be extended by including examinee-specific or examiner-specific characteristics in the misclassification parameters, allowing for the understanding of the potential heterogeneity in the scoring behavior of the examiners. Unfortunately, there is no available information about the specific characteristics of the examiners in the ST study and we do not pursue this here. However, tooth position, gender, and age of the examinee are considered in Section 4.2.

Following García-Zattera et al. (2010), García-Zattera et al. (2012) and García-Zattera et al. (2016), the following restricted parameter spaces for the misclassification parameters are considered to avoid identification problems,

$$\left\{\left({\eta }_{(q,j)},{\alpha }_{(q,j)}\right)\in [0,1{]}^2:{\eta }_{(q,j)}+{\alpha }_{(q,j)}>1\right\},q=1,\dots ,Q,j=1,\dots ,J.$$

3.3. The Implied Statistical Models and Stochastic Representations

Regardless of the misclassification model, the assumptions (A.1) – (A.5), along with the joint probability model for the time-to-event responses (4) and the BNP prior for the baseline probability distribution (5), imply that the joint probability model for the observed binary indicators and unobserved time-to-event variables for each subject is given by

$$\begin{array}{cc}\hfill p({\mathbf{D}}_1,\dots ,{\mathbf{D}}_N,{\mathbf{T}}_1,\dots ,{\mathbf{T}}_N& \mid \mathit{\alpha },\mathit{\eta },\mathit{\beta },\mathit{\rho },c,\mathit{\theta })=\prod _{i=1}^{N}p({\mathbf{D}}_i\mid {\mathbf{T}}_i,\mathit{\alpha },\mathit{\eta })p({\mathbf{T}}_i\mid \mathit{\beta },\mathit{\rho },c,\mathit{\theta }),\hfill \\ \hfill & =\prod _{i=1}^N\left\{\prod _{j=1}^J\prod _{k=1}^{K_i}p(D_{(i,j,k)}\mid {\mathbf{T}}_{(i,j)},{\eta }_{({\xi }_{(i,k)},j)},{\alpha }_{({\xi }_{(i,k)},j)})\right\}\times \hfill \\ \hfill & \int p({\mathbf{T}}_i\mid \mathit{\beta },\mathit{\rho },F_0)p(F_0\mid c,\mathit{\theta })d{F}_0,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill p(D_{(i,j,k)}\mid T_{(i,j)},& {\eta }_{({\xi }_{(i,k)},j)},{\alpha }_{({\xi }_{(i,k)},j)})\hfill \\ \hfill & ={\left\{{\alpha }_{({\xi }_{(i,k)},j)}^{D_{(i,j,k)}}{\left(1-{\alpha }_{({\xi }_{(i,k)},j)}\right)}^{1-D_{(i,j,k)}}\right\}}^{\mathbb{I}(T_{(i,j)}{)}_{\left\{T_{i,j)}\in \left(0,v_{(i,k)}\right]\right\}}}\times \hfill \\ \hfill & {\left\{{\left(1-{\eta }_{({\xi }_{(i,k)},j)}\right)}^{D_{(i,j,k)}}{\eta }_{({\xi }_{(i,k)},j)}^{1-D_{(i,j,k)}}\right\}}^{\mathbb{I}(T_{(i,j)}{)}_{\left\{T_{i,j)}\in \left(v_{(i,k)},+\infty \right)\right\}}},\hfill \\ \hfill & =\prod _{l=1}^k{\left({\alpha }_{({\xi }_{(i,k)},j)}^{D_{(i,j,k)}}{\left(1-{\alpha }_{({\xi }_{(i,k)},j)}\right)}^{1-D_{(i,j,k)}}\right\}}^{\mathbb{I}(T_{(i,j)}{)}_{\left\{T_{i,j)}\in \left(v_{(i,l-1)},v_{(i,l)}\right]\right\}}}\times \hfill \\ \hfill & \prod _{l=k+1}^{K_i+1}{\left\{{\left(1-{\eta }_{({\xi }_{(i,k)},j)}\right)}^{D_{(i,j,k)}}{\eta }_{({\xi }_{(i,k)},j)}^{1-D_{(i,j,k)}}\right\}}^{\mathbb{I}(T_{(i,j)}{)}_{\left\{T_{i,j)}\in \left(v_{(i,l-1)},v_{(i,l)}\right)\right\}}},\hfill \end{array}$$

and p(T_i ∣ β, π, F₀) is given by f_{x(i,1),…,x(i,J)} (T_(i,1), … , T_(i,J) ∣ β, π, F₀ under each specific time-to-event marginal model assumption ((1) – (3)). Therefore, the likelihood function for observed data is given by

$$\begin{array}{cc}\hfill p({\mathbf{D}}_1,\dots ,{\mathbf{D}}_N\mid \alpha ,\eta ,\beta ,\rho ,c,\theta )& =\prod _{i=1}^N{\int }_{{\mathbb{R}}_{+}^J}p({\mathbf{D}}_i\mid {\mathbf{T}}_i,\alpha ,\eta )p({\mathbf{T}}_i\mid \beta ,\rho ,c,\theta ,\tau )d{\mathbf{T}}_i,\hfill \\ \hfill & =\prod _{i=1}^N{\int }_{{\mathbb{R}}_{+}^J}\left\{\prod _{j=1}^J\prod _{k=1}^{K_i}p(D_{(i,j,k)}\mid {\mathrm{T}}_{(i,j)},{\eta }_{({\xi }_{(i,k)},j)},{\alpha }_{({\xi }_{(i,k)},j)})\right\}\times \hfill \\ \hfill & \int p({\mathbf{T}}_i\mid \beta ,\rho ,F_0)p(F_0\mid c,\theta )d{F}_{0}d{\mathbf{T}}_i.\hfill \end{array}$$ (7)

An alternative stochastic representation of the joint model for the unobserved time-to-events greatly simplifies the posterior computation for the proposed models. Under this representation, the time-to-events are viewed as transformed Gaussian random variables,

$$T_{(i,j)}=F_{x_{(i,j)}}^{-1}\left(\mathrm{\Phi }\left(Z_{(i,j)}\right)\right),$$

where

$${\mathit{Z}}_i=(Z_{(i,1)},\dots ,Z_{(i,J)})\mid \mathit{\rho }\stackrel{i.i.d.}{\sim }{N}_J({\mathbf{0}}_J,{\mathit{R}}_{\rho }),$$

i = 1, … , N, with N_d(m, S) denoting a d-variate Normal distribution with mean m and covariance matrix S, and density denoted by ϕ_d (· ∣ m, S). The joint density implied by this transformation is then given by

$$\prod _{j=1}^J\left\{\frac{f_{x_{(i,j)}}(t_j)}{\varphi \left(F_{x_{(i,j)}}^{-1}(\mathrm{\Phi }(t_j))\right)}\right\}{\varphi }_J\left(F_{x_{(i,1)}}^{-1}(\mathrm{\Phi }(t_1)),\dots ,F_{x_{(i,J)}}^{-1}(\mathrm{\Phi }(t_J))\mid {\mathbf{0}}_J,{\mathit{R}}_{\rho }\right),$$

which is equivalent to f_{x(i,1),…,x(i,J)} (t₁, … , t_j ∣ , β, ρ, F₀). This distribution can also be viewed as the marginal distribution for T_i arising from the joint model

$$p({\mathbf{T}}_i\mid {\mathit{Z}}_i,\mathit{\beta },F_0)p({\mathit{Z}}_i\mid \mathit{\rho }),$$

where p (· ∣ Z_i, β, F₀) is a degenerate probability distribution arising from

$$T_{(i,j)}\mid Z_{(i,j)},\beta ,F_0\stackrel{ind.}{\sim }p(\cdot \mid Z_{(i,j)},\beta ,F_0)={\delta }_{F_{x_{(i,1)}}^{-1}{\left(\mathrm{\Phi }\left(Z_{(i,j)}\right)\right)}^{(\cdot )}},$$

j = 1, … , J, where δ_a(·) is the Dirac measure at a. Based in this, the data augmented hierarchical representation of the proposed models, along with the employed prior distributions, is given by

$$\begin{array}{c}\hfill D_{(i,j,k)}\mid T_{(i,j)},{\eta }_{({\xi }_{(i,k)},j)},{\alpha }_{({\xi }_{(i,k)},j)}\stackrel{ind.}{\sim }p(\cdot \mid T_{(i,j)},{\eta }_{({\xi }_{(i,k)},j)},{\alpha }_{({\xi }_{(i,k)},j)}),\hfill \\ \hfill \hfill \\ \hfill T_{(i,j)}\mid Z_{(i,j)},\beta ,F_0\stackrel{ind.}{\sim }p(\cdot \mid Z_{(i,j)},\beta ,F_0),\hfill \\ \hfill \hfill \\ \hfill Z_{(i,j)}\mid \mathit{\rho }\stackrel{ind.}{\sim }{N}_J({\mathbf{0}}_J,{\mathit{R}}_{\rho }),\hfill \\ \hfill \hfill \\ \hfill \left({\eta }_{(q,j)},{\alpha }_{(q,j)}\right)\mid a^{(\eta ,0)},a^{(\eta ,1)},a^{(\alpha ,0)},a^{(\alpha ,1)}\stackrel{ind.}{\sim }\text{Beta}(a^{(\eta ,0)},a^{(\eta ,1)})\times \text{Beta}(a^{(\alpha ,0)},a^{(\alpha ,1)})\times \hfill \\ \hfill \hfill \\ \hfill \mathbb{I}{\left({\eta }_{(q,j)},{\alpha }_{(q,j)}\right)}_{\left\{({\eta }_{(q,j)},{\alpha }_{(q,j)}):{\eta }_{(q,j)}+{\alpha }_{(q,j)}>1\right\}},\hfill \\ \hfill \hfill \\ \hfill \mathit{\beta }\mid {\mathbf{m}}_{\beta },{\mathit{V}}_{\beta }\sim N_p({\mathbf{m}}_{\beta },{\mathit{V}}_{\beta }),\hfill \\ \hfill \hfill \\ \hfill F_0\mid c,\mathit{\theta }\sim {\text{TFP}}^J({\Pi }^{\theta },{\mathcal{A}}^c),\hfill \\ \hfill \hfill \\ \hfill \mathit{\theta }\mid {\mathbf{m}}_{\theta },{\mathit{V}}_{\theta }\sim N_2({\mathbf{m}}_{\theta },{\mathit{V}}_{\theta }).\hfill \end{array}$$

A similar hierarchical representation is obtained under the misclassification model assuming equal misclassification parameters across variables for each examiner. The model specification is completed by assuming a prior distribution on the parameters of the Gaussian copula model ρ, which depends on the parameterization of the correlation matrix R_ρ. We assume priors on ρ such that the resulting prior on the correlation matrix R_ρ is uniform on the corresponding space of correlation matrices.

3.4. Main Aspects of the Posterior Computation

Samples from the posterior distribution for the model parameters are obtained by using a Gibbs sampler algorithm based on the augmented posterior distribution described in the previous section. In this Gibbs sampler, blocks of parameters are updated using Metropolis-Hastings steps (Tierney, 1994) or directly sampled from the corresponding conditional distributions. The parameters defining the conditional tailfree probabilities are updated in a single block by using the adaptive Gaussian random-walk proposal described by (Haario et al., 2001), where the candidate generating covariance matrix is tuned to get acceptance rates in the 20% to 50% range. The underlying time-to-event variables Z_i, i = 1, … , n, the regression parameters β and the parameters of the centering distribution of the tailfree process θ can be updated in a similar way.

Assumptions (A.1) – (A.5), along with the assumptions of the semiparametric time-to-event models for clustered data, imply that the full conditionals for the misclassification parameters under the more general misclassification model are truncated beta distributions given by

$${\eta }_{(q,j)}\mid \cdots \sim \text{Beta}\left(a^{(\eta ,0)}+n_{(q,j)}^{00},a^{(\eta ,1)}+n_{(q,j)}^{+0}-n_{(q,j)}^{00}\right)\mathbb{I}{\left({\eta }_{(q,j)}\right)}_{\left\{{\eta }_{(q,j)}:{\eta }_{(q,j)}>1-{\alpha }_{(q,j)}\right\}},$$

and

$${\alpha }_{(q,j)}\mid \cdots \sim \text{Beta}\left(a^{(\alpha ,0)}+n_{(q,j)}^{11},a^{(\alpha ,1)}+n_{(q,j)}^{+1}-n_{(q,j)}^{11}\right)\mathbb{I}{\left({\alpha }_{(q,j)}\right)}_{\left\{{\alpha }_{(q,j)}:{\alpha }_{(q,j)}>1-{\eta }_{(q,j)}\right\}},$$

where

$$\begin{array}{cc}\hfill n_{(q,j)}^{00}& =\sum _{i=1}^N\sum _{k=1}^{K_i}I{\left(D_{(i,j,k)},T_{(i,j)}\right)}_{{{\left\{D_{(i,j,k)}=0,T_{(i,j)}\in \left(v_{(i,k)},+\infty \right)\right\}}^{\mathbb{I}\left({\xi }_{(i,k)}\right)}}_{\{q\}},}\hfill \\ \hfill & n_{(q,j)}^{+0}=\sum _{i=1}^N\sum _{k=1}^{K_i}I{\left(T_{(i,j)}\right)}_{{{\left\{T_{(i,j)}\in \left(v_{(i,k)},+\infty \right]\right\}}^{I\left({\xi }_{(i,k)}\right)}}_{\{q\}},}\hfill \\ \hfill n_{(q,j)}^{11}& =\sum _{i=1}^N\sum _{k=1}^{K_i}I{\left(D_{(i,j,k)},T_{(i,j)}\right)}_{{{\left\{D_{(i,j,k)}=1,T_{(i,j)}\in \left(0,v_{(i,k)}\right]\right\}}^{\mathbb{I}\left({\xi }_{(i,k)}\right)}}_{\{q\}},}\hfill \end{array}$$

and

$$n_{(q,j)}^{+1}=\sum _{i=1}^N\sum _{k=1}^{K_i}I{\left(T_{(i,j)}\right)}_{{{\left\{T_{(i,j)}\in \left(0,v_{(i,k)}\right]\right\}}^{I\left({\xi }_{(i,k)}\right)}}_{\{q\}}.}$$

Similar expressions are obtained for the model assuming the same examiner-specific misclassification parameters for each variable.

The updating scheme for the association parameters of the Gaussian copula model, ρ, depends on the parametrization of the correlation matrix R_ρ. Under an unstructured correlation matrix, parameter expansion for data augmentation strategies can be used (Liu & Wu, 1999; van Dyk & Meng, 2001; Imai & van Dyk, 2005). A compound symmetric parameterization, with off-diagonal elements equal and positive, allows for a simpler marginal joint likelihood of the proposed models. Specifically, a compound symmetry parameterization of the correlation matrix can be obtained from the stochastic representation Z_ij = γ_i + ϵ_ij, where ${\gamma }_i\mid \rho \stackrel{i.i.d.}{\sim }N(0,\rho )$ and ${ϵ}_{ij}\mid \rho \stackrel{i.i.d.}{\sim }N(0,1-\rho )$. Thus, given γ_i, the conditional CDF for T_(i,j) is given by

$$F_{x_{(i,j)}}(t\mid {\gamma }_i)=\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(F_{x_{(i,j)}}(t))-{\gamma }_i}{\sqrt{1-\rho }}\right),$$

and p (D_i ∣ γ_i, α, η, β, ρ, F₀) is given by

$$\prod _{j=1}^J\left\{\sum _{k=1}^{K_i+1}{A}_{(i,j,k)}\left[\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(F_{x_{(i,j)}}(v_{(i,k)}))-{\gamma }_i}{\sqrt{1-\rho }}\right)-\mathrm{\Phi }\left(\frac{{\mathrm{\Phi }}^{-1}(F_{x_{(i,j)}}(v_{(i,k-1)}))-{\gamma }_i}{\sqrt{1-\rho }}\right)\right]\right\},$$ (8)

Where $A_{(i,j,k)}={\prod }_{l=k}^{K_i}{\alpha }_{({\xi }_{(i,l)},j)}^{D_{(i,j,l)}}{\left(1-{\alpha }_{({\xi }_{(i,l)},j)}\right)}^{1-D_{(i,j,l)}}{\prod }_{l=1}^{k-1}{\eta }_{({\xi }_{(i,l)},j)}^{1-D_{(i,j,l)}}{\left(1-{\eta }_{({\xi }_{(i,l)},j)}\right)}^{D_{(i,j,l)}}$. A detailed description of the MCMC algorithm employed under a general correlation matrix is given in Appendix B of the online supplementary material.

4. A Simulation Study

To validate the proposed models, we conducted an analysis of simulated datasets. The main aim of this study is to provide empirical evidence that under the proposed semiparametric marginal approach to modeling misclassified time-to-event data the model parameters can be estimated from the observed data only, without the need of external information about the misclassification parameters. It is important to emphasize that external information beyond the observed data is often required for misclassified data in other settings. The simulation study is also used to evaluate the performance of classical model selection criteria in identifying among the time-to-event model assumptions, to show the effect of performing naive analyses neglecting the misclassification process, and to assess the effect on inferences under a wrong time-to-event model.

4.1. The Simulation Settings

Three different marginal models are considered for the underlying time-to-event data T_(i,j). Specifically, we consider PH, AFT, and PO marginal assumptions in the definition of the true model, respectively. Under the three models we considered J = 4 teeth and the joint model was completed by considering a Gaussian copula function. For all models, a bimodal baseline distribution is assumed by considering F₀(·) = 0.5 × LN(· ∣ −0.5, 0.8²) + 0.5 × LN(· ∣ 0.5, 0.3²), where LN(· ∣ μ, σ²) refers to the CDF of a log-Normal distribution with location μ and scale parameter σ². For each model we set x_(i,j) = (x_(i,j,1), x_(i,j,2)), where $x_{(i,j,1)}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }\text{Bernoulli}(0.5)$, $x_{(i,j,2)}\stackrel{\mathrm{i}.\mathrm{i}.\mathrm{d}.}{\sim }\text{Uniform}(0,1)$. The true time-to-event marginal models are shown in Appendix C of the online supplementary material.

For each marginal model, three different simulation scenarios were considered. In Scenario I, a compound symmetry correlation matrix and common effects of the predictors across teeth were assumed. In this case, we set ρ = 0.2 and β_j = (−0.5, 1), for every j. The true time-to-events were interval-censored by simulating the “visit” times for each subject. We considered K_i = 10. The first visit time was randomly chosen from an LN(−1.0, 2²) distribution. The time between the consecutive visits, υ_i,k – υ_i,k–1,, was drawn from an LN(−0.7, 0.2²) distribution. We assumed that the assessment of the occurrence of the event was performed by Q = 4 examiners, allocated randomly to each subject and visit. We further assumed common misclassification parameters for each examiner across variables and set α = (0.95, 0.90, 0.85, 0.80) and η = (0.80, 0.85, 0.90, 0.95).

In Scenario II, a general correlation matrix was assumed, keeping everything else the same as in Scenario I. In this case, we set

$${\mathit{R}}_{\rho }=\left(\begin{array}{cccc}\hfill 1.0\hfill & \hfill {\rho }_{12}\hfill & \hfill {\rho }_{13}\hfill & \hfill {\rho }_{14}\hfill \\ \hfill {\rho }_{21}\hfill & \hfill 1.0\hfill & \hfill {\rho }_{23}\hfill & \hfill {\rho }_{24}\hfill \\ \hfill {\rho }_{31}\hfill & \hfill {\rho }_{32}\hfill & \hfill 1.0\hfill & \hfill {\rho }_{34}\hfill \\ \hfill {\rho }_{41}\hfill & \hfill {\rho }_{42}\hfill & \hfill {\rho }_{43}\hfill & \hfill 1.0\hfill \end{array}\right)=\left(\begin{array}{cccc}\hfill 1.0\hfill & \hfill 0.4\hfill & \hfill 0.2\hfill & \hfill 0.1\hfill \\ \hfill 0.4\hfill & \hfill 1.0\hfill & \hfill 0.4\hfill & \hfill 0.2\hfill \\ \hfill 0.2\hfill & \hfill 0.4\hfill & \hfill 1.0\hfill & \hfill 0.4\hfill \\ \hfill 0.1\hfill & \hfill 0.2\hfill & \hfill 0.4\hfill & \hfill 1.0\hfill \end{array}\right).$$

In Scenario III, data were generated using the same setup as Scenario II, but we allowed tooth-specific misclassification parameters and predictor effects for each of the four examiners in estimation. For each simulation scenario and true marginal model, we considered three different sample sizes N = 100, 200, and 300. For each scenario, true marginal model, and sample size, 200 datasets were generated.

To evaluate the ability to identify among the correct time-to-event modeling assumption, AFT,PH, and PO versions of the proposed marginal model were fit to each dataset, using the algorithms described in Section 3.4. Under Scenarios I and II, we considered versions of the proposed model assuming common effects of the predictors across teeth and common misclassification parameters across teeth for each examiner. In this case, we set m_β = m_θ = 0₂, V_β = V_θ = 10³ × I₂, and constrained uniform priors distributions were assumed for the misclassification parameters by taking $a_{(1)}^{(\alpha ,0)}=a_{(1)}^{(\alpha ,1)}=\cdots =a_{(Q)}^{(\alpha ,0)}=a_{(Q)}^{(\alpha ,1)}=1$ and $a_{(1)}^{(\eta ,0)}=a_{(1)}^{(\eta ,1)}=\cdots =a_{(Q)}^{(\eta ,0)}=a_{(Q)}^{(\eta ,1)}=1$. Under Scenario I a compound symmetry correlation matrix was assumed with an uniform prior for ρ. Under Scenario II an unstructured correlation matrix was assumed with a uniform Haar prior over all correlation matrices. Under Scenario III, on the other hand, we considered versions of the proposed model assuming different effects of the predictors across teeth, an unstructured correlation matrix, and different misclassification parameters across teeth for each examiner. In this case, we set m_β = m_θ = 0₈, V_β = V_θ = 10³ × I₈, and considered a uniform prior for the general correlation matrix and constrained uniform priors for the misclassification parameters. For all models we set c = 1.

For each model and dataset, we obtain a posterior sample of size 5,000, after a burn-in period of 20,000 and thinning of every other 5 scans of the posterior distribution. The three versions of the proposed marginal model fit for each dataset were compared by means of the pseudo Bayes factor (PsBF), originally developed by Geisser & Eddy (1979) and further considered by Gelfand Dey (1994). The PsBF for the comparison of M_i versus M_j corresponds to the ratio between the pseudo marginal likelihood (PML) for model M_i and model M_j. In our context, the PML for model M_i is defined as

$${\text{PML}}_{M_i}=\prod _{i=1}^N\prod _{j=1}^J{p}_{M_i}\left(D_{(i,j,1)},\dots ,D_{(i,j,K_i)}\mid {\mathbf{D}}^{[-(i,j)]}\right),$$

where p_Mi(D_(i,j,1), … , D_(i,j,Ki)∣D^[−(i,j)]) is the predictive distribution for observations associated with the jth tooth of the ith subject, based on the data D^[−(i,j)] and under model M_i, with D^[−(i,j)] being the observed data matrix that excludes the observation for the jth tooth of subject i. Therefore, PsBF for model M_i versus model M_j is defined as

$${\text{PBF}}_{M_i,M_j}=\prod _{i=1}^N\prod _{j=1}^J\frac{p_{M_i}\left(D_{(i,j,1)},\dots ,D_{(i,j,K_i)}\mid {\mathbf{D}}^{[-(i,j)]}\right)}{p_{M_i}\left(D_{(i,j,1)},\dots ,D_{(i,j,K_i)}\mid {\mathbf{D}}^{[-(i,j)]}\right)}.$$ (9)

The method suggested by Gelfand & Dey (1994) was used to obtain estimates of CPO statistics from the MCMC output. Under a compound symmetry correlation matrix, the CPO can be computed as

$$\begin{array}{cc}\hfill p_{M_i}& \left(D_{(i,j,1)},\dots ,D_{(i,j,K_i)}\mid {\mathbf{D}}^{[-(i,j)]}\right)\hfill \\ \hfill & ={\left\{E_{{\gamma }_i,\alpha ,\eta ,\beta ,\rho ,F_0\mid \mathbf{D}}\left(\frac{1}{p\left({\mathbf{D}}_{(i,j)}\mid {\gamma }_i,\alpha ,\eta ,\beta ,\rho ,F_0\right)}\right)\right\}}^{-1},\hfill \\ \hfill & \approx {\left\{\frac{1}{B}\sum _{b=1}^B\left(\frac{1}{p\left({\mathbf{D}}_{(i,j)}\mid {\gamma }_i^{(b)},{\alpha }^{(b)},{\eta }^{(b)},{\beta }^{(b)},{\rho }^{(b)},F_0^{(b)}\right)}\right)\right\}}^{-1},\hfill \end{array}$$

Where (${\gamma }_i^{(b)}$, α^(b), η_(b), β_(b), ρ_(b), $F_0^{(b)}$), b = 1, … , B, are MCMC samples from the posterior distribution, and p(D_(i,j) ∣ γ_i, α, η, β, ρ, F₀) can be derived from expression (8). The expression forapproximating the CPO under an unstructured correlation matrix is given in Appendix D of the online supplementary material.

To assess the effect of ignoring the misclassification process on the statistical inferences we performed naive analyses to data generated under misclassification. Specifically, we implemented the semiparametric marginal models described in Section 3.1 for regular interval-censored data. These models were fit to the data that arises by assuming that the identification of the interval of time where each event occurred is free of error, leading to regular interval-censored data. In this case, each response was assumed to lie in the corresponding kth interval, where k is the first interval where D_(i,j,k) = 1, regardless of the values of D_(i,j,k+1), … , D_(i,j,Ki). The naive analyses were performed for the data generated under Scenario I, using the same MCMC and prior specification as for the corresponding semiparametric marginal models taking into account the misclassification process.

Finally, to assess the effect on the inferences of the use of a wrong time-to-event model, we also simulate data from an extended hazard (EH) model (see,e.g, Li et al., 2015). The EH model assumes the following relationship among the baseline survival distribution, the predictors, and the marginal survival distributions:

$$1-F_{x_{(i,j)}}(t)=(1-F_0(\text{exp}\{{\mathit{x}}_{(i,j)}^{\prime }\zeta \}t){)}^{\text{exp}\{x_{(i,j)}^{\prime }\beta \}},$$

where β and ζ are vectors of regression coefficients. The EH model is a more flexible survival model, including AFT and PH as special cases.

4.2. The Results

The results suggest that the regression and association parameters can be estimated with only minimal bias and with reasonable precision under all simulation settings. Table 1 shows the means, across simulations, the biases, and the MSE of the posterior mean of the parameters from the different versions of the semiparametric model, from the different time-to-event modeling assumptions under Scenario I. The results under Scenarios II, III, and a variation of Scenario I with a different baseline time-to-event distribution (Scenario IV), are shown in Appendix E of the online supplementary material.

Table 1:

Simulated data - Scenario I. True value, Monte Carlo mean, bias, and mean square error (MSE) of the posterior mean of the time-to-event model parameters. The results are presented for different group sample sizes (N) and true underlying time-to-event model assumptions (PH, AFT and PO). In this table, the same true time-to-event model is assumed to simulate and to fit the data.

			True Marginal Model
			PH			AFT			PO
N	Parameter	True Value	Mean	Bias	MSE	Mean	Bias	MSE	Mean	Bias	MSE
100	β1	−0.5	−0.502	0.002	0.036868	−0.495	0.005	0.005954	−0.502	0.002	0.036868
	β2	1.0	1.032	0.032	0.114593	1.004	0.004	0.016145	1.032	0.032	0.114593
	ρ	0.2	0.2350	0.035	0.005422	0.226	0.026	0.004412	0.244	0.044	0.006299
200	β1	−0.5	−0.496	0.004	0.007412	−0.502	0.002	0.002504	−0.479	0.021	0.019762
	β2	1.0	1.022	0.022	0.025133	1.015	0.015	0.008689	1.070	0.070	0.067400
	ρ	0.2	0.218	0.018	0.002634	0.214	0.014	0.002304	0.217	0.017	0.002817
300	β1	−0.5	−0.504	0.004	0.005200	−0.505	0.005	0.001625	−0.502	0.002	0.015133
	β2	1.0	1.001	0.001	0.017162	0.997	0.003	0.004365	1.029	0.029	0.046210
	ρ	0.2	0.212	0.012	0.001533	0.212	0.012	0.00168	0.214	0.014	0.001809

Similar results regarding bias and MSE were observed for the misclassification parameters for all simulation settings. Figures 1 and 2 show the results for Scenario I. In general the MSE is similar for the misclassification parameters across true time-to-event models and there is a larger variability of the estimates of the specificity parameters. This is explained by the distribution of the visit times. In fact, assessment intervals were simulated to roughly capture all possible survival times, i.e. approximately cover the support of the true survival distributions. However, relatively more assessment visits are toward the tail of the survival distribution. Therefore, less information is available to estimate the specificity parameters.

Figure 1:

Simulated data- Scenario I: True value (×), mean of the posterior mean across simuplations (●) $\pm 1.96\times \sqrt{\text{MSE}}$ for the sensitivity and specificity of each examiner. The results for = 100, N = 200 and N = 300 are displayed as solid, dashed and dotted lines, respectively. Panels (a) and (b), (c) and (d), and (e) and (f) display the results under a true PH, AFT and PO marginal time-to-event model, respectively. Panels (a), (c) and (e) display the results for the sensitivity. Panels (b), (d) and (f) display the results for the specificity.

Figure 2:

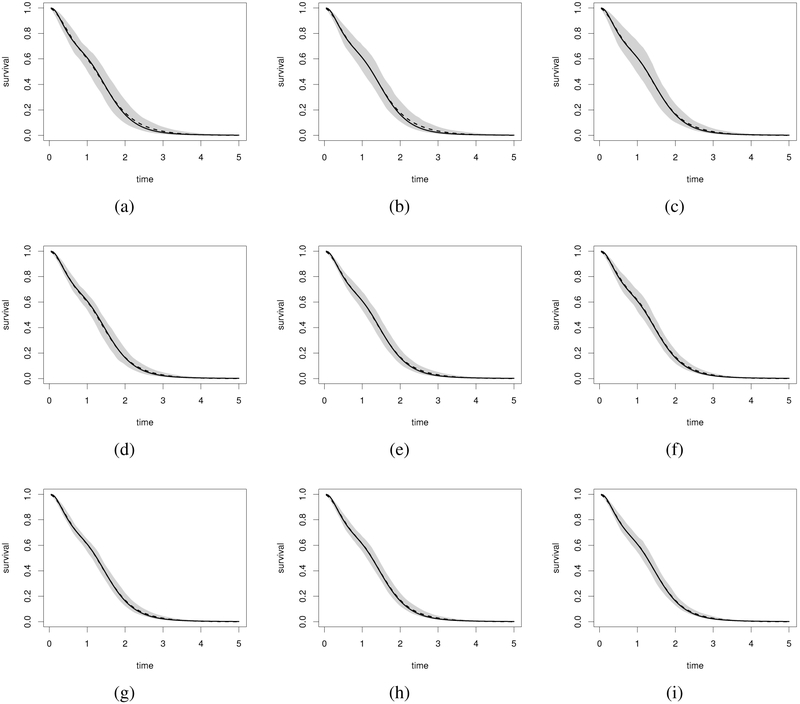
Simulated data - Scenario I. Mean across simulations of the posterior mean of the baseline survival function (dashed line), point-wise 95% confidence region (shaded). The true survival function is represented as a solid line. Panels (a), (b), and (c) display the results for N = 100 under a true PH, AFT and PO marginal model, respectively. Panels (d), (e), and (f) display the results for N = 200 under a true PH, AFT and PO marginal model, respectively. Panels (g), (h), and (i) display the results for N = 300 under a true PH, AFT and PO marginal model, respectively

As illustrated in Table 1, Figure 1, and Figure 2 for Scenario I, important reductions in the MSE were observed for all parameters when the sample size increased for all simulation settings, suggesting that the posterior mean is a consistent estimator of the model parameters. These results on bias, MSE, and consistency strongly suggest that prior information on the misclassification parameters is not needed to obtain nearly unbiased and precise estimates for the regression coefficients, association parameters and misclassification parameters. Thus, the model parameters can be estimated from the observed data without extra information on the misclassification parameters.

Table 2 displays the results on the behavior of the model selection criteria under Scenario I. This table shows the percentage of time across simulations in which the logarithm of the PML (LPML) selects the correct time-to-event model assumption. The results show that the LPML is an adequate model selection criteria and that the power for selecting the correct regression model assumption is high even for sample sizes as small as N = 100. Furthermore, the power of LPML for selecting the correct model assumption rapidly increases with the sample size. The less power observed for the LPML for detecting the correct regression assumption under the PH and PO model is explained by the distribution of the visit times. More assessment visits are toward the tail of the time-to-event distribution under the PH and PO models, in comparison with the AFT model.

Table 2:

Simulated data - Scenario I. Percentage of time, across simulations, in which the LPML favors the correct true underlying time-to-event regression model assumption. The results are shown for the different group sample sizes (N) and true underlying time-to-event regression model assumption.

	True Marginal Model
N	PH	AFT	PO
100	67.5	84.0	67.5
200	87.1	94.4	81.0
300	90.0	98.4	86.2

Table 3 and Figure 3 show the results for the naive analysis assuming no misclassification. The increased bias and MSE strongly support the benefits of the proposed model under the presence of misclassification. Indeed, systematic and strong bias were observed for the regression coefficients and variance components. The posterior mean of the regression coefficients under the naive model were biased towards the null effect. Furthermore, an underestimation of the correlation is obtained under a naive analysis. As expected from the results obtained for the model parameters under a naive analysis, the posterior mean is a strongly biased estimator of the baseline survival function if the misclassification process is not taken into account. Most of the marginal survival probabilities are significantly underestimated by the posterior mean under the naive analysis.

Table 3:

Simulated data - Scenario I. True value, and Monte Carlo mean, bias and mean square error (MSE) of the posterior mean of the time-to-event model parameters for different sample sizes. The results are presented for naive fitting of AFT, PO, and PH models. In this table, the same true time-to-event model is assumed to simulate and to fit the data.

		Fitted Model
			PH			AFT			PO
N	Parameter	True Value	Mean	Bias	MSE	Mean	Bias	MSE	Mean	Bias	MSE
100	β1	−0.5	−0.308	0.192	0.046564	−0.386	0.114	0.017434	−0.325	0.175	0.059050
	β2	1.0	0.686	0.314	0.129580	0.791	0.209	0.057670	0.735	0.265	0.165507
	ρ	0.2	0.146	0.054	0.005063	0.141	0.059	0.005210	0.144	0.056	0.005398
200	β1	−0.5	−0.312	0.188	0.040296	−0.390	0.11	0.014599	−0.347	0.153	0.037034
	β2	1.0	0.710	0.290	0.100839	0.798	0.202	0.048498	0.717	0.283	0.125007
	ρ	0.2	0.125	0.075	0.006762	0.125	0.075	0.006812	0.130	0.070	0.006303
300	β1	−0.5	−0.315	0.185	0.037274	−0.386	0.114	0.014451	−0.332	0.168	0.038471
	β2	1.0	0.713	0.287	0.095330	0.809	0.191	0.040722	0.687	0.313	0.128777
	ρ	0.2	0.120	0.080	0.007240	0.118	0.082	0.007573	0.122	0.078	0.006896

Figure 3:

Simulated data - Scenario I. Mean across simulations of the posterior mean of the baseline survival function (dashed line), point-wise 95% confidence region (shaded) under the a naive analysis ignoring the misclassification process. The true survival function is represented as a solid line. Panels (a), (b), and (c) display the results for N = 100 under a true PH, AFT and PO marginal model, respectively. Panels (d), (e), and (f) display the results for N = 200 under a true PH, AFT and PO marginal model, respectively. Panels (g), (h), and (i) display the results for N = 300 under a true PH, AFT and PO marginal model, respectively

Finally, when an incorrect probability model is fit to the data, it is expected to observe misleading inferences associated with parameters with different interpretations across models (e.g., the regression coefficients) and parameters highly influenced by the model assumptions (e.g., the marginal survival functions, which varies as a function of predictors in different ways under the different models). However, no or little effects are expected on parameters with a common interpretation, such as the association structure and misclassification parameters. A more detailed discussion on this aspect is provided in Appendix F of the online supplementary material.

5. The analysis of the Signal-Tandmobiel^® data

In this section analyses of the ST study data are presented. We are interested in the evaluation of the marginal effect of gender, age at baseline, age when brushing starts, number of between-meal snacks (two or less a day versus more than two a day), and geographical location of the school, expressed in terms of the x– and y–coordinates, on the time-to-CE for permanent first molars: teeth 16, 26 on the maxilla (upper quadrants), and teeth 36 and 46 on the mandible (lower quadrants). The inclusion of the geographical components, was motivated by the results of exploratory data analyses without correcting for misclassification, that showed a significant East-West gradient in the apparent prevalence of CE in Flanders (estimated as the number of teeth testing positive to CE by the dentists divided by the number of teeth in the sample, and shown in Figure 10 of Appendix G of the online supplementary material). Therefore, one of the research questions is whether there is a geographical trend in the true prevalence of CE or the observed trend in the apparent prevalence is completely explained by the geographic distribution of the dentists. In fact, and for practical reasons, the dentists were active in a relatively restricted geographical area. For instance, the spatial distribution of the dentist in the first year of examination of the ST is shown in Figure 11 of Appendix G of the online supplementary material. Thus, a possible cause for the apparent trend in CE is a different scoring behavior of the 16 dental examiners and their non–homogeneous spatial distribution in the study area. The proposed model address this question by correcting for the misclassification of the examiners and, at the same time, evaluating the effect of the geographic location of the school on the underlying distribution of the time-to-CE. Notice that the identification of the two possible sources of the geographic trend are possible because in each year there was more than one examiner active in each geographical area and there was some overlapping between the area where each examiner was active and the regions. For instance, for the first year of examination at least 4 examiners were active in each province and 14 out of the 16 examiners were active in more than one province.

Different versions of the proposed models were fit the to ST data. Specifically, we considered different marginal modeling assumptions, common or tooth-specific regression coefficients, compound symmetry (structured) or unstructured correlation matrices, nonlinear and linear models for the effects of the geographic location of the schools, and common or covariate specific misclassification parameters. For the geographic location of the schools we considered a model based on tensor product of spline basis functions for x and y (i.e., nonlinear and with interaction) (Hennerfeind et al., 2006), additive spline basis for x and y (i.e., nonlinear and without interaction), linear terms for x and y with an interaction term, and a linear version without interaction. For the misclassification parameters, we considered models assuming common sensitivity and specificity parameters across teeth for every examiner, along with a model where these parameters were allow to vary with tooth’s position, child’s gender and age at baseline.

The models were fit by assuming similar priors to the ones described in the analyses of simulated data. For each model, we ran the Markov chain cycle described in Section 3.4 a conservative total number of 1,000,000 samples. The full chain was subsampled every 50 iterations after a burn-in period of 250,000 samples, to give a reduced chain of length 15,000. Standard MCMC tests (not shown), suggested convergence of the chains.

Table 4 shows the LPML for the different models. The results suggest that, from a predictive point of view, the PO version of the Bayesian semiparametric marginal model predicts these data the best. Furthermore, the results show that the simplest version of the model better fits the data. Specifically, we conclude that there is no need for a “nonparametric” modeling of the geographic information or evidence of spatial interaction, interaction between the predictors and the tooth’s location, an unstructured correlation matrix, different misclassification parameters across teeth or predictor-dependent misclassification parameters. More importantly, the results also suggest that the marginal models outperform the flexible AFT frailty model proposed by García-Zattera et al. (2016) for these data. In fact, the LPML for the frailty AFT model considering the same predictors and misclassification model was −5560 versus −5543 for the simplest PO model.

Table 4:

Signal-Tandmobiel^® data. Log pseudo marginal likelihood (LPML) for the considered models. For the geographic location of the schools the tensor product of spline basis functions for x and y, additive spline basis for x and y, linear terms for x and y with an interaction term, and a linear version without interaction are represented by g(x, y), g_x(x) + g_y(y), x + y + x × y, and x + y, respectively.

Marginal model	β (across teeth)	Rρ	x and y	α and η	LPML
AFT	Common	Structured	x + y	Common	−5552
PH	Common	Structured	x + y	Common	−5545
PO	Common	Structured	x + y	Common	−5543
PO	Common	Unstructured	x + y	Common	−5828
PO	Common	Structured	x + y	Different	−5610
PO	Common	Structured	x + y	Depending on x	−5547
PO	Different	Structured	x + y	Common	−5556
PO	Common	Structured	g(x, y)	Common	−5544
PO	Common	Structured	gx(x) + gy(y)	Common	−5545
PO	Common	Structured	x + y + x × y	Common	−5546

To assess the goodness of fit of the proposed model two different measures were considered. Specifically, we consider a posterior predictive check strategy (Gelman et al., 2014), where we compare the predictive distribution of the error-corrupted binary variables with the observed ones. A summary of the results for the ST data under different models is given in Appendix H of the online supplementary material. The results show there is no evidence of lack of fit for the selected model. For instance, the 95% credible band from the posterior predictive distribution contains the observed count in all cases. Furthermore, the PO versions of the proposed model (under a compound symmetry correlation matrix and under an unstructured correlation matrix) showed the best performance. In fact, the posterior predictive mean (95% credible interval) of the “chi-square” goodness of fit statistics was 48.76 (17.67, 118.34), 47.54 (19.22, 118.87), 83.28 (48.44, 153.12), 53.62 (19.55, 144.49), and 65.06 (31.42, 138.80), for the PO model under a compound symmetry correlation matrix, for the PO model under an unstructured correlation matrix, for a parametric version of a PO model (with a compound symmetry correlation matrix) using a Weibull baseline distribution, for the for the PH version of the model, for the AFT version of the model, respectively.

As a second measure of goodness of fit we consider the posterior predictive distribution for the latent time-to-event residuals and compare it with the theoretical distribution, assuming that the model is correct. The results for the different teeth under the PO version of the proposed model are given in Appendix H of the online supplementary material for a compound symmetry correlation matrix and under an unstructured correlation matrix. The results do not show significant deviations from the theoretical distribution for all teeth. The PO model under an unstructured correlation matrix shows a slightly better performance, where the point-wise 95% credible band for the quantiles of the latent residuals cover the theoretical straight line completely. For the PO model under a compound symmetry correlation matrix, the point-wise 95% credible band for the quantiles of the latent residuals cover most of the theoretical straight line, with small deviations observed for tooth 46.

Table 5 shows the posterior means and 95% highest posterior density (95% HPD) credible intervals for the regression and association parameters under the selected PO semiparametric model. The 95%HPD interval for each regression coefficient suggest that gender, age, age when brushing starts, and the geographical location (y-coordinate) has a significant effect on the marginal odds of CE at any given time. To evaluate the posterior evidence about the effect of the predictors on the time to CE, we also computed the pseudo contour probability (PsCP) for each of these hypotheses. The PsCP was computed based on equi-tailed credible bands and is defined as one minus the smallest credible level for which the null hypothesis parameter value is contained in the corresponding credible bands. The PsCP was 0.007 for the marginal effect of gender, 0.001 for the marginal effect of both age and age when brushing starts, 0.185 for the number of between-meal snacks, 0.275 for the x-coordinate, and 0.006 for the y-coordinate. These results suggest that there is strong posterior evidence against several of the corresponding null hypotheses: namely, boys have greater odds of developing CE and that the older the child is when he/she starts brushing, the greater the odds of developing CE. Furthermore, the results on β₅ and β₆ support the hypothesis that the observed geographical gradient is indeed explained by real local geographical differences and not due to the different scoring behavior of the examiners.

Table 5:

Signal-Tandmobiel^® data. Posterior mean (95% credible interval) for the time-to-event model parameters under the PO version of the proposed model (PO), a semiparametric version of the PO model for error-free interval-censored data, neglecting the misclassification process (PO naive), and for a Weibull parametric PO model, taking into account the misclassification process (PO parametric).

	Model
Parameter	PO	PO naive	PO parametric
β1(Gender; Girl)	0.2853 ( 0.0677 ; 0.5049)	0.2126 ( 0.0018 ; 0.4242)	0.3742 ( 0.1420 ; 0.5730)
β2 (Age at baseline; years)	0.2275 ( 0.1343 ; 0.3266)	0.1927 ( 0.1165 ; 0.2667)	0.2381 ( 0.1348 ; 0.3376)
β3 (Age when brushing starts; years)	−0.3108 (−0.5082; −0.1202)	−0.2642 (−0.4042; −0.1139)	0.1362 (−0.0649 ; 0.3059)
β4 (In between–meal snacks; ≥ 2 a day)	0.1609 (−0.0718 ; 0.4039)	0.1554 (−0.0565 ; 0.3804)	0.1947 (−0.0323 ; 0.4258)
β5 (x-coordinate)	1.2029 (−0.9065 ; 3.2985)	1.1348 (−0.6141 ; 2.6372)	2.0010 (−0.1179 ; 3.8020)
β6 (y-coordinate)	−8.5588 (−14.7564 ; −2.7341)	−7.9773 (−12.8916 ; −3.1642)	−4.0854 (−9.8616 ; 1.9983)
ρ	0.6935 ( 0.6520 ; 0.7309)	0.5536 ( 0.4672 ; 0.6512)	0.4241 ( 0.3342 ; 0.4966)

Figure 4 shows the posterior mean and 95% HPD credible interval for the sensitivity and specificity of each examiner under the selected PO model. The results under the corresponding AFT and PH models are also displayed in this figure. The results suggest a greater variability in the sensitivity than in the specificity estimates, which can be explained by the low prevalence of CE at this age. All examiners showed a sensitivity greater than 0.75, with rather narrow 95% HPD credible intervals, with one exception. The latter result is explained by the fact that this examiner (examiner 9) was only involved in the first two years of the ST study, having less information for the estimation of his parameters. The posterior means for the specificity parameters were higher than 0.93 for all examiners.

Figure 4:

Signal-Tandmobiel^® data. Posterior mean (●) and 95% highest posterior density intervals for the misclassification parameters for each examiner. Panels (a) and (b), (c) and (d), and (e) and (f) display the results under a PH, AFT and PO marginal time-to-event model, respectively. Panels (a), (c) and (e) display the results for the sensitivity. Panels (b), (d) and (f) display the results for the specificity.

To illustrate the contributions of both the nonparametric and misclassification components of the proposed model for the ST data, we also implemented and fit parametric versions of the proposed models and performed naive analyses by considering a Bayesian semiparametric models for error-free interval-censored data (i.e., neglecting the misclassification process). The results show the need of the Bayesian nonparametric component in the time-to-event model. As a matter of fact, the LPML for parametric counterparts of the simplest PH, AFT, and PO versions of the model were −5570, −5583, and −5564, respectively. In these cases, the parametric models were fit using a Weibull baseline distribution, the same predictors, and the same misclassification model.

Table 5 shows the results of the regression parameters under a semiparametric PO model using a naive analysis. Not taking into account the misclassification process for the ST data causes an attenuation of the effects of the predictors towards zero. Also, the power for detecting differences is reduced. The results also show that the correction of the point estimates of predictor effects obtained under the model taking into account the misclassification, in comparison with the naive analysis, does not come with an increase in variability, which is an important advantage with respect to contexts where the data does not contain information on the misclassification parameters (see, e.g., Luan et al., 2015). On the other hand, the results under a Weibull parametric PO model show that the differences in the posterior inferences do not follow a systematic pattern, with coefficients taking higher or smaller values than observed under the semiparametric PO model. More importantly, the significant effect of the age when brushing starts variable and geographic location are not detected under the parametric version of the model.

Figures 5 and 6 display the estimated survival functions for some combinations of the predictors under the different models. The results also show that significantly different inferences are obtained when the objects of interest are the predictor-dependent marginal survival functions. The inferences under naive analyses not taking into account the misclassification process and a parametric version of the model can even produce survival point estimates that are outside the credible region under the PO model (please also see Figures 14 and 15 in the online supplementary material).

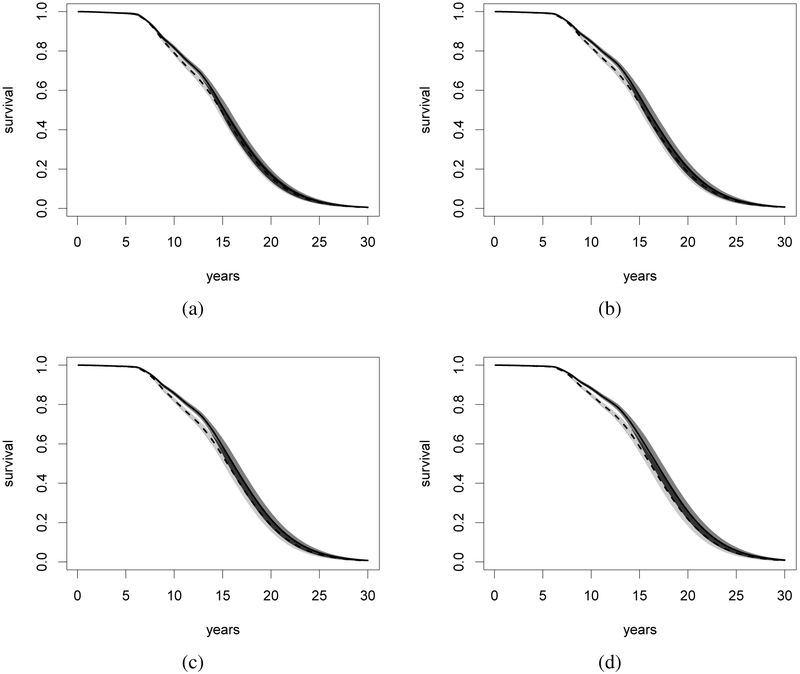
Figure 5:

Signal-Tandmobiel^® data - PO model - misclassification. Posterior predictive mean of the survival function under the selected model (solid line) and under a semiparametric PO model neglecting the misclassification process (dashed line). The pointwise 60% credible bands for each model are displayed as gray areas. Panel (a) displays the results for a girl, 7.2 years old at baseline, 3 years old when brushing starts, having two or fewer snacks in-between meals, and sample mean x– and y– coordinates. Panel (b) displays the results for a girl, 7.2 years old at baseline, 2 years old when brushing starts, having two or fewer snacks in-between meals, and sample mean x– and y–coordinates. Panel (c) displays the results for a boy, 7.2 years old at baseline, 3 years old when brushing starts, having two or fewer snacks in-between meals, and sample mean x– and y–coordinates. Panel (d) displays the results for a boy, 7.2 years old at baseline, 2 years old when brushing starts, having two or fewer snacks in-between meals, and sample mean x– and y–coordinates.

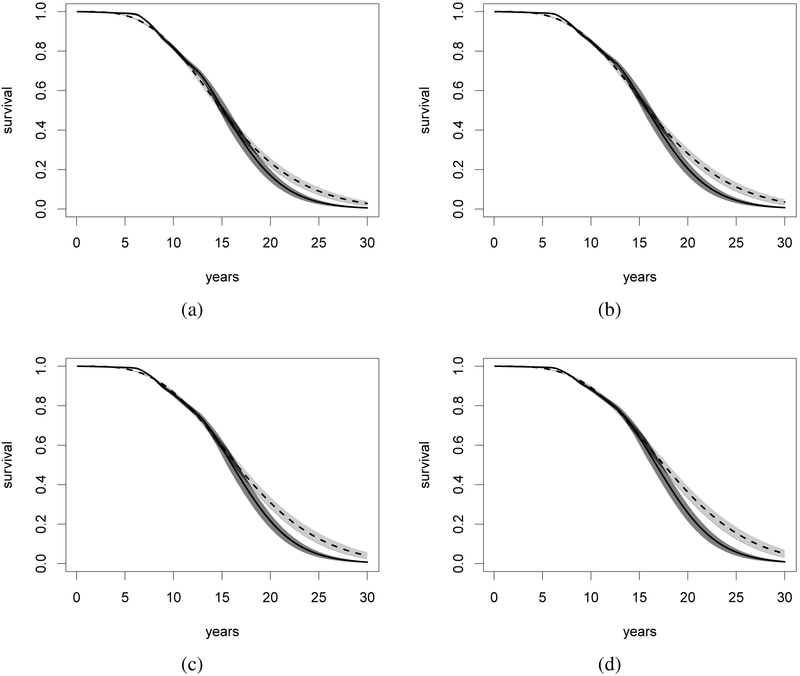
Figure 6:

Signal-Tandmobiel^® data - PO model - nonparametric. Posterior predictive mean of the survival function under the selected model (solid line) and under a Weibull parametric PO model (dashed line). The pointwise 60% credible bands for each model are displayed as gray areas. Panel (a) displays the results for a girl, 7.2 years old at baseline, 3 years old when brushing starts, having two or fewer snacks in-between meals, and sample mean x– and y–coordinates. Panel (b) displays the results for a girl, 7.2 years old at baseline, 2 years old when brushing starts, having two or fewer snacks in-between meals, and sample mean x– and y–coordinates. Panel (c) displays the results for a boy, 7.2 years old at baseline, 3 years old when brushing starts, having two or fewer snacks in-between meals, and sample mean x– and y–coordinates. Panel (d) displays the results for a boy, 7.2 years old at baseline, 2 years old when brushing starts, having two or fewer snacks in-between meals, and sample mean x– and y–coordinates.

6. Concluding Remarks

We have proposed a Bayesian semiparametric approach for the marginal modeling of misclassified correlated interval-censored data and showed that models under this framework can outperform standard frailty models, even when they are specified in a flexible way regarding the distributional assumptions. Although the methodology was motivated by an oral health application, it can be applied to any situation where correlated responses are of interest, they can only be determined to lie in an interval of time, and the assessment of the event is subject to misclassification. Examples include studies about kidney failure or vision loss. An important aspect associated with the Bayesian nonparametric formulation of the model is that, by assuming the same flexible model for the baseline marginal time-to-event distribution function F₀, the different regression model assumptions are placed on common ground. Furthermore, parametric models are special cases of the nonparametric models. Thus, differences in the performance of the models can be attributed to the regression model assumption only, rather than to additional possible differences in nonparametric models or estimation methods. The proposed approach is illustrated under the three most commonly used regression assumptions (PH, AFT and PO). However, it can be easily extended for other specifications, such EH (see,e.g, Li et al., 2015) or to fully nonparametric specification of the marginal distributions (see, e.g. Jara et al., 2010). As a matter of fact, we also fit a EH version of the proposed mode for the ST data. However, the LPML for this model was −5564 and thus the LPML still favors the simplest and PO version of the proposed model.

We provided empirical evidence showing that under simple restrictions on the parameter space, the model parameters in the proposed model can be estimated from the observed data obtained from a longitudinal study, where the follow-up for individuals and variables continues after the first positive result, thus avoiding the need of external information on the misclassification parameters. The results suggest that even under the use of uniform priors on the misclassification parameters, the posterior mean of the model parameters is unbiased, precise, and consistent. We noted that if external information on the misclassification parameters is available, this can be easily incorporated into the model specification.

The generalization of the proposed modeling approach to account for potential time trends in the misclassification parameters is also of interest in some applications, for instance, when the examiners follow a learning-by-doing process. The most important question in such generalizations of the models are related to the potential lack of identification of the model parameters. In the context of models for categorical data, the assumption of constant misclassification parameters is a necessary and sufficient identification restriction when at least three time points are considered (García-Zattera et al., 2010, 2012). The empirical results provided in this paper suggest that this constraint is at least a sufficient identification restriction when more time points are considered. These and other generalizations are the subject of ongoing research.

The MCMC algorithms were coded in C++. The code were compiled into a shared library and linked into R via “Rcpp” package’s foreign language interface. For a simulated data of size N = 100 and J = 4, the computation time to obtain a Markov chain of length 45,000 is on average 25 minutes, based on an IMAC machine with 3.2 GHz intel Core i5 and 16 GB 1600 MHz DDR3. When the number of covariates is increased from 2 to 10, the computation time for n = 100 increases to 30 minutes. On the other hand, if the sample size is N = 300, the computation time is one hour on average.