The increasing lifespan variation gradient by area-level deprivation: A decomposition analysis of Scotland 1981–2011

Abstract

Life expectancy inequalities are an established indicator of health inequalities. More recent attention has been given to lifespan variation, which measures the amount of heterogeneity in age at death across all individuals in a population. International studies have documented diverging socioeconomic trends in lifespan variation using individual level measures of income, education and occupation. Despite using different socioeconomic indicators and different indices of lifespan variation, studies reached the same conclusion: the most deprived experience the lowest life expectancy and highest lifespan variation, a double burden of mortality inequality. A finding of even greater concern is that relative differences in lifespan variation between socioeconomic group were growing at a faster rate than life expectancy differences. The magnitude of lifespan variation inequalities by area-level deprivation has received limited attention. Area-level measures of deprivation are actively used by governments for allocating resources to tackle health inequalities. Establishing if the same lifespan variation inequalities emerge for area-level deprivation will help to better inform governments about which dimension of mortality inequality should be targeted. We measure lifespan variation trends (1981–2011) stratified by an area-level measure of socioeconomic deprivation that is applicable to the entire population of Scotland, the country with the highest level of variation and one of the longest, sustained stagnating trends in Western Europe. We measure the gradient in variation using the slope and relative indices of inequality. The deprivation, age and cause specific components driving the increasing gradient are identified by decomposing the change in the slope index between 1981 and 2011. Our results support the finding that the most advantaged are dying within an ever narrower age range while the most deprived are facing greater and increasing uncertainty. The least deprived group show an increasing advantage, over the national average, in terms of deaths from circulatory disease and external causes.

1. Background

It is now well established that there are systematic differences in life expectancy between otherwise comparable countries, and that the most deprived socioeconomic groups within all countries can expect to live the shortest lives (Mackenbach et al., 2008, 2016; Marmot et al., 2008; McCartney, 2012). An additional, but not yet routinely measured, dimension of mortality inequality is the amount of variation in age at death (lifespan variation) that exists across all individuals within an entire country, or that exists across all individuals within predefined socioeconomic groups (van Raalte et al., 2018).

This is an important dimension of inequality to measure because decreasing lifespan variation means that deaths are being compressed around a common age, and that age at death is becoming more homogenous between individuals (Smits and Monden, 2009; Tuljapurkar, 2010). A more homogenous age at death is beneficial at both the societal level and individual level: lower inequality in age at death equates to less uncertainty which is important to consider when forecasting pensions, estimating demands on health care and social security systems and planning personal savings and investments for the future (van Raalte et al., 2018).

Lifespan variation is diverging between socioeconomic groups in the few countries where it is has been examined, which includes countries as diverse as Finland (van Raalte et al., 2014), Spain (Permanyer et al., 2018) and the USA (Sasson, 2016b). In these cases, lifespan variation among the most advantaged SES groups has declined over the past three to five decades, while lifespan variation among the least advantaged groups has been stagnant or even increased. This is worrisome, as it implies that higher SES groups are becoming more homogenous and are increasingly able to plan their life course, while the lower SES groups face increasing uncertainty in the timing of death.

Long time series of data by socioeconomic status are scarce. Many countries do not record educational status on the death certificate, or if it is done, records are often not linked to census populations leading to potentially biased estimates of mortality differences (O'Reilly et al., 2008; Shkolnikov et al., 2007). Likewise, administrative records detailing income or occupational position are rarely linked to death and population registers. Household surveys capture many of these dimensions, but their application to study trends in lifespan variation are limited because they often fail to include the entire age range of the population, they do not contain a long enough time series, or they lack the statistical power because of their small sample sizes.

Increasingly, governments and researchers are turning to area-based indicators as a valuable data source for studying social inequality, health and mortality (Allik et al., 2016; Eibner and Sturm, 2006; Kearns et al., 2000; Montez et al., 2016; Noble et al., 2010; Salmond and Crampton, 2012; Saunders et al., 2008). Lifespan variation by a measure of relative area-level deprivation has received limited attention. This is an important issue to address because area-level measures of deprivation are actively used when deciding how to allocate and distribute resources for reducing health inequalities (Allik et al., 2016; Diez Roux, 2001; The Scottish Government and National Statistics, 2012). Area-level measures have a further advantage over individual measures, in that they can be applied to all individuals, regardless of age. Individual-based markers of SES are usually only applied once individuals enter early adulthood and changes between SES groups are minimal. As a consequence, age-at-death distributions are left-truncated in such analyses. The extent to which this truncation underestimates true SES-gradients in lifespan variation is unknown.

While most countries have experienced declines in lifespan variation in lockstep with increases in life expectancy (Németh, 2017; Vaupel et al., 2011), Scotland is a country that has been highlighted as an exception: its population level lifespan variation trend demonstrated one of the longest sustained stagnating trends in Western Europe, which has only recently returned to declining (Seaman et al., 2016a). In addition, Scotland was found to have experienced higher lifespan variation at shared levels of life expectancy with its closest comparator country England and Wales (Seaman et al., 2016b). The mortality problem in Scotland peaked following the 1980s. The peak coincided with increasing social and economic polarisation, as poverty rates in Scotland grew while wealth became ever more concentrated (Mooney and Johnstone, 2000).

Alcohol and drug related deaths were, and still continue to be, key determinants of premature mortality in Scotland (Leyland et al., 2007; McCartney et al., 2016; Schofield et al., 2016). Of all deaths in Scotland in 2015, 6.5% were attributable to alcohol consumption (Tod et al., 2018). Scotland also had the highest drug related death rate in Europe in 2016 with 160 deaths per million. This is striking relative to the UK average of 60 per million (National Records of Scotland, 2017a). Increasing drug related mortality has parallels to current unfolding crises in other Anglo-Saxon countries, particularly the USA. In this regard, it is important to determine whether stagnant national trends in lifespan variation were the result of stagnant population-wide heterogeneity in age at death, or were driven by different trends in lifespan variation for more and less advantaged groups.

We have four objectives in the current paper. First, we examine the development of socioeconomic inequality in lifespan variation for Scotland and determine whether the diverging trends seen internationally among individual-based SES groupings (Permanyer et al., 2018; Sasson, 2016b; van Raalte et al., 2014) are also found when using an area-level measure of deprivation. Second, we formally quantify the gradient in lifespan variation by calculating the slope and relative indices of inequality. Third, we examine the impact of age truncation, by comparing the magnitude of the gradient from birth and from age 35. Fourth, we identify the contributions of each deprivation quintile, age and cause of death to the lifespan variation gradient by decomposing the change in the slope index of inequality between 1981 and 2011.

1.1. Measuring lifespan variation

Early studies using lifespan variation as an outcome measure centred around the debate initiated by Fries (1984): would future mortality reductions result in mortality compression or shifts in the age-distribution of mortality to ever higher ages? Theoretically, the interest was in senescent mortality, i.e. mortality purged of exogenous causes. This led to a focus on mortality at older ages. In their study of the USA between 1962 and 1979, Myers and Manton (1984) noted that a decrease in lifespan variation (as measured by the standard deviation) was apparent when taking all ages into account. When measured as conditional upon survival to age 60, they reported that lifespan variation was increasing. In response, Fries (1984) commented that age 60 was an arbitrary age for truncation and that it introduced statistical bias because the proportion of the population included in the analysis increased between the two time points (from around 66%–75%).

To remove some of the arbitrariness of defining an old-age cut-off point, Kannisto (2001) suggested to measure the standard deviation above the modal age at death. This would reduce the “built-in tendency” for dispersion to increase when mortality was declining and the bulk of deaths were moving to higher ages. In doing so, Kannisto found that lifespan variation in the USA declined steadily from the early 1930s to the early 1990s, as life expectancy increased. Horiuchi et al. (2013) further found that increases in the modal age at death were faster than increases in life expectancy conditional upon survival to age 55 (e55), age 65 (e65) or age 75 (e75).

More recent work turned away from using indicators of lifespan variation to resolve the compression versus shifting senescent mortality debate, toward the value of monitoring lifespan variation in and of itself. In these studies, lifespan variation is seen as an indicator of both population-level heterogeneity and individual-level uncertainty in the timing of death (Smits and Monden, 2009; van Raalte et al., 2018). For either interpretation, the whole population is of interest. However, covering the whole population can have important implications when comparing across variability indices which are sensitive to infant mortality (van Raalte and Caswell, 2013) and do not put the same weight on the same features of the age distribution of death (Anand et al., 2001). Therefore the direction and pace of trends are known to differ between indices and concurrence across indices can depend upon the age at which survival is conditioned on (Anand et al., 2001; Shkolnikov et al., 2003).

Despite these known sensitivities, measures of lifespan variation facilitate international and intertemporal comparisons of inequality between individuals in age at death irrespective of SES-group membership (Anand et al., 2001). When truncating the distributions at ages 10 or 15 years (where mortality is usually at a minimum) lifespan variation trends for most industrialized countries have decreased and converged. There are some exception countries that have experienced stagnating adult mortality and subsequent stagnating lifespan variation trends (Edwards and Tuljapurkar, 2005; Smits and Monden, 2009). Scotland has not followed the desired decreasing trend: it demonstrated the longest stagnating variation trend in Western Europe between 1989 and 2011 (Seaman et al., 2016a) and higher variation at a shared level of life expectancy with England and Wales (Seaman et al., 2016b). Both studies included the favourable contributions from large reductions in infant mortality in their calculations. This makes the finding for Scotland even more concerning because it indicates that premature adult mortality, at the national level, was not being obscured when using the full age spectrum. While it is well established that premature adult mortality is strongly patterned by socioeconomic inequality, the impact on lifespan variation inequalities has not yet been documented for Scotland.

1.2. Socioeconomic inequalities in lifespan variation

A growing number of studies have analysed socioeconomic trends in lifespan variation within countries (Brønnum-Hansen, 2017; Permanyer et al., 2018; Sasson, 2016b; Shkolnikov et al., 2003; van Raalte et al., 2014). Appendix 1 summarises the studies we are aware of that have measured lifespan variation stratified by a measure of socioeconomic position at any given time period and in any given country.

van Raalte et al. (2011) measured cross-sectional differences in lifespan variation by educational attainment within 11 European countries using the standard deviation. Brown et al. (2012) did the same in the USA using the standard deviation above the modal age of death. Both studies found higher lifespan variation amongst the lowest educated groups. Trends in lifespan variation by education for ages 20–64 years old were presented for Russia by Shkolnikov et al. (2003). This study demonstrated the properties of the Gini-coefficient and in doing so identified that the magnitude of the educational gradient, in relative terms, was greater and had increased more over time for variation in age at death than life expectancy. van Raalte et al. (2014) analysed trends in lifespan variation for occupational social classes in Finland over the period 1971–2010. Sasson (2016b) extended the analysis of trends by using an education-based indicator for SES for the USA from 1990 to 2010. A restriction with all of these studies is that the age distributions had to be truncated because of data availability and the theoretical relevance of the socioeconomic indicators used. Two exception studies are Brønnum-Hansen (2017) and van Raalte et al. (2018) which stratified on household-based measures of income that are theoretically applicable to all ages.

Despite the different socioeconomic indicators used and different indices of lifespan variation estimated, each of these studies reached the same conclusion: the most deprived groups experience the lowest life expectancy and highest amount of variation in age at death, a double burden of mortality inequality. A finding that is perhaps of even greater concern is that relative differences in lifespan variation by SES group were growing at a faster rate than differences in life expectancy in each of the above mentioned studies. In Russia the improvements in variation were smallest for the lowest educational group (Shkolnikov et al., 2003). In Finland and Denmark, the most disadvantaged groups were experiencing stagnating or slightly increasing trends in lifespan variation, despite continuous gains to life expectancy (Brønnum-Hansen, 2017; van Raalte et al., 2014). In the USA, the lowest educated whites experienced increasing lifespan variation alongside decreasing (females) or stagnating (males) life expectancy. Blacks from all levels of education experienced stagnating variation alongside increasing life expectancy (Sasson, 2016b). At the same time, in all countries, no matter how socioeconomic inequality was measured, the least disadvantaged groups experienced continuous mortality compression and decreasing variation. We extend the literature by measuring lifespan variation inequality by area-level deprivation.

1.3. Area-level deprivation

Governments’ actively use area-level measures of deprivation for monitoring health inequalities and for allocating resources to tackle them (National Audit Office, 2010; The Scottish Government and National Statistics, 2012). Area-level measures of relative deprivation are used to better understand the influence that contextual deprivation may have on health and mortality, independent of individual level socioeconomic circumstance (Carstairs and Morris, 1989; Macintyre et al., 2002; Tunstall et al., 2011). Area-level indicators, that are informed by a strong theoretical framework, can be a powerful tool for capturing the features of shared physical and social environments that are most important for the health of populations (Dearden et al., 2018; Kearns et al., 2000).

They also have a number of empirical advantages over individual level indicators. For example, the higher geographies used in area-level measures are built up from postcodes. Postcodes are deemed to be the most convenient way of allocating an area reference to individuals based on their home address. Since home address is routinely recorded for individuals across services, for example hospital admissions and GP registers, this unit of measurement has an immediate advantage over markers of SES position that are not routinely collected, such as social class or occupation. This means area-level measures are valuable for increasing the opportunities available to help explain the causes of health inequalities (Carstairs and Morris, 1989). Area-level measures also provide an opportunity to capture subgroups of the population that have historically been excluded from traditional measures of occupation based social class, in particular women, younger age groups and the unemployed (Morgan and Baker, 2006).

Area-level inequality in Scotland is a particularly important issue because it contains 59 of the 100 consistently most deprived areas in Britain (Dearden et al., 2018). We add to the existing international body of lifespan variation literature by stratifying the population of Scotland by an area-level measure of deprivation, the Carstairs Score. This measure is theoretically meaningful for the entire population of Scotland, it was constructed specifically for measuring health inequalities and covers a substantial time period (Allik et al., 2016; Carstairs and Morris, 1989; Krieger et al., 2002). We quantify the magnitude of the gradient in lifespan variation between deprivation quintiles by calculating the slope index and relative index of inequality. Decomposition is used to identify the quintiles, ages and causes of death driving the change in the gradient between 1981 and 2011.

2. Data and measurement

Data obtained were individual level death records and census population estimates by single year of age (0–85+) and sex for small geographical areas (postcode sector) at each of the four most recent census years in Scotland (1981, 1991, 2001, 2011). The population size of each postcode sector at each census year is approximately 5,000 (see Table 1 for more details). Census population estimates are the most robust population estimates in Scotland and these are used as the baseline for all subsequent mid-year population estimates (National Records of Scotland, 2017b). Individual deaths were aggregated for the years surrounding each census year to increase the number of events (1980–1982, 1991–1992, 2000–2002, 2010–2012). Only two years’ worth of data could be aggregated for 1991 because of geographical boundary changes occurring in 1990. Census population estimates were adjusted to match the year-grouping of deaths. Death counts and population estimates by postcode sector were then matched with the relevant Carstairs score for each year.

Table 1. Cause-specific mortality rates.

Year	Number of part postcode sectors	Mean population size of part postcode sector (SD)
1981	1010	4982.47 (1178.53)
1991	1001	4993.02 (1653.67)
2001	1010	5011.89 (1542.42)
2011	1012	5232.61 (1568.05)

2.1. The Carstairs score

The Carstairs score is an established measure used to capture relative deprivation within the population and aims to reflect the material resources, services, amenities, and physical environment which are seen as expected in society (Carstairs and Morris, 1989). The Carstairs score is derived from four census variables: overcrowding; male unemployment; car ownership; and low social class. The Carstairs score is calculated from the unweighted combination of the four variable's z-scores. A z-score of zero means the score is the same as the population mean score. A higher score indicates higher deprivation and a lower score (below zero) indicates lower deprivation.

2.2. Constructing life tables

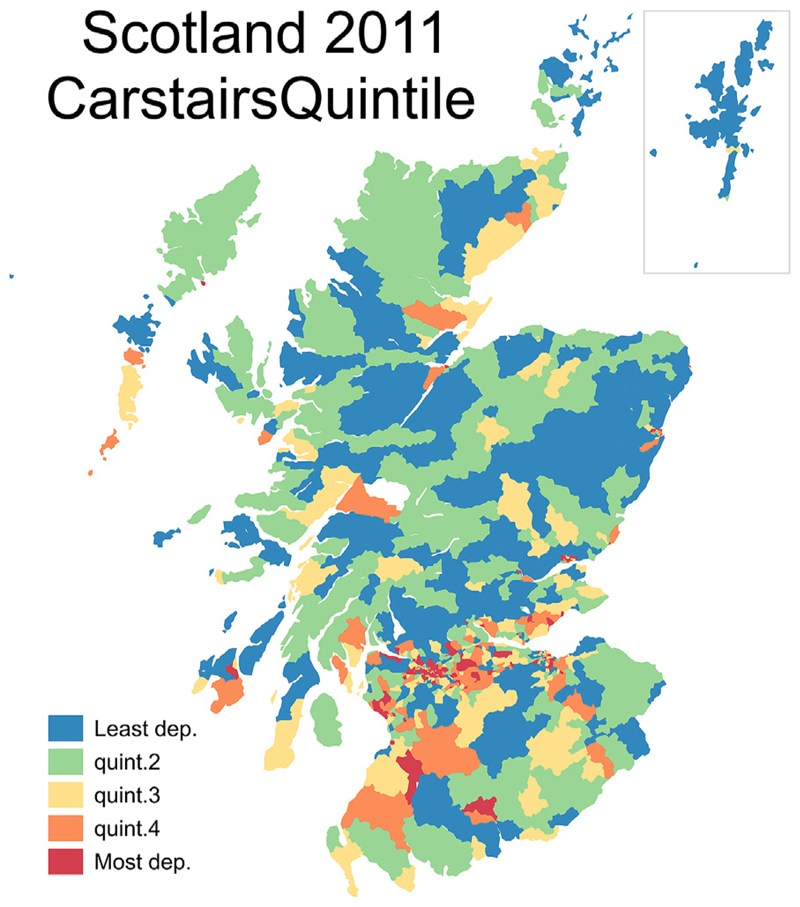
The matched data for each postcode sector were then assigned to population-weighted quintiles of the z-score distribution, each representing 20% of the Scottish population. Deaths and populations by age and sex were aggregated within deprivation quintiles and around each census year. Fig. 1 is a map of Scotland showing the quintile that each postcode sector was assigned to in 2011. The most deprived areas are concentrated within the major cities of Scotland where the geographical size of the postcode sectors is smallest.

Fig. 1. Map of Scotland Showing the Quintile of Deprivation that each Postcode Sector is Assigned to in 2011.

Life tables were constructed for each deprivation quintile and stratified by sex and census year (40 separate life tables). Analyses of quintiles of deprivation over time reflect a consistent concept of deprivation: although absolute levels of deprivation have changed there is always 20% of the population defined as most deprived compared to 20% of the population defined as least deprived. We report results for quintiles of deprivation because they are the preferred analytical grouping for routine reporting of health measures in Scotland (NHS Public Health and Intelligence, 2017).

Population quintiles contained the aggregated data from the small areas (part postcode sectors) in Scotland. Each of our life tables are based on a population of around 500,000. Although this population size is far above the recommended minimum population size for accurate estimates, there are a number of challenges that exist when estimating confidence intervals for life tables based on small population sizes (Congdon, 2014; Scherbov and Ediev, 2011; Silcocks et al., 2001; Toson and Baker, 2003).

One issue is the impact of ages with zero deaths. Before smoothing and extrapolating, our data contained 3,440 combinations of census year, sex, deprivation quintile and ages. Of these, 51 cells contained zero deaths. The impact of this problem has been extensively explored for small populations by replacing zero entries with a small positive value (Scherbov and Ediev, 2011; Silcocks et al., 2001; Toson and Baker, 2003). The conclusions from existing studies are that zero deaths are found to have limited impact for calculations based on populations of over 5,000. The final open ended age category can also present challenges for small population sizes, especially because the population structure at older ages can differ greatly between populations (Scherbov and Ediev, 2011; Silcocks et al., 2001). The smoothing and extrapolation methods we used to address the open ended age category problem are outlined next.

2.3. Smoothing and extrapolation of all-cause mortality rates

Census population estimates obtained were available up to different open-ended age intervals; 1981 was 85+, 1991 was 90+, 2001 was 85 + and 2011 was 95+. According to the 2011 Scottish female period life table, over 45 percent of women survived to ages older than 85 (Human Mortality Database, 2018). Given the likely differences in survivorship by deprivation quintile, using an open-ended age interval risked introducing biases in lifespan variation according to the proportions surviving to age 85.

We used the smoothing method used by Human Mortality Database (HMD), a Kannisto logistic model, to extrapolate mortality rates to age 110 + for each year, sex, and quintile separately. Specifically, we apply equations 64 and 65 from the HMD Methods Protocol version 6 (Wilmoth et al., [version 27/11/2017]), but modified to use information from ages 75 + rather than 80+. We report results using the extrapolated mortality rate from age 85 to an open age category of 110+. All-cause mortality for ages 1–84 was smoothed using penalized splines (Camarda, 2012). We did not smooth or adjust infant mortality rates.

2.4. Sensitivity checks

We tested the impact of our extrapolation approach against three alternative approaches available in the MortalityLaws R package (Pascariu, 2018). The three comparison approaches were an alternative Kannisto, a Gompertz, and a Quadratic. We selected the HMD Kannisto logistic model because it is a widely reported age pattern that emerges in high quality datasets (Barbi et al., 2018; Gampe, 2010). Although there is not a consensus about this age pattern (Gavrilov and Gavrilova, 2011; Newman, 2018) it is actively used by the HMD and many national statistical offices for period life tables (Wilmoth et al., [version 27/11/2017]). In our study the choice of extrapolation method was not a consequential decision as the alternative extrapolations lead to the same conclusions (see appendix 2 and appendix 3 for the lifespan variation estimates calculated using the alternative transformations compared with the main results; see appendix 4 for the slope index and relative index results estimated using alternative extrapolations.

2.5. Cause-specific mortality rates

ICD codes were used to estimate age-cause specific mortality rates by sex, quintile of deprivation and Census year from five broad underlying causes of death: circulatory diseases, respiratory diseases, neoplasms, external causes and other causes. All deaths in our data included an ICD code entry; however, deaths that were ill defined or did not refer to an identifiable ICD code were classified as ‘other’. Cause of death categories were mutually-exclusive, and harmonisation ensured comparability of causes over time. The ICD codes included in each category are available in appendix 5. The absolute number of deaths and proportions of deaths in each cause-specific category are given below in Table 2.

Table 2. Number of deaths and percentage by sex and census year.

	1981				1991
	males		females		males		females
Circulatory	47087	50.1	51189	53.2	26715	46.2	30429	48.6
Respiratory	10689	11.4	9805	10.2	6349	11.0	7010	11.2
Cancers	21717	23.1	19784	20.6	15288	26.4	14510	23.2
External	6156	6.5	4510	4.7	3681	6.4	2399	3.8
Other	8404	8.9	10911	11.3	5793	10.0	8249	13.2
Total	94053	100%	96199	100%	57826	100%	62597	100%
	2001				2011
	males		females		males		females
Circulatory	31471	38.6	36762	40.8	23102	29.9	24816	28.1
Respiratory	8908	10.9	10699	11.9	9420	12.2	11388	12.9
Cancers	22867	28.0	22065	24.5	23739	30.7	22798	25.8
External	7643	9.4	3979	4.4	7156	9.3	3867	4.4
Other	10685	13.1	16513	18.3	13923	18.0	21532	28.9
Total	81574	100%	90018	100%	77340	100%	84401	100%

Cause specific mortality rates in single ages by quintiles exhibit random fluctuations in some ages. Although random noise has little impact on indices such as life expectancy and lifespan variation it is helpful to smooth mortality rates to identify the most important patterns in the decomposition results. For each sex and quintile separately, we smoothed cause-specific rates over age using the penalized splines technique for all-cause mortality (Camarda, 2012). Cause-specific rates were then constrained to sum to our smoothed all-cause rates.

2.6. Measures of lifespan variation

We measure inequality in age at death using $e_x^{†}.$ This is the average of remaining life expectancy at each age, weighted by the number of lifetable deaths at each age. It has an intuitive public health interpretation: the average number of years remaining at death and it measures average life years lost when a death occurs (Vaupel and Canudas Romo, 2003). The high correlation between alternative indices of lifespan inequality suggests that the overall conclusions would not have changed had an alternative measure been used (Németh, 2017; van Raalte and Caswell, 2013; Vaupel et al., 2011; Wilmoth and Horiuchi, 1999).

Our main results report $e_0^{†}.$ Unlike education, occupation and income measures, area-level deprivation is applicable to all ages. Reporting $e_0^{†}$ is consistent with the standard reporting of life expectancy at birth. A robustness check was carried out using $e_{35}^{†}.$ We report $e_{35}^{†}$ trends in appendix 6. Appendix 7 shows the Slope Index of Inequality (SII) and the Relative Index of Inequality (RII) estimates using $e_{35}^{†}.$ A conditional age of 35 was selected to compare to previous studies of lifespan variation by an individual-based measure of SES. This is an age where education, occupation and income indicators are all theoretically applicable.

2.7. Quantifying the lifespan variation gradient

To analyse the gradient in lifespan variation by area-level deprivation, the SII and the RII were used. The SII communicates the absolute level of inequality in a health variable for social groups. The RII communicates the inequality in relative terms (Mackenbach et al., 1997). The SII and RII are valuable methods of analysis to use because they allow trends to be assessed by taking into account all of the data points not just the extremes (Munoz-Arroyo and Sutton, 2007). These tools were originally developed to calculate the gradient in age-standardized death rates by socioeconomic status (Pamuk, 1985). In work that more closely resembles are own, they have been used to calculate the gradient in life expectancy across area-levels of deprivation in the USA ((Singh and Siahpush, 2006) and regional inequality in New Zealand (Pearce and Dorling, 2006).

2.8. The slope index and relative index of inequality

The SII is an attempt to estimate the absolute survival difference between the most and least deprived groups. In our study, it is interpreted as the absolute effect on lifespan variation from moving from the lowest ranking socioeconomic group to the highest ranking socioeconomic group (Munoz-Arroyo and Sutton, 2007). Carstairs quintiles of socioeconomic deprivation rank the categories from 1 (least deprived) to 5 (most deprived). The population of each socioeconomic deprivation category are part of the cumulative total population. Each socioeconomic deprivation category is assigned a variable which refers to the midpoint of their range in the cumulative distribution of the total population. This is straight forward when using population weighted quintiles, as each contains 20% of the population. Therefore the first 20% has a range from 0% to 20% and the midpoint is 0.10; the final 20% of the population has a range from 80% to 100% and is assigned a midpoint value of 0.90 (Munoz-Arroyo and Sutton, 2007). The SII is the value of the slope coefficient of an ordinary least squares regression between the dependent survival variable and the independent deprivation cumulative population variable: the larger the coefficient the greater the impact of deprivation (Allik et al., 2016). However, if the mean level of health in all socioeconomic groups changes by the same proportion the SII will increase. This is a limitation for comparing trends across populations.

The RII is an alternative approach that is not sensitive to changes in the mean level of health. The RII reported in this study was obtained by dividing the SII value by the mean value of the outcome variable across all socioeconomic deprivation (Regidor, 2004).

For lifespan variation, the SII is interpreted as the absolute difference in years between the notionally most deprived and least deprived quintiles. In this paper the relative index of inequality is interpreted as how much higher, in percentage terms, lifespan variation of the most deprived quintile is compared to the population average.

2.9. Monte Carlo simulations

Confidence intervals were produced for $e_0^{†}$ and the SII and RII estimates by using 1,000 random Poisson draws of all-cause death counts in each age (0–110+), sex and quintile combination. Assuming the same population exposures, we use the simulated death counts to produce 1000 mortality rate schedules, each implying a new lifetable. Confidence intervals were selected using the standard approach of selecting 0.025 and 0.975 quantiles of the distribution of the statistic of interest. The general recommended number of repetitions is between 1000 and 2000 (Carpenter and Bithell, 2000). Appendix 8 shows the stability of $e_0^{†}$ estimates up to 2000 repetitions).

2.10. Decomposing the gradient

We decomposed the change in the slope index of inequality for lifespan variation by age, cause of death and quintile of deprivation. We applied the pseudo-continuous decomposition method proposed by Horiuchi et al. (2008) using the DemoDecomp R package (Riffe, 2018). This is a general decomposition method that can be used to decompose any aggregate index into the contribution of its parameters. To our knowledge, we are the first to apply this method to the decomposition of the slope index of inequality for a lifetable variation measure. This provides evidence for why the lifespan variation gradient by area-level deprivation in Scotland changed between 1981 and 2011.

All R scripts used for our analysis are freely available via the Open Science Framework (DOI: 10.17605/OSF.IO/T8UXM).

3. Results

3.1. Trends by socioeconomic deprivation

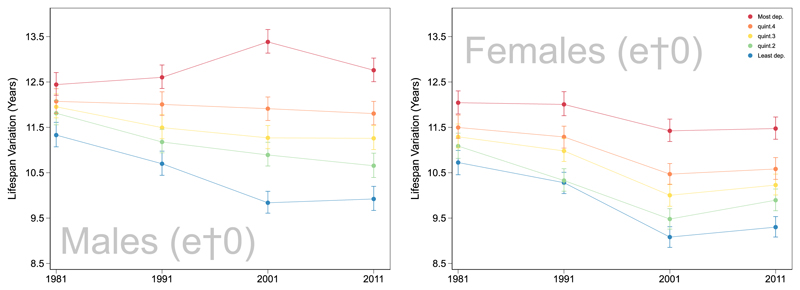
Fig. 2 shows the $e_0^{†}$ trends for each deprivation quintile for males and females.

Fig. 2. Trends in $e_0^{†}$ by sex and quintile of area-level deprivation, Scotland, 1981–2011.

The trend graphs reveal that in the earliest time point lifespan variation estimates were more similar across deprivation quintiles. In 1981 variation for males from the most deprived areas was 12.4 years but was 1.1 years lower for the least deprived (11.3 years). Over the study period the gap between each deprivation quintile increases. This is the case for males and females. In 2011 lifespan variation for males in the most deprived was 12.8 years compared with 9.9 years for the least deprived.

There are some differences between the deprivation-specific trends for males compared with females. Notably there is a stronger convergence of trends for females, with the exception of the most deprived quintiles. Although the markers for females cluster and the confidence intervals overlap quintile 5 remains an outlier. Males exhibit no such convergence of trends.

Our sensitivity analysis found the same general trends for $e_0^{†}$ and $e_{35}^{†}$ but the absolute level of lifespan variation is higher when measured at age 0. The direction of the trends does not change for any quintile when measured using $e_0^{†}$ or $e_{35}^{†}$ for males or for females. This provides some reassurance for studies based on left truncated data due to the use of individual SES measures.

3.2. Quantifying the socioeconomic gradient

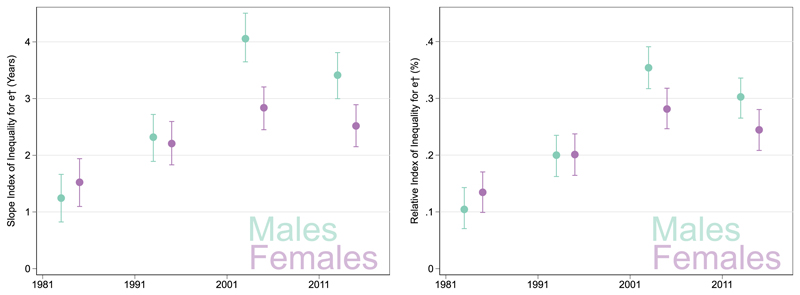
Fig. 3 compares the socioeconomic gradient for lifespan variation using $e_0^{†}.$ The figure shows the gradient in absolute terms (years) by presenting trends in the slope index of inequality and in relative terms (%) by presenting the relative index of inequality. These results formally quantify the diverging inequalities that were visualised in Fig. 2: the socioeconomic gradient has steepened over time with it being steepest in 2001 and showing some improvement in 2011. Still, the magnitude of inequality in 2011 is higher than it was in 1981.

Fig. 3. Slope and Relative indices of inequality for lifespan variation at birth by sex and Census year, Scotland.

For $e_0^{†},$ the SII for males in 1981 shows a 1.2 year difference between the most and least deprived quintile (95% CI 0.8–1.7 years). By 2011 the $e_0^{†}$ difference had increased to 3.4 years (95% CI 3.0 years–3.8 years). The RII shows that, in 1981, $e_0^{†}$ was 10.4% (95% CI 7.0%–14.3%) higher for males from the most deprived quintile compared to the population average. By 2011 $e_0^{†}$ was 30.3% higher for males from the most deprived quintile compared to the population average (95% CI 26.5%–33.5%).

For $e_0^{†},$ the SII for females in 1981 shows a 1.5 year difference between the most and least deprived quintile. By 2011 the $e_0^{†}$ difference had increased to 2.5 years. The RII shows that, in 1981, $e_0^{†}$ was 13.4% higher for females from the most deprived quintile compared to females from the least deprived quintile. By 2011 $e_0^{†}$ was 24.5% higher for females from the most deprived quintile compared to females from the least deprived quintile.

The sensitivity check using $e_{35}^{†}$ showed that the SII and RII had increased over time for males and females but the increase between 1981 and 2011 was lower in magnitude. Between 2001 and 2011 there was a decrease in $e_0^{†}$ but $e_{35}^{†}$ showed a stagnation.

Decomposing the slope index can help to identify the components contributing to the steepening lifespan variation gradient between 1981 and 2011.

3.3. Decomposing the change in the slope index between 1981 and 2011

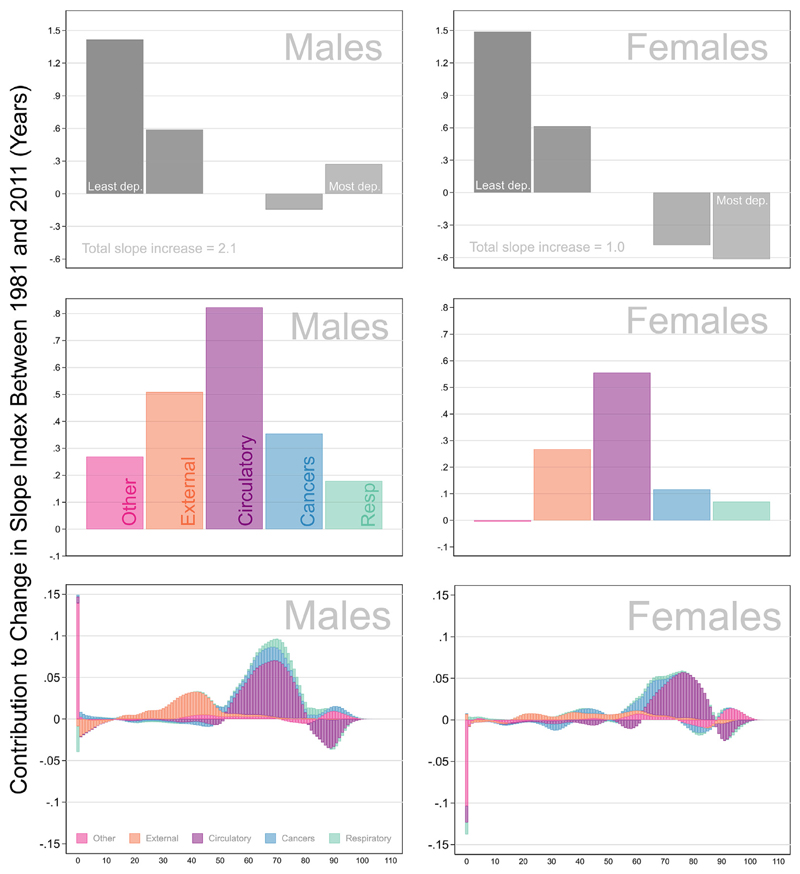
Fig. 4 shows the quintile contributions, the cause-specific contributions and the age-and cause-specific contributions to the change in the slope index between 1981 and 2011 for males and females separately. The sum of values represented in each graph is the total change in the slope index of inequality: 2.1 years for males and 1.0 year for females.

Fig. 4. Change in Slope Index of Inequality between 1981 and 2011 decomposed into (a) quintile contributions (b) cause specific contributions and (c) age and cause specific contributions.

3.3.1. Quintile contributions

The top row of Fig. 4 shows the contribution from each quintile. Contributions above the line mean the quintiles were diverging from the national average causing the gradient to steepen. Contributions below the zero line mean the quintiles converged toward the national average. For both males and females the least deprived quintile makes the largest contribution to the increase in the slope index. This means the least deprived were leading the way and moving further away from the national average. The contributions from the most deprived quintile differ between males and females. Males from the most deprived quintile contributed to the steepening gradient meaning that they were lagging further behind the national average. In contrast females from the most deprived quintile contributed to a decrease in the gradient meaning they were converging toward the national average.

3.3.2. Cause of death contributions

The middle row shows the cause-specific components of the change in the slope index. Here we see that the two largest contributing causes to the slope index of inequality are circulatory diseases and external causes of death. This is the case for males and for females. This means that divergences in these two causes of death account for increasing inequality in age at death.

3.3.3. Age and cause of death contributions

The bottom row shows how the cause-specific contributions are distributed across all ages. Spikes above the zero line reflect the ages at which the change in mortality rates over time increased the lifespan variation gradient (quintiles diverged from the national average). Spikes below the zero line reflect the ages at which the change in mortality rates over time has reduced the lifespan variation gradient (quintiles converged toward the national average). Each spike reflects the cumulative total of the contributions made by each cause of death at that single year of age.

Overall, the age and cause specific mortality changes which led to divergence in lifespan variation between quintiles was concentrated over ages 50 to 80 (for circulatory diseases) and ages 20 to 50. External causes of death were more pronounced among males than females.

The fact that mortality change at age 0 has a different impact on the lifespan variation gradient for males compared to females was an unexpected result. Infant mortality rates improved substantially for all deprivation quintiles during the study period. However, when examining the infant deaths in isolation, the SII for the infant mortality contributions to $e_0^{†}$ increased for males but decreased for females (appendix 9). Why there is a stronger socioeconomic dimension to male infant mortality is unclear. We suspect that it is related to potential socioeconomic differences in the known weakening male disadvantage in infant mortality that has been occurring since the 1970s (Drevenstedt et al., 2008), but this would require an investigation over a finer infant age scale.

4. Discussion

4.1. Summary of findings

Consistent with studies using individual-level measures, more deprived areas experienced higher lifespan variation than more advantaged areas. Area-level differences widened between 1981 and 2011, causing the socioeconomic gradient to steepen. Males from the most deprived quintile lagged further behind the national average and contributed to the steepening gradient. Females from the most deprived quintile were converging toward the national average and contributed to a decrease in the gradient. Males and females from the least deprived areas diverged away from the national lifespan variation average. Circulatory diseases and external causes of death diverged over the time period and accounted for increasing inequality in age at death. These contributions were strongly patterned by age: circulatory over ages 50 to 80 contributed to the increasing gradient and external causes of death demonstrated notable contributions over ages 20 to 50, particularly for males.

4.2. Interpretation of increasing socioeconomic gradient

Our use of an area-level indicator of deprivation in Scotland confirms patterns that have been observed at the individual level elsewhere: lower SES groups experience higher lifespan variation, and differences between SES groups in lifespan variation are widening. The increasing slope and relative index of inequality demonstrates that this pattern is not restricted to comparisons of extreme SES groups, as previous studies have done, but rather it is reflective of higher lifespan variation with increasing levels of socioeconomic deprivation.

Area-level measures of deprivation are not directly comparable with individual-level indicators used in the existing literature. The measurement of socioeconomic position has evolved over time and no single authoritative measure exists. Rather a number of measures are available each capturing different social and economic characteristics across different levels (e.g. individuals, households or areas) and across different stages of the life course (e.g. infancy, childhood, adolescence and adulthood) (Bailey et al., 2003; Krieger et al., 1997). The inability for one measure to adequately capture all dimensions of socioeconomic position reflects the complexity of this construct (Galobardes et al., 2006). It is also important to recognise that optimal indicators of socioeconomic position may change over time and the relevance of indicators may differ between populations or cohorts (Næss et al., 2005).

It is therefore important to consider the conceptual basis of different measures of socioeconomic position to ensure that an adequate measure is used, results are interpreted appropriately, and that the measure used is appropriate for making the intended comparisons (Rose et al., 2005). Despite these distinct differences in how socioeconomic inequality can be measured, when the growing body of evidence is taken together the implications are that individuals who are the most disadvantaged face increasing uncertainty in the timing of death in all settings where trends have been examined (Brønnum-Hansen, 2017; Sasson, 2016b; Shkolnikov et al., 2003; van Raalte et al., 2014).

Brown et al. (2012) and Sasson (2016b) discuss the implications of widening SES differences in lifespan variation specifically in relation to education. The lower lifespan variation experienced by highly educated groups is seen as manifestation of the individual material and nonmaterial advantages that enable the most educated to maximize their life chances even as social, political, and environmental contexts change (Brown et al., 2012). This reflects a fundamental causes explanation developed by Link and Phelan (1995): Educational indicators can act as a proxy for human, social, and cultural capital that enable individuals to mitigate current health risks and access the highest level of care (Brown et al., 2012). However, in their study of US states, Montez et al. (2019) highlight that the relationship between individual educational characteristics and mortality is context dependent. It would be overly simplistic to interpret area-level deprivation as a proxy measure for the same pathways linking individual resources to mortality. Instead, increasing lifespan variation by area-level deprivation may reflect inequality at the societal level rather than disparities in individual level resources (Townsend, 1987).

In contrast to the protective power advantage that education or income gives individuals, increasing differences in terms of area-level deprivation may cause profound negative psychosocial responses for the entire population (Marmot and Wilkinson, 2001). This is evidenced by the finding that countries with the steepest socioeconomic gradients also experience the worst population health (Wilkinson and Pickett, 2007). The relationship between life expectancy and lifespan variation can be interpreted as support for this perspective: those countries with the highest level of life expectancy also demonstrate the lowest levels of variation (inter-individual inequality) (Popham et al., 2013; Vaupel et al., 2011). All empirical indicators aim to capture the important role socioeconomic circumstances have for mortality with an emphasis being placed on the finding that socioeconomic position is now more important for mortality than gender (Sasson, 2016b). However, indicators differ in the extent to which they can be interpreted from an individual or population perspective of inequality which has direct implications for implementing the most appropriate policy responses.

The heterogeneous trajectories in lifespan variation, that we document, demonstrate that social factors exert a strong influence on age patterns of mortality in addition to biological factors. Nearly 60 years ago, Strehler and Mildvan (1960) found a log-linear correlation between the initial level of mortality and rate of aging parameters of the Gompertz equation. This SM-correlation, as it is known, would mechanistically lead to lower lifespan variation with mortality improvement if it were universally applicable. Empirical evidence for SM-correlation has been mixed, with Yashin et al. (2002) finding that the slope of the SM-correlation changed after the 1950s. After this time, mortality change was better characterized by mortality shifting (Bongaarts and Feeney, 2002; Yashin et al., 2002). More recently, Zheng et al. (2011) found heterogeneous patterns of SM-correlation depending on the country and period. Our findings add to the growing body of evidence that national trends in life expectancy and lifespan variation mask important subnational differences in age-specific patterns of survival. This supports the Zheng et al. (2011) argument that the impact of social and environmental factors on aging need to be better understood and incorporated into general theories of aging.

4.3. Comparisons with international studies

4.3.1. Age truncation

Lifespan variation is an important, but not yet routinely measured, indicator for understanding national and socioeconomic inequalities. Studies of national trends are able to make use of long running trend data that include full population estimates and complete mortality data. These studies have generally found that improvements in lifespan variation have been driven by mortality reductions at younger ages. A limitation within existing studies of socioeconomic trends is that they have generally been forced to use conditional age distributions because of the availability and theoretical relevance of education, income, or occupation as indicators of SES.

Our sensitivity checks demonstrated that the magnitude of inequalities in age at death was greater when measuring variation from birth. This is not an unexpected result as van Raalte et al. (2014) previously noted that the extent of any diverging trends between socio-economic groups may be underestimated because of age truncation. Sensitivity analysis carried out by van Raalte et al. (2014) measured lifespan variation conditional upon survival to age 40 compared to the reported lifespan variation in the results which was conditional upon survival to age 31. They demonstrated that the divergence in lifespan variation trends between socioeconomic groups was larger when reporting from age 31 because it included ages where the mortality differences due to external causes were more extreme. By quantifying the socioeconomic difference by both unconditional, and conditional on survival to age 35 distributions (to compare with previous individual-based studies of SES) we have shown that these previous studies may underestimate the full extent of the between-SES group differences in lifespan variation, particularly for males. Mortality in infancy, childhood, adolescence, and young adulthood were shown to have strong social patterning, which is consistent with the long-standing literature (Leon et al., 1992; Leyland, 2004; Phillimore et al., 1994; Singh and Yu, 1995). Future research should aim to explicitly test the impact of age truncation on the magnitude of the lifespan variation gradient. This will help to identify how much variation in age at death traditional measures of socioeconomic inequality are unable to capture.

4.3.2. External causes of death

Another important finding of our study is demonstrating the role external mortality has played in impacting national trends. Rising premature mortality from external causes of death including; drugs, alcohol, suicides, accidents and assaults has been documented in several countries (Aburto et al., 2016; Rudd et al., 2016). Particular attention has been given to the role these causes have played in the USA (Denney et al., 2013; Ho and Hendi, 2018; Sasson, 2016a). The recent emergence of this problem in the USA differs to Scotland where external causes of death have been identified as a public health problem for over a decade (Leyland et al., 2007; Leyland and Dundas, 2010; Schofield et al., 2016; Tod et al., 2018). Alcohol and drug related deaths are problematic in Scotland compared to opioid use in the USA (Ho and Hendi, 2018; Tod et al., 2018). It is too soon to determine whether the introduction of the minimum unit alcohol pricing policy in Scotland in 2018 will have the intended impact on reducing alcohol related deaths (Holmes et al., 2014). However, it is already the case in both countries that these premature deaths are substantial enough to have implications for national level mortality trends (Ho and Hendi, 2018; Seaman et al., 2016b): in Scotland the impact is evident in relation to it having one of the lowest life expectancies in Western Europe (McCartney et al., 2012) alongside a stagnating lifespan variation trend (Seaman et al., 2016a), while the USA has experienced increasing lifespan variation since 2010 (van Raalte et al., 2018).

Highlighting external mortality further stresses its role in preventing continued mortality compression and reductions in lifespan variation for developed countries. For countries that have been shown to have comparatively high lifespan variation (particularly for their overall level of mortality), external mortality has played an outsized role. For example, traffic accidents and homicides accounted for the same proportion of the variation difference between the USA (higher variation) and Sweden (lower variation) as heart disease and cancers combined (Nau and Firebaugh, 2012). While in Central and Eastern European countries, changes in alcohol consumption were directly linked to fluctuating lifespan variation (Aburto and van Raalte, 2017). The role external causes of death play in determining lifespan variation levels extents to studies of population subgroups (Lariscy et al., 2016; Nau and Firebaugh, 2012; van Raalte et al., 2018). The value of lifespan variation is that it is sensitive to these mortality premature mortality crises. This is in contrast to life expectancy, a mean outcome metric, which may not capture premature mortality especially as the bulk of deaths shifts to older ages.

4.4. Strengths and limitations

Reporting lifespan variation at birth is consistent with the established reporting of life expectancy at birth, and this is an advantage of using an area-level indicator of deprivation. A further advantage, over individual-level measures of socioeconomic inequality, is that governments actively use area-level measures of deprivation when allocating resources (Galobardes, 2012; Kearns et al., 2000; Macintyre et al., 1993). However, area-level measures are not without limitations: they assume social homogeneity when in reality deprived individuals do not exclusively live in deprived areas and vice-versa (Sloggett and Joshi, 1994). The Carstairs score has been criticised for including car ownership without recognising that the meaning of car ownership differs between urban and rural contexts (Fischbacher, 2014). Alternatively, we could have used the Scottish Index of Multiple deprivation (SIMD); however, it is only available from 2001/02, already contains indicators of health and mortality within the index, and uses geographic groupings for which the exposure population cannot be easily identified for earlier census data. For these reasons we preferred to measure deprivation by the Carstairs score, which was derived specifically for studying health inequalities (Carstairs and Morris, 1989).

Moreover, the composition of areas contained within each quintile may have changed over the study period. However, we are following the experiences of synthetic rather than actual cohorts. In that sense we are estimating the gradient of heterogeneity in mortality conditions by area-level deprivation under different time periods in a purely relative sense: There is always a 20% most deprived group being compared to the 20% least deprived group in relation to deprivation at each time period.

5. Conclusion

The conclusions of this study provide further evidence for increasing mortality inequalities in developed countries: there is a clear area-level gradient for lifespan variation that increased during the study period. Using area-level deprivation data for Scotland adds to the existing body of international evidence showing that the most advantaged groups are dying within an ever narrower age range while the most disadvantaged groups are facing greater and increasing uncertainty about their survival. Increasing uncertainty in age at death has far reaching implications for individual level decision making and societal level planning.

Supplementary Material

Supplementary data to this article can be found online at https://doi.org/10.1016/j.socscimed.2019.04.008.