Self-Similar Dynamics of Nuclear Packing in the Early Drosophila Embryo

Abstract

Embryonic development starts with cleavages, a rapid sequence of reductive divisions that result in an exponential increase of cell number without changing the overall size of the embryo. In Drosophila, the final four rounds of cleavages occur at the surface of the embryo and give rise to ∼6000 nuclei under a common plasma membrane. We use live imaging to study the dynamics of this process and to characterize the emergent nuclear packing in this system. We show that the characteristic length scale of the internuclear interaction scales with the density, which allows the densifying embryo to sustain the level of structural order at progressively smaller length scales. This is different from nonliving materials, which typically undergo disorder-order transition upon compression. To explain this dynamics, we use a particle-based model that accounts for density-dependent nuclear interactions and synchronous divisions. We reproduce the pair statistics of the disordered packings observed in embryos and recover the scaling relation between the characteristic length scale and the density both in real and reciprocal space. This result reveals how the embryo can robustly preserve the nuclear-packing structure while being densified. In addition to providing quantitative description of self-similar dynamics of nuclear packings, this model generates dynamic meshes for the computational analysis of pattern formation and tissue morphogenesis.

Significance

Quantitative models of embryogenesis require information about cell packings in developing tissues. Here, we use live imaging, computational modeling, and tools from the theory of random heterogeneous materials to quantify dynamics of nuclear packings in the early Drosophila embryo, during the stage when the blastoderm is formed and patterned by maternal morphogen gradients. We discovered that nuclear packings display self-similar dynamics as the number of nuclei in the blastoderm grows exponentially. This behavior can be quantitatively explained through a particle-based model, in which pairwise mechanical interactions between nuclei depend on nuclear-packing density. Our computational model of dynamic nuclear packings in the blastoderm provides dynamic meshes for further studies of embryo patterning and morphogenesis.

Introduction

Some of the key variables in computational models of embryonic development describe the number of cells in the embryo and their spatial arrangements during progression from a fertilized egg to patterned tissues and organs (1, 2, 3). For organisms in which cell fate specification starts during the early cleavage divisions, these variables must reflect detailed information about specific cell lineages (4). When patterning starts only after a significant number of cleavages, cell arrangements are most naturally described within a statistical framework. Here, we focus on the early Drosophila embryo, an example of the latter, during the stage when the syncytial blastoderm is established by synchronized nuclear cleavages and maternal morphogen gradients are formed (5). Decades of work on this system led to some of the most advanced computational models of developmental cell cycles (6, 7), pattern formation (8, 9, 10, 11, 12), and morphogenesis (13). However, most of these models focus on an isolated process, and their integration into a common developmental trajectory is yet to be accomplished.

Nuclear cleavages after fertilization of the Drosophila egg proceed in two distinct phases (14). During the first nine divisions, mitotic cell cycles induce cytoplasmic flows that distribute zygotic nuclei throughout the egg volume and eventually carry them to the surface of the embryo (15). During the second phase, most of the nuclei can be found under a common plasma membrane, where they divide four more times, resulting in a blastoderm embryo with ∼6000 identical nuclei (14, 16). The second phase of cleavages coincides with the formation of maternal morphogen gradients—nonuniform distributions of concentration or nuclear localization of proteins that provide positional control of zygotic transcription. For instance, the transcription factor Dorsal, which patterns the dorsoventral axis of the embryo, is distributed in the ventral-to-dorsal gradient of nuclear localization (8, 17). Another transcription factor, Capicua, forms a nuclear localization profile along the anteroposterior axis and is involved in both anteroposterior and dorsoventral patterning systems (18). Progressive increase of nuclear numbers could play an active role in shaping both of these nuclear localization profiles, which requires a quantitative framework for describing nuclear-packing dynamics.

Here, we take a step toward establishing this framework capitalizing on ideas from the theory of random heterogeneous materials, which provides powerful approaches for dealing with assemblies of identical objects (19), such as suspensions of colloidal particles (20) or cell packings in tissues (21). The structure of random materials has been characterized by scalar descriptors, e.g., the bond-orientational order parameter (22, 23, 24); however, a more comprehensive description is provided by the radial distribution function (RDF), which characterizes pairwise correlations between particle positions (25) in real space, and the structure factor, which quantifies the pair statistics of the packing in reciprocal space, revealing the characteristic wavelengths of density fluctuations in the system.

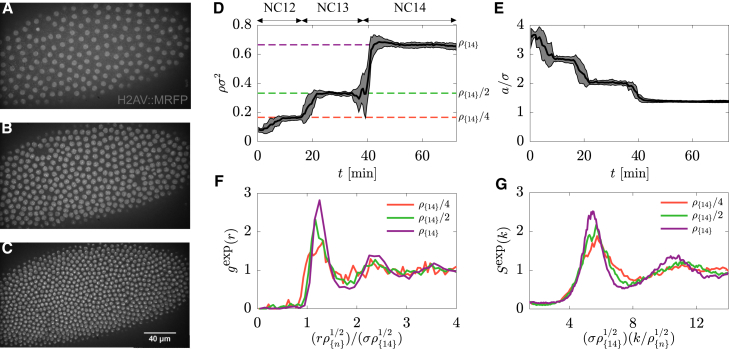
This is the approach we take in this study, focusing on the second phase of nuclear division cycles (NCs) (Fig. 1, A–C; Materials and Methods; Video S1). During this time, the nuclear number density ρ doubles in steps (Fig. 1 D), leading to the formation of a dense final packing of disk-shaped nuclei (Fig. S2), in which neighboring nuclei are on average separated by only ∼1.4 times the average nuclear diameter σ = (4.62 ± 0.12)μm (Fig. 1 E). We discovered that as the nuclear cleavages progress, the RDFs and structure factor corresponding to NC12-14 can be collapsed upon rescaling lengths. Below, we demonstrate that the observed self-similar dynamics of the packing can be explained using a particle-based model that accounts for repulsive internuclear interactions and nuclear divisions in the blastoderm. In addition to providing quantitative description of self-similar dynamics of nuclear packings, this model generates dynamic meshes for the computational analysis of pattern formation and tissue morphogenesis.

Figure 1.

(A–C) Maximal-intensity-projection images of syncytial embryo with histone-RFP marker during NC12, 13, and 14 (A–C, respectively). (D) The total nuclear number density ρ as a function of time is shown. The scale bar in (C) is 40 μm. At each division, ρ abruptly doubles, whereas the average nearest-neighbor distance a decreases in a similar stepwise fashion (E). RDFs (F) and structure factor (G) of packings at the end of NC12, 13, and 14 are shown (red, green, and purple curves, respectively). Positions of g(r) and S(k) peaks collapse after rescaling distances by (ρ/ρ_{14})^1/2. The results in (D)–(G) are averaged over six embryos. Gray regions in (D) and (E) represent the interval of two SDs centered at mean. To see this figure in color, go online.

Materials and Methods

Live imaging and image analysis

Embryos were collected from flies expressing H2AV::mRFP to visualize nuclei. Embryos were dechorionated with 50% bleach, washed, and mounted on Biofoil membrane (Kenneth Technologies, Flemmington, NJ) in halocarbon 27 oil. Embryos were then imaged on the NIKON TI-E microscope (Nikon, Tokyo, Japan) with the YOKOGAWA spinning disk (CSU-21) module (Yokogawa Electric Corporation, Tokyo, Japan) using the 561 laser to visualize nuclei at 30 s intervals. To process these videos, we first used MATLAB’s (The MathWorks, Natick, MA) adaptive image binarization algorithm, which follows the Bradley method (26) to identify the pixels corresponding to the nuclei. A recursive clustering algorithm was employed to extract both the average two-dimensional (2D)-projected area of the nuclei A as well as the in-plane positions of their centroids r_i(t) = (x_i(t), y_i(t)). The finite-size effects in calculating the RDF were eliminated by extracting a square sample from each image and extending the data periodically along both dimensions (Fig. S1).

Particle-based model

We developed a particle-based model, in which the nuclei are represented by disks with an effective hard-core and soft-shoulder interaction (21, 27, 28). The motion of the nuclei is dominated by dissipative forces because of strong friction with the environment. Such dynamics can be described by the overdamped equation of motion:

$$\frac{\text{d}{\mathit{r}}_i}{\text{d}t}=\frac{1}{\gamma }\sum _{j\ne i}{\mathit{F}}_{ij}+\sqrt{2D}{\mathit{\xi }}_i,$$ (1)

where F_ij is the pairwise interaction force, D is the effective diffusion coefficient, and γ is the friction coeffecient, whereas ξ_i is the Gaussian white noise with properties $\langle {\xi }_{i\alpha }\rangle =0$ and $\langle {\xi }_{i\alpha }\left(t\right){\xi }_{j\beta }\left(t\text{'}\right)\rangle ={\delta }_{\alpha \beta }{\delta }_{ij}\delta \left(t-t\text{'}\right)$ for α, β ∈ {x, y}.

The pairwise interaction force is given by

$${\mathit{F}}_{ij}=\{\begin{array}{ll}\left[f\left(\sigma -r_{ij}\right)+k\sigma \right]\frac{{\mathit{r}}_{ij}}{r_{ij}}\hfill & r_{ij}<\sigma \hfill \\ k\frac{\mathit{\lambda }\sigma -r_{ij}}{\mathit{\lambda }-1}\frac{{\mathit{r}}_{ij}}{r_{ij}}\hfill & \sigma \le r_{ij}\le \mathit{\lambda }\sigma \hfill \\ \mathbf{0}\hfill & r_{ij}>\mathit{\lambda }\sigma \hfill \end{array},$$ (2)

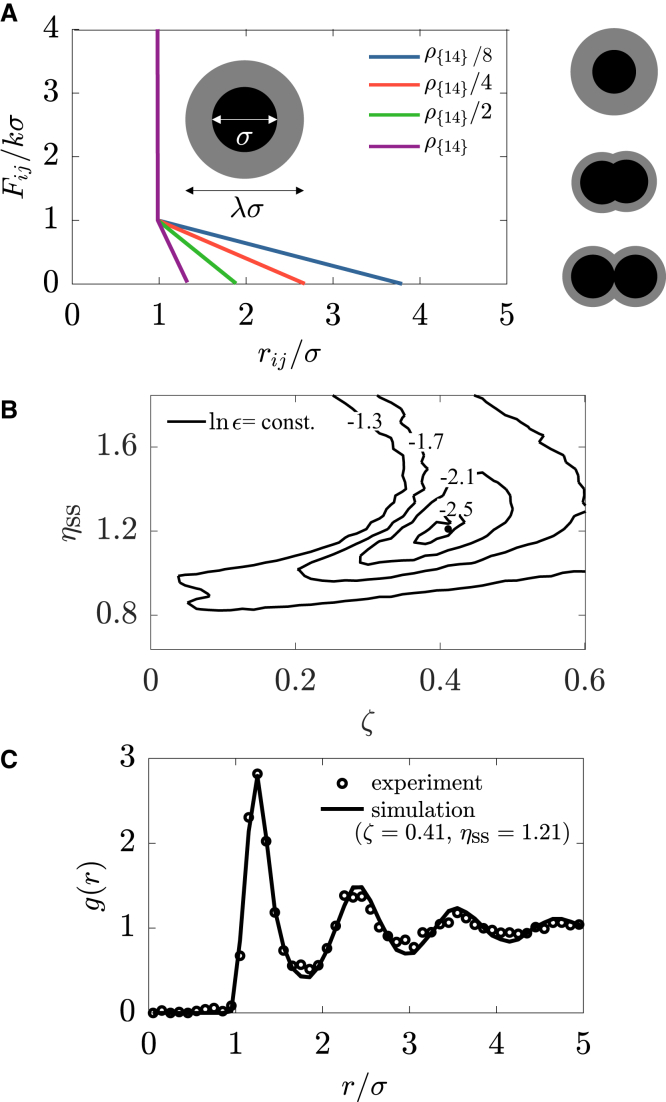
where λ describes the range of the soft-shoulder interaction, r_ij = r_i − r_j is the displacement between nuclei i and j, and r_ij = |r_ij|. The parameters f and k are the effective spring constants associated with particle-particle and shoulder-shoulder overlap, respectively (Fig. 2 A). In the limit $f\gg k$, the repulsion due to particle-particle overlap effectively acts as a hard-core repulsion; we choose f = 1000k. In turn, the shoulder-shoulder overlap mimics the repulsive interaction of the nuclei at distances greater than σ (Fig. 2 A) because of overlapping microtubule asters radiating from the nuclei close to the embryo’s apical surface (29, 30, 31). As shown in an earlier study, the interpolar microtubules exert repulsive forces on their surrounding because of polymerization (32). These forces decrease with the distance from the centrosome because of decreasing density of microtubules. Assuming the same type of interaction for astral microtubules, we describe the shoulder-shoulder overlap by a repulsive force that decreases linearly with the internuclear separation (Eq. 2). This gives rise to another interaction-associated length scale, λ, that describes the range of the shoulder-shoulder interaction. A previous in vitro imaging of dividing syncitial nuclei extracted from the Drosophila blastoderm confirmed the existence of such a length scale and showed that it is determined solely by the cytoskeletal networks (33).

Figure 2.

(A) Pairwise force as a function of the internuclear distance. Inset gives a schematic of a nucleus, which is represented by a hard core (black circle) and a soft shoulder (gray circle). Nuclei experience strong repulsion when their hard cores overlap (r_ij < σ) and soft repulsion when their soft shoulders overlap (σ ≤ r_ij ≤ λσ), whereas they do not interact for r_ij > λσ. Right column gives schematics of the division. A dividing nucleus is treated as a pair of daughter particles repelling each other by a repulsive force F_div. At each division, the diameter of the shoulder is decreased by a factor of $\sqrt{2}$, whereas the hard core does not change. (B) The logarithm of the discrepancy ε between the simulated and the experimentally measured RDF as a function of ζ and η_ss in NC14 is shown. (C) A comparison is shown between the experimentally measured RDF (circles) and the simulated RDF (solid curve) in NC14 for ζ = 0.41 and η_ss = 1.21. To see this figure in color, go online.

The characteristic nuclear diameter σ, the repulsive force at the maximal shoulder-shoulder overlap $k\sigma$, and the characteristic timescale τ₀ = γ/k set the characteristic units of length, force, and time, respectively. We further define a dimensionless parameter $\zeta =\sqrt{2D\gamma /k{\sigma }^2}$, which compares an effective thermal energy due to fluctuations with the energy associated with shoulder-shoulder internuclear interactions.

We modeled nuclear division by particle duplication such that a single nucleus is replaced by a pair of daughter particles (Fig. 2 A). During division, the two daughter particles interact via a strong repulsive force given by

$${\mathit{F}}_{\text{div}}=\frac{q}{{\left(r_0+r_{ij}\right)}^2}\frac{{\mathit{r}}_{\mathit{ij}}}{r_{ij}},$$ (3)

where q = 10kσ³ and r₀ = 0.1σ (32, 34, 35). The particles become two separated nuclei as soon as the distance between them exceeds σ (Fig. 2 A). The force F_div effectively captures the net force between centrosomes during spindle pole separation contributed by the activity of dynein motor, Ncd motor, and polymerization of interpolar microtubules (32).

Nuclear division introduces another timescale, associated with separating the daughter particles, τ_div ∼ (γσ³/6q)[1 + 3(r₀/σ) + 3(r₀/σ)²] ≈ 0.023τ₀, which we take here to be much shorter than the NC length (Supporting Materials and Methods). As a consequence, nuclei divide synchronously, and the number density doubles with each division:

$${\rho }_{\left\{n\right\}}=2{\rho }_{\left\{n-1\right\}}$$ (4)

such that at n-th NC ρ_{n} = 2^{(n − 14)}ρ_{14} (Fig. 1 D).

The experimentally observed self-similarity of RDF suggests that the length scale associated with the internuclear interaction should scale with nuclear number density as ρ^−1/2 (Fig. 1 F). Therefore, to capture this unique structural dynamics by our model, we redefine the shoulder-shoulder interaction range λ at the beginning of n-th nuclear cycle as

$${\mathit{\lambda }}_n=\frac{{\mathit{\lambda }}_{n-1}}{\sqrt{2}}$$ (5)

such that at n-th NC, λ_n = 2^{−(n − 14)/2}λ₁₄, where λ₁₄ is the interaction range in NC14. This could effectively describe the redistribution of actin and microtubule networks after each mitosis (22, 23, 30). Because the characteristic nearest-neighbor distance is signifciantly larger than the range of the effective hard-core repulsion σ, we assume for simplicity that σ does not depend on the density.

Given that the number density ρ and the interaction range λ are rescaled in each nuclear cycle by 2 and $1/\sqrt{2}$, respectively, we define a dimensionless parameter describing the range of pairwise interactions as

$${\eta }_{\text{ss}}={\rho }_{\left\{n\right\}}{\sigma }^2{\mathit{\lambda }}_n^2=\text{const}\text{.}$$ (6)

Thus, our model contains only two free parameters, ζ and η_ss.

Results

Structural order of dynamic nuclear packings

To quantify the structural properties of nuclear packings, we calculated the RDF, g^(exp)(r), defined as the ratio of the average density at a radial distance r from a given nucleus and the bulk density (25), at the end of NC12, 13, and 14 (Fig. 1 F; Video S1. Live Video of Nuclear Cycle 11–14 of Early Drosophila Embryo Expressing H2AV::mRFP, Document S2. Article plus Supporting Material A). g^exp(r) approaches 1 in the limit r → ∞, indicating the absence of long-range positional order, whereas the position of the first peak in g^exp(r) moves to smaller distances while the nuclear cycles progress, which suggests that the system exhibits a density-dependent characteristic length scale. Motivated by this observation, we rescaled interparticle distances by (ρ_{n}/ρ_{14})^1/2, where ρ_{n} is the number density at the n-th nuclear cycle; ρ_{14} = (0.67 ± 0.02)/σ² is the number density in NC14 (Fig. 1 C). Upon this rescaling, we observed almost perfect collapse of the peaks corresponding to NC12–14 (Fig. 1 F).

Next, we quantified the packing in reciprocal space by computing the structure factor (Fig. S3 B; Video S2), defined as $S^{\text{exp}}\left(\mathit{k}\right)={\left|\left(1/N\right){\sum }_{i=1}^N\text{exp}\left(\text{i}\mathit{k}\cdot {\mathit{r}}_i\right)\right|}^2$, where r_i are the in-plane positions of centers of mass of the nuclei, N is the total number of nuclei, and k = (k_x, k_y) is the wavevector (19, 21, 25). We found that, similarly to g(r), peak positions of S^exp(k), where k = |k|, also collapse upon rescaling distances by (ρ_{n}/ρ_{14})^1/2. Furthermore, in the long-wavelength limit (k → 0), S^exp approaches a density-independent nonzero value (Fig. 1 G). This implies that similarly to the short-range order, the density fluctuations of nuclear packings at long wavelengths also remain unchanged by nuclear divisions.

Thus, the nuclear packing preserves its structure at progressively smaller length scales during densification. This makes the system distinct from other known disordered systems with short-range interactions. For example, packings of identical nonoverlapping hard disks exhibit short-range positional order with the first RDF peak at r = σ and undergo a structural phase transition as the number density is increased (36, 37). On the other hand, when confined, particles interacting only via long-range repulsive forces, e.g., Coulomb interactions, form ordered structures with a density-dependent characteristic length scale (38, 39). These model systems are clearly different from what we observe for nuclear packings in the embryo (Fig. 1; Fig. S4).

Model parameter estimation

To explore origins of the self-similar dynamics of the nuclear packings (Fig. 1, A–C), we used a particle-based model (Materials and Methods; Fig. 2 A)). Both free model parameters, ζ and η_ss, were estimated from experimental data as described below.

Because the internuclear interactions in our model are short-ranged, the effects of the embryo’s curvature are expected to be negligible. Therefore, we started our analysis on a flat surface by simulating the nuclear-packing dynamics in a square box with periodic boundary conditions (Video S3). Initially, we randomly distributed N = 64 nuclei along the surface of the simulation domain by random sequential addition (19, 40). The side of the simulation box L = (8N/ρ_{14})^1/2 = 27.74σ was kept constant throughout simulation. We assumed that the NC lengths were much longer than the time needed for the system to reach the steady state (Fig. S5) and let the system minimize its total potential energy at each NC before triggering the next division.

To determine the values of the two remaining free parameters η_ss and ζ, we varied them and compared the RDF of the simulated and the experimentally measured packings at the end of NC14. In particular, we calculated the mean-square error of g(r), defined as ${\mathrm{ϵ}}^2=\left(1/r_{\text{max}}\right){\int }_0^{r_{\text{max}}}\text{d}r{\left[g\left(r\right)-g^{\text{exp}}\left(r\right)\right]}^2$, and plotted contours of lnϵ in the (ζ, η_ss) plane (Fig. 2 B). Here, we chose the upper limit of the integration interval r_max = 5σ because this is the distance at which g(r) first saturates to unity. We found the best agreement between the two at ζ = 0.41 and η_ss = 1.21 (Fig. 2 C).

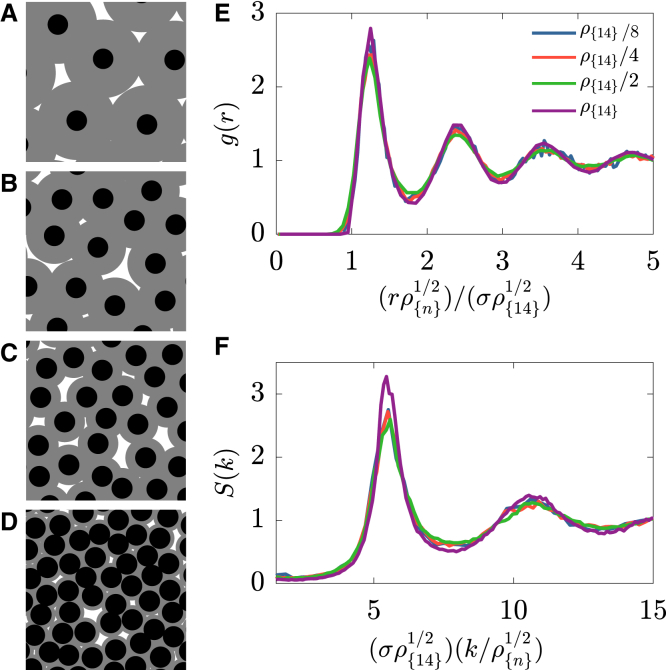
This set of model parameters not only matches the structure of the packings at the end of NC14 but also describes the dynamics throughout the course of NC11–14. Fig. 3, A–D show representative simulation snapshots of the steady-state packings in each of the four NCs. We quantified their structural properties by calculating time-averaged g(r) and S(k) (Fig. S3, C and D).

Figure 3.

(A–D) Simulation snapshots of representative structures in NC11–14 at η_ss = 1.21 and ζ = 0.41. RDFs (E) and structure factor (F) are shown for packings at η_ss = 1.21 and ζ = 0.41 in NC11–14 (blue, red, green, and purple curves, respectively). RDFs and structure factor collapse after rescaling distances by (ρ/ρ_{14})^1/2. Note that this collapse is not commonly observed in typical packing models. The simulation was done in a square box of size L = 55.49 starting with N = 256 particles. To see this figure in color, go online.

In agreement with experiments, the simulated packings exhibit short-range structural order that is unaffected by the density and preserve the suppression of density fluctuations at large wavelengths. This is demonstrated by the collapse of g(r) in real space and S(k) in reciprocal space upon rescaling distances by (ρ_{n}/ρ_{14})^1/2 (Fig. 3, E and F). Thus, the nuclear packings are characterized by a considerable level of both short and long-range correlated (dis)order. In contrast to common disordered materials, in which these types of structures can be observed only at high density, in nuclear packings, the level of (dis)order persists over a wide range of densities.

As expected, because of the short-range pairwise interaction potential, the RDF of the final nuclear-packing structure remains largely unchanged when the model is implemented on a prolate spheroid with the aspect ratio of the real embryo (Fig. 4, A and B; Supporting Materials and Methods). For direct comparison with the imaging data at all densities (NC12–14), we projected positions of the nuclei at the end of NC14 from a spheroid onto a plane, mimicking the maximal-intensity-projection plane in experiments. We calculated the statistical properties of the 2D-projected images to show that although the projection does not affect the positions of the peaks in the RDF, it significantly affects their maxima and minima (Fig. 4 C). In particular, the amplitude of the first peak of g(r) predicted by the model increases with nuclear density, in contrast to the 2D model (Fig. 3 E) and consistent with what we observe experimentally (Fig. 1 F).

Figure 4.

(A) Snapshot of the nuclear packing in NC14 with N = 6000 nuclei on the surface of a prolate spheroid with the aspect ratio 3:1. (B) Comparison between the experimentally measured RDF (circles) and the simulated RDF (solid curve) in NC14 is shown for ζ = 0.47 and η_ss = 1.15. (C) Heights of the first peak in RDF, g(r^∗), are shown for nuclear packings at the end of NC12–14. Empty circles represent mean of six experimentally measured values (error bars denote SD), whereas full circles represent results calculated from simulations on a prolate spheroid after projecting the packings onto the maximal-intensity-projection plane. To see this figure in color, go online.

Characterization of the degree of order

A variety of different order metrics have been devised to characterize packings (41), but the commonly used ones only incorporate local order (e.g., bond-orientational order) (24). Here, we characterize the level of structural order of the nuclear packing by computing the scalar order metric τ, which is defined in 2D as (42)

$$\tau =\rho {\int }_0^{2r_{\text{max}}}2\pi r\text{d}r{\left[g\left(r\right)-1\right]}^2.$$ (7)

For a spatially uncorrelated Poisson point pattern, τ = 0 because g(r) = 1 for all r. Thus, a deviation of τ from zero, which can only be positive for either positive or negative correlations, measures translational order with respect to the fully uncorrelated case across length scales. Moreover, τ diverges for any perfect crystal. We computed τ from RDF of packings in embryos and found substantial order across lengthscales (Video S1. Live Video of Nuclear Cycle 11–14 of Early Drosophila Embryo Expressing H2AV::mRFP, Video S3. Simulation in a Square Box from NC11 to NC14 at ρ{14}=0.67, ηss=1.21, and ζ=0.41 C). In particular, at the final density in NC14 (ρ_{14} = 0.67/σ²), τ = 7.9 ± 0.9, which is considerably higher compared to packings of identical nonoverlapping disks at the same density, where τ ≈ 4.7, for example.

Next, we used τ to explore the general behavior of our model throughout the (ζ, η_ss) parameter space at fixed ρ_{14} = 0.67/σ². Surprisingly, we found that τ is a nonmonotonic function of η_ss (Fig. 5 A; Video S1. Live Video of Nuclear Cycle 11–14 of Early Drosophila Embryo Expressing H2AV::mRFP, Document S2. Article plus Supporting Material A). Specifically, ordered structures appear at η_ss ∼ 1.3 and small values of ζ (Fig. 5, A and B). In turn, these structures become increasingly disordered when either η_ss diverges from ∼1.3 or ζ is increased (Fig. 5, A–D).

Figure 5.

(A) Order parameter τ as a function of ζ and η_ss in NC14 (ρ = ρ_{14} = 0.67/σ²). (B–D) Representative snapshots of the nuclear packing in steady state are shown at (ζ, η_ss) = (0, 1.27), (0.41, 1.21), (0.16, 0.7), respectively. (E) τ is shown as a function of the final number density ρ_{14} at η_ss = 1.21 and ζ = 0.41 in NC 11–14. Blue, red, green, and purple curves correspond to NC11–14, respectively. To see this figure in color, go online.

A question remains, though, as to why the syncytial embryo stops its divisions at the particular value of the nuclear density, ρ_{14} ≈ 0.67/σ² (Fig. 1 D), and how the structure of the nuclear packing would change upon changing this density. To address these questions, we computed τ at fixed ζ = 0.41 and η_ss = 1.21, varying the final nuclear density ρ_{14}. In agreement with constant height of the first peak of g(r) and S(k) in the 2D model (Fig. 3, E and F), τ also does not significantly vary among NCs. However, the final packings in NC14 become increasingly ordered when ρ_{14} is increased beyond ≈0.7/σ². This is seen from divergence of τ in NC14 from that in NC11–13 (Fig. 5 E; Fig. S6 B). This divergence occurs because of significant contribution of the steric repulsion at large densities. Interestingly, the critical density 0.7/σ² is close to the experimentally measured density in NC14, ρ_{14} = 0.67/σ² (Fig. 1 D), and also to the maximal density at which nonoverlapping disks can be packed by random sequential addition (19, 40). These results suggest that the embryo maximizes the final nuclear density while still preserving the level of structural order throughout syncytial divisions.

Discussion

We discovered that during rapid densification by synchronous mitotic divisions, nuclear packings display self-similar dynamics that preserves both long and short-range correlated disorder (Fig. 1). This type of dynamics is fundamentally different from what is commonly observed in densifying systems of particles interacting via short-range forces, such as collections of nonoverlapping disks and Lennard-Jones fluids, which undergo phase transitions at increasing particle densities (41, 43, 44, 45).

Self-similar dynamics of nuclear packings can be quantitatively explained using a particle-based model with density-dependent short-range interaction potential (Fig. 2). The model has only two free parameters, which are uniquely identifiable from imaging data (Figs. 2, 3, and 4). In the future, this description could be extended to address the role of (a)synchrony of divisions. In particular, it is not known how the packing structure would change upon varying both durations of NCs and the speed of mitotic waves (23, 46, 47, 48, 49). Another possible extension of our model would be to allow deformation of the cytoskeletal components to ensure confluency of the overall packing and explore its role in establishing the structure of the nuclear packing (30). A more challenging future direction would be to design controlled experiments on biologically perturbed embryos to test the scope of our simplified theoretical model.

Computationally generated nuclear positions on the surface of a prolate spheroid provide time-dependent grids for solving the reaction-diffusion problems describing the anteroposterior, dorsoventral, and terminal patterning cues. The one-dimensional models that have been proposed for the Bicoid, Dorsal, and Capicua gradients (17, 18, 50) can be implemented in two dimensions, providing a coherent description of the joint dynamics of the anteroposterior, dorsoventral, and terminal patterning systems. In the future, our computational framework can be extended to the next stages of embryogenesis, including zygotic transcription, cellularization, and epithelial morphogenesis, paving the way for self-consistent modeling of multiple consecutive stages of development.

Author Contributions

S.T., S.Y.S., and M.K. designed research. S.D., N.J.-V.D., and M.K. performed research. S.D. analyzed data. S.D., N.J.-V.D., S.T., S.Y.S., and M.K. wrote the manuscript.

Editor: Mark Alber.

Supporting Citations

References (51, 52, 53, 54) appear in the Supporting Material.