Voltage-Dependent Profile Structures of a Kv-Channel via Time-Resolved Neutron Interferometry

Abstract

Available experimental techniques cannot determine high-resolution three-dimensional structures of membrane proteins under a transmembrane voltage. Hence, the mechanism by which voltage-gated cation channels couple conformational changes within the four voltage sensor domains, in response to either depolarizing or polarizing transmembrane voltages, to opening or closing of the pore domain's ion channel remains unresolved. Single-membrane specimens, composed of a phospholipid bilayer containing a vectorially oriented voltage-gated K⁺ channel protein at high in-plane density tethered to the surface of an inorganic multilayer substrate, were developed to allow the application of transmembrane voltages in an electrochemical cell. Time-resolved neutron reflectivity experiments, enhanced by interferometry enabled by the multilayer substrate, were employed to provide directly the low-resolution profile structures of the membrane containing the vectorially oriented voltage-gated K⁺ channel for the activated, open and deactivated, closed states of the channel under depolarizing and hyperpolarizing transmembrane voltages applied cyclically. The profile structures of these single membranes were dominated by the voltage-gated K⁺ channel protein because of the high in-plane density. Importantly, the use of neutrons allowed the determination of the voltage-dependent changes in both the profile structure of the membrane and the distribution of water within the profile structure. These two key experimental results were then compared to those predicted by three computational modeling approaches for the activated, open and deactivated, closed states of three different voltage-gated K⁺ channels in hydrated phospholipid bilayer membrane environments. Of the three modeling approaches investigated, only one state-of-the-art molecular dynamics simulation that directly predicted the response of a voltage-gated K⁺ channel within a phospholipid bilayer membrane to applied transmembrane voltages by utilizing very long trajectories was found to be in agreement with the two key experimental results provided by the time-resolved neutron interferometry experiments.

Significance

Voltage-gated cation channels are central to neurological signal transmission. How they change conformation in response to changes in the transmembrane voltage remains unresolved. Time-resolved neutron interferometry experiments have determined directly the dependence of the profile structure of a voltage-gated K⁺ channel within single phospholipid bilayers and of the distribution of water within that structure on the transmembrane voltage. These two key results were compared with their counterparts predicted by three different computational approaches for modeling the activated, open and deactivated, closed states of three different voltage-gated K⁺ channels in hydrated phospholipid bilayers. Only one was found to be in agreement with the two key results. Thus, these time-resolved neutron interferometry experiments provide a crucial test for the computational modeling approaches.

Introduction

Nav and Kv channels are voltage-gated ion channels (VGICs) selective for sodium or potassium, respectively, that are responsible for the generation and propagation of action potentials in neurological signal transmission (1). The mechanism of coupling conformational changes within the four voltage sensor domains (VSDs) in response to a change in the transmembrane voltage, either depolarizing or polarizing relative to the resting voltage, to opening or closing the channel within the pore domain (PD) remains unknown (2, 3). The VSDs of VGICs are deactivated at the resting transmembrane voltage of −60 to −70 mV and experience the absence of a transmembrane voltage only transiently during the course of an action potential of a few milliseconds’ duration (4). To date, higher-resolution three-dimensional (3-D) structures for VGICs have only been provided by conventional techniques (x-ray crystallography, cryo-electron microscopy) in the absence of a transmembrane voltage (e.g., 5, 6, 7). This seriously complicates any investigation into the mechanism of electromechanical coupling. For example, in the case of Kv channels for which the first high-resolution structures were obtained, the channel within the PD was found to be open, and the conformations of the VSDs were assumed to be activated because 0 mV would be sufficiently depolarizing (5, 8). In the absence of a structure for the deactivated, closed state of Kv channels, numerous models were developed employing various computational approaches, each relying on specific assumptions (2, 3). Several incorporated restraints based on experimental results provided by indirect techniques (9, 10, 11, 12, 13). For example, one utilized pairs of site-directed cysteine mutations and measurements of metal cross-linking as a function of the transmembrane voltage (14). Other approaches attempted to induce the deactivated, closed state by applying hyperpolarizing transmembrane voltages (e.g., 15, 16, 17). The most successful of these utilized very long 250 μs MD simulations (18). Overall, such studies demonstrated a high degree of similarity in the atomic models, thereby achieving a “consensus” structure for the deactivated, closed state of Kv channels (2). However, despite the “consensus” noted, experimental validation utilizing one or more direct techniques remains essential.

Some developments were needed to investigate the voltage-dependent structures of VGICs directly, without having to resort to one or more site-directed mutations and subsequent labeling with bulky chromophores or heavy metals. We first developed two methods for the fabrication of single-membrane specimens, composed of a phospholipid bilayer containing a vectorially oriented voltage-gated K⁺ channel protein at high in-plane density, tethered to the surface of an inorganic multilayer substrate to allow for the application of transmembrane voltages in an electrochemical cell (19, 20). The structures of the tethered single-membrane specimens were then characterized by both x-ray reflectivity (19) and neutron reflectivity (21), each enhanced by interferometry enabled by the multilayer substrate (20, 22). The electrical properties of the membranes were characterized by electrical impedance spectroscopy (EIS). With these essential developments, we then utilized time-resolved x-ray and neutron interferometry to investigate the dependence of the so-called “profile structure” of the isolated VSD of the prokaryotic Kv channel KvAP on physiologically relevant transmembrane voltages that were nonpolarizing, polarizing, and depolarizing with respect to the transmembrane resting voltage (23). The profile structure is the projection of the 3-D structure of the membrane parallel to the membrane plane onto the membrane normal and is dominated by the protein component at the high in-plane density. In these time-resolved, “pump-probe” experiments, the three voltages were applied cyclically, and the interferometry data were collected separately for each voltage and subsequently averaged. For the x-ray case employing a pulsed synchrotron source, radiation damage to the specimens was detected after only three voltage cycles, although the incident photon flux was sufficiently high to provide accurate x-ray scattering-length density (xSLD) profiles for each voltage within a single cycle. For the neutron case utilizing a pulsed spallation source, the incident neutron flux was dramatically lower, therefore requiring many voltage cycles to provide accurate neutron scattering-length density (nSLD) profiles made possible by the absence of any detectable radiation damage to the specimens. The voltage-dependent xSLD and nSLD profile structures for the isolated VSD of KvAP determined from these time-resolved experiments were found to be in good agreement with long (multi-μs) molecular dynamics (MD) simulations of the same VSD protein within a hydrated phospholipid bilayer membrane investigated as a function of similar physiologically relevant transmembrane voltages (24).

In this work, we extended our time-resolved neutron interferometry approach to investigate the dependence of the profile structure of the complete homotetrameric prokaryotic Kv channel KvAP, vectorially oriented within a phospholipid bilayer membrane at a solid-liquid interface, on the transmembrane voltage. A cyclic sequence of hyperpolarizing and depolarizing voltage pulses, whose amplitudes and duration were judiciously selected to circumvent the inactivation exhibited by the complete homotetrameric channel (25), was synchronized with the pulsed neutron source. Averaging the data for each of the hyperpolarizing and depolarizing voltage pulses collected over many cycles provided the nSLD profile structure of the membrane for the deactivated, closed state (hyperpolarized) and activated, open state (depolarized) of the channel, as well as the profile structure for water within the Kv channel for these two end states, the latter enabled by using neutrons (20). There were two key experimental results from this study, namely the difference ΔnSLD profile structures for both the membrane and for water within the membrane, each calculated as the nSLD profile for the deactivated, closed state (hyperpolarized) minus the nSLD profile for the activated, open state (depolarized). The two key results were then compared with those predicted by three fundamentally different computational approaches to modeling these same two states for three different voltage-gated K⁺ channels in hydrated phospholipid bilayer membranes. They included a targeted MD simulation applied to the prokaryotic KvAP channel (13), ROSETTA membrane protein structure prediction followed by MD simulation applied to the transmembrane domain of the eukaryotic Kv1.2 channel (9, 10, 11), and a state-of-the-art, 250 μs timescale MD simulation (18) applied to the transmembrane domain of the eukaryotic Kv1.2/2.1 chimera channel. Only one of these computational approaches was found to be in agreement with both of the two key experimental results for the KvAP channel provided by our time-resolved neutron interferometry experiments.

Materials and Methods

Expression and purification of KvAP protein

The KvAP gene (coding for residues 14–295 of the protein) was amplified from a PQE60 plasmid that was kindly provided by Dr. Rod McKinnon (Rockefeller University). The gene was inserted into the in-house pETCH vector (26), which supplies a C-terminal His₆ tag. The plasmid was inserted into C41(DE3) cells, which were grown in Luria-Bertani medium at 37°C. When the OD₆₀₀ value reached 0.8, protein expression was induced by addition of 0.4 mM isopropylthiogalactoside; 10 mM BaCl₂ was added to the medium at the same time. Cells were harvested after 4 h, washed with water, and frozen.

All purification steps were carried out at 4°C. Cells were lysed in 20 mM Tris (pH 8), 100 mM KCl (buffer A) using an Emulsiflex cell disruptor (Avestin Inc., Ottawa, Ontario, Canada) operating at 20,000 psi. The lysate was centrifuged at 14,000 × g for 15 min, after which the supernatant was centrifuged at 200,000 × g for 1 h to isolate the membrane fraction. The membrane pellet was resuspended in buffer A, and n-decyl-β-D-maltopyranoside (DM) was added to a final concentration of 1.9% (w/v). After 1 h, the suspension was centrifuged again at 200,000 × g for 1 h. The supernatant was filtered and applied to a 1 mL HisTrap-HP column (GE LifeSciences, Pittsburgh, Pennsylvania) equilibrated with buffer A + 0.24% DM. KvAP was eluted with a gradient from 0 to 400 mM imidazole. Fractions containing KvAP were pooled and dialyzed versus buffer A + 0.24% DM. The protein was then reduced with 1 mM tris(2-carboxyethyl)phosphine for an hour, after which it was concentrated to ∼10 mg/mL. DM concentrations in the concentrated protein sample were measured by analytical thin-layer chromatography (27) and were typically found to be ∼5% (w/v). A sample of the concentrated protein was analyzed by size-exclusion chromatography on a Sephacryl S-200 column in buffer A + 0.24% DM and found to migrate as a tetramer. Aliquots of the concentrated protein were flash-frozen in liquid nitrogen.

Specimens for x-ray interferometry and time-resolved neutron interferometry experiments

We used a modified version of the self-assembly method (19) to tether the homotetrameric KvAP solubilized in DM, designated as KvAP-DM, to the surface of an Si-Ge-Si multilayer on silicon substrates to result in a unique vectorial orientation of the KvAP protein with respect to the normal to the substrate surface. The modifications included utilizing 3-aminopropyldimethylethoxysilane (Gelest, Morrisville, PA) to alkylate the silicon oxide surface of the substrate, followed by sequential reaction with three linkers—succinic anhydride (Sigma-Aldrich, St. Louis, MO), 1-ethyl-3(3-dimethylaminopropyl)carbodiimide hydrochloride (Pierce Biotechnology, Rockford, IL), and N-hydroxysuccinimide (Pierce)—followed by surface functionalization with N_α,N_α-Bis(carboxymethyl)-L-lysine hydrate (Sigma-Aldrich) to produce an alkylated substrate surface possessing nitrilotriacetate endgroups. The modifications resulted in improved specimen-to-specimen reproducibility for tethering KvAP-DM to the surface of the Si-Ge-Si multilayer on silicon substrates. Each silicon or germanium layer in the multilayer was of ∼20 Å thickness, fabricated by magnetron sputtering at the Advanced Photon Source, Argonne National Laboratory. The detergent was subsequently exchanged for 1-palmitoyl-2-oleoylphosphatidylcholine (POPC; Avanti Polar Lipids, Alabaster, AL) following the self-assembly method (19).

Electrochemical cell for time-resolved neutron interferometry experiments

The basic features of the electrochemical cells used for the time-resolved neutron interferometry experiments reported herein were similar to those for the cells used previously for the closely related experiments with the isolated VSD from KvAP (23). Here, instead of an Si-Ni-Si multilayer on silicon substrate as in the reference, the working electrode was provided by an Si-Ge-Si multilayer on a silicon substrate, the latter being heavily doped with phosphorus to make it sufficiently conductive (R < 1 Ωcm²), which was held at ground potential. The electric potential (voltage) was applied to the membrane on the surface of the Si-Ge-Si multilayer substrate via a platinum counterelectrode in the aqueous electrolyte composed of 0.1 M KCl in 1 mM Tris buffer at pH 8. For either the isolated VSD studied previously (23) or KvAP itself tethered to the substrate surface via a His-tag on the protein’s C-terminus in this study, this is exactly opposite to the electrophysiological convention in which the extracellular side of the membrane is at ground potential and the electric potential is applied to the cytoplasmic side.

Design of the neutron interferometry “pump-probe” experiment to avoid KvAP inactivation

In a classic “pump-probe” experiment, the membrane containing the vectorially oriented Kv channel is subjected to a periodic alternating sequence of polarizing and depolarizing pulses with respect to the resting transmembrane voltage, each of constant amplitude and finite duration, and the membrane structure is synchronously probed with a small number of neutron pulses for each voltage pulse applied to the membrane. This approach has the absolute requirement that both the activation of the four VSDs and subsequent opening of the channel within the PD produced by the depolarizing voltage pulse and the deactivation of the four VSDs and closing of the channel within the PD produced by the polarizing voltage pulse be completely reversible. Utilizing a pulsed neutron source like the Spallation Neutron Source at Oak Ridge National Laboratory, although the incident neutron pulses are of only ∼10 μs duration, the momentum transfer $\stackrel{\rightharpoonup }{Q}$ (see Supporting Materials and Methods, Section a) for each scattered neutron is determined by time of flight (TOF), which requires 16.5 ms. Hence, the number of neutron pulses employed for each voltage pulse depends on the duration of the TOF, down to the lower limit of one neutron pulse for a voltage pulse of 16.5 ms duration.

However, all Nav and Kv channels exhibit inactivation, even those that do not possess the additional cytoplasmic domain of eukaryotic channels but only a transmembrane domain, like the prokaryotic Kv channel KvAP utilized in this work. For an ensemble of channels, only a fraction of the ensemble can be activated in response to a second, sufficiently depolarizing voltage pulse to result in pore opening and a measurable potassium current if the first depolarizing pulse is of too long a duration. For KvAP, using polarizing pulses of −120 mV and depolarizing pulses of +100 mV (electrophysiological convention), each of 150 ms duration, only about one third of the ensemble can be activated by a second depolarizing pulse (25). After four pulses, the entire ensemble is inactivated. Unfortunately, reactivation occurs only on a much longer timescale, namely ∼90 s for KvAP incorporated into a planar phospholipid bilayer composed of POPC:1-palmitoyl-2-oleoylphosphatidylglycerol (POPG)-decane (25). This situation would render such a “pump-probe” experiment as described above essentially impossible because the experiment would be exceedingly inefficient, utilizing only an infinitesimal fraction (1/600) of the incident neutron flux available, noting the incident neutron pulse rate of 60 Hz, to achieve the requirement of complete reversibility. However, a judicious choice of both the amplitude and duration of the polarizing and depolarizing voltage pulses can be used to circumvent inactivation for a particular Kv channel depending on its membrane environment. As shown in Fig. 4 of (25), choosing more hyperpolarizing pulses of −150 mV and less depolarizing pulses of +20 mV, each of only 50 ms duration, can be employed to eliminate any measurable inactivation for KvAP in a planar phospholipid bilayer composed of POPC:POPG-decane. As a result of the above considerations, we employed three neutron pulses for each hyperpolarizing or depolarizing voltage pulse, this number averaging over the complete activation of the KvAP channel ensemble upon application of each depolarizing voltage pulse from inspection of Fig. 1 of (25).

X-ray interferometry data collection

X-ray interferometry data were collected from several specimens, each composed of either a KvAP-DM monolayer or a KvAP-POPC membrane after POPC-DM exchange, tethered to the surface of the same Si-Ge-Si multilayer substrate. The specimens were maintained in a hydrated state with moist He at 95% relative humidity in a thermoregulated specimen chamber with Kapton windows. Specular x-ray reflectivity data were collected at 8.048 keV (1.543 Å), using a rotating-anode x-ray source, singly bent LiF monochromator incident beam optics, a Huber 4-circle diffractometer (Huber, Rimsting, Germany), an Si(111) analyzer, and a scintillation detector, via θ-2θ scans as described previously (19). These data were subsequently corrected for the incident beam footprint on the planar specimen depending on the angle of incidence and for off-specular background scattering.

Time-resolved neutron interferometry data collection

Time-resolved neutron interferometry data were collected with the Magnetism Reflectometer on Beamline 4A at the Spallation Neutron Source, Oak Ridge National Laboratory (28). Several specimens were investigated, composed of either a KvAP-POPC membrane tethered to the surface of an Si-Ge-Si multilayer substrate (four) or just the self-assembled monolayer (SAM) used to tether KvAP-DM to the substrate as a voltage-insensitive “control” (two). The incident neutron pulses are polychromatic and of ∼10 μs duration at a repetition rate of 60 Hz. 16.5 ms is required to determine the momentum transfer vector $\stackrel{\rightharpoonup }{Q}$ of each reflected neutron via TOF. The cyclic sequence of hyperpolarizing voltage pulses of 150 mV and depolarizing voltage pulses of 20 mV, each of 50 ms duration and constant amplitude, were synchronized with the incident neutron pulses so that there were three neutron pulses for each voltage pulse. To achieve acceptable reflected neutron counting statistics, reflectivity data were collected from each specimen for 3–200 min, for each of the six angles of incidence employed to span the range of Q_z accessed using the polychromatic neutron pulses. The time required increased with angle of incidence, and the reflected neutrons for each triplet of neutron pulses were collected separately and subsequently averaged over each of the hyperpolarizing or depolarizing voltage pulses. Given the incident neutron pulse rate, this implies that the reflectivity data for each transmembrane voltage were averaged over 10³–10⁶ cycles of the voltage pulse sequence. The time-averaged specular reflectivity data for each transmembrane voltage was then calculated, and the time-averaged data were subsequently corrected for the incident beam footprint on the planar specimen depending on the angle of incidence and for off-specular background scattering.

X-ray interferometry data analysis

The specular x-ray interferometry data for the KvAP-DM monolayer and KvAP-POPC membrane specimens were analyzed using a constrained refinement approach analogous to that described previously (19) to provide their respective xSLD profile. The formalism and its implementation are fully described in the Supporting Materials and Methods, Section a.

Time-resolved neutron interferometry data analysis

The time-averaged specular neutron interferometry data for either the hyperpolarizing or the depolarizing voltage pulses was analyzed, using a constrained refinement approach analogous to that first described previously for a tethered protein monolayer at the solid-gas interface (29), to provide the nSLD profile for each voltage. The formalism and its implementation are fully described in the Supporting Materials and Methods, Section a.

Estimation of error propagation in the x-ray and neutron interferometry data analysis

As described in the Supporting Materials and Methods, Section a, our data analysis employs the Fresnel-normalized x-ray or neutron interferometry data R(Q_z)/R_F(Q_z), in which the specular reflectivity data R(Q_z) containing the standard errors determined by the photon/neutron counting statistics has been divided by an analytic function R_F(Q_z) describing the reflectivity from a single ideal interface. The constrained refinement approach employs Fourier transformations to produce the xSLD or nSLD profile structures that obscure the standard errors in the reflectivity data. For the x-ray case, the propagation of errors from the data into the xSLD profiles was estimated utilizing a region of the profile that should be of constant xSLD. As shown in Fig. 2 A, this occurs for the KvAP-DM specimens over the region 50 Å < z < 100 Å, which is occupied by only the moist helium environment. The low-amplitude oscillations about zero xSLD in this region arise from error propagation with a wavelength determined by the truncation of the inverse Fourier transformation at a maximal Q_z of 0.427 Å⁻¹. For the neutron case, the time-resolved experiments employed “control” specimens composed of only the Si-Ge-Si multilayer substrate on silicon and the organic SAM, otherwise used to tether the KvAP-POPC membrane to the substrate’s surface. These control specimens were not expected to exhibit any dependence on the transmembrane voltage applied to the KvAP-POPC membrane specimens. As shown in Fig. 4 C, the difference ΔnSLD profile for the SAM specimen (hyperpolarizing − depolarizing) over the region 0 Å < z < 100 Å, otherwise occupied by the KvAP-POPC membrane when present, exhibits only low-amplitude oscillations about zero nSLD in this region. These low-amplitude oscillations arise from error propagation with a wavelength determined by the truncation of the inverse Fourier transformation at a maximal Q_z of 0.194 Å⁻¹. Because errors propagate in difference ΔnSLD profiles as the square root of the sum of the squares of the errors in each nSLD profile contributing to the difference profile, the standard errors in each contributing nSLD profile are then smaller by a factor of 1/$\sqrt{2}$.

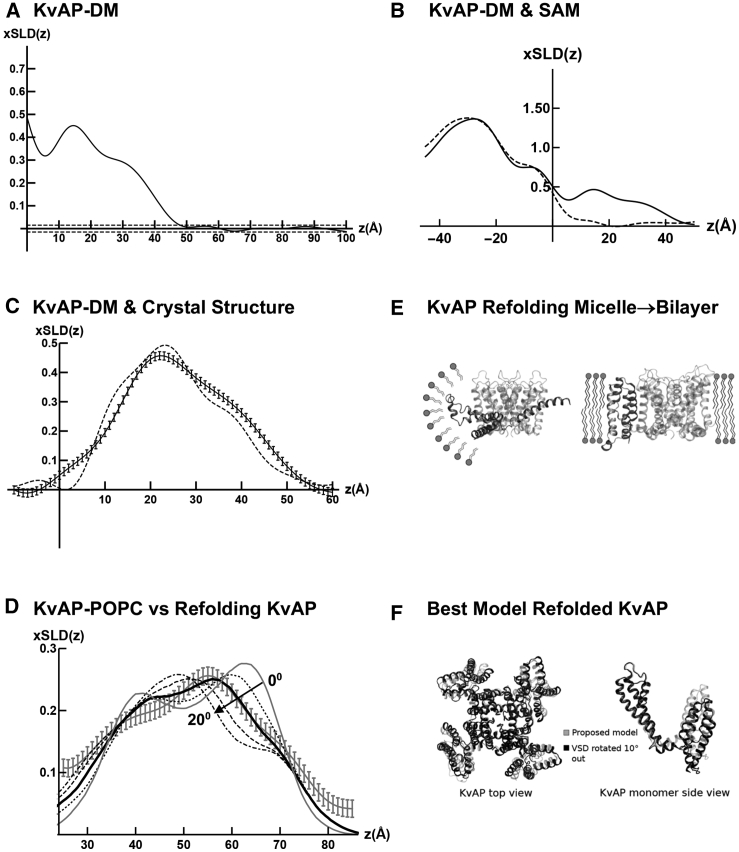
Figure 2.

Folding KvAP at the solid-liquid interface. (A) The xSLD(z) profile for a KvAP-DM monolayer tethered to the surface of an Si-Ge-Si multilayer substrate is shown. The horizontal dashed lines above and below the abscissa were used to estimate the propagation of errors. (B) The xSLD(z) profiles for an Si-Ge-Si multilayer substrate with only the organic SAM used to tether the KvAP-DM monolayer to its surface (dashed) and for a slightly different Si-Ge-Si multilayer substrate with a KvAP-DM monolayer tethered to its surface (solid) are shown. The xSLD profiles for the multilayer substrates occur for z < 0 Å, whereas those for the SAM or tethered KvAP-DM monolayer occur for z > 0 Å. (C) The xSLD(z) profile for the tethered KvAP-DM monolayer (solid) with estimated errors is shown, compared with the xSLD(z) profile calculated from the x-ray crystal structure for KvAP-DM (dashed). (D) The xSLD(z) profile for the KvAP-POPC membrane after POPC-DM exchange (gray with estimated errors) is shown, compared with the xSLD(z) profiles calculated for the model proposed for KvAP (gray solid) within a phospholipid bilayer environment described in (E), as well as for rotations of 5° (dotted), 10° (black solid), 15° (dashed), and 20° (dash-dot) less than the 90° originally proposed. (E) An illustration is given showing the proposed (31) refolding of the S1 helix to form a four-helix bundle structure for the VSDs and reorientation of the bundle axis relative to the pore axis of KvAP via a rotation of ∼90° upon the transformation from a detergent micelle environment (left side) to a phospholipid bilayer environment (right side). One VSD is shown in the foreground (black) with the PD in the background (gray). (F) Top view and side view (of one subunit) of the 3-D structure proposed for KvAP in a phospholipid bilayer environment from (31) is shown in a ribbon representation (gray), compared with that for a rotation of the VSDs by 10° less (black) than originally proposed. The xSLD(z) profiles are in units of electron density, e⁻/ų.

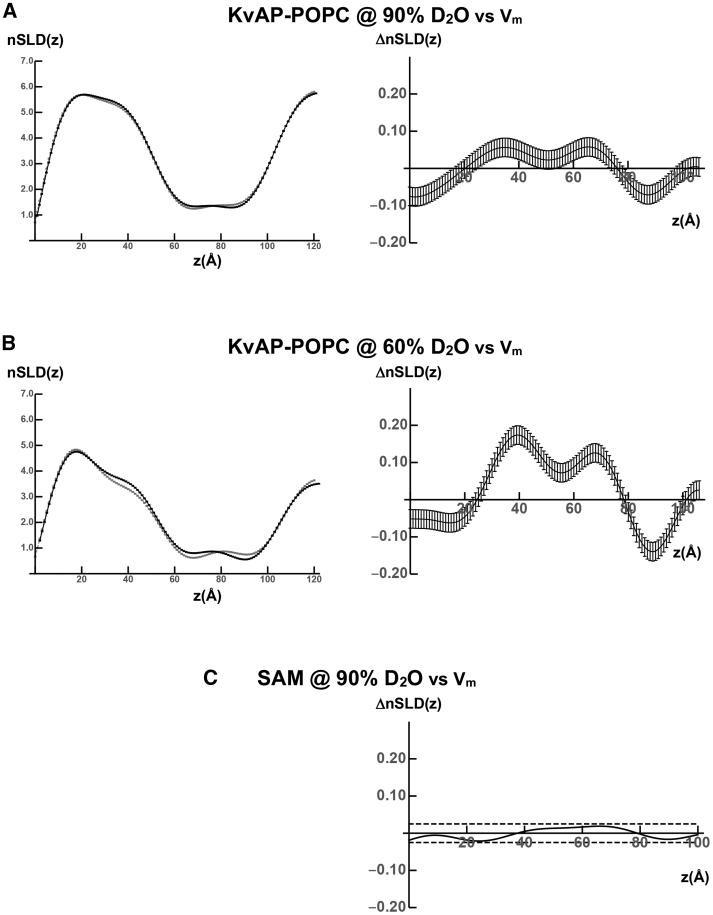
Figure 4.

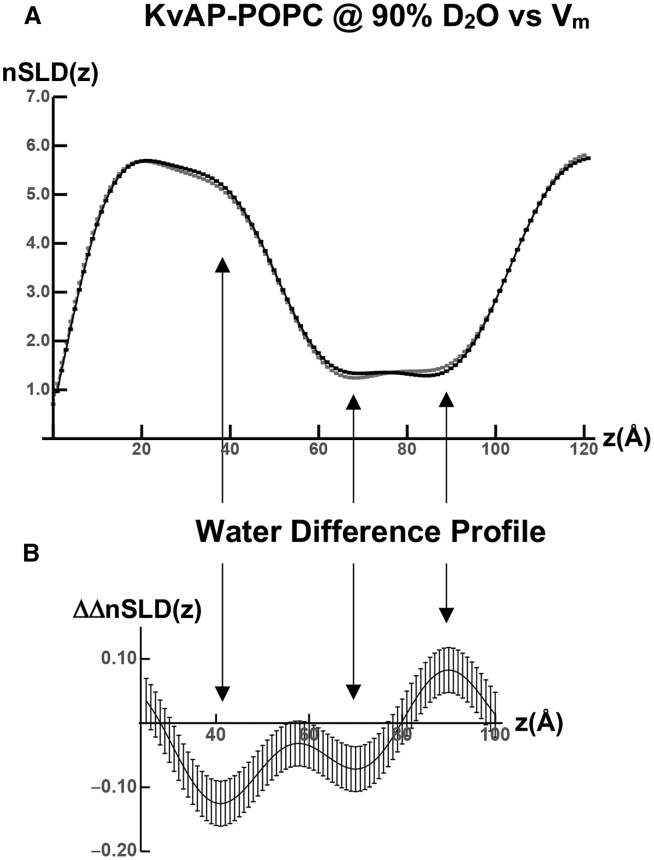
Experimental voltage-dependent profile structures for the KvAP-POPC membrane. (A) Left side shows the nSLD(z) profiles for the KvAP-POPC membrane of specimen S2 (black hyperpolarized, gray depolarized) at a solvent contrast of 90% D₂O/10% H₂O. The profile for the membrane is at negative contrast relative to 90% D₂O. (A) Right side shows the difference ΔnSLD(z) profile (hyperpolarized minus depolarized) at the same contrast of 90% D₂O/10% H₂O. (B) Left side shows the nSLD(z) profiles for the same specimen S2 at a contrast of 60% D₂O/40% H₂O. The profile for the membrane is also at negative contrast relative to 60% D₂O. (B) Right side shows the difference ΔnSLD(z) profile (hyperpolarized minus depolarized) at the same contrast of 60% D₂O/40% H₂O. (C) Right side shows the ΔnSLD(z) profile (hyperpolarized minus depolarized) for the organic SAM on the inorganic Si-Ge-Si multilayer substrate’s surface, but otherwise lacking the tethered KvAP-POPC membrane, for specimen S1 at a solvent contrast of 90% D₂O/10% H₂O. The horizontal dashed lines above and below the abscissa were used to estimate the propagation of errors into the difference ΔnSLD(z) profiles and hence the nSLD(z) profiles contributing to the difference. The nSLD(z) profiles are in units of 10⁻⁶/Ų.

Modeling the voltage-dependent nSLD profiles for the KvAP-POPC membrane

We believe that it is essential that all-atom MD simulation be incorporated in any approach to modeling either the activated, open state or the deactivated, closed state of a Kv-channel protein within a hydrated phospholipid bilayer environment for two reasons. First, the elastic scattering experiment (neutron interferometry) is sensitive only to the time average over the dynamics inherent in such a membrane system. Second, upon embedding a particular state of the protein within the hydrated phospholipid bilayer, the protein must be allowed to relax in response to its environment within the bilayer, and conversely, the hydrated bilayer must be allowed to relax in response to the embedded protein. These processes cannot be accurately modeled using static structure representations. In Supporting Materials and Methods, Section c, we describe in detail the modeling of the activated, open and deactivated, closed states of three Kv channels in a hydrated phospholipid bilayer. These include the transmembrane domain of the eukaryotic Kv1.2/2.1 chimera, the transmembrane domain of the eukaryotic Kv1.2, and the prokaryotic KvAP. Importantly, we also describe how the atomic-level detail in the MD simulations is utilized to produce the time-averaged nSLD profiles for either the entire membrane or the nSLD profiles for the separate protein, lipid, and water components for comparison with their experimental counterparts. A portion of the MD trajectories for either the activated, open state or the deactivated, closed state of Kv channel in the hydrated POPC bilayer was selected over which the system demonstrated stability. These portions were the same length for each state and were sampled at uniform intervals to generate a number of instantaneous configurations of the system used to calculate the time-averaged nSLD profiles. For the membrane, the atom selection included the protein, water, and lipid within a cylinder of defined radius that extended from the center of the protein outward perpendicular to the transmembrane axis. Each selected atom was binned into 0.5 Å steps along the transmembrane axis for each of the sampled configurations. The neutron atomic scattering lengths were summed for each bin, and these values were averaged over all sampled configurations to construct the time-averaged nSLD profile for each state of the Kv channel. The origin was defined as the protein center of mass for each configuration. Different deuteration ratios were achieved by randomly selecting a fraction of the hydrogen atoms on water and polar hydrogens on the protein to replace with deuterium. The same approach was employed to calculate the separate time-averaged nSLD profiles for the protein, lipid, and water components of the membrane as determined by the atom selection.

For the activated, open state of both the Kv1.2/2.1 chimera and the KvAP channel in a hydrated POPC bilayer membrane, we also calculated the resolution-limited nSLD profiles of the separate protein and lipid components. This was accomplished by the least-squares fitting of slab models (21), based on a finite sum of error functions, to the time-averaged nSLD profiles for either the activated, open state of the protein or the host POPC bilayer, each hydrated with 100% D₂O. Their resolution-limited counterparts were then calculated via Fourier transformation into momentum transfer space (Q_z), followed by inverse Fourier transformation back into real space (z) at somewhat higher spatial resolution than in the experimental nSLD profiles using twice the maximal value of Q_z (i.e., 2 × 0.194 Å⁻¹) in the time-resolved neutron interferometry experiments (see Supporting Materials and Methods, Section a). Thus, the minimal wavelength component in these resolution-limited nSLD profiles is half that of the experimental nSLD profiles, allowing important visualization of the influence of somewhat finer details in the model profiles on their overall shape at the experimental spatial resolution. Linear combinations of the separate resolution-limited nSLD profiles for the activated, open state of the protein and the host POPC bilayer hydrated with D₂O were then calculated, thereby allowing for manipulation of the lipid/protein mole ratio to match that of the experimental KvAP-POPC membrane employed in the time-resolved neutron interferometry experiments. This was essential for the Kv1.2/2.1 chimera protein because the MD simulation cell contained twice the amount of POPC compared with that for the experimental KvAP-POPC membrane.

Supporting material

The analysis of the x-ray interferometry data and the time-resolved neutron interferometry data is fully described in Supporting Materials and Methods, Section a, and specimen-to-specimen reproducibility with regard to the time-resolved neutron interferometry experiments is addressed in Supporting Materials and Methods, Section b. The details of the MD simulations for modeling the activated, open state and the deactivated, closed state of three Kv channels in a hydrated POPC bilayer membrane environment, including the Kv1.2/2.1 chimera, Kv1.2, and KvAP, are described in Supporting Materials and Methods, Section c. The effect of the experimental spatial resolution on our ability to detect smaller translations of the S4 helix within the VSDs of the Kv channels associated with the transition between the activated, open state and the deactivated, closed state is described in Supporting Materials and Methods, Section d.

Results

Folding KvAP at the solid-liquid interface

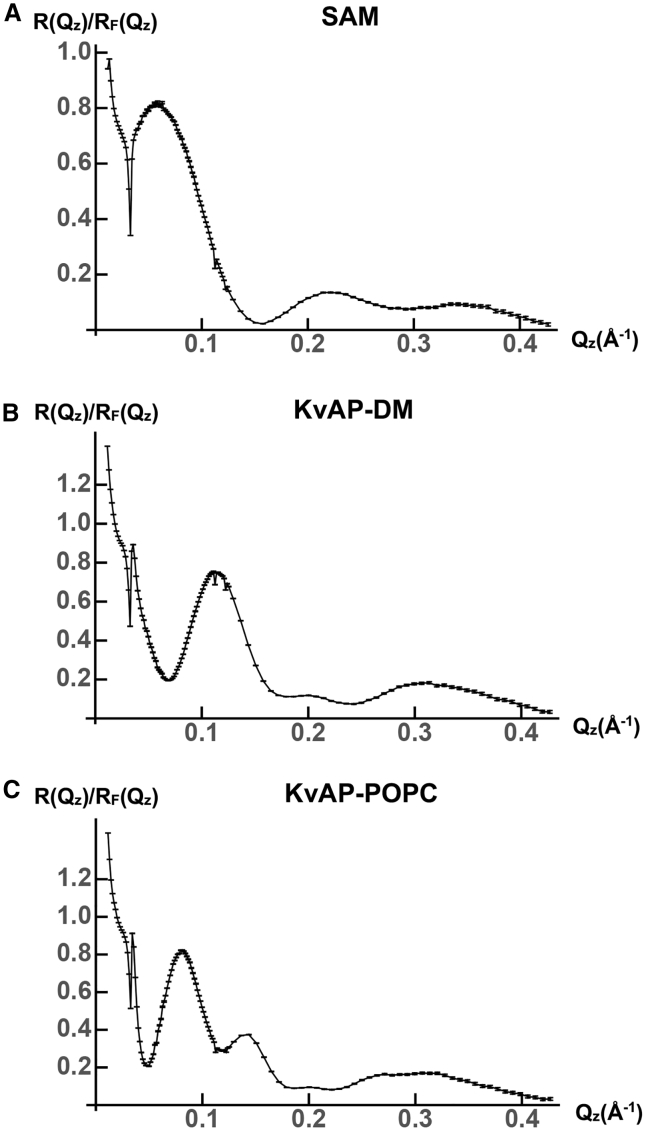
Based on a comparison of the x-ray crystal structures for the prokaryotic KvAP channel determined in a detergent micellar environment (30) and the eukaryotic Kv1.2 channel determined in a mixed phospholipid-detergent micellar environment (8), it was proposed (31) that the VSDs of KvAP would undergo refolding to form a four-helix bundle motif and a substantial reorientation of the bundle axis upon transfer from a micellar detergent environment to that of a phospholipid bilayer. Thus, we first investigated the profile structure of KvAP-DM within a monolayer tethered to the surface of an Si-Ge-Si multilayer substrate and subsequently the profile structure of the tethered KvAP-POPC membrane after detergent-phospholipid exchange employing the self-assembly method, performing x-ray interferometry after each stage of fabrication in a moist helium environment (19). Numerous specimens were investigated using both Si-Ge-Si multilayer substrates (four) as well as monolayer graphene on Si-Ge-Si multilayer substrates (four). For the latter, tethering the KvAP-DM monolayer to the graphene surface was achieved as in (32). In Fig. 1, we show typical Fresnel-normalized specular x-ray reflectivity data for the specimens on Si-Ge-Si multilayer substrates. Fig. 1 A shows the data for the substrate possessing only the organic self-assembled monolayer (SAM) used subsequently to tether the KvAP-DM monolayer to its surface, Fig. 1 B for the substrate with the tethered KvAP-DM monolayer on its surface, and Fig. 1 C for the substrate with the tethered KvAP-POPC membrane on its surface after POPC-DM exchange. The error bars are based on the photon-counting statistics. In Fig. 2 A, we show the xSLD profile for a typical KvAP-DM monolayer on the surface of either an Si-Ge-Si multilayer substrate or a monolayer graphene on Si-Ge-Si multilayer substrate using the constrained refinement approach. The horizontal dotted lines above and below the abscissa were used to estimate the propagation of errors from the reflectivity data into the xSLD profiles, described in Estimation of Error Propagation in the X-Ray and Neutron Interferometry Data Analysis. For the tethered KvAP-DM monolayers on either substrate, the xSLD profile of the monolayer occurred relatively close to the substrate’s surface. In Fig. 2 B, we show the xSLD profiles for the Si-Ge-Si multilayer substrate with the KvAP-DM monolayer on its surface compared with only the SAM on its surface. The best xSLD profile for the KvAP-DM monolayer itself is the difference of these two profiles as shown in Fig. 2 C with estimated propagated error bars as described. Also shown in Fig. 2 C, the xSLD profile for the KvAP-DM monolayer can be seen to agree fairly well with that calculated from the x-ray crystal structure from (30). All specimens for the tethered KvAP-DM monolayer exhibited similar xSLD profiles. As shown in Fig. 2 D, there is a substantial change in the xSLD profile for the KvAP-POPC membrane after exchange of POPC for DM. The membrane is further from the substrate surface, and thus, subtraction of the xSLD profile of the substrate with the SAM on its surface is not required. The estimated propagated errors are the same as for the KvAP-DM monolayer, noting the small change in ordinate scale. In Fig. 2 D, we have also superimposed the xSLD profiles calculated for the model proposed in (31), as described in Fig. 2 E, as well as for rotations of the axis of the four-helix bundle VSDs of 5°, 10°, 15°, and 20° less than the 90° rotation originally proposed. As can be seen from Fig. 2 D, a rotation by only 10° less than the 90° rotation originally proposed brings the model into close agreement with the experimental xSLD profile for the KvAP-POPC membrane dominated by the KvAP protein. Based on the estimated propagated errors in the experimental xSLD profile, we estimate that the rotation has been determined with a precision of about ±2°. In Fig. 2 F, we compare the 3-D structure for KvAP originally proposed (31) with that found in our experiments.

Figure 1.

Fresnel-normalized x-ray interferometry data R(Q_z)/R_F(Q_z) with regard to folding KvAP at the solid-liquid interface. (A) R(Q_z)/R_F(Q_z) data for the organic self-assembled monolayer (SAM) used to tether the KvAP-DM monolayer to the surface of an Si-Ge-Si multilayer substrate are shown. (B) R(Q_z)/R_F(Q_z) data for a KvAP-DM monolayer tethered to the surface of an Si-Ge-Si multilayer substrate are shown. (C) R(Q_z)/R_F(Q_z) data for a KvAP-POPC membrane tethered to the surface of the same Si-Ge-Si multilayer substrate are shown. Error bars are based on the photon-counting statistics.

A majority of the specimens exhibited xSLD profiles for the KvAP-POPC membrane as shown in Fig. 2 D, whereas a minority exhibited xSLD profiles intermediate between that for the precursor KvAP-DM monolayer and that for the KvAP-POPC membrane, suggesting incomplete exchange. EIS indicated a substantial increase in the resistance of the overlayer on the substrate’s surface upon the transformation from the tethered KvAP-DM monolayer to a tethered KvAP-POPC membrane for all specimens. The resistance of the KvAP-POPC membrane tethered to the surface of graphene was 2.3 × 10⁵–1.3 × 10⁶ Ωcm², whereas that for the membrane tethered to the surface of silicon was 1.2 × 10⁶– 4.7 × 10⁶ Ωcm². Typical EIS data are shown in Fig. S1 for the SAM on a monolayer of graphene on an Si-Ge-Si multilayer substrate in Fig. S1 A, for the KvAP-POPC membrane on the same substrate in Fig. S1 B, and for a KvAP-POPC membrane on an Si-Ge-Si substrate in Fig. S1 C, along with the best model fits to the EIS data. The model utilized one R-RC circuit to represent the substrate and a second RC circuit in series to represent the bio-organic overlayer on its surface, either the SAM or the KvAP-POPC membrane. Thus, we concluded that a properly folded KvAP homotetramer within the POPC bilayer membrane, structurally homologous with Kv1.2 and capable of sensing changes in the transmembrane voltage, had been achieved.

Time-resolved “pump-probe” neutron interferometry

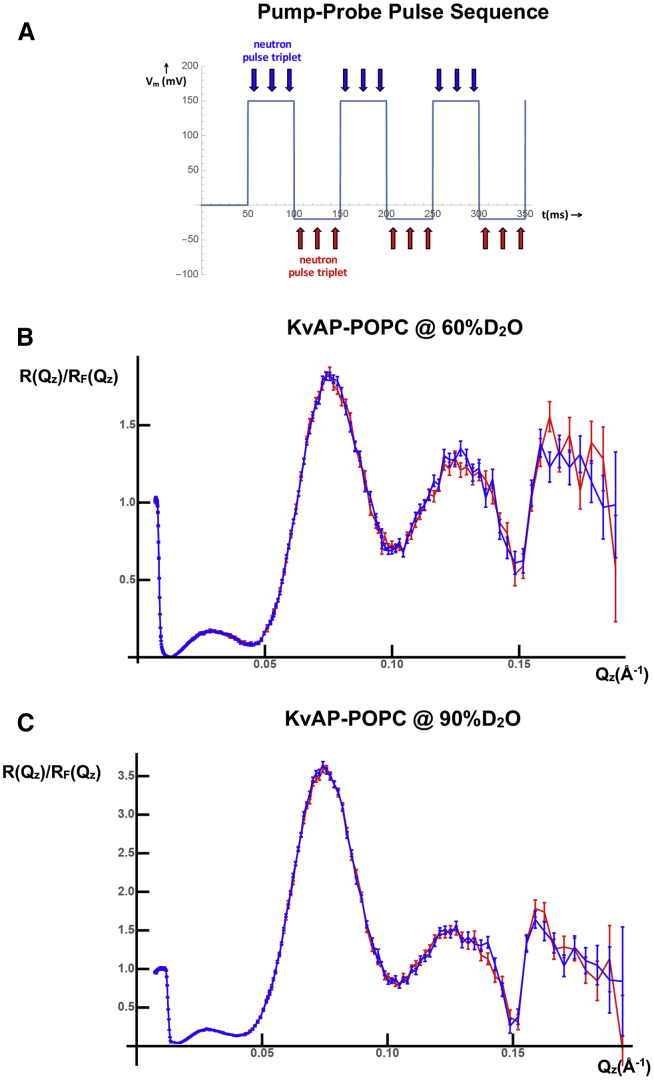
We utilized a cyclic sequence of hyperpolarizing voltage pulses of 150 mV and depolarizing voltage pulses of 20 mV, each of 50 ms duration, to circumvent inactivation of the KvAP channel ensemble within a POPC bilayer membrane. The sequence of voltage pulses and synchronized neutron pulse triplets is depicted in Fig. 3 A. The Fresnel-normalized neutron interferometry data R(Q_z)/R_F(Q_z) for one KvAP-POPC membrane (specimen S2), averaged over either the hyperpolarizing or depolarizing voltage pulses with standard errors based on the neutron counting statistics, are shown for aqueous solvent contrasts of 60% D₂O/40% H₂O in Fig. 3 B and 90% D₂O/10% H₂O in Fig. 3 C. There are experimentally significant differences in the mean of the R(Q_z)/R_F(Q_z) data that exceed the standard errors consistently over small ranges of momentum transfer Q_z for both contrasts, becoming more evident with increasing Q_z and somewhat larger for 60% D₂O/40% H₂O. Four different KvAP-POPC membrane specimens were investigated, and specimen-to-specimen reproducibility is addressed in Supporting Materials and Methods, Section b.

Figure 3.

Time-resolved “pump-probe” neutron interferometry. (A) The cyclic sequence of hyperpolarizing and depolarizing transmembrane voltage pulses, together with the triplet of incident neutron pulses utilized for each voltage (blue hyperpolarizing, red depolarizing), employed in the time-resolved neutron interferometry experiment is shown. (B) Fresnel-normalized neutron reflectivity R(Q_z)/R_F(Q_z), averaged over the hyperpolarizing voltage pulses (blue), is shown compared with that averaged over the depolarizing voltage pulses (red) for the KvAP-POPC membrane of specimen S2 at an aqueous solvent contrast of 60% D₂O/40% H₂O. (C) Similar Fresnel-normalized neutron reflectivity R(Q_z)/R_F(Q_z) is shown for the same specimen at a contrast of 90% D₂O/10% H₂O. The standard errors for each are based on the reflected neutron counting statistics.

The nSLD profiles for specimen S2 at the aqueous solvent contrasts provided by 90% D₂O/10% H₂O and 60% D₂O/40% H₂O, derived from the R(Q_z)/R_F(Q_z) data using the constrained refinement approach, are shown in Fig. 4. The nSLD profile for the Si-Ge-Si multilayer substrate occurs for z < 0 Å (data not shown), whereas the nSLD profile for the KvAP-POPC membrane occurs within the interval 30 Å < z < 110 Å with the membrane centroid located at z ∼75 Å. The nSLD profiles for the membrane appear at negative contrast with respect to the average nSLD of both electrolytes shown in Fig. 4 A (left side) for 90% D₂O and in Fig. 4 B (left side) for 60% D₂O. The changes in the membrane nSLD profiles for the hyperpolarizing versus the depolarizing voltage pulses occur within the interval 65 ± 35 Å for both contrasts. In general, they demonstrate a loss of nSLD within the extracellular half of the membrane for z > 75 Å and a gain of nSLD within the cytoplasmic half of the membrane for z < 75 Å, that exceed the estimated propagated errors, for the deactivated, closed state of the channel (hyperpolarized) relative to the activated, open state (depolarized). The difference ΔnSLD profiles, hyperpolarized minus depolarized, were calculated after superposition of the centroids of the nSLD profiles for the membrane at the maximal contrast provided by 90% D₂O for each transmembrane voltage. This was done so that the small shift in the centroid of the membrane nSLD profile for the hyperpolarizing voltage toward the substrate surface of less than 1 Å relative to that for the depolarizing voltage did not otherwise contribute to the difference ΔnSLD profiles. With this minor adjustment, the difference ΔnSLD profiles manifest the changes noted, as shown in Fig. 4 A (right side) for 90% D₂O and in Fig. 4 B (right side) for 60% D₂O, and although the changes are similar for both contrasts, they are larger for 60% D₂O. The difference ΔnSLD profile for the control specimen S1 lacking the KvAP-POPC membrane is nearly featureless on the same ordinate scale as shown in Fig. 4 C. The horizontal dashed lines above and below the abscissa in Fig. 4 C were used to estimate the propagation of errors from the reflectivity data into the ΔnSLD profiles and the nSLD profiles described in Estimation of Error Propagation in the X-Ray and Neutron Interferometry Data Analysis. The different magnitudes of the features in the ΔnSLD profiles for the different contrasts arise from H-D exchange for both water and protein within the membrane profile because POPC possesses no exchangeable hydrogens.

The double-difference profile, ΔΔnSLD, shown in Fig. 5 for 90% D₂O minus 60% D₂O and hyperpolarizing minus depolarizing voltages, provides the dependence of the H-D exchange profile on the transmembrane voltage. However, any water-accessible sites within the KvAP protein that might be unexposed for one state (e.g., deactivated, closed) and become exposed for the other state (e.g., activated, open) would all undergo H-D exchange because of cycling between the hyperpolarizing and depolarizing voltages. Hence, the double-difference profile, ΔΔnSLD, in Fig. 5 is that for only water. The double-difference profile demonstrates that water is lost from the cytoplasmic half of the membrane for z < 75 Å, especially at the surface of the cytoplasmic side of the membrane at z ∼35–45 Å, and water is gained within the extracellular half of the membrane for z ∼85–95 Å, for the deactivated, closed state of the channel (hyperpolarized) relative to the activated, open state (depolarized). In Fig. 5, the nSLD profiles at 90% D₂O (hyperpolarized and depolarized) are shown in Fig. 5 A juxtaposed above the double-difference profile ΔΔnSLD in Fig. 5 B for reference. The error bars in the double-difference profile ΔΔnSLD are $\sqrt{2}$ larger than those in the $\mathit{\Delta }$nSLD profiles, contributing to the difference described in Estimation of Error Propagation in the X-Ray and Neutron Interferometry Data Analysis.

Figure 5.

Experimental voltage-dependent profile structure for water within the KvAP-POPC membrane. (A) For reference, the nSLD(z) profiles for specimen S2 and an aqueous solvent contrast of 90% D₂O/10% H₂O from Fig. 4 are shown juxtaposed to better delineate those more relevant regions of the membrane profile exhibiting changes in the ΔnSLD(z) profile for water only (vertical arrows). (B) The double-difference ΔΔnSLD(z) profile for solvent contrasts of 90% D₂O/10% H₂O minus 60% D₂O/40% H₂O and for hyperpolarizing minus depolarizing transmembrane voltages is shown for specimen S2. The estimated errors in the double-difference ΔΔnSLD(z) profile are $\sqrt{2}$ larger than for the ΔnSLD(z) profiles shown in Fig. 4.

Note that any model for the deactivated, closed state of the Kv channel relative to the activated, open state of the channel should predict both the ΔnSLD difference profiles and the ΔΔnSLD double-difference profile from these time-resolved neutron interferometry experiments. This is because the experiments are directly sensitive to the voltage dependence of the profile structure of the Kv channel and to the voltage dependence of water within that profile structure in these single phospholipid bilayer membranes containing the vectorially oriented channel at high in-plane density. We compare several models for these two states of Kv channels in the sections that follow.

Modeling the nSLD profile for the activated, open state of the KvAP protein within a hydrated POPC bilayer membrane

We first address whether the nSLD profile structure determined for the KvAP-POPC membrane using a depolarizing transmembrane voltage to produce the activated, open state of the channel in our time-resolved neutron interferometry experiments is consistent with what is known about both the high-resolution structure of this Kv channel and the structure of a hydrated POPC bilayer. However, there is no x-ray crystal structure for a properly folded KvAP protein in the activated, open state. Instead, there is a model (31) based on a proposed structural homology for KvAP with the transmembrane domain of Kv1.2 determined by x-ray crystallography (8) employing a more “membrane-like” crystallization environment, as described in Folding KvAP at the Solid-Liquid Interface. In Supporting Materials and Methods, Section c, we describe the construction of an improved model for this state of KvAP based on the result that the isolated VSD of KvAP was shown to undergo a substantial conformational change for depolarizing transmembrane voltages compared with the absence of a voltage (23, 24). There are high-resolution x-ray crystal structures for the eukaryotic Kv channels, Kv1.2 (8) and the Kv1.2/2.1 chimera (5), with the highest resolution achieved for the latter. Given the proposed structural homology noted above, we first compare the time-averaged nSLD profile for the transmembrane domain of the Kv1.2/2.1 chimera protein in a hydrated POPC bilayer under a depolarizing transmembrane voltage from the MD simulation of (18), as described in Supporting Materials and Methods, Section c. We then compare the time-averaged nSLD profile for the improved model for KvAP in a hydrated POPC bilayer environment under a depolarizing transmembrane voltage in a MD simulation also described in Supporting Materials and Methods, Section c.

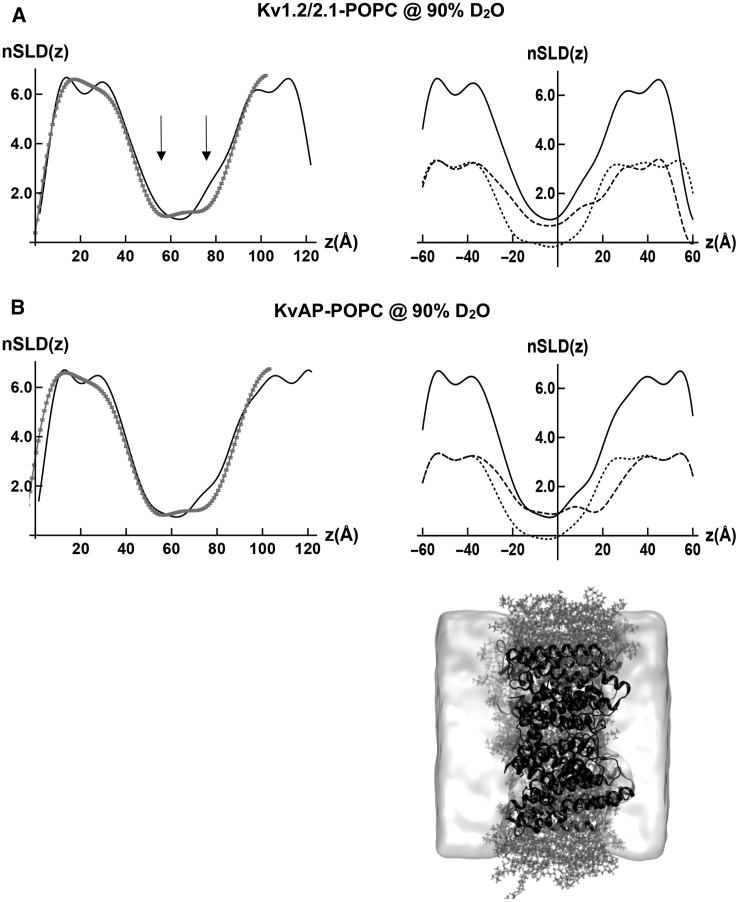
In Fig. 6 A, the left-side panel compares the time-averaged, resolution-limited nSLD profile of the activated, open state for the Kv1.2/2.1 chimera, based on the MD simulation within a hydrated POPC bilayer, with the experimental nSLD profile for the KvAP-POPC membrane at a depolarizing transmembrane voltage. The nSLD profile for the Kv1.2/2.1 chimera within a hydrated POPC bilayer was adjusted to match the lipid/protein mole ratio of the experiment. The right-side panel shows the separate resolution-limited nSLD profiles for both the Kv1.2/2.1 chimera protein and the POPC bilayer in D₂O, as well as their sum. In Fig. 6 B, the left-side panel compares the time-averaged, resolution-limited nSLD profile for the activated, open state of the KvAP protein, based on the MD simulation of the improved model within a hydrated POPC bilayer, with the experimental nSLD profile for the KvAP-POPC membrane at a depolarizing transmembrane voltage. The right-side panel shows the separate resolution-limited nSLD profiles for both the KvAP protein and the POPC bilayer in D₂O, as well as their sum.

Figure 6.

Modeling the nSLD profile for the activated, open state of KvAP in a hydrated POPC bilayer membrane. The nSLD profiles for the membranes in (A) and (B) below are at negative contrast relative to 90–100% D₂O. (A) Left side shows the experimental nSLD(z) profile for the KvAP-POPC membrane at a contrast of 90% D₂O/10% H₂O (gray) compared with that of the resolution-limited model based on MD simulation for the Kv1.2/2.1 chimera channel within a hydrated, POPC bilayer at a contrast of 100% D₂O (black) at twice the spatial resolution of the experimental profile. The two arrows point out the “double-well” shape of the experimental nSLD(z) profile. (A) Right side shows the separate contributions of the Kv1.2/2.1 protein (dashed) and the POPC bilayer (dotted) in 100% D₂O to the model profile and their sum (solid). (B) Left side shows the experimental nSLD(z) profile for the KvAP-POPC membrane at a contrast of 90% D₂O/10% H₂O (gray) compared with that of the resolution-limited model based on MD simulation of an improved model for this state of the KvAP channel within a hydrated, POPC bilayer at a contrast of 100% D₂O (black) at twice the spatial resolution of the experimental profile. (B) Right side shows the separate contributions of the KvAP protein (dashed) and the POPC bilayer (dotted) in 100% D₂O to the model profile, and their sum (solid). Juxtaposed below, we show to scale a rendering of an instantaneous configuration of the KvAP protein (black ribbon) embedded with the POPC bilayer (gray licorice) in a water slab (white shaded) from the MD simulation of the improved model for this state of the KvAP channel.

In Fig. 6 B, the time-averaged, resolution-limited nSLD profile for the activated, open state of the KvAP protein within a hydrated POPC bilayer appears to be in reasonable agreement with the “double-well” geometric shape of the experimental nSLD profile for the KvAP-POPC membrane at a depolarizing transmembrane voltage. In Fig. 6 A, there is slightly less agreement between the time-averaged, resolution-limited nSLD profile for the activated, open state of the Kv1.2/2.1 chimera protein within a hydrated POPC bilayer and the “double-well” geometric shape of the experimental nSLD profile for the KvAP-POPC membrane at a depolarizing transmembrane voltage. This is not surprising based on the structural homology between the two proteins. For both the Kv1.2/2.1 chimera in Fig. 6 A and KvAP in Fig. 6 B, the more detailed features provided by the somewhat higher spatial resolution of the nSLD profiles for the models predict that the deeper minimum of the “double-well” geometric shape occurs within the cytoplasmic half of the membrane, as exhibited by the experimental nSLD profile, but to a lesser extent. Note that the separate nSLD profiles for the host POPC bilayer component are very similar, whereas the nSLD profiles for the protein component are more different, as shown in the right-side panels. Thus, any differences in the nSLD profiles for their respective membranes arise from the protein component. Lastly, if the spatial resolution in the resolution-limited nSLD profiles is reduced to approach that of the experimental profiles, the “double-well” geometric shape exhibited by the experimental profile is reproduced.

Modeling the difference ΔnSLD profiles between the deactivated, closed state and activated, open state of the KvAP protein within a hydrated POPC bilayer membrane

We next address whether any of the three fundamentally different computational approaches to modeling the deactivated, closed state and the activated, open state of a Kv channel mentioned in the Introduction can predict the experimental difference ΔnSLD profiles for the KvAP protein within a hydrated POPC bilayer membrane. Like for the experimental KvAP-POPC membrane, the difference ΔnSLD profiles described below were all calculated as the nSLD profile for the deactivated, closed state minus that for the activated, open state, after the superposition of the membrane centroids for each state of the respective Kv channel. Furthermore, the difference ΔnSLD profiles for each of the three models were calculated from their respective MD simulations described in Supporting Materials and Methods, Section c and smoothed via convolution with a Gaussian function (σ = 5 Å).

In Fig. 7 A, we show the difference ΔnSLD profile from the experiment for the KvAP-POPC membrane, with respect to the z = 0 Å origin at the substrate surface, for an aqueous solvent contrast of 60% D₂O. We chose the higher contrast for this comparison because the signal/noise level is higher than for 90% D₂O, and the following difference ΔnSLD profiles for the models are shown at the same contrast (60% D₂O). In Fig. 7, B–D, we show the difference ΔnSLD profiles for only the Kv1.2/2.1 chimera protein, for only the Kv1.2 protein, and for only the KvAP protein, respectively. In all of the ΔnSLD profiles for only the Kv-channel proteins, the z = 0 Å origin is at the membrane centroid.

Figure 7.

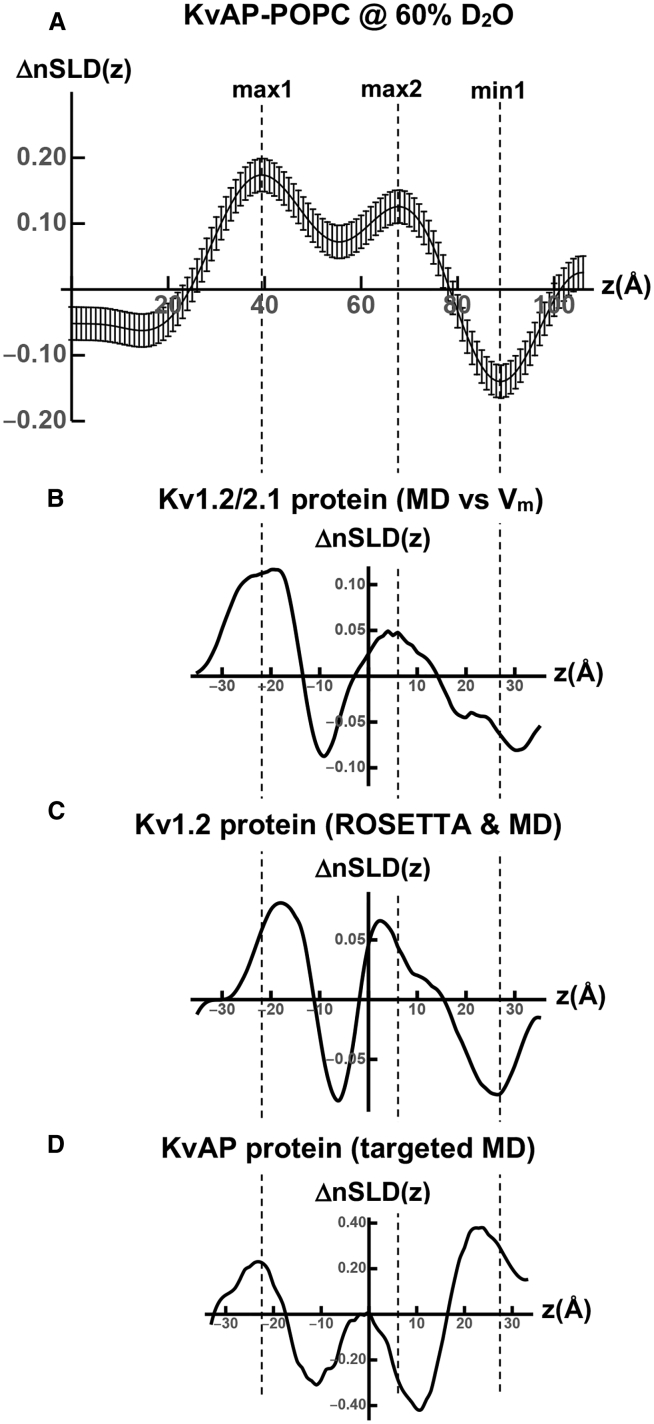
Modeling the difference ΔnSLD profile between the deactivated, closed and activated, open states of KvAP in a hydrated POPC bilayer membrane. (A) The experimental difference ΔnSLD(z) profile (hyperpolarized − depolarized) for the KvAP-POPC membrane is shown at a contrast of 60% D₂O/40% H₂O from Fig. 4B with respect to the z = 0 Å origin at the multilayer substrate surface. (B) The difference ΔnSLD(z) profile (hyperpolarized − depolarized) for the Kv1.2/2.1 protein within a hydrated POPC bilayer membrane is shown at a contrast of 60% D₂O/40% H₂O with respect to the centroid of the membrane. The difference ΔnSLD(z) profile was calculated from MD simulations that utilized transmembrane voltages (V_m) to generate the deactivated, closed and activated, open states. (C) The difference ΔnSLD(z) profile for the Kv1.2 protein within a hydrated POPC bilayer membrane is shown at a contrast of 60% D₂O/40% H₂O with respect to the centroid of the membrane. The difference ΔnSLD(z) profile was calculated from the MD simulations of ROSETTA models for the deactivated, closed and activated, open states. (D) The difference ΔnSLD(z) profile for the KvAP protein within a hydrated POPC bilayer membrane is shown at a contrast of 60% D₂O/40% H₂O with respect to the centroid of the membrane. The difference ΔnSLD(z) profile was calculated from targeted MD simulations to generate the deactivated, closed and activated, open states. The vertical dashed lines serve only to guide the eye.

There are three main features evident in the experimental difference ΔnSLD profile for the KvAP-POPC membrane shown in Fig. 7 A, namely the two maxima (max1, max2) and the minimum (min1) spanning ∼70 Å of the membrane profile. These three features are very similar to those exhibited by the Kv1.2/2.1 chimera protein in Fig. 7 B and the Kv1.2 protein in Fig. 7 C, each spanning ∼70 Å of their simulated membrane profile. The only exception is that the minimum between the two maxima within the cytoplasmic half of the membrane for the Kv1.2/2.1 and Kv1.2 proteins is much deeper than for the experimental KvAP-POPC membrane. This difference vanishes when the ΔnSLD profiles for the Kv1.2/2.1 and Kv1.2 proteins are convoluted with a broader Gaussian (e.g., σ ∼10 Å) that matches the spatial resolution of the experimental ΔnSLD profile for the KvAP-POPC membrane. The similarity noted comparing the difference ΔnSLD profiles for only the protein components of the simulated membranes for Kv1.2/2.1 and Kv1.2 suggests that the experimental difference ΔnSLD profile for the KvAP-POPC membrane is dominated by its protein component. However, despite utilizing an improved model for the activated, open state of the KvAP protein, the major features in the difference ΔnSLD profile for only the protein in Fig. 7 D differ substantially from those for the experimental KvAP-POPC membrane in Fig. 7 A, especially within the extracellular half of the membrane.

With respect to the three main features in the experimental difference ΔnSLD profile in Fig. 7 A, the larger maximum occurs near the cytoplasmic surface of the membrane separated from a second maximum within the cytoplasmic half of the membrane by 28 Å, whereas the minimum occurs within the extracellular half of the membrane separated from the first maximum by 50 Å. The two separations of these three main features are the only unique attributes of the experimental ΔnSLD profile. It is notable that the ΔnSLD profiles for both the simulated Kv1.2/2.1 chimera protein and the simulated Kv1.2 protein within their respective POPC bilayer membranes exhibit the same three features, namely two maxima and one minimum that span their respective membrane profiles. As can be seen in Table 1, in which the separations noted utilize the centroids of the features, the two unique separations for the ΔnSLD profile of the Kv1.2/2.1 chimera protein match those of the KvAP protein to within less than 1 Å. However, the two unique separations for the ΔnSLD profile of the Kv1.2 protein are 6–8 Å smaller than for the KvAP protein. Thus, the question arises as to whether our time-resolved neutron interferometry experiments could have detected these smaller separations given the relatively low spatial resolution of the experimental nSLD profiles for the KvAP-POPC membrane at hyperpolarizing and depolarizing transmembrane voltages. The answer is “yes,” as is demonstrated in Supporting Materials and Methods, Section d.

Table 1.

Separations between Features in the ΔnSLD Profiles

	Exp ΔnSLD KvAP	ΔnSLD Kv1.2/2.1	ΔnSLD Kv1.2
|Δ(max1 − max2)|	28 Å	28 Å	20 Å
|Δ(max1 − min1)|	50 Å	51 Å	44 Å

Modeling the difference ΔnSLD profile for water between the deactivated, closed state and activated, open state of the KvAP protein within a hydrated POPC bilayer membrane

Lastly, we address whether any of the three fundamentally different computational approaches to modeling the deactivated, closed state and the activated, open state of a Kv channel mentioned in the Introduction can predict the experimental difference ΔnSLD profile for water within the KvAP protein in a hydrated POPC bilayer membrane. As for the experimental KvAP-POPC membrane, the difference ΔnSLD profiles for water described below were calculated as the nSLD profile water for the deactivated, closed state minus that for the activated, open state after the superposition of the membrane centroids for each state of the respective Kv channel. Furthermore, the difference ΔnSLD profiles for water in each of the three models were calculated from their respective MD simulations described in Supporting Materials and Methods, Section c and smoothed via convolution with a Gaussian function (σ = 5 Å).

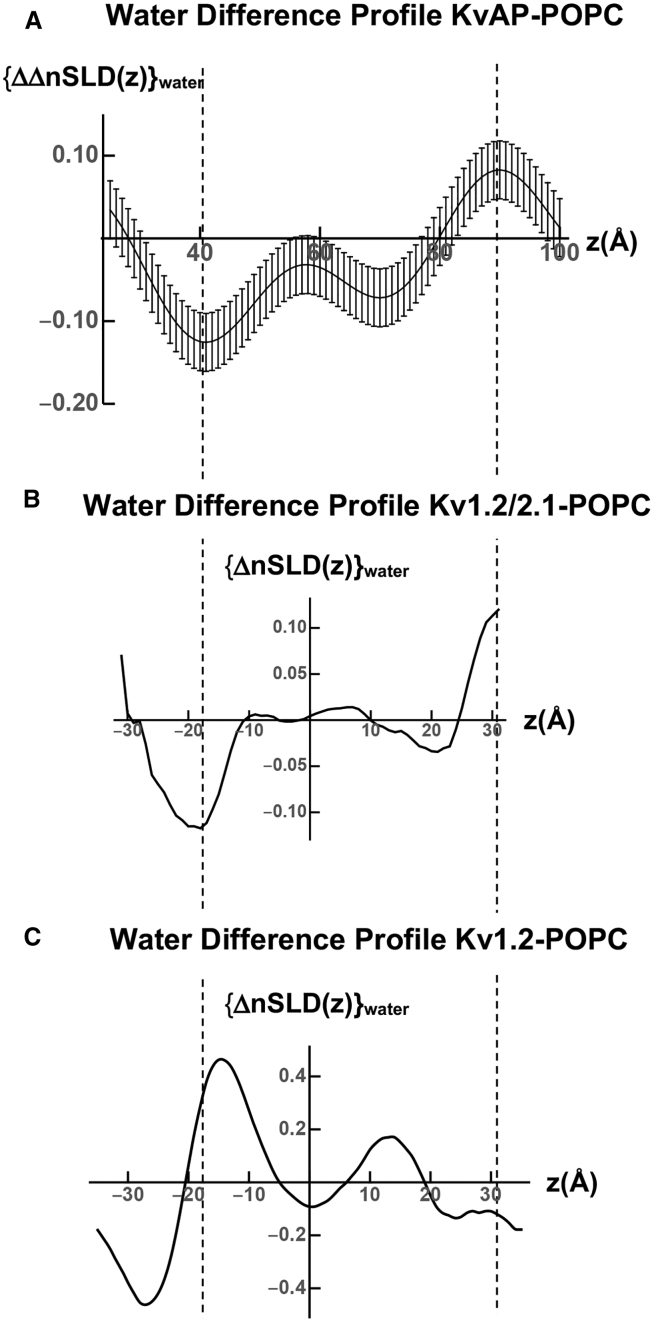
In Fig. 8 A, we show the experimental difference ΔnSLD profile for water within the KvAP-POPC membrane, namely the double-difference ΔΔnSLD profile from Fig. 5 B. In Fig. 8 B, we show the difference ΔnSLD profile for water within the transmembrane domain of the Kv1.2/2.1 protein within a hydrated POPC bilayer. The agreement between the experimental and simulated difference nSLD profiles for water is seen to be very good, particularly with regard to both the amplitudes and signs of their major features, corresponding to the loss of water from the cytoplasmic half of the membrane, nearer the membrane surface, and the gain of water within the extracellular half of the membrane, nearer the membrane surface. They differ somewhat within the interior region of the membrane profile structure in between the two membrane surfaces, with some water being lost from the interior region for KvAP versus essentially none for the transmembrane domain of the Kv1.2/2.1 chimera. In Fig. 8 C, we show the difference ΔnSLD profile for water within the Kv1.2-POPC membrane. In this case, the difference ΔnSLD profile for water within the Kv1.2-POPC membrane bears no resemblance to that for the experimental KvAP-POPC membrane in terms of both amplitudes and signs of their respective features.

Figure 8.

Modeling the difference ΔnSLD profile for water between the deactivated, closed and activated, open states of KvAP within a hydrated POPC bilayer membrane. (A) Experimental double-difference ΔΔnSLD(z) profile for water within the experimental KvAP-POPC membrane from Fig. 5B is shown. (B) The difference ΔnSLD(z) profile for water within the simulated Kv1.2/2.1-POPC membrane shown here with respect to the centroid of the nSLD profile for the membrane is shown. (C) The difference ΔnSLD(z) profile for water within the simulated Kv1.2-POPC membrane shown here with respect to the centroid of the nSLD profile is shown. The vertical dashed lines serve only to guide the eye.

Discussion

We chose to focus this investigation on the activated, open state and the deactivated, closed state of the prokaryotic KvAP channel, the endpoints of the electromechanical coupling mechanism in which all four VSDs of each channel in the ensemble are in the same fully activated or fully deactivated state. Intermediate states are also thought to play a role in the mechanism (3). Such intermediates can arise when some fraction of the four VSDs within each channel of the ensemble are either activated or deactivated. They can also arise when the VSDs are only partially activated or deactivated, with the translation of the S4 helices within the VSDs at some fraction of the maximal translation between the endpoints, e.g., 1/4, 1/2, or 3/4. We sought to avoid such intermediate states by utilizing depolarizing and hyperpolarizing transmembrane voltages whose amplitudes and duration were not only sufficient to circumvent inactivation but also sufficient to attain either full activation or deactivation of all four VSDs within each channel of the ensemble. The agreement achieved, as described in the next paragraph, suggests that we were successful.

The ΔnSLD profile for the Kv1.2/2.1 chimera protein from the MD simulations of (18) contains the effects of both a relatively large inward translation of the S4 helix within the VSDs of ∼15 Å along the membrane profile, toward the cytoplasmic side of the membrane, and the closing of the channel of the PD in response to the hyperpolarizing transmembrane voltage. We found that the large inward translation of the S4 helix within the VSDs actually dominates the ΔnSLD profile over almost its full extent for the Kv1.2/2.1 protein except for the extreme cytoplasmic side of the profile, where changes in the PD near the C-terminus of the S6 helices also make a contribution, as shown in Fig. S3. In these simulations, the hyperpolarizing voltage was much larger than in our experiments, which could have contributed to the magnitude of this translation of the S4 helices (2). The agreement in terms of both the amplitudes and positions of the major features within the experimental ΔnSLD profile for the KvAP-POPC membrane and those in the ΔnSLD profile for the Kv1.2/2.1 chimera protein itself from the MD simulation is seen to be very good in Fig. 7, as quantified in Table 1. Although the major features in the difference ΔnSLD profile for the Kv1.2 protein in Fig. 7 C are qualitatively similar to those for both the Kv1.2/2.1 chimera protein in Fig. 7 B and for KvAP within the KvAP-POPC membrane in Fig. 7 A, the separations between the three features are 6–8 Å less for the Kv1.2 protein, using the vertical dashed lines as guides in Fig. 7 and as quantified in Table 1. It is noteworthy in this regard that the ΔnSLD profile from the simulation for the Kv1.2 protein contains the effects of both a smaller inward translation of the S4 helix within the VSDs of ∼7 Å along the membrane profile, toward the cytoplasmic side of the membrane, and the closing of the channel within the PD (10). As for the Kv1.2/2.1 protein chimera, we found that the smaller inward translation of the S4 helix within the VSDs also dominates the ΔnSLD profile over almost its full extent for the Kv1.2 protein. The differences in the separations of the main features in the difference ΔnSLD profiles for the Kv1.2/2.1 chimera protein versus the Kv1.2 protein noted above indicate the sensitivity of these difference ΔnSLD profiles to the magnitude of the translation of the S4 helix within the VSDs. Importantly, our time-resolved neutron interferometry experiments would have been capable of detecting such a smaller translation of the S4 helix within the VSDs of ∼7 Å were it to have occurred in the experimental KvAP-POPC membrane despite the relatively low spatial resolution of the experiment.

Based on the comparisons of the experimental ΔnSLD profile with those for the models of the Kv1.2/2.1 chimera and Kv1.2 noted in the preceding paragraph, our time-resolved neutron interferometry experiments demonstrate directly that the magnitude of the inward translation of the S4 helix upon the transition between the activated, open state and the deactivated, closed state is ∼15 Å for KvAP. The magnitude of the translation associated with this transition for Kv channels has been controversial in the past as reviewed in (3), possibly because of the investigation of different channels in differing environments coupled with the indirect techniques utilized. Nevertheless, there are several such experiments that support a translation of this relatively large magnitude (14, 33, 34, 35).

Conclusions

We have demonstrated good agreement between the difference ΔnSLD profile (hyperpolarized minus depolarized) for the experimental KvAP-POPC membrane from our time-resolved neutron interferometry experiments and that for the transmembrane domain of the Kv1.2/2.1 chimera protein embedded within a hydrated POPC bilayer from the MD simulations of (18). This agreement indicates that the inward translation of the S4 helices within the VSDs of KvAP upon the transition between the activated, open state and the deactivated, closed state is ∼15 Å along the membrane profile. We have also demonstrated good agreement between the difference ΔnSLD profile (hyperpolarized minus depolarized) for water within the experimental KvAP-POPC membrane and that for water within the transmembrane domain of the Kv1.2/2.1 chimera protein. Thus, there is a “de-wetting” of the cytoplasmic half of the pore within the PD of KvAP associated with this transition like that predicted from the MD simulations of the Kv1.2/2.1 chimera. The other two fundamentally different computational approaches for modeling these same two states in hydrated phospholipid bilayer membranes were unable to provide agreement with both of these two key results from our time-resolved neutron interferometry experiments.

Author Contributions

A.Y.T. performed the experimental measurements (EIS, x-ray interferometry, and time-resolved neutron interferometry). L.J.M., K.C.G., and P.J.L. designed and carried out the expression and purification of the KvAP protein. H.A.A., A.A.P., and V.L. configured the hardware and software associated with the Magnetism Reflectometer at the Spallation Neutron Source to implement the time-resolved “pump-probe” neutron interferometry experiments. A.D.G. manipulated the model proposed for the 3-D structure of KvAP and calculated the corresponding xSLD profiles; constructed the models and performed MD simulations on the activated, open states for the KvAP protein within hydrated POPC bilayers; and performed MD simulations on the activated, open and deactivated, closed states for the Kv1.2 protein within hydrated POPC bilayers. J.A.F. calculated the time-averaged nSLD profiles from the coordinates provided from simulation 6 of the MD simulation for Kv1.2/2.1-T1(−). J.K.B. designed the time-resolved neutron interferometry experiments and analyzed the x-ray and neutron interferometry data. J.K.B., A.D.G., J.A.F., and D.J.T. wrote the manuscript.

Editor: Michael Grabe.

Supporting Citations

References (36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50) appear in the Supporting Material.