Statistical notes for clinical researchers: the independent samples t-test

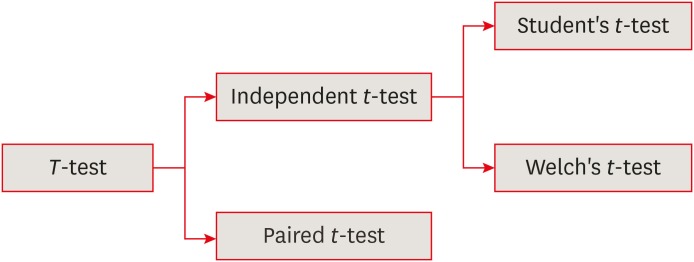
The t-test is frequently used in comparing 2 group means. The compared groups may be independent to each other such as men and women. Otherwise, compared data are correlated in a case such as comparison of blood pressure levels from the same person before and after medication (Figure 1). In this section we will focus on independent t-test only. There are 2 kinds of independent t-test depending on whether 2 group variances can be assumed equal or not. The t-test is based on the inference using t-distribution.

Figure 1. Types of 2-sample t-test.

T-DISTRIBUTION

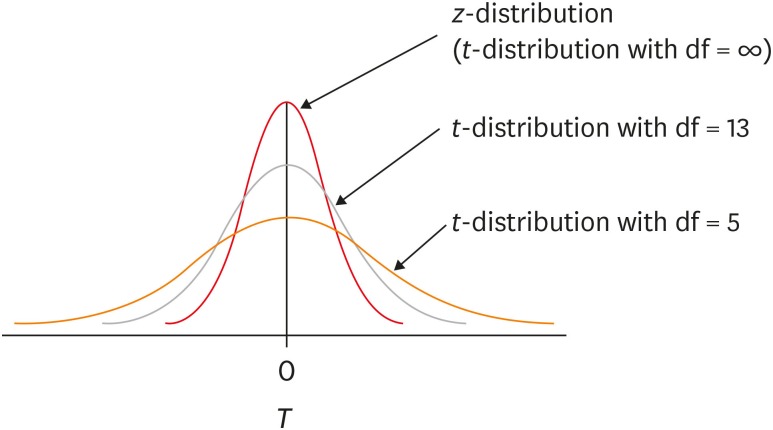
The t-distribution was invented in 1908 by William Sealy Gosset, who was working for the Guinness brewery in Dublin, Ireland. As the Guinness brewery did not permit their employee's publishing the research results related to their work, Gosset published his findings by a pseudonym, “Student.” Therefore, the distribution he suggested was called as Student's t-distribution. The t-distribution is a distribution similar to the standard normal distribution, z-distribution, but has lower peak and higher tail compared to it (Figure 2).

Figure 2. The t-distribution with various degrees of freedom (df) compared to z-distribution.

According to the sampling theory, when samples are drawn from a normal-distributed population, the distribution of sample means is expected to be a normal distribution. When we know the variance of population, σ², we can define the distribution of sample means as a normal distribution and adopt z-distribution in statistical inference. However, in reality, we generally never know σ², we use sample variance, s², instead. Although the s² is the best estimator for σ², the degree of accuracy of s² depends on the sample size. When the sample size is large enough (e.g., n = 300), we expect that the sample variance would be very similar to the population variance. However, when sample size is small, such as n = 10, we could guess that the accuracy of sample variance may be not that high. The t-distribution reflects this difference of uncertainty according to sample size. Therefore the shape of t-distribution changes by the degree of freedom (df), which is sample size minus one (n − 1) when one sample mean is tested.

The t-distribution appears to be a family of distribution of which shape varies according to its df (Figure 2). When df is smaller, the t-distribution has lower peak and higher tail compared to those with higher df. The shape of t-distribution approaches to z-distribution as df increases. When df gets large enough, e.g., n = 300, t-distribution is almost identical with z-distribution. For the inferences of means using small samples, it is necessary to apply t-distribution, while similar inference can be obtain by either t-distribution or z-distribution for a case with a large sample. For inference of 2 means, we generally use t-test based on t-distribution regardless of the sizes of sample because it is always safe, not only for a test with small df but also for that with large df.

INDEPENDENT SAMPLES T-TEST

To adopt z- or t-distribution for inference using small samples, a basic assumption is that the distribution of population is not significantly different from normal distribution. As seen in Appendix 1, the normality assumption needs to be tested in advance. If normality assumption cannot be met and we have a small sample (n < 25), then we are not permitted to use ‘parametric’ t-test. Instead, a non-parametric analysis such as Mann-Whitney U test should be selected.

For comparison of 2 independent group means, we can use a z-statistic to test the hypothesis of equal population means only if we know the population variances of 2 groups, ${\sigma }_1^2$ and ${\sigma }_2^2$, as follows;

$$Z = \frac{{\stackrel{-}{X}}_1 - {\stackrel{-}{X}}_2}{\sqrt{\frac{{\sigma }_1^2}{n_1} + \frac{{\sigma }_2^2}{n_2}}}$$ (Eq. 1)

where X̄₁ and X̄₂, ${\sigma }_1^2$ and ${\sigma }_2^2$, and n₁ and n₂ are sample means, population variances, and the sizes of 2 groups.

Again, as we never know the population variances, we need to use sample variances as their estimates. There are 2 methods whether 2 population variances could be assumed equal or not. Under assumption of equal variances, the t-test devised by Gosset in 1908, Student's t-test, can be applied. The other version is Welch's t-test introduced in 1947, for the cases where the assumption of equal variances cannot be accepted because quite a big difference is observed between 2 sample variances.

1. Student's t-test

In Student's t-test, the population variances are assumed equal. Therefore, we need only one common variance estimate for 2 groups. The common variance estimate is calculated as a pooled variance, a weighted average of 2 sample variances as follows;

$$s_p^2 = \frac{(n_1 - 1)}{\left(n_1 - 1\right)+(n_2 - 1)}{s}_1^2 + \frac{(n_2 - 1)}{\left(n_1 - 1\right)+(n_2 - 1)}{s}_2^2$$ (Eq. 2)

where $s_1^2$ and $s_2^2$ are sample variances.

The resulting t-test statistic is a form that both the population variances, ${\sigma }_1^2$ and ${\sigma }_1^2$, are exchanged with a common variance estimate, $s_{\mathrm{p}}^2$. The df is given as n₁ + n₂ − 2 for the t-test statistic.

$$t = \frac{{\stackrel{-}{X}}_1 - {\stackrel{-}{X}}_2}{\sqrt{\frac{s_p^2}{n_1} + \frac{s_p^2}{n_2}}} = \frac{{\stackrel{-}{X}}_1 - {\stackrel{-}{X}}_2}{s_p\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}~t_{(n_1 + n_2 - 2)}$$ (Eq. 3)

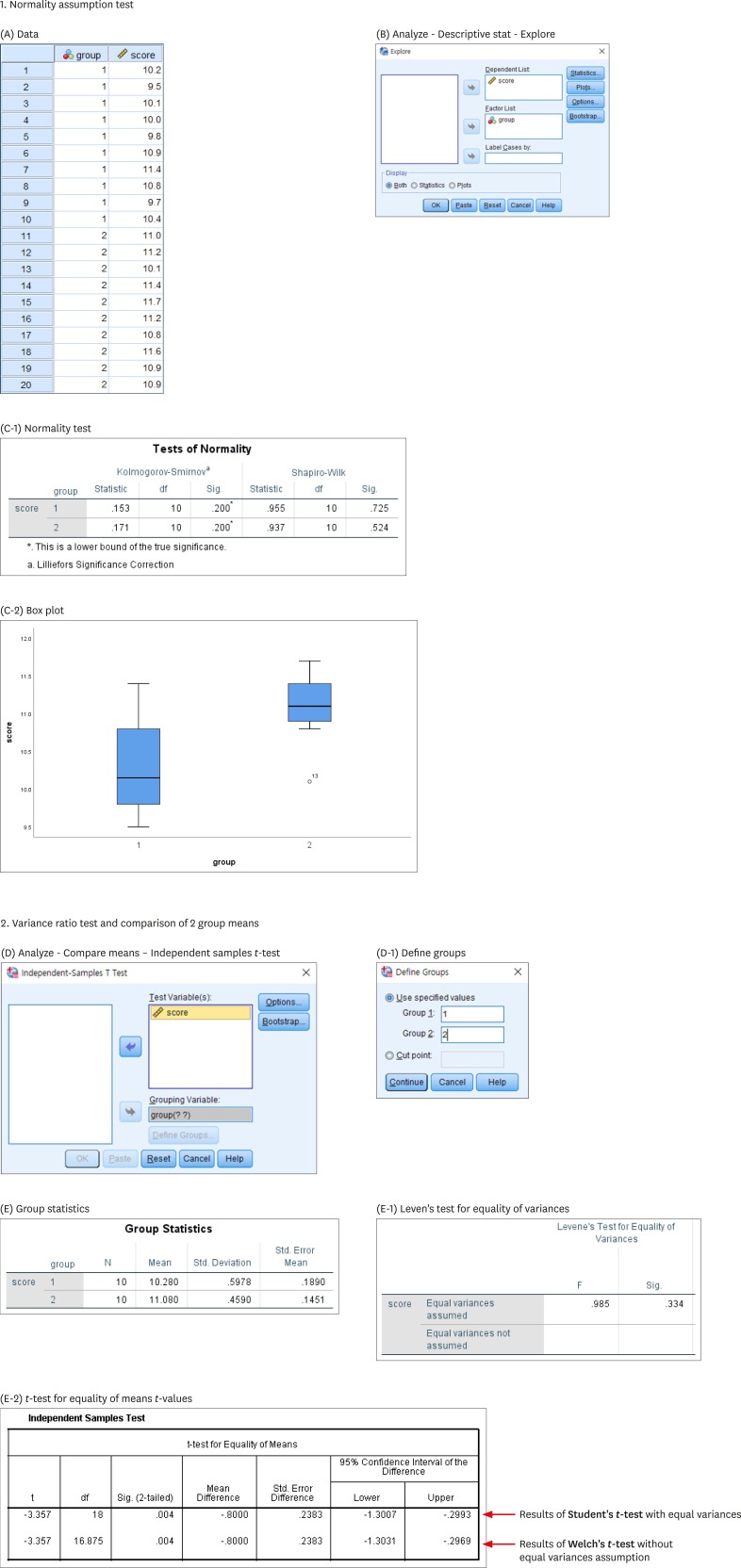
In Appendix 1, ‘(E-1) Leven's test for equality of variances’ shows that the null hypothesis of equal variances was accepted by the high p value, 0.334 (under heading of Sig.). In ‘(E-2) t-test for equality of means t-values’, the upper line shows the result of Student's t-test. The t-value and df are shown −3.357 and 18. We can get the same figures using the formulas Eq. 2 and Eq. 3, and descriptive statistics in Table 1, as follows.

Table 1. Descriptive statistics and result of the Student's t-test.

Group	No.	Mean	Standard deviation	p value
1	10	10.28	0.5978	0.004
2	10	11.08	0.4590

$$s_p^2\mathrm{ }=\mathrm{ }\frac{\left(10 - 1\right) \times {0.5978}^2 + \left(10 - 1\right) \times {0.4590}^2}{\left(10 - 1\right) + (10 - 1)} = \frac{5.1124}{18} = 0.2840 = {\left(0.5329\right)}^2$$

$$t = \frac{{\stackrel{-}{X}}_1 -{ \stackrel{-}{X}}_2}{s_p\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} = \frac{10.28 - 11.08}{0.5329\sqrt{\frac{1}{9} + \frac{1}{9}}} = \frac{-0.80}{0.2512} = -3.18$$

df = n₁ + n₂ − 2 = 10 + 10 − 2 = 18

The result of calculation is a little different from that by SPSS (IBM Corp., Armonk, NY, USA) of Appendix 1, maybe because of rounding errors.

2. Welch's t-test

Actually there are a lot of cases where the equal variance cannot be assumed. Even if it is unlikely to assume equal variances, we still compare 2 independent group means by performing the Welch's t-test. Welch's t-test is more reliable when the 2 samples have unequal variances and/or unequal sample sizes. We need to maintain the assumption of normality.

Because the population variances are not equal, we have to estimate them separately by 2 sample variances, $s_1^2$ and $s_2^2$. As the result, the form of t-test statistic is given as follows;

$$t = \frac{{\stackrel{-}{X}}_1 - {\stackrel{-}{X}}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}~t_{\nu }$$ (Eq. 4)

where ν is Satterthwaite degrees of freedom.

$$\nu = \frac{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}{{\left(\frac{s_1^2}{n_1}\right)}^2/\left(n_1 - 1\right) + {\left(\frac{s_2^2}{n_2}\right)}^2/\left(n_2 - 1\right)}$$ (Eq. 5)

In Appendix 1, ‘(E-1) Leven's test for equality of variances’ shows an equal variance can be successfully assumed (p = 0.334). Therefore, the Welch's t-test is inappropriate for this data. Only for the purpose of exercise, we can try to interpret the results of Welch's t-test shown in the lower line in ‘(E-2) t-test for equality of means t-values’. The t-value and df are shown as −3.357 and 16.875.

$$t = \frac{{\stackrel{-}{X}}_1 - {\stackrel{-}{X}}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}} = \frac{10.28 - 11.08}{\sqrt{\frac{{0.5978}^2}{10} + \frac{{0.4590}^2}{10}}} = \frac{-0.80}{0.2383} = -3.357$$

$$\upsilon = \frac{{(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2})}^2}{{\left(\frac{s_1^2}{n_1}\right)}^2/\left(n_1 - 1\right) + {\left(\frac{s_2^2}{n_2}\right)}^2/\left(n_2 - 1\right)} = \frac{{(\frac{{0.5978}^2}{10} + \frac{{0.4590}^2}{10})}^2}{\frac{{\left(\frac{{0.5978}^2}{10}\right)}^2}{10-1} + \frac{{\left(\frac{{0.4590}^2}{10}\right)}^2}{10-1}}\mathrm{ }=\mathrm{ }\frac{{0.05679}^2}{0.0001419 + 0.0000493} = \frac{.003225}{0.0001912} \cong 16.87$$

We've confirmed nearly same results by calculation using the formula and by SPSS software.

The t-test is one of frequently used analysis methods for comparing 2 group means. However, sometimes we forget the underlying assumptions such as normality assumption or miss the meaning of equal variance assumption. Especially when we have a small sample, we need to check normality assumption first and make a decision between the parametric t-test and the nonparametric Mann-Whitney U test. Also, we need to assess the assumption of equal variances and select either Student's t-test or Welch's t-test.

Appendix 1

Procedure of t-test analysis using IBM SPSS

The procedure of t-test analysis using IBM SPSS Statistics for Windows Version 23.0 (IBM Corp., Armonk, NY, USA) is as follows.