Genome-wide association analyses of risk tolerance and risky behaviors in over one million individuals identify hundreds of loci and shared genetic influences

Abstract

Humans vary substantially in their willingness to take risks. In a combined sample of over one million individuals, we conducted genome-wide association studies (GWAS) of general risk tolerance, adventurousness, and risky behaviors in the driving, drinking, smoking, and sexual domains. Across all GWAS we identified hundreds of associated loci, including 99 loci associated with general risk tolerance. We report evidence of substantial shared genetic influences across risk tolerance and the risky behaviors: 46 of the 99 general risk tolerance loci contain a lead SNP for at least one of our other GWAS, and general risk tolerance is genetically correlated ($\left|{\widehat{r}}_g\right|$ ~ 0.25 to 0.50) with a range of risky behaviors. Bioinformatics analyses imply that genes near general-risk-tolerance-associated SNPs are highly expressed in brain tissues and point to a role for glutamatergic and GABAergic neurotransmission. We found no evidence of enrichment for genes previously hypothesized to relate to risk tolerance.

INTRODUCTION:

Choices in important domains of life, including health, fertility, finance, employment, and social relationships, rarely have consequences that can be anticipated perfectly. The degree of variability in possible outcomes is called risk. Risk tolerance—defined as the willingness to take risks, typically to obtain some reward—varies substantially across humans and has been actively studied in the behavioral and social sciences. An individual’s risk tolerance may vary across domains, but survey-based measures of general risk tolerance (e.g., “Would you describe yourself as someone who takes risks?”) have been found to be good all-around predictors of risky behaviors such as portfolio allocation, occupational choice, smoking, drinking alcohol, and starting one’s own business^1–3.

Twin studies have established that various measures of risk tolerance are moderately heritable (h²~30%, although estimates in the literature vary^3–5). Discovery of specific genetic variants associated with general risk tolerance could provide insights into underlying biological pathways; advance our understanding of how genetic influences are amplified and dampened by environmental factors; enable the construction of polygenic scores (indexes of many genetic variants) that can be used as overall measures of genetic influences on individuals; and help distinguish genetic variation associated with general versus domain-specific risk tolerance.

Although risk tolerance has been one of the most studied phenotypes in social science genetics, most claims of positive findings have been based on small-sample candidate gene studies (Supplementary Table 1), whose limitations are now appreciated⁶. To date, only two loci associated with risk tolerance have been identified in genome-wide association studies (GWAS)^7,8.

Here, we report results from large-scale GWAS of self-reported general risk tolerance (our primary phenotype) and six supplementary phenotypes: “adventurousness” (defined as the self-reported tendency to be adventurous vs. cautious); four risky behaviors: “automobile speeding propensity” (the tendency to drive faster than the speed limit), “drinks per week” (the average number of alcoholic drinks consumed per week), “ever smoker” (whether one has ever been a smoker), and “number of sexual partners” (the lifetime number of sexual partners); and the first principal component (PC) of these four risky behaviors, which we interpret as capturing the general tendency to take risks across domains. All seven phenotypes are coded such that higher phenotype values are associated with higher risk tolerance or risk taking. Table 1 lists, for each GWAS, the datasets we analyzed and the GWAS sample sizes.

Table 1 |.

GWAS results

GWAS	Cohorts analyzed	n	Mean χ2	LD Score intercept (SE)	# lead SNPs	# loci	# cond. assoc.	SNP h2 (SE)
General risk tolerance (disc. GWAS)	UKB; 23andMe	939,908	1.85	1.04 (0.01)	124	99	91	0.046 (0.001)
General risk tolerance (repl. GWAS)	10 indep. cohorts	35,445	1.03	1.00 (0.07)	0	0	0	--
General risk tolerance (disc. + repl.)	UKB; 23andMe; 10 indep. cohorts	975,353	1.87	1.04 (0.01)	132	107	97	0.045 (0.001)
Adventurousness	23andMe	557,923	1.98	1.05 (0.01)	167	137	126	0.098 (0.002)
Automobile speeding propensity	UKB	404,291	1.53	1.03 (0.01)	42	36	33	0.079 (0.003)
Drinks per week	UKB	414,343	1.61	1.03 (0.01)	85	62	61	0.085 (0.003)
Ever smoker	UKB; TAG Consortium44	518,633	1.97	1.05 (0.01)	223	183	172	0.109 (0.003)
Number of sexual partners	UKB	370,711	1.77	1.04 (0.01)	117	97	88	0.128 (0.003)
First PC of the four risky behaviors	UKB	315,894	1.77	1.05 (0.01)	106	89	84	0.156 (0.004)

The table provides an overview of the GWAS of our primary and supplementary phenotypes. Replication analysis of the lead SNPs’ association results in independent cohorts was only conducted for the discovery GWAS of general risk tolerance. “n”: GWAS sample size; “Mean χ²”: mean GWAS chi-squared statistics across HapMap3 SNPs with minor allele frequency (MAF) greater than 0.01; “LD Score intercept”: estimate of the intercept from a LD Score regression¹¹ using HapMap3 SNPs with MAF greater than 0.01; “# lead SNPs”: number of approximately independent (pairwise r² < 0.1) lead SNPs; “# loci”: number of associated loci; “# cond. assoc.”: number of conditional associations in the COJO analysis¹³; “SNP h²”: SNP heritability estimated with the Heritability Estimator from Summary Statistics (HESS) method¹⁷ using 1000 Genomes phase 3 SNPs with MAF greater than 0.05; “disc.”: discovery; “repl.”: replication; “indep.”: independent.

RESULTS:

Association analyses

All seven GWAS were performed in European-ancestry subjects; included controls for the top 10 (or more) principal components of the genetic relatedness matrix and for sex and birth year (Supplementary Table 2); and followed procedures described in a pre-specified analysis plan (see URLs) and in the Supplementary Note.

In the discovery phase of our GWAS of general risk tolerance (n = 939,908), we conducted a GWAS using the UK Biobank (UKB, n = 431,126) and then performed a sample-size-weighted meta-analysis of those results with GWAS results from a sample of research participants from 23andMe (n = 508,782). The UKB measure of general risk tolerance is based on the question: “Would you describe yourself as someone who takes risks? Yes / No.” The 23andMe measure is based on a question about overall comfort taking risks, with five response options ranging from “very comfortable” to “very uncomfortable.” The genetic correlation⁹ between the UKB and 23andMe cohorts (${\widehat{r}}_g$ = 0.77, SE = 0.02) is smaller than one but high enough to justify our approach of pooling the two cohorts (see Section 2 in the Supplementary Note of ref.¹⁰ for a theoretical demonstration of the merits of pooling cohorts despite moderate heterogeneity of phenotype measures).

The Q-Q plot (Supplementary Fig. 1a) from the discovery GWAS exhibits substantial inflation (λ_GC = 1.41). According to the estimated intercept from a linkage disequilibrium (LD) Score regression¹¹, only a small share of this inflation (~5%) in test statistics is due to confounding biases such as cryptic relatedness and population stratification. To account for these biases, we inflated GWAS standard errors by the square root of the LD Score regression intercept¹².

We identified 124 approximately independent SNPs (pairwise r² < 0.1) that attained genome-wide significance (P < 5×10^–8). These 124 “lead SNPs” are listed in Supplementary Table 3 and shown in Fig. 1a. All have coefficients of determination (R²’s) below 0.02%, and the SNP with the largest per-allele effect is estimated to increase general risk tolerance by ~0.026 standard deviations in our discovery sample (Supplementary Fig. 2). To test if the lead SNPs’ effect sizes are heterogeneous across the 23andMe and UKB cohorts, we generated an omnibus test statistic by summing Cochran’s Q statistics across all lead SNPs; consistent with our genetic correlation estimate of less than unity between the two cohorts, we rejected the null hypothesis of homogeneity (P = 4.32×10^–5; Supplementary Note). To define genomic loci around the lead SNPs, we took the physical regions containing all SNPs in LD (pairwise r² > 0.6) with the lead SNPs and merged loci within 250 kb of each other; the 124 lead SNPs are located in 99 such loci (Supplementary Table 3). We supplemented those analyses with a conditional and joint multiple-SNP (COJO) analysis¹³, which identified 91 genome-wide significant “conditional associations” (Supplementary Table 3).

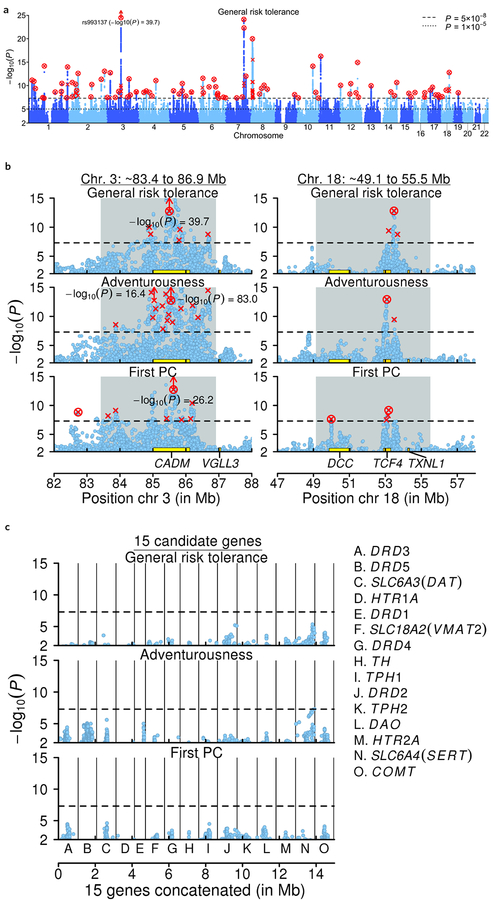
Figure 1 |. Manhattan plots.

In all panels, the x-axis is chromosomal position; the y-axis is the GWAS P value on a −log₁₀ scale (based on a two-tailed z-test); each lead SNP is marked by a red “×”; each conditional association is marked by a red “o”; and each SNP that is both a lead SNP and a conditional association is marked by a red “⊗”. a, Manhattan plots for the discovery GWAS of general risk tolerance (n = 939,908). b, Local Manhattan plots of a long-range LD region on chromosome 3 and a candidate inversion on chromosome 18 that contain lead SNPs for all seven of our GWAS. The gray background marks the locations of long-range LD or candidate inversion regions. c, Local Manhattan plots of the areas around the 15 most commonly tested candidate genes in the prior literature on the genetics of risk tolerance. Each local plot shows all SNPs within 500 kb of the gene’s borders that are in weak LD (r² > 0.1) with a SNP in the gene. The 15 plots are concatenated and shown together in the panel, divided by the black vertical lines. The 15 genes are not particularly strongly associated with general risk tolerance or the risky behaviors, as can be seen by comparing the results within each row across panels b and c (the three rows correspond to the GWAS of general risk tolerance, adventurousness (n = 557,923), and the first PC of the four risky behaviors (n = 315,894)).

In the replication phase of our GWAS of general risk tolerance (combined n = 35,445), we meta-analyzed summary statistics from ten smaller cohorts. Additional details on cohort-level phenotype measures are provided in Supplementary Table 4. The cohorts’ survey questions differ in terms of their exact wording and number of response categories, but all questions ask subjects about their overall or general attitudes toward risk. The genetic correlation⁹ between the discovery and replication GWAS is 0.83 (SE = 0.13). 123 of the 124 lead SNPs were available or well proxied by an available SNP in the replication GWAS results. Out of these 123 SNPs, 94 have a concordant sign (P = 1.7×10^–9) and 23 are significant at the 5% level in one-tailed t tests (P = 4.5×10^–8) (Supplementary Fig. 3). This empirical replication record closely matches theoretical projections that take into account sampling variation and the winner’s curse (Supplementary Note).

In the UKB we tested and confirmed that a much higher fraction of males (34%) than females (19%) described themselves as risk tolerant on the general risk tolerance measure (t-test P < 1 × 10⁻¹⁰⁰; Supplementary Fig. 4), consistent with much prior research^14,15. We used bivariate LD Score regression¹² to calculate the genetic correlation between GWAS performed separately in the sample of females and in the sample of males in the UKB. Our estimate (${\widehat{r}}_g$ = 0.822, SE = 0.033) is high enough to justify our approach of pooling males and females in our other analyses to maximize statistical power¹⁰. Nonetheless, our estimate is significantly smaller than unity, suggesting that the autosomal genetic factors contributing to general risk tolerance, while largely similar across sexes, are not identical.

Our six supplementary GWAS—of adventurousness, the four risky behaviors, and their principal component (n = 315,894 to 557,923; Supplementary Tables 4–5)—were conducted using methods comparable to those in the primary GWAS, except that they had no replication phases and most involved a single large cohort. Supplementary Fig. 1 shows Q-Q plots and Supplementary Fig. 5 shows Manhattan plots.

Table 1 provides a summary overview of the seven GWAS. We identified a total of 864 “lead associations”: the sum total of the 124 general-risk-tolerance lead SNPs together with the 740 lead SNPs from the six supplementary GWAS. (These 864 lead associations were obtained by considering each of our seven phenotypes separately and using the standard genome-wide significance P value threshold of 5×10^–8. If we instead consider the seven GWAS jointly and use a Bonferroni-corrected P value threshold of 7.1×10⁻⁹ (= 5×10⁻⁸/7), we obtain 566 lead associations across the seven GWAS.) Since we did not have the data to conduct replication analyses of the lead associations from the supplementary GWAS, we calculated the “maxFDR”¹⁶, a theoretical upper bound on the false discovery rate (FDR), for each GWAS. The maxFDR estimates were low across all GWAS (the highest estimate was 1.22×10⁻³, for automobile speeding propensity), thus providing reassurance about the robustness of the lead associations.

Applying our locus definition, we identified a total of 703 “locus associations”: the sum total of the 99 general-risk-tolerance loci together with the 604 loci from the supplementary GWAS (Supplementary Note). Pooling the loci corresponding to the 703 locus associations, and merging loci within 250 kb from each other, yields 444 distinct loci. COJO analyses¹³ identified a sum total of 655 conditional associations across all seven GWAS. (If we instead consider the seven GWAS jointly and use a Bonferroni-corrected P value threshold of 7.1×10⁻⁹ (= 5×10⁻⁸/7), we obtain 464 locus associations and 505 conditional associations across the seven GWAS.) We verified that the results of the COJO analyses are consistent with those from multiple regressions using individual-level genotype-dosage data from the UKB (Supplementary Note). Supplementary Tables 3 and 6–7 report the lead SNPs, the genomic loci, and the results of the COJO analyses. Table 1 also shows the SNP heritabilities¹⁷ of the seven phenotypes, calculated from the GWAS results; the SNP heritabilities range from ~0.05 (for general risk tolerance) to ~0.16 (for the first PC of the four risky behaviors).

We note that 212 of the 864 lead associations are located within long-range LD regions¹⁸ or candidate inversions (i.e., genomic regions that are highly prone to inversion polymorphisms; Supplementary Note). Of these, only 109 are also conditional associations, and 46 are in loci that contain no conditional associations, thus indicating that many lead associations in the long-range LD regions or candidate inversions may tag causal variants that are also tagged by other lead associations. We discuss some of these regions in the next section.

Genetic overlap

There is substantial overlap across the results of our GWAS. For example, 46 of the 99 general-risk-tolerance loci contain a lead SNP of at least one of the other GWAS, and 72 of the 124 general-risk-tolerance lead SNPs are in weak LD (pairwise r² > 0.1) with a lead SNP of at least one of the other GWAS (including 45 for adventurousness and 49 for at least one of the four risky behaviors or their first PC). To empirically assess if this overlap could be attributed to chance, we conducted resampling exercises under the null hypothesis that the lead SNPs of our supplementary GWAS are distributed independently of the general-risk-tolerance loci and lead SNPs. We strongly rejected this null hypothesis (P < 0.0001; Supplementary Note).

Several long-range LD regions, candidate inversions, and LD blocks¹⁹ stand out for being associated both with general risk tolerance and with all or most of the supplementary phenotypes. We tested whether the signs of the lead SNPs located in these regions tend to be concordant across our primary and supplementary GWAS. We strongly rejected the null hypothesis of no concordance (P < 3×10^–30; Supplementary Note), suggesting that these regions represent shared genetic influences, rather than colocalization of causal SNPs. Fig. 1b and Supplementary Fig. 6 show local Manhattan plots for some of these long-range LD regions and candidate inversions. The long-range LD region¹⁸ on chromosome 3 (~83.4 to 86.9 Mb) contains lead SNPs from all seven GWAS as well as the most significant lead SNP from the general-risk-tolerance GWAS, rs993137 (P = 2.14×10^–40), which is located in the gene CADM2. Another long-range LD region, on chromosome 6 (~25.3 to 33.4 Mb), covers the HLA-complex and contains lead SNPs from all GWAS except drinks per week. Three candidate inversions on chromosomes 7 (~124.6 to 132.7 Mb), 8 (~7.89 to 11.8 Mb), and 18 (~49.1 to 55.5 Mb) contain lead SNPs from six, five, and all seven of our GWAS, respectively. Finally, four other LD blocks¹⁹ that do not overlap known long-range LD or candidate inversion regions each contain lead SNPs from five of our GWAS (including general risk tolerance). While many of the lead SNPs in these regions are not conditional associations, the above results regarding the numbers of GWAS with lead SNPs in these regions also hold if we only consider the conditional associations instead of the lead SNPs in those regions. The two long-range LD regions and the three candidate inversions have previously been found to be associated with numerous phenotypes, including many cognitive and neuropsychiatric phenotypes²⁰.

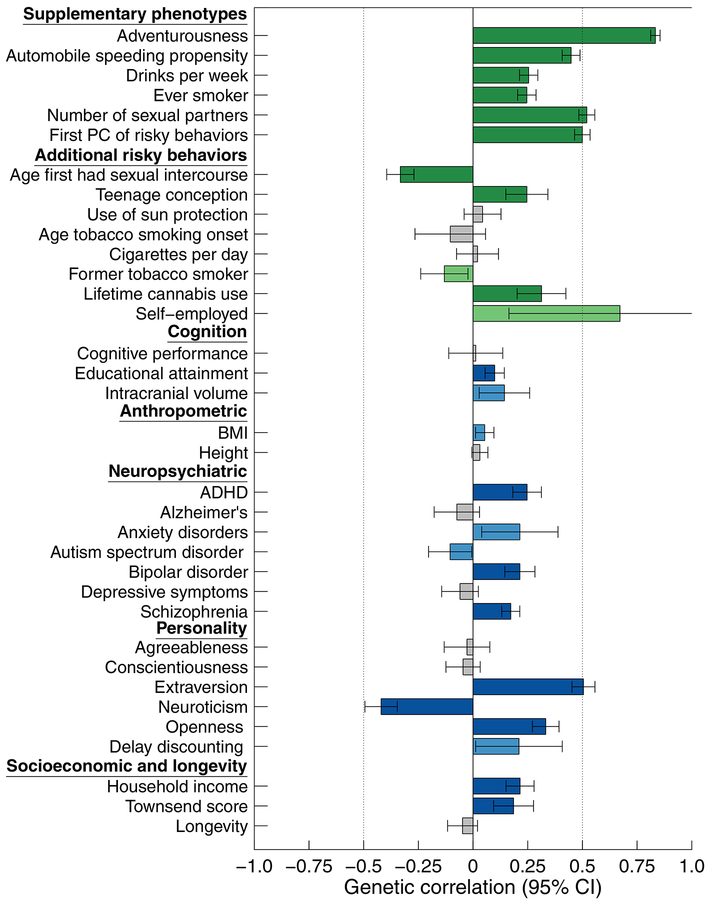
To investigate genetic overlap at the genome-wide level, we estimated genetic correlations with self-reported general risk tolerance using bivariate LD Score regression⁹. (For this and all subsequent analyses involving general risk tolerance, we used the summary statistics from the combined meta-analysis of our discovery and replication GWAS.) The estimated genetic correlations with our six supplementary phenotypes are all positive, larger than ~0.25, and highly significant (P < 2.3×10^–30; Fig. 2), indicating that SNPs associated with higher general risk tolerance also tend to be associated with riskier behavior. The largest estimated genetic correlations are with adventurousness (${\widehat{r}}_g$ = 0.83, SE = 0.01), number of sexual partners (0.52, SE = 0.02), automobile speeding propensity (0.45, SE = 0.02), and the first PC of the four risky behaviors (0.50, SE = 0.02).

Figure 2 |. Genetic correlations with general risk tolerance.

The genetic correlations were estimated using bivariate LD Score (LDSC) regression⁹. Error bars show 95% confidence intervals. For the supplementary phenotypes and the additional risky behaviors, green bars represent significant estimates with the expected signs, where higher risk tolerance is associated with riskier behavior. For the other phenotypes, blue bars represent significant estimates. Light green and light blue bars represent genetic correlations that are statistically significant at the 5% level, and dark green and dark blue bars represent correlations that are statistically significant after Bonferroni correction for 35 tests (the total number of phenotypes tested). Grey bars represent correlations that are not statistically significant at the 5% level. The two dotted vertical lines indicate genetic correlations of −0.5 and 0.5, respectively. All significance tests are two-sided.

Our estimates of the genetic correlations between general risk tolerance and the supplementary risky behaviors are substantially higher than the corresponding phenotypic correlations (Supplementary Tables 8 and 9). Although measurement error partly accounts for the low phenotypic correlations, the genetic correlations remain considerably higher even after adjustment of the phenotypic correlations for measurement error. The comparatively large genetic correlations support the view that a general factor of risk tolerance partly accounts for cross-domain correlation in risky behavior^21,22 and imply that this factor is genetically influenced. The lower phenotypic correlations suggest that environmental factors are more important contributors to domain-specific risky behavior^23,24.

To increase the precision of our estimates of the SNPs’ effects on general risk tolerance, we leveraged the high degree of genetic overlap across our phenotypes by conducting Multi-Trait Analysis of GWAS (MTAG)¹⁶. We used as inputs the summary statistics of our GWAS of general risk tolerance, of our first five supplementary GWAS (i.e., not including the first PC of the four risky behaviors), and of a previously published GWAS on lifetime cannabis use²⁵ (Supplementary Note). MTAG increased the number of general-risk-tolerance lead SNPs from 124 to 312 (Supplementary Fig. 7 and Supplementary Table 10).

We also estimated genetic correlations between general risk tolerance and 28 additional phenotypes (Fig. 2 and in Supplementary Table 9). These included phenotypes for which we could obtain summary statistics from previous GWAS, as well as five phenotypes for which we conducted new GWAS. The estimated genetic correlations for the personality traits extraversion (${\widehat{r}}_g$ = 0.51, SE = 0.03), neuroticism (–0.42, SE = 0.04), and openness to experience (0.33, SE = 0.03) are significantly distinguishable from zero after Bonferroni correction and are substantially larger in magnitude than previously reported phenotypic correlations²⁶, pointing to shared genetic influences among general risk tolerance and these traits. After Bonferroni correction, we also found significant positive genetic correlations with the neuropsychiatric phenotypes ADHD, bipolar disorder, and schizophrenia. Viewed in light of the genetic correlations we found with some supplementary phenotypes and additional risky behaviors classified as externalizing (e.g., substance use, elevated sexual behavior, and fast driving), these results suggest the hypothesis that the overlap with the neuropsychiatric phenotypes is driven by their externalizing component²⁷.

Polygenic prediction

We constructed polygenic scores of general risk tolerance to gauge their potential usefulness in empirical research (Supplementary Note). We used the Add Health, HRS, NTR, STR, UKB-siblings, and Zurich cohorts as validation cohorts (Supplementary Table 5 provides an overview of these cohorts; the UKB-siblings cohort comprised individuals with at least one full sibling in the UKB). For each validation cohort, we constructed the score using summary statistics from a meta-analysis of our discovery and replication GWAS that excluded the cohort (for the UKB-siblings cohort, we reran our UKB GWAS after excluding individuals from that cohort). Our measure of predictive power is the incremental R² (or pseudo-R²) from adding the score to a regression of the phenotype on controls for sex, birth year, and the top ten principal components of the genetic relatedness matrix.

Our preferred score was constructed with LDpred²⁸. Our largest validation cohort (n ~ 35,000) is the UKB-siblings cohort. In that validation cohort, the score’s predictive power is 1.6% for general risk tolerance, 1.0% for the first PC of the four risky behaviors, 0.8% for number of sexual partners, 0.6% for automobile speeding propensity, and ~0.15% for drinks per week and ever smoker. Across our validation cohorts, in which other phenotypes are measured, the score is also predictive of several personality phenotypes and a suite of real-world measures of risky behaviors in the health, financial, career, and other domains (Supplementary Figs. 8–9 and Supplementary Tables 11–14). The incremental R² we observe for general risk tolerance is consistent with our theoretical prediction, given the GWAS sample sizes, the SNP heritability of general risk tolerance (Table 1), and the imperfect genetic correlations across the GWAS and validation cohorts^29,30 (Supplementary Note).

Biological annotation

To gain insights into the biological mechanisms through which genetic variation influences general risk tolerance, we conducted a number of bioinformatics analyses using the results of the combined meta-analysis of our discovery and replication GWAS of general risk tolerance.

First, we systematically reviewed the literature that aimed to link risk tolerance to biological pathways (Supplementary Note). Our review covered studies based on candidate genes (i.e., specific genetic variants used as proxies for biological pathways), pharmacological manipulations, biochemical assays, genetic manipulations in rodents, as well as other research designs. Our review identified 132 articles that matched our search criteria (Supplementary Table 1). This previous work has focused on five main biological pathways: the steroid hormone cortisol, the monoamines dopamine and serotonin, and the steroid sex hormones estrogen and testosterone. Using a MAGMA³¹ competitive gene-set analysis, we found no evidence that SNPs within genes associated with these five pathways tend to be more associated with general risk tolerance than SNPs in other genes (Supplementary Table 15). Furthermore, none of the other bioinformatics analyses we report below point to these pathways.

We also examined the 15 most commonly tested autosomal genes within the dopamine and serotonin pathways, which were the focus of most of the 34 candidate-gene studies identified by our literature review. We verified that the SNPs available in our GWAS results tag most of the genetic variants typically used to test the 15 genes. Across one SNP-based test and two gene-based tests, we found no evidence of non-negligible associations between those genes and general risk tolerance (Fig. 1c and Supplementary Table 16). (We note, however, that some brain regions identified in analyses we report below are areas where dopamine and serotonin play important roles.)

Second, we performed a MAGMA³¹ gene analysis to test each of ~18,000 protein-coding genes for association with general risk tolerance (Supplementary Note). After Bonferroni correction, 285 genes were significant (Supplementary Fig. 10 and Supplementary Table 17). To gain insight into the functions and expression patterns of these 285 genes, we looked them up in the Gene Network³² co-expression database.

Third, to identify relevant biological pathways and identify tissues in which genes near general-risk-tolerance-associated SNPs are expressed, we applied the software tool DEPICT³³ to the SNPs with P values less than 10^–5 in our GWAS of general risk tolerance (Supplementary Note).

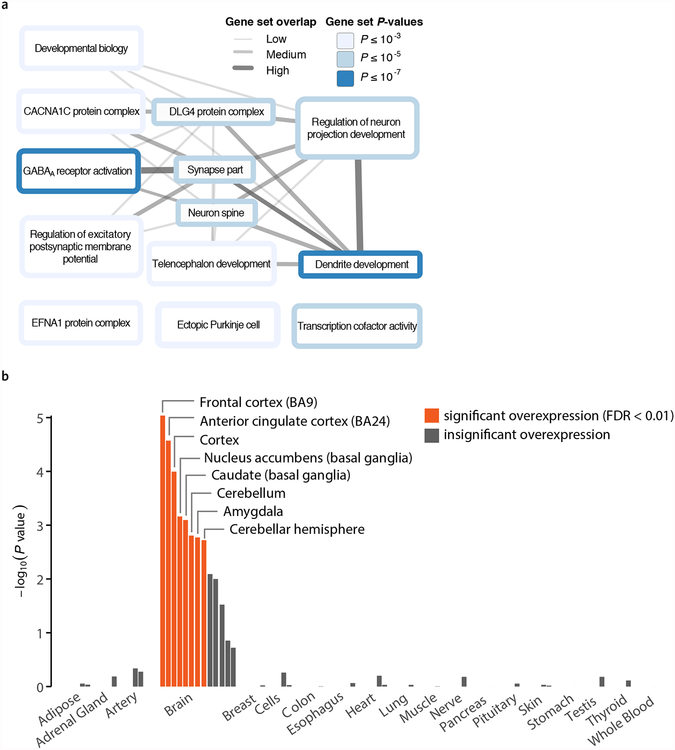
Both the Gene Network and the DEPICT analyses separately point to a role for glutamate and GABA neurotransmitters, which are the main excitatory and inhibitory neurotransmitters in the brain, respectively³⁴ (Fig. 3a and Supplementary Tables 18 and 19). To our knowledge, with the exception of a recent study³⁵ prioritizing a much larger number of genes and pathways, no published large-scale GWAS of cognition, personality, or neuropsychiatric phenotypes has pointed to clear roles both for glutamate and GABA (although glutamatergic neurotransmission has been implicated in recent GWAS of schizophrenia³⁶ and major depression³⁷). Our results suggest that the balance between excitatory and inhibitory neurotransmission may contribute to variation in general risk tolerance across individuals.

Figure 3 |. Results from selected biological analyses.

a, DEPICT gene-set enrichment diagram. We identified 93 reconstituted gene sets that are significantly enriched (FDR < 0.01) for genes overlapping DEPICT-defined loci associated with general risk tolerance; using the Affinity Propagation method⁴³, these were grouped into the 13 clusters displayed in the graph. Each cluster was named after its exemplary gene set, as chosen by the Affinity Propagation tool, and each cluster’s color represents the permutation P value of its most significant gene set. The “synapse part” cluster includes the gene set “glutamate receptor activity,” and several members of the “GABA_A receptor activation” cluster are defined by gamma-aminobutyric acid signaling. Overlap between the named representatives of two clusters is represented by an edge. Edge width represents the Pearson correlation ρ between the two respective vectors of gene membership scores (ρ < 0.3, no edge; 0.3 ≤ ρ < 0.5, thin edge; 0.5 ≤ ρ < 0.7, intermediate edge; ρ ≥ 0.7, thick edge). b, Results of DEPICT tissue enrichment analysis using GTEx data. The panel shows whether the genes overlapping DEPICT-defined loci associated with general risk tolerance are significantly overexpressed (relative to genes in random sets of loci matched by gene density) in various tissues. Tissues are grouped by organ or tissue type. The orange bars correspond to tissues with significant overexpression (FDR < 0.01). The y-axis is the significance on a −log₁₀ scale. See Supplementary Note for additional details.

The Gene Network and the DEPICT tissue enrichment analyses also both separately point to enrichment of the prefrontal cortex and the basal ganglia (Fig. 3b and Supplementary Tables 18, 20, and 21). The cortical and subcortical regions highlighted by DEPICT include some of the major components of the cortical-basal ganglia circuit, which is known as the reward system in human and non-human primates and is critically involved in learning, motivation, and decision-making, notably under risk and uncertainty^38,39. We caution, however, that our results do not point exclusively to the reward system.

Lastly, we used stratified LD Score regression⁴⁰ to test for the enrichment of SNPs associated with histone marks in 10 tissue or cell types (Supplementary Note). Central nervous system tissues are the most enriched, accounting for 44% (SE = 3%) of the heritability while comprising only 15% of the SNPs (Supplementary Fig. 11a and Supplementary Table 22). Immune/hematopoietic tissues are also significantly enriched. While a role for the immune system in modulating risk tolerance is plausible given prior evidence of its involvement in several neuropsychiatric disorders^36,37, future work is needed to confirm this result and to uncover specific pathways that might be involved.

DISCUSSION:

Our results provide insights into biological mechanisms that influence general risk tolerance. Our bioinformatics analyses point to the role of gene expression in brain regions that have been identified by neuroscientific studies on decision-making, notably the prefrontal cortex, basal ganglia, and midbrain, thereby providing convergent evidence with that from neuroscience^38,39. Yet our analyses failed to find evidence for the main biological pathways that had been previously hypothesized to influence risk tolerance. Instead, our analyses implicate genes involved in glutamatergic and GABAergic neurotransmission, which were heretofore not generally believed to play a noteworthy role in risk tolerance.

Although our focus has been on the genetics of general risk tolerance and risky behaviors, environmental and demographic factors account for a substantial share of these phenotypes’ variation. We observe sizeable effects of sex and age on general risk tolerance in the UKB data (Supplementary Fig. 4), and life experiences have been shown to affect both measured risk tolerance and risky behaviors (e.g., refs.^41,42). The GWAS results we have generated will allow researchers to construct and use polygenic scores of general risk tolerance to measure how environmental, demographic, and genetic factors interact with one another.

For the behavioral sciences, our results bear on an ongoing debate about the extent to which risk tolerance is a “domain-general” as opposed to a “domain-specific” trait. Low phenotypic correlations in risk tolerance across decision-making domains have been interpreted as supporting the domain-specific view^23,24. Across the risky behaviors we study, we found that the genetic correlations were considerably higher than the phenotypic correlations (even after the latter are corrected for measurement error) and that many lead SNPs are shared across our phenotypes. These observations suggest that the low phenotypic correlations across domains are due to environmental factors that dilute the effects of a genetically-influenced domain-general factor of risk tolerance.

URLs.

Publicly archived analysis plan for this project, https://osf.io/cjx9m/;

Social Science Genetic Association Consortium (SSGAC), https://www.thessgac.org/data;

BCFtools, https://samtools.github.io/bcftools/bcftools.html;

BEAGLE, http://faculty.washington.edu/browning/beagle/b3.html;

BOLT-LMM v.2.3.2, https://data.broadinstitute.org/alkesgroup/BOLT-LMM/;

DEPICT (Retrieved Feb 2015), https://data.broadinstitute.org/mpg/depict/;

EasyQC v9.0, http://www.uni-regensburg.de/medizin/epidemiologie-praeventivmedizin/genetische-epidemiologie/software/;

GCTA, http://cnsgenomics.com/software/gcta;

HESS, http://bogdan.bioinformatics.ucla.edu/software/hess/;

IMPUTE2, http://mathgen.stats.ox.ac.uk/impute/impute_v2.html;

IMPUTE4, https://jmarchini.org/impute-4/;

LD Score Regression (ldsc), https://github.com/bulik/ldsc/;

LDpred, https://bitbucket.org/bjarni_vilhjalmsson/ldpred;

Mach2QTL, http://csg.sph.umich.edu/yli/mach/download/mach2qtl.source.V112.tgz;

MAGMA, https://ctg.cncr.nl/software/magma;

Minimac2, https://genome.sph.umich.edu/wiki/Minimac2;

MTAG software, https://github.com/omeed-maghzian/mtag;

PBWT, https://github.com/richarddurbin/pbwt;

PLINK, http://zzz.bwh.harvard.edu/plink/plink2.shtml;

Python v2.7, https://www.python.org/download/releases/2.7/;

QCtool v2, http://www.well.ox.ac.uk/~gav/qctool_v2/;

R, https://www.r-project.org/;

REGSCAN v0.2.0, https://www.geenivaramu.ee/en/tools/regscan;

Rstudio, https://www.rstudio.com/;

ShapeIT, http://mathgen.stats.ox.ac.uk/genetics_software/shapeit/shapeit.html;

SMR, https://cnsgenomics.com/software/smr/;

SNPTEST, https://mathgen.stats.ox.ac.uk/genetics_software/snptest/snptest.html;

Stata v14.2, https://www.stata.com/install-guide/windows/download/.

ONLINE METHODS:

This article is accompanied by a Supplementary Note with further details. Further information on experimental design is also available in the Life Sciences Reporting Summary linked to this article.

Phenotype definitions, GWAS, quality control, and meta-analysis

For our discovery GWAS of general risk tolerance (n = 939,908), we performed a sample-size-weighted meta-analysis of results from the UK Biobank (UKB, n = 431,126) and a sample of research participants from 23andMe (n = 508,782). For our replication GWAS of general risk tolerance (n = 35,445), we performed a sample-size-weighted meta-analysis of results from ten smaller cohorts from seven studies: Army STARRS, BASE-II, NFBC 1966, RSIII, STR, UKHLS, and VIKING. The exact measures for the general risk tolerance phenotype vary across cohorts in wording and number of response categories, but all measures are similar and ask about one’s tendency, preparedness, or willingness to take risks in general (Supplementary Table 4).

For our GWAS of adventurousness, we analyzed data from a sample of research participants from 23andMe (n = 557,923). We analyzed responses to the question: “If forced to choose, would you consider yourself to be more cautious or more adventurous?”, with possible responses ranging from “[1] Very cautious” to “[5] Very adventurous.” For our GWAS of three of the four risky behaviors—automobile speeding propensity (n = 404,291), drinks per week (n = 414,343), and number of sexual partners (n = 370,711)—and for the first principal component (PC) of the four risky behaviors (n = 315,894), we analyzed UKB data. For the remaining risky behavior, ever smoker (n = 518,633), we meta-analyzed GWAS results from the UKB and from the TAG Consortium⁴⁴. Our automobile speeding propensity phenotype is based on responses to the question: “How often do you drive faster than the speed limit on the motorway?”, with possible responses ranging from “[1] Never/rarely” to “[4] Most of the time.” We dropped individuals who answered “[5] Do not drive on the motorway,” and then we normalized the categorical variable for males and females separately. Our drinks per week phenotype was constructed based on responses to a series of questions about drinking habits and is defined as the number of alcoholic drinks consumed per week. Our ever-smoker phenotype in the UKB is a dummy variable that equals one if a respondent reported being a current or previous smoker and zero if the respondent reported never smoking or only smoking once or twice; our ever smoker phenotype from the TAG Consortium is the Consortium’s “smoking initiation” phenotype (which TAG also refers to as “ever versus never regular smoker”)⁴⁴. Our number of sexual partners phenotype is based on responses to the question: “About how many sexual partners have you had in your lifetime?”; respondents who reported more than 99 lifetime sexual partners were asked to confirm their responses. We assigned a value of zero to participants who reported having never had sex, and we again normalized this measure separately for males and females. Our first PC phenotype is the first PC obtained from a principal component analysis (PCA) in the UKB of the four risky behaviors (Supplementary Table 23). All seven phenotypes were coded such that higher phenotype values are associated with higher risk tolerance or risk taking. Table 1 lists, for each GWAS, the datasets we analyzed and the GWAS sample size. The Supplementary Note and Supplementary Tables 4 and 5 provide additional details on the cohorts and phenotype definitions.

All GWAS were performed at the cohort level in European-ancestry subjects according to a pre-specified and publicly archived analysis plan (see URLs). All GWAS included controls for the top 10 (or more) principal components of the genetic relatedness matrix and for sex and birth year. Genotyping was performed using a range of commercially available genotyping arrays. We applied extensive quality-control (QC) procedures to the cohort-level summary statistics, including but not limited to the EasyQC protocol developed by the GIANT consortium⁴⁵. We used Haplotype Reference Consortium v1.1 (HRC) data to construct our main reference panel, which we used for quality control of the GWAS summary statistics and to determine the independence of significant loci. For the 23andMe and UKB cohorts, only SNPs with minor allele frequency (MAF) greater than 0.001 were analyzed. All meta-analyses were restricted to SNPs with a sample size greater than half of the maximum sample size across all the SNPs in the GWAS. In total, 9,284,738 SNPs were analyzed in the discovery GWAS of general risk tolerance; 9,339,358 SNPs were analyzed in the GWAS of adventurousness; and ~11,515,000 SNPS were analyzed in the GWAS of the four risky behaviors and their first PC. To adjust standard errors for the possible effects of population stratification, we inflated them by the square root of the estimated intercept from an LD Score regression¹² (for the replication GWAS of general risk tolerance, which meta-analyzed different cohorts, we inflated them at the meta-analysis level). Additional details are provided in the Supplementary Note and Supplementary Tables 2 and 24–26.

To identify approximately independent lead SNPs, we applied to the GWAS results a clumping algorithm. Our clumping algorithm begins by selecting the SNP with the lowest P value as the lead SNP in the first clump, and includes in the first clump all SNPs that have r² greater than 0.1 with the lead SNP and that have GWAS P value less than 1×10^–4. Next, the SNP with the second-lowest P value outside the first clump becomes the lead SNP of the second clump, and the second clump is created analogously but using only the SNPs outside of the first clump. This process continues until every genome-wide significant SNP (i.e., every SNP with a GWAS P value less than 5×10^–8) is either designated as a lead SNPs or is clumped to another lead SNP. We also defined non-overlapping, continuous genomic loci around the lead SNPs using Ripke et al.’s⁴⁶ locus definition, and we performed conditional and joint multiple-SNP analyses (COJO)¹³. Ripke et al. defined a locus as “the physical region containing all SNPs correlated at r² > 0.6 with [one of the lead] SNPs”, and merged associated loci within 250 kb of each other. To define the set of distinct loci that contain all the loci corresponding to the locus associations from across the seven GWAS, we pooled the loci corresponding to the locus associations and merged loci within 250 kb from each other. For the COJO analyses, for each of the seven main GWAS we restricted the analysis to the set of SNPs that (1) pass all GWAS quality control filters, and (2) are located within the loci of the phenotype (which includes all of the lead SNPs).

Supplementary Tables 3, 6, 7, and 27 report the lead SNPs, the loci, the results of the COJO analyses, and the results of a lookup of the lead SNPs in the NHGRI-EBI GWAS Catalog database²⁰ for our seven main GWAS; Supplementary Fig. 12 shows the GWAS estimates of general-risk-tolerance lead SNPs in the 23andMe and UKB cohorts and in the replication GWAS, and Supplementary Data 1 shows LocusZoom plots for all the loci identified in the seven GWAS.

Testing for population stratification

To assess the extent to which population stratification may bias our GWAS estimates, we conducted three tests. First, we estimated LD Score intercepts using the summary statistics of the discovery and replication GWAS of general risk tolerance and of the GWAS of our four main risky behaviors and their first PC¹². Second, following Okbay et al. (2016)¹⁰, we conducted sign tests that compare the signs of the estimates from our discovery GWAS of general risk tolerance (but excluding all full siblings from the UKB cohort) to the signs of the estimates from within-family (WF) GWAS of general risk tolerance. If our discovery GWAS estimates were entirely driven by stratification, then the signs of the WF estimates—which are immune to stratification—should be independent of the signs of the discovery GWAS estimates, in which case we would expect a sign concordance of roughly 50%. A higher degree of sign concordance would suggest that at least some of the signal from the GWAS comes from true genetic effects. Across four sign tests, we strongly reject the null hypothesis of 50% sign concordance for all of the sign tests (P < 5 × 10⁻¹⁰ in all four tests), implying that at least some of the signal from the GWAS comes from true genetic effects. Our third test of population stratification, the “within-family regression test,” compares both the signs and magnitudes of the discovery and WF GWAS of general risk tolerance. The Supplementary Note, Supplementary Tables 28, 29, and Supplementary Fig. 13 provide further details on the three tests and report their results. All three tests imply no more than low levels of population stratification.

Replication of the general-risk-tolerance lead SNPs and maxFDR calculation

To assess the credibility of the lead SNPs from our discovery GWAS of general risk tolerance, we compared those results to the estimates from our replication GWAS of general risk tolerance. (We did not attempt replication of the results of our six supplementary GWAS in independent data, because we did not have access to such data for these phenotypes.) We first filtered out SNPs with sample size less than one-half the maximum sample size in the replication GWAS. After applying this filter, 122 of the 124 lead SNPs were directly available in the replication GWAS summary statistics, and one of the two remaining lead SNPs was well proxied by a SNP in high LD (r² > 0.8) with it. For the resulting 123 SNPs, we conducted a (one-sided) binomial sign test to assess whether the directions (i.e., the signs) of the effects of the lead SNPs are more concordant across the discovery and the replication GWAS than expected by chance. We also conducted a (one-sided) binomial test to assess whether a larger fraction of the lead SNPs are significant at the 5% level in one-sided tests in the replication GWAS than expected by chance. We then followed the procedure outlined in Okbay et al. (2016)⁴⁷ and conducted a Bayesian analysis to obtain estimates of the posterior distributions of the 123 SNPs’ true effect sizes (the β_j ‘s), given their GWAS estimates. We used the SNPs’ estimated posterior distributions to estimate their expected replication record in the two binomial tests, and compared their actual and expected replication records.

To calculate the “maxFDR,” an upper bound on the false discovery rate (FDR) for a GWAS, we used the MTAG software¹⁶ and followed the methodology described in section 1.4.3 of Turley et al.’s Supplementary Information¹⁶. The maxFDR is defined as the maximum theoretical FDR over a range of possible fractions of null SNPs (π_null).

The Supplementary Note and Supplementary Fig. 3 provide additional details.

Estimation of genome-wide SNP heritability

We used the Heritability Estimator from Summary Statistics (HESS)⁴⁸ method to estimate the genome-wide SNP heritability of our seven main phenotypes. For the results reported in Table 1, we used the summary statistics from the GWAS listed in the table for all 1000 Genomes phase 3 SNPs with MAF greater than 0.05. We did not apply GC prior to estimating heritability with HESS. The Supplementary Note, Supplementary Table 30, and Supplementary Fig. 14 provide additional details, and also report estimates of the SNP heritability of our seven main phenotypes estimated with the GCTA⁴⁹, LD Score regression¹², and HESS methods, using only summary statistics from the UKB GWAS for comparability across phenotypes and methods (except for adventurousness, which is not available in the UKB and for which we used the 23andMe summary statistics).

Genetic correlations

We used bivariate LD Score regression⁹ to estimate genetic correlations between general risk tolerance and various phenotypes. We used the scores computed by Finucane et al.⁵⁰, which are based on genotypic data from the European-ancestry samples in the 1000 Genomes Project and only HapMap3 SNPs. As is common in the literature, we restricted our analyses to SNPs with MAF > 0.01. We used the summary statistics of the meta-analysis combining our discovery and replication GWAS of general risk tolerance to estimate genetic correlations with general risk tolerance, and we used the summary statistics of our GWAS of adventurousness, our four main risky behaviors, and their first PC to estimate genetic correlations with those phenotypes. For most other phenotypes, we used published GWAS results. We obtained the summary statistics from the GWAS of lifetime cannabis use²⁵ and of ADHD⁵¹ from the International Cannabis Consortium and the Psychiatric Genomics Consortium, respectively. We conducted our own GWAS using the first release of the UKB data for five phenotypes: age first had sexual intercourse (n = 98,956), teenage conception among females (n = 40,077), use of sun protection (n = 111,560), household income (n = 97,059), and Townsend deprivation index score (n = 112,192). The sex-specific GWAS of general risk tolerance used to estimate the genetic correlation between males and females were conducted in the full release of UKB data, separately for males and females, following the same methodology and QC protocol as for our other GWAS in the full release of UKB data. The Supplementary Note and Supplementary Tables 9, 31 provide additional details. Also, the Supplementary Note, Supplementary Table 32, and Supplementary Fig. 15 report the results of proxy-phenotype analyses in which we examined whether the general-risk-tolerance lead SNPs tend to also be associated with related phenotypes.

Multi-trait analysis of GWAS (MTAG)

We used Multi-Trait Analysis of GWAS (MTAG)¹⁶ to increase the precision of our estimates of the SNPs’ effects on general risk tolerance. We used as inputs the summary statistics of the meta-analysis combining our discovery and replication GWAS of general risk tolerance; the summary statistics of our GWAS of adventurousness, automobile speeding propensity, drinks per week, ever smoker, and number of sexual partners; and the summary statistics of a previously published GWAS on lifetime cannabis use⁵². Because SNPs that have no effect on one phenotype but a sizeable effect on another can bias MTAG results, we excluded from this analysis SNPs in the proximity of several genes implicated in biological processes that are likely to be specific only to one of the phenotypes. Specifically, we excluded all SNPs located within 1Mb of the genes CHRNA5 and CHRNB3 (nicotinic receptors), CNR1 and CNR2 (cannabinoid receptors), and ADH1B (Alcohol Dehydrogenase). We imposed a MAF filter of 0.01 and a sample size filter that selected, for each GWAS, the SNPs with sample sizes larger than two-thirds of the ninth decile of the GWAS’s sample size. MTAG limited the analysis to the 5,869,552 SNPs analyzed in all GWAS (and that satisfied these filters). To identify approximately independent lead SNPs for general risk tolerance, we applied the clumping algorithm described above. The Supplementary Note, Supplementary Table 10, and Supplementary Fig. 7 provide further details.

Polygenic prediction

We assessed the predictive power of polygenic scores of general risk tolerance in six different validation cohorts: Add Health, HRS, NTR, STR, UKB-siblings, and Zurich. (The UKB-siblings cohort comprised all individuals with at least one full sibling in the UKB.) We constructed three polygenic scores. Our first two polygenic scores were constructed with the LDpred²⁸ method, which accounts for the linkage disequilibrium (LD) between SNPs. The first used the summary statistics from the meta-analysis of the discovery and replication GWAS of general risk tolerance, while the second used the MTAG summary statistics. (The LDpred method relies on a Gaussian mixture weight that corresponds to the assumed fraction of SNPs that are causal. For each of our first two polygenic scores, we first generated LDpred scores for each of the following mixture weights: 1, 0.3, 0.1, 0.03, 0.01, 0.003, 0.001, 0.0003, and 0.0001⁵³. The LDpred-score results we present in this paper for our first two polygenic scores are for the scores based on a Gaussian mixture weight of 0.3 (our “preferred score”), which consistently performed well across cohorts and phenotypes.) Our third polygenic score was constructed with the classical method, which simply weights SNPs by their GWAS effect size^54,55, using the summary statistics from the meta-analysis of the discovery and replication GWAS of general risk tolerance.

We used the subset of all the SNPs (i.e., we did not impose a P value threshold) in the HapMap consortium phase 3 release⁵⁶ with an imputation quality of more than 0.7 to generate all three scores. For every validation cohort that was also included in the discovery or replication GWAS or in the MTAG analysis, we reran the GWAS and MTAG analyses without the validation cohort to generate the summary statistics we used to construct the scores. Due to data access limitations, the 23andMe cohort could not be included in the meta-analysis whose summary statistics we used to construct the polygenic scores in the NTR, STR, and Zurich cohorts. The second polygenic score (using the MTAG summary statistics) was only constructed for the Add Health, HRS, and UKB-siblings cohorts.

Our measure of a score’s predictive power for a predicted phenotype is the incremental R² (or incremental pseudo-R²) from adding the score to a regression of the phenotype on controls for sex, birth year, birth-year squared, birth-year cubed, as well as the interactions between sex and the three birth-year variables, and the first ten principal components of the genetic relatedness matrix. We used the bootstrap method with 1,000 iterations to estimate 95% percentile confidence intervals for the incremental R² estimates. For continuous phenotypes, we estimated ordinary least squares (OLS) regressions; for binary phenotypes (e.g., ever smoker), we estimated probit models; and for censored phenotypes (e.g., equity share, which is nonnegative), we estimated tobit models. For binary and censored phenotypes, we used McFadden’s pseudo-R² to calculate the incremental pseudo-R².

The Supplementary Note provides additional details, including a description of how the predicted phenotypes were constructed. Results are presented in Supplementary Figs. 8–9 and Supplementary Tables 11–14.

Biological annotation: testing hypotheses about specific genes and gene sets

We conducted a comprehensive review of the literature on biological pathways that have been hypothesized to influence risk tolerance. The 132 articles identified by review are compiled in Supplementary Table 1. The Supplementary Note and Supplementary Tables 15, 16, and 33–34 provide further details and report the results of the various analyses we conducted to assess whether the pathways and genes that have previously been hypothesized to relate to risk tolerance do indeed show evidence of association with risk tolerance.

Biological annotation: additional bioinformatics analyses

We conducted a series of additional bioinformatics analyses using the results of the combined meta-analysis of our discovery and replication GWAS of general risk tolerance. We conducted a gene analysis with MAGMA³¹ to test each of 18,224 genes for association with general risk tolerance in a hypothesis-free manner (the 18,224 genes are the set of all genes containing at least one SNP in our combined meta-analysis results). We used our main reference panel to estimate LD. Bonferroni correction was applied to account for multiple testing, counting each gene as an independent test. We then used the Gene Network³² co-expression database to gain insight into the functions of the significant MAGMA genes.

We also used DEPICT³³ (release 194) to prioritize tissues, gene sets, and genes that are implicated by our GWAS results. Only SNPs with GWAS P values less than 10^–5 were used as input, and DEPICT-defined loci were defined by clumping these SNPs (see the Supplementary Note for the clumping parameters used for this analysis). Locus boundaries were then defined using a LD r² threshold of 0.5, and overlapping loci were merged, yielding 464 autosomal loci comprising 1,060 genes.

To partition the SNP-based heritability of general risk tolerance, we used stratified LD Score regression⁵⁰, following the procedure described by Finucane et al.⁵⁰. We estimated stratified LD Score regressions both for the functional genomic regions of the “baseline model” and for the tissue-level annotations provided by Finucane et al. To correct for multiple hypothesis testing, we applied a Bonferroni correction for 52 two-sided tests in the baseline model (i.e., for 52 annotations) and for 10 two-sided tests in the tissue type models (i.e., for 10 tissue types).

The Supplementary Note, Supplementary Tables 17–22 and 35–39, and Supplementary Figs. 10–11 and 16 provide further details and report the results of these and other bioinformatics analyses, including a transcriptome-wide analysis with Summary-based Mendelian Randomization (SMR)⁵⁷, and an ascertainment of whether the lead SNPs and their LD partners (SNPs with an r² > 0.6 with a lead SNP and no more than 250 kb from it) are protein-altering variants or are associated with cis-gene expression in distinct human tissues, among other analyses. The Supplementary Note also highlights the most important results of the bioinformatics analyses and summarizes the conclusions we derive from them.

DATA AVAILABILITY STATEMENT:

GWAS summary statistics can be downloaded from www.thessgac.org/data. SNP-level summary statistics from analyses based entirely or in part on 23andMe data can only be reported for up to 10,000 SNPs. For general risk tolerance, we provide association results for all SNPs that passed quality-control filters in a GWAS meta-analysis of general risk tolerance that excludes the research participants from 23andMe; we also provide association results from the complete GWAS (which includes data from 23andMe) for all lead SNPs identified in our discovery GWAS and MTAG analysis of general risk tolerance, and for the next 4,000 most significant SNPs in the discovery GWAS. For adventurousness, we provide association results from the complete GWAS (which includes only data from 23andMe) for all lead SNPs and for the next 4,000 most significant SNPs. For automobile speeding propensity, drinks per week, ever smoker, number of sexual partners, and the first PC of the four risky behaviors, we provide association results from the complete GWAS for all SNPs that passed quality-control filters. Contact information for the cohorts included in this paper can be found in the Supplementary Note.