Phase-locking and bistability in neuronal networks with synaptic depression

Abstract

We consider a recurrent network of two oscillatory neurons that are coupled with inhibitory synapses. We use the phase response curves of the neurons and the properties of short-term synaptic depression to define Poincaré maps for the activity of the network. The fixed points of these maps correspond to phase-locked modes of the network. Using these maps, we analyze the conditions that allow short-term synaptic depression to lead to the existence of bistable phase-locked, periodic solutions. We show that bistability arises when either the phase response curve of the neuron or the short-term depression profile changes steeply enough. The results apply to any Type I oscillator and we illustrate our findings using the Quadratic Integrate-and-Fire and Morris-Lecar neuron models.

1. Introduction

Coherent activity in deterministic networks of coupled oscillators often takes the form of phase-locked activity. In this situation, relative to some common reference point, each network element is assigned a phase that is periodic over time. The relative phase differences between the network elements can then be computed to determine potential phase-locked states. Such networks arise in a variety of physical and biological contexts, such as cardiac networks [49], central pattern generating neuronal networks [9], and those described by weakly-coupled Kuramoto oscillators [26].

Various mathematical approaches have been developed to understand phase-locking. One of the most common methods relies on weak coupling among the network elements, so that the technique of averaging can be applied. This allows the phase relationship between the network elements to be systematically reduced to the study of sets of equations on a torus, whose roots correspond to phase-locked states [21]. Another common method uses the phase response curve (PRC) to derive maps whose fixed points correspond to phase-locked solutions [17]. The PRC measures the response of an oscillator to perturbations given at specific phases of the oscillation cycle. The PRC is a mapping with domain given by the perturbation phase and range equal to the change of phase of the periodic trajectory. A positive (negative) value of the PRC implies that a perturbation given at that phase causes the oscillator to increase (decrease) its phase relative to a specified reference point. Neuronal models for which the PRC is strictly of one sign are Type I, while those in which the PRC changes sign are Type II [19].

Oscillators may also be subject to inputs that are not necessarily weak. In this case, the spike-time response curve characterizes how the timing of the next spike is affected by an input. By normalizing against the intrinsic period of the neuron, one effectively obtains a phase response curve, albeit one that may not quantitatively match the one obtained from weak perturbations. A synaptic current from a presynaptic neuron can be thought of as a (not necessarily weak) input to a postsynaptic cell that may affect its phase. While there are a wide variety of synapses, we will focus on inhibitory synapses that exhibit short-term synaptic depression where the strength of the synapse increases as a function of period of the presynaptic neuron. We are interested in finding situations where more than one stable periodic solution exists as a result of the shortterm synaptic depression.

Multistability of solutions refers to the existence of multiple stable solutions for the same set of parameters. Each of these solutions has a basin of attraction defined as the set of initial conditions for which the starting trajectory asymptotically approaches this solution. Multistability is thought to be of importance to a neuronal network in that each of the stable solutions corresponds to a different network output state. Thus, the capabilities of a network are expanded in the presence of multistability. It has been shown previously that synaptic depression can lead to bistable states in neuronal networks [7, 30, 33]. Synaptic depression can enhance information about stimuli in competitive networks that display a multitude of dominance times [25], but can also detract from multistability of dominance times in noise induced switching in excitatory networks [32].

In this study, we show that bistability of different phase-locked states can arise in a pair of Type I neurons in which just one of the synapses exhibits short-term depression. Further, we develop a technique for finding the phase-locked states that relies on knowing only the PRC of each neuron, rather than the specific mathematical equations needed to describe the evolution of a model’s voltage variable. Calculating a PRC of a neuron is a feed-forward process in that the timing of the perturbation to a neuron can be externally controlled. There is significant work on approximating PRCs from experimental data; for example see [36]. The maximal synaptic strength as a function of cycle period or frequency (synaptic plasticity profile) can also be calculated in a feed-forward manner [47]. Huang [24] developed a method to combine these two types of feed-forward information into a feedback Poincaré map. The stable (unstable) fixed points of this map corresponded to stable (unstable) phase-locked solutions of the reciprocally coupled inhibitory system. Using Huang’s method, we derive two distinct 2-D maps. For each of these maps, we derive conditions for the existence of bistable solutions. Our analysis reveals that bistability occurs when either the PRC of the neuron or the synaptic plasticity profile of the synapse has a sufficiently steep derivative in a neighborhood of a fixed point. To illustrate our proposed methods, we use the Quadratic Integrate-and-fire (QIF) model [23] and the Morris-Lecar (ML) model [34]. The QIF is the normal form of saddle-node bifurcation of fixed points. From it, one can derive the theta model which is the canonical Type I phase model. We use the QIF model because we can analytically derive its PRC. The ML model is perhaps the most basic, biophysically based planar model of a neuron and is widely used in mathematical and computational studies.

This paper is organized as follows. In Section 2, we describe the coupled systems governed by either the QIF or ML models, together with their respective PRCs. In Section 3 we first derive three distinct maps. The first map is 1-D, previously derived in Dror et al [17], that describes the behavior of two coupled neurons in which the synapses are static (not depressing). The second two maps are the aforementioned 2-D maps. We show that a stable fixed point of the 1-D map has a corresponding fixed point of either of the 2-D maps, however its stability may be different. In this section, we also utilize a geometric method, developed in [4], to determine existence of bistable solutions. Section 4 concludes with a Discussion.

2. Models and Methods

The main results of this paper hold for neuronal models that display Type I dynamics as described below. We will analytically (numerically) calculate a family of phase response curves (PRCs) for the QIF (ML) models. We will use this family of PRCs to construct a 2-D map that determines the existence and stability of phase locked solutions of a reciprocally coupled set of two inhibitory neurons. We will also use the model equations to conduct simulations and show that the results agree with those obtained from the 2-D map.

2.1. Intrinsic neuron models: QIF and ML

The Quadratic Integrate-and-Fire (QIF) [23] model is given by

$$\begin{gathered} \frac{dV}{dt}=1+V^2 \\ V\left(t_{sp}^{+}\right)=V_r,\text{\hspace{1em}when\hspace{0.17em}}V\left(t_{sp}^{-}\right)=V_t\left(V_r<V_t\right) \end{gathered}$$ (1)

where V_t > V_r are the spike threshold and the resting potential, respectively. As soon as the voltage V reaches the threshold V_t at a spike time t_sp, V is reset to the resting potential V_r. While we consider homogeneous neurons in this study, there is no problem in extending this to consider heterogeneity. To do so, one could simply choose different values of V_t or V_r for the two neurons.

The Morris-Lecar [34] neuron is a conductance-based model neuron that contains leak (L), potassium (K) and calcium (Ca) currents. The maximal conductance and reversal potential of a given current X are denoted by $\overline{g}X$ and E_X, respectively. The Ca current depends on an instantaneous function $m_{\infty }$ of the membrane voltage (V) and is given by $I_{Ca}={\overline{g}}_{Ca}{m}_{\infty }\left(V\right)\left(V-E_{Ca}\right)$ where $m_{\infty }\left(V\right)=0.5(1+\tanh \left(\left(V-{\upsilon }_1/k_1\right)\right)$. The parameter v₁ is the half-activation value of the Ca current and k₁ is the reciprocal of the slope at that point. The leak current is given by $I_L={\overline{g}}_L\left(V-E_L\right)$. The K current involves a dynamic activation variable w and is given by $I_K={\overline{g}}_{K}w\left(V-E_K\right)$.

The equations for the membrane voltage V and activation variable w are given by

$$\begin{gathered} \frac{dV}{dt}=\left(I_{app}-I_L-I_K-I_{Ca}\right)/C \\ \frac{dw}{dt}=\frac{w_{\infty }\left(V\right)-w}{{\tau }_w\left(V\right)} \end{gathered}$$ (2)

where w_∞(V ) = 0.5(1 + tanh((V − v₂)/k₂)) and τ_w(V ) = 1/(ϕ cosh((V − v₂)/2k₂)). The parameters v₂, k₂ and ϕ govern the K kinetics. The parameter C denotes the membrane capacitance and I_app denotes the current externally injected to the neuron. Depending on parameters, the Morris-Lecar equations can model either a Type I or Type II oscillator. We choose parameters such that it is the former. For the parameters we choose, the amount of time that the voltage spends above a prescribed threshold V_th = 0 is almost fixed. We shall assume that it is constant and call it t_burst. This gives the width of the action potential. The time between spikes can vary based on the input a cell may receive. Heterogeneity between cells can be introduced by varying Iapp.

2.2. Phase response curves

The phase response curve of an oscillator describes how the period of the oscillator changes depending on the phase at which it receives a perturbation. In general, the PRC can be computed numerically (for model neurons) or experimentally (for biological neurons) by injecting a brief perturbing current (such as a small current pulse) and measuring the effect of this perturbation on the cycle length as a function of the phase of the perturbing input. If the perturbation is infinitesimally small, then an infinitesimal phase response curve (iPRC) of the model neuron can be obtained by linearizing the governing differential equations about the limit cycle and solving the adjoint equation. For appropriate choices of parameters, the iPRCs of the QIF and ML models are called Type I since they are each of one sign. These type of model neurons delay their firing in response to inhibitory inputs independent of the phase that the input is given.

Throughout this study, we use the term PRC to refer to responses calculated by direct synaptic inputs. Denote by P₀ the intrinsic period of a cell. Suppose a perturbing input is given at time dt after the firing of the cell. This yields a phase ϕ = dt/P₀ at the time of the perturbation. Let P_c denote the new cycle period which is the time between when a cell fires prior to a perturbation and the subsequent firing of the cell when a perturbation is given at phase ϕ. We define the PRC as

$$Z\left(\varphi \right)=\frac{P_0-P_c}{P_0}$$ (3)

We assume that the effects of a perturbation to the current cycle of a neuron only last for that cycle. Any effects that may linger to subsequent cycles are ignored here, but treatment of such cases can be found elsewhere [42].

The PRC of a QIF neuron can analytically be calculated using equations (1). It is given by

$$Z\left(\varphi \right)=\frac{\arctan \left(\tan \left(P_0\varphi +\arctan V_r\right)-g\right)-\arctan V_r}{P_0}-\varphi$$ (4)

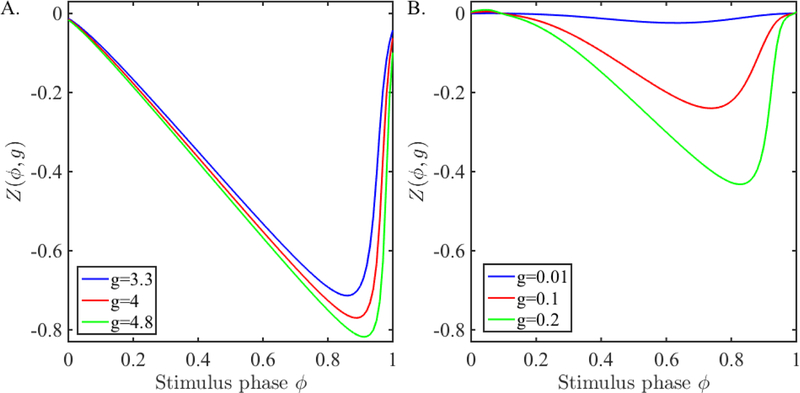
where g > 0 denotes the strength of the perturbation. In Figure 1A, we show examples of the QIF PRC for a few different choices of inhibitory synaptic strength. Note that as g increases, the PRCs have larger amplitudes shifting to larger perturbation phases. Also note, that for the set of g values chosen, the PRC is quite large with changes of phase up to as much as 0.8, with large gradients for large ϕ.

Figure 1:

PRC due to synaptic input. A. The PRCs obtained from the QIF model (1) for different synaptic strengths. B. The PRCs obtained from the ML model (2) for different synaptic strengths.

We compute the PRC of a ML model neuron numerically. We choose parameters so that the oscillations arise through a saddle node on invariant circle (SNIC) bifurcation. Neurons that oscillate through a SNIC bifurcation have a Type 1 iPRC [19]. A PRC obtained from our model neurons for a range of synaptic strength is shown in Figure 1B where we created the PRC by applying a perturbation of the form

$$I_{syn}=g_{pre\to post}\text{H}\left({\text{V}}_{\text{pre}}-{\text{V}}_{\text{th}}\right)\left[{\text{V}}_{\text{post}}-{\text{E}}_{\text{inh}}\right].$$

This is a type of perturbation that mimics a synaptic input in that it contains the driving force V_post − E_inh where E_inh is the inhibitory synaptic reversal potential. The reference point to compute the PRC is chosen to be when V crosses V_th in the positive direction. Note again that this method of computing the PRC is different from computing the iPRC of a spiking neuron which yields a strictly Type 1 PRC. The PRC we obtain is very similar, but there is a small, insignificant, region of the PRC that is positive near small stimulus phases due to the longer active duration of the ML neuron. Also note that for the smallest shown conductance of g = 0.01, the PRC is very small in amplitude and has small gradients for all ϕ.

2.3. Modeling synaptic inputs

When a presynaptic cell rises above threshold, it sends an inhibitory input to the postsynaptic cell. In the situation where the synapse exhibits synaptic depression, the strength of this input is an increasing function of the interspike interval, or alternatively a decreasing function of the spiking frequency. For the QIF model, we use a model for depression due to Abbott et al [1]. We let r denote the amount of available synaptic resources normalized to lie between zero and one. The equations governing r are given by

$$\begin{array}{l}\frac{dr}{dt}=\frac{1-r}{{\tau }_r}\text{\hspace{0.17em}between spikes of the presynaptic neuron}\\ r^{+}=f\cdot r^{-}\text{\hspace{0.17em}when the presynaptic neuron fires.}\end{array}$$ (5)

Here, the amount of available synaptic resources is reset by a fraction f ∈ (0, 1] at the instant that the neuron fires and recovers to 1 with time constant τ_r after the spike. Hence, the value of the depression variable r depends on the cycle period of the neuron. To model a non-depressing synapse, we simply choose f = 1.

When the presynaptic neuron is firing with a fixed period of P, the depression variable r oscillates between a minimum and a maximum value at the steady state. This maximum value attained at the onset of a spike at the steady state can be obtained from equation (5) as

$$r_{ss}\left(P\right)=\frac{1-e^{-P/{\tau }_r}}{1-f{e}^{-P/{\tau }_r}}.$$ (6)

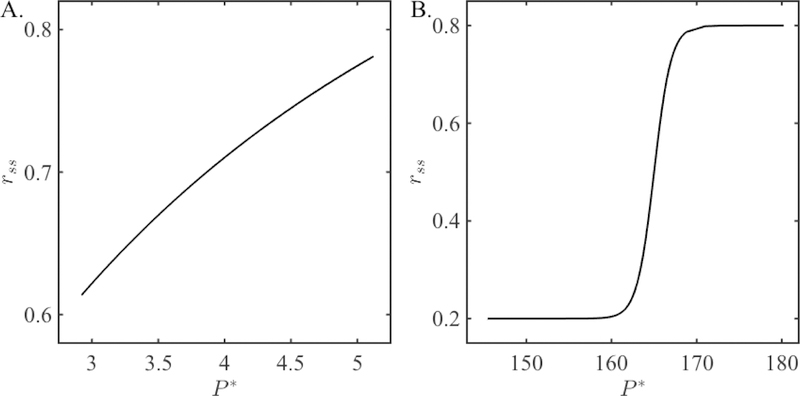
The function r_ss(P ) is called the steady state synaptic plasticity profile and is shown in Figure 2A. Observe that r_ss(P ) is a monotone increasing function.

Figure 2:

Steady state synaptic plasticity profiles r_ss(P ) for the two synaptic models. A. The plasticity profile for the QIF model (6). B. The plasticity profile for the ML model (11). Notice the difference in the scaling of the y-axes; the value of the depression variable changes over a much larger range for the synapse considered for the ML model.

For the ML model, we use an adapted version of the Abbott model, as in [35], that takes into account the length of the action potential as well as making the recovery from depression more strongly dependent on the cycle period. The model involves two variables r and s. As above, r keeps track of the amount of depression in the synapse. The variable s will be used to transmit information about r to the postsynaptic cell whenever the presynaptic cell exhibits a spike at time t_sp.

$$\frac{dr}{dt}=\frac{r_{\infty }\left(P_c\right)-r}{{\tau }_{\alpha }}{H}_{\infty }\left(V_{th}-V_{pre}\right)-\frac{r}{{\tau }_{\beta }}{H}_{\infty }\left(V_{pre}-V_{th}\right)$$ (7)

$$\frac{ds}{dt}=0$$ (8)

$$r_{\infty }\left(P_c\right)=\frac{1}{2}(1+\alpha \tanh \left(\left(P_c-P_h/k_h\right)\right)$$ (9)

$$s^{+}\left(t_{sp}\right)=r^{-}\left(t_{sp}\right)$$ (10)

The function r_∞(P ) is the target level of recovery that the depressing synapse is trying to reach for a given cycle period P_c. The parameter α = 0.6 is chosen to limit the bounds of r_∞ between 0.2 and 0.8, P_h is the half-activation period and k_h is the reciprocal of the slope at that point. The variable P_c is calculated and updated on a cycle-by-cycle basis. In Section 3.5, in order to illustrate the dependence of bistability on the steady state plasticity profile, we shall choose different functional foms of r_∞ (P ) to be used in equation (9). If we wish to model a non-depressing synapse, we take s⁺(t_sp) = 1.

Just as above for the spiking neuron model, when an ML-based neuron is firing periodically with period P, the value of the depression variable oscillates between a maximum and a minimum value. In this case, it is straightforward to show that the steady state value of the depression at the onset of a spike is given by

$$r_{ss}\left(P\right)=r_{\infty }\left(P\right)\frac{1-e^{-\left(P-t_{burst}\right)/{\tau }_{\alpha }}}{1-e^{-t_{burst}/{\tau }_{\beta }}{e}^{-\left(P-t_{burst}\right)/{\tau }_{\alpha }}}.$$ (11)

If we let $f=e^{-t_{burst}/{\tau }_{\beta }}$ and then take the limit as t_burst → 0 in the term (P − t_burst), equation (11) reduces to a form that is similar to equation (6) except that the maximum is given by r_∞(P ) instead of one. Note that for narrow action potentials, the term exp(−t_burst/τ_β) is close to one. Moreover, the steady state period will be relatively large. Thus the fraction in (11) is effectively equal to one. Thus $r_{ss}\left(P\right)\approx r_{\infty }\left(P\right)$. We shall use this approximation throughout the duration of the paper. The function r_ss is plotted in Figure 2B.

2.4. Coupled equations

We shall consider a coupled system of neurons A and B. The synapse from A to B will always be non-depressing (f = 1 or s⁺(t_sp) = 1) and will have a fixed synaptic conductance ${\overline{g}}_{A\to B}$. The synapse from B to A can be either depressing or non-depressing depending on the case we are considering and will clearly be noted in the subsequent text.

For the QIF model, the effect on the postsynaptic cell of this input is to decrease its voltage by an amount $g_{pre\to post}{r}^{-}$. That is

$$V_{post}^{+}=V_{post}^{-}-g_{pre\to post}{r}^{-}$$

This decrease can be modeled using a Dirac delta function δ(t) in the coupled set of equations below.

$$\frac{d{V}_A}{dt}=1+V_A^2-g_{B\to A}{r}^{-}\delta \left(t-t_{B,sp}\right)$$

$$\frac{d{V}_B}{dt}=1+V_B^2-{\overline{g}}_{A\to B}\delta \left(t-t_{A,sp}\right)$$

$$V_A\left(t_{A,sp}^{+}\right)=V_r,\text{\hspace{1em}when\hspace{0.17em}}{V}_A\left(t_{A,sp}^{-}\right)=V_t\left(V_r<V_t\right)$$

$$V_B\left(t_{B,sp}^{+}\right)=V_r,\text{\hspace{1em}when\hspace{0.17em}}{V}_B\left(t_{B,sp}^{-}\right)=V_t\left(V_r<V_t\right)$$

where t_*,sp represents the time of the spike of A or B The dynamics for the r variable are given by equation (5). Note that the term r⁻ only appears in the equation for dV_A/dt.

For the ML model, let f (V, w) = (I_app − I_L − I_K − I_Ca)/C. The coupled equations for neurons A and B are

$$\begin{gathered} \frac{d{V}_A}{dt}=f\left(V_A,w_A\right)-g_{B\to A}{s}^{+}\left(t_{sp,B}\right)H_{\infty }\left(V_B-{\upsilon }_{th}\right)\left[V_A-E_{inh}\right] \\ \frac{d{w}_A}{dt}=\frac{w_{\infty }\left(V_A\right)-w_A}{{\tau }_w\left(V_A\right)} \\ \frac{d{V}_B}{dt}=f\left(V_B,w_B\right)-{\overline{g}}_{A\to B}{H}_{\infty }\left(V_A-{\upsilon }_{th}\right)\left[V_B-E_{inh}\right] \\ \frac{d{w}_B}{dt}=\frac{w_{\infty }\left(V_B\right)-w_B}{{\tau }_w\left(V_B\right)} \end{gathered}$$ (12)

where the Heaviside function H_∞ (V − V_th) is 0 if V < V_th and 1 otherwise. The variable s⁺(t_sp,B) which appears only in the dV_A/dt equation is governed by the synaptic equations (7)–(10). Thus at the moment that neuron B spikes, neuron A receives a synaptic input of $g_{B\to A}{s}^{+}\left(t_{sp},B\right)$ and then remains constant through the duration of the action potential of B.

2.5. Intrinsic and actual phase

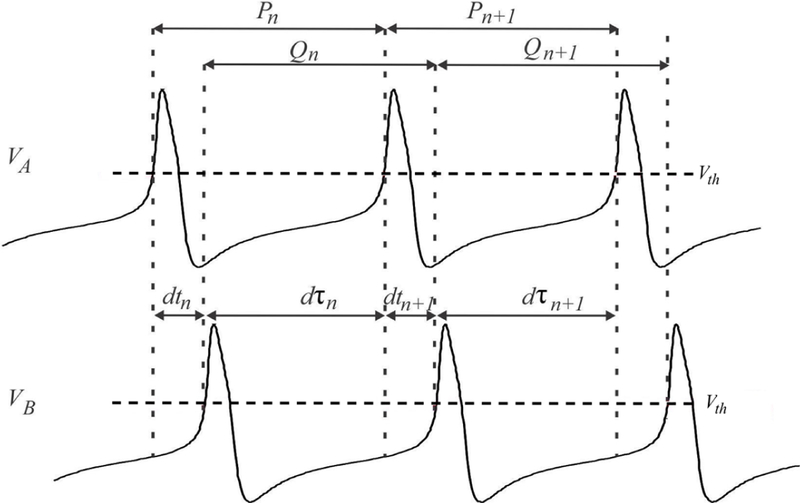
We use a Poincaré section to define the phase of each cell at each cycle. This will lead to a sequence of crossing times when a particular trajectory crosses the Poincaré section at the nth cycle, which in turn will lead to a sequence of phases. A schematic that depicts various quantities of interest needed to derive the Poincaré maps is shown in Figure 3.

Figure 3:

The variables that are used to define the Poincaré maps are shown on the simulation of ML neurons. The cycle length P_n of cell A in cycle n (measured when voltage crosses V_th) can be divided into the delay between cell A activity to cell B activity (dt_n) and the opposite (dτ_n). The cycle period Q_n of cell B in cycle n is dτ_n+dτ_n+1.

Choose the Poincaré section to be at V_A = V_th. The amount of time in the nth cycle that passes after cell A fires until cell B fires is denoted by dt_n, while the amount of time after cell B fires until cell A fires is denoted by dτ_n (Figure 3). The (activity) phase of neuron A (or B) is defined as the firing time dt_n (or dτ_n) normalized by the cycle length. Therefore, the phases of A and B are, respectively, given by

$$\begin{array}{l}{\widehat{\varphi }}_n=d{t}_n/P_n\\ {\widehat{\theta }}_n=d{\tau }_n/Q_n.\end{array}$$ (13)

In the derivations of the maps, we will make use of the PRCs of A and B which are defined in terms of P₀ and Q₀, the intrinsic periods of A and B. To simplify these derivations we introduce the notation of the “intrinsic phase” of neurons A and B which are defined, respectively, as

$${\varphi }_n=d{t}_n/P_0$$ (14)

$${\theta }_n=d{\tau }_n/Q_0.$$ (15)

Because we will be considering both static and depressing cases, we need separate notation to demarcate each of the PRCs of neuron A. Our convention will be the following. We let $Z_A\left(\varphi ,{\overline{g}}_{B\to A}\right)$ denote the PRC when it is created with a static synapse. We let Z_A(ϕ, _gB→Ar⁻) denote the PRC when it depends on the strength of the synaptic conductance. What differs is the choice of the second variable. In the former case the maximal conductance ${\overline{g}}_{B\to A}$ is fixed, while in the latter, the maximal conductance _gB→Ar⁻ depends on cycle period through either equation (5) for the QIF model or equation (7) for the ML model. The PRC of cell B is always created with a static synapse of strength ${\overline{g}}_{A\to B}$ and is simply denoted by Z_B(θ). At steady state, the actual phase is related to the intrinsic phase through the following:

$$\widehat{\theta }=\frac{\theta }{1-Z_B\left(\theta \right)}$$

$$\widehat{\varphi }=\frac{\varphi }{1-Z_A\left(\theta ,g\right)},$$

where $g={\overline{g}}_{B\to A}$ for the static synapse and g = g_B→Ar_ss for the dynamic synapse, where r_ss is given by equation (6) for QIF or (11) for ML.

3. Results

3.1. Derivation of the maps

For completeness, we start with the derivation of the Poincaré map for the relative firing times of the neurons when they are connected with static synapses [4]. Rewriting the PRC relationship (3), we can obtain the cycle lengths of each cell in cycle n as

$$P_n=P_0\left[1-Z_A\left({\varphi }_n,{\overline{g}}_{B\to A}\right)\right]$$ (16)

$$Q_n=Q_0\left[1-Z_B\left({\theta }_n\right)\right].$$ (17)

Note that we use the PRC $Z_A\left(\varphi ,{\overline{g}}_{B\to A}\right)$ where the value in the second argument is chosen for the non-depressing, static case. The following equations relate the firing times of the two cells

$$d{t}_n+d{\tau }_n=P_n$$ (18)

$$d{\tau }_n+d{t}_{n+1}=Q_n.$$ (19)

From the equations (15), (16) and (18), θ_n can be written in terms of ϕ_n:

$$\begin{gathered} \begin{array}{l}{\theta }_n=\frac{d{\tau }_n}{Q_0}=\frac{1}{Q_0}\left[P_n-d{t}_n\right]=\frac{1}{Q_0}\left[P_0\left(1-Z_A\left({\varphi }_n,{\overline{g}}_{B\to A}\right)\right)-P_0{\varphi }_n\right]\\ \\ =\frac{P_0}{Q_0}\left[1-Z_A\left({\varphi }_n,{\overline{g}}_{B\to A}\right)-{\varphi }_n\right].\end{array} \end{gathered}$$ (20)

Similarly, ϕ_n+1 can be expressed in terms of θ_n:

$$\begin{gathered} {\varphi }_{n+1}=\frac{d{t}_{n+1}}{P_0}=\frac{1}{P_0}\left(Q_n-d{\tau }_n\right)=\frac{1}{P_0}\left[Q_0\left(1-Z_B\left({\theta }_n\right)\right)-Q_0{\theta }_n\right] \\ =\frac{Q_0}{P_0}\left(1-Z_B\left({\theta }_n\right)-{\theta }_n\right). \end{gathered}$$ (21)

using the equations (17) and (19). Thus, plugging equation (20) into equation (21) defines the following 1-D map for the intrinsic phase of cell A (14) when the 1:1 firing order between the cells is maintained:

$$\begin{gathered} \begin{array}{l}{\varphi }_{n+1}=\text{Π}\left({\varphi }_n\right)\\ \\ =\frac{Q_0}{P_0}\left[1-Z_B\left(\frac{P_0}{Q_0}\left(1-Z_A\left({\varphi }_n,{\overline{g}}_{B\to A}\right)-{\varphi }_n\right)\right)\right]-1+Z_A\left({\varphi }_n,{\overline{g}}_{B\to A}\right)+{\varphi }_n.\end{array} \end{gathered}$$ (22)

The condition for 1:1 phase-locking is ϕ_n = ϕ_n+1 = ϕ*. Plugging this into the map gives the condition for a fixed point as

$$P_0\left[1-Z_A\left({\varphi }^{*},{\overline{g}}_{B\to A}\right)\right]=Q_0\left[1-Z_B\left({\theta }^{*}\right)\right]$$

where ${\theta }^{*}=\frac{P_0}{Q_0}\left[1-Z_A\left({\varphi }^{*},{\overline{g}}_{B\to A}\right)-{\varphi }^{*}\right]$.

To determine conditions for 1:1 phase-locked activity, it is sufficient to rule out cases where either of the two neurons fires consecutively. To avoid the case where B fires twice for every one firing of A, dτ_i + P_i+1 < Q_i+1 + Q₀ must hold. This is equivalent to $Z_A\left({\varphi }_{i+1},{\overline{g}}_{B\to A}\right)>1-Q_0/P_0\left[2-{\theta }_i-Z_B\left({\theta }_i\right)\right]$. Since ${\varphi }_{i+1}=Q_0/P_0\left[1-{\theta }_i-Z_B\left({\theta }_i\right)\right]$, $Z_A\left({\varphi }_{i+1},{\overline{g}}_{B\to A}\right)>1-Q_0/P_0-{\varphi }_{i+1}$. So to obtain a 1:1 phase-locked solution, the fixed point ${\varphi }^{*}=Q_0/P_0\left(1-{\theta }^{*}-Z_B\left({\theta }^{*}\right)\right)$ should satisfy $Z_A\left({\varphi }^{*},{\overline{g}}_{B\to A}\right)>1-Q_0/P_0-{\varphi }^{*}$. Geometrically, at the fixed point, the PRC of A, $Z_A\left({\varphi }^{*},{\overline{g}}_{B\to A}\right)$, should lie above the line Z_A = 1 − Q₀/P₀ − ϕ. To avoid the case of A firing twice in succession, we need the condition Q_i+1 < dτ_i + P₀, equivalently, Z_B(θ_i) > 1 − P₀/Q₀ − θ_i. Locally, this amounts to Z_B(θ*) > 1 − P₀/Q₀ − θ*, i.e., the PRC of B, Z_B(θ), should lie above the line Z_B = 1 − P₀/Q₀ − θ at the fixed point.

Next, we derive maps to predict the network activity in the presence of synaptic depression. In the first case, we shall use the dynamic equation (5) to derive a 2-D map for the phase ϕ_n and the depression variable r_n. This approach allows the transients due to different initial conditions to potentially play a role in the convergence of the map to a fixed point. In the second case, we derive a 2-D map for the phase ϕ_n and the period P_n. For this case, we use the steady state plasticity profile given in equation (9). This approach assumes that the depression variable quickly reaches its steady state plasticity value and as a result, we only need to track how the cycle period changes. We note that the fixed points of either of the two maps correspond to the same phase-locked solutions.

For the first approach, assume that the strength of the B to A synapse changes according to the dynamics of the depression variable r equation (5) and is given by g_B→Ar_n in cycle n. Assume that we know the values ϕ_n and r_n. Then we can compute the period of neuron A in cycle n using the expression

$$P_n=P_0\left[1-Z_A\left({\varphi }_n,g_{B\to A}{r}_n\right)\right].$$ (23)

We next modify equation (20) by rewriting P_n as given in (23) to obtain the phase of neuron B in cycle n as

$${\theta }_n=\frac{P_0}{Q_0}\left[1-Z_A\left({\varphi }_n,g_{B\to A}{r}_n\right)-{\varphi }_n\right].$$ (24)

Equation (17) giving the cycle length of neuron B becomes

$$Q_n=Q_0\left[1-Z_B\left(\frac{P_0}{Q_0}\left[1-Z_A\left({\varphi }_n,g_{B\to A}{r}_n\right)-{\varphi }_n\right]\right)\right]$$ (25)

in cycle n. Plugging (24) into (21) and computing the depression variable using (5) over one cycle gives a a 2-D map Π^dyn for the evolution of the intrinsic phase of cell A and the synaptic depression variable from cell B to cell A

$$\begin{array}{l}{\varphi }_{n+1}={\Pi }_1^{dyn}\left({\varphi }_n,r_n\right)\\ =\frac{Q_0}{P_0}\left[1-Z_B\left(\frac{P_0}{Q_0}\left(1-Z_A\left({\varphi }_n,g_{B\to A}{r}_n\right)-{\varphi }_n\right)\right)\right]-1+Z_A\left({\varphi }_n,g_{B\to A}{r}_n\right)+{\varphi }_n\\ r_{n+1}={\Pi }_2^{dyn}\left({\varphi }_n,r_n\right)\\ =1-\left[1-f{r}_n\right]\exp \left(-\frac{Q_0}{{\tau }_r}\left(1-Z_B\left[\frac{P_0}{Q_0}\left(1-Z_A\left({\varphi }_n,g_{B\to A}{r}_n\right)-{\varphi }_n\right)\right)\right]\right).\end{array}$$ (26)

Observe that the first equation is the same as (22) except that now the second argument of Z_A depends on _gB→Ar_n as opposed to ${\overline{g}}_{B\to A}$.

For the second approach, we derive the map where the synaptic strength from neuron B to A changes according to the steady-state synaptic plasticity profile in equation (9) and is given by _gB→Ar_∞(Q_n) in cycle n. Assume that we know the values ϕ_n and P_n. The phase of neuron B in cycle n can be found using (15) and (18) as

$${\theta }_n=\left(P_n-{\varphi }_n{P}_0\right)/Q_0.$$ (27)

Plugging this into (17) immediately yields the expression for the cycle length of neuron B in cycle n as

$$Q_n=Q_0\left[1-Z_B\left(\left(P_n-{\varphi }_n{P}_0\right)/Q_0\right)\right].$$ (28)

We can now obtain the phase of neuron A in cycle n + 1 using equations (15) and (19) as

$$Q_{n+1}=\left[Q_n-d{\tau }_n\right]/P_0=\left[Q_n-{\theta }_n{Q}_0\right]/P_0.$$ (29)

We can use this phase to obtain the cycle length of neuron A in cycle n + 1 as

$$P_{n+1}=P_0\left[1-Z_A\left({\varphi }_{n+1},g_{B\to A}{r}_{\infty }\left(Q_n\right)\right)\right].$$ (30)

Similar to equation (23), the period of neuron A is determined by Z_A which is a function of two variables. However, in this case the synaptic strength received by neuron A in cycle n + 1 depends directly on the cycle length of neuron B in cycle n. The map Π^ss for the activity of the network can be obtained by plugging the equations (27) and (28) into (29) and (30) as

$$\begin{array}{l}{\varphi }_{n+1}={\Pi }_1^{ss}\left({\varphi }_n,P_n\right)\\ =\frac{Q_0}{P_0}\left[1-Z_B\left(\frac{P_n-{\varphi }_n{P}_0}{Q_0}\right)\right]-\frac{P_n}{P_0}+{\varphi }_n\\ P_{n+1}={\Pi }_2^{ss}\left({\varphi }_n,P_n\right)\\ =P_0[1-Z_A(\frac{Q_0}{P_0}\left[1-Z_B\left(\frac{P_n-{\varphi }_n{P}_0}{Q_0}\right)\right]-\frac{P_n}{P_0}+{\varphi }_n,\\ g_{B\to A}{r}_{\infty }\left(Q_0\left[1-Z_B\left(\frac{P_n-{\varphi }_n{P}_0}{Q_0}\right)\right]\right))].\end{array}$$ (31)

A fixed point (ϕ*, r*) of the map (26) corresponds to a 1:1 solution. This 1:1 solution is also represented by a fixed point of the map (31) which occurs at (ϕ*, P*), where P* is the steady-state value obtained from (23) at (ϕ*, r*). Thus the fixed points of the map Π^dyn (26) and Π^ss (31) are equivalent. In the subsections below, we will discuss two distinct ways to find fixed points of these 2-D maps. One way is to use information obtained from the 1-D static map (22) as shown in Section 3.2. The second way is to use a geometric method developed in [4] as shown in Section 3.6.

3.2. Relating fixed points of the static and depressing maps

We now use the 1-D map Π (22) to find fixed points of the 2-D maps that utilize depression. Since we have already shown above how to relate Π^dyn to Π^ss, we will restrict our attention to the relationship between Π and Π^dyn. In particular, we will show that for every value of conductance ${\overline{g}}_{B\to A}$ that produces a fixed point of the 1-D map Π, there exists a corresponding value of g_B→A that produces a fixed point of the 2-D map Π^dyn. Bistability can occur when this relationship is non-invertible.

At a periodic steady state, a depressing synapse behaves like a non-depressing one in that the value r_n converges to r_ss as derived in equation (6), but where the period is determined by the actual period of the feedback network. In particular, at the steady state, at each spike, the voltage of the postsynaptic cell is changed an amount g_B→Ar_ss. This same change can be achieved in a non-depressing model by choosing ${\overline{g}}_{B\to A}{=}_{g_{B\to A}}{r}_{ss}$. In other words, for any steady state value of a depressing synapse given by the pair g_B→A and r_ss, there exists a corresponding value ${\overline{g}}_{B\to A}$ of a non-depressing synapse that yields the same synaptic output. Alternatively, given a value ${\overline{g}}_{B\to A}$ for a non-depressing synapse, we will show there exists a pair g_B→A and r_ss such that ${\overline{g}}_{B\to A}{=}_{g_{B\to A}}{r}_{ss}$. That such a pair exists is not so obvious, because the value r_ss is determined by the steady state period which is itself a function of g_B→A.

A fixed point (ϕ*, r*) of the map Π^dyn (31) satisfies

$$\begin{array}{l}{Q}_0\left[1-Z_B\left(\frac{P_0}{Q_0}\left[1-{\varphi }^{*}-Z_A\left({\varphi }^{*},g_{B\to A}{r}^{*}\right)\right]\right)\right]=P_0\left[1-Z_A\left({\varphi }^{*},g_{B\to A}{r}^{*}\right)\right]\\ Z_B\left(\frac{P_0}{Q_0}\left[1-{\varphi }^{*}-Z_A\left({\varphi }^{*},g_{B\to A}{r}^{*}\right)\right]\right)=1-\frac{{\tau }_r}{Q_0}\ln \left(\frac{1-f{r}^{*}}{1-r^{*}}\right).\end{array}$$ (32)

At the fixed point, the steady state period P* is found by substituting the values ϕ* and r* into equation (23) to obtain P* = P₀[1 − Z_A(ϕ*, g_B→Ar*)]. Because of periodicity, the value r* = r_ss(P*) is calculated from (6) by evaluating at P*. Thus if we were to try to use the depressing map Π^dyn alone, we would end up with an implicit equation for r* which is difficult to solve. Instead, let us exploit the relationship between the 1- and 2-D maps to compute P* independently of r*.

Assume that the 1-D map Π yields a steady-state phase ϕ* of neuron A when the synaptic strength from B to A equals ${\overline{g}}_{B\to A}$. The response $Z_A\left({\varphi }^{*},{\overline{g}}_{B\to A}\right)$ of neuron A to perturbations received at the phase ϕ* is obtained from its PRC given by the equation (4). This determines the steady-state period of neuron A determined by using (16) and is given by $P^{*}=P_0\left[1-Z_A\left({\varphi }^{*},{\overline{g}}_{B\to A}\right)\right]$. We can now use this value of P* with equation (6) to obtain r*. To be able to have the same steady-state solution with the 2-D map, the phase and period must equal ϕ* and P*, respectively and ${\overline{g}}_{B\to A}=g_{B\to A}{r}^{*}$. Thus if the 1-D map Π has a fixed point ϕ* with maximal conductance ${\overline{g}}_{B\to A}$, the 2-D map Π^dyn will have a fixed point at the same fixed phase ϕ* if the following holds

$$P^{*}=P_0\left[1-Z_A\left({\varphi }^{*},{\overline{g}}_{B\to A}\right)\right]$$ (33)

$$r^{*}=\frac{1-\exp \left(P^{*}/{\tau }_r\right)}{1-f\exp \left(P^{*}/{\tau }_r\right)}$$ (34)

$$g_{B\to A}=\frac{{\overline{g}}_{B\to A}}{r^{*}}$$ (35)

To summarize, for a given ${\overline{g}}_{B\to A}$ and associated steady state phase ϕ* of the 1-D map Π, solve (33) to find P*. Substitute this expression into equation (34) to find r*, and in turn use this value in equation (35) to find g_B→A. This procedure yields g_B→A as a function of ${\overline{g}}_{B\to A}$. That is there exists a function h such that

$$\begin{gathered} \begin{array}{l}{g}_{B\to A}=h\left({\overline{g}}_{B\to A}\right)\\ \\ ={\overline{g}}_{B\to A}\frac{1-f\exp \left(P_0\left[1-Z_A\left({\varphi }^{*},{\overline{g}}_{B\to A}\right]\right)/{\tau }_r\right)}{1-\exp \left(P_0\left[1-Z_A\left({\varphi }^{*},{\overline{g}}_{B\to A}\right]\right)/{\tau }_r\right)}.\end{array} \end{gathered}$$ (36)

Alternatively, assume that the 2-D map is used to obtain a fixed point of (ϕ*, r*) with the synaptic conductance from B to A equal to g_B→A. Then the 1-D map can be used with the synaptic strength from B to A equal to ${\overline{g}}_{B\to A}{=}_{g_{B\to A}}{r}^{*}$ to obtain the same steady-state phase of ϕ*. However, a priori, there is no guarantee that the there is a unique pair g_B→A and r* whose product is ${\overline{g}}_{B\to A}$. Uniqueness will occur if the function $h\left({\overline{g}}_{B\to A}\right)$ is invertible. When it is not, bistability can occur.

The potential lack of invertibility of $h\left({\overline{g}}_{B\to A}\right)$ is directly related to the stability of the fixed points of the 2-D map Π^dyn. Indeed while fixed points of the one-dimensional map Π are stable for a large range of ${\overline{g}}_{B\to A}$ values, the 2-D map undergoes two-distinct saddle-node bifurcations as g_B→A is varied. This will be discussed in detail below in Section 3.4.

3.3. Conditions for bistability

We now analyze the relationship $g_{B\to A}=h\left({\overline{g}}_{B\to A}\right)$ given in (36). If this function is invertible, then for each g_B→A there exists a unique value of ${\overline{g}}_{B\to A}$ such that ϕ* is a fixed phase of both the 1-D and 2-D maps. Clearly, this will occur if and only if $h\left({\overline{g}}_{B\to A}\right)$ is monotonic. In the trivial case where there is no depression (f = 1) or if the PRC is zero, g_B→A equals ${\overline{g}}_{B\to A}$, and h is an increasing function. To find where bistability may be possible, let us derive conditions under which $h\left({\overline{g}}_{B\to A}\right)$ can be decreasing on some interval.

For ease of notation, let us temporarily suppress the subscript B → A. Then we can express $h\left(\overline{g}\right)$ as

$$h\left(\overline{g}\right)=\frac{\overline{g}}{r\left(\overline{g}\right)},$$ (37)

where $r\left(\overline{g}\right)$ is found from equation (34). The derivative of the function h is

$$\frac{dh}{d\overline{g}}=\frac{r\left(\overline{g}\right)-\frac{dr}{d\overline{g}}\cdot \overline{g}}{{\left(r\left(\overline{g}\right)\right)}^2}.$$

It is sufficient to find condition under which the numerator is negative. That is, we require the following inequality to hold

$$r\left(\overline{g}\right)<\frac{dr}{d\overline{g}}\cdot \overline{g}.$$

Use the chain rule to find

$$r\left(\overline{g}\right)<\frac{dr}{dP}\cdot \frac{dP}{d\varphi }\cdot \frac{d\varphi }{d\overline{g}}\cdot \overline{g}.$$ (38)

For bistability to occur, equation (38) must be satisfied at the fixed point (ϕ*, r*). Observe that $r\left(\overline{g}\right)$ is always positive, so the right hand side of the inequality has to be positive. By definition, the synaptic conductance $\overline{g}$ is always positive. The derivative dr/dP depends on the steady state plasticity profile which is also always positive by definition. The derivative dP/dϕ depends on the PRC of the neuron, in fact, it equals −dZ/dϕ, which can be positive or negative. The derivative $d\varphi /d\overline{g}$ is obtained from the 1-D map (22). As $\overline{g}$ increases, neuron A receives more inhibition, recovers later, causing θ to increase and ϕ to decrease, hence $d\varphi /d\overline{g}$ is always negative. Thus for the right-hand side of (38) to be positive, dP/dϕ must be negative, or, equivalently, dZ/dϕ must be positive. Therefore, bistability is possible only if the fixed point occurs on the increasing branch of the PRC. This is possible for networks coupled with small synaptic conductances, since small $\overline{g}$ gives large ϕ which falls on the increasing branch of PRC (Figure 1).

So, the first condition for bistability is that, the conductance ${\overline{g}}_{B\to A}$ must be small. In this case, to satisfy the inequality (38), the product of the derivatives on the right hand side must be large enough to compensate the small $\overline{g}$ value. So, we expect to get bistability when these derivatives are large in absolute value. We will next show that we can achieve bistable phase locking solutions with either a PRC that has a steep increasing branch (equivalently large |dP/dϕ|) or with a steady state depression profile that increases rapidly with increasing period (large dr/dP ). If $d\varphi /d\overline{g}$ is large enough, we should also be able to get bistability. However, we do not have direct control over this term, so it is difficult to assess its impact. We will use the QIF model, that has a steep PRC even for small synaptic conductances (Figure 1A) to show that bistability occurs even with a weak depression property (Figure 2A) when |dP/dϕ| is large. We will next show using the ML model if the PRC is small in amplitude for small synaptic conductances (Figure 1B), then a much steeper plasticity profile (Figure 2B) is necessary, i.e., dr/dP has to be large to achieve bistability.

3.4. Bistability with depression in QIF neurons

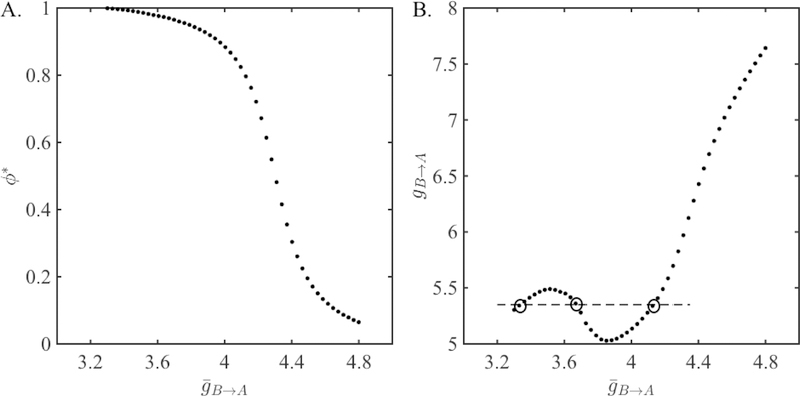
Consider two identical QIF neurons (V_tA = V_tB = 7, V_rA = V_rB = −8). Let the synaptic strength from A to B be fixed at ${\overline{g}}_{A\to B}=4$. We vary ${\overline{g}}_{B\to A}$, the strength from B to A in a range from 3.3 to 4.8. The steady-state phase ϕ* of neuron A obtained from the 1-D map (22) Π as a function of ${\overline{g}}_{B\to A}$ is shown in Figure 4A. We use these values of ϕ* in equation (33) to find P*. Then use equation (34) to determine the value of the depression variable at the steady state (f = 0.5 and τ_r = 5). Finally, use equation (35) to find the value of g_B→A necessary to obtain the same phase locking from the depressing map Π^dyn (26). The non-monotonic relationship $h\left({\overline{g}}_{B\to A}\right)$ between the two synaptic conductances is shown in Figure 4B. Clearly for an interval of values in the range, there exist more than one value of ${\overline{g}}_{B\to A}$ corresponding to a single value of g_B→A. This means that there is more than one solution to the 2-D map for these values of synaptic conductance.

Figure 4:

Phase locking of QIF neurons with static synapses. A. Steady-state intrinsic phase of neuron A obtained from the map Π given in equation (22) as a function of the synaptic coupling strength ${\overline{g}}_{B\to A}$. B. The relationship $g_{B\to A}=h\left({\overline{g}}_{B\to A}\right)$ between the synaptic strengths of the static map Π and the depressing map Π^dyn given in equation (26) obtained from equations (33–35). The dashed horizontal line at g_B→A = 5.35 intersects $h\left({\overline{g}}_{B\to A}\right)$ at three points (inside circles). Two of these are points that correspond to bistability in the presence of synaptic depression.

To understand where this region of non-montonicity lies, we will briefly discuss the bistability conditions for the case of QIF neurons. Note that as the synaptic strength ${\overline{g}}_{B\to A}$ is increased, the phase of neuron A decreases (Figure 4A). The firing period of the network at the steady state is determined by this phase through the PRC of neuron A. A Type I PRC first increases and then decreases in absolute value with increasing phase (Figure 1). Therefore, the network period P* first increases and then decreases as ${\overline{g}}_{B\to A}$ is increased. The steady-state value of depression r* is an increasing function of P*. As a result, r* also first increases and then decreases with increasing ${\overline{g}}_{B\to A}$.

The networks coupled with larger synaptic strengths yield smaller steady-state phases of neuron A (Figure 4A). The PRC is increasing in amplitude for this range of phases. Therefore, for larger synaptic strengths, r* decreases as ${\overline{g}}_{B\to A}$ is increased. The synaptic strength g_B→A equals the ratio ${\overline{g}}_{B\to A}/r^{*}$. Hence, for larger synaptic strengths, g_B→A is always an increasing function of ${\overline{g}}_{B\to A}$, since the numerator ${\overline{g}}_{B\to A}$ is increasing and the denominator r* is decreasing.

On the other hand, for smaller synaptic strengths, the phase locking occurs at`larger phases (Figure 4A), where the PRC is decreasing in amplitude with increasing phase. Here, increasing ${\overline{g}}_{B\to A}$ would yield a smaller phase, a larger period, and a larger r* value. In this case, whether g_B→A is an increasing or a decreasing function of ${\overline{g}}_{B\to A}$ depends on the derivative of r* with respect to ${\overline{g}}_{B\to A}$. When the PRC has a larger derivative (or when the derivative of the plasticity profile is large enough as will be shown next) the increase in r* is large, causing a decrease in g_B→A. The non-monotonicity between the two conductances is observed for smaller ${\overline{g}}_{B\to A}$ (Figure 4B) and bistability occurs for synaptic conductances falling in this range as expected. The intersection of the dashed horizontal line at g_B→A = 5.35 with the graph of $h\left({\overline{g}}_{B\to A}\right)$ illustrates the correspondence of three different ${\overline{g}}_{B\to A}$ values with it.

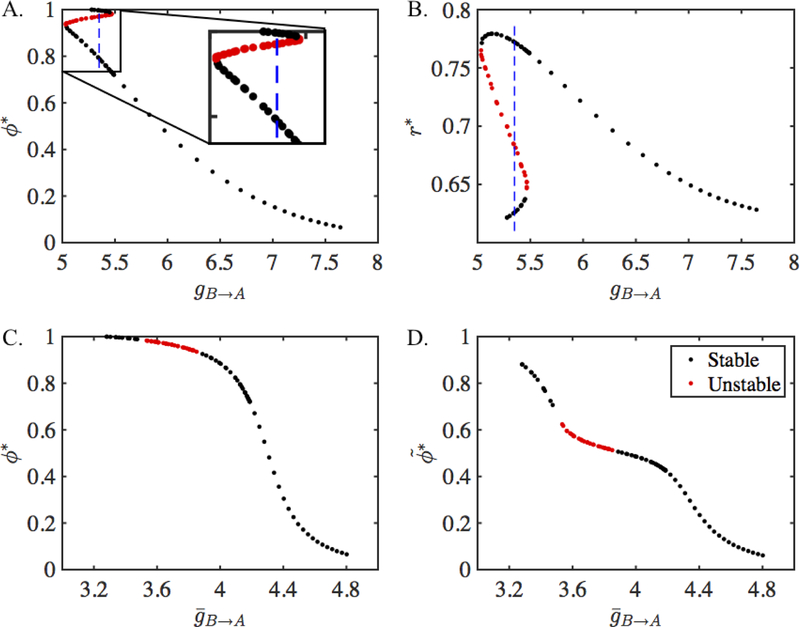
Having discussed conditions for bistability, we now plot the steady-state phase values obtained from the 2-D map. Figure 5 shows the fixed points of the map Π^dyn as a function of g_B→A. The steady-state phases ϕ* are shown in Figure 5A and the value of the depression variable r* is shown in Figure 5B. The stability of the fixed points can be found numerically as explained below. The stable solutions are shown in black and the unstable solutions are shown in red in the figure. For g_B→A small, there are three fixed points, two of which are stable. Therefore, the network has bistability for this range of synaptic strength and is capable of exhibiting hysteresis. We plot the results of the 2-D map as a function of the total synaptic conductance ${\overline{g}}_{B\to A}{=}_{g_{B\to A}}{r}^{*}$ in Figure 5C. The fixed points agree with the ones obtained from the 1-D map Π which are shown in Figure 4A. Solutions corresponding to an interval of g_B→A values obtained from the 2-D map are unstable (red dots) while others are stable (black dots). In contrast, all the solutions obtained from the 1-D map are stable. Finally, we show the activity phases ${\tilde{\varphi }}^{*}$ of neuron A in Figure 5D. These are the actual phases (13) of neuron A at the steady state.

Figure 5:

Fixed points of the 2-D map Π^dyn given in Equation (26) and their equivalence with the fixed points of the map Π given in Equation (22). A. Steady-state intrinsic phase of neuron A obtained from Π^dyn as a function of $g_{B\to A}$. Dashed vertical line at g_B→A = 5.35 lies within the region of bistablity which is also shown in the inset. B. The steady-state value of the depression variable obtained from Π^dyn as a function of $g_{B\to A}$. C. The steady-state intrinsic phase of neuron A obtained from the depressing map Π^dyn is equivalent to the phase obtained from the static map Π (compare with Figure 4A) when plotted as a function of ${\overline{g}}_{B\to A}{=}_{g_{B\to A}}{r}^{*}$ = g_B→Ar*. D. The steady state activity phase ${\tilde{\varphi }}^{*}$ of neuron A obtained from Π^dyn.

The bistability occurs in this model due to saddle-node bifurcations occuring as g_B→A varies. To understand the origin of these saddle-node bifurcations, consider first the stability condition for fixed points of the 1-D map as derived in [17]. If ϕ* is a fixed point of Π, with a corresponding θ* value, then the fixed point is (asymptotically) stable if $\left|\left({Z^{\prime }}_A\left({\varphi }^{*},{\overline{g}}_{B\to A}\right)+1\right)\left(Z_B^{\prime }\left({\theta }^{*}\right)+1\right)\right|<1$. For a large range of values of ${\overline{g}}_{B\to A}$, this condition is met and fixed points of the 1-D map are stable.

To determine whether the corresponding fixed point x* = (ϕ*, r*) of the 2-D map (26) is stable, we compute the eigenvalues µ₁ and µ₂ of the Jacobian matrix, A, obtained by linearizing about a fixed point. These eigenvalues depend continuously on parameters and, in particular, on g_B→A. If none of the eigenvalues lie on the unit circle, i.e., $\left\{\mu \in ℂ:\left|\mu \right|=1\right\}=\varnothing$, then the point x* is hyperbolic. The hyperbolicity condition can be violated in three ways leading to different bifurcations. If one of the eigenvalues, say µ₁, passes through 1, then a saddle-node bifurcation occurs. If µ₁ passes through −1, then a flip bifurcation occurs. If both eigenvalues µ₁ and µ₂ are complex and pass through $\left|{\mu }_1\right|=\left|{\mu }_2\right|=1$, then a Neimark-Sacker bifurcation occurs.

The Jacobian matrix is given by

$$A=\left(\begin{array}{cc}\frac{\partial {\Pi }_1^{dym}}{\partial \varphi }& \frac{\partial {\Pi }_1^{dyn}}{\partial \varphi }\\ \frac{\partial {\Pi }_2^{dym}}{\partial \varphi }& \frac{\partial {\Pi }_2^{dyn}}{\partial \varphi }\end{array}\right).$$

The partial derivatives are

$$\begin{gathered} \frac{\partial {\text{Π}}_1^{dyn}}{\partial \varphi }=\left[Z_B^{\prime }\left(\theta \right)+1\right]\left[\frac{\partial Z_A}{\partial \varphi }\left(\varphi ,g_{B\to A}r\right)+1\right] \\ \frac{\partial {\text{Π}}_1^{dyn}}{\partial r}=\left[Z_B^{\prime }\left(\theta \right)+1\right]\frac{\partial Z_A}{\partial r}\left(\varphi ,g_{B\to A}r\right) \\ \frac{\partial {\text{Π}}_2^{dyn}}{\partial \varphi }=\frac{P_0}{{\tau }_r}{Z}_B^{\prime }\left(\theta \right)\left[1-fr\right]\left[1+\frac{\partial Z_A}{\partial \varphi }\left(\varphi ,g_{B\to A}r\right)\right]\exp \left(\frac{Q_0}{{\tau }_r}\left[1-Z_B\left(\theta \right)\right]\right) \\ \frac{\partial {\text{Π}}_2^{dyn}}{\partial r}=\left[f+\frac{P_0}{{\tau }_r}{Z}_B^{\prime }\left(\theta \right)\left[1-fr\right]\frac{\partial Z_A}{\partial r}\left(\varphi ,g_{B\to A}r\right)\right]\exp \left(\frac{Q_0}{{\tau }_r}\left[1-Z_B\left(\theta \right)\right]\right) \end{gathered}$$ (39)

where $\theta =\frac{P_0}{Q_0}\left[1-\varphi -Z_A\left(\varphi ,g_{B\to A}r\right)\right]$ and $Z_B^{\prime }$ denotes derivative with respect to ϕ. The PRC of the QIF model neuron is given in Equation (4). Taking derivatives of the PRCs of neurons A and B yields

$$\begin{array}{l}{Z}_B^{\prime }\left(\theta \right)=\frac{{\sec }^2\left(Q_0\theta +\arctan V_{r_B}\right)}{1+{\left[\tan \left(Q_0\theta +\arctan V_{r_B}\right)+{\overline{g}}_{A\to B}\right]}^2}-1,\\ \frac{\partial Z_A}{\partial \varphi }\left(\varphi ,g_{B\to A}r\right)=\frac{{\sec }^2\left(P_0\varphi {+}_{g_{B\to A}}tan{V}_{r_A}\right)}{1+{\left[\tan \left(P_0\varphi +\arctan V_{r_A}\right)+g_{B\to A}\right]}^2}-1,\\ \frac{\partial Z_A}{\partial r}\left(\varphi ,g_{B\to A}r\right)=\frac{{\overline{g}}_{B\to A}}{P_0+\left[1+{\left[\tan \left(P_0\varphi +\arctan V_{r_A}\right){+}_{g_{B\to A}}r\right]}^2\right]}.\end{array}$$ (40)

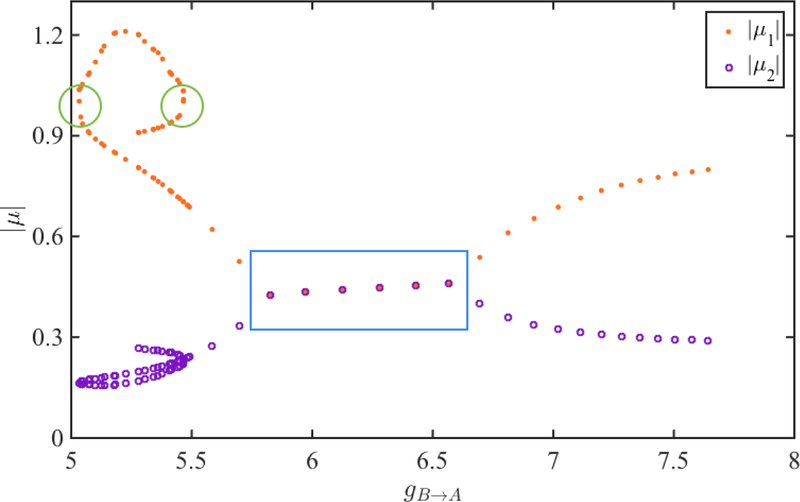
We numerically evaluate the Jacobian matrix A at a the fixed point x* = (ϕ*, r*) of the map. The absolute values of the two eigenvalues µ₁ (orange dots) and µ₂ (purple circles) corresponding to each fixed point are shown in Figure 6. When the eigenvalues are both complex, their absolute values are equal (blue box). We see that the absolute value of one of the eigenvalues (µ₁) exceeds 1 (green circles) when g_B→A is small. We find that as g_B→A varies, two distinct saddle node bifurcations occur as µ₁ passes through the value 1 when g_B→A equals 5.06 and 5.47. Thus when g_B→A lies between these values, there are multiple fixed points some of which are stable and others unstable. It is in this region in parameter space that bistability of solutions occurs.

Figure 6:

The dependence of the eigenvalues µ₁ and µ₂ of the depressing map (26) on the parameter g_B→A. The absolute values of µ₁ and µ₂ are shown in orange and purple, respectively. These values overlap for complex eigenvalues (blue box). The fixed points are stable when both eigenvalues are less than 1 in absolute value. The fixed points lose (regain) stability via saddle-node bifurcation when µ₁ is greater (less) than 1 (green circles).

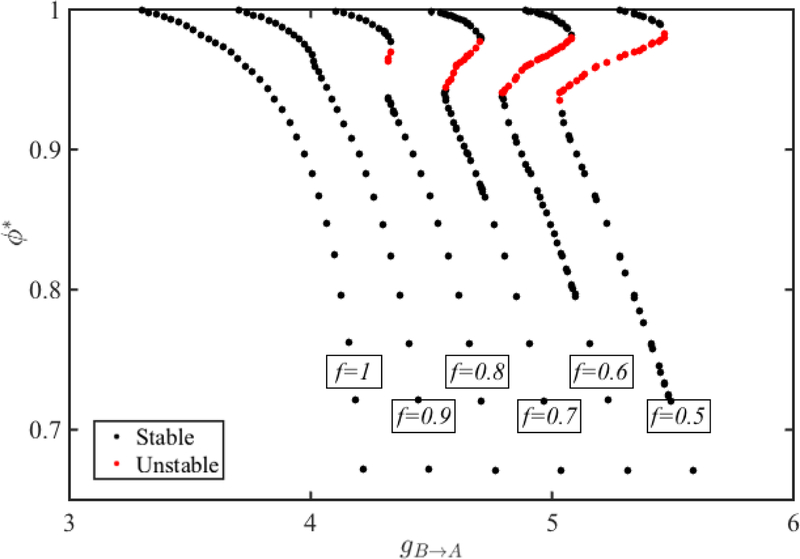
We also note that for fixed g_B→A, stability depends on the depression parameters f and τ_r as can be seen in Equations (39) and (40). Figure 7 demonstrates the change in the bistability region for QIF neurons as the parameter f that controls the extent of synaptic depression is varied. Using the same approach as above, we first obtain the fixed points of the map Π and use the equivalence relations given by equation (33)–(35) to obtain the fixed points of the map Π^dyn. We keep the parameters that govern the neuronal and synaptic dynamics same except the parameter f is varied from 0.5 to 1.

Figure 7:

The dependence of bistability in QIF neurons on the parameters that govern synaptic depression (5). The unstable region increases and the region of bistability changes as f is decreased from left to right. A similar change is observed as τ_r is increased.

When f = 1, there is no depression and only one stable fixed point exists for each value of g_B→A. As f decreases, the extent of the depression becomes larger and a region of bistability emerges. The region of unstable solutions occurs over a larger interval of g_B→A values as f decreases. But the range of stable phases covered on the upper branch for each value of f does not change much. The region of bistability along the lower branch does shift to smaller phases. Therefore, as the synapse from B to A gets more depressing, the smaller stable phase of neuron A gets smaller in the bistability region. An effect similar to the one observed when f is decreased exists when τ_r gets larger since this also results in stronger synaptic depression.

3.5. Bistability with Depression in ML Neurons

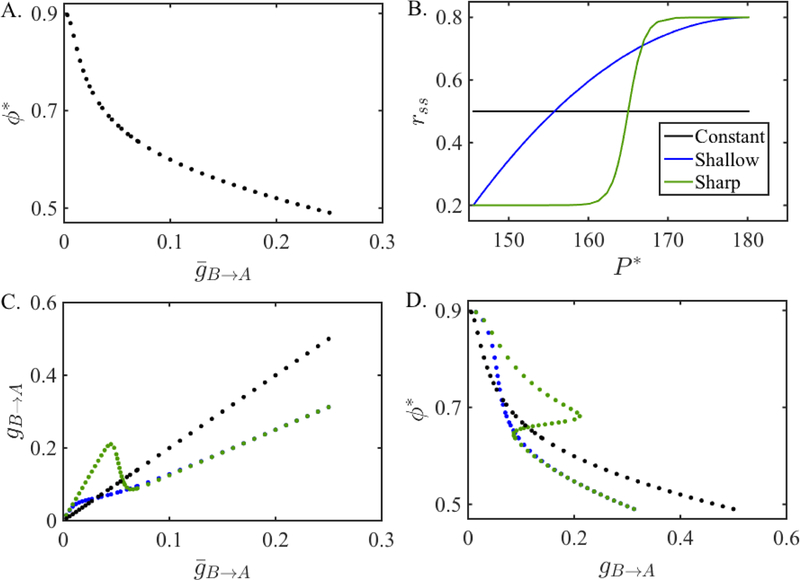
We now show how ML neurons can exhibit bistability. We first couple two ML neurons with static synapses. We let ${\overline{g}}_{A\to B}$ be fixed at 0.1 and find the steady state network phase for a set of ${\overline{g}}_{B\to A}$ varying between 0.001 and 0.25. The steady state phase ϕ* of neuron A changes between 0.5 and 0.9 for this range of synaptic strengths and is shown in Figure 8A.

Figure 8:

Existence of bistability in ML neurons depending on the steady state plasticity profile. A. The steady-state intrinsic phase of neuron A obtained from the static map Π given in equation (22) as a function of the synaptic conductance ${\overline{g}}_{B\to A}$. B. Different steady state plasticity profiles r_ss used in the depressing map Π^ss given in equation (31). C. The relationship between the synaptic conductances of the static map Π and the depressing map Π^ss for different r_ss. D. The steady-state intrinsic phase ϕ* of neuron A obtained from the map Π^ss for different r_ss as a function of the synaptic conductance g_B→A. Notice that the bistability region exists only when a sharp steady state profile is used.

Since the increasing branch of the ML PRC is not as steep as that of the QIF, in order to obtain bistability, we need to rely on the synaptic plasticity profile changing quickly enough. To show the dependency on the derivative of the plasticity profile, we use three different steady state synaptic plasticity profiles r_ss. To change the synaptic plasticity profile r_ss, we will change the function r_∞ in equation (9). Based on the approximation $r_{ss}\approx r_{\infty }$, we will assume that the changes are made directly to the function r_ss itself.

The first synaptic plasticity profile we use is constant, r_ss(P ) = 0.5 (black line in Figure 8B). It gives results equivalent to the case when there is no depression at all and is shown for comparison purposes with the other profiles. As the second plasticity profile, we choose a quadratic function (blue curve in Figure 8B) that compares with the plasticity profile used for the QIF model (Figure 2A). The minimum and maximum values of the depression variables are denoted by r_min and r_max and are chosen to have the values 0.2 and 0.8, respectively. It is given by the function r_ss(P ) = (r_max − r_min)((P − P_max)/(P_min − P_max))² + r_max, where P_min and P_max are the minimum and maximum values the period of the neuron B takes at the steady state when coupled with static synapses. The third plasticity profile is modeled by a hyperbolic tangent function given in equation (9) (green curve in Figure 8B). We shall refer to the plasticity profiles modeled by the constant, quadratic and hyperbolic tangent functions as the constant, shallow and sharp plasticity profiles, respectively.

Although the equations (33)–(35) are derived for the map Π^dyn, we can adjust them for the map Π^ss given by equation (31) and find the value of the synaptic conductance value g_B→A of the depressing map Π^ss corresponding to the solution of the static map Π for each conductance ${\overline{g}}_{B\to A}$. The relations between the two conductances for each plasticity profile are shown in Figure 8C. We see that for the constant r_ss function, the relation between the conductances (black line) is simply linear $\left(g_{B\to A}={\overline{g}}_{B\to A}/2\right)$ and always increasing as expected. For the shallow r_ss function, the relation between the conductances (blue curve) is nonlinear but still increasing. On the other hand, for the sharp r_ss function, the curve that shows the relation between the conductances (green curve) first increases, then decreases for a region of small conductance values and then increases again. We expect to get bistability for conductances that fall in this range of nonmonotonicity as there are three ${\overline{g}}_{B\to A}$ values for a given g_B→A.

We next compute the steady state phase ϕ* of neuron A using the map Π^ss for each g_B→A as shown in Figure 8D. We do this by plotting the phases found from the 1-D map Π on the g_B→A axis. For the constant r_ss function, the phase ϕ* is the same with the phase obtained from the map Π (compare with Figure 8A). When the shallow r_ss function is used, the curve defining the relation between the phase ϕ* and the synaptic conductance g_B→A slightly bends for small synaptic conductances but no bistability is observed. However, when the sharp r_ss function is used, we can see that there are three steady states for a range of small synaptic conductances. We find that the middle phase is unstable, therefore there are two stable steady states for this range of synaptic conductances.

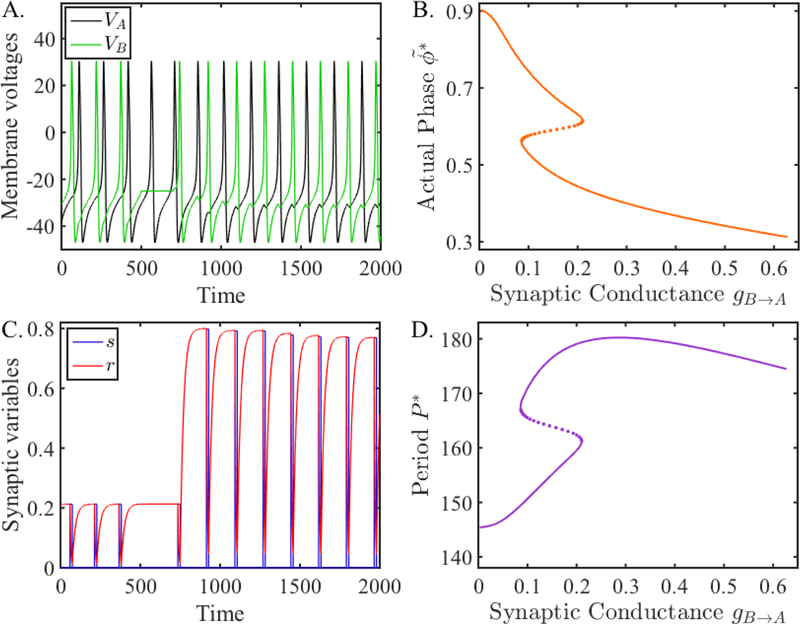
Next we show this bistability in a simulation of the coupled network. We numerically solved (12) using XPPAUT [20]. Figure 9 shows an example of bistability exhibited by this network. Panel A shows the voltage traces of the two neurons, while panel C shows the evolution of the r variable. At the start of the simulation, the two neurons are oscillating out of phase with one another. Cell A (black trace) sends a fixed synaptic conductance g_A→B = 0.1 to B (green trace), while the conductance from B to A has a maximum given by r_ssg_B→A = 0.212 ∗ 0.125 = 0.0265. Thus the maximal synaptic conductance from A to B is stronger than B to A and thus A delays the firing of B more than vice versa. At t = 900, we transiently hyperpolarized neuron B for a duration of t = 200 msecs. During this time, the r variable is being primed to grow because the cycle period of B will become much longer. Indeed, when B is released from the hyperpolarization, r is seen to grow very rapidly as the cycle period P_c has been updated yielding a new target r_∞(P_c) for r to approach. The steady state configuration that the cells settle into is nearly anti-phase where the time between successive spikes is almost identical. This is reflected in the synaptic conductance r_ssg_B→A = 0.767 ∗ 0.125 = 0.0959 being almost equal to ${\overline{g}}_{B\to A}=0.1$. Panel B shows a graph of the actual phase (13) of neuron A and panel D shows a graph of network period versus g_B→A. The Z- and S-shaped curves in these panels indicate the existence of bistability. The simulation shown in panel A was conducted at g_B→A = 0.125 which is within the region of bistability. The lower (upper) parts of the curve in panel D (B) corresponds to the early part of the time traces in panels A and C. Here the synapse from B to A is weak because the period of the network is small and vice versa, namely, the period is small because the synapse from B to A is weak. The upper (lower) portion of the curve in panel D (B) corresponds to the latter part of the time traces after the network again reaches a steady state. Now the period is long giving the chance for the synapse from B to A to strengthen and because the synapse is strong, the period is long.

Figure 9:

Simulation of coupled ML neurons compared with fixed points of the map Π^ss (31). A. Membrane voltages of two ML neurons coupled with inhibitory synapses when the B to A synapse is depressing. The network locks at two different phases. From t = 900 to 1, 100, neuron B is hyperpolarized, causing the network to switch to the other phase-locked solution. B. Activity phase versus synaptic conductance obtained from the map Π^ss. C. The evolution of the synaptic variables from neuron B to A. D. Period of neuron A (also neuron B) versus synaptic conductance obtained from the map Π^ss. The Z-shaped (S-shaped) curve in panel B (panel D) shows the different phases (periods) that exist over a range of conductance values of g_B→A. The lower and upper branches represent stable solutions, while the dotted middle branch represents unstable solutions. The simulations in the left two panels occur for g_B→A = 0.125, where for t < 900, the phase-locked solution corresponds to a point on the upper (lower) branch, and for t > 1100, the solution converges to a phase-locked solution on the lower (upper) branch.

3.6. Geometric Approach to Finding Fixed Points

In the previous section, we found fixed points of the 2-D map Π^ss by utilizing information obtained from the 1-D map. We now describe an alternate, geometric way to find fixed points of 2-D maps that we had developed in a separate paper [4]. To briefly describe the idea consider first a generic 1-D map, x_n+1 = f (x_n). The geometric method that one would use to find fixed points would be to look for intersections of the graph of y = f (x) with the diagonal y = x. The generalization of this idea to a generic 2-D map x_n+1 = F (x_n, y_n), y_n+1 = G(x_n, y_n) is to view the graphs of F (x, y) and G(x, y) as surfaces in appropriate spaces and look for their intersection with relevant planes. By then projecting the resulting curves onto a common plane, we can identfiy intersections of those two curves as fixed points of the 2-D map.

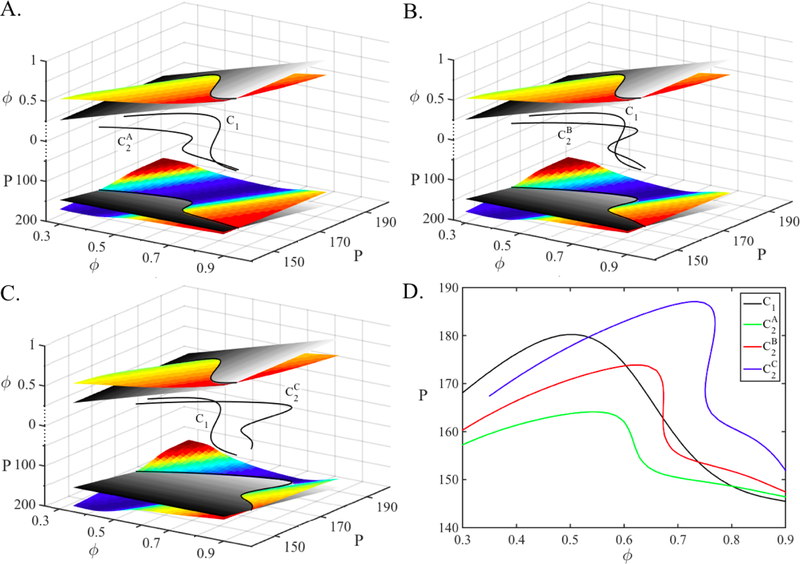
A fixed point (ϕ*, P*) of the map Π^ss given in equation (31) occurs when ${\varphi }^{*}={\Pi }_1^{ss}\left({\varphi }^{*},P^{*}\right)$ and $P^{*}={\Pi }_2^{ss}\left({\varphi }^{*},P^{*}\right)$. The two functions $z_1={\Pi }_1^{ss}\left(\varphi ,P\right)$ and $z_2={\Pi }_2^{ss}\left(\varphi ,P\right)$ each define 2-D surfaces. Both functions have the same domain, but have different ranges; the former lies in the ϕ direction and the other in the P direction. We can visualize how the fixed points are obtained by plotting these surfaces in an augmented ℝ³ space. We plot the surfaces ${\Pi }_1^{ss}\left(\varphi ,P\right)$ and ${\Pi }_2^{ss}\left(\varphi ,P\right)$ on the same coordinate axis, above and below the z = 0 plane, respectively in Figure 10A–C. The first condition for fixed points, ϕ* = Π^ss(ϕ*, P*) lies along the curve obtained at the intersection of the surface $z_1={\Pi }_1^{ss}\left(\varphi ,P\right)$ and the plane z₁ = ϕ. Similarly, the condition $P^{*}={\Pi }_2^{ss}\left({\varphi }^{*},P^{*}\right)$ is satisfied along the curve obtained at the intersection of the surface $z_2={\Pi }_2^{ss}\left(\varphi ,P\right)$ and the plane z₂ = P. In each case, we are intersecting two, 2-D surfaces which results in a 1-D curve. These intersection curves are shown in black above and below the z = 0 plane. Their projections on the z = 0 plane are also shown which are denoted by C₁ and C₂, respectively. The fixed points of the must lie on both curves; hence it lays on their intersection as shown on the z = 0 plane.

Figure 10:

Fixed points of the map Π^ss (31). A–C. The creation of fixed points of the map for different sets of parameters. The surfaces ${\Pi }_1^{ss}\left(\varphi ,P\right)$ and ${\Pi }_2^{ss}\left(\varphi ,P\right)$ are drawn above and below the z = 0 plane denoted by the axes z₁ = ϕ and z₂ = P, respectively. The intersection of the surface $z_1={\Pi }_1^{ss}\left(\varphi ,P\right)$ with the plane z₁ = ϕ and the intersection of the surface $z_2={\Pi }_2^{ss}\left(\varphi ,P\right)$ with the plane z₂ = P yield the two black curves above and below the z = 0 plane. The fixed points of the maps lay on the intersection of the two fixed point curves whose projections C₁ and C₂ on the z = 0 plane are shown. There is one fixed point in A and C while there are three fixed points in B, depending on the value of the g_B→A. D. The projections of the fixed point curves, C₁ and C₂ are drawn on the same coordinate axes for three parameter sets. The curveC₁ is the same for all parameter sets while C₂ changes. Creation and annihilation of multiple fixed points with changing parameters is observed.

The graphs of the surfaces $z_1={\Pi }_1^{ss}\left(\varphi ,P\right)$ and $z_2={\Pi }_2^{ss}\left(\varphi ,P\right)$ clearly depend on the choice of steady state synaptic plasticity profile and associated parameters. For this section we use the sharp plasticity profile as defined in equation (9). The parameters are the same in all subfigures and are given in Section 3.5 except the conductance g_B→A We choose g_B→A to equal 0.075, 0.125 and 0.225 in A, B and C, respectively. We expect to get one fixed point when g_B→A equals 0.075 or 0.225 as these values lay to the left and right of the bistability region, respectively, and three fixed points when g_B→A equals 0.125, as shown in Figure 8D.

The curve C₁ is common to all three cases. The reason that C₁ is fixed for all three cases is that when the value g_B→A changes, only the PRC Z_A changes. So, the only term that differs in the map Π^ss for the three cases is Z_A. The term Z_A only appears in the ${\text{Π}}_2^{ss}$ equation and it does not appear in the ${\text{Π}}_1^{ss}$ equation. Therefore, when g_B→A changes, only the curve C₂ moves and C₁ stays constant. The curve $C_2^A$ lies mostly below the curve C₁ and they intersect at only one point in Figure 10A. Hence there is only one fixed point when g_B→A = 0.075, as expected. When g_B→A is increased to 0.125, the curve $C_2^B$ bends and is pushed more in the P direction (y axis), creating three intersections with C₁ in Figure 10B. The intersections, hence the fixed points occur at smaller phase and larger period values compared to case A. When g_B→A is increased to 0.225, the curve $C_2^C$ is pushed more in the P direction, and lies mostly above C₁ and only one fixed point remains. This fixed point has a smaller phase and a larger period value compared to the cases A and B.

The projections of the fixed point curves, C₁ and C₂, are drawn on the same coordinate axes for three parameter sets in Figure 10D. The black curve is C₁, the intersection of the surface $z_1={\Pi }_1^{ss}\left(\varphi ,P\right)$ and the plane z₁ = ϕ and, as discussed above, is the same for the three parameter sets. The colored curves are C₂, the intersections of the surfaces $z_2={\Pi }_2^{ss}\left(\varphi ,P\right)$ and the planes z₂ = P. As C₂ moves and its intersection with C₁ changes, the number of fixed points and their values change. It is easier to see in this figure that as the value of g_B→A increases, the curve C₂ moves up causing fixed points with smaller phase and larger period values. It is also easy to see that fixed points are gained and lost through saddle-node bifurcations of fixed points, similarly to the QIF model.

4. Discussion

Numerous theoretical and computational studies have utilized PRCs to explore phase-locking in oscillatory neuronal networks [2, 4, 11, 18, 17, 23, 41, 44]; see [10] for a review. Some studies assume short or weak perturbations and use iPRCs [11, 18], while others use more general PRCs [37, 41] obtained from inputs that are not necessarily weak. In the case of strong inputs, PRCs do not necessarily scale linearly with input strength. Additionally, experimental work has shown that PRCs computed using realistic synaptic inputs can differ significantly from those computed with either weak or strong current pulse injections [22]. In turn, these differences can lead to qualitative and quantitative differences in phase-locking properties of coupled neurons.

An additional level of complexity arises when dealing with realistic neuronal networks. Namely, the amplitude of the synaptic current may change with the short-term history of activity. This property, known as short-term synaptic plasticity, is observed in most synaptic connections and, in oscillatory networks, results in gain modulation, or a modification of synaptic strength as a function of presynaptic firing rate. If the presynaptic activity approaches a periodic state, the synaptic strength approaches a steady state. In models of synaptic transmission, this leads to a maximum and minimum value of the variables governing the synaptic dynamics along the periodic solution [8, 12]. In [4], we defined the steady-state plasticity profile to correspond to the maximum value of the synaptic strength as a function of presynaptic frequency. We further showed how to use this function, together with PRCs, to determine phase locking in a pair of inhibitory cells in which the underlying equations governing the activities of the cells and synapses need not be known.

Bistability of periodic firing patterns in the presence of synaptic plasticity has been studied by us [7, 8, 14] and others [33, 50]. In most of these cases, some sort of model equations were utilized to conduct the analysis. Here, using the methods developed in [24] and [4], we show how synaptic depression gives rise to bistability of periodic solutions in reciprocally connected networks when the only cellular information that is available is the PRCs of the neurons. For neurons that display Type I PRCs [19], we derived two distinct but related 2-D maps whose fixed points correspond to phase-locked solutions of the coupled network. As the maximal strength of the depressing synapse is changed, the fixed points of these map undergo two distinct saddle-node bifurcations that bookend a region of bistability and hysteresis.

Through our analysis, we obtained a condition in the form of an inequality that dictates when bistability can occur. This condition depends on both neuronal and synaptic dynamics and requires a strong postsynaptic response that is either phase or period dependent. This strong effect can either be achieved if the neuron has a steep PRC (phase dependency) or a steep steady state depression profile (period dependency). We showed each of these situations, respectively, in the context of QIF and ML model neurons.

In the case of QIF neurons, the amplitude of the PRC is relatively large and the increasing branch of the PRC is very steep (Figure 1A). This steepness implies that the delay caused by a synaptic perturbation depends heavily on the phase of the perturbation received, i.e., the neuron is phase-sensitive to perturbations even for small synaptic strengths. In networks of such neurons, a weak short-term synaptic depression property (as in Figure 2A) is enough to create bistable phase locking modes of the network.

In the case of ML neurons, the PRC changes significantly as synaptic strength is changed (Figure 1B). However, the PRC has a small derivative for small synaptic conductances, which are of interest here. In this case, a weak short-term synaptic depression property is not enough to create bistable phase locking modes. This was demonstrated by choosing different forms of the steady state depression profile and showing that only those profiles that exhibit sharp changes (as in Figure 2B) lead to bistability, either in numerical simulations (Section 3.5) or via the geometric method of intersecting surfaces (Section 3.6).

The techniques derived in this paper build on the work of many other researchers who have used maps, based on inter-spike intervals, to derive conditions for phase locking (see, e.g., [11, 13, 17, 41]). As in the present study, in most of these studies, qualitative as well as quantitative properties of the PRC are used to conduct the analysis. Oprisan [39] developed similar geometric methods that depended on the shape of the PRC in order to assess phase locking, but synaptic plasticity was not considered. Very recently, Oprisan and Austin [40] have introduced a method to incorporate the response of two stimuli within a single cycle of oscillation. They develop a two-stimulus response surface which shares similarities in approach to our geometric method involving surfaces of PRCs. From a methodological viewpoint, our approach in the current study demonstrates the usefulness of developing maps that simultaneously track the dynamics of short-term synaptic plasticity and the PRC effects in order to explore the stable states of recurrent networks.

Few experimental studies have definitively demonstrated the functional roles of short-term synaptic plasticity at the network and behavior levels. However, the role of synaptic dynamics in network output is a rapidly growing area of research [5]. Short-term depression plays a prominent role in the activity of several oscillatory networks, including the thalamocortical system [15], electrosensory processing in weakly electric fish [6], olfactory processing [43], auditory processing [38] and central pattern generation [47]. The proposed mechanism in our study, that the shape of the PRC and depression profiles may result in the existence of bistability, indicates a form of short-term memory that can arise in such oscillatory networks, similar to those proposed for working memory [45]. Additionally, a simple modification of the PRC or depression profiles, for example by neuromodulation, may lead to transitions of the network in or out of states that allow for such activity-dependent short-term memory states. The existence and modulation of these bistable states may allow for gating information flow, especially in the context of sensory processing.