Aggrecan Nanoscale Solid—Fluid Interactions Are a Primary Determinant of Cartilage Dynamic Mechanical Properties

Abstract

Poroelastic interactions between interstitial fluid and the extracellular matrix of connective tissues are critical to biological and pathophysiological functions involving solute transport, energy dissipation, self-stiffening and lubrication. However, the molecular origins of poroelasticity at the nanoscale are largely unknown. Here, the broad-spectrum dynamic nanomechanical behavior of cartilage aggrecan monolayer is revealed for the first time, including the equilibrium and instantaneous moduli and the peak in the phase angle of the complex modulus. By performing a length scale study and comparing the experimental results to theoretical predictions, we confirm that the mechanism underlying the observed dynamic nanomechanics is due to solid–fluid interactions (poroelasticity) at the molecular scale. Utilizing finite element modeling, the molecular-scale hydraulic permeability of the aggrecan assembly was quantified (k_aggrecan = (4.8 ± 2.8) × 10⁻¹⁵ m⁴/N • s) and found to be similar to the nanoscale hydraulic permeability of intact normal cartilage tissue but much lower than that of early diseased tissue. The mechanisms underlying aggrecan poroelasticity were further investigated by altering electrostatic interactions between the molecule’s constituent glycosaminoglycan chains: electrostatic interactions dominated steric interactions in governing molecular behavior. While the hydraulic permeability of aggrecan layers does not change across species and age, aggrecan from adult human cartilage is stiffer than the aggrecan from newborn human tissue.

Graphical Abstract

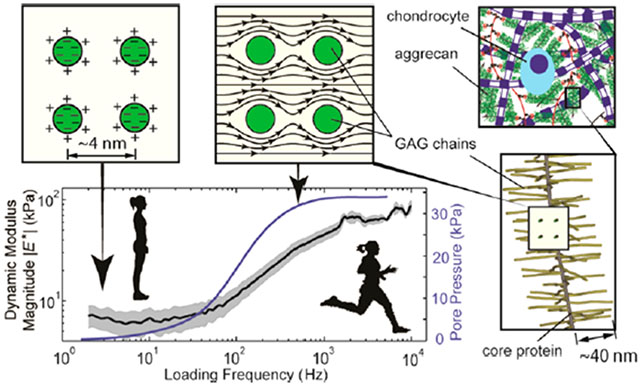
An area of significant interest and techological importance has been the nanoscale mechanisms underlying the macroscopic dynamic mechanical properties of hydrated biological and non-biological materials that are responsible for important functions such as fluid permeation, solute and drug transport,^1–3 energy dissipation and self-stiffening,^4,5 and lubrication and cellular mechanotransduction.^6–8 Recent advances in instrumentation have enabled the quantification of nanoscale-time-dependent properties in various hydrated tissues,^9–12 hydrogels^6,13,14 and macromolecules.^11,15–21 It has been hypothesized that two molecular mechanisms underlie the observed nanoscale dynamic mechanical properties: solid–fluid interactions (poroelasticity) or fluid flow-independent intrinsic macromolecular viscoelasticity.^22,23 The poroelasticity mechanism obeys a specific length scale dependence (e.g., the length scale over which fluid flows),^5,24 while intrinsic molecular viscoelasticity does not show this dependence.^25,26 The limited frequency bandwidth of experimental instruments utilized to date has precluded measurement of the broad dynamic spectrum necessary to decouple poro- and viscoelastic phenomena based on length scale tests. In the present study, we utilized a custom-built high-bandwidth (frequency range, f ~1 Hz to 10 kHz) atomic force microscope (AFM)-based nanorheology system⁴ to quantify the broad spectrum dynamic nanomechanical behavior of a model biomacromolecular system, cartilage aggrecan, and to subsequently identify the mechanisms underlying molecular rheology.

Cartilage is an important hydrated biomacromolecular tissue (70–80% water by weight) that exhibits rate-dependent macroscopic dynamic mechanical properties and allows for proper physiological joint function over a wide range of frequencies.²⁷ The two major structural constituents of cartilage are a self-assembled gel of aggrecan monomers enmeshed within a self-assembled network of collagen fibrils. The negative charges on the glycosaminoglycan (GAG) chains of aggrecan (Figure 1a), along with their associated counterions, exert high nanoscale electrical double layer repulsive forces and associated osmotic interactions that result in a high intramolecular and intratissue water content. We chose aggrecan as a model biomacromolecule for this study because it has been hypothesized that the small spacing between neighboring GAG chains (~3 nm²⁸), which is much smaller than the average spacing between collagen fibrils (~100 nm²⁹), determines the fluid permeability of the aggrecan gel and is therefore the molecular origin of poroelasticity in cartilage. Aggrecan was also chosen as a model system because of its critical role in the pathophysiology of diseases such as osteoarthritis (OA).^30—32 At the earliest stages of OA, proteolytic degradation of GAG-containing aggrecan (16) makes cartilage especially susceptible to degradation during high-rate (dynamic) joint activities.⁴ Since mechanical loading of many tissues upregulates cell synthesis and deposition of a locally enriched aggrecan gel (e.g., in the intervertebral disc and the fibrocartilaginous regions of tendons and ligaments,^33,34 and even in regulating structural and dynamical plasticity in the microenvironment of nervous system³⁵), the basic work in this study is broadly relevant to many examples of mechanobiology.

Figure 1.

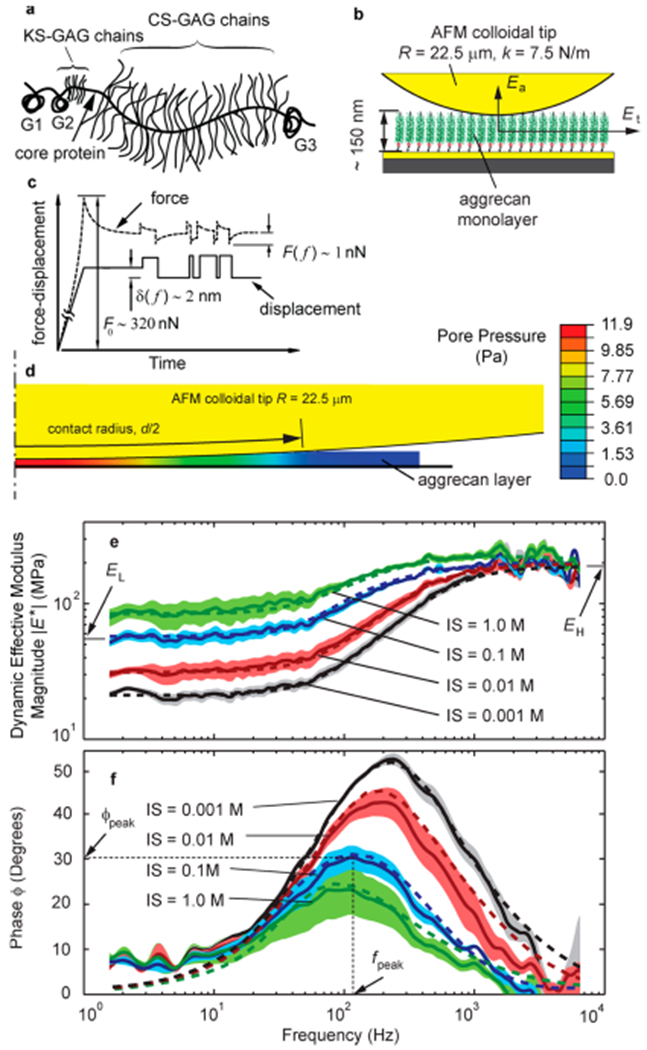
High frequency atomic force microscope (AFM)-based rheology of aggrecan monolayer. (a) Schematic drawing of aggrecan showing chondroitin sulfate (CS) GAG, keratan sulfate (KS) GAG, core protein and globular domains G1, G2 and G3. (b) Aggrecan monolayer is end-grafted on a gold-coated substrate and indented by gold-coated AFM colloids. (c) Loading profile is composed of an initial indentation at a specified force, followed by a random binary sequence (RBS) in displacement with step size of 2 nm covering the frequency range of 1 Hz to 10 kHz. (d)The fluid pressurization due to dynamic mechanical loading and the resulting fluid flow along the contact distance are simulated by finite element modeling. (e and f) The magnitude and phase of the dynamic effective modulus of newborn human aggrecan is measured at different ionic strength of 0.001, 0.01, 0.1, and 1 M in NaCl solution (solid lines). The mean (solid line) and 95% confidence interval (shaded area) are based on n = 6 different locations on the substrate. The simulation by the transversely isotropic finite element model (dashed lines) shows a close match to the experimental data.

The goals of the current study are to (1) quantify the broad spectrum (frequency range, f ~1 Hz to 10 kHz) dynamic nanomechanical behavior of a biomimetic, end-grafted cartilage aggrecan monolayer assembly (Figure 1b), including the low frequency (equilibrium) modulus E_L, high frequency (instantaneous) modulus E_H, and the characterstic frequency f_peak (the frequency at which the phase of the complex dynamic modulus E* peaks, see Figure 1e,f); (2) determine the scaling law relationship between characteristic frequency f_peak and characteristic length scale d, the distance over which the fluid flows during dynamic loading and can be varied by changing the AFM tip radius (see Figure 1d), to confirm whether poroelasticiy is the underlying mechanism governing dynamic behavior; (3) estimate the nanoscale hydraulic permeability k by using finite element modeling (with the aggrecan monolayer modeled as a anisotropic poroelastic material); (4) find the role of electrostatic and steric interactions in the poroelastic properties of aggrecan by changing the ionic strength of the salt solution (to screen electrostatic interactions between neighboring double layers) and changing the initial offset load during dynamic nanoindentation; and (5) to compare the nanoscale dynamic mechanical properties of aggrecan across cartilage age and species from which the aggrecan molecules are extracted.

RESULTS/DISCUSSION

Fluid Solid Interactions Govern the Dynamic Nanomechanics of Aggrecan.

We measured the nanomechanics of brush layers of aggrecan over a four-decade frequency range using a newly developed high-frequency AFM-based nanorheology system,³⁶ and an efficient loading profile where the AFM tip is displaced by 2 nm steps, applied in a “random binary sequence” (RBS, Figure 1c; see the Supporting Information for more details). The first full spectrum measurement of newborn human aggrecan nanomechanics, reported as the magnitude and phase of the effective dynamic modulus over the frequency range of 1 Hz to 10 kHz (Figure 1e,f), exhibits the following distinct features: a low frequency asymptote E_L and high frequency asymptote E_H of the magnitude of modulus |E*|, and a phase angle ϕ between the applied probe tip displacement and measured force that exhibits a peak at frequency f_peak. E_L reflects the equilibrium compressive modulus of the aggrecan monolayer due to its solid content only, with no contribution from fluid flow because it is measured at very low frequency (i.e., the quasi-equilibrium state). E_H reflects the modulus of the monolayer at high frequencies, equivalent to instantaneous loading, where the mixture of the solid and pressurized fluid behaves as an incompressible material.³⁷ At mid frequencies, the interactions between solid and fluid dominate and the phase angle, the tangent of which is an indicator of energy dissipation,³⁸ peaks at frequency f_peak.

We showed that the mechanism underlying the observed frequency-dependent nanomechanics of aggrecan is nanoscale-poroelasticity by means of an experimental length-scale study. According to linear poroelasticity,^5,24 the peak frequency f_peak is proportional to the product of the equilibrium modulus E and the hydraulic permeability k of the material, and inversely proportional to the characteristic contact distance d between the AFM tip and aggrecan (shown in Figure 1d):

$$f_{\mathrm{peak}}\propto \frac{\mathit{Ek}}{d^2}$$ (1)

This dependence of f_peak with the length scale d is a definitive approach to confirming the hypothesis that solid–fluid interactions are the origin of the observed dynamic nanomechanics (rather than, e.g., a purely solid-phase viscoelastic mechanism, which would not scale with contact distance d). We performed this dynamic nanomechanical test on newborn human aggrecan with two different-sized AFM colloidal probe tips having diameters of 45 and 5 μm (Figure 2). The difference in tip diameter resulted in a difference in the contact distance of d_45-μm = 3.1 μm versus d_5-μm = 1.5 μm at near-physiological ionic strength conditions of 0.1 M NaCl. (The contact distance between aggrecan monolayer and AFM tip is estimated using Hertzian contact geometry. The indentation depth at a given applied force, estimated from the height-force curves of Supporting Information Figure S1, is the difference of the initial height (zero force) and the height at the applied force.) The peak frequency was measured f_peak-45-μm = 124 ± 9 Hz when the 45 μm diameter tip was used. Equation 1 predicts that when the dynamic tests are performed with the 5 μm tip, at similar loading conditions to the 45-μm tip to keep E and k unchanged, the peak frequency f_peak shifts to 529 Hz. The peak frequency with the 5 μm tip was measured as f_{peak-5 μ}m = 518 ± 34 Hz (Figure 1a), which shows close agreement to the prediction of eq 1. This consistency of the length scale dependence of the dynamic modulus phase angle with the prediction of eq 1 over a wide range of ionic strengths (IS = 0.1, 0.01, and 0.001 M NaCl), together with the observation of the key features of poroelastic response, such as E_L, E_H, and f_peak, all confirm that poroelasticity is the dominant mechanism underlying the dynamic nanomechanics of the aggrecan monolayer. Intrinsic viscoelastic behavior, associated with molecular friction and configurational changes within and between macromolecules, is another energy dissipation mechanism in soft tissues, but has been shown to be independent of fluid-flow length scale.^22,26 In addition, intrinsic viscoelastic relaxation times in cartilage have been found to be much longer than those associated with the nanomechanical poroelastic behavior of aggrecan revealed in the present study.^22,39

Figure 2.

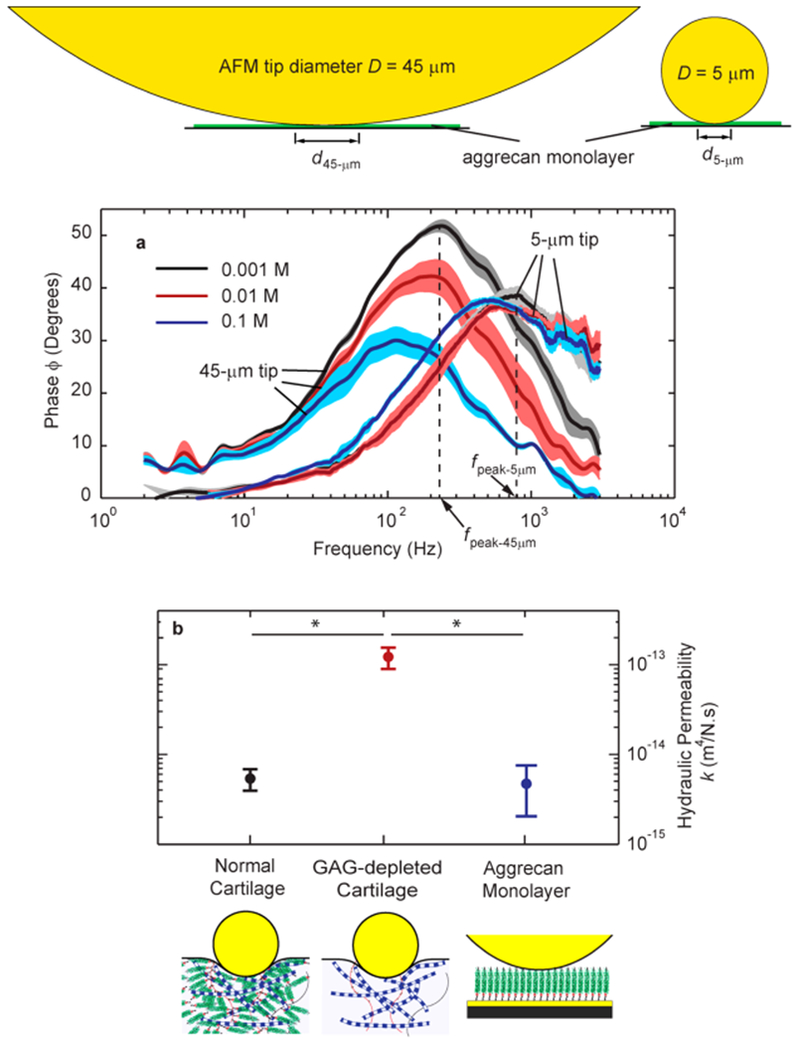
Aggrecan fluid solid interactions play the dominant role in dynamic nanomechanical properties of cartilage. (a) The length-scale analysis at different ionic strength confirms our hypothesis that the governing mechanism in the dynamic mechanical function of aggrecan monolayer is poroelasticity. On the basis of poroelasticity theory, f_peak ~ 1/d², i.e., if the contact distance d_45μm decreases to d_5μm, the peak frequency of the phase angle of the dynamic modulus increases from f_peak-45-μm = 124 Hz to f_peak-5-μm = 529 Hz. Our experimental data, here using fetal bovine aggrecan, shows that the peak frequency increased to f_{peak-5 μm} = 518 ± 34 Hz for the 5 μm-tip, which is in close agreement to the theoretical prediction of 529 Hz. (b) The hydraulic permeability of normal newborn bovine cartilage, with main constituents of aggrecan GAGs and collagen, is close to the hydraulic permeability of the fetal bovine aggrecan monolayer (no statistical significance), and they are both significantly lower than the hydraulic permeability of GAG-depleted newborn bovine cartilage (representative of early changes in cartilage after joint injury to young individuals, leading to post-traumatic osteoarthritis). This further confirms that the mechanical properties of the matrix that are dependent on solid–fluid interactions, such as hydraulic permeability, are determined by the aggrecan network. (*p < 0.05; using t test, and the reported data is mean ± SE. For normal and GAG-depleted cartilage, N = 4 animals, where k of each animal is the average over M = 4 plugs, and m = 4 different locations on each plug. For aggrecan, N = 3 plates, where for each plate, the k and E_L are averaged over M = 6 different locations.).

A finite element model was implemented to estimate the intrinsic poroelastic properties of the aggrecan monolayer, such as the hydraulic permeability and Young’s modulus. End-grafting of each aggrecan monomer to the substrate confines the aggrecan monolayer from lateral motion at the bottom of the layer (Figure 1b), resulting in a higher effective stiffness in the transverse direction compared to the axial direction. To incorporates this anisotropy in the lateral vs axial direction, we utilized a transversely isotropic model.⁴⁰ Due to axisymmetric geometry of the tip-sample, the model parameters are reduced to the following: hydraulic permeability k, axial equilibrium modulus E_a, and transverse equilibrium modulus E_t (see Supporting Information for more details about the model). The predictions of the theoretical FEM simulation closely match the experimental data for the magnitude and phase of the dynamic modulus over the wide frequency range of 1 Hz to 10 kHz, and at different ionic strengths of 0.001, 0.01, 0.1, and 1 M NaCl. The close match between theoretical and experimental spectrum of dynamic modulus further confirms the hypothesis that the observed nanomechanics of the aggrecan layer is governed by linear poroelasticity.

Hydraulic Permeability of Aggrecan at the Molecular Level.

We estimated the hydraulic permeability of the dense aggrecan layer at the molecular level for the first time using the measured f_peak together with the poroelastic finite element model. The hydraulic permeability of fetal bovine aggrecan was found to be k = (4.8 ± 2.8) × 10 ⁻¹⁵ m⁴/N·s. This value is close to the hydraulic permeability of the normal ECM of newborn bovine cartilage (Figure 2b), where it is hypothesized that aggrecan is the main determinant of the hydraulic permeability of the tissue. (The volumetric concentration of aggrecan layer is c_monolayer = 43 ± 10 mg/mL at 0.1 M ionic strength,⁴¹ close to the physiological range of 20–80 mg/mL in human and animal cartilage ECM.) In cartilage, the type II collagen network mesh size is 60–200 nm,⁴² while the distance between GAG chains on aggrecan is only 2–4 nm apart from each other.²⁸

Thus, the pore size and hence the hydraulic permeability of cartilage is hypothesized to be determined by aggrecan. In a previous study,⁴ we applied the same high-bandwidth AFM-based rheology system to estimate the hydraulic permeability of normal and GAG-depleted cartilage ECM. In the normal tissue, both aggrecan and collagen network contribute to the nanomechanics of matrix. However, in cartilage where the aggrecan GAG chains were enzymatically depleted, the collagen network, which was still intact, has the major nanomechanical contribution. In this previous study, we measured the hydraulic permeability of the normal cartilage to be k_normal = (5.4 ± 2.0) × 10⁻¹⁵ m⁴/N•·s, while the hydraulic permeability of the GAG-depleted matrix was more than an order of magnitude higher, k_GAG-depleted = (1.3 ± 0.7) × 10 ⁻¹³ m⁴/N·s. Comparing the hydraulic permeability of these three bovine systems: aggrecan monolayer, intact ECM, and aggrecan-depleted ECM (Figure 2b), we further confirmed the dominant role of aggrecan in determining the hydraulic permeation of cartilage ECM.

We also calculated the equilibrium modulus E_L of the aggrecan monolayer and of normal and GAG-depleted cartilage (Supporting Information Figure S3) to be E_L,normal = 141.1 ± 34 kPa, E_{L,GAG-depleted} = 90.5 (18 kPa, and E_L,aggrecan = 20.5 ± 1.0 kPa, and showed that the effect of the aggrecan on equilibrium stiffness E_L is less dramatic than its effect on hydraulic permeation of the matrix. From the comparison of E_L among the three systems, we directly conclude that both aggrecan and collagen play a major role in determining the compressive stiffness of the ECM at the nanoscale; this conclusion has been shown previously only at the macroscale.⁴³

Mechanisms Underlying Fluid–Solid Interactions in Aggrecan Monolayers.

We explored the mechanisms underlying molecular level poroelasticity of aggrecan by measuring the changes in hydraulic permeability and stiffness of newborn human aggrecan caused by electrostatic and steric interactions. Macroscale⁴³ and nanoscale studies^41,44 have shown that the electrostatic interactions between the highly charged GAGs of aggrecan contribute significantly to the cartilage equilibrium stiffness (a fluid flow-independent property). Here, we explored the role of electrostatic interactions on hydraulic permeability (a fluid flow-dependent property) as well as stiffness of the aggrecan layer by changing the ionic strength of the solution, from 0.001 to 1.0 M NaCl. Bath ionic strength regulates electrostatic interactions by shielding of the fixed charge groups of the GAG chains. Steric interactions were studied by changing the initial indentation strain of the brush layer (from 0.2 to 0.7) under which the poroelastic properties were measured, while keeping the ionic strength constant.

By quantifying the axial modulus of the newborn human aggrecan layer E_a (Figure 3a) from the full spectrum dynamics at different ionic strengths and preindentation strains (Supporting Information Figure S4), we observed that the stiffness of aggrecan monolayers was less sensitive to strain than to ionic strength. The axial modulus E_a of aggrecan at low ionic strength (0.001 M) showed negligible changes with static strains ranging from 0.2 to 0.7, implying that aggrecan behaves as a linear material (i.e., strain-independent) over a wide strain range under low ionic strength conditions. At a higher ionic strength of 0.01 M, E_a showed a slight increase with strain. By further increasing the ionic strengths to 0.1 M (near physiological), the equilibrium modulus increased from ~15 kPa measured at strain of 0.3, to ~50 kPa at the large strain of 0.65. This strain-dependence of the equilibrium modulus becomes even more amplified when the ionic strength is further increased to 1.0 M. The lateral modulus E_t (shown in Supporting Information Figure S5) did not show significant dependence on strain at different ionic strengths as the endgrafted aggrecan monolayer is confined laterally.

Figure 3.

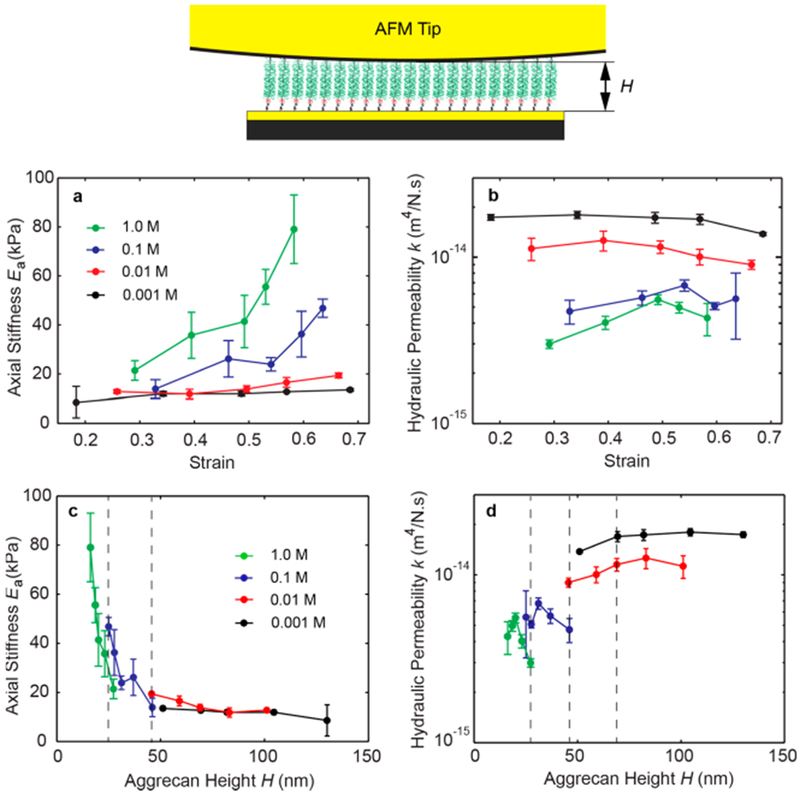
Decoupling the electrostatic and steric interactions between GAG-chains. (a and b) The axial stiffness E_a and hydraulic permeability k of the newborn human aggrecan is estimated using the transversely isotropic finite element model at solutions with ionic strength of 0.001,0.01,0.1, and 1 M NaCl under strain values in the range of 0.2–0.7. The axial stiffness E_a has shown statistically significant strain-dependence for IS = 0.01, 0.1, and 1.0 M, but not for IS = 0.001. The hydraulic permeability k showed statistically significant strain-dependence for IS = 0.001,0.01, and 0.1 M, but not for IS = 1.0 M (p <0.05; using one way analysis of variance; data are mean ± SE). (c and d) The dependence of axial stiffness E_a and hydraulic permeability k on the height of the aggrecan monolayer, H, at which the dynamic measurement is performed. The height of the aggrecan is altered by changes in the ionic strength (i.e., data points with different colors) and by applying compressive stress via the AFM tip (changes in height within each color; see Supporting Information Figure S1).

The hydraulic permeability of the aggrecan monolayer showed strong dependence on ionic strength, and weaker dependence on strain (Figure 3b). At low ionic strength of 0.001 and 0.01 M, where the electrostatic interaction is maximum, the hydraulic permeability showed a slight decrease when the strain is increased. At higher ionic strength of 0.1 and 1.0 M, the variation in hydraulic permeability was large and no significant trend was observed. At a fixed strain, however, the hydraulic permeability dropped significantly by increasing the ionic strength. Taking the data on equilibrium stiffness and hydraulic permeability together, we found that the electrostatic interactions between the GAG chains play a dominant role in determining the intrinsic poroelastic properties of aggrecan, which were altered significantly by ionic strength. The electrostatic repulsion between the charged GAG chains plays a key role in the stiffness and persistence length of the GAG chains and the core protein of aggrecan, as was shown previously via course-grained modeling,⁴⁵ and via direct measurement at low ionic strength.²⁸ By increasing the ionic strength, the fixed negative charges of the GAG chains are shielded, resulting in lower persistence lengths. As a result, at a constant applied force via the AFM probe tip, the lack of electrostatic repulsion at high ionic strength results in a collapse of the GAG chains. Hence, the intra- intermolecular steric interaction begins to compete with electrostatic interactions at higher ionic strength, where we observe a change in the poroelastic properties of aggrecan by increasing strain as well as ionic strength.

The full spectrum dynamic nanomechanics of aggrecan provided interesting facts about other aspects of fluid–solid interactions, i.e., the energy dissipation and self-stiffening of aggrecan at different applied strain values. The self-stiffening represented here by the ratio of E_H to E_L, i.e., the increase in stiffness due to loading rate (Supporting Information Figure S4a), and the energy dissipation, represented here by the peak angle ϕ_p (Supporting Information Figure S4b), are lowered by increasing strain (Supporting Information Figure S4). It is well-known thatthe modulus of an ideal elastic material does not change with frequency, so for a purely elastic material where there is no energy dissipation: E_H/E_L = 1, and ϕ_p = 0. Therefore, at higher ionic strengths, the aggrecan exhibits more elastic-like material behavior (Supporting Information Figure S4).

Previous macroscale experiments have shown that the stiffness of a GAG-rich extracellular matrix increases as the ionic strength of the solution decreases.^43,46 This seems to contradict the molecular level data that is reported here (Figure 1e, and Figure 3a); however, we showed that if the loading conditions are consistent, our molecular level results are consistent with the macroscale data. We compared load-control and height-control (i.e., displacement-control) loading before applying the dynamic random binary sequence. These two cases are shown in Supporting Information Figure S2, where the height of the patterned aggrecan monolayer (Supporting Information Figure S2a) is shown at different applied forces by the AFM tip at IS = 0.1 M (blue) and 0.01 M (red). The measurement at constant offset load of 320 nN (load-control) is performed at the AFM height/force shown, while for the approximately constant GAG spacing measurement (height-control) 320 nN is applied at 0.1 M, and 950 nN is applied at 0.01 M.

When the dynamic measurement is performed in load control (as in Figure 1e,f), the stiffness increases with increasing ionic strength. When the dynamic measurement is performed in height-control, the stiffness decreases with increasing ionic strength (as shown in Supporting Information Figure S2c). To interpret this difference in the measured dynamic stiffness in response to load-control versus height-control, we note that in Supporting Information Figure S1, the height of the aggrecan monolayer, for a given applied force, decreases dramatically with increasing ionic strength due to shielding of repulsive electrostatic interactions between GAG chains. The resulting decrease in GAG–GAG spacing leads to enhanced steric interactions, which then dominate over any remaining electrostatic interactions. At 1.0 M NaCl in Figure 1e, for example, the aggrecan monolayer behaves more like a fully compressed elastic material having a relatively high, frequency-independent dynamic modulus that no longer exhibits poroelastic self-stiffening. Under these conditions, steric interactions between GAG chains provide the resistance to indentation of aggrecan. In contrast, when aggrecan height is maintained constant, the effects of altered ionic strength can be interpreted in the context of almost constant GAG–GAG spacing (Supporting Information Figure S2a). Under these conditions, a decrease in ionic strength (e.g., 0.1 down to 0.001 M NaCl) results in a ~ 10-fold increase in the electrical Debye length;as a result, the probe tip would have to apply a much bigger force to maintain constant GAG-GAG spacing (aggrecan height), leading to a higher apparent dynamic modulus. (Similarly, native cartilage tissue is stiffer at lower ionic strength.)

Additional insight into this important difference in the response to load-control versus height-control-based dynamic stiffness can be seen in Figure 3c,d. Here, we use the aggrecan height data of Supporting Information Figure S1 and replot the data of Figure 3 to report axial stiffness and hydraulic permeability versus aggrecan height. At 0.001 and 0.01 M NaCl, axial stiffness is essentially constant in the 50–130 nm height regime (Figure 3c). This is expected since, under this range of ionic strength conditions, the Debye length is greater than GAG–GAG spacing (the latter being ~2–4 nm along and between adjacent aggrecan core proteins,⁴⁴ and electrostatic repulsive interactions between GAGs remain essentially constant). With the use of Poisson–Boltzmann theoretical simulations, just such a result was previously predicted.⁴³ However, further increases in ionic strength to 0.l M reduces electrostatic interactions, and by 1.0 M NaCl, electrostatic interactions are completely shielded. In this regime, aggrecan height is so greatly diminished that GAG-GAG steric interactions yield a much higher axial compressive stiffness (Figure 3c). Simlarly, the decrease in aggrecan height at high ionic strength and the resulting decrease in GAG–GAG spacing leads to a much smaller equivalent pore size for fluid flow, consistent with a decrease in hydraulic permeability (Figure 3d).

Aggrecan Stiffness and Hydraulic Permeability Across Age and Species.

The effect of age and species on the aggrecan nanostructure and nanomechanics is of critical importance to understand the fundamental molecular processes that take place in age-related disease such as osteoarthritis. In previous studies in which aggrecan was imaged via AFM, the two key structural parameters, the trace length of the GAG chain, L_GAG and the trace length of the core protein, L_CP, were quantified for fetal bovine, newborn human, and adult human aggrecan (Figure 4a–c).^28,47 L_GAG and L_CP were measured to be similar in fetal bovine and newborn human aggrecan. However, the adult human has a significantly shorter L_GAG and L_CP than the fetal bovine and newborn human, where the lower LCP in adult aggrecan is due in part to the accumulation of enzymatically cleaved aggrecan core protein with increasing age.⁴⁸ Thus, AFM-based visualization of aggrecan has shown significant age-dependent (fetal/newborn vs adult) structural alterations, while species-dependence (bovine vs human) for similar relative age did not as dramatic variations in structural properties.

Figure 4.

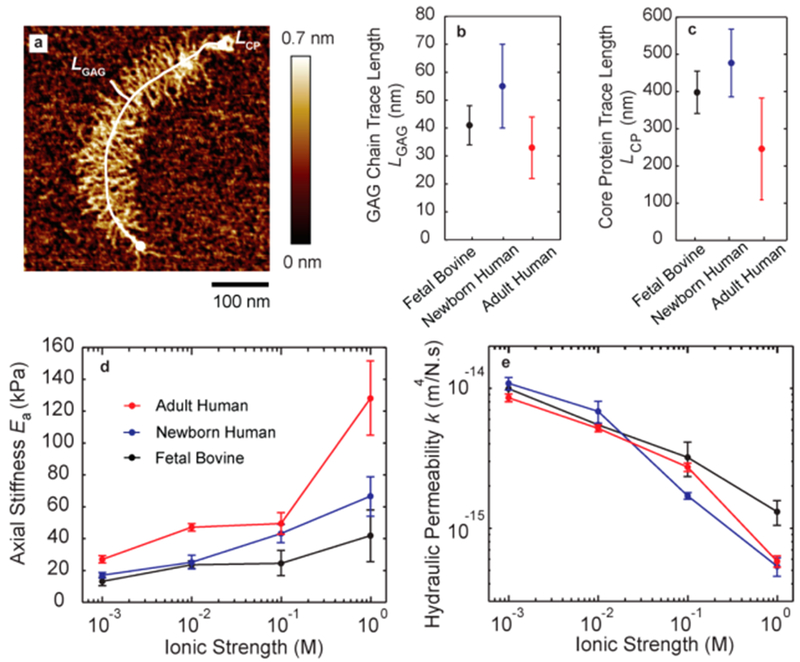
Poroelastic properties of aggrecan estimated across species and ages. (a) AFM images of individual aggrecan molecule have been used to quantify structural properties such as core protein length L_CP and GAG chain length L_GAG (image reproduced with permission from ref 47. Copyright 2012 Elsevier). (b) GAG chain length and (c) core protein length of aggrecan varies across age and species (data from refs 28 and 47). (d) The axial stiffness E_a of adult human aggrecan is higher than that of newborn human and fetal bovine (two-way ANOVA, p < 0.05). E_a is not significantly different between newborn human and fetal bovine. (e) The hydraulic permeability k for adult human, newborn human and fetal bovine aggrecan did not show any significant differences.

Here, by high-bandwidth measurement of the dynamic modulus of aggrecan, we correlated the nanomechanical functions of aggrecan such as E_a and k, to the structural properties L_GAG and L_CP reported previously.^28,47 We observed that adult human aggrecan exhibits higher axial stiffness E_a compared to newborn human and fetal bovine aggrecan, implying the effect of age on the nanomechanical function of aggrecan. The difference in E_a of newborn human and fetal bovine aggrecan is not statistically significant, which implies species-independence of nanomechanics of aggrecan for similar relative ages. In adult human aggrecan, we also observed a stronger dependence of axial stiffness E_a on ionic strength compared to fetal and newborn aggrecans. In contrast to the observed age-dependence of the stiffness E_a, we did not observe significant differences in hydraulic permeability k of aggrecan across age or species. Given that shorter L_GAG and L_CP in adult human aggrecan resulted in higher stiffness, while the hydraulic permeability remained unaffected, we suggest that the age-associated structural differences in aggrecan core protein and GAG chains do not change the pore size for a given applied molecular-scale load, which is determined by the distance between GAG chains. In other words, the electrostatic interaction between GAG chains, which we showed to be the dominant determinant of hydraulic permeability and pore size, does not change across age, despite the changes in L_GAG and L_CP. However, the alterations in L_GAG and L_CP affect the persistence length and stiffness of the aggrecan layer, as shown in Figure 4a, and previously for quasi-static loading.^28,47 While our approach cannot determine whether L_GAG or L_CP contributes most to the stiffness properties of the aggrecan layer, we hypothesize that L_GAG and GAG–GAG spacing are dominant due to electrostatic interactions. A model that incorporates these specific contributions of GAG chains and core proteins individually may better bridge the gap between the structure and function of aggrecan macromolecules.

CONCLUSIONS

Cartilage in human joints functions optimally in a wide range of loading rates during daily activities ranging from standing and walking to running and very high impact. Highly specialized matrix molecules like aggrecan are synthesized and secreted then assembled outside the cells to form a microenvironment that adjusts its stiffness and energy dissipation according to the rate of loading presented to the cells. In this work, we investigated the molecular origin of the dynamic mechanical functions of cartilage, and showed that aggrecan solid–fluid interactions form the dominant mechanism underlying these functions (Figure 5). Utilizing a custom-made high bandwidth atomic force microscope-based rheology system, we directly explored the solid–fluid interactions of the GAG-rich proteoglycan aggrecan over a wide spectrum to cover the frequency content of loading in daily activities (1 Hz to 10 kHz, the higher frequencies relevant to impact joint loading). Our methodology to estimate the key parameters governing solid–fluid interactions in isolated aggrecan molecules revealed the following: (1) we observed the key nanomechanical functions of aggrecan including their equilibrium stiffness at low frequencies, the increase in stiffness with increasing loading rate, and a peak in the phase angle of the complex modulus indicative of poroelastic behavior at the nanoscale. These features have recently been observed in native cartilage ECM⁴ where both aggrecan and the collagen network are present. The observation of similar dynamic behavior in isolated aggrecan confirmed the hypotheses that (i) aggrecan solid–fluid interactions govern the dynamic nanomechanical functions of the extracellular matrix at higher frequency loading (Figure 5b), while (ii) electrostatic repulsion between GAG chains in the absence of fluid flow govern the quasi-static stiffness of the aggrecan constituents (Figure 5a). (2) The length scale analysis further confirmed the above hypothesis that fluid–solid interactions are the main mechanism underlying the observed dynamic nanomechanical response. (3) For the first time, the hydraulic permeability of aggrecan layers was measured atthe molecular level and was quantified by finite element modeling to be k = (4.8 ± 2.8) × 10 ⁻¹⁵ m⁴/N·s for fetal bovine aggrecan, which closely matches both the nanoscale and macroscale hydraulic permeability of native newborn bovine ECM. (4) We also showed that electrostatic interaction between the GAG chains plays a significant role in determining the equilibrium stiffness and hydraulic permeability while the steric interactions contribute mostly at higher ionic strength where the fixed charges of aggrecan GAGs are shielded.

Figure 5.

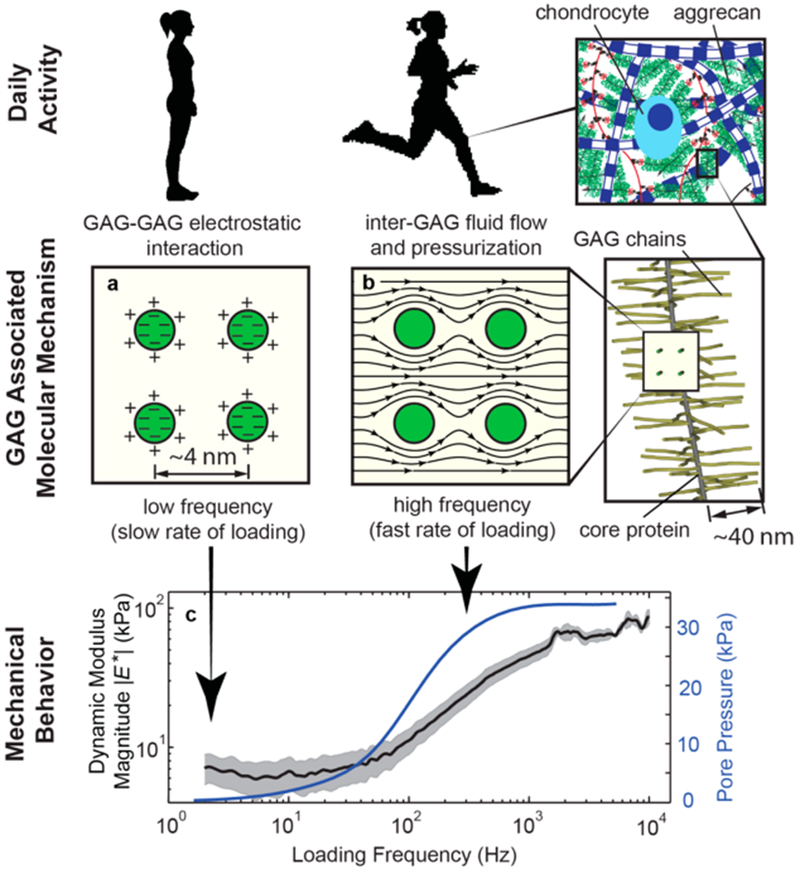
Molecular mechanism of cartilage dynamic mechanical behavior is governed by electrostatic and solid–fluid interactions between GAG chains. (a) Cross section of neighboring GAG chains is shown. The mechanical function of aggrecan in quasi-static loading is controlled by the electrostatic and steric interaction between GAG side chains. (b) In dynamic loading, as it happens during fast rate of loading such as in running, solid–fluid interaction determines the mechanical functions of aggrecan by viscous drag effects and fluid pressurization. (c) The fluid pressurization due to solid–fluid viscous interaction (simulated and shown by the blue line) results in self-stiffening, which is the increase in dynamic modulus by loading frequency (experimentally measured and shown by black line; the shade around the black line is the 95% confidence interval).

As an immediate application, we utilized this methodology to correlate the nanostructure of aggrecan to its poroelastic properties such as the equilibrium modulus and hydraulic permeability across age and species. Aggrecan from adult human tissue showed higher equilibrium modulus than aggrecan from newborn human or fetal bovine tissue, while the hydraulic permeability did not change significantly among these groups. This implies that the alteration in structural dimensions of aggrecan may affect the persistence lengths of the molecule, but not the pore size (i.e., GAG-GAG spacing) that determines the hydraulic permeability. A further application directly linked to our findings concerns the transport of peptides and therapeutic drugs into tissues having highly charged matrix constituents in which both electrostatic and solid–fluid interactions become critical factors in delivery of such drugs. For example, the mucins in mucus,⁴⁹ the hyaluronan in desmoplastic tumors,^50,51 and the aggrecan–GAGs in cartilage,⁵² are major determinants of diffusivity and transport of potential therapeutics. For the case of cartilage, electrostatic interactions can increase the uptake of charged nanoparticles up to 400-fold compared to neutral particles having the same size and molecular weight. This dramatic dependence of transport into tissues with fixed charges is best understood by separating electrostatic from solid–fluid interactions, for which we present a molecular level approach in this work.

METHODS

Aggrecan Purification.

The cartilage samples were washed in ice-cold 50 mM sodium acetate, pH 7.0, containing a mixture of protease inhibitors, and stored on ice for the next step. The tissue was cut into small pieces (~3 mm × 3 mm) and extracted in 4 M guanidinium hydrochloride, 100 mM sodium acetate, pH 7.0, with protease inhibitors for 48 h. Unextracted tissue residues were separated by centrifugation and the clarified supernatant was dialyzed against two changes of 100 vol of 0.1 M sodium acetate, pH 7.0, with protease inhibitors.⁵³ Purified aggrecan fractions were obtained by Guanidine HCL extraction followed by dissociative CsCl density gradient centrifugation as described,^28,47 and then dialyzed consecutively against 500 vol of 1 M NaCl and deionized water to remove excess salts. Aggrecan yield was determined by the dimethyl methylene blue (DMMB) dye-binding assay.⁵⁴

Endgrafting.

Purified fetal bovine epiphyseal,²⁸ adult (38 years old) and newborn human aggrecan⁴⁷ were chemically end-grafted to gold-coated planar substates (6 mm × 6 mm) via thiol-gold binding.⁵⁵ Aggrecan was end-functionalized by reaction with 1 μM dithiobis (sulfosuccinimidyl propionate) and 0.1 mM dithiothreitol (Pierce) for 1 h. Excess reactants were removed by spinning (3500 rpm, 6 h) with a centrifugal filter (Centricon, Millipore, 10 kDa cutoff). Approximately 30 μL of 1 mg/mL modified aggrecan solution in deionized water was deposited onto freshly cleaned gold-coated surfaces and incubated for ~48 h in a humidity chamber. Prior to nanomechanical measurements, the surfaces were thoroughly rinsed with deionized water. With this protocol, the volumetric concentration of aggrecan layer is c_monolayer = 43 ± 10 mg/mL at 0.1 M ionic strength,⁴¹ close to the physiological range of 20–80 mg/mL in cartilage ECM.

Microcontact Printing.

Aggrecan height was measured versus normal force using microcontact printing and contact mode AFM imaging with probe of tip radius 22.5 μm (same as the one used in dynamic nanoindentation). Aggrecan was end-grafted within circular patterns (15 μm in diameter; a typical height image is shown in Supporting Information Figure S2b) and an OH-SAM filled the area outside of the circular area, as described previously.⁵⁵

AFM Imaging in Contact Mode.

The heights were measured in 0.001 −1 M NaCl using ~0–1300 nN normal force (scan rate = 60 μm/s) and were averages of eight 30 μm line scans (256 points/line) (Supporting Information Figure S1). The initial height of the aggrecan layer is considered to be the height at zero force. The height at a certain loading is obtained from the height-force curve (shown for 0.01 and 0.1 M in Supporting Information Figure S2a; for height-force curves at all IS, see the Supporting Information). The strain is calculated as the ratio of the height at the loading time by the initial height. The stress is calculated as the force exerted on the AFM tip normalized by the effective area under the AFM tip.

High-Frequency AFM-Based Nanorheology System.

The complex dynamic modulus of cartilage was measured over a wide frequency range (1 Hz to 10 kHz), using a recently developed a high-frequency rheology system coupled to the commercial AFM, MFP-3D (Asylum Research, Santa Barbara, CA).^4,36 We coupled a high-frequency actuating system to the commercial AFMs. The secondary piezo, which is chosen to be small compared to the primary piezo of the commercial AFM (2 × 2 × 2 mm³; Physik Instrumente, Auburn, MA), maximizes the feasible frequency range by pushing the resonance frequency of the combined piezo system to frequencies as high as 10 kHz. The displacement of the secondary piezo is load-independent by applying a permanent prestress to the piezo by clamping it between a beam and the substrate. The clamp system has its own mechanical resonances, which were diminished by optimizing the beam geometry and material. To have a low weight-to-stiffness ratio, we fashioned the beam from carbon fiber.

Loading Profile: Random Binary Sequence (RBS).

We used the random binary sequence signal to maximize the signal-to-noise ratio (Figure 1c). The advantage of the RBS over the more traditional signals such as sinusoid sweep is stimulating the system with lower crest factor (defined in Supporting Information). The lower crest number is equivalent to higher stimulus power, which results in a less noisy system identification of the system.^56,57 For details of generation of the RBS signal see the Supporting Information.

Finite Element Model.

The aggrecan is end-grafted covalently to the gold-coated substrate, where the substrate confines the aggrecan monolayer from lateral motion at the bottom of the layer (Figure 1b). This lateral confinement results in higher stiffness in the lateral direction compared to the axial direction. A transversely isotropic model⁴⁰ was implemented using the general purpose commercial finite element software ABAQUS (Version 6.9, SIMULIA, Providence, RI) Because of the symmetry of the problem, the specimen was modeled using axisymmetric, poroelastic elements (CAX4P). The probe tip indenter was modeled as a rigid surface since the spherical tip is much stiffer than the aggrecan monolayer. The probe tip was assigned a displacement history as described in Figure 1c), and a zero-displacement boundary condition was assumed at the lower aggrecan–substrate interface. The indenter and the substrate surface were assumed to be impermeable to fluid flow, and the indenter–aggrecan contact region was assumed to be frictionless due to the hydrophilic, highly charged nature of aggrecan.^58,59 The pore pressure was set to zero at the top surface of the aggrecan (excluding the indenter contact surface) and the side surfaces of the aggrecan to simulate free draining of the interstitial fluid from the aggrecan at those surfaces. We note that, for the frequency and amplitude ranges specific to our dynamic measurements, previous studies have shown that hydrodynamic drag associated with fluid flow along the probe tip is negligible.^60,61 The relevant mechanical properties in this anisotropic model are the Young’s modulus in axial direction E_a, the Young’s modulus in transverse direction E_t, and the hydraulic permeability, k.. (For parametric studies on model sensitivity to these parameters, see Supporting Information Figure S6.) The remaining parameters such as the Poisson’s ratios ϑ_a, ϑ_at and the transverse shear modulus G_t are assumed to be zero. The equilibrium Young’s modulus in the axial direction E_a is taken as the limiting low-frequency dynamic modulus E_L, and is directly obtained from experimental data (see Supporting Information Figure S6a,b). Once E_a is obtained, the Young’s modulus in transverse direction and the ratio of E_t/E_a is estimated from E_H/E_L, the ratio of the high-frequency modulus E_H to low-frequnecy modulus E_L (see Supporting Information Figure S6c and d). Having the moduli E_a and E_t, we directly estimated the hydraulic permeability k from the peak frequency of the phase angle, f_peak, which is linearly proportional to k (see Supporting Information Figure S6e,f).

Statistical Analysis.

All the data are the result of a minimum of three independent experiments. Statistics were calculated with Matlab. The significance was calculated using a one-way ANOVA method, followed by independent Student’s t test.