One- and two-photon absorption properties of quadrupolar thiophene-based dyes with acceptors of varying strength

Abstract

The one-photon (1P) and two-photon (2P) absorption properties of three quadrupolar dyes, featuring thiophene as donor and acceptors of varying strength, are determined by a combination of experimental and computational methods employing density functional theory (DFT). The emission shifts in different solvents are well reproduced by time-dependent DFT calculations with the linear response and state specific approaches in the framework of the polarizable continuum model. The calculations show that the energies of both 1P- and 2P- active states decrease with an increase of the strength of the acceptor. The 2P absorption cross-sections predicted by response theory are accounted for by considering just one intermediate state (S₁) in the sum-over-states formulation. For the chromophore featuring the stronger acceptor, the energetic positions of the 1P- and 2P- active states prevent exploitation of the theoretically predicted very high 2P activity due to the competing 1P absorption into the S₁ state.

Graphical Abstract

Introduction

Emissive materials have numerous applications, including in biological optical imaging.[1,2] Near infrared (NIR) fluorescent probes present interest for medical diagnostics as well as for some therapeutic applications.[1,2] Typically imaging probes are based on small organic dyes that absorb and emit light in the therapeutic window of 650−1400 nm. [3,4]

A suitable strategy for development of organic NIR emitters is to employ large conjugated systems featuring electron donating (D) and acceptor (A) groups. [5] A wide variety of existing donor and acceptor building blocks allows for efficient tuning of the electronic and optical properties of molecular fluorophores. [6]

Among donor-acceptor derivatives, donor-acceptor-donor (DAD) thiophene-based molecules make up a special group of dyes, which have already proven useful in construction of single material organic solar cells (SMOC), fabrication of one‐component external resonator-free organic lasers, as well as fluorescent probes for visualization of protein dynamics in living cells. [7–10] In addition to being used directly as fluorescent probes, DAD dyes have also been employed as antennae to boost absorption of otherwise poorly-absorbing luminescent silicon nanocrystals (SiNC). [11–15] DAD chromophores are also known for their often very large two-photon absorption (2PA) cross sections. [16], which make them attractive as probes for two-photon (2P) microscopy - an optical imaging method that allows for increase in imaging resolution simultaneously with reduction in photodamage.

In general, the development of 2P probes for fluorescence-based imaging pursues two main goals: 1) tuning the emission into the NIR spectral region, and 2) increasing 2PA. The effect of acceptors in DAD systems on one-photon (1P) absorption properties has been recently investigated [17], demonstrating that stronger acceptors in DAD systems lower the transition energy.

Nonlinear optical properties of families of DAD compounds featuring benzothiadiazole or thiadiazole-quinoxaline acceptors have also been reported [18–21]. However, clear understanding of the interplay between the optical properties and the strength of the acceptor group for a given donor, supported by systematic experimental and computational investigation, is still lacking.

In this study we performed such an investigation by considering three DAD dyes featuring thiophene as a donor and increasingly strong acceptor groups (see Fig.1): 4,7-di(thiophen-2-yl)benzo[c][1,2,5]thiadiazole (TBT), 5,7-di(thiophen-2-yl)thieno[3.4-b]pyrazine (TPT) and 4,6-di(thiophen-2-yl)thieno[3.4-c][1.2.5]thiadiazole (TTzT). We report complete photophysical characterization of these three DAD chromophores, including their solvatochromic and 2PA properties. The experimental results are complemented by quantum chemical calculations of the spectroscopic properties as well as of the fluorescence solvatochromism. 2PA properties are computed using the response theory and rationalized based on the sum-over-states (SOS) formalism.

Fig. 1.

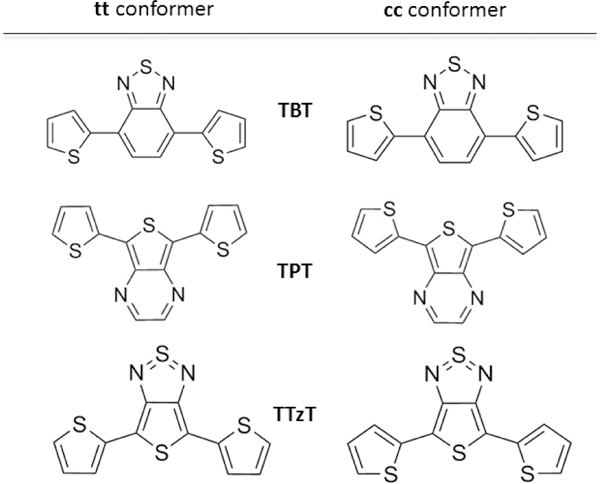
The two symmetric conformers of the DAD chromophores investigated in this work. From top to bottom, the acceptor group is benzothiadiazole (B), thienopyrazine (P), thienothiadiazole (Tz).

Quantum chemical calculations

Ground and excited state structures, solvent effects on one-photon absorption and emission spectra

The molecular structures of TBT, TPT and TTzT chromophores were optimized using density functional theory (DFT), CAM-B3LYP long range-corrected hybrid functional and 6–31G* basis set. It is known that time-dependent DFT calculations (TD-DFT) can erroneously predict the ordering of charge transfer states. To circumvent this deficiency, we ran all the calculations using the long-range corrected CAM-B3LYP functional.[22] Three possible conformers were considered in the calculations of the ground state properties to assess their relative stabilities in vacuum and in solvents. The geometries of the three DAD systems in their lowest excited states (S₁) were also optimized at the TD-CAM-B3LYP level in vacuum and in solvents, using the polarizable continuum model.[23, 24] Optimization of the excited state geometries in solvents was performed using the classical linear-response (LR-PCM) approach [25,26]. In order to obtain a more accurate description of the solvent effects on excitation energies, the state-specific self-consistent procedure model (SS-PCM) [27,28] was also considered and applied to the optimized excited state geometry. Unlike in LR PCM, in SS PCM solvent’s fast degrees of freedom are allowed to equilibrate with the ground state electron density and a more accurate description of solvent effects is expected.[27] In this case the procedure for calculating the fluorescence spectra of the solvated dyes included LR-PCM to determine the excited-state structures and, next, single point vertical SS-PCM calculations using these geometries. LR-PCM and SS-PCM results were compared.

The reorganization energy upon excitation was estimated according to the adiabatic potential approach, namely via a two point-based calculation using the potential energy surfaces of the ground and excited states (see Fig. S1) and via calculation of Huang–Rhys (HR) factors $S_v$ (see the ESI for additional details). [29]

The Stokes shifts in various solvents were determined experimentally as the a difference between the maxima of the absorption and emission spectra. The Stokes shifts were also determined by quantum chemical calculations as a sum of the electronic and a vibronic energy terms, where both are dependent on the solvent. The former term is the difference between the adiabatic S₀-S₁ excitation energy in absorption (solvent equilibrated with the ground state) and in emission (solvent equilibrated with the excited state). The vibronic term was determined for each solvent as the difference between the maxima of the two vibronic profiles simulated starting from the same 0–0 origin. The absorption and emission vibronic profiles were simulated including Franck-Condon activities based on the evaluation of Huang-Rhys factors (see ESI for details).

All of the above quantum chemical calculations were carried out using the Gaussian 09 suite of programs. [30]

Two photon spectra

For linearly polarized light the rotationally averaged 2P transition probability $\delta$ is given by [31]:

$$\delta =2{\delta }_F+4{\delta }_G=2\sum _{ab}\frac{1}{30}{S}_{aa}{S}_{bb}+4\sum _{ab}\frac{1}{30}{S}_{ab}{S}_{ab}$$ (1)

where $S_{ab}$ are the two photon transition matrix elements defined according to the SOS expressions as [31]:

$$S_{ab}=\sum _p\left[\frac{\langle i\text{|}{\mu }_a\text{|}p\rangle \langle p\text{|}{\mu }_b\text{|}f\rangle }{E_{ip}-\omega }+\frac{\langle i\text{|}{\mu }_b\text{|}p\rangle \langle p\text{|}{\mu }_a\text{|}f\rangle }{E_{ip}-\omega }\right]$$ (2)

where $\mu$ is the dipole moment operator (with indexes $a,b$ running over the cartesian components $x,y,z$), $E_{ip}$ is the excitation energy of the electronic state p, $\omega$ is the photon energy, $i$ and $f$ represent the initial (ground) and final electronic states, while the sum runs over p, the intermediate electronic states included in the SOS expansion, including the initial and final states.

The $S_{ab}$ can be calculated also by the response theory which includes implicitly the full SOS and the $S_{ab}$ are obtained from the single residue of the quadratic response function. It has been shown that the CAM-B3LYP functional gives a description of two-photon absorption comparable to the coupled cluster model CC2. [32] Therefore, here we employed density functional response theory to compute 2P absorption cross sections at TD-CAM-B3LYP/6–31G* level of theory as implemented in the Dalton 2016 software package.[33, 34] In particular, a Lorentzian bandshape with the full-width half-maximum (FWHM) of 0.1 eV is assumed in Dalton for the calculation of two photon cross sections [31], which is narrower than the usual experimental linewidth, leading to an overestimate of computed 2P absorption intensities.[15, 35]

The SOS expressions of $S_{ab}$ and $\delta$ were employed to rationalize the Dalton-computed 2P transition probabilities in terms of a few states model and to dissect the role of the resonance enhancement. To this end transition dipole moments between excited states were computed as the double residue of the quadratic response function.

Experimental

Synthesis

Compounds TBT, TPT and TTzT were prepared according to procedures reported in literature. [36–38]. Spectroscopic characterizations, 1H-NMR and 13C-NMR, of the investigated compounds were recorded on a Varian Mercury-400 spectrometer equipped with a 5 mm probe. Chemical shifts were calibrated using the internal CDCl3 resonance which was referenced to TMS.

Photophysical measurements

The experiments were carried out using air-equilibrated solution at 298 K unless otherwise noted. UV–vis absorption spectra were recorded with a PerkinElmer λ40 spectrophotometer using quartz cells with path length of 1.0 cm. Emission spectra were obtained with either a Perkin Elmer LS-50 spectrofluorometer, equipped with a Hamamatsu R928 phototube, or an Edinburgh FLS920 spectrofluorometer equipped with a Ge-detector for detection in the NIR spectral region. Emission lifetimes were measured by the above-mentioned Edinburgh FLS920 spectrofluorimeter equipped with a TCC900 card for data acquisition in time-correlated single-photon counting experiments (0.2 ns time resolution) with a 340 nm pulsed diode and a LDH-P-C 405 pulsed diode laser. Emission quantum yields were measured following the method of Demas and Crosby [39] (standard used: [Ru(bpy)₃]²⁺ in air-equilibrated aqueous solution Φ = 0.040 [40] and HITCI (1,1′,3,3,3′,3′-hexamethyl-indotricarbocyanine iodide) in EtOH Φ = 0.30).[41] The estimated experimental errors are 2 nm on the band maxima, 5% for the molar absorption coefficient and luminescence lifetime, 10% for the emission quantum yields.

Electrochemical measurements

The electrochemical experiments were carried out using argon-purged CH₂Cl₂ solutions at 298 K. In the cyclic voltammetry (CV) setup, the working electrode was a glassy carbon electrode (0.08 cm²), the counter electrode was a Pt spiral, and a silver wire was employed as a quasi-reference electrode (AgQRE). The potentials reported are referred to SCE, whereby the AgQRE potential was measured with respect to ferrocene (E_1/2 = 0.51 V vs SCE for Fc⁺/Fc). The concentration of the compounds examined was on the order of 1 × 10⁻³ M; 0.1 M tetrabutylammonium hexafluorophosphate (TBAPF₆) was added as a supporting electrolyte. Cyclic voltammograms were obtained at the scan rates in the range of 0.05–5 V s⁻¹. The estimated experimental error on the E_1/2 value is ± 10 mV.

Two-photon absorption

Two-photon absorption spectra were measured by the relative two-photon fluorescence excitation (TPFE) method using solutions of the dyes in CDCl₃ and Rhodamine B in MeOD as a reference. We assumed no changes in the photophysical properties of the dyes (spectra and emission quantum yields) in deuterated solvents relative to those in the respective protonated solvents [42–43]. The excitation source was a Ti:Sapphire laser (Chameleon Ultra II, Coherent) producing pulses (FWHM ˜110 fs) at the repetition rate of 80 MHz. The emission spectra were recorded with an intensified CCD camera (ANDOR) coupled to a monochromator (Princeton Instruments). Short-pass filters were used to exclude the excitation light. The dependencies of emission intensities on the excitation flux were recorded at multiple wavelengths throughout the excitation range to ensure that the measurements were not confounded by saturation effects and/or the residual linear absorption. A detailed description of the experimental apparatus and the procedures can be found in the Supporting Information.

Results and discussion

Ground and excited state equilibrium structures

The three DAD dyes investigated here have typical quadrupolar structures along the long molecular axes (from D to D), but the static dipole moments are oriented perpendicular to these axes. Several conformers may exist, and some were computationally investigated previously.[44] We determined the equilibrium structures and energies of the three conformers corresponding to different orientations of the two donor groups with respect to the acceptor, labelled tt, cc and ct. The first two structures are shown in Fig. 1. Some of these conformers are slightly twisted around the DA bond with angles on the order of 1^o. The only significant deviation from planarity occurs in the case of the cc conformer of TBT with the dihedral angle of ca. 20^o. The relative stabilities of the conformers may be influenced by solvation as a result of their different dipole moments (Table S1). Indeed, in vacuum the tt conformer of TBT is more stable than the cc conformer by about 1.5 kcal/mol (Fig. 2), but the two become isoenergetic in polar solvents as a result of a larger dipole moment of the cc conformer. Similarly, the cc conformer of TTzT is slightly more stable in vacuum than the tt conformer, but the latter becomes more stable in polar solvents owing to its larger dipole moment (Fig. 2).The equilibrium structures of the lowest excited states of the three dyes were determined by TD-CAM-B3LYP calculations in vacuum and in different solvents. The lowest excited state is dominated by the (H→L, i.e. HOMO→LUMO) excitation in all of the systems (see Table S2). For both tt and cc conformers of the three chromophores, HOMO and LUMO are delocalized over the entire conjugated framework, owing to the almost complete co-planarity of the molecular fragments. The HOMO is slightly more localized on the donor and the LUMO is slightly more localized on the acceptor (see Fig. 3), thereby conveying some CT character to the lowest excited state.

Fig.2.

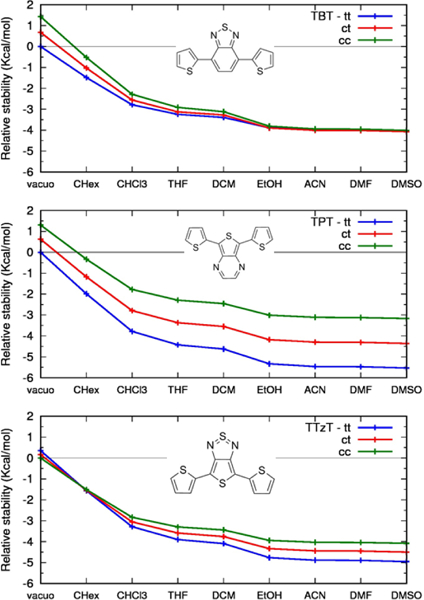
The relative stability of the tt, ct, cc conformers of (top) TBT, (middle) TPT, (bottom) TTzT chromophores as a function of solvent. From CAM-B3LYP/6-31G* calculations. Solvent described by PCM.

Fig. 3.

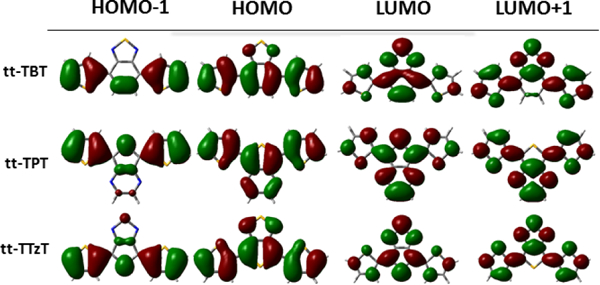
CAM-B3LYP/6-31G* frontier molecular orbitals of TBT, TPT and TTzT

Because of the LUMO’s shape, the excitation to S₁ imprints a quinoidal character to the phenyl ring with a concomitant shortening of the CC bond connecting the donor and acceptor in TBT (see Fig. S2). This shortening, however, is not associated with changes in dihedral angles, since the chromophores are mostly planar in their ground states. Similarly, large bond length changes occur upon excitation of TPT, with the pyridine ring acquiring marked quinoidal character (see Fig. S3), accompanied by a moderate inversion of the CC bond lengths in the donor units, including shortening of the CC bond connecting the donor and acceptor. For TTzT the largest changes occur for the CS and NS bonds of the acceptor, both subject to elongation due to the anti-bonding character of the LUMO orbital (Fig. 3). The carbon skeleton undergoes changes in the excited state (see Fig. S4), as previously reported for similar systems[17]. Overall, the most significant changes in the geometry impact the bond lengths, but do not involve dihedral angles. These bond length changes lead to notable reorganization energies of 640 meV, 680 meV and 540 meV for TBT, TPT and TTzT, respectively, which result in significant Stokes shifts (see below).

One photon spectra and solvatochromism.

The experimental absorption spectra of the three dyes, TBT, TPT and TTzT (see the top part of Fig. 4–6), show similar features, all common for DAD chromophores[15,20], i.e. strong absorption in the lower energy region, which shifts to the red for stronger acceptors, followed by the second group of intense absorption bands above 400 nm, which also migrate to the red upon increase in the acceptor strength.

Fig. 4.

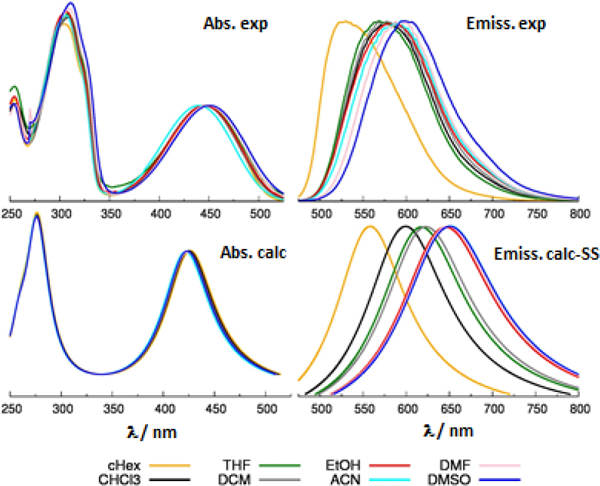
Comparison between computed (bottom) and experimental (top) absorption (left) and emission (right) spectra of TBT. Computed results from TD-CAM-B3LYP/6-31G* calculations, solvent described with PCM in the SS formalism. To facilitate the comparison with experiment, computed vertical excitations are broadened with a Lorentzian linewidth of 0.4 eV.

Fig. 6.

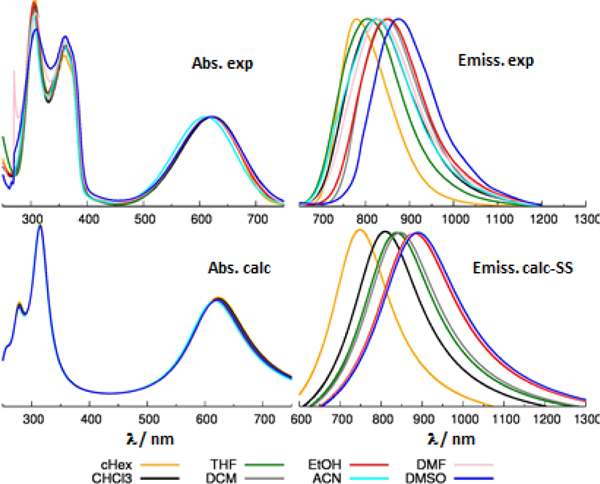
Comparison between computed (bottom) and experimental (top) absorption (left) and emission (right) spectra of TTzT. Computed results from TD-CAM-B3LYP/6-31G* calculations, solvent described with PCM in the SS formalism. Computed emission energies shifted by 0.2 eV, see the discussion in the text. To facilitate the comparison with experiment, computed vertical excitations are broadened with a Lorentzian linewidth of 0.4 eV.

TBT, TPT and TTzT have high molar absorption coefficients, and strong fluorescence (Table 1). The shapes of the absorption spectra are similar in all studied solvents, with small differences in the positions of the low energy absorption bands. In polar solvents the emission spectra undergo red shifts of 0.24 eV for TBT, 0.17 eV for TPT and 0.19 eV for TTzT with respect to cyclohexane. The quantum yields decrease with an in increase in the polarity of the solvent. The highest quantum yields (in cyclohexane) are 0.75, 0.12 and 0.16 for TBT, TPT and TTzT, respectively.

Table 1.

Photophysical properties of TBT, TPT and TTzT in different solvents at room temperature

TBT
solvent	λAbs(nm)	λEm (nm)	Φ	τ (ns)
CHex	446	536	1.07a	11.1
CHCl3	446	582	1.03	13.8
THF	446	569	0.85	14.6
DCM	445	577	0.90	16.3
EtOH	447	588	0.63	12.2
ACN	440	594	0.83	15.4
DMF	449	588	0.83	13.8
DMSO	451	598	0.71	14.9
TPT
solvent	λAbs (nm)	λEm (nm)	Φ	τ (ns)
CHex	537	644	0.118	8.8
CHCl3	532	699	0.021	1.4
THF	529	686	0.084	3.7
DCM	529	695	0.041	2.4
EtOH	524	699	0.005	0.2
ACN	519	698	0.017	1.6
DMF	526	701	0.026	1.7
DMSO	531	705	0.012	1.3
TTzT
solvent	λAbs(nm)	λEm (nm)	Φ	τ (ns)
CHex	623	750	0.162	9.8
CHCl3	623	815	0.036	2.0
THF	620	811	0.060	3.5
DCM	619	826	0.039	2.5
EtOH	618	823	0.007	0.3
ACN	610	833	0.016	1.6
DMF	618	826	0.013	1.5
DMSO	620	850	0.020	1.3

^aThe reported value is 1.0 within the experimental error.

Such strong solvatochromism as well as the large Stokes shifts are an indication of strongly polar excited states.

All the compounds have similar absorption bands in the 300–400 nm region and charge transfer (CT) bands in the visible region. The latter are progressively shifted towards long wavelengths upon increase in the electron-withdrawing strength of the central acceptor moiety (TBT<TPT<TTzT). The emission spectra show trends similar to those in the S₀-S₁ absorption.

Cyclic voltammetry (see Fig. S5) measurements show that all the compounds undergo reversible reduction and irreversible oxidation. An increase in the electron withdrawing ability of the central acceptor leads to a decrease in both the oxidation and reduction potentials as well as in their difference (ΔV).

The main absorption features are well reproduced by the calculations (see Figs. 4-6 left, bottom part) while the excitation energies are generally overestimated (see also Fig. S6) which is typical in the case of absorption, for the long-range corrected functional CAM-B3LYP. [45–48] For higher excited states the absorption intensities were underestimated due to the limited number of excited states included in the calculations. Although other range-separated functionals and more accurate procedures, such as the ‘gap tuning’, which were recently employed for related DAD dyes [6], potentially could improve the accuracy, we emphasize that the central objective of our study was to describe the charge transfer character of the emitting state, solvent effects on the emission spectra along with the 2P activities of low lying excited states, rather than to perform accurate prediction of the excitation energies. The CAM-B3LYP functional has been rigorously tested and shown to be appropriate in terms of the goals of the present study. [32,49]

The first absorption band is due to the intense S₀→S₁ transition, which is dominated by the H→L excitation. The decrease in the energy of this band with an increase in the strength of the acceptor is well reproduced by the calculations and is in agreement with the concomitant decrease in the H-L gap (see Table S3). We note that the trend in the computed energies of HOMO’s and LUMO’s as a function of the acceptor strength (Table S3) is in agreement with the electrochemical data, which show a decrease in both oxidation and reduction potentials with an increase of the strength of the acceptor.

For all chromophores in the series, computations predicted another low-lying strongly electric dipole allowed state, dominated by (H→L+1) excitation. Therefore, the second experimentally observed intense transition in the one-photon absorption (1PA) spectra of TBT, TPT and TTzT (Figs. 4-6 left) was attributed to this higher excited state, as has been done previously for TBT derivatives.[15]

Associated with the charge transfer from the donor to acceptor upon (H→L) excitation (see Fig. 3), there is also a redistribution of charge along the short molecular axis, which results in a remarkably large dipole moment in the S₁ state, persisting in the optimized geometry (see Table S1). This large dipole moment accounts for the observed solvatochromism, since polar states are stabilized in polar solvents.[44]

Solvatochromism was further investigated by computing emission energies in different solvents using both the LR-PCM and SS-PCM approaches. The computational and experimental results are presented in Table S4 and Fig. S7. It can be seen that the absolute emission energies are generally quite accurately predicted by both models, with slight differences in accuracy for the three dyes, possibly owing to the different distributions and types of heteroatoms. [50–51] Indeed, almost all the computed emission energies are slightly underestimated (see Table S4), and the degree of underestimation is similar and close to 0.2 eV for the two molecules featuring the thiadiazole ring (TBT and TTzT). A comparison between experimental and SS-PCM simulated spectra is shown in Figs. 4-6 right. To facilitate the comparison between the trend in Fig. 6 (bottom, right) we reported the spectra of TTzT uniformly shifted by 0.2 eV. The uncorrected computed emissions are compared with experimental data in Figs. S8.

It is of interest to focus on the relative shifts of the transition energies as a function of the solvents’ dielectric constants, taking as reference the data in e.g. DMSO (Fig. 7). It can be seen that the energy shifts computed by LR-PCM and SS-PCM methods follow the same trend as the experimentally measured shifts, whereby the experimental data fall, in some cases, in between the two sets of the computed shifts. Both experimental and theoretical results show that the changes in the shifts as a function of the solvent polarity tend to saturate for all of the investigated compounds. A closer inspection shows that while the relative shifts predicted by the LR-PCM method, ~0.15 eV, is almost identical for the three dyes, the shifts computed by SS-PCM are much more sensitive to the nature of the dye and, most importantly, they more accurately reproduce the experimental data. Indeed, the emission shifts, as they change from DMSO to cyclohexane, are experimentally observed to be 0.24, 0.17 and 0.19 eV for TBT, TPT and TTzT, respectively, and computed by the SS-PCM method as 0.32, 0.19 and 0.26 eV, a result in agreement with the more accurate description of dynamical solvent effects by this model.[27]

Fig. 7.

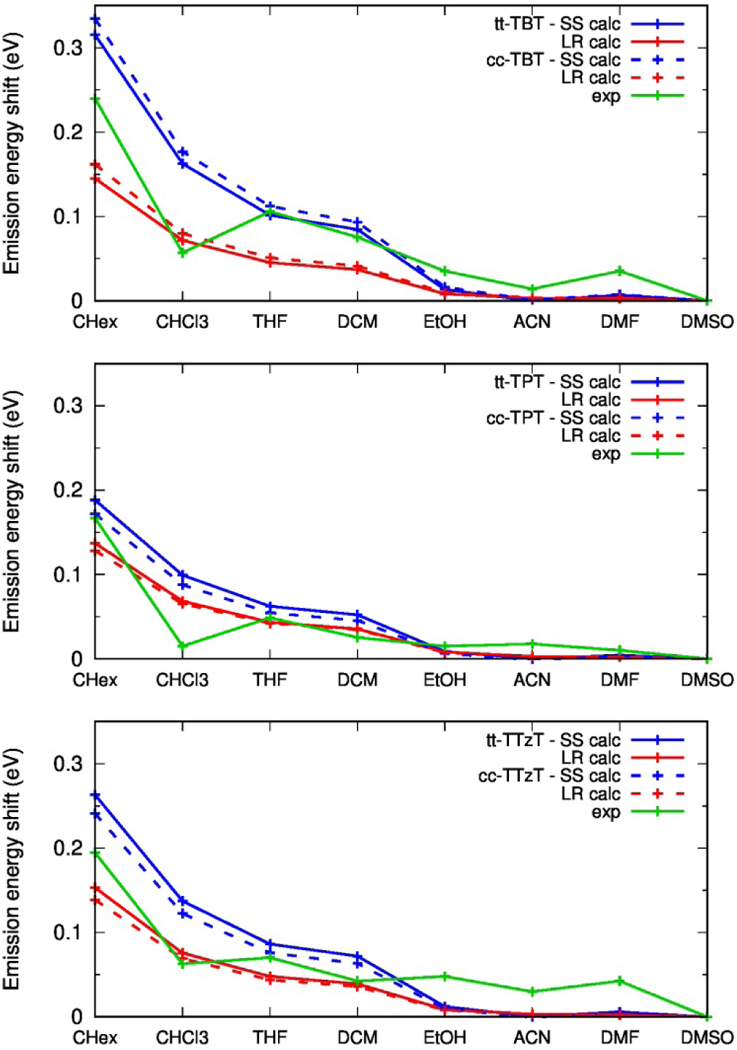
Shift of the emission energy in various solvents, with respect to that in DMSO. (green) Experimental, (red) computed, from LR-PCM calculations, (blue) computed, from SS-PCM calculations.

Unlike the computed vertical emission energies discussed above, an accurate simulation of the Stokes shift (whose magnitude is relevant for the design of emitting dyes in the NIR) requires the evaluation of vibrational frequencies and vibronic progressions which may also be influenced by solvent polarity. Therefore, we determined the Stokes shift in different solvents by including vibronic progressions in simulated absorption and emission spectra whose 0–0 electronic transition energy was determined, as above, with the LR-PCM and SS-PCM models. The remarkably different Stokes shifts obtained experimentally by changing solvents (Table S5, last column) are compared with the simulated values in Fig. 8. The experimental solvent dependence is reasonably well predicted by both LR-PCM and SS-PCM models, with the latter showing a more marked sensitivity to the chromophore, in better agreement with experiment.

Fig. 8.

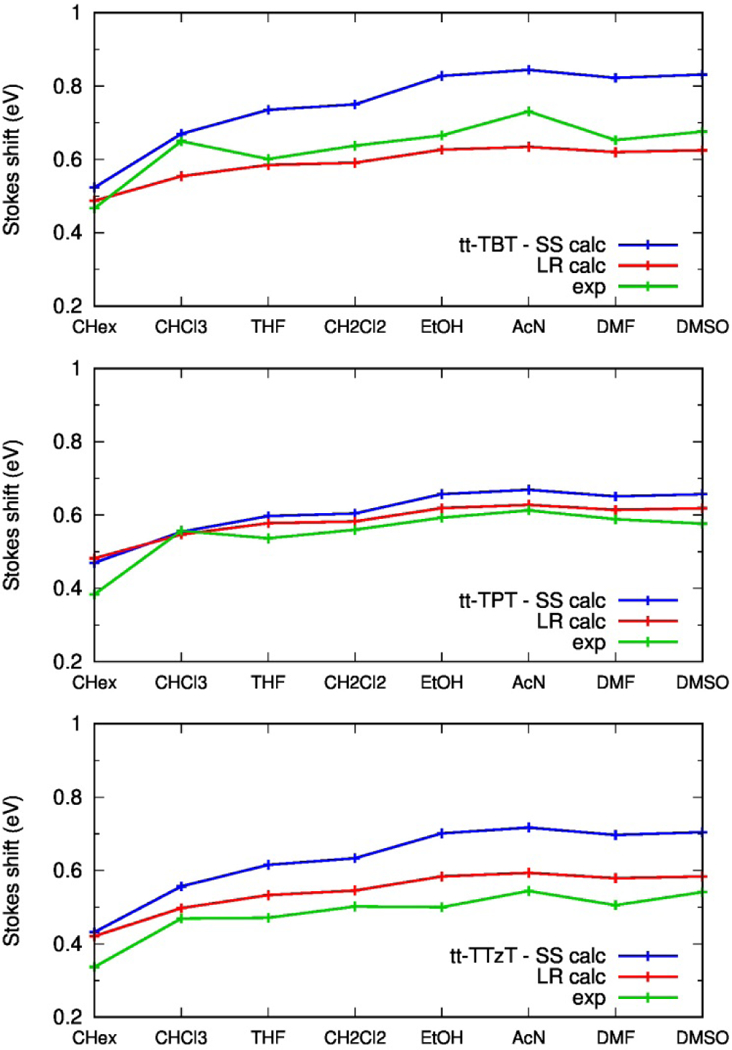
Comparison between experimental and computed Stokes shifts in various solvents. (green) Experimental, (red) computed, from LR-PCM calculations, (blue) computed, from SS-PCM calculations.

Two photon absorption properties.

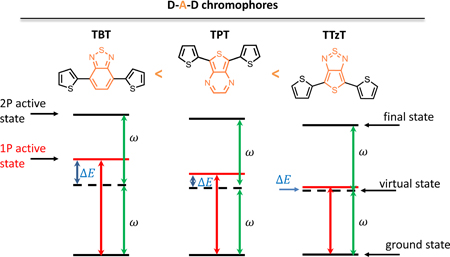
For centrosymmetric quadrupolar DAD chromophores [35,52], the S₀→S₁ transition is usually strongly electric dipole-allowed, while the S₀→S₂ transition, which in some cases is dominated by the (H-1→L) excitation, is forbidden. The chromophores investigated in this work do not formally belong to any symmetry group that includes the inversion of symmetry operation, and yet the (H-1→L) excitation in these molecules is nearly forbidden, similar to truly centrosymmetric systems. In the more stable tt conformers, the (H-1→L) excitation is predicted to dominate the S₂ state of TBT [15], S₄ state of TPT and S₃ state for TTzT, according to TD-CAM-B3LYP calculations (see Table S2). Previously, we have shown that the S₂ state is the lowest energy 2P-active state in TBT derivatives[15]. Therefore, here we investigated states S₄ and S₃, for TPT and TTzT, respectively, in view of their origin in the same (H-1→L) excitation. We note that the predicted excitation energies decrease along the series from 4.4 eV for TBT to 4.04 eV for TTzT in vacuum, suggesting that stronger acceptors influence not only 1PA but also 2PA properties.

The computed 2PA cross-sections (response theory) are presented in Table 2 and Table S6. Note that the negligible cross-section for the S₀→S₁ band indicates that the selection rules for centrosymmetric molecules still prevail for these dyes, despite the lack of an inversion center, as observed for other non-centrosymmetric chromophores.[15] The calculations show that an increase in the acceptor strength results not only in a decrease of the lowest 2P-active state energy but also in an increase of the corresponding 2PA cross-section. In the case of TTzT the nearly completely 1P-forbidden state (S₃) has an extremely large 2PA cross-section. It is worth noting here that 2PA cross-sections computed using the Dalton package typically come out overestimated, which is in part due to a too narrow linewidth parameter (0.1 eV) set in the software.[35] Nevertheless, the very large cross-section computed for TTzT is unlikely to be solely due to the overestimation, but is rather a result of a strong resonance enhancement effect which explains also the unusually large 2PA cross-section of the 1P active S₂ state (see below).

Table 2.

1P and 2P absorption properties of TBT, TPT and TTzT from TD-CAM-B3LYP/6-31G* calculations in vacuo.

Excited state	Energy/eV	σ(2) / GM a	fb	Wavefunction composition
tt-TBT
S2	4.40	528	0.04	(H-1→L)
tt-TPT
S4	4.30	851	0.07	(H-1→L)
tt-TTzT
S2	4.00	2820	0.50	(H→L+1)
S3	4.04	5.3×105	0.05	(H-1→L)

^a2P absorption cross-section for linearly polarized light

^b1P oscillator strength.

In order to carry out the analysis of 2PA activities in terms of the SOS model we computed the transition dipole moments between all the relevant electronic states (Table S7) along with the transition probabilities $\delta ,{\delta }_F$ and ${\delta }_G$ according to eq. (1). We considered either only one intermediate state S₁ or several intermediate states. The results (Table S8) show that in all cases S₁ state is responsible for most of the computed 2P activity. The SOS expression for the amplitude M_i->f^(2P) of two-photon transition from initial state i to the final state f can be written as [53]:

$$M_{i\to f}^{\left(2P\right)}\propto \frac{\left({\mu }_{ff}-{\mu }_{ii}\right){\mu }_{if}}{\omega }{+}_{\square }\sum _{p\ne i,f}\left[\frac{{\mu }_{fp}{\mu }_{pi}}{E_{ip}-\omega }\right]$$ (3)

where indexes p denote the intermediate states. In the cases when the final state is 1P-forbidden (μ_if=0) and S₁ state plays the dominant role as an intermediate state, transition dipole moments ${\mu }_{f.S1}$ and ${\mu }_{S1.i}$ are expected to be large. (see Table S7).

Having established that the intermediate state S₁ accounts for the most of the predicted 2P activity, we note that in the case of TTzT the resonance enhancement effect is particularly strong because the denominator in the corresponding term in eq. (3) approaches zero, as shown schematically in Fig. 9. Indeed, the energy of S₁ is predicted to be very close to one-half the energy of either S₂ or S₃ states. Obtaining more realistic values for 2PA cross-sections would require introduction of a larger damping factor Γ either in the SOS or response theory formalism.[54] These computational results show that the relative positions of the lowest 1P- and 2P-active excited states are such that in spite of the large predicted 2P activities, especially in the case of TTzT, experimental measurements of 2PA cross-sections into the 2P states are likely to be difficult (see below).

Fig. 9.

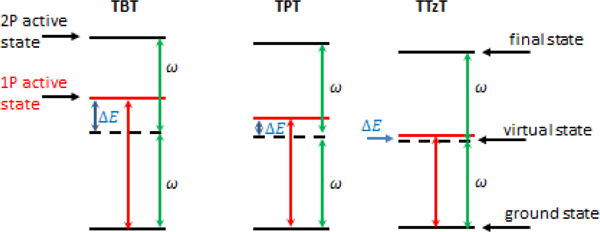
Schematic representation of the lowest energy 1P and 2P active stats of TBT, TPT and TTzT. $\omega$ is the photon energy in the 2P absorption.

Two-photon absorption spectra of the dyes were measured in CDCl₃ using a modification of a previously described setup [55]. The choice of a deuterated solvent was dictated by the fact that in the NIR region overtones of C-H bond vibrations may absorb light [56] and hence interfere with 2PA measurements. To confirm that the observed signals were solely due to the 2PA by a chromophore of interest, dependencies of the emission intensity on the excitation flux were measured at several wavelengths throughout the excitation range (see ESI Figs. S11-S13) and were found to be strictly quadratic (Fig. 10 and S14), as expected for the 2P excitation mechanism. The tunability range of the excitation source used in our experiments was 680–1080 nm. Therefore, for TBT the upper energy limit (680 nm) was determined by the available laser spectrum, while for TPT and TTzT the measurements had to be truncated already at 760 nm and 940 nm, respectively. Such truncation was dictated by the interfering 1P absorption into the lowest vibronic levels of S₁ state and consequently significant deviations from the quadratic behavior at all higher energies.

Fig. 10.

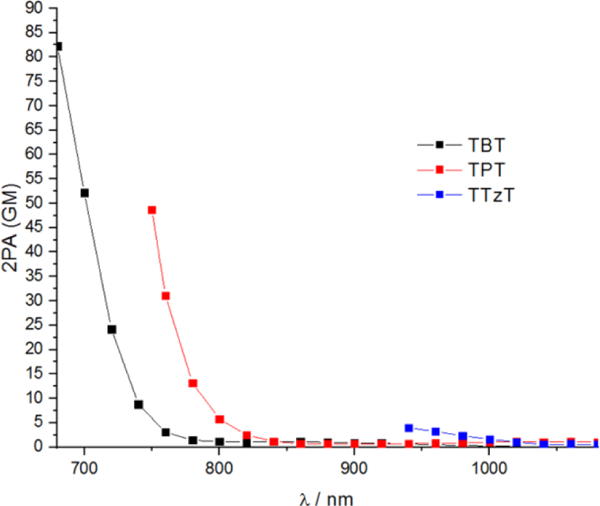
2P absorption of TBT, TPT and TTzT in CDCl3.

The rather low energies at which 1PA becomes a strongly interfering or even the dominant absorption mechanism are explained by the very large differences between the values of 1PA and 2PA cross-sections. It is likely that 1P transitions originating in thermally excited vibrational levels of the ground state are largely responsible for the observed less-than-quadratic power dependencies, as suggested in some previous publications [57].

The TD-DFT 2PA spectra show a progressive increase in the 2PA cross-section of the 2P-active band and concomitant narrowing of the gap between the energies of the excitation photons and S₁ state (Fig. 9). As a result, the experimentally accessible region where the 2PA cross-sections can be reliably measured decreases in the series TBT, TPT, TTzT (Fig. 10 and S14). As the photon energy approaches that of S₁ state, 1PA starts to get in the way, and measurements must be truncated well below the actual 2PA maximum is reached. This effect is particularly dramatic in the case of TTzT, where just a tail of the 2PA band could be observed, while the 2PA cross-section at the band maximum is expected to be the largest in the series.

Consistent with the computational predictions, the measured 2P activity at 750 nm is much larger for TPT than for TBT, which is a result of the lower energy of the 2P active state and a larger resonance enhancement effect in the case of TPT due to the reduced gap between the S₁ state and the energy of the excitation photons.

Conclusions

The 1P and 2P properties of three DAD dyes featuring thiophene as donor and acceptors of varying strength are determined by a combination of experimental and computational methods. The marked solvatochromism is investigated experimentally by measuring the emission spectra in different solvents and rationalized in terms of the increased dipole moment of the lowest excited state compared to the ground state. The emission shifts in different solvents are well reproduced by the calculations with the LR-PCM and SS-PCM models. However, only the SS-PCM model correctly captures the specificity of the chromophore and predicts different emission shifts for the three dyes, in agreement with the experimental results.

The effect of the acceptor on the 2PA properties of the DAD dyes has been determined. The predicted 2PA cross-sections can be accounted for by considering just one intermediate state, i.e. S₁ state. The energies of both 1P- and 2P- active states decrease with an increase in the strength of the acceptor. In the case of TTzT the energetic positions of these states prevent exploitation of the theoretically predicted very high 2PA efficiency due to the competing 1P absorption into the S₁ state.

In conclusion, the above data and analysis suggest that 2PA properties of DAD chromophores can be efficiently tuned by modulating the acceptor strength. However, when designing DAD dyes one should take into account possible resonance overlap between the energies of excitation photons and intermediate states. Future investigation should consider effects of different donors as well as substituents conveying partial diradical character [58,59] to the dyes in order to create chromophores with improved 2PA properties and high emissivity.

Fig. 5.

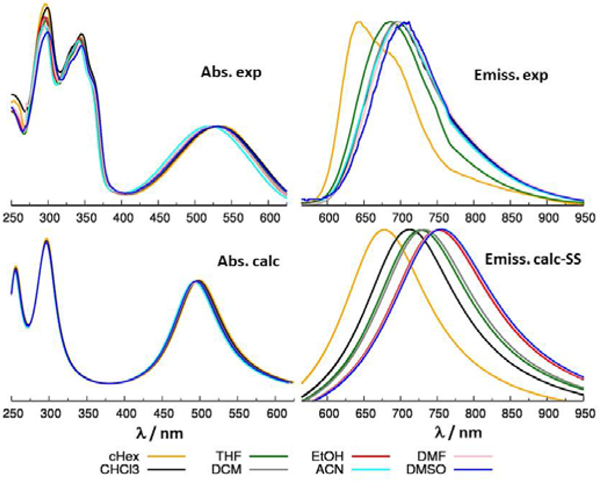
Comparison between computed (bottom) and experimental (top) absorption (left) and emission (right) spectra of TPT. Computed results from TD-CAM-B3LYP/6-31G* calculations, solvent described with PCM in the SS formalism. To facilitate the comparison with experiment, computed vertical excitations are broadened with a Lorentzian linewidth of 0.4 eV.