Abstract
Background
Prostate-specific antigen (PSA)–based screening for prostate cancer has been widely performed, but its accuracy is unsatisfactory. To improve accuracy, building an effective statistical model using machine learning methods (MLMs) is a promising approach.
Methods
Data on continuous changes in the PSA level over the past 2 years were accumulated from 512 patients who underwent prostate biopsy after PSA screening. The age of the patients, PSA level, prostate volumes, and white blood cell count in urinalysis were used as input data for the MLMs. As MLMs, we evaluated the efficacy of three different techniques: artificial neural networks (ANNs), random forest, and support vector machine. Model performance was evaluated using area under the receiver operating characteristic curve (AUC) and compared with the PSA level and the conventional PSA–based parameters: PSA density and PSA velocity.
Results
When using two annual PSA testing, all receiver operating characteristic curves of the three MLMs were above the curve for the PSA level, PSA density, and PSA velocity. The AUCs of ANNs, random forest, and support vector machine were 0.69, 0.64, and 0.63, respectively. Those values were higher than the AUCs of the PSA level, PSA density, and PSA velocity, 0.53, 0.41, and 0.55, respectively. The accuracies of the MLMs (71.6% to 72.1%) were also superior to those of the PSA level (39.1%), PSA density (49.7%), and PSA velocity (54.9%). Among the MLMs, ANNs showed the most favorable AUC. The MLMs showed higher sensitivity and specificity than conventional PSA–based parameters. The model performance did not improve when using three annual PSA testing.
Conclusion
The present retrospective study results indicate that machine learning techniques can predict prostate cancer with significantly better AUCs than those of PSA density and PSA velocity.
Keywords: Machine leaning method, Prostate cancer, Prostate-specific antigen
1. Introduction
Prostate-specific antigen (PSA)–based screening for prostate cancer (PCA) has been widely performed in many countries. PSA is produced by prostate epithelium; therefore, it is organ specific but is not a PCA-specific marker. PSA can be elevated in patients with benign prostate hypertrophy, prostatitis, or other non-PCA conditions. The low specificity of PSA can lead to unnecessary biopsy. The sensitivity of PSA is also unsatisfactory—it is limited to around 50% based on a widely used cutoff level of 4 ng/ml. To improve the accuracy of screening systems, various approaches such as measurements of free PSA, PSA density, PSA velocity, and introduction of the age-specific PSA reference range have been proposed.1, 2, 3 The results are promising; however, they do not show sufficiently strong diagnostic accuracy on their own.
To overcome these obstacles, building an effective statistical model using various predictive variables is a promising approach. For this purpose, machine learning techniques have been used extensively in the field of clinical medicine, especially when used for the construction of prediction models. For prediction of PCA, the machine learning technique most evaluated is artificial neural network (ANN).4, 5, 6, 7, 8, 9, 10, 11, 12 ANNs show high area under the curve (AUC) values compared with PSA alone (total PSA or other PSA-based assessments), ranging from 0.67 to 0.87 depending on the selected variables and the examined population. More recently, as alternative machine learning methods (MLMs), support vector machine (SVM) and random forest (RF) have been applied to PSA screening.13, 14 These new algorithms may help to improve diagnosis, but available information is limited.
Partly because of the low sensitivity and specificity of PSA, many participants in PSA screening receive repeat PSA testing annually. In general, participants with PSA above the cutoff levels are encouraged to undergo prostate biopsy. However, conservative attitudes toward making the decision to receive an invasive procedure sometimes cause participants to select repeat PSA testing rather than promptly opt for prostate biopsy. In addition, several guidelines recommend annual PSA testing for men with PSA below 4 ng/ml. The Japanese Urological association (JUA) recommends annual PSA testing for men with PSA levels 1–4 ng/ml.15 The NCCN Prostate Cancer Early Detection Panel recommends PSA testing at 1- to 2-year interval for men with PSA levels 1–3 ng/ml in the age group of 45–75 years.16 Such a frequent follow-up leads to multiple normal or intermediately abnormal PSA test values. It can result not only in psychological distress for participants but also in inefficient use of medical resources.
Based on this background, we conducted the present retrospective study with the objective of building an effective statistical model using two or three annual PSA testing before prostate biopsy. For this purpose, we evaluated the efficacy of SVM and RF in addition to the traditional machine learning technique, ANNs. To our knowledge, there are no previous studies using annual PSA testing to improve the accuracy of PSA screening.
2. Patients and methods
2.1. Patients
The study was approved by the independent ethics committee of Hitachi General Hospital. Between October 2002 and June 2016, 3,911 patients underwent prostate biopsy at Hitachi General Hospital. We accumulated data on continuous changes in the PSA level over the past 2 years from 3911 patients and excluded those patients who received drugs (e.g. dutasteride) that might affect the PSA level. As a result, the overall study cohort (n = 512) was selected from 3911 patients. In addition, three continuous and annually measured PSA values were available for 304 patients. All patients underwent transurethral ultrasound sonography (TRUS) before biopsy. The TRUS examinations were performed by well-trained technicians. The PSA density was calculated by dividing the PSA by the prostate volume (approximate values of ellipsoid: anteroposterior diameter × lateral diameter × vertical diameter × π/6). The PSA velocity was calculated as the rate of PSA change using the first and last values only and the equation pn − p1/tn − t1 [n = total number of PSA tests, p = PSA value, and t = time at PSA test (yr)].
Of 512 patients, 193 (37.7%) were diagnosed with PCA on the first prostate biopsy, which was performed using the 10-core transrectal approach. Table 1 shows the baseline characteristics of the patients. The mean PSA level and PSA distribution were not significantly different between the patients diagnosed with PCA and those not diagnosed with PCA. The mean prostate volume was significantly higher in the former group compared with the latter group, but there was no significant difference in PSA density and PSA velocity between the two groups. Among 319 patients not diagnosed with PCA at the first biopsy, 112 patients underwent a second or more prostate biopsies. The rebiopsy was performed using the 12-core transperitoneal approach. Of the 112 patients, 57 were eventually diagnosed with PCA.
Table 1.
Distribution of diagnostic variables in 512 patients who underwent the first biopsy.
| Characteristics | Patients diagnosed with PCA |
Patients with negative biopsy |
P value |
|---|---|---|---|
| N = 193 | N = 319 | ||
| Age (year) | 0.52 | ||
| 50–59 | 7 | 30 | |
| 60-69 | 82 | 149 | |
| ≧70 | 104 | 140 | |
| Mean PSA level (ng/ml)a) | 8.6 | 4.5 | 0.08 |
| PSA (ng/ml)a) | 0.67 | ||
| <4 | 2 | 9 | |
| 4 < PSA<10 | 149 | 260 | |
| 10 ≦ PSA<20 | 38 | 47 | |
| ≧20 | 4 | 3 | |
| Mean prostate volume (cc) | 55.6 | 44.8 | <0.05 |
| Mean PSA density (ng/ml/cc) | 0.20 | 0.19 | 0.87 |
| Mean PSA velocity (ng/ml/year) | 0.96 | 0.71 | 0.08 |
PCA, prostate cancer; PSA, prostate-specific antigen.
Average of two serial PSA testing
2.2. Machine learning methods
Three types of supervised machine learning algorithms (ANNs, SVM, and RF) were applied in this study. A set of input variables comprising age of patients, PSA level (maximum, minimum, median, mean, and variance level), prostate volumes, white blood cell (WBC) count in urinalysis, and result of biopsy was used to create the PCA prediction model. Age of patients, PSA level, and prostate volumes were entered as continuous variables, and the WBC count in urinalysis was entered as seven categorical variables from below 1 WBC/high-power field to 50-99 WBC/high-power field. The results of biopsy were entered as binary: 1 (PCA) and 0 (non-PCA).
The machine learning models were fit using scikit-learn 0.18 modules of python throughout this study. The ANN models were fit using the multilayer perceptron Classifier class. The multilayer perceptron is a feedforward ANN model that maps sets of input data onto sets of appropriate outputs. There can be one or more nonlinear hidden layers between the input and the output. The input neurons send information to the hidden layer, and the hidden layer sends data to the output layer. Every neuron in the hidden layer has weighted inputs, a nonlinear activation function (which defines the output, given an input), and one output. There are two main tuning parameters: the number of nodes in the hidden layer and activation function. Training is the weight optimization process in which the error of predictions is minimized and the network reaches a specified level of accuracy. The SVM model is a machine learning model that finds an optimal boundary between the possible outputs. SVM identifies the optimal separating hyperplane that maximizes the margin between the output and input. The SVM models were fit using the SVC class of scikit-learn. There are three main tuning parameters: penalty parameter C, kernel type, and gamma. Parameter C handles the trade-off between maximizing the margin and minimizing the training error; increasing the value improves the classification accuracy for the training data but could lead to overfitting. Kernel type defines the type of nonlinear kernel function (tanh, radial basis function (RBF), polynomial) used for the separation. Gamma is used for kernel functions. Increasing the gamma value improves the classification accuracy for the training data, but this could lead to overfitting. The RF model is a machine learning model built on decision trees. In the decision tree, each node of the tree splits the data into two groups using a cutoff value within one of the features. As the depth increases, the decision tree tends to overfit the training data; the tree fits details of particular data rather than the overall properties of the distributions. The RF method is able to minimize the effect of the overfitting problem by creating an ensemble of randomized decision trees, each of which overfits the data and averages the results to find a better classification. Increasing the number of trees improves the accuracy for the training, but the cost in terms of computation time for learning is increased.
For all the three models, the parameters of the estimator were optimized by 10-fold cross-validated grid search over a parameter grid. For each of the 10 “folds,” a model was trained using nine of the folds as training data and the resulting model was validated on the remaining part of the data. For each parameter set in the parameter grid, 10-fold cross-validations were evaluated and the best parameter set was selected.
2.3. Statistical analysis
Continuous variables were compared using the independent sample Student t test. Model performance was evaluated using area under the receiver operating characteristic (ROC) curve (AUC), which provides a measure of the discriminatory performance of the model17; sensitivity, which is the proportion of true positives that are classified as such; specificity, which measures the proportion of correctly identified true negatives; and accuracy, which is the proportion of correct predictions.
3. Results
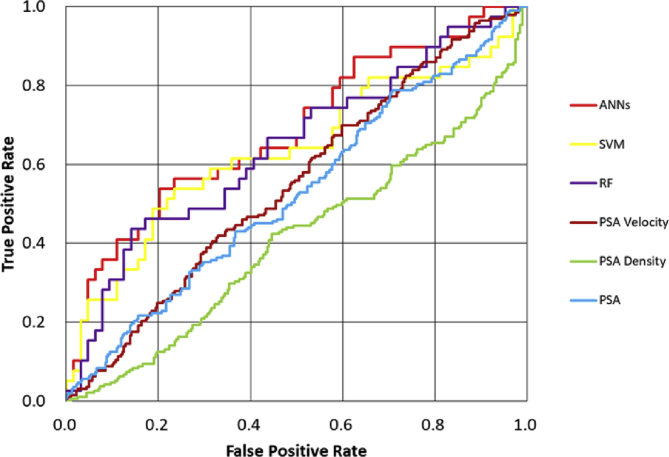
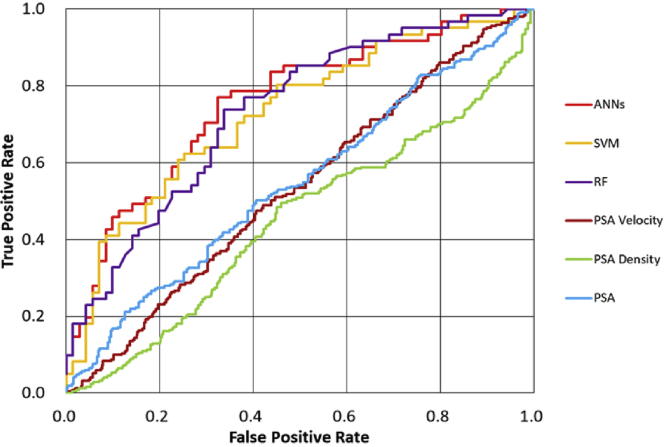
Fig. 1 shows the corresponding ROC curves for ANNs, SVM, and RF using two annual PSA testing to predict pathological diagnosis of the first biopsy in 512 patients. The results were compared with those of the PSA level (cutoff of 4 ng/ml), PSA density (cutoff of 0.20 ng/ml/cc), and PSA velocity (cutoff of 0.75 ng/ml/year). As shown in Fig. 1, all the ROC curves of the three MLMs were above the curve for the PSA level, PSA density, and PSA velocity. In addition, we compared the ROC curves of those methods to predict the result of the second or more biopsy in combination with the results of the first biopsy. After subsequent biopsies, 250 of 512 patients were finally diagnosed as having PCA. In this case, the ROC curves of the three MLMs were above the curve for the PSA level, PSA density, and PSA velocity (Fig. 2).
Fig. 1.
Receiver operating characteristic curve for prediction of prostate cancer diagnosis on the first therapy is shown.
ANNs, artificial neural networks; PSA, prostate-specific antigen; RF, random forest; SVM, support vector machine.
Fig. 2.
Receiver operating characteristic curve for prediction of prostate cancer diagnosis on the first and second therapies is shown.
ANNs, artificial neural networks; PSA, prostate-specific antigen; RF, random forest; SVM, support vector machine.
Table 2 shows the AUC, sensitivity, specificity, and accuracy of each prediction method for the results of the first biopsy. When using AUC as a measure of predictive model performance, as shown in Table 2, the AUC of ANNs was 0.69. It was superior to those of RF and SVM (0.64 and 0.63, respectively). The AUCs of the PSA level, PSA density, and PSA velocity were 0.53, 0.41, and 0.55, respectively, which were lower than those of the MLMs.
Table 2.
Diagnostic performance of different prediction methods using two serial PSA testing and PSA-related parameter.
| Outcome | Artificial neural network | Random forest | Support vector machine | PSA density | PSA velocity | PSA |
|---|---|---|---|---|---|---|
| AUC | 0.69 | 0.64 | 0.63 | 0.41 | 0.55 | 0.53 |
| Sensitivity (%) | 56.4 | 66.7 | 59.0 | 37.2 | 47.1 | 99.0 |
| Specificity (%) | 76.6 | 56.2 | 68.7 | 57.3 | 60.8 | 2.8 |
| Accuracy (%) | 71.6 | 72.1 | 71.6 | 49.7 | 54.9 | 39.1 |
AUC, area under the receiver operating characteristic curve; PSA, prostate-specific antigen.
As show in Table 2, the accuracies of the three MLMs were also superior to those of the PSA level, PSA density, and PSA velocity. The sensitivities of the MLMs were 56.4 to 66.7%, which were higher than those of PSA density and PSA velocity. Furthermore, the specificities of the MLMs tended to be higher than conventional PSA–related parameters.
We further analyzed the predictive performance of the three MLMs using three annual PSA testing. As shown in Table 3, AUCs of ANNs, RF, and SVM were 0.70, 0.68, and 0.71, respectively. Those were slightly superior to AUCs using two annual PSA testing. In addition, the accuracies, sensitivities, and specificities were higher than those using two annual PSA testing.
Table 3.
Diagnostic performance of different prediction methods using three serial PSA testing.
| Outcome | Artificial neural network | Random forest | Support vector machine |
|---|---|---|---|
| AUC | 0.70 | 0.68 | 0.71 |
| Sensitivity (%) | 59.1 | 72.7 | 68.2 |
| Specificity (%) | 64.1 | 64.1 | 79.5 |
| Accuracy (%) | 72.4 | 65.8 | 74.1 |
AUC, area under the receiver operating characteristic curve; PSA, prostate-specific antigen.
4. Discussion
As machine learning techniques, ANNs were first introduced into PCA diagnosis in 1994 by Snow et al. .4 The authors used age, PSA level, digital rectal examination (DRE), and TRUS findings as input data and reported the excellent AUC of 0.87. Since then, ANNs have been widely used for this purpose. However, reported AUCs ranged from 0.67 to 0.88 depending on the selected variables and the examined population. According to reviews by Schroder and Kattan,12 seven of the eight ANN studies used DRE findings as variables. In six studies, percent free PSA was also introduced as a variable. Here, we showed that machine learning techniques using the more simple predictors as input data can efficiently predict PCA. Our analyses have provided the following interesting findings.
In the present study, we used age, PSA level, prostate volume, and WBC count in urinalysis as variables. The WBC count in urinalysis was selected in attempting to exclude PSA elevation due to prostatitis. We excluded DRE as a variable to avoid subjective factors. The three examined MLMs revealed both favorite AUCs of 0.63 to 0.69, which were better than that of the PSA level, PSA density, and PSA velocity. We further analyzed the predictive performance of the models by adding PSA density and PSA velocity as variables, but this failed to further improve AUC (data not shown). Therefore, it is possible that these models had already learned factors associated with PSA density and PSA velocity.
As the JUA recommends annual PSA testing for men with PSA levels 1–4 ng/ml,15 a number of Japanese PSA screening participants have prior two or more annual PSA data. Present prediction models can help decision-making for prompt prostate biopsy or further PSA follow-up. However, the model using three annual PSA testing did not improve predictive performance, as shown in Table 3. Therefore, it is possible that PSA levels over the past 2 years were sufficient for this purpose. Although the JUA recommends annual PSA testing, recently, individualized rescreening interval is being proposed for men with PSA levels in the range 1–4 ng/ml. Randazzo et al.18 conducted a population-based prospective screening study and proposed a retest interval of every 3–4 years for men with the baseline PSA of 1–2 ng/ml. The European Association of Urology recommendation is to postpone PSA follow-up interval to 8 years for men with PSA of <2 ng/ml at the age of 60 years .19 In the future, if prediction models using PSA testing at optimal interval are developed, they could be a powerful tool for a more individualized and scientific rescreening strategy.
Because there are no previous studies using annual PSA testing, we compared three different models using the same variables and population to identify the most suitable prediction model. In a clinical situation, a relatively large number of variables compared with the sample size have a tendency for overfitting bias in machine learnings. The RF model is known to be less prone to overfitting than the traditional ANNs or SVM.20 Therefore, RF may be a candidate for a suitable model when using annual PSA testing. However, in the present study, the AUC of RF was not superior to those of ANNs, and our study did not have enough power to draw conclusion on this point.
Although our study revealed important findings, there are several limitations to our analysis. First, the sample size was relatively small; therefore, further investigation is needed to establish a prediction model. Second, many potential biases resulting from the retrospective design of the analysis must be considered. Third, information about the decision-making process for prostate biopsy selection was not fully available.
In conclusion, the present retrospective study showed that machine learning techniques could predict a PCA diagnosis with significantly better AUCs than those of PSA density and PSA velocity. It is possible that the three MLMs developed a tendency to detect PCA from input data more effectively than human intelligence.
Conflicts of interest
No potential conflict of interest relevant to this article was reported.
Acknowledgments
This study was supported by Hitachi Ltd.
References
- 1.Gann P.H., Hennekens C.H., Stampfer M.J. A prospective evaluation of plasma prostate-specific antigen for detection of prostatic cancer. JAMA. 1995;273(4):289–294. [PubMed] [Google Scholar]
- 2.Djavan B., Zlotta A., Kratzik C., Remzi M., Seitz C., Schulman C.C. PSA, PSA density, PSA density of transition zone, free/total PSA ratio, and PSA velocity for early detection of prostate cancer in men with serum PSA 2.5 to 4.0 ng/mL. Urology. 1999;54(3):517–522. doi: 10.1016/s0090-4295(99)00153-3. [DOI] [PubMed] [Google Scholar]
- 3.Kitagawa Y., Izumi K., Sawada K., Mizokami A., Nakashima K., Koshida K. Age-specific reference range of prostate-specific antigen and prostate cancer detection in population-based screening cohort in Japan: Verification of Japanese Urological Association Guideline for prostate cancer. Int J Urol. 2014;21(11):1120–1125. doi: 10.1111/iju.12523. [DOI] [PubMed] [Google Scholar]
- 4.Snow P.B., Smith D.S., Catalona W.J. Artificial neural networks in the diagnosis and prognosis of prostate cancer: A pilot study. J Urol. 1994;152:1923–1926. doi: 10.1016/s0022-5347(17)32416-3. [DOI] [PubMed] [Google Scholar]
- 5.Joseph B., Herbert F., Alberto A., Vijaya B., Dennis A.J., William N. Performance of a neural network in detecting prostate cancer in the prostate-specific antigen reflex range of 2.5 to 4.0 ng/ml. Urology. 2000;56:1000–1006. doi: 10.1016/s0090-4295(00)00830-x. [DOI] [PubMed] [Google Scholar]
- 6.Bob D., Mesut R., Alexandre Z., Christian S., Peter S., Michael M. Novel artificial neural network for early detection of prostate cancer. J Clin Oncol. 2002;20:921–929. doi: 10.1200/JCO.2002.20.4.921. [DOI] [PubMed] [Google Scholar]
- 7.Carsten S., Henning C., Axel S., Eleftherios P.D., Leon F.A.W., Michael L. Multicenter evaluation of an artificial neural network to increase the prostate cancer detection rate and reduce unnecessary biopsies. Clin Chem. 2002;48:1279–1287. [PubMed] [Google Scholar]
- 8.Carsten S., Hellmuth-Alexander M., Maciej K., Franz R., Henning C., Stefan A.L. A (−5, −7) proPSA-based artificial neural network to detect prostate cancer. Eur Urol. 2006;50:1014–1020. doi: 10.1016/j.eururo.2006.04.011. [DOI] [PubMed] [Google Scholar]
- 9.Carsten S., Chuanliang X., Henning C., Markus G., Alexander H., Hartwig H. Assay-specific artificial neural networks for five different PSA assays and populations with PSA 2–10 ng/ml in 4480 men. World J Urol. 2007;25:95–103. doi: 10.1007/s00345-006-0132-9. [DOI] [PubMed] [Google Scholar]
- 10.Felix K.-H.C., Markus G., Alberto B., Andrea G., Julia H., Michael W.K. Initial biopsy outcome prediction—Head-to-head comparison of a logistic regression-based nomogram versus artificial neural network. Eur Urol. 2007;51:1236–1243. doi: 10.1016/j.eururo.2006.07.021. [DOI] [PubMed] [Google Scholar]
- 11.Carsten S., Chuanliang X., Patrik F., Henning C., Hellmuth-Alexander M., Michal L. Comparison of two different artificial neural networks for prostate biopsy indication in two different patient populations. Urology. 2007;70:596–601. doi: 10.1016/j.urology.2007.04.004. [DOI] [PubMed] [Google Scholar]
- 12.Schröder F., Kattan M.W. The comparability of models for predicting the risk of a positive prostate biopsy with prostate-specific antigen alone: A systematic review. Eur Urol. 2008;54(2):274–290. doi: 10.1016/j.eururo.2008.05.022. [DOI] [PubMed] [Google Scholar]
- 13.Nhung N.T., Khuong V.T., Huy V.Q., Bao P.T. Classifying prostate cancer patients based on total prostate-specific antigen and free prostate-specific antigen features by support vector machine. J Cancer Res Ther. 2016;12(2):818–825. doi: 10.4103/0973-1482.172133. [DOI] [PubMed] [Google Scholar]
- 14.Xiao L.H., Chen P.R., Gou Z.P., Li Y.Z., Li M., Xiang L.C. Prostate cancer prediction using the random forest algorithm that takes into account transrectal ultrasound findings, age, and serum levels of prostate-specific antigen. Asian J Androl. 2017;19(5):586–590. doi: 10.4103/1008-682X.186884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.http://www.urol.or.jp/cms/files/info/16/20171023.pdf.
- 16.Carroll P.R., Parsons J.K., Andriole G., Bahnson R.R., Barocas D.A., Catalona W.J. Prostate cancer early detection, version 1.2014. Featured updates to the NCCN Guidelines; National comprehensive cancer network. J Natl Compr Canc Netw. 2014;12(9):1211–1219. doi: 10.6004/jnccn.2014.0120. quiz 1219. [DOI] [PubMed] [Google Scholar]
- 17.Hanley J.A., McNeil B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143:29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
- 18.Randazzo M., Beatrice J., Huber A., Grobholz R., Manka L., Chun F.K. Is further screening of men with baseline PSA<1 ng ml(-1) worthwhile? The discussion continues-Results of the Swiss ERSPC (Aarau) Int J Cancer. 2015;137(3):553–559. doi: 10.1002/ijc.29420. [DOI] [PubMed] [Google Scholar]
- 19.http://uroweb.org/wp-content/uploads/EAU-Guidelines-Prostate-Cancer-2016-1.pdf.
- 20.Askland K.D., Garnaat S., Sibrava N.J., Boisseau C.L., Strong D., Mancebo M. Prediction of remission in obsessive compulsive disorder using a novel machine learning strategy. Int J Methods Psychiatr Res. 2015;24(2):156–169. doi: 10.1002/mpr.1463. [DOI] [PMC free article] [PubMed] [Google Scholar]