Item Response Tree Models to Investigate Acquiescence and Extreme Response Styles in Likert-Type Rating Scales

Abstract

Item response tree (IRTree) models are recently introduced as an approach to modeling response data from Likert-type rating scales. IRTree models are particularly useful to capture a variety of individuals’ behaviors involving in item responding. This study employed IRTree models to investigate response styles, which are individuals’ tendencies to prefer or avoid certain response categories in a rating scale. Specifically, we introduced two types of IRTree models, descriptive and explanatory models, perceived under a larger modeling framework, called explanatory item response models, proposed by De Boeck and Wilson. This extends the typical application of IRTree models for studying response styles. As a demonstration, we applied the descriptive and explanatory IRTree models to examine acquiescence and extreme response styles in Rosenberg’s Self-Esteem Scale. Our findings suggested the presence of two distinct extreme response styles and acquiescence response style in the scale.

A Likert-type rating scale is widely used in many disciplines to measure individual differences in attributes, attitudes, or traits. In this type of scale, the response categories are written to represent different levels of endorsement (e.g., “Strongly agree” to “Strongly disagree”). Despite the wide uses of the rating scales, this response format has been a concern because the respondents may tend to prefer or avoid particular categories, regardless of the levels of trait being measured. This phenomenon has been referred to as response style, response set, or response bias in the literature (Cronbach, 1946; Jackson & Messick, 1958; Paulhus, 1991). In this study, we used the term response style to express this phenomenon.

The adverse effects of response styles have been widely discussed elsewhere (e.g., Kam & Fan, 2017; Moors, 2012; Weijters, Cabooter, & Schillewaert, 2010). The presence of response styles can cause biases in the measurement of the true trait as well as affecting the meanings of scores. For example, if the respondents prefer the extreme categories (e.g., “Strongly agree” and “Strongly disagree”), their responses can overestimate or underestimate the true levels of the trait, and therefore their scores are possibly biased. In more extreme cases, the scale scores may be seriously biased by response styles, and they cannot be interpreted as representing the trait of interest. Furthermore, response styles may distort the associations among variables measured by the scales because the biased scale scores can deflate or inflate the correlations among the variables.

Because of these undesirable effects, there have been many reports of investigating the presence of response styles (e.g., Hurley, 1998; Meisenberg & Williams, 2008; Moors, 2008, 2012; Schneider, 2016; Weijters et al., 2010). Different response styles have been conjectured to occur while responding to a Likert-type rating scale. Among them, the most commonly reported are the acquiescence response style, disacquiescence response style, extreme response style, and midpoint response style. A comprehensive summary of these response styles can be found in Baumgartner and Steenkamp (2001) and Van Vaerenbergh and Thomas (2013).

Generally, response styles have been examined by two different approaches depending on how the response styles are captured. The first approach incorporates items that are external to the substantive trait being measured in order to track the response style of interest (Greenleaf, 1992b; Weijters, Geuens, & Schillewaert, 2010). The other approach uses only the internal items of a scale that are originally designed to measure the substantive trait (Bolt & Johnson, 2009). This approach does not require extra measures or items; individuals’ response patterns to the internal items are inspected to capture the response styles. Both approaches are equally common and sometimes used concurrently (e.g., Wetzel & Carstensen, 2017).

In addition to the ways of capturing response styles, different statistical techniques were applied to investigate response styles. The simplest is to look at descriptive statistics such as frequency counts, mean, and standard deviation of the item scores (Bachman & O’Malley, 1984; Reynolds & Smith, 2010). Although relatively straightforward, descriptive statistics are not very illuminating because this approach cannot tease apart the response styles from the trait being measured. This makes it hard for researchers to inspect whether the responses reflect the response styles, true traits, or both. Because of this limitation, this approach was only recommended when researchers can include external items to detect the response styles (Greenleaf, 1992a).

Other more advanced techniques were proposed within two modeling frameworks: structural equation modeling and item response theory (IRT). With structural equation modeling, response styles were often modeled as continuous latent variables using confirmatory factor analysis (Billiet & McClendon, 2000; Welkenhuysen-Gybels, Billiet, & Cambré, 2003). At times, response styles were modeled as categorical latent variables, and latent class analysis was applied to identify subgroups of individuals who display different preference/avoidance when selecting the response categories (Moors, 2003, 2010; Van Rosmalen, Van Herk, & Groenen, 2010). As for the IRT approach, some studies proposed a multidimensional nominal response model to inspect and control for the extreme response style (Bolt & Johnson, 2009; Bolt & Newton, 2011; Johnson & Bolt, 2010). For others, polytomous IRT models such as partial credit model were extended to mixture models to identify latent groups of distinct response styles (e.g., Austin, Deary, & Egan, 2006). Recently, a tree-structure-based IRT model, item response tree (IRTree) models (also known as multiprocess IRT models or multinomial processing tree models) were used to study response styles (Böckenholt & Meiser, 2017; Khorramdel & von Davier, 2014; Plieninger & Meiser, 2014).

Among the proposed techniques, IRTree models are considered a promising tool due to its capacity to directly hypothesize the response processes by a tree structure (Böckenholt, 2017). By applying IRTree models, researchers can model the hypothesized processes involved in responding to the items, and in so doing permits an examination of the response styles associated with different processes. Moreover, IRTree models enable the researchers to disentangle response styles from the substantive trait based only on the internal items, although incorporating external items is also permissible. These benefits of the IRTree models, as a way of studying response styles, are well documented in the recent demonstrations (Böckenholt, 2017; Böckenholt & Meiser, 2017; Khorramdel & von Davier, 2014; Plieninger & Meiser, 2014; Thissen-Roe & Thissen, 2013; Zettler, Lang, Hülsheger, & Hilbig, 2016). However, most of these pioneer studies, if not all, aimed to examine only the extreme and/or midpoint response styles. There was little work on how the IRTree model can be extended to investigate other response styles.

This article aims to show that IRTree models can be used to investigate a variety of hypotheses about response styles. To do so, this study holds the view that IRTree models are part of a larger modelling framework, called explanatory item response model, proposed by De Boeck and Wilson (2004). Taking this view allows greater flexibility in thinking about IRTree models, including models that have not been considered in previous applications.

The remaining article is organized as follows. We first give an overview of IRTree models. We then explicate how IRTree models can be used to inspect response styles in explanatory item response modeling framework. Next, to demonstrate the flexibility of IRTree models, we showcase its applications to study acquiescence, disacquiescence, and extreme response styles in a 4-point Likert-type Rosenberg Self-Esteem Scale.

Overview of IRTree Models

IRTree models are a type of IRT model that is specified via a tree structure. It was introduced as an alternative to modeling the responses of Likert-type rating scales (Böckenholt, 2012; De Boeck & Partchev, 2012). The basic idea of IRTree models is that the observed responses are the results from a series of decision processes, which can be represented by a tree structure. This feature is particularly beneficial because it allows the study of various response behaviors involved in each process (e.g., the extreme response style is a response behavior occurring in the process of deciding whether to choose extreme or mild response categories). By stipulating different response processes, researchers can study a variety of response behaviors that are conjectured to occur.

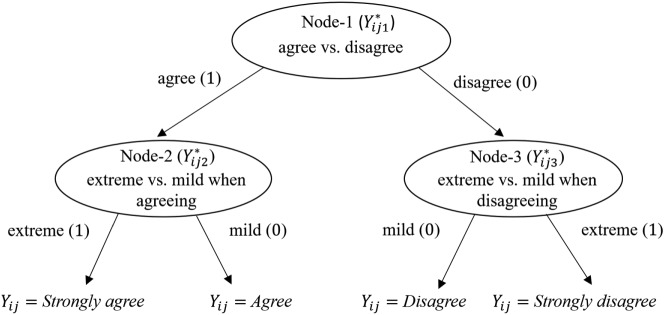
As an example, we illustrate one way of specifying the tree structure of a 4-point Likert-type scale consisting of Strongly agree (SA), Agree (A), Disagree (D), and Strongly disagree (SD). The tree structure in Figure 1 postulates that individuals’ item responses are derived through the following decision processes: (1) the respondents first decide whether they agree or disagree with a given statement and (2) they further determine how strongly they agree or disagree with a given statement. The decision processes are depicted by a series of nodes and branches. Each node represents a decision query, and the branches represent the decisions made at each node.

Figure 1.

An example tree structure for a 4-point Likert-type rating scale.

To model the postulated decision processes, the original categorical item responses ($Y_{\mathrm{ij}}$) from person i to item j are recoded by the n nodes ($Y_{\mathrm{ijn}}^{*}$) and the branches of each node. This recoding reflects the postulated processes that lead to the final four response categories. In Figure 1, Node-1 recodes whether the agree categories (SA, A) or disagree categories (SD, D) were chosen (agree = 1, leading to the left branch; disagree = 0, leading to the right branch). If the decision at the first node is 1 (i.e., A or SA was chosen), Node-2 recodes whether the extreme category (SA) or mild category (A) was chosen (extreme = 1; mild = 0). If the decision at the first node is 0 (i.e., D or SD was chosen), Node-3 recodes whether the extreme category (SD) or mild category (D) was chosen (extreme = 1; mild = 0).

Following the nodes and branches in Figure 1, the four response categories can be as in Table 1. This table summarizes the recoding scheme according to the postulated decision processes and is referred to as the mapping matrix (De Boeck & Partchev, 2012). Note that decision process that is irrelevant to a specific response category is recoded as “not applicable” (NA). For Node-2, the decision is to choose between the agree categories of SA and A, so the disagree categories of SD and D are not part of the decision process and therefore coded as NA. For Node-3, the situation is reversed. The decision is to choose between the disagree categories of SD and D, so the agree categories of SA and A are irrelevant and coded as NA.

Table 1.

The Recoding Scheme (Mapping Matrix) for the IRTree Models in Figure 1.

Original responses ($Y_{\mathrm{ij}})$	Node-1 ($Y_{\mathrm{ij}1}^{*}$)	Node-2 ($Y_{\mathrm{ij}2}^{*}$)	Node-3 ($Y_{\mathrm{ij}3}^{*}$)
Strongly agree	1	1	NA
Agree	1	0	NA
Disagree	0	NA	0
Strongly disagree	0	NA	1

Note. IRTree = item response tree; NA= not applicable.

Applying the recoding scheme in Table 1, Table 2 shows how the individuals’ original responses data are restructured. For example, Mary’s original choice for Item-1 “Agree” is recoded to (1, 0, NA) for the three nodes, and her choice for Item-2 “Strongly disagree” is recoded to (0, NA, 1) for the three nodes.

Table 2.

An Example Data Matrix After Applying the Recoding Scheme.

Person	Item (original responses)	Node-1 ($Y_{\mathrm{ij}1}^{*}$)	Node-2 ($Y_{\mathrm{ij}2}^{*}$)	Node-3 ($Y_{\mathrm{ij}3}^{*}$)
Mary	Item-1 (A)	1	0	NA
Mary	Item-2 (SD)	0	NA	1
. . .	. . .	. . .	. . .	. . .
Bob	Item-1 (D)	0	NA	0
Bob	Item-2 (SA)	1	1	NA
. . .	. . .	. . .	. . .	. . .

Note. A = agree; SA = strongly agree; D = disagree; SD = strongly disagree; NA = not applicable.

After recoding and restructuring individuals’ original responses based on the postulated tree structure, an IRT model is specified for each node $Y_{\mathrm{ijn}}^{*}$ to estimate node-specific latent variables (aka., “theta” in IRT terminology) and item parameters. In so doing, it examines the response behaviors involved in each process represented by a node. In the example in Figure 1, a binary IRT model is fitted to each of the three nodes because the node is specified to lead to binary outcomes (agree vs. disagree or mild vs. extreme). Thus, the probability of $Y_{\mathrm{ijn}}^{*}=1$ (i.e., the probability of the branch coded as 1 being chosen) is given as follows:

$$\pi (Y_{\mathrm{ijn}}^{*}=1|{\theta }_{\mathrm{in}})=g^{-1}({\theta }_{\mathrm{in}}+{\beta }_{\mathrm{jn}}),$$ (1)

where ${\theta }_{\mathrm{in}}$ denotes person i’s latent trait that involves in the nth node. The notation ${\beta }_{\mathrm{jn}}$ denotes the item parameter for item j in the nth node. The notation $g^{-1}$ denotes the inverse of the link function (typically a logit or probit link).

Note that a node could have more than two branches. In such case, the polytomous IRT models (ordered or not ordered) should be fitted (see Jeon & De Boeck, 2016). We will briefly comment on models with nonbinary branches in the Discussion section. In the following, we will discuss a broader psychometric framework for studying item responses, called explanatory item response modeling, and explain how the IRTree models can be formulated within this framework.

Explanatory Item Response Model

Explanatory item response model is a framework proposed by De Boeck and Wilson (2004) with two major themes described below.

Generalized Linear/Nonlinear Mixed Models

An explanatory item response model takes the view that all item response models are a form of generalized linear or nonlinear mixed models (Baayen, Davidson, & Bates, 2008; De Boeck & Wilson, 2004; Rijmen, Tuerlinckx, De Boeck, & Kuppens, 2003). Item response models are “generalized” models because the item response data are often categorical and are modeled via a link function. The mathematical function of the item response models can either be linear or nonlinear. For example, the 1PL (one-parameter logistic) model that fixes the item discrimination parameters to be equal across all items are linear models, whereas the 2PL and 3PL models that allow item-specific discrimination parameters are nonlinear models. Meanwhile, most popular item response models can be seen as a “mixed” model because they include both fixed and random effects. In the typical 1PL, 2PL, and 3PL IRT models, the latent trait variables, usually denoted by θs, are treated as the random effects of persons, and the item parameters are treated as fixed effects of items.

Indicator and Property Predictors

The second feature of the explanatory item response modelling framework is the classification of two types of item response models: descriptive and explanatory. The key distinction lies in the attribute of the predictors included in the mixed model—indicator or property (De Boeck & Wilson, 2004). A descriptive item response model includes only the indicator variable (e.g., item ID) as a predictor in the mixed model. Therefore, the focus is to examine the effect of the indicator (e.g., the effect of each item) on the responses. The widely used 1PL to 3PL binary IRT models as well as common polytomous IRT models, such as the graded response model (Samejima, 1969), the partial credit model (Masters, 1982), and the nominal response model (Bock, 1972) are all descriptive item response models. In contrast, an explanatory item response model includes at least one property variable (e.g., item keying direction) as a predictor in the mixed model. As such, the focus is to examine the effect of the property (e.g., the effect of item keying direction) on the responses. The linear logistic test model by Fischer (1973) and its extensions are examples of such models.

It is important to point out that the distinction made between an indicator and a property predictor applies not only to items but also to persons and response categories as well (see De Boeck & Wilson, 2004). In the mixed model, researchers can consider treating the indicator and property predictors of persons, items, and categories as either random or fixed effects, which gives great flexibility in model specification. This flexibility permits researchers to specify the most suitable models for their research questions and data at hand.

IRTree Model as Explanatory Item Response Model

In this article, we maintain that, like traditional IRT models, IRTree models can be formulated under the explanatory item response modeling framework. Adopting this framework, IRTree models can be extended to include property variables of persons, items, and categories in a mixed model, leading to an explanatory IRTree model. Previous IRTree models for studying response styles were limited to a descriptive model, including only the indicator predictors. To our best knowledge, explanatory IRTree models that include property predictors have never been considered in the study of response styles. Moreover, as far as we know, IRTree models have only been applied to study extreme and middle tendency in responding to a 5-point rating scale. By way of specifying both descriptive and explanatory IRTree models, this article will showcase how IRTree models can help to inspect two distinct extreme response styles as well as acquiescence and disacquiescence response styles in a 4-point scale. The specification of descriptive and explanatory IRTree models will be discussed in detail in the Method section.

Response Styles in This Study

Extreme Response Style

Extreme response style refers to a tendency to use the extreme categories. In the literature, respondents’ preference for the extreme categories is often called extreme response style, while the avoidance of extreme categories (therefore preference for mild categories) is called mild response style. These two styles describe the opposite phenomena of using the extreme categories (Hurley, 1998; Moors, 2008). In this study, we define extreme response style as a tendency to use the extreme categories, irrelevant to the trait being measured.

The extreme response style was regarded as a trait-irrelevant factor contaminating the measurement of the true trait. Previous studies often assumed the extreme response style to be unidimensional and focused on controlling its effect at the scale level. Yet the possibility of multidimensionality of the extreme response style and their effects at item level have not been widely discussed. For instance, in a rating scale having two extreme categories (e.g., “Strongly agree” and “Strongly disagree”), the behavior in choosing these two extreme categories might be quite different and point to two distinct extreme response styles. Moreover, researchers can look into where and how the different extreme response styles occur in items. This information can provide rich and in-depth insights on extreme response styles. To this end, the present study will examine the possibility of two distinct extreme styles at both the scale level and item level.

Acquiescence and Disacquiescence Response Styles

The acquiescence response style describes a tendency to agree with the statements in the items, irrelevant to trait being measured. On the contrary, the disacquiescence response style describes a tendency to disagree with the statements. For example, if the respondents tend to agree with the statements by selecting the agree categories (i.e., SA, A) in the items measuring self-esteem (e.g., “On the whole, I am satisfied with myself”), their self-esteem scores are very likely to be inflated. On the contrary, the respondents’ tendency to disagree with the statements by selecting the disagree categories (i.e., SD, D) can deflate their self-esteem scores. Obviously, both the acquiescence and disacquiescence styles are a concern because their presence can bias the measurement of the true trait and contaminate the meaning of scores.

To minimize the effects of acquiescence and disacquiescence response styles, it is a common practice to construct a balanced scale where half of the items are positively keyed, and the other half are negatively keyed (Billiet & McClendon, 2000). Positively keyed items are phrased to represent a relatively high level of the trait by agreeing with the statements (e.g., “I am proud of myself” for measuring self-esteem), whereas negatively keyed items are phrased to represent a relatively high level of trait by disagreeing with the statements (e.g., “I certainly feel useless at times” for measuring self-esteem). The use of positively and negatively keyed items is believed to prevent the individuals’ scores from being inflated or deflated by the acquiescence and disacquiescence response styles. That is, when there are equal number of positively and negatively keyed items, it is believed that the effects of these two styles can be offset at the scale level.

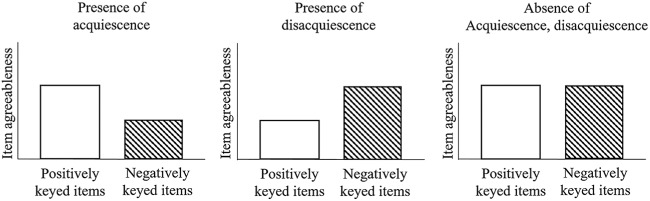
In this article, we attest that the data of a balanced scale contain useful information to detect the presence of acquiescence and disacquiescence response styles. Specifically, these two styles can be revealed by the item agreeableness statistics (aka, item easiness statistics in a cognitive or aptitude test). The item agreeableness statistic indicates how likely the response categories in an item, representing a high level of the trait, will be chosen. With mixed keyed items having four categories of SA, A, D, and SD, the item agreeableness statistic of a positively keyed item indicates the likelihood of selecting the agree categories (i.e., A and SA) that reflect a high level of the trait. On the contrary, the item agreeableness statistic of a negatively keyed item indicates the likelihood of selecting the disagree categories (i.e., D and SD) that also reflect a high level of the trait. If respondents tend to choose the agree categories across items (i.e., acquiescence), this tendency will raise the item agreeableness levels of the positively keyed items, while it will lower the item agreeableness levels of the negatively keyed items. This will result in the agreeableness levels of the positively keyed items being higher than those of the negatively keyed items. On the contrary, if respondents tend to choose the disagree categories across items (i.e., disacquiescence), this tendency will raise the item agreeableness levels of the negatively keyed items, while it will lower the item agreeableness levels of the positively keyed items. This will lead to the agreeableness levels of the negatively keyed items being higher than those of the positively keyed items. Following the same reasoning, when there is no acquiescence or disacquiescence, the item agreeableness levels will be similar between positively keyed and negatively keyed items. These three scenarios are presented in Figure 2.

Figure 2.

Presence of acquiescence and disacquiescence based on the pattern of item agreeableness levels of the positively and negatively keyed items.

In the following section, we demonstrate the examination of extreme, acquiescence, and disacquiescence response styles using descriptive and explanatory IRTree models based on the responses to the Rosenberg Self-Esteem Scale.

Method

Measure and Sample

Rosenberg’s Self-Esteem Scale is a 10-item Likert-type rating scale widely used for measuring individuals’ global self-worth. In the scale, each item has a statement about an individual’s general feelings about oneself and requires respondents to indicate how strongly they agree or disagree with the statement. The scale is balanced with five positively keyed items and five negatively keyed items. In all 10 items, there are four response categories of SA, A, D, and SD (see the appendix for the actual items). Data were retrieved from the open source of the 2005 Longitudinal Study of Generation in California (Silverstein & Bengtson, 2008). A total of 1,596 participants were included in the analysis (male = 43.2%, female = 56.8%, $M_{\mathrm{age}}$ = 49.37 years, $S{D}_{\mathrm{age}}$ = 18.89).

Model Specification

Tree Structure

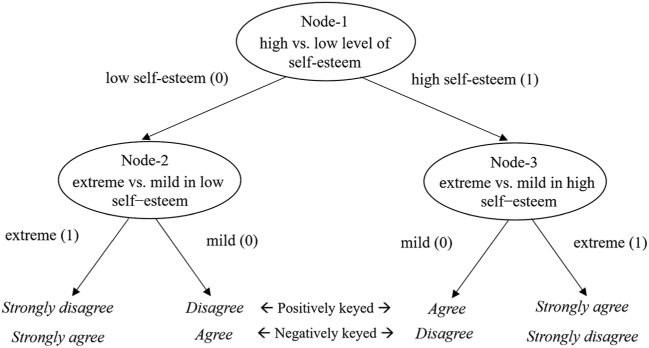
To inspect extreme, acquiescence, and disacquiescence response styles by IRTree models, we postulated the following response processes as shown in Figure 3. First, respondents determine whether they have positive feelings about themselves (i.e., a high level of self-esteem) or negative feelings about themselves (i.e., a low level of self-esteem). Second, they decide how strong their feelings are. The two-step decision processes are described by a tree structure with three nodes in Figure 3. Node-1 recodes whether the respondents choose the categories reflecting a high level of self-esteem (coded as 1) or the categories reflecting a low level of self-esteem (coded as 0). Thus, this node is referred to as trait direction. For the categories reflecting a low level of self-esteem (i.e., when Node-1 branches out to 0), Node-2 further recodes whether the respondents choose the extreme category (coded as 1) or the mild category (coded as 0). This node is referred to as extremity in low self-esteem direction. For the categories reflecting a high level of self-esteem (i.e., when Node-1 branches out to 1), Node-3 further recodes whether the respondents choose the extreme category (coded as 1) or the mild category (coded as 0). This node is referred to as extremity in high self-esteem direction. The participants’ original choices of the four response categories were all recoded according to this tree structure. Note that response categories in positively and negatively keyed items are recoded accordingly as the categories can reflect a high or low level of self-esteem depending on the item keying direction.

Figure 3.

Tree structure for detecting extreme, acquiescence, and disacquiescence response styles in the 4-point Rosenberg’s Self-Esteem Scale.

Based on the tree structure, we specified the IRTree models by fitting a 1PL IRT for each node. Remember that a variety of descriptive or explanatory IRTree models can be specified depending on whether an indicator or property variable (of person, item, and category) is included as a predictor. To examine extreme, acquiescence, and disacquiescence response styles, we specified descriptive and explanatory IRTree models. Both the descriptive and explanatory models are generalized linear mixed models; hence, all models could be estimated by the lme4 package in R using maximum likelihood estimator (Bates, Mächler, Bolker, & Walker, 2015).

Descriptive IRTree Model for Extreme Response Style

We first specify the descriptive IRTree model to examine the possibility of two distinct extreme response styles, controlling for self-esteem. The descriptive IRTree model includes only the indicator predictors of persons and items. For all three nodes in Figure 3, the effects of persons are specified as random (latent variables), and the effects of items are specified as fixed (item parameters). The corresponding lme4 R code for this model specification is glmer(DV ~ 0 + nodes:item + (0 + nodes|person)).

This model results in three random effects of persons (also known as three thetas in IRT) for the three nodes. The first random effect of persons represents individuals’ levels of self-esteem (${\theta }_{\mathrm{trait}\mathrm{direction}}$ for Node-1). The second and third random effects of persons represent individuals’ extreme response styles in the low self-esteem direction (${\theta }_{\mathrm{extremity}\left(\mathrm{low}\mathrm{trait}\right)}$ for Node-2) and in the high self-esteem direction (${\theta }_{\mathrm{extremity}\left(\mathrm{high}\mathrm{trait}\right)}$ for Node-3), while controlling for self-esteem of Node-1. The two random effects for Node-2 and Node-3 allow us to examine the presence of two extreme response styles in the opposite trait directions. To determine extreme response styles in the scale, we compare the model fit of the model specifying two distinct extreme styles to those of more constrained models—one with no extreme response styles at all, and the other with only one extreme response style regardless of the trait directions.

In addition to the three random effects of persons, the model gives three sets of 10-item parameters as the fixed effects of items, ${\beta }_{\mathrm{jn}}$, one set for each of the three nodes (n = 1, . . ., 3 for node, j = 1, . . ., 10 for item). The item parameters show how likely the categories in each item are chosen. The set of 10-item parameters for Node-1 (${\beta }_{\mathrm{trait}\mathrm{direction}:\mathrm{item}}$) indicates the item agreeableness statistics for items, showing how likely the categories reflecting a high level of self-esteem would be chosen. These estimates help to control for the variation due to item contents while examining the extreme response styles. The item parameters for Node-2 and Node-3 provide the information about extreme response styles at the item level. The set of 10-item parameters for Node-2 (${\beta }_{\mathrm{extremity}\left(\mathrm{low}\mathrm{trait}\right):\mathrm{item}}$) indicates how likely the extreme category in the low self-esteem direction (SD in positively keyed items and SA in negatively keyed items) would be chosen. Likewise, the set of 10-item parameters for Node-3 (${\beta }_{\mathrm{extremity}\left(\mathrm{high}\mathrm{trait}\right):\mathrm{item}}$) shows how likely the extreme categories in the high trait direction (SA in positively keyed items and SD in negatively keyed items) would be chosen. These item parameters of Node-2 and Node-3 evaluate extreme response styles at the item level.

Explanatory IRTree Model for Acquiescence and Disacquiescence Response Styles

To inspect the presence of acquiescence and disacquiescence response styles, the explanatory IRTree model is specified by including the predictors of person indicators and the item property variable (i.e., keying direction). Because item property of keying direction is included as a predictor, this model is explanatory with regard to items. As for being fixed or random, the effects of persons are treated as random (latent variables) and the effects of item property are treated as fixed (item parameters) for each node in the tree structure. It is worth noting that the item indicators are also included as random effects to control for the response variability due to item-by-item differences (e.g., due to contents). This specification is similar to the linear logistic test model with error as discussed by De Boeck (2008). The corresponding lme4 R code for this model specification is glmer(DV ~ 0 + nodes:item_keying + (0 + nodes|person) + (0+nodes|item)).

The explanatory model results in three random effects of person indicators for the three nodes, representing individuals’ levels of self-esteem and two extreme response styles (${\theta }_{\mathrm{trait}\mathrm{direction}}$, ${\theta }_{\mathrm{extremity}\left(\mathrm{low}\mathrm{trait}\right)}$, ${\theta }_{\mathrm{extremity}\left(\mathrm{high}\mathrm{trait}\right)}$) as well as three random effects of item indicators for the three nodes, representing item-by-item differences ($u_{\mathrm{trait}\mathrm{direction}}$, $u_{\mathrm{extremity}\left(\mathrm{low}\mathrm{trait}\right)}$, and $u_{\mathrm{extremity}\left(\mathrm{high}\mathrm{trait}\right)}$).

The model also yields three sets of two item parameters as the fixed effects, ${\beta }_{\mathrm{jn}}$, one set for each of the three nodes (n = 1, . . ., 3 for node, j = 1 or 2 for item keying direction). The two item parameters for Node-1 (${\beta }_{\mathrm{trait}\mathrm{direction}:\mathrm{positively}\mathrm{keyed}}$ and ${\beta }_{\mathrm{trait}\mathrm{direction}:\mathrm{negatively}\mathrm{keyed}}$) indicate the overall item agreeableness levels for positively and negatively keyed items, respectively. The relative sizes of these two item agreeableness statistics reveal the presence of acquiescence and disacquiescence response styles (i.e., a higher agreeableness level for positively keyed items indicates acquiescence, and a higher agreeableness level for negatively keyed items indicates disacquiescence). The sets of item parameters for Node-2 (${\beta }_{\mathrm{extremity}\left(\mathrm{low}\mathrm{trait}\right):\mathrm{positively}\mathrm{keyed}}$, ${\beta }_{\mathrm{extremity}\left(\mathrm{low}\mathrm{trait}\right):\mathrm{negatively}\mathrm{keyed}}$) and Node-3 (${\beta }_{\mathrm{extremity}\left(\mathrm{high}\mathrm{trait}\right):\mathrm{positively}\mathrm{keyed}}$, ${\beta }_{\mathrm{extremity}\left(\mathrm{high}\mathrm{trait}\right):\mathrm{negatively}\mathrm{keyed}}$) indicate the potential effect of item keying direction on selecting the extreme categories. These two sets of parameters show how likely the extreme categories would be chosen in the positively and negatively keyed items, which helps to evaluate whether the extreme response styles would occur differently depending on item keying direction.

Results

Descriptive IRTree Model

The descriptive model examined the extreme response styles at the scale and item levels. At the scale level, the presence of the two distinct extreme response styles were evaluated by model fit comparisons. The results in Table 3 showed that the descriptive IRTree model with two extremity factors (in the third row) fits noticeably better to the data, compared to the two other models—one posing no extremity factor (1a in Table 3) and the other posing a single extremity factor (2a in Table 3). This suggests the existence of two extreme response styles differentiated by the trait direction. The variance components (i.e., random effects) of these two extremity factors were noticeably greater than zero (${\theta }_{\mathrm{extremity}\left(\mathrm{low}\mathrm{trait}\right)}$ = 1.810 and ${\theta }_{\mathrm{extremity}\left(\mathrm{high}\mathrm{trait}\right)}$ = 6.427), while controlling for the self-esteem factor (${\theta }_{\mathrm{trait}\mathrm{direction}}$ = 4.461).

Table 3.

Model Fits of Descriptive and Explanatory IRTree Models.

Models	−2 LL	AIC	BIC
1a.Descriptive model with one trait factor and no ERS factors	23316.2	23378.0	23637.0
2a.Descriptive model with one trait factor and one ERS factor	22683.6	22730.0	22922.0
3a.Descriptive model with one trait factor and two ERS factors	22457.0	22529.0	22830.0
2.Explanatory model with one trait factor and two ERS factors	22620.8	22657.0	22807.0

Note. Trait represents self-esteem. IRTree = item response tree; ERS = extreme response style; −2 LL = −2 times log likelihood; AIC = Akaike information criterion; BIC = Bayesian information criterion. Lower values of −2 LL, AIC, and BIC indicate that the model fits better to the data.

To examine the two distinct extreme response styles at the item level, fixed effects of item indicators (βs) for Node-2 and Node-3 were evaluated (see Table 4). The estimates for Node-2 on the top panel of Table 4 show where and how the extreme response style in the low-trait direction occurs in items. For all items, the estimates were negative, suggesting that extreme categories reflecting low self-esteem (SD in the positively keyed items and SA in the negatively keyed items) were less likely to be chosen, controlling for self-esteem (random effect of persons for Node-1) and item agreeableness (item parameters for Node-1). Likewise, the estimates for Node-3 on the bottom panel of Table 4 show the extreme response style in the high-trait direction (SD in the negatively keyed items and SA in the positively keyed items). The results showed no consistent pattern among the items. The extreme categories in Items 1, 2, 3, 5, and 10 were more likely to be chosen, whereas the mild categories in Items 4, 6, 7, 8, and 9 were more likely to be chosen, controlling for self-esteem and item agreeableness.

Table 4.

Estimates of Fixed Effects for Items in the Descriptive IRTree Model.

Node-2: Extremity (low trait)	Item	${\beta }_{\mathrm{extremity}\left(\mathrm{low}\mathrm{trait}\right):\mathrm{item}}$	SE	p
	Item 1	−0.877	0.443	.048
	Item 2	−1.164	0.617	.059
	Item 3	−1.646	0.356	<.001
	Item 4	−2.302	0.383	<.001
	Item 5	−1.657	0.368	<.001
	Item 6	−3.173	0.462	<.001
	Item 7	−2.676	0.377	<.001
	Item 8	−1.901	0.204	<.001
	Item 9	−2.751	0.294	<.001
	Item 10	−2.424	0.326	<.001
Node-3: Extremity (high trait)	Item	${\beta }_{\mathrm{extremity}\left(\mathrm{high}\mathrm{trait}\right):\mathrm{item}}$	SE	p
	Item 1	0.925	0.099	<.001
	Item 2	0.228	0.097	.019
	Item 3	0.966	0.100	<.001
	Item 4	−0.682	0.099	<.001
	Item 5	0.499	0.099	<.001
	Item 6	−1.143	0.101	<.001
	Item 7	−1.151	0.101	<.001
	Item 8	−0.991	0.107	<.001
	Item 9	−0.388	0.102	<.001
	Item 10	0.647	0.101	<.001

Note. IRTree = item response tree; SE = standard error. Results of Node-1 are not reported. Negatively keyed items are underlined.

Explanatory IRTree Model

The explanatory IRTree models included the six random effects. The first three were the random effects of persons for the three nodes corresponding to the self-esteem factor and two extremity factors (the variance components of ${\theta }_{\mathrm{trait}\mathrm{direction}}$ = 4.253, ${\theta }_{\mathrm{extremity}\left(\mathrm{low}\mathrm{trait}\right)}$ = 1.833, ${\theta }_{\mathrm{extremity}\left(\mathrm{high}\mathrm{trait}\right)}$ = 6.337). The second set of three effects was the random effects of items that reflect item-by-item differences (the variance components of $u_{\mathrm{trait}\mathrm{direction}}$ = 0.964, $u_{\mathrm{extremity}\left(\mathrm{low}\mathrm{trait}\right)}$ = 0.345, and $u_{\mathrm{extremity}\left(\mathrm{high}\mathrm{trait}\right)}$ = 0.579). These effects were controlled for while examining the presence of acquiescence and disacquiescence response styles.

To evaluate the presence of acquiescence and disacquiescence styles, the fixed effects of item keying direction for Node-1 (βs), corresponding to the item agreeableness, were examined in Table 5. The results showed that the item agreeableness levels were noticeably higher for the positively keyed items than for the negatively keyed items, suggesting the presence of acquiescence response style. Furthermore, the fixed effects of item keying for Node-2 and Node-3 were examined to evaluate the respondents’ uses of extreme categories in positively and negatively keyed items. The results showed that individuals tended to avoid using the extreme categories reflecting a low level of trait for both item keying directions (see the negative estimates for Node-2 in Table 5). The extent of the avoidance was fairly comparable between positively and negatively keyed items. There was no significant preference or avoidance of the extreme categories reflecting a high level of trait for both positively and negatively keyed items (see the estimates for Node-3 in Table 5).

Table 5.

Estimates of Fixed Effects for Item Keying in the Explanatory IRTree Model

Node 1: Trait direction	Item keying	${\beta }_{\mathrm{trait}\mathrm{direction}:\mathrm{keying}}$	SE	p
	Positively keyed	4.756	0.447	<.001
	Negatively keyed	3.193	0.440	<.001
Node-2: Extremity (low trait)	Item keying	${\beta }_{\mathrm{extremity}\left(\mathrm{low}\mathrm{trait}\right):\mathrm{keying}}$	SE	p
	Positively keyed	−2.075	0.383	<.001
	Negatively keyed	−2.015	0.343	<.001
Node-3: Extremity (high trait)	Item keying	${\beta }_{\mathrm{extremity}\left(\mathrm{high}\mathrm{trait}\right):\mathrm{keying}}$	SE	p
	Positively keyed	−0.363	0.342	.289
	Negatively keyed	0.143	0.342	.676

Note. IRTree = item response tree; SE = standard error.

Discussion

This study extended the applicability of an IRTree model in the study of response styles. We conceptualized the IRTree models in the explanatory item response modeling framework delineated by De Boeck and Wilson (2004) and demonstrated its application for studying response styles. More specifically, we showcased how IRTree models, either descriptive or explanatory, can be stipulated from the vantage point of a generalized linear mixed model. As a demonstration, the extreme response style as well as the acquiescence and disacquiescence response styles were examined based on the responses to the Rosenberg’s Self-Esteem Scale. Our findings suggested the existence of two distinct extreme response styles in the low and high trait directions. The two extremity styles were further examined at the item level. In all items, people tended to avoid the extreme categories that reflect a low level of self-esteem. In contrast, only in some items but not all, people tended to avoid the extreme categories that reflect a high level of self-esteem. These two response styles did not occur differently depending on item keying direction. Moreover, our findings pointed to acquiescence response style when responding to the Rosenberg Self-Esteem Scale.

The present study makes new contributions in several ways. First, it explored the possibility of two distinct extreme response styles. Not only that, it evaluated the two extreme response styles in depth by looking into where and how the response styles occurred in items. Second, we introduced the explanatory IRTree models, which have not been considered in previous studies of response styles. Our study demonstrated the explanatory IRTree model by incorporating item keying direction as a predictor and showed how the acquiescence and disacquiescence response styles can be indirectly detected without entailing external measures. Last, this article showcased the versatility of the IRTree models, when conceived under an explanatory item response modeling framework. A variety of IRTree models can be specified by combining different predictors, either as an indicator or a property, for person, item, and response category. This permits the researchers to build a variety of models tailored to their own research interest.

The IRTree technique permits researchers to disentangle response styles from the substantive trait by modeling the content-relevant and -irrelevant factors as separate nodes in the tree. This feature empowers the researchers to differentiate those respondents who carry a response style from those who do not. For example, following the tree structure in Figure 3, it is possible to distinguish a respondent with extremely high self-esteem but no extreme response style (Respondent A) from another respondent with a high level of self-esteem and an extreme response style (say, preferring extreme responses in both trait directions; Respondent B). These two respondents could have the same response to an item (SD or SA), hence follow the same path in the tree structure. However, Respondent A would be estimated to have a higher score on ${\theta }_{\mathrm{trait}\mathrm{direction}}$, compared to Respondent B. On the contrary, Respondent B would be estimated to have a higher score on the extreme response style factors (${\theta }_{\mathrm{extremity}\left(\mathrm{low}\mathrm{trait}\right)}$, ${\theta }_{\mathrm{extremity}\left(\mathrm{high}\mathrm{trait}\right)}$), compared to Respondent A. However, it should be noted that the IRTree models would not be able to distinguish these two respondents if they have exactly the same responses to all the items.

It is reasonable to conjecture that the response styles identified in this study travel well to other measures of self-esteem that have the same response format (i.e., 4-point Likert-type rating scale consisting of positively and negatively keyed items). However, these findings should not be generalized to measures of other constructs, measures in different response formats, and/or specific populations such as children, senior, and clinical populations without further empirical evidence. We encourage future studies to verify these specific generalizations. Moreover, the findings of the present study were based on a single response data set, and a cross-validation is needed. In several previous studies, response styles were investigated based on multiple sources of evidence. For example, Zettler et al. (2016) used the self- and observer-report measures of personality traits for the same individuals to detect response styles. They emphasized that the consistency in findings from cross-source data is essential to verify the presence of response styles. In other reports, external measures were employed to verify the response styles (e.g., Plieninger & Meiser, 2014). Our findings were not based on cross-source data nor were they compared to any external criteria. In this regard, we encourage future investigations to cross-validate the current findings.

Finally, in our applications, we only fitted the 1PL IRTree models. It is important to note that IRTree models are not restricted to the 1PL parameterization. It is possible to incorporate other types of item parameters, resulting in a 2PL or 3PL model. In such cases, the IRTree model will be a generalized nonlinear mixed model (Jeon & De Boeck, 2016). Equally important, the nodes do not have to be binary (two branches). A node can have multiple branches depending on the researchers’ questions and data at hand. In these cases, multinomial or ordinal IRTree models are most appropriate, and statistical packages that can handle multiple categories such as the flirt by Jeon and Rijmen (2016) can be considered.

Appendix

Appendix.

Rosenberg’s Self-Esteem Scale.

Item	Statement
Item 1	I feel that I’m a person of worth, at least on an equal basis with others.
Item 2	I feel that I have a number of good qualities.
Item 3	All in all, I am inclined to feel that I am a failure.
Item 4	I am able to do things as well as most other people.
Item 5	I feel I do not have much to be proud of.
Item 6	I take a positive attitude toward myself.
Item 7	On the whole, I am satisfied with myself.
Item 8	I wish I could have more respect for myself.
Item 9	I certainly feel useless at times.
Item 10	At times I think I am no good at all.