Abstract
This study discusses quantile regression methodology and its usefulness in education and social science research. First, quantile regression is defined and its advantages vis-à-vis vis ordinary least squares regression are illustrated. Second, specific comparisons are made between ordinary least squares and quantile regression methods. Third, the applicability of quantile regression to empirical work to estimate intervention effects is demonstrated using education data from a large-scale experiment. The estimation of quantile treatment effects at various quantiles in the presence of dropouts is also discussed. Quantile regression is especially suitable in examining predictor effects at various locations of the outcome distribution (e.g., lower and upper tails).
Keywords: quantile regression, instrumental variables, interim assessments, achievement gap, field experiment, OLS regression
Empirical quantitative analyses in education, psychology and the social sciences typically use linear statistical models such as ordinary least squares (OLS) regression, analysis of variance or covariance, or weighted linear models (e.g., multilevel) to compute either average estimates of associations between a dependent and an independent variable or group differences in the dependent variable controlling for the other independent variables included in the model. The regression coefficients produced by such linear modeling approaches are mean estimates adjusted usually by the effects of the covariates that are present in the model, especially when observational or quasi-experimental data are analyzed. For example, in OLS regression, one of the most commonly used modeling approaches in the social sciences, a regression coefficient indicates the “effect” of an independent variable x on the mean of the dependent variable y given the effects of the remaining independent variables (also called predictors) in the model. This statistical approach is often known as conditional-mean modeling (see Hao & Naiman, 2007).
Consider the following example from education. Suppose a researcher is interested in whether teacher certification has an impact on student mathematics performance. In a simple regression model, one would regress mathematics scores on teacher certification which for simplicity can be coded as a binary indicator variable taking the value of 1 if a teacher is certified and the value of 0 if the teacher is not certified. The regression estimate in this case is the mean difference in mathematics scores between students who have certified teachers and students who have not. A positive and significant mean difference would suggest that students who have certified teachers have a significantly higher mean in mathematics than students who have noncertified teachers. If covariates or statistical controls such as student background, prior student ability, as well as other teacher and school characteristics were to be included in the regression model the regression estimate of the teacher certification variable would be modified to a degree, unless teacher certification was by design orthogonal to covariates (in a randomized experiment).
Although the mean is the most widely computed measure of central tendency/location of a distribution of scores it is sensitive to outliers and can be influenced by imbalances of extreme scores in the upper or lower tails of a distribution of scores. When the distribution of scores is considerably skewed the mean is typically pooled toward the tail with the most extreme scores. That is, in a highly skewed distribution the mean value will be affected by the extreme outliers either in the upper or the lower tails of the distribution. In such cases, the mean is not an accurate measure of the central location. For that reason, the estimation of the median, a more robust index of central tendency, has also been proposed in the literature in cases where the normality assumption of the distribution of scores does not hold. With regard to linear modeling the median regression can be used instead of a mean regression to provide robust estimates of central tendency/location of an outcome y (Hao & Naiman, 2007).
To illustrate the sensitivity of the mean to extreme outliers consider an example from education. Suppose an education researcher is interested in the average effect of a school resource such as class size on mathematics achievement in the third grade. For simplicity, suppose class size is coded as a binary indicator variable which takes the value of 1 if a student is in a small class and 0 otherwise. Suppose also that the outcome is standardized. One can then run a simple OLS regression where mathematics scores are regressed on the class size dummy variable to estimate the regression estimate of the class size variable. Empirically, the mean difference between small and regular size classes in mathematics is estimated to be 0.11 standard deviations (SDs) favoring students in small classes. Similarly, one can run a median regression to compute the median difference between small and regular size classes. The median parameter estimate is, in this example also, 0.11 SDs. These results indicate that the distribution of the dependent variable is most likely not skewed. Now, suppose one were to substitute the three largest mathematics scores of students in large classes (3.00, 3.70, and 3.70) with three extreme values (60) and rerun the OLS and the median regressions. The results indicate that the mean and the median estimates are no longer similar. The parameter estimate of the median remained the same (0.11 SD), but the mean parameter estimate changed dramatically and is now 0.01 SD. This shows that the three extreme outliers in the large class reduced the mean difference in mathematics between small and regular classes to essentially 0. In this example, the standard errors (SEs) of the estimates were as large as the estimates, and thus, statistical significance was not achieved in either model.
In addition, the mean estimates produced by typical regression models do not provide any information about the effect of an independent variable at different points of the outcome distribution of scores. That is, the typical regression model is unable to provide estimates for noncentral locations in the distribution of scores. However, in many occasions in education research investigators are interested in estimate teacher and school effects for different groups of students (e.g., low- vs. middle-achievers) and reduce the achievement gap.
Specifically, many education researchers study educational inequality. Suppose the main research question of interest is whether teacher certification effects vary by the level of student achievement. In this example, the researcher is interested in determining whether the teacher certification effects are consistent across the distribution of scores or whether they differ for low-, median-, or high-achievers. Suppose that teacher certification signals higher levels of teacher quality or effectiveness and is hypothesized to improve student learning. One hypothesis would be that certified teachers focus on improving learning especially for students who struggle at school (i.e., lower-achieving students). If that hypothesis were true, one would expect a larger potential benefit (i.e., a larger regression coefficient) for students in the lower end of the achievement distribution (e.g., at the 25th or 10th percentiles) than for other students. In contrast, if higher achieving students were to take advantage of this school resource (teacher certification) to a higher degree than other students, then one would expect a larger benefit for students in the upper tail of the achievement distribution (e.g., 75th or 90th percentile) than for other students. Another hypothesis would be that teacher certification effects are larger for middle-achievers than for lower-or higher-achievers.
These three scenarios suggest that a school resource or treatment could have varying effects at different levels of achievement either by design or by happenstance (e.g., a byproduct of the treatment implementation in classrooms). A fourth noteworthy scenario is that the effect of certified teachers on student achievement is uniform or consistent across the distribution of achievement scores. If that were true, then the potential benefit would be similar for lower-, middle-, or higher-achieving students (i.e., the regression estimates across the achievement distribution would be similar in magnitude). There are of course many variations to these four hypotheses. Although these four hypotheses may not capture all possible effects, they demonstrate that the effects of a school resource or treatment could differ by achievement level by design, hidden mechanisms, or circumstances in the classrooms. The typical linear modeling approach that estimates means would not be able to capture this potential inconsistency of the effects throughout the entire distribution of scores.
Quantile regression was introduced nearly 30 years ago in the econometric literature as a method that is an extension of the typical regression model and addresses the caveats of the typical regression model because it allows the analyst to conduct conditional estimation at various points (called quantiles) in a distribution of scores (Koenker & Bassett, 1978). In that sense, the median regression is a special case of the quantile regression model because the median is the 0.50 quantile (or the 50th percentile). Quantile regression is an appropriate method to estimate effects at different quantiles including points in the upper and lower tails of the achievement distribution (Porter, 2015). For instance, a researcher who focuses on lower achievers can estimate teacher and school effects at the 25th, 20th, 10th, or 5th percentiles separately. In the same vein, quantile-specific estimates for multiple predictors can be obtained in the upper tail of the distribution at the 75th, 80th, 90th, or 95th percentiles separately. Nowadays statistical software (e.g., STATA) allows the analyst to conduct conditional estimation at predetermined quantiles or equally spaced quantiles (e.g., 10% increments) throughout the entire distribution of scores. These estimates paint a more comprehensive portrait of the effects independent variables can have on the outcome distribution of scores. Quantiles are very similar to percentiles and percentile ranks and can be interpreted as such. For example, the 0.25 quantile is at the 25th percentile and indicates that 25% of the scores are below that point in the distribution of scores.
The quantiles are specific values or points at various locations of an ordered array of population values of a variable y. For a specific cumulative distribution function (CDF) of a certain variable the qth quantile of this particular distribution is the value of the inverse of the CDF at that quantile q. For instance, suppose we work with the standard normal distribution and the quantile of interest is 0.75 (the third quartile). Then, the value of the inverse of the standard normal CDF at the 0.75 quantile is a z-score of 0.67. The proportion of the population with z-values less than 0.67 is 0.75 or that 75% of the values are less than 0.67. It follows that the proportion of the population with z-values greater than 0.67 is 0.25 or that 25% of the values are greater than 0.67.
Quantile regression not only yields robust estimates of independent variables in the presence of extreme outliers (in the dependent variable) at different points (quantiles) of the outcome distribution and at the same time allows researchers to compute regression estimates of multiple predictors at various quantiles separately, it also relaxes the homoscedasticity assumption about the residuals of y. Specifically, the OLS regression model assumes that the residuals of y are distributed identically with a constant population variance (e.g., ). However, there may be occasions where some residuals or different groups of residuals have different variances. In such cases, the residual variance is nonconstant and the error term is heteroscedastic. Heteroscedasticity does not affect the estimation of the regression coefficients. It affects however, the SEs of the regression coefficients which are a function of the residual variance. Specifically, the SEs of the regression estimates are not correct and are typically underestimated. That means, the precision with which a regression coefficient is estimated is affected upward (i.e., the precision is inflated and thus erroneous). As a result, the likelihood of committing a Type I error is increased because due to an underestimated SE the test statistic (the ratio of the regression estimate to its SE) of the regression estimate will be larger than it should have been had residual heteroscedasticity been taken into account.
When heteroscedasticity is evident the SEs of the regression estimates produced from the OLS regression are biased downward. To address this caveat of OLS regression, some statistical software packages (e.g., STATA) offer a post hoc solution that corrects the SEs of the regression estimates. For instance, STATA can compute robust or Huber–White SEs (White, 1980) that are a function of the variability among the predictors in the model as well as the variance matrix of the residuals with diagonal elements that can differ for each residual or for groups of residuals.
In quantile regression the analyst can compute SEs of the regression estimates that are robust to heteroscedasticity using a resampling approach (Angrist & Pischke, 2009; Hao & Naiman, 2007). Specifically, the bootstrap approach introduced by Efron (1979) can be modified to compute robust SEs of quantile regression estimates. This is an iterative sampling approach of a large number of samples of size n with replacement from the actual data at hand. Suppose the data represent the dependent variable y. In each bootstrap sample one can compute the value of the quantile of interest (e.g., q = 0.20) in the outcome y. Suppose we repeat this sampling approach 100 times and compute each time the value of the quantile of interest. Then, eventually we have a sample of 100 values of the specific quantile and as a result we can compute the SD of these estimates, which is the SE of the estimate of the quantile (Angrist & Pischke, 2009). In quantile regression this iterative approach is slightly modified. For instance, for a certain quantile (e.g., q = 0.10) one can draw samples of size n with replacement from pairs of the dependent variable (y) and one independent variable (e.g., x1) for each observation i to estimate the parameter estimate between y and x1 (e.g., ) (Angrist & Pischke, 2009; Hao & Naiman, 2007). Suppose 100 parameter estimates are computed from 100 bootstrap samples. Then, the SE of is the SD of the 100 estimates at the 0.10 quantile (Porter, 2015). This procedure is repeated for each predictor at the 0.10 quantile, and then for each of the quantiles of interest and for the predictors in the model. Notice that this approach takes into account the variability of the parameter estimate of each predictor at each quantile. The bootstrapped SEs make no assumptions about the outcome distribution and as result they are preferable (Hao & Naiman, 2007). Previous work has shown that bootstrap SEs are robust to heteroscedasticity (Hahn, 1995).
OLS and Quantile Regression
Consider a simple population regression model for individual i
| (1) |
where y is the dependent variable, x is the independent variable, is the residual of y, and the s are the mean regression parameters. The estimation involves the minimization of the sum of squared residuals with respect to the s, namely,
| (2) |
where is the fitted value, and the estimate of the parameter is computed from the data at hand (i.e., y and x) using a formula that is a direct function of the covariation between the two variables, namely
| (3) |
In multiple regression the fitted value is where x is a vector of values of multiple predictors for observation i and is a vector of regression estimates of these predictors. The corresponding solution of regression estimates for multiple predictors is
| (4) |
where X is the design matrix of the predictor variables and y is the dependent variable vector.
The quantile regression model that corresponds to the simple linear regression model in Equation (1) for quantile q is
| (5) |
where q indicates the specific quantile and 0 < q < 1 (Hao & Naiman, 2007; Koenker & Bassett, 1978). The estimation in this case involves the minimization of the weighted sum of the absolute values of the residuals for quantile q, namely,
| (6) |
where , and q and (1 −q) are the weights. In particular, q is the weight assigned to positive residuals (i.e., ) and (1 −q) is the weight assigned to negative residuals (i.e., ). It follows that for the median (q = 0.5) the estimation involves the minimization
| (7) |
because at the median q = 1 −q, and as a result , and thus, the weighted sum of the absolute values of the residuals creates Equation (7). To illustrate the mechanism suppose we want to estimate the quantile regression coefficients at the 0.25 quantile (first quartile). Then, the weights are q = 0.25 for the positive residuals and (1 −q) = 0.75 for the negative residuals. In other words, in this example the data points of y that are above the regression line are given a weight 0.25 and the data points below the regression line are given the weight 0.75 (see Hao & Naiman, 2007; Porter, 2015). That means the estimation of the regression coefficients at any quantile q involves weighting the data of the entire sample accordingly (Hao & Naiman, 2007).
When multiple predictors are used in the quantile regression model the fitted value is where x is a vector of values of multiple predictors for observation i and is a vector of regression estimates of these predictors at quantile q. That is, at any quantile q the regression estimates computed are as many as the independent variables or predictors in the model. For example, if there are five predictors used in the model at quantile q there will be also five corresponding regression estimates at quantile q. It is prudent to use the same predictors at each quantile to facilitate comparisons across various quantiles.
A slightly modified version of Equation (6) is usually reported in published articles. Specifically, the quantile regression estimates are estimated by minimizing the function
| (8) |
where is called the check function and is a certain quantile (Angrist & Pischke, 2009). The check function weighs positive and negative residuals using different weights, that is, is the weight assigned to positive residuals (i.e., ) and (1 –) is the weight assigned to negative residuals (i.e., ). Because differentiation is not possible to estimate the quantile regression coefficients an optimization method called linear programming is used instead to minimize Equation (8) and produce quantile regression estimates (Angrist & Pischke, 2009; Porter, 2015).
Using Quantile Regression to Estimate Intervention Effects in Education
To demonstrate the usefulness of quantile regression in estimating treatment effects we analyzed education data from a large-scale randomized experiment. Specifically, we used quantile regression to estimate treatment effects of interim assessments across the achievement distribution.
Background
High-stakes accountability ordinances introduced more than a decade ago created systems across states that required reports of school annual performances. Consequently, data-driven school assessment programs were instigated in multiple states to improve classroom instruction and ultimately student performance (Bracey, 2005; Sawchuk, 2009). One type of these assessment-based solutions is standardized assessments that are administered several times throughout the school year, known as diagnostic or interim assessments (Perie, Marion, Gong, & Wurtzel, 2007). Teachers in turn receive training to analyze these assessment-based data to evaluate students’ progress accurately. Once the evaluation is completed teachers modify their instruction accordingly to match students’ learning needs and help them increase their performance.
The underlying hypothesis is that as student performance data become available more frequently, teachers with adequate training should be able to analyze these data to diagnose the level of learning for each student and then fine-tune their instructional practices accordingly to improve student learning. Within this framework, teachers use recurrent evidence of student performance to better monitor student learning and through targeted instructional practices aspire to increase student performance.
An important component of interim assessments is targeted differentiated instruction that meets student ability and knowledge closely (Tomlinson, 2000). Differentiated instruction maximizes each student’s probability of individual success by recognizing students’ individual knowledge sets and needs. Through an iterative series of assessments, teachers use assessment-based data to diagnose students’ weaknesses and strengths and modify instruction to match students’ abilities, knowledge, and learning needs. The objective is that teachers identify and enact the most effective personalized instructional practice for each student to boost his or her learning trajectory.
Although interim assessments should equip teachers with tools that enable learning and lead to improvements in student achievement for all students at various levels of achievement, it is possible that these assessments could be especially helpful for students at different achievement levels. For example, recent work has reported that assessment programs sometimes focus on struggling students (Datnow & Hubbard, 2015). Through interim assessment processes teachers may be able to identify with higher accuracy low-achievers’ learning needs and differentiate instruction to help them improve further. Hence, it is possible that struggling students may benefit more from interim assessments than average- or high-achievers.
To test this hypothesis, we examine the effects of interim assessments across the mathematics and reading distributions of scores. The primary research question is whether the effects are consistent or vary by achievement level. First, we estimate the effects of interim assessments for low-, median- and high-achievers and then compare the differences between these effects to determine potential changes in the achievement gap between lower- and higher-achievers. To accomplish this goal, we use quantile regression that produces estimates in the middle as well as in the lower and upper tails of the achievement distribution. We use data from a large-scale experiment conducted in Indiana during the 2010-2011 school year.
Review of the Literature
Although the literature has provided some evidence about the average effects of interim assessments on student achievement (e.g., Konstantopoulos, Miller, & van der Ploeg, 2013; Slavin, Cheung, Holmes, Madden, & Chamberlain, 2013) little is known about the effects of interim assessments on the achievement gap between lower and higher achievers. The main evidence in the literature is about the effects of formative assessments on low-achievers (e.g., Black & Wiliam, 1998). However, the achievement gap between low- and high-achievers continues to be an important issue in educational research and practice. School interventions such as interim assessments may have the potential to reduce achievement differences between lower and higher achievers via differentiated instruction. For example, in order to respond successfully to information garnered from interim assessments that identify students’ weaknesses in learning the material, teachers may reteach important concepts and skills. Reteaching could have a larger benefit for students who did not grasp the material well the first time, who are likely to be lower achieving students. Although interim assessments are hypothesized to improve student achievement for all students, it is unclear whether the effects of these assessment systems are the same for all students at various achievement levels, or whether they vary by achievement level.
The literature thus far has not documented well the consistency or variability of the effects of interim assessments on student achievement across the achievement distribution. Prior reviews have reported some evidence that formative assessments may produce additional benefits for lower-achieving students compared with other students (Black & Wiliam, 1998). More recent evidence about the effects of interim assessments across the achievement distribution has indicated beneficial effects in Grades 3 to 8 in mathematics (Konstantopoulos, Li, Miller, & van der Ploeg, 2016). These effects were by and large uniform across the achievement distribution and did not vary by achievement level. In this study, we report additional evidence about the effects of interim assessments on various levels of student achievement using data from a large-scale experiment conducted in 2010-2011 in Indiana.
Two conditions seem plausible with respect to the consistency or variability of the effects of interim assessments on student performance. First, if differentiated instruction has a uniform effect across the achievement distribution one would expect comparable potential benefits for students at different achievement levels (i.e., low-, median-, or high-achievers). If this hypothesis were true, the treatment effect would not vary by achievement level and would have no effect on the achievement gap between higher-, median-, or lower-achievers because lower and higher scoring students would benefit equally from differentiated instruction.
Second, if differentiated instruction varies by student achievement level (e.g., additional benefit for low- or high-achievers) one would expect more pronounced effects of interim assessments at different parts of the achievement distribution. Under this condition, two scenarios seem plausible. First, if differentiated instruction benefits low-achievers more than other students, one would expect a more pronounced treatment effect in the lower tail of the achievement distribution than in the middle or in the upper tail. If this hypothesis were true, the treatment effect would vary by achievement level and would reduce the achievement gap between lower- and higher-achievers because low-achievers would benefit more from differentiated instruction. Second, if differentiated instruction benefits high-achievers more than others one would expect a more pronounced treatment effect in the upper tail of the achievement distribution than in the middle or the lower tail. If this hypothesis were true, the treatment effect would again vary by achievement level and would increase the achievement gap between higher- and lower-achievers because higher scoring students would benefit more from differentiated instruction.
Method
Data
Indiana’s assessment program incorporated two commercial products: in Grades K to 2, Wireless Generation’s mCLASS and in Grades 3 to 8, CTB/McGraw-Hill’s Acuity (Indiana State Board of Education, 2006). Vendors worked with Indiana staff and teachers to align their assessments, instructional resources, and training curricula to Indiana’s content standards and instructional scope. Students throughout Indiana took the same assessments and were tested at the same time points during the school year statewide.
We conducted a randomized experiment in Indiana during the 2010-2011 school year and included K-8 public schools that had volunteered to be part of the intervention in the spring of 2010. We used a cluster randomized design (see Boruch, Weisburd, & Berk, 2010) where schools were randomly assigned to a treatment or a control condition. The sample was drawn from a list of 157 schools that had volunteered in the spring of 2010 to participate in the interim assessments program in Indiana during the 2010-2011 school year. A priori statistical power analysis had suggested that nearly 55 schools would be required to detect the average treatment effect with a probability higher than .80.
We anticipated approximately a 20% attrition rate and, as a result, we first selected randomly a sample of 70 schools from the list. Second, we assigned randomly these 70 schools to a treatment or a control condition aiming for a balanced design. Thirty-six schools were assigned to the treatment condition and 34 schools were assigned to the control condition. The actual attrition rate was nearly 20% and as a result, the sample of schools that participated in the experiment was reduced to 55 with 28 schools in the treatment condition and 27 schools in the control condition. Nearly 20,000 students participated in the study during the 2010-2011 school year. The schools in the treatment condition received mCLASS or Acuity, and the training associated with each product. The control schools did not receive access to these assessments and their associated trainings, operating under business-as-usual conditions.
Measures
In Grades 3 to 8, the outcomes were mathematics and reading scores of ISTEP+ which is Indiana’s standardized state-wide accountability test. Indiana’s ISTEP+, like most state tests, does not extend below the third grade. As a result, in Grades K to 2, the outcomes were Terra Nova scores in mathematics and reading. The Terra Nova test is frequently used in early grades and was administered by the research team. Terra Nova is developed and maintained by CTB/McGraw-Hill’s educational assessment unit, which also develops and maintains the ISTEP+. Domain and conceptual overlap between the two assessment batteries is considerable. To simplify interpretation of estimates, we standardized the achievement scores (i.e., mean = 0 and SD = 1).
The main independent variable indicated school assignment to the treatment (i.e., mCLASS or Acuity) or not. The treatment variable was coded as a binary indicator taking the value of 1 for treatment schools who received mCLASS or Acuity and 0 otherwise. The coefficient of the treatment is a standardized mean difference between treatment and control groups. The student-level covariates included gender (a binary indicator for female students—male students being the reference category), age (in months), race (multiple binary indicators for Black, Latino, and other race students—White students being the reference category), low socioeconomic status that represents economic disadvantage (a binary indicator for free or reduced price lunch eligibility—no eligibility being the reference category), special education status (a binary indicator for special education students—no special education status being the reference category) and limited English proficiency status (a binary indicator for students with limited English proficiency—English proficiency being the reference category). The school-level covariates were percent of female, minority, lower socioeconomic status, special education and limited English proficiency students, as well as school urbanization categories (binary indicators for rural, suburban, and small town—urban being the reference category).
Statistical Analysis
To estimate the effects of interim assessments at different levels of achievement, we used quantile regression (Buchinsky, 1998; Hao & Naiman, 2007; Koenker & Bassett, 1978). Specifically, we examined treatment effects in the lower tail (i.e., 0.10 and 0.25 quantiles), the middle (0.50 quantile), and the upper tail (i.e., 0.75 and 0.90 quantiles) of the achievement distribution. We conducted analyses across different groups of grades (i.e., K-2, 3-8, and K-8).
At each quantile the empirical model for student i was
| (9) |
where y is the outcome variable (mathematics or reading scores), is the constant term, is the estimate of the treatment effect, Tj is a binary indicator of being in a treatment or a control group, ST represents student predictors, is a column vector of regression estimates of student predictors, SC represents school predictors, is a column vector of regression estimates of school predictors, G represents differences across grades (i.e., grade fixed effects—dummies), is a column vector of grade fixed effects estimates, and is a student error. The estimator at τth quantile is defined as
| (10) |
where is the check function that weighs positive and negative residuals differently (see Koenker & Bassett, 1978). Because we were interested in including in the model specification multiple covariates as Equation (9) indicates we ran conditional quantile regression models.
Seven control schools and eight treatment schools did not participate in the experiment but provided student and school data. To deal with the potential nonrandom dropout and address the potential threat to the internal validity of the treatment estimates, we used an instrumental variables (IV) approach coupled with quantile regression (see Abadie, Angrist, & Imbens, 2002). This approach is based on the framework developed by Imbens and Angrist (1994) that creates four latent groups of units in an experiment according to their compliance behavior: never-takers, compliers, defiers, and always-takers.
In particular, the never-takers are the units that would not participate in the interim assessment program regardless of their initial assignment. The never-takers in the specific data set were the 15 schools that did not participate in the experiment. The compliers are the units that would comply according to their initial assignment (i.e., receive treatment if assigned to the treatment group and not receive treatment if assigned to the control group). The compliers in the specific data set were the 55 schools that participated in the experiment according to their assignment. In the treatment group, the compliers were 28 schools. The defiers are the units that would receive the opposite treatment from the one they were originally assigned to (i.e., units switch from the control to the treatment group and vice versa). There were no defier schools in the data set. The always-takers are the units that would receive the treatment regardless of their initial assignment. There were no always-takers in the data set. Imbens and Angrist (1994) showed that under the monotonicity assumption (i.e., the nonexistence of defiers), the IV approach can provide valid estimates of the average causal treatment effect for the compliers in the treatment group.
We used random assignment in the original sample (i.e., the 70 schools) as the instrumental variable. This approach involves two steps. The first step uses a logistic regression model where the outcome is binary (i.e., 1 for the 28 schools assigned to the treatment that actually received the treatment and 0 for the 32 remaining schools). The predictors include random assignment (1 for schools assigned randomly to treatment and 0 otherwise) which served as the instrument, and student and school predictors (as described in the variables section). Specifically, in the first stage the logistic model for student i was
| (11) |
where is the probability of complying with the initial assignment of receiving the treatment. The predicted values from the logistic model above are then used to construct weights that account for the propensity of schools in the treatment group that complied with random assignment. Since complier is a latent compliance type that cannot be observed directly, Abadie et al. (2002) proposed a way of identifying the probability that a participating unit is a complier (i.e., schools assigned to the treatment condition that received the treatment). Specifically, the authors proposed constructing weights to identify compliers, namely,
| (12) |
where Zj is the instrument (random assignment in the initial sample of 70 schools), and is estimated through a logistic regression model in the first stage.
Once the weights are computed, they are used in the second-stage estimation. The intuition is that in the second-stage weighted estimation the treatment schools that complied with initial random assignment would receive different weights than other schools. In particular, Abadie et al. (2002) showed that the treatment effects at the τth quantile can be consistently estimated through a weighted quantile regression with as the weight, namely,
| (13) |
The weights account for the propensity of schools (and students) that complied with random assignment and these treatment schools (and students) have a higher weight than other schools. The unit of analysis in the first and second stages is the student. We used the ivqte command in STATA to conduct the IV quantile regression analysis (see, Frolich & Melly, 2010). The IV method analyzed data from the full sample of students (nearly 30,000 students).
We computed cluster bootstrap SEs that take into account the two-stage procedure and potential clustering effects. Specifically, in the IV analysis, the cluster bootstrap approach resampled schools (instead of students) 400 times (replications). The cluster bootstrap SE was the SD of the 400 treatment effects estimates obtained from the 400 replications. Cameron and Trivedi (2010) suggest that cluster bootstrap SEs are robust to heteroscedasticity and account for clustering effects.
We also conducted analyses to estimate the effect of the intention to treat (ITT) using the initial sample of schools used in random assignment (i.e., 70 schools and nearly 30,000 students). The ITT analysis provides estimates of the treatment effect for schools that were assigned randomly to the treatment condition as opposed to the control condition. The data are analyzed as was intended by initial random assignment regardless of whether schools participated in the study. Fifteen of the 70 schools (7 control schools and 8 treatment schools) did not participate in the experiment but were part of the initial random assignment and provided student and school data, and thus, were included in the ITT analyses. These schools and their students were included in the analyses under the assumption that they had participated in the study.
Finally, we also conducted analysis to estimate the effect of the treatment on the treated (TOT) using the sample of schools that participated in the experiment (i.e., 55 schools and nearly 20,000 students). The treatment effect in this case captures the difference in student achievement between schools that were assigned randomly to the treatment group and actually received the treatment and schools that were assigned randomly to the control group and remained in the experiment in that group. Fifteen of the 70 schools dropped out of the experiment after random assignment and if this attrition were nonrandom and differential (i.e., treatment schools that dropped out of the experiment are different on average than control schools that also dropped out of the experiment), the treatment and control schools that stayed in the experiment may not be equivalent on average. This is a potential caveat of the TOT estimates. The quantile regression models used in the ITT and TOT analyses are described in Equation (9).
For the ITT and TOT analyses, we used the qreg2 routine in STATA. To account for potentially clustering effects (i.e., students nested in schools) we computed cluster robust SEs in the ITT and the TOT analyses (see, Parente & Santos Silva, 2016). According to Parente and Santos Silva (2016), the cluster robust SEs take into account heteroscedasticity and potential clustering effects. We conducted analyses using data across all grades (i.e., K through 8) to estimate treatment effects for both mCLASS and Acuity. We also conducted analyses using either K to 2 data or 3 to 8 data to estimate mCLASS or Acuity effects separately. Prior ISTEP+ scores were available in Grades 4 to 8 and thus we also ran models that included or omitted prior student achievement as a covariate to determine the stability of the results.
Finally, we constructed tests to determine potential differences in treatment effects between pairs of quantiles. Specifically, we used t-tests to compare differences in estimates of pairs of quantiles across the achievement distribution (e.g., 10th vs. 90th quantiles, or 25th vs. 75th quantiles, and so forth). We used a bootstrap procedure to compute the SEs of the mean differences (see Kolenikov, 2010).
Results
The initial task was to conduct analyses that examine whether random assignment was successful as intended by design using pretest scores. We inspected baseline equivalence in prior scores between treatment and control groups at various quantiles. Only ISTEP+ prior scores were available in Grades 4 to 8. We used quantile regression pooling data across Grades 4 to 8 and conducted analyses in mathematics and reading. We estimated baseline differences from the 0.05 to the 0.95 quantiles in five-percentile increments (i.e., 0.05, 0.10, 0.15, . . ., 0.85, 0.90, and 0.95). Prior scores were standardized to have a mean of 0 and an SD of 1. The unit of analysis was the student. We computed cluster robust SEs for all quantile estimates (Parente & Santos Silva, 2016). We used both a graphical device and a table to report the results of this analysis (Bitler, Domina, Penner, & Hoynes, 2015). Specifically, the results are illustrated in Figures 1 and 2 and in Table 1.
Figure 1.
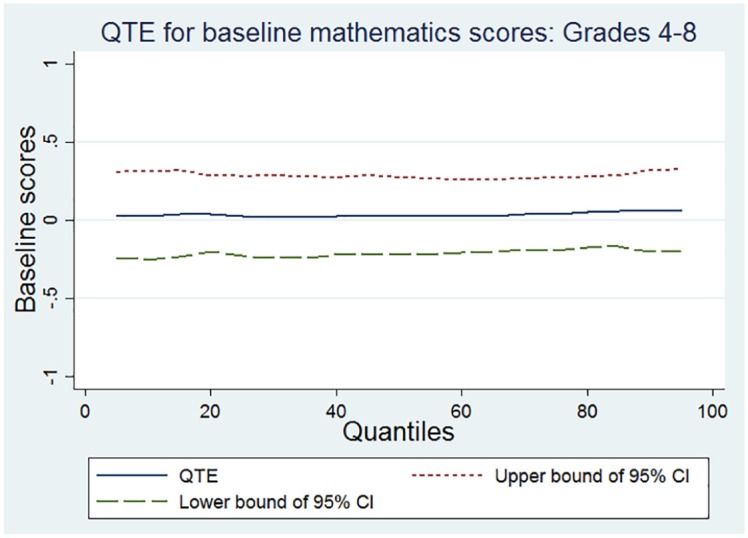
Quantile treatment estimates (QTEs) of Acuity interim assessment on baseline mathematics scores.
Figure 2.
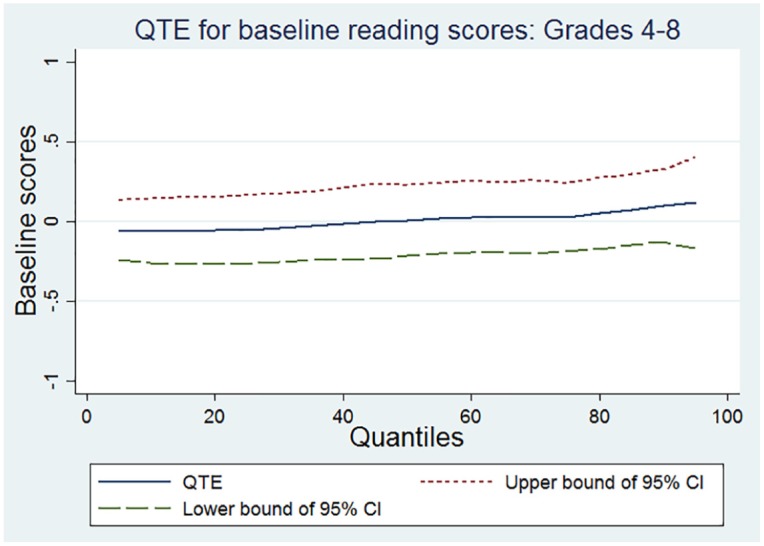
Quantile treatment estimates (QTEs) of Acuity interim assessment on baseline reading scores.
Table 1.
Mean Differences Between Treatment and Control in Prior Scores at Various Quantiles: Random Assignment Check in Grades 4 to 8.
| Quantiles | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5th | 10th | 15th | 20th | 25th | 30th | 35th | 40th | 45th | 50th | 55th | 60th | 65th | 70th | 75th | 80th | 85th | 90th | 95th | |
| Mathematics | |||||||||||||||||||
| Estimate | 0.034 | 0.029 | 0.042 | 0.042 | 0.027 | 0.021 | 0.018 | 0.026 | 0.032 | 0.029 | 0.024 | 0.027 | 0.027 | 0.042 | 0.037 | 0.052 | 0.061 | 0.059 | 0.064 |
| SE | 0.140 | 0.143 | 0.141 | 0.125 | 0.130 | 0.135 | 0.132 | 0.126 | 0.129 | 0.125 | 0.123 | 0.119 | 0.119 | 0.115 | 0.119 | 0.115 | 0.115 | 0.133 | 0.132 |
| Reading | |||||||||||||||||||
| Estimate | −0.053 | −0.059 | −0.057 | −0.056 | −0.051 | −0.041 | −0.027 | −0.015 | 0.000 | 0.007 | 0.020 | 0.029 | 0.025 | 0.030 | 0.029 | 0.050 | 0.075 | 0.099 | 0.117 |
| SE | 0.095 | 0.103 | 0.107 | 0.106 | 0.111 | 0.110 | 0.108 | 0.114 | 0.120 | 0.113 | 0.114 | 0.114 | 0.112 | 0.116 | 0.109 | 0.114 | 0.113 | 0.116 | 0.145 |
Note. SE = standard error.
Figure 1 shows baseline differences in prior mathematics scores across various quantiles in Grades 4 to 8. The quantile estimates were all very close to 0 and the upper and lower bounds of the 95% confidence interval always included 0. This graph indicates that the treatment is balanced in baseline mathematics achievement. Figure 2 portrays the results in prior reading scores. The quantile estimates were all close to 0 and the upper and lower bounds of the 95% confidence interval always included 0. The graph indicates that the treatment is also balanced in baseline reading achievement. The estimates in Table 1 provide additional support about baseline equivalence in mathematics and reading scores. All quantile estimates were statistically nonsignificant and close to 0. These results indicate that random assignment was successful as expected by the research design.
Table 2 reports sample sizes, means, and SDs of outcomes and predictor variables used in the analyses for treatment and control groups and the full sample. The first four rows in Table 2 report descriptive statistics for the outcome variables (i.e., posttest mathematics and reading scores) in Grades K to 2 (Terra Nova) and 3 to 8 (ISTEP+). All posttest scores were standardized to have a mean of 0 and an SD of 1. The Terra Nova mathematics and reading mean scores were higher in the control group than in the treatment group. These mean differences were found to be statistically significant in the quantile regression analyses (see Table 3). Approximately 6,000 students in Grades K to 2 had Terra Nova scores. The ISTEP+ mathematics and reading mean scores were only slightly higher in the control group than in the treatment group. These mean differences were found to be statistically nonsignificant in the quantile regression analyses (see Table 3). Nearly 25,000 students in Grades 3 to 8 had ISTEP+ scores. The average student age was 10.75 years (129 months) and was similar in treatment and control groups. Fifty percent of the students in the control group were females as opposed to 48% in the treatment group. Overall, 53% of the students were White, while in the treatment group the percentage was slightly higher (55%). Nearly 27% of the students were Blacks, while almost twice as many Latino students were in the control group than in the treatment group (15% vs. 8%). The rate of economically disadvantaged students (i.e., eligible for free or reduced-price lunch) was about 57%.
Table 2.
Means, Standard Deviations, and Samples Sizes for Variables of Interest.
| Treatment |
Control |
Full sample |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | SD | N c | Mean | SD | N c | Mean | SD | N | |
| Outcomes | |||||||||
| Terra Nova Reading scores | −0.145 | 0.967 | 3,058 | 0.138 | 1.012 | 3,212 | 0.000 | 1.000 | 6,270 |
| Terra Nova Mathematics scores | −0.138 | 0.964 | 3,050 | 0.131 | 1.016 | 3,199 | 0.000 | 1.000 | 6,249 |
| ISTEP + Reading scores | 0.003 | 1.024 | 12,073 | −0.003 | 0.977 | 12,670 | 0.000 | 1.000 | 24,743 |
| ISTEP + Mathematics score | 0.028 | 1.006 | 12,149 | −0.026 | 0.994 | 12,719 | 0.000 | 1.000 | 24,868 |
| Predictors | |||||||||
| Age (months) | 127.410 | 33.936 | 18,381 | 130.982 | 32.623 | 17,682 | 129.161 | 33.346 | 36,063 |
| Female | 0.477 | 0.499 | 18,392 | 0.500 | 0.500 | 17,695 | 0.488 | 0.500 | 36,087 |
| Race | |||||||||
| White | 0.548 | 0.498 | 18,376 | 0.506 | 0.500 | 17,651 | 0.527 | 0.499 | 36,027 |
| Black | 0.295 | 0.456 | 18,376 | 0.253 | 0.435 | 17,651 | 0.274 | 0.446 | 36,027 |
| Latino | 0.078 | 0.268 | 18,376 | 0.154 | 0.361 | 17,651 | 0.115 | 0.320 | 36,027 |
| Other | 0.079 | 0.269 | 18,376 | 0.087 | 0.281 | 17,651 | 0.083 | 0.275 | 36,027 |
| Limited English proficiency | 0.042 | 0.200 | 19,108 | 0.045 | 0.208 | 18,451 | 0.043 | 0.204 | 37,559 |
| Low socioeconomic status: Free or reduced-price lunch | 0.571 | 0.495 | 18,400 | 0.565 | 0.496 | 17,702 | 0.568 | 0.495 | 36,102 |
| Special education | 0.194 | 0.395 | 19,108 | 0.180 | 0.384 | 18,451 | 0.187 | 0.390 | 37,559 |
Note. SD = standard deviation.
Table 3.
Ordinary Least Squares and Quantile Regression Estimates in Mathematics and Reading Achievement.
| Mathematics |
Reading |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean regression | Median regression | 10th | 25th | 75th | 90th | Mean regression | Median regression | 10th | 25th | 75th | 90th | |
| IV | ||||||||||||
| Grades K to 8 | ||||||||||||
| Treatment effect | 0.004 | −0.027 | 0.000 | −0.034 | −0.047 | −0.088 | −0.036 | −0.061 | −0.077 | −0.053 | −0.027 | −0.054 |
| SE | 0.073 | 0.062 | 0.070 | 0.066 | 0.069 | 0.080 | 0.058 | 0.059 | 0.057 | 0.054 | 0.063 | 0.073 |
| Number of schools | 70 | 70 | ||||||||||
| Number of students | 29,757 | 29,671 | ||||||||||
| Grades K to 2 | ||||||||||||
| Treatment effect | −0.225* | −0.191 | −0.246 | −0.217 | −0.206* | −0.271* | −0.198* | −0.169 | −0.221* | −0.185* | −0.162* | −0.300 |
| SE | 0.045 | 0.099 | 0.202 | 0.129 | 0.068 | 0.097 | 0.042 | 0.121 | 0.108 | 0.077 | 0.075 | 0.155 |
| Number of schools | 30 | 30 | ||||||||||
| Number of students | 6,159 | 6,180 | ||||||||||
| Grades 3 to 8 | ||||||||||||
| Treatment effect | 0.099 | 0.047 | 0.074 | 0.035 | 0.036 | −0.028 | 0.040 | −0.010 | −0.037 | −0.012 | 0.027 | 0.047 |
| SE | 0.094 | 0.074 | 0.091 | 0.079 | 0.092 | 0.098 | 0.073 | 0.062 | 0.077 | 0.070 | 0.081 | 0.090 |
| Number of schools | 70 | 70 | ||||||||||
| Number of students | 23,598 | 23,491 | ||||||||||
| ITT | ||||||||||||
| Grades K to 8 | ||||||||||||
| Treatment effect | 0.003 | −0.004 | 0.032 | −0.003 | −0.000 | −0.009 | −0.026 | −0.029 | −0.059 | −0.030 | 0.002 | −0.013 |
| SE | 0.053 | 0.053 | 0.057 | 0.057 | 0.054 | 0.053 | 0.043 | 0.044 | 0.046 | 0.042 | 0.042 | 0.053 |
| Number of schools | 70 | 70 | ||||||||||
| Number of students | 29,757 | 29,671 | ||||||||||
| Grades K to 2 | ||||||||||||
| Treatment effect | −0.225* | −0.191* | −0.246* | −0.218* | −0.205* | −0.271* | −0.198* | −0.169* | −0.221* | −0.185* | −0.162* | −0.292* |
| SE | 0.045 | 0.050 | 0.057 | 0.055 | 0.038 | 0.033 | 0.043 | 0.042 | 0.058 | 0.049 | 0.043 | 0.072 |
| Number of schools | 30 | 30 | ||||||||||
| Number of students | 6,159 | 6,180 | ||||||||||
| Grades 3 to 8 | ||||||||||||
| Treatment effect | 0.066 | 0.057 | 0.112 | 0.059 | 0.063 | 0.046 | 0.027 | 0.012 | −0.012 | 0.015 | 0.043 | 0.078 |
| SE | 0.062 | 0.061 | 0.060 | 0.069 | 0.064 | 0.064 | 0.049 | 0.047 | 0.052 | 0.050 | 0.049 | 0.060 |
| Number of schools | 70 | 70 | ||||||||||
| Number of students | 23,598 | 23,491 | ||||||||||
| TOT | ||||||||||||
| Grades K to 8 | ||||||||||||
| Treatment effect | −0.045 | −0.039 | −0.000 | −0.038 | −0.054 | −0.095 | −0.054 | −0.055 | −0.071 | −0.039 | −0.043 | −0.062 |
| SE | 0.061 | 0.063 | 0.066 | 0.064 | 0.061 | 0.072 | 0.050 | 0.049 | 0.052 | 0.044 | 0.052 | 0.070 |
| Number of schools | 55 | 55 | ||||||||||
| Number of students | 19,300 | 19,280 | ||||||||||
| Grades K to 2 | ||||||||||||
| Treatment effect | −0.206* | −0.173* | −0.234* | −0.191* | −0.177* | −0.270* | −0.206* | −0.168* | −0.247* | −0.200* | −0.142* | −0.313* |
| SE | 0.055 | 0.058 | 0.063 | 0.056 | 0.047 | 0.044 | 0.048 | 0.047 | 0.065 | 0.050 | 0.046 | 0.090 |
| Number of schools | 26 | 26 | ||||||||||
| Number of students | 5,666 | 5,685 | ||||||||||
| Grades 3 to 8 | ||||||||||||
| Treatment effect | 0.030 | 0.055 | 0.066 | 0.049 | 0.023 | −0.066 | 0.010 | 0.004 | −0.011 | 0.024 | 0.012 | 0.046 |
| SE | 0.079 | 0.076 | 0.071 | 0.086 | 0.091 | 0.089 | 0.061 | 0.059 | 0.060 | 0.055 | 0.065 | 0.083 |
| Number of schools | 49 | 49 | ||||||||||
| Number of students | 13,634 | 13,595 | ||||||||||
Note. SE = standard error; IV = instrumental variables; ITT = intention to treat; TOT = treatment on the treated.
p≤ .05.
The main results of the analyses are reported in Table 3. The treatment effect estimates indicate differences in SDs between treatment and control groups at various quantiles. Positive estimates indicate a positive treatment effect, while negative estimates indicate a negative effect. OLS mean estimates are also reported next to the median estimates. Table 3 reports first IV estimates at various quantiles in mathematics and reading, then reports ITT estimates at various quantiles in mathematics and reading, and finally reports TOT estimates at various quantiles in mathematics and reading.
The results produced from the IV quantile regression analyses indicated that in Grades K to 8 all treatment effect estimates, in mathematics and reading, were close to 0 and statistically nonsignificant. That is, the effects of interim assessments (mCLASS or Acuity) at various quantiles were not statistically different from 0. The effects were uniform across the achievement distribution, that is, students across different achievement levels did not benefit from these assessment programs.
The IV estimates in Grades 3 to 8 were similar to those reported in Grades K to 8. The estimates were small, statistically nonsignificant and uniform across the achievement distribution. The mathematics and reading estimates obtained from the Grades K to 2 analysis, however, were all negative and almost 0.20 SDs on average (i.e., one fifth of an SD). In Grades K to 2, 50% of the IV estimates were statistically significant mainly in the upper tail in mathematics and in the lower tail in reading. The median estimates were not significant, however. The IV estimates were overall uniform across the achievement distributions and did not appear to vary by achievement level. The K to 2 results indicate that mCLASS had a negative impact on mathematics and reading scores regardless of achievement level. Along the same lines the, Grades 3 to 8 results suggest that Acuity did not have any impact on mathematics and reading scores regardless of achievement level.
The ITT quantile regression estimates in Grades K to 8 were close to 0, typically smaller than their SEs and hence, statistically nonsignificant in the middle and in the tails of the achievement distributions. These results were similar to the results of the IV analyses. However, the results varied by interim assessment program. The Grade K to 2 analyses produced negative and statistically significant estimates that were approximately as large as 0.20 SDs on average (i.e., one fifth of an SD) across the achievement distribution. The median estimate in mathematics was close to 0.20 SDs while the estimate in reading was slightly smaller. The estimates in the 0.10 and the 0.90 quantiles were much larger and nearly one quarter of an SD or larger. The effects were overall uniform across the achievement distributions and did not appear to vary by achievement level. In contrast, the ITT estimates in Grades 3 to 8, both in mathematics and reading, were very similar to those reported in Grades K to 8. The estimates were small, statistically nonsignificant and similar in magnitude across the achievement distribution. The ITT estimates were overall similar to the IV estimates and suggest that mCLASS negatively affected student achievement across different achievement levels, while Acuity did not have any impact on mathematics and reading scores regardless of achievement level.
The TOT results in Grades K to 8 followed similar patterns as the IV and the ITT results. All treatment effect estimates both in mathematics and reading were close to 0, statistically nonsignificant, and uniform across the achievement distributions. The results by interim assessment program also followed a similar pattern as the IV and ITT estimates. The effects were virtually 0 in Grades 3 to 8 and negative, statistically significant, and nearly 0.20 SDs on average (i.e., one fifth of an SD) in Grades K to 2 across various quantiles. The effects were overall uniform across the achievement distributions and did not vary by achievement level.
The OLS regression means were similar in magnitude to the median regression estimates across all three analyses. These results suggest by and large that interim assessment programs had uniform effects across achievement levels and neither reduced nor increased the achievement gap.
In Grades 4 to 8, we were able to conduct sensitivity analyses by including or excluding prior achievement ISTEP+ scores as covariates in the regression models. The objective was to determine whether controlling for prior scores would change the results considerably (i.e., a robustness check). The OLS, IV, and ITT estimates of this analysis are summarized in Table 4. By and large, the coefficients were statistically nonsignificant, which suggests that including or excluding prior achievement in the model did not influence the estimates (i.e., the estimates were robust). The OLS means were similar in magnitude to the median estimates. Overall, the pattern of these results was similar to that in Table 3. There were two exceptions, however. The 0.10 and 0.25 quantile estimates in reading that had been obtained from the ITT analyses that included prior scores as covariates were negative and statistically significant. The SEs of the estimates in the analyses that included prior scores as covariates were overall smaller. That is, the estimation was more precise as one would expect when prior scores are controlled for in regression models. Overall, the effects reported in Table 4 were consistent across the achievement distribution, and thus, the treatment did not seem to have an impact on the achievement gap between lower- and higher-achievers.
Table 4.
Ordinary Least Squares and Quantile Regression Estimates in Mathematics and Reading Achievement With and Without Prior Scores.
| Mathematics |
Reading |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean regression | Median regression | 10th | 25th | 75th | 90th | Mean regression | Median regression | 10th | 25th | 75th | 90th | |
| Prior scores included | ||||||||||||
| IV | ||||||||||||
| Grades 4 to 8 | ||||||||||||
| Treatment effect | −0.024 | −0.040 | −0.022 | −0.035 | −0.041 | −0.058 | −0.045 | −0.045 | −0.064 | −0.056 | −0.039 | −0.057 |
| SE | 0.043 | 0.043 | 0.051 | 0.039 | 0.051 | 0.063 | 0.035 | 0.034 | 0.045 | 0.040 | 0.040 | 0.063 |
| Number of schools | 70 | 70 | ||||||||||
| Number of students | 18,836 | 18,714 | ||||||||||
| ITT | ||||||||||||
| Grades 4 to 8 | ||||||||||||
| Treatment effect | −0.016 | −0.028 | −0.002 | −0.026 | −0.005 | −0.003 | −0.030 | −0.026 | −0.051* | −0.046* | −0.016 | −0.029 |
| SE | 0.029 | 0.024 | 0.026 | 0.025 | 0.030 | 0.041 | 0.023 | 0.018 | 0.025 | 0.022 | 0.020 | 0.033 |
| Number of schools | 70 | 70 | ||||||||||
| Number of students | 18,836 | 18,714 | ||||||||||
| Prior scores excluded | ||||||||||||
| IV | ||||||||||||
| Grades 4 to 8 | ||||||||||||
| Treatment effect | 0.081 | 0.022 | 0.047 | 0.033 | 0.001 | −0.071 | 0.032 | −0.008 | −0.047 | −0.011 | 0.006 | 0.046 |
| SE | 0.096 | 0.086 | 0.089 | 0.085 | 0.096 | 0.114 | 0.076 | 0.077 | 0.084 | 0.075 | 0.086 | 0.101 |
| Number of schools | 70 | 70 | ||||||||||
| Number of students | 20,052 | 19,977 | ||||||||||
| ITT | ||||||||||||
| Grades 4 to 8 | ||||||||||||
| Treatment effect | 0.053 | 0.044 | 0.093 | 0.056 | 0.044 | 0.026 | 0.021 | 0.012 | −0.021 | 0.021 | 0.039 | 0.062 |
| SE | 0.063 | 0.061 | 0.061 | 0.072 | 0.061 | 0.064 | 0.051 | 0.049 | 0.053 | 0.051 | 0.052 | 0.058 |
| Number of schools | 70 | 70 | ||||||||||
| Number of students | 20,052 | 19,977 | ||||||||||
Note. SE = standard error; IV = instrumental variables; ITT = intention to treat; TOT = treatment on the treated.
p≤ .05.
Finally, we investigated potential differences between any two quantile-specific estimates across the entire achievement distribution of scores using t tests. To construct the numerator of the t-test we subtracted the estimated treatment effect in one quantile from the estimated treatment effect in a different quantile (e.g., the estimate at the 0.90 quantile minus the estimate at the 0.10 quantile). In this example, a positive difference would indicate that high-achievers benefited more from the treatment than low-achievers. That is, a positive difference would indicate an increase in the achievement gap between high- and low-achievers. In contrast, a negative difference would indicate a decrease in the achievement gap between high- and low-achievers. The SEs computed for each mean difference took into account the dependency of the estimates. These mean differences and their SEs are reported in Table 5. The results suggest that the mean differences between quantile treatment effects at any two quantiles are generally not different from 0. Only 6 of the 180 t tests were statistically significant at the .05 level (4 in mathematics and 2 in reading). It appears therefore that the treatment effects were consistent across the achievement distribution and did not have any systematic impact on the achievement gap. This finding is consistent with results reported from a recent study (Konstantopoulos et al., 2016).
Table 5.
Differences Among Quantile Regression Estimates.
| Mathematics |
Reading |
|||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 90th vs. 10th quantile | 90th vs. 25th quantile | 90th vs. 50th quantile | 90th vs. 75th quantile | 75th vs. 10th quantile | 75th vs. 25th quantile | 75th vs. 50th quantile | 50th vs. 10th quantile | 50th vs. 25th quantile | 25th vs. 10th quantile | 90th vs. 10th quantile | 90th vs. 25th quantile | 90th vs. 50th quantile | 90th vs. 75th quantile | 75th vs. 10th quantile | 75th vs. 25th quantile | 75th vs. 50th quantile | 50th vs. 10th quantile | 50th vs. 25th quantile | 25th vs. 10th quantile | |
| IV | ||||||||||||||||||||
| Grades K to 8 | ||||||||||||||||||||
| Treatment effect difference | −0.088 | −0.054 | −0.060 | −0.041 | −0.047 | −0.013 | −0.019 | −0.028 | 0.006 | −0.034 | 0.023 | −0.001 | 0.007 | −0.027 | 0.051 | 0.026 | 0.034 | 0.017 | −0.008 | 0.025 |
| SE | 0.061 | 0.052 | 0.045 | 0.032 | 0.044 | 0.032 | 0.022 | 0.034 | 0.020 | 0.025 | 0.056 | 0.045 | 0.037 | 0.031 | 0.040 | 0.027 | 0.019 | 0.034 | 0.019 | 0.023 |
| Grades K to 2 | ||||||||||||||||||||
| Treatment effect difference | −0.026 | −0.054 | −0.081 | −0.066 | 0.040 | 0.012 | −0.015 | 0.055 | 0.027 | 0.028 | −0.079 | −0.115 | −0.131 | −0.138 | 0.059 | 0.023 | 0.007 | 0.052 | 0.016 | 0.037 |
| SE | 0.147 | 0.112 | 0.094 | 0.062 | 0.103 | 0.069 | 0.047 | 0.074 | 0.037 | 0.053 | 0.131 | 0.116 | 0.104 | 0.078 | 0.086 | 0.072 | 0.049 | 0.071 | 0.051 | 0.043 |
| Grades 3 to 8 | ||||||||||||||||||||
| Treatment effect difference | −0.102 | −0.062 | −0.075 | −0.063* | −0.038 | 0.001 | −0.011 | −0.027 | 0.012 | −0.039 | 0.084 | 0.059 | 0.057 | 0.020 | 0.064 | 0.039 | 0.037 | 0.027 | 0.002 | 0.025 |
| SE | 0.078 | 0.061 | 0.047 | 0.031 | 0.063 | 0.044 | 0.029 | 0.048 | 0.025 | 0.033 | 0.058 | 0.051 | 0.042 | 0.034 | 0.042 | 0.032 | 0.022 | 0.036 | 0.022 | 0.029 |
| ITT | ||||||||||||||||||||
| Grades K to 8 | ||||||||||||||||||||
| Treatment effect difference | −0.041 | −0.007 | −0.005 | −0.009 | −0.032 | 0.002 | 0.004 | −0.036 | −0.001 | −0.035 | 0.046 | 0.017 | 0.017 | −0.015 | 0.061 | 0.032 | 0.031 | 0.030 | 0.000 | 0.029 |
| SE | 0.054 | 0.045 | 0.037 | 0.027 | 0.039 | 0.029 | 0.018 | 0.028 | 0.017 | 0.021 | 0.045 | 0.037 | 0.033 | 0.025 | 0.031 | 0.021 | 0.016 | 0.026 | 0.015 | 0.019 |
| Grades K to 2 | ||||||||||||||||||||
| Treatment effect difference | −0.025 | −0.054 | −0.081 | −0.066 | 0.041 | 0.012 | −0.015 | 0.056 | 0.027 | 0.029 | −0.070 | −0.107 | −0.122 | −0.129 | 0.059 | 0.023 | 0.007 | 0.052 | 0.016 | 0.037 |
| SE | 0.111 | 0.094 | 0.075 | 0.054 | 0.087 | 0.068 | 0.043 | 0.065 | 0.048 | 0.043 | 0.128 | 0.106 | 0.099 | 0.078 | 0.077 | 0.057 | 0.042 | 0.077 | 0.051 | 0.048 |
| Grades 3 to 8 | ||||||||||||||||||||
| Treatment effect difference | −0.066 | −0.013 | −0.010 | −0.017 | −0.049 | 0.004 | 0.006 | −0.055 | −0.003 | −0.053* | 0.089* | 0.063 | 0.065* | 0.034 | 0.055 | 0.029 | 0.031 | 0.024 | −0.002 | 0.026 |
| SE | 0.061 | 0.050 | 0.040 | 0.028 | 0.048 | 0.035 | 0.022 | 0.037 | 0.022 | 0.025 | 0.044 | 0.037 | 0.030 | 0.022 | 0.034 | 0.026 | 0.018 | 0.027 | 0.018 | 0.023 |
| TOT | ||||||||||||||||||||
| Grades K to 8 | ||||||||||||||||||||
| Treatment effect difference | −0.095 | −0.057 | −0.056 | −0.041 | −0.054 | −0.016 | −0.015 | −0.039 | −0.001 | −0.038 | 0.010 | −0.022 | −0.007 | −0.018 | 0.028 | −0.004 | 0.011 | 0.017 | −0.015 | 0.032 |
| SE | 0.070 | 0.059 | 0.046 | 0.035 | 0.053 | 0.039 | 0.023 | 0.040 | 0.024 | 0.028 | 0.060 | 0.050 | 0.040 | 0.029 | 0.045 | 0.033 | 0.023 | 0.038 | 0.023 | 0.027 |
| Grades K to 2 | ||||||||||||||||||||
| Treatment effect difference | −0.035 | −0.078 | −0.097 | −0.093 | 0.057 | 0.014 | −0.004 | 0.061 | 0.018 | 0.043 | −0.066 | −0.113 | −0.146 | −0.172 | 0.106 | 0.059 | 0.026 | 0.080 | 0.033 | 0.047 |
| SE | 0.140 | 0.111 | 0.097 | 0.067 | 0.105 | 0.076 | 0.054 | 0.076 | 0.051 | 0.051 | 0.154 | 0.127 | 0.115 | 0.095 | 0.094 | 0.069 | 0.051 | 0.089 | 0.053 | 0.057 |
| Grades 3 to 8 | ||||||||||||||||||||
| Treatment effect difference | −0.132 | −0.115 | −0.121* | −0.089* | −0.043 | −0.026 | −0.032 | −0.011 | 0.007 | −0.017 | 0.057 | 0.022 | 0.041 | 0.034 | 0.023 | −0.012 | 0.007 | 0.016 | −0.020 | 0.035 |
| SE | 0.087 | 0.071 | 0.055 | 0.036 | 0.068 | 0.051 | 0.033 | 0.050 | 0.031 | 0.035 | 0.064 | 0.056 | 0.045 | 0.034 | 0.053 | 0.040 | 0.026 | 0.042 | 0.027 | 0.033 |
Note. SE = standard error; IV = instrumental variables; ITT = intention to treat; TOT = treatment on the treated.
p≤ .05.
In sum, the effects obtained from the various analyses appeared to be uniform across the achievement distributions. The t tests between any two quantile estimates were generally statistically nonsignificant. Thus, mCLASS and Acuity effects had consistent effects in various quantiles and did not vary by achievement level. This indicates that these two products do not seem to affect the achievement gap between lower- and higher-achievers. Thus, the hypothesis that interim assessments may benefit some groups of students more than others was not supported with these data. The findings indicate that interim assessments do neither decrease nor increase the achievement gap.
The internal validity of the estimates produced from the IV and ITT analyses is high. The field experiment was conducted without problems and thus the IV and ITT analyses should produce causal estimates. Baseline equivalence of observed school variables was established at various levels of achievement and suggested that random assignment was successful. As a result, it is reasonable to assume unbiased estimation of the treatment effects. The fact that the TOT estimates were very similar to the IV and ITT estimates also suggests that attrition did not compromise the treatment effect estimates.
The external validity of the estimates may be somewhat limited. The sample was drawn from a subset of Indiana public schools that volunteered in the spring of 2010 to implement Indiana’s assessment program in 2010-2011. It is unclear what motivated these schools to volunteer to participate in the experiment that year. Schools’ motivations may differ from year to year and schools that were part of this study may be different from schools that volunteered for the assessment programs in the previous or the following years. Hence, these results should be generalizable to schools that aspired to use technology-supported interim assessments in Indiana in 2010-2011. The generality of the findings beyond that specific group of schools, however, is debatable.
Conclusion
This study demonstrated the utility of quantile regression in point estimation across the entire outcome distribution of scores beyond measures of central location such as the mean. OLS regression and analysis of variance–type models are used recurrently in education, psychology, and the social sciences to estimate average associations of interest or differences among group means. However, one of the caveats of these popular statistical models is that they are not as robust to considerable skewness in the outcome distributions. As a result, typical regression mean estimates may be biased in the presence of extreme outliers located mainly in one of the tails of a distribution of scores. Median regression is a good alternative to typical regression models when asymmetry in a distribution is sizeable, because the median is a more robust index of central tendency. Median regression is a special case of quantile regression, a statistical tool that provides researchers with the opportunity to estimate predictor “effects” at various points in the outcome distribution. In many occasions mean estimation is not enough and does not capture the associations between the predictors and the outcome at various locations of the outcome distribution.
In the field of education, many researchers are interested in identifying school resources and instructional practices that potentially reduce the achievement gap. Quantile regression can be used to examine such research questions. For example, the effects of class size, teacher professional development, or a new mathematics curriculum vis-à-vis a traditional curriculum can be estimated across the achievement distribution of scores using quantile regression. The effects of school resources are estimated in the middle and the lower and upper tails of the achievement distribution and researchers can determine which groups of students (e.g., low-, middle- or high-achievers) benefit more from these resources.
A potential limitation of quantile regression modeling is that the analyses generate many more estimates than the typical regression model. For example, a regression model with five predictors would produce five corresponding regression estimates. In contrast, a quantile regression model that estimates the associations between the five predictors and the outcome at five different quantiles (e.g., 0.10, 0.25, 0.50, 0.75, 0.90) will produce 25 corresponding regression estimates. Nonetheless, as the figures and tables in this study show, a carefully selected representation of the generated output can be summarized efficiently.
In sum, quantile regression is an additional, valuable statistical tool that researchers can use to obtain robust estimates of associations or group differences at different locations in the outcome distribution of scores. It is a good alternative to regression and ANOVA models especially when researchers are interested in examining effects in the lower and upper tails of the outcome distribution of scores.
Footnotes
Declaration of Conflicting Interests: The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This research was supported by a grant from the Institute of Education Sciences, U.S. Department of Education (R305E090005).
ORCID iD: Spyros Konstantopoulos  https://orcid.org/0000-0003-1393-2440
https://orcid.org/0000-0003-1393-2440
References
- Abadie A., Angrist J., Imbens G. (2002). Instrumental variables estimates of the effect of subsidized training on the quantiles of trainee earnings. Econometrica, 70, 91-117. [Google Scholar]
- Angrist J. D., Pischke J.-F. (2009). Mostly harmless econometrics: An empiricist’s companion. Princeton, NJ: Princeton University Press. [Google Scholar]
- Bitler M., Domina T., Penner E., Hoynes H. (2015). Distributional analysis in educational evaluation: A case study from the New York City Voucher Program. Journal of Research on Educational Effectiveness, 8, 419-450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Black P., Wiliam D. (1998). Assessment and classroom learning. Educational Assessment: Principles, Policy and Practice, 5, 7-74. [Google Scholar]
- Boruch R., Weisburd D., Berk R. (2010). Place randomized trials. In Piquero A., Weisburd D. (Eds.), Handbook of quantitative criminology (pp. 481-502). New York, NY: Springer. [Google Scholar]
- Bracey G. W. (2005, June). No child left behind: Where does the money go? (Policy Brief No. EPSL-0506-114-EPRU). Tempe: Education Policy Studies Laboratory, Arizona State University. [Google Scholar]
- Buchinsky M. (1998). Recent advances in quantile regression models: A practical guideline for empirical research. Journal of Human Resources, 33, 89-126. [Google Scholar]
- Cameron A. C., Trivedi P. K. (2010). Microeconometrics using Stata (rev. ed.). College Station, TX: Stata Press. [Google Scholar]
- Datnow A., Hubbard L. (2015). Teachers’ use of assessment data to inform instruction: Lessons from the past and prospects for the future. Teachers College Record, 117, 1-26. [Google Scholar]
- Efron B. (1979). Bootstrap methods: Another look at the jackknife. Annals of Statistics, 7, 1-26. [Google Scholar]
- Frolich M., Melly B. (2010). Estimation of quantile treatment effects with STATA. STATA Journal, 3, 423-457. [Google Scholar]
- Hahn J. (1995). Bootstrapping quantile regression estimators. Econometric Theory, 11, 105-121. [Google Scholar]
- Hao L., Naiman D. Q. (2007). Quantile regression. Thousand Oaks, CA: Sage. [Google Scholar]
- Imbens G., Angrist J. D. (1994). Identification and estimation of local average treatment effects. Econometrica, 62, 467-476. [Google Scholar]
- Indiana State Board of Education. (2006). A long-term assessment plan for Indiana: Driving student learning. Indianapolis, IN: Author. [Google Scholar]
- Koenker R., Bassett G. (1978). Regression quantiles. Econometrica, 46, 33-50. [Google Scholar]
- Kolenikov S. (2010). Resampling variance estimation for complex survey data. Stata Journal, 10, 165-199. [Google Scholar]
- Konstantopoulos S., Li W., Miller S. R., van der Ploeg A. (2016). Effects of interim assessments across the achievement distribution: Evidence from an experiment. Educational and Psychological Measurement, 76, 587-608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konstantopoulos S., Miller S., van der Ploeg A. (2013). The impact of Indiana’s system of Interim assessments on mathematics and reading achievement. Educational Evaluation and Policy Analysis, 35, 481-499. [Google Scholar]
- Parente P. M., Santos Silva J. (2016). Quantile regression with clustered data. Journal of Econometric Methods, 5, 1-15. [Google Scholar]
- Perie M., Marion S., Gong B., Wurtzel J. (2007). The role of interim assessments in a comprehensive assessment system: A policy brief. Dover, NH: National Center for the Improvement of Educational Assessment. [Google Scholar]
- Porter S. R. (2015). Quantile regression: Analyzing changes in distributions instead of means. In Paulsen M. B. (Ed.), Higher education: Handbook of theory and research (Vol. 30, pp. 335-381). Cham, Switzerland: Springer. [Google Scholar]
- Sawchuk S. (2009, May 12). Testing faces ups and downs amid recession. Education Week, 28, pp. 1, 16-17. [Google Scholar]
- Slavin R. E., Cheung A., Holmes G. C., Madden N. A., Chamberlain A. (2013). Effects of a data-driven district reform model on state assessment outcomes. American Educational Research Journal, 50, 371-396. [Google Scholar]
- Tomlinson C. A. (2000). Differentiation of instruction in the elementary grades. Champaign: ERIC Clearinghouse on Elementary and Early Childhood Education, University of Illinois. [Google Scholar]
- White H. (1980). A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica, 48, 817-838. [Google Scholar]


