Abstract
Researchers frequently use machine-learning methods in many fields. In the area of detecting fraud in testing, there have been relatively few studies that have used these methods to identify potential testing fraud. In this study, a technical review of a recently developed state-of-the-art algorithm, Extreme Gradient Boosting (XGBoost), is provided and the utility of XGBoost in detecting examinees with potential item preknowledge is investigated using a real data set that includes examinees who engaged in fraudulent testing behavior, such as illegally obtaining live test content before the exam. Four different XGBoost models were trained using different sets of input features based on (a) only dichotomous item responses, (b) only nominal item responses, (c) both dichotomous item responses and response times, and (d) both nominal item responses and response times. The predictive performance of each model was evaluated using the area under the receiving operating characteristic curve and several classification measures such as the false-positive rate, true-positive rate, and precision. For comparison purposes, the results from two person-fit statistics on the same data set were also provided. The results indicated that XGBoost successfully classified the honest test takers and fraudulent test takers with item preknowledge. Particularly, the classification performance of XGBoost was reasonably good when the response time information and item responses were both taken into account.
Keywords: machine learning, XGBoost, extreme gradient boosting, test security, item compromise, item preknowledge
The interest in utilizing statistical tools to identify fraud in testing has a long history and can be traced back to as early as the 1920s (Bird, 1927). Numerous methods focused on identifying unusual response similarity among examinees, particularly in the context of paper-and-pencil testing (e.g., Angoff, 1974; Bay, 1995; Belov, 2011; Holland, 1996; Maynes, 2005; Saupe, 1960; Sotaridona & Meijer, 2002, 2003; van der Linden & Sotaridona, 2006; Wollack, 1997). However, the response similarity indices may not be useful in dealing with different types of test security issues such as advance knowledge of the items administered in a testing program. Item preknowledge and item compromise have become significant concerns for many testing programs that deliver test content in online and computer-based platforms. Examinees with item preknowledge may have similar response patterns if they all have access to the same set of items and respond consistently with what they have accessed. In such a scenario, one can expect that the response similarity indices will identify some pairs of test takers in this group, and Wollack and Maynes (2017) present an application. However, item preknowledge may be more complicated in reality. Different people may have access to different sets of items, and they may not remember or may misremember what they have seen. In such a case, response similarity indices will be less successful at identifying these people due to lesser degrees of similarity because the response similarity indices are not explicitly designed for detecting item preknowledge. Additionally, response similarity indices do not take into account response time data, which may be a significant source of information in detecting item preknowledge.
Because of the limitations of response similarity indices in identifying item preknowledge, there has been an increasing number of methods specifically developed and proposed in the past decade for identifying examinees with item preknowledge, and Eckerly (2017) provides a detailed review of these methods. Some of these methods use only raw item responses (e.g., Belov, 2014, 2016; Eckerly, Babcock, & Wollack, 2015; McLeod, Lewis, & Thissen, 2003; O’Leary & Smith, 2017; Shu, Henson, & Luecht, 2013; Sinharay, 2017; Wang, Liu, & Hambleton, 2017), while some others use only response time data (e.g., Boughton, Smith, & Ren, 2017; Lee, 2018; Qian, Staniewska, Reckase, & Woo, 2016; van der Linden & Guo, 2008; van der Linden & Krimpen-Stoop, 2003), and a few combine the information from both response time and item response data (e.g., Wang, Xu, Shang, & Kuncel, 2018). A common characteristic of these proposed methods is that they all use traditional psychometric and statistical models to identify individuals with item preknowledge. The goal of the current study is to contribute to this growing literature by exploring the utility of a recently developed state-of-the-art machine-learning algorithm, Extreme Gradient Boosting (XGBoost; Chen & Guestrin, 2016), in identifying examinees with item preknowledge using a real data set. Researchers frequently use machine-learning algorithms in many fields. In the area of test security, there has been relatively few studies that have utilized these methods to identify potential testing fraud (Kim, Woo, & Dickison, 2017; Man, Sinharay, & Harring, 2018; Sotaridona, 2003). In the very first attempt, Sotaridona (2003) explored the performance of Backpropagation, a supervised learning algorithm, in detecting examinees with item preknowledge in a small simulation study. Later, Kim et al. (2017) used another supervised learning algorithm, Market Basket Analysis, for identifying aberrant response patterns. More recently, Man et al. (2018) compared the performance of several data mining algorithms in detecting test fraud. In the current article, XGBoost, a highly effective gradient tree-boosting algorithm as has been demonstrated in many data science competitions, is investigated. Since its development and introduction in 2014, XGBoost became a de facto method for many data science competitions and won a majority of these competitions at the Kaggle platform. In the following section, a technical introduction of how XGBoost performs classification is first provided, and this is followed by a small-scale conceptual illustration. The purpose of this conceptual illustration is to provide readers with a better understanding of how XGBoost actually works. Then, the XGBoost algorithm is applied to a larger data set that was made publicly available by Cizek and Wollack (2017) to assess how XGBoost performs when identifying test takers flagged for potential item preknowledge in this data set. For comparison purposes, the results from two person-fit statistics proposed in the literature (de la Torre & Deng, 2008; Sinharay, 2018) are also provided. Finally, some issues to consider while working with these machine-learning algorithms are discussed, particularly in detecting testing fraud.
Extreme Gradient Boosting
Let denote a vector of observed values for the ith observation on j features, where and , and is the value of the target outcome for the ith observation. A tree ensemble model is specified to predict the outcome using additive functions as
| (1) |
where T is the number of trees, and is the corresponding tree structure. Each tree is defined by a function q that maps an observation to the lth leaf, where and a weight (w) on each leaf is defined as
| (2) |
Once the tree structure is developed and the weights are estimated, a predicted outcome can be obtained by first assigning an observation to a leaf on each tree based on the values of the feature set and then summing the weights on the corresponding leaves.
The algorithm optimizes the following objective function to develop a number of trees:
| (3) |
where is a differentiable loss function to measure the distance between the observed and predicted outcomes, and Ω is a regularization term to control the complexity of the model in order to avoid overfitting. In the context of a classification problem with two outcomes as in this study, can be defined as a logistic loss function:
| (4) |
Regularization term in Equation (3) is defined as
| (5) |
where L is the number of leaves in the tree structure, and γ and λ are the parameters to penalize the complexity of the tree. The term λ||w||2 in the equation represents a form of L2 regularization on the leaf weights.1
The objective function in Equation (3) is optimized in an additive manner. This procedure starts with a constant prediction, and a new tree that minimizes the loss function is searched and added at each iteration as the following:
Therefore, the objective function at the iteration t can be written as
| (6) |
Chen and Guestrin (2016) used a second-order Taylor approximation to quickly optimize this objective function. The second-order Taylor approximation of is
| (7) |
where and are, respectively, the first- and second-order gradient statistics on the loss function with respect to the predicted value in the previous step, , and they can be computed as
| (8) |
| (9) |
For a fixed tree structure at iteration t, Chen and Guestrin (2016) showed that the optimal weight on the lth leaf could be computed by
| (10) |
and whether or not a particular tree structure improves the prediction can be checked by computing a gain score using the equation
| (11) |
where represents a set of observations assigned to the lth leaf.
Equation (11) is used to evaluate every potential split when developing trees and adding new branches to the trees. The XGBoost algorithm starts from a single leaf for each structure and keeps adding branches as long as a split with a positive gain is found. In the next section, a detailed numerical illustration is provided to present a better conceptual understanding of how XGBoost grows the tree structures and performs classification using a small data set.
A Numerical Illustration of the XGBoost Algorithm
A small data set is available in Table 1 for 30 subjects with two feature variables (RT1 and RT2) and one target variable (y). The feature variables represent the response time of each subject for two test items, and the target variable represents whether or not the subject had item preknowledge (0 = No, 1 = Yes). The goal is to develop a tree structure for predicting the target outcome from the two feature variables. These are all the inputs that a user needs to provide to the XGBoost algorithm. For the sake of demonstration, the values of λ = 1.5 and γ = 1 are used as the regularization parameters for this illustration. The rest of the columns in Table 1 will be explained in the remaining of this section.
Table 1.
A Small Data Set With 30 Observations and Their Values on Two Feature Variables and One Target Variable and the Summary of First Tree Iterations From XGBoost Search.
| Iteration 1 (Tree 1) |
Iteration 2 (Tree 2) |
Iteration 3 (Tree 3) |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RT1 | RT2 | y | g (1) | h (1) | w (1) | g (2) | h (2) | w (2) | g (3) | h (3) | w (3) | Pr | |||||
| 1 | 114 | 36 | 1 | 0 | −0.5 | 0.25 | −0.15 | −0.15 | −0.54 | 0.25 | −0.30 | −0.45 | −0.61 | 0.24 | 0.31 | −0.14 | .46 |
| 2 | 92 | 121 | 1 | 0 | −0.5 | 0.25 | −1.04 | −1.04 | −0.74 | 0.19 | −0.30 | −1.34 | −0.79 | 0.16 | −0.43 | −1.76 | .15 |
| 3 | 49 | 24 | 1 | 0 | −0.5 | 0.25 | 0.80 | 0.80 | −0.31 | 0.21 | −0.30 | 0.50 | −0.38 | 0.23 | 0.31 | 0.81 | .69 |
| 4 | 58 | 30 | 1 | 0 | −0.5 | 0.25 | −0.15 | −0.15 | −0.54 | 0.25 | −0.30 | −0.45 | −0.61 | 0.24 | 0.31 | −0.14 | .46 |
| 5 | 40 | 17 | 1 | 0 | −0.5 | 0.25 | 0.80 | 0.80 | −0.31 | 0.21 | −0.30 | 0.50 | −0.38 | 0.23 | 0.31 | 0.81 | .69 |
| 6 | 67 | 66 | 1 | 0 | −0.5 | 0.25 | −1.04 | −1.04 | −0.74 | 0.19 | −0.30 | −1.34 | −0.79 | 0.16 | 0.31 | −1.03 | .26 |
| 7 | 30 | 79 | 1 | 0 | −0.5 | 0.25 | −1.04 | −1.04 | −0.74 | 0.19 | 0.47 | −0.57 | −0.64 | 0.23 | 0.31 | −0.26 | .44 |
| 8 | 19 | 14 | 1 | 0 | −0.5 | 0.25 | 0.80 | 0.80 | −0.31 | 0.21 | 0.47 | 1.27 | −0.22 | 0.17 | 0.31 | 1.58 | .83 |
| 9 | 33 | 8 | 1 | 0 | −0.5 | 0.25 | 0.80 | 0.80 | −0.31 | 0.21 | 0.47 | 1.27 | −0.22 | 0.17 | 0.31 | 1.58 | .83 |
| 10 | 172 | 38 | 1 | 0 | −0.5 | 0.25 | −0.15 | −0.15 | −0.54 | 0.25 | −0.30 | −0.45 | −0.61 | 0.24 | 0.31 | −0.14 | .46 |
| 11 | 55 | 37 | 0 | 0 | 0.5 | 0.25 | −0.15 | −0.15 | 0.46 | 0.25 | −0.30 | −0.45 | 0.39 | 0.24 | 0.31 | −0.14 | .46 |
| 12 | 103 | 79 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | −0.30 | −1.34 | 0.21 | 0.16 | 0.31 | −1.03 | .26 |
| 13 | 68 | 117 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | −0.30 | −1.34 | 0.21 | 0.16 | −0.43 | −1.76 | .15 |
| 14 | 194 | 17 | 0 | 0 | 0.5 | 0.25 | −0.15 | −0.15 | 0.46 | 0.25 | −0.30 | −0.45 | 0.39 | 0.24 | 0.31 | −0.14 | .46 |
| 15 | 68 | 84 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | −0.30 | −1.34 | 0.21 | 0.16 | −0.43 | −1.76 | .15 |
| 16 | 48 | 127 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | −0.30 | −1.34 | 0.21 | 0.16 | −0.43 | −1.76 | .15 |
| 17 | 48 | 200 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | −0.30 | −1.34 | 0.21 | 0.16 | −0.43 | −1.76 | .15 |
| 18 | 61 | 47 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | −0.30 | −1.34 | 0.21 | 0.16 | 0.31 | −1.03 | .26 |
| 19 | 37 | 155 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | −0.30 | −1.34 | 0.21 | 0.16 | −0.43 | −1.76 | .15 |
| 20 | 58 | 84 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | −0.30 | −1.34 | 0.21 | 0.16 | −0.43 | −1.76 | .15 |
| 21 | 139 | 97 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | −0.30 | −1.34 | 0.21 | 0.16 | −0.43 | −1.76 | .15 |
| 22 | 99 | 84 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | −0.30 | −1.34 | 0.21 | 0.16 | −0.43 | −1.76 | .15 |
| 23 | 47 | 50 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | −0.30 | −1.34 | 0.21 | 0.16 | 0.31 | −1.03 | .26 |
| 24 | 41 | 54 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | −0.30 | −1.34 | 0.21 | 0.16 | 0.31 | −1.03 | .26 |
| 25 | 29 | 90 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | 0.47 | −0.57 | 0.36 | 0.23 | −0.43 | −0.99 | .27 |
| 26 | 117 | 31 | 0 | 0 | 0.5 | 0.25 | −0.15 | −0.15 | 0.46 | 0.25 | −0.30 | −0.45 | 0.39 | 0.24 | 0.31 | −0.14 | .46 |
| 27 | 44 | 104 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | −0.30 | −1.34 | 0.21 | 0.16 | −0.43 | −1.76 | .15 |
| 28 | 34 | 62 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | −0.30 | −1.34 | 0.21 | 0.16 | 0.31 | −1.03 | .26 |
| 29 | 83 | 20 | 0 | 0 | 0.5 | 0.25 | −0.15 | −0.15 | 0.46 | 0.25 | −0.30 | −0.45 | 0.39 | 0.24 | 0.31 | −0.14 | .46 |
| 30 | 64 | 57 | 0 | 0 | 0.5 | 0.25 | −1.04 | −1.04 | 0.26 | 0.19 | −0.30 | −1.34 | 0.21 | 0.16 | 0.31 | −1.03 | .26 |
| Loss function | 20.79 | 15.15 | 14.34 | 13.56 | |||||||||||||
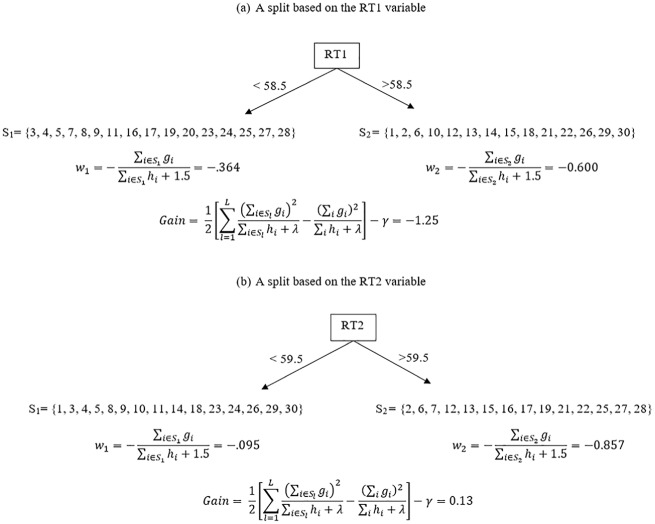
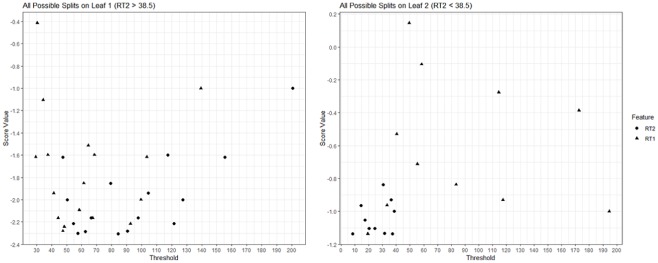
First, the algorithm starts with an initial guess (. To develop the first tree, the algorithm computes the first- and second-order gradient statistics (g(1) and h(1)) based on Equations (8) and (9) given y and . Then, the algorithm searches for the best split among all possible splits based on these two features. For instance, Figure 1 provides two possible splits of observations based on RT1 and RT2 with their respective gain scores and leaf weights computed using Equations (10) and (11). The gain score for the first split is negative, thus indicating that this split would not improve our prediction. On the other hand, the gain score for the second split is positive, thus indicating that this split would improve our prediction. The algorithm computes the gain score for each possible split, and then finds the best one. Figure 2 provides the gain score for all potential splits. The best split was based on the threshold value of 38.5 on the RT2 feature, yielding a gain score of 3.512. Therefore, the first step to develop the first tree is to divide the observations into two leaves, observations with the RT2 values larger than 38.5 and observations with the RT2 values smaller than 38.5. Then, for the observations on each leaf, the algorithm again computes a gain score for all potential splits based on RT1 and RT2 to see if there is a new branch that can be added with a positive gain. Figure 3 provides the gain scores for all possible splits based on RT1 and RT2 using the observations on both leaves of the first split. As it can be seen, there is only one split that actually provides a positive gain. This is a split based on the threshold value of 49.5 on the RT1 feature on the second leaf (RT2 < 38.5), and it yields a gain score of 0.148. If the depth of the tree is limited by two and the algorithm stops here, our resulting structure for the first tree is presented in Figure 4. The depth of the tree can be increased, and the algorithm can be forced to search additional branches. The greater the depth is, the higher the level of interactions between features can be accounted for. However, the algorithm is stopped here for the sake of simplicity. Based on the first tree structure in Figure 4, there are three leaves and the weight for each leaf is also computed based on Equation (10). Once these weights are estimated, the assigned weight for each observation can be added to our initial prediction () and the new prediction () at the end of Iteration 1 can be obtained. At the bottom of Table 1, the value obtained from the loss function is also reported for these new predictions. As seen, the loss function value for our constant predictions was 20.79, but now it decreased to 15.15.
Figure 1.
Two sample splits of observations based on the RT1 and RT2 features and their respective leaf weights and gain scores.
Figure 2.
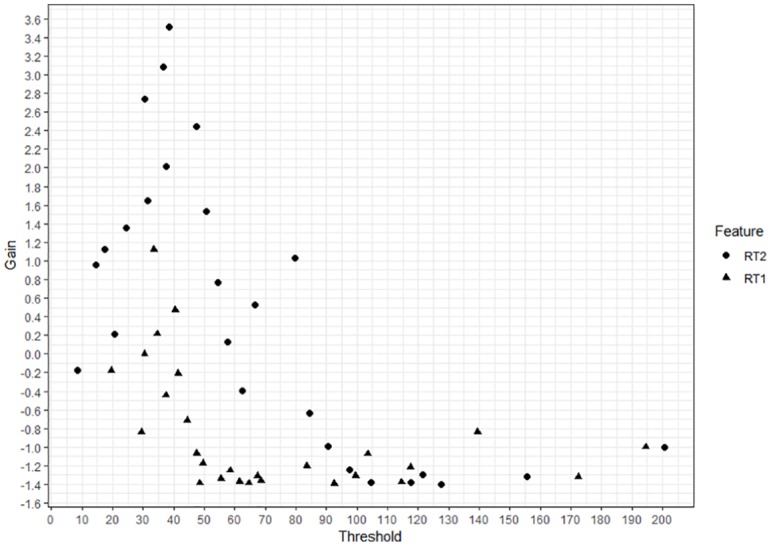
Gain scores of all potential first splits in Tree 1 based on RT1 and RT2 features.
Figure 3.
Gain scores for all possible splits on the first and second leaves of the first split in Tree 1.
Figure 4.
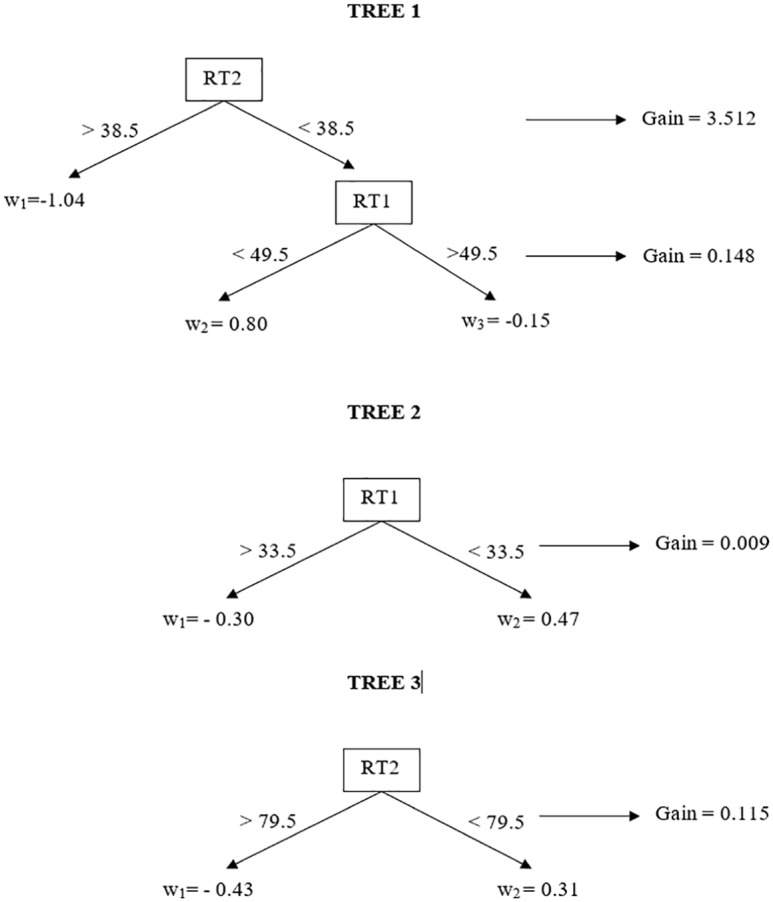
Tree structures developed after three iterations as a result of the XGBoost algorithm.
This process continues until a certain predetermined number of trees is developed or until no tree structure with a positive gain score is found. Additional columns in Table 1 provide the new gradient statistics (g(2) and h(2)) based on as Iteration 2 starts. Following a similar process, the algorithm again computes the gain scores for all possible splits based on RT1 and RT2 using g(2) and h(2). The best split is now based on the threshold value of 33.5 on the RT1 feature, yielding a gain score of 0.009. Therefore, in the second tree, the observations are divided into two leaves, observations with the RT1 values larger than 33.5 and observations with the RT1 values smaller than 33.5. None of the further splits on the leaves of the first split in the second tree yielded a positive gain, and so the algorithm stops and computes the weights for the leaves of the first split in the second tree. Then, the assigned weight for each observation to our predictions from the first iteration () can be added and the new prediction () at the end of Iteration 2 can be obtained. The loss function value now decreased to 14.34 at Iteration 2. In Iteration 3, the new gradient statistics are computed (g(3) and h(3)) and the best split is found to be based on the threshold value of 79.5 on the RT2 feature, yielding a gain score of 0.115. None of the further splits on the leaves of the first split on the third tree yielded a positive gain, and Iteration 3 ended. The new weights for each observation were added to the predictions from Iteration 2 and the new predictions () were obtained. The loss function value at the end of Iteration 3 is 13.56. The whole search process ended at Iteration 3 because no further split in Iteration 4 provided a positive gain. The whole developed tree structure can be seen in Figure 4. In the last column of Table 1, the predicted probabilities for the observations in the training data set were also provided after transforming from logit to probability.
If a new observation comes with a different set of values on RT1 and RT2, the probability can be predicted using this developed tree structure. For instance, suppose a student’s response times on the first item (RT1) and second item (RT2) are 80 and 40, respectively. This student would be in Leaf 1 on Tree 1 (w = −1.04), in Leaf 1 on Tree 2 (w = −0.30), and in Leaf 2 on Tree 3 (w = 0.31). Therefore, the sum of the corresponding leaf weights is equal to −1.03 on the logit scale, yielding a value of 0.26 after transformation, which is the probability that a student with an RT1 equal to 80 and an RT2 equal to 40 has item preknowledge. Conversely, suppose a student’s values for RT1 and RT2 are 25 and 15, respectively. This student would be in Leaf 2 on Tree 1 (w = 0.80), in Leaf 2 on Tree 2 (w = 0.47), and in Leaf 2 on Tree 3 (w = 0.31). The sum of the corresponding leaf weights for this student is equal to 1.58, yielding a probability of 0.83 for item preknowledge. Notice that the smaller the response time that a student has, the higher the probability of item preknowledge that the tree ensemble model predicts.
As one can imagine, this search process becomes exhaustive and computationally very demanding when the number of features and sample size increase. XGBoost applies a number of novel techniques to make this search process manageable, such as an approximate exact greedy algorithm, a weighted quantile sketch, sparsity-aware split finding, the use of parallel computing, cache optimization, and distributed computing. A more comprehensive treatment of the technical details can be found in Chen and Guestrin (2016), Mehta et al. (2018), and Nielsen (2016).
A Practical Guide to Identify Examinees With Item Preknowledge Using XGBoost
Description of the Real Data Sets
The data set used in the current study comes from Cizek and Wollack (2017) and includes two test forms with sample sizes of 1,636 and 1,644 from a single year of testing for a computer-based program. Each test form contains 170 operational test items, and there are 87 common items between the two test forms. The unique characteristic of this data set is that it is known to include examinees who engaged in fraudulent test behavior, such as illegally obtaining live test content before the exam. There are 94 candidates for both forms who were flagged by the testing company as likely cheaters. To maximize the information used by the XGBoost model, these two data sets were merged into a single big data set with 3,280 examinees and 253 operational items. In this combined data set, each examinee responded to 170 items, while the responses were missing to the remaining form-specific 83 items. Out of 3,280 examinees, 94 candidates were flagged as likely cheaters, while the remaining candidates were treated as honest examinees. The whole data set is first randomly divided into two subsets: a training data set and a test data set. The training data set included 2,624 candidates (80%), and the test data set included 656 candidates (20%). Table 2 provides a summary of the frequencies for the test and training data sets regarding the flagged and nonflagged individuals.
Table 2.
The Number of Flagged and Nonflagged Individuals for the Training and Test Data Sets.
| Flagged individuals | Nonflagged individuals | Total | |
|---|---|---|---|
| Training data set | 77 | 2,547 | 2,624 |
| Test data set | 17 | 639 | 656 |
| Total | 94 | 3,186 | 3,280 |
Both data sets included the dichotomous responses (correct/incorrect), nominal responses (A, B, C, and D), and response time information on each item for each examinee. To explore the relative contribution of using different types of information on the predictive power of the XGBoost model, both the training and test data sets were structured in four different ways using (a) only dichotomous item responses, (b) only nominal item responses, (c) both dichotomous item responses and response times, and (d) both nominal item responses and response times. The nominal responses are categorical and, therefore, are recoded using a procedure known as one hot encoding before model training. For instance, if the nominal response vector for an examinee to three hypothetical items is {A,D,C}, then this response vector is transformed into a numerical vector as {1,0,0,0,0,0,0,1,0,0,1,0}. The first four elements of the transformed vector {1,0,0,0} correspond to nominal response A for the first item. The second four elements of the transformed vector {0,0,0,1} correspond to nominal response D for the second item, and the last four elements of the transformed vector {0,0,1,0} correspond to nominal response C for the third item. The four different types of data sets that are used to train the four different XGBoost models in the current study are shown in Table 3 for a hypothetical three-item test.
Table 3.
Four Different Type of Data Sets Used in Training Different XGBoost Models for a Hypothetical Three-Item Test.
| Input features (predictors) | Target output (1 = flagged, 0 = nonflagged) | |
|---|---|---|
| Dichotomous response data | ||
| Nominal response data | ||
| Dichotomous response data + Response time data | ||
| Nominal response data + Response time data |
Model Training
In the context of the item preknowledge that is addressed in this article, the problem for the XGBoost model should be categorized as a classification problem. Assuming that a training data set is available with item responses and response times as input features and with a target variable for each examinee (flagged or nonflagged), XGBoost models can be trained to map the patterns in the input features to the target variable. In this case, it could be assumed that obtaining the test content prior to exam and possibly studying and memorizing these items gave an advantage to the flagged individuals such that they are more likely to give a correct response to the items they had accessed with a much shorter response time. Therefore, the data patterns for these individuals on the items they had access before should be different from the data patterns for items they had not seen. In the model training phase, XGBoost can learn from these different patterns using the information in the training data set. Once the model is trained and a tree ensemble model is developed, the model can be used to predict the probability of outcome based on the same input features for individuals in the test data set or for any future observation.
Training an XGBoost model is a complicated process due to the large number of parameters that one can control during the optimization process, and there are no straightforward guidelines. Here, some essential parameters to consider and the approach used for the current study are briefly introduced.
η is a learning rate parameter representing the degree of shrinkage for the leaf weights. It can take values from 0 to 1. In the above numerical illustration, it is assumed that η = 1. Instead, one could multiply the weights by a smaller constant when updating the predictions at each iteration, thus yielding a smaller improvement in the model fit rather than full optimization. This typically helps prevent overfitting.
γ is a regularization parameter functioning as a kind of Lagrangian multiplier that controls the complexity. The higher the value is, the higher the regularization. It can take values from 0 to ∞, where 0 indicates no regularization.
α and λ are the L1 and L2 regularization terms for the leaf weights, respectively. These two terms function as penalization terms for the complexity of the model.
T is the maximum number of trees (iterations) that the algorithm continues to develop.
Maximum depth is the maximum depth of a tree. The higher the value is, the more complex the model and the higher order of interactions the model can capture.
h min is the minimum sum of the second-order gradient statistics on a leaf. If the sum of the second-order gradient statistics on a leaf becomes less than this, the algorithm stops further partitioning. This parameter is also used to control overfitting, and higher values prevent a model from learning relations that might be highly specific to a particular sample.
Maximum δ step is particularly useful for classification problems when the categories are highly imbalanced, and setting this to a finite number (e.g., 1) helps convergence if the goal is to predict the true probability instead of rank ordering the prediction.
Scaling positive weights is also a parameter to help the convergence by controlling the balance of positive and negative weights for unbalanced classes. A typical suggestion is to use a value obtained by dividing the sum of the negative cases (nonflagged individuals) by the sum of the positive cases (flagged individuals).
A typical application in machine-learning algorithms is known as “parameter tuning,” which is a mysterious art in machine-learning practice. Each of these parameters can take an infinite number of values, and one can run an extensive grid search to find the optimal combination of values for all the parameters in an ideal world with a supercomputer. However, this is not realistic, particularly if the size of the training data set is very large. Instead, the size of the search can be significantly reduced and made manageable when these parameters are tuned one by one or in pairs. Although this approach may not give the best solution, all one needs to do is to find a combination that is good enough. This tuning procedure is implemented in the training data set with cross-validation (e.g., 10-fold). Once the parameters are tuned to give the best performance for the training data using cross-validation, the final model is calibrated using the optimized values for all parameters. In the current study, a gradual step-by-step approach is applied when tuning the parameters. At each step, a particular parameter or a pair of parameters were tuned while fixing all other parameters at their default values or their tuned values in a previous step. I adopted this approach after reading suggestions on several posts written by people who successfully used the XGBoost in practice (e.g., see Jain, 2016; Lemagnen, 2018; Zhang, 2015). The steps that were used in the parameter tuning procedure are summarized in Table 4, and the values that were used in the final calibration of the XGBoost models are given in Table 5.
Table 4.
Parameter Tuning Procedure.
| No. of iterations (T) | Parameters |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| η | h min | max_depth | γ | Max δ step | λ | α | Scale positive weight | ||
| Parameter range | [0,1] | [0,Inf] | [0,Inf] | [0,Inf] | [0,Inf] | [0,Inf] | [0,Inf] | [0,Inf] | |
| Steps | |||||||||
| 1: Tune η | 1,000 | {0, 0.01, . . ., 0.3} | 1 | 6 | 0 | 1 | 1 | 0 | 1 |
| 2: Tune max_depth and hmin | 1,000 | Step 1 value | {0, 0.05, . . ., 1} | {3, 4, . . ., 30} | 0 | 1 | 1 | 0 | 1 |
| 3: Tune γ | 1,000 | Step 1 value | Step 2 value | Step 2 value | {0, 0.1, . . ., 1} | 1 | 1 | 0 | 1 |
| 4: Tune max δ step | 1,000 | Step 1 value | Step 2 value | Step 2 value | Step 3 value | {0, 0.1, . . ., 3} | 1 | 0 | 1 |
| 5: Tune λ | 1,000 | Step 1 value | Step 2 value | Step 2 value | Step 3 value | Step 4 value | {0, 0.1, . . ., 1.5} | 0 | 1 |
| 6: Tune α | 1,000 | Step 1 value | Step 2 value | Step 2 value | Step 3 value | Step 4 value | Step 5 value | {0, 0.1, . . ., 1} | 1 |
| 7: Tune scale positive weight | 1,000 | Step 1 value | Step 2 value | Step 2 value | Step 3 value | Step 4 value | Step 5 value | Step 6 value | {0, 0.1, . . ., 3} |
| Final model calibration | 10,000 | Step 1 value | Step 2 value | Step 2 value | Step 3 value | Step 4 value | Step 5 value | Step 6 value | Step 7 value |
Note. Inf = infinity.
Table 5.
Parameters Used in the Final Calibration Model After the Tuning Procedure for Each Different Data Set.
| No. of iterations (T) | Parameters |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| η | h min | max_depth | γ | Max δ step | λ | α | Scale positive weight | ||
| Dichotomous responses | 10,000 | 0.01 | 0.25 | 5 | 0 | 1.5 | 1.0 | 0.0 | 1 |
| Nominal responses | 10,000 | 0.01 | 0.60 | 7 | 0 | 1.0 | 1.0 | 0.0 | 1 |
| Dichotomous responses + Response time | 10,000 | 0.01 | 0.00 | 5 | 0 | 1.0 | 1.5 | 0.0 | 1 |
| Nominal responses + Response time | 10,000 | 0.05 | 1.20 | 3 | 0 | 0.5 | 0.6 | 0.3 | 1 |
There are two important parameters that are not considered in the current study: sampling by rows and sampling by columns. Both parameters can take values from 0 to 1 and indicate the proportion of the data that should be used for growing trees during the optimization process. For instance, setting both parameters to 0.7 would mean that the algorithm will randomly select 70% of the observations (rows) and 70% of the features (columns) in the data set at each iteration to use in order to reduce the chance of overfitting by introducing randomness in the learning procedure. However, the values for both parameters in the current study were set to 1, thus indicating that no subsampling occurs for rows and columns and that all data are used. This is to ensure the reproducibility of the results presented in the current article. By tuning these two parameters, the given results in the current study could be improved while not necessarily being able to be precisely replicated by anyone else due to the random nature of the sampling for both the columns and rows during model training. Therefore, these two parameters were set to 1 and not optimized. I used the available xgboost package in R (Chen et al., 2018) for all analyses.
Results From the XGBoost Analysis
Each of the four different XGBoost models are trained using different data sets with different sets of features, as described in Table 3. Once they are calibrated using the tuned parameters on the training data sets, these models are used to predict the outcome for examinees in the test data set. Since the problem in the current study is a classification problem (0 = honest, 1 = cheater), when the XGBoost model is used to predict the outcomes in the test data set, it computes and assigns a probability-like score between 0 and 1 for each individual based on the pattern of input features of these examinees. The higher this probability-like score is, the more likely the predicted outcome is 1 (the individual is flagged as a cheater). Since the assigned labels in the test data are known for individuals, the probability-like scores can be compared with the actual assigned binary labels to evaluate the performance of these models. While examining the performance of these four models, the following outcome measures were used: the area under the receiver operating characteristic curve (AUROC), the true-positive rates (power), and the positive predictive value (precision) at a certain threshold level that is determined based on a fixed level of false-positive rates.
Table 6 shows the overall performance of these models based on AUROC. The AUROC is conceptually a measure of how well the two classes (flagged and nonflagged individuals in the test data) are separated based on the estimated probability-like scores. Not surprisingly, the model that makes the use of only nominal responses is more powerful than the model that uses only dichotomous responses. The additional contribution of the response time information to the predictive power of the model for both dichotomous and nominal responses is very obvious and important. When the response time information is included in the model to predict whether an examinee in the test data set had item preknowledge, the AUROC exceeded .9, which indicates reasonably good predictive power.
Table 6.
The Predictive Performance of Four XGBoost Models on the Test Data Set Based on Area Under the Receiver Operating Characteristic Curve (AUROC).
| AUROC | |
|---|---|
| Dichotomous responses | 0.636 |
| Nominal responses | 0.785 |
| Dichotomous responses + Response time | 0.914 |
| Nominal responses + Response time | 0.930 |
Another way to evaluate the performance of these models is to look at their true-positive rates at certain levels of false-positive rates. As mentioned before, once the final calibrated XGBoost models are used to predict the outcomes for the individuals in the test data set, it computes and assigns a predicted probability-like score between 0 and 1 for each examinee. To predict the designated class, users have to decide the cutoff score to be used. For instance, Figure 5 shows the predicted probability-like scores for all candidates in the test data set (N = 656) for one of these models and three hypothetical cutoff scores (horizontal lines in the plot). The true-positive rate would be the number of black triangles above the horizontal line divided by 17, which is the total number of candidates flagged by the testing agency in the test data set (assumed to be the fraudulent test takers). The false-positive rate would be the number of gray circles above the horizontal line divided by 656, which is the number of candidates not flagged by the testing agency (assumed to be the honest test takers) in the test data set. The cutoff score choice depends on how conservative one would prefer to be to avoid falsely identified honest examinees, while identifying as many as possible as true fraudulent test takers. In most of the studies in the test security literature, researchers considered false-positive rates of 0.01 and 0.05 while evaluating the performance of traditional statistical indices. Therefore, the cutoff levels such that the false-positive rate would be as close to 0.01 and 0.05 were identified for each model and then the outcome measures were computed at these cutoff scores to compare the four different XGBoost models. These numbers are presented in Table 7. The XGBoost model that uses the nominal responses and response time information successfully identified 10 and 13 candidates out of the 17 candidates previously flagged by the testing agency when the false-positive rate is 0.011 and 0.05, respectively. Another measure reported in Table 7 is precision. Precision is computed as the proportion of the number of truly identified examinees to the number of all identified individuals. Precision is important as it measures the degree of accuracy among all identified individuals. As can be seen from Table 7, the precision was equal to 58.8% at the false-positive rate of 0.01, a level very likely to be used in practice.
Figure 5.
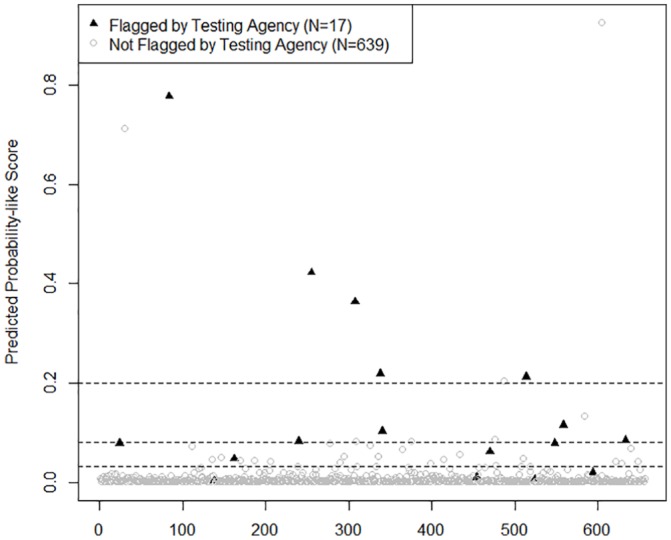
The predicted probability-like score from an XGBoost model for candidates flagged and nonflagged by the testing agency.
Table 7.
True-Positive Rates of Four XGBoost Models on the Test Data Set at Two Different Levels of False-Positive Rates (0.01 and 0.05).
| Model | Cutoff score | No. of falsely identified examinees (false-positive rate) | No. of truly identified examinees (true-positive rate) | Precision |
|---|---|---|---|---|
| False-positive rate of 0.01 | ||||
| Dichotomous responses | 0.053 | 7 (1.1%) | 4 (23.5%) | 36.3% |
| Nominal responses | 0.052 | 7 (1.1%) | 6 (35.3%) | 46.1% |
| Dichotomous responses + Response time | 0.043 | 7 (1.1%) | 7 (41.1%) | 50.0% |
| Nominal responses + Response time | 0.078 | 7 (1.1%) | 10 (58.8%) | 58.8% |
| False-positive rate of 0.05 | ||||
| Dichotomous responses | 0.010 | 32 (5.0%) | 5 (29.4%) | 13.5% |
| Nominal responses | 0.021 | 32 (5.0%) | 8 (47.0%) | 20.0% |
| Dichotomous responses + Response time | 0.014 | 32 (5.0%) | 12 (70.5%) | 35.3% |
| Nominal responses + Response time | 0.032 | 32 (5.0%) | 13 (76.5%) | 28.8% |
Interpretation of the XGBoost Predictions
A common concern of using methods such as XGBoost in practice is their black-box nature. The results of these tree ensemble models can be easily explained and interpreted when the model has a small number of trees and each tree has a small depth, such as the one used for the numerical illustration in this article. However, as the number of trees and/or the depth of trees increases, the model becomes so complex that it is very difficult to explain why a certain outcome is produced as a result of the input features. This black-box nature of these models can bring many challenges with regard to describing the outcome of these models to people who are affected or to legal entities. That being said, the readers should keep in mind that there are some efforts to make the results of these models more interpretable (Foster, 2017), and there may be more tools made available for practitioners in the future. In this section, I provide some examples of how to visualize the results from XGBoost to get a better understanding of its predictions using the xgboostExplainer package in R.
After fitting an XGBoost model, the first thing one can look at is the relative importance of features in the predictive model. Suppose one considers the most successful model that used both response time and nominal item responses as predictive features. Note that there were 1,265 features in this model as a result of one hot encoding of 253 items with four nominal categories and a response time variable for each of 253 items. Figure 6 provides the most important 15 features in this model. On the x-axis of Figure 6, importance score indicates how valuable a feature is in the construction of boosted trees within the model. The importance score is calculated for a single tree by the amount that each attribute split point improves the performance (as measured by gain weighted by the number of observations in each leaf) and then averaged across all trees within the model. On the y-axis, there are labels for features. For instance, the most important feature turns out to be the response time for Item 58 in Form B (B58.RT), and the second most important feature is the response time for Item 30 in Form A (A30.RT). This plot is important as it helps contextualize why a certain individual’s predicted probability is high. For instance, the model predicted a probability of 0.804 for Examinee 84 to have item preknowledge. Suppose one wants to understand why Examinee 84 has a high probability of item preknowledge. Figure 7 provides a breakdown of this prediction into the impact of each individual feature on the logit scale. The first bar is the intercept displaying the logit value of −3.71 with a corresponding probability of 0.024. The second bar indicates that the base prediction changes by 1.28 based on the response time of Examinee 84 on Item 58 in Form B and the new prediction is now −2.43 with a corresponding probability of 0.081. Similarly, the third bar indicates that the prediction changes by 0.6 based on the response time of Examinee 84 on Item 145 in Form A and the new prediction becomes −1.83 with a corresponding probability of 0.138. This continues until each feature makes a negative or positive contribution to the prediction based on Examinee 84’s response data, and the final prediction for Examinee 84 is 1.41 corresponding to a probability of 0.804.
Figure 6.
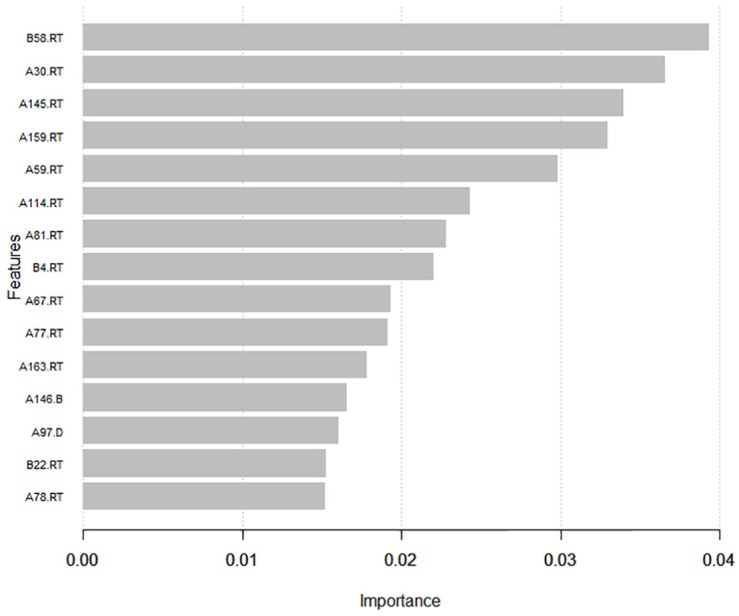
The most important 15 features from the predictive model that used both response time and nominal item responses as features.
Figure 7.
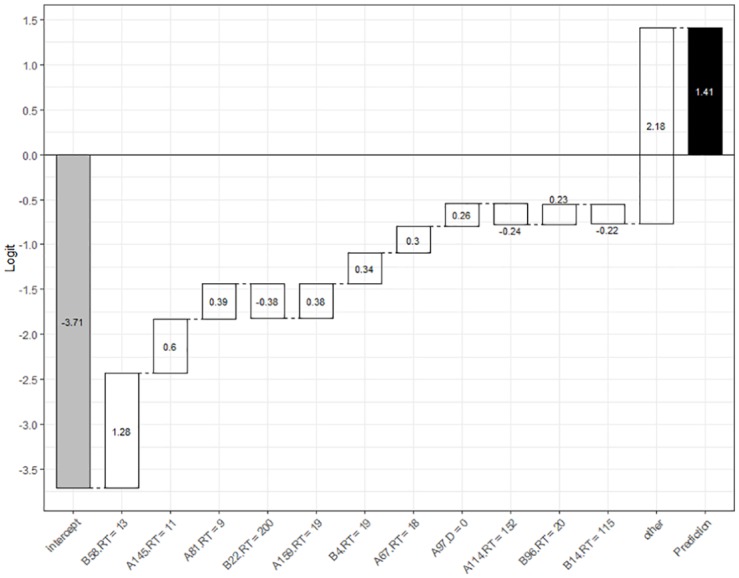
Breakdown of model prediction for Examinee 84 into the impact of each individual feature on the logit scale.
Notice that the short response time on Items 4, 58, and 96 in Form B and Items 67, 81, 145, and 159 in Form A makes a positive contribution that increases the probability, while long response time on Items 14 and 22 in Form B and Item 114 in Form A makes a negative contribution that decreases the probability. It is no coincidence that most of these features can actually be seen in Figure 6 among the most important 15 features. Only features with an absolute impact larger than .2 are displayed in Figure 7 for the sake of simplicity. The collective contribution of all other features is displayed as “other” on the x-axis. In addition, one can even show how a certain value of a feature affects the logit as shown in Figure 8 for Item 58 in Form B. Each point in Figure 8 is an examinee in the test data set. The x-axis represents the response time of the examinees in the test data set for Item 58 in Form B and the y-axis represents how much the predicted logit changes for each data point. This kind of plotting can help better understand how the model works in general and how and why a certain predicted value is computed for a particular examinee.
Figure 8.
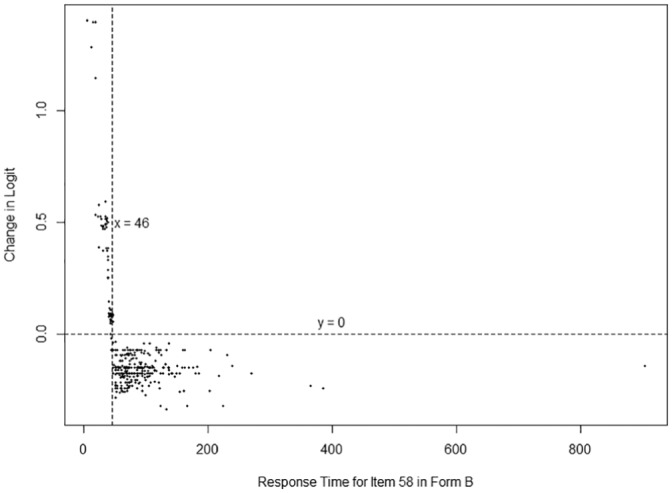
The relationship between the response time for Item 58 in Form B and the change in logit.
Results From Alternative Methods
In this section, the results from more traditional person-fit statistics were provided to identify the individuals with potential item preknowledge in the test data set. Particularly, two item response theory (IRT)–based person-fit indices were considered, one based on the response time (Sinharay, 2018) and the other based on the item responses (de la Torre & Deng, 2008). Sinharay (2018) recently proposed a new person-fit statistic based on van der Linden’s (2006) lognormal response time model. In this model, it is assumed that the conditional distribution of the log of response times is normal.
| (12) |
where is the latent working speed parameter of the ith person, and and are the time intensity and time discrimination parameters for the jth item, respectively. Given the known item parameters, van der Linden (2006) showed that the maximum likelihood estimate of can be obtained by
| (13) |
Sinharay (2018) derived and showed that the sum of the residuals, , has a chi-squared distribution with J − 1 degrees of freedom, where the residual term for the ith person on the jth item is defined as
| (14) |
To compute this statistic for the individuals in the test data set, the response time model in Equation (12) was first fit to the training data set, and time intensity and time discrimination parameters were estimated using Stan (Stan Development Team, 2018). Then, the maximum likelihood estimates for all individuals in the test data set were estimated based on Equation (13) given the estimated item parameters and the sum of the squared residuals were computed for each individual.
A procedure to imitate supervised learning was used for the person-fit index to make a fair comparison with XGBoost. In this procedure, a threshold value for the sum of the squared residuals was identified such that the proportion of false positives (Type I error rate) is equal to 0.01. This threshold value was computed as 195.2. There were eight individuals out of 656 in the test data set above this threshold, and only one of them was flagged by the testing agency. These results yielded a false-positive rate of 0.011, a true-positive rate of 0.059, and a precision of 0.125.
Another popular person-fit statistic is the standardized log likelihood of a response vector (lz; Drasgow, Levine, & Williams, 1985) for the IRT models. The lz statistic is computed as
| (15) |
where l0 is the observed log likelihood of a response vector, and E(l0) and are its expected value and standard error, respectively. These elements are equal to
| (16) |
| (17) |
and
| (18) |
respectively, where Xk is the observed response for the kth item for an examinee, and Pk(θ) is the probability of a correct response for the kth item for the examinee with ability θ. The true ability θ is typically replaced by its estimate () in these calculations. de la Torre and Deng (2008) proposed a modified procedure by correcting for unreliability and adjusting the corresponding reference distribution by constructing an empirical null distribution through simulation. Although this modified procedure seems to be computationally laborious, the results indicated better control of the Type I error rates and improved power when the modified lz (lz*) was used for detecting cheaters. The item parameters were first estimated by fitting the one-parameter logistic IRT model to the training data set, and then the modified lz statistic and its associated p value were computed for each individual in the test data set using the procedure described by de la Torre and Deng (2008). A similar procedure to imitate a supervised learning was used to make a fair comparison with XGBoost. First, a cutoff p value was computed such that the proportion of false positives is equal to 0.01. This cutoff p value was computed as 0.002. There were six individuals out of 656 in the test data set with a p value below this cutoff, and none of them were flagged by the testing agency. These results yielded a false-positive rate of 0.009, a true-positive rate of 0, and a precision of 0.
Discussion
As the use of computerized (adaptive) testing is increasing, a small group of examinees can take a test at frequent adjacent intervals, and this can cause issues regarding the security of any testing program. Securing the item bank is crucial to maintaining the integrity of test scores. Many test programs are likely to take preventive measures such as controlling the item exposure rate and retiring a certain number of items after a certain amount of time or exposure. However, regardless of how many preventive measures are being taken, there may be occasions where there is a need to screen the item response data for potential test fraud, particularly for item preknowledge. The current study contributes to the growing literature about statistical methods to identify the examinees with potential item preknowledge by demonstrating the use of a recently developed machine-learning algorithm, XGBoost, on a real data set known to include examinees who engaged in fraudulent test behavior by potentially illegally obtaining test content before the exam. The results are promising and indicate that XGBoost can be a successful tool for classifying the honest and fraudulent test takers with item preknowledge. The classification performance of the XGBoost models as measured by AUROC is reasonably good (>.9) for the models where the response time information is included along with item responses as predictive features.
A critical feature of the machine-learning algorithms such as XGBoost is that they can handle a large amount of data in a very effective manner. In the current study, only the response time and item responses were considered as predictive input features when training the model. More quantitative and qualitative information such as gender, ethnicity, country, test center, age, whether or not an examinee is taking the test first time, and the number of times an examinee had taken the test before can be included in these models along with the response time and item responses. Test companies can consider any information that they think is valuable to identify the examinees with item preknowledge, and this information would potentially improve the performance of these models even more. In the current study, variables other than item responses and response time were not considered because there has been some debate about whether these trained machine-learning models may be reflective of societal bias and human prejudices (e.g., for some discussion of these issues, see Baer & Kamalnath, 2017; Kh, 2018; Knight, 2017; Rosso, 2018; Stephen, 2018). Therefore, it would be essential to be cautious before introducing demographic variables into these models as predictive features.
It should also be noted that the application in the current study might have restricted use in practice. XGBoost is a supervised learning algorithm that requires training data with known outcome labels (honest test takers vs. fraudulent test takers). To train an XGBoost model, a testing company would need a data set including examinees known to have item preknowledge and examinees known to be honest test takers. Then, this XGBoost model can be used to predict a probability-like score for future examinees who are administered the same set of items or a subset of the items. However, on many occasions, test companies do not have such a data set. It is necessary to think of different ways of obtaining a training data set. One idea may be to fit the hierarchical IRT model (van der Linden, 2007) to the data set under investigation, simulate a hypothetical data set with item responses and response times based on the hierarchical IRT model, and then mimic fraudulent response behavior (e.g., item preknowledge) for some examinees on some items in this hypothetical data set. Then, this hypothetical data set with the embedded fraudulent test behavior that is based on the same item parameters from the data set under investigation can be used for training a model. However, the success of such a model trained with a hypothetical data set will be highly dependent on how realistic the simulated fraudulent test behavior in the hypothetical data set is and how it reflects what may have been happening in the reality under investigation. Another potential approach may be generative adversarial networks (GANs) from machine-learning literature. One of the applications of GANs is realistic data generation especially in fields where real data are scarce. GANs can learn to mimic any distribution of data and can be used to create worlds similar to our own in domains such as images, music, speech, and prose. Regardless, there is a variety of different ways to continue studying and exploring the use of XGBoost and other machine-learning algorithms in the field of test security.
Appendix
Training XGBoost model and predicting the outcome for the data set with nominal responses and response time
# Load the following libraries for the analysis
require(xgboost)
require(pROC)
# Import Train and Test datasets
train <- read.csv(“train.csv”)
test <- read.csv(“test.csv”)
for(i in 1:1266) { train[,i] = as.numeric(train[,i])}
for(i in 1:1266) { test[,i] = as.numeric(test[,i])}
dtrain <- xgb.DMatrix(data = data.matrix(train[,1:1265]),label=train$Flagged)
dtest <- xgb.DMatrix(data = data.matrix(test[,1:1265]),label=test$Flagged)
# Train the model
watchlist <- list(train=dtrain, test=dtest)
bst <- xgb.train(data=dtrain,
nround = 10000,
eta = .05,
min_child_weight = 1.2,
max_depth = 3,
gamma = 0,
max_delta_step=.5,
subsample = 1,
colsample_bytree = 1,
lambda =.6,
alpha =0.3,
scale_pos_weight =1,
num_parallel_tree = 1,
nthread = 1,
watchlist=watchlist,
objective = “binary:logistic”,
eval_metric=“rmse”,predict=TRUE,
early.stop.round = 1000,
seed = 123)
# Predict the outcome on the test dataset
test$prob <- predict(bst,dtest)
# Create the plot for predicted scores
# for flagged and unflagged examinees
plot(test$prob,
pch=ifelse(test$Flagged==0,1,17),
col=ifelse(test$Flagged==0,”gray”,”black”),
xlab=““,
ylab=“Predicted Probability-like Score”,
main = ““)
legend(“topleft”,
c(“Flagged by Testing Agency (N=17)”,”Not Flagged by Testing Agency (N=639)”),
pch=c(17,1),
col=c(“black”,”gray”))
# AUC estimate
auc(test$Flagged,test$prob)
# Determine the thresholds for the false positive rates of 0.05 and 0.01
th = quantile(test[test$Flagged==0,]$prob,c(.95,.99))
th
# Compute the True Positive Rates for the cut-off scores
a = table(test$Flagged,test$prob>th[1])
a
a[1,2]/sum(a[1,])
a[2,2]/sum(a[2,])
a = table(test$Flagged,test$prob>th[2])
a
a[1,2]/sum(a[1,])
a[2,2]/sum(a[2,])
Note that the original XGBoost algorithm also uses a form of L1 regularization by adding the term when computing . This is not included here because it was not mentioned in the original paper by Chen and Guestrin (2016). However, it can be seen in the source code the algorithm is implemented (https://github.com/dmlc/xgboost/blob/master/src/tree/param.h, see Line 43-44, Lines 135-138, Lines 295-301).
Footnotes
Declaration of Conflicting Interests: The author declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author received no financial support for the research, authorship, and/or publication of this article.
ORCID iD: Cengiz Zopluoglu  https://orcid.org/0000-0002-9397-0262
https://orcid.org/0000-0002-9397-0262
References
- Angoff W. H. (1974). The development of statistical indices for detecting cheaters. Journal of the American Statistical Association, 69(345), 44-49. [Google Scholar]
- Baer T., Kamalnath V. (2017, November). Controlling machine-learning algorithms and their biases. Retrieved from https://www.mckinsey.com/business-functions/risk/our-insights/controlling-machine-learning-algorithms-and-their-biases
- Bay L. (1995, April). Detection of cheating on multiple-choice examinations. Paper presented at the annual meeting of the American Educational Research Association, San Francisco, CA. [Google Scholar]
- Belov D. I. (2011). Detection of answer copying based on the structure of a high-stakes test. Applied Psychological Measurement, 35, 495-517. [Google Scholar]
- Belov D. I. (2014). Detecting item preknowledge in computerized adaptive testing using information theory and combinatorial optimization. Journal of Computerized Adaptive Testing, 2(3), 37-58. [Google Scholar]
- Belov D. I. (2016). Comparing the performance of eight item preknowledge detection statistics. Applied Psychological Measurement, 40, 83-97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bird C. (1927). The detection of cheating in objective examinations. School & Society, 25(635), 261-262. [Google Scholar]
- Boughton K. A., Smith J., Ren H. (2017). Using response time data to detect compromised items and/or people. In Cizek G. J., Wollack J. A. (Eds.), Handbook of quantitative methods for detecting cheating on tests (pp. 177-192). New York, NY: Routledge. [Google Scholar]
- Chen T., Guestrin C. (2016, August). Xgboost: A scalable tree boosting system. Paper presented at the Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA. [Google Scholar]
- Chen T., He T., Benesty M., Khotilovich V., Tang Y., Cho H., . . . Li Y. (2018). xgboost: Extreme Gradient Boosting (R package Version 0.71.2). Retrieved from https://cran.r-project.org/web/packages/xgboost/index.html
- Cizek G. J., Wollack J. A. (Eds.). (2017). Handbook of quantitative methods for detecting cheating on tests. New York, NY: Routledge. [Google Scholar]
- de la Torre J., Deng W. (2008). Improving person-fit assessment by correcting the ability estimate and its reference distribution. Journal of Educational Measurement, 45, 159-177. [Google Scholar]
- Drasgow F., Levine M. V., Williams E. A. (1985). Appropriateness measurement with polychotomous item response models and standardized indices. British Journal of Mathematical and Statistical Psychology, 38, 67-86. [Google Scholar]
- Eckerly C. (2017). Detecting preknowledge and item compromise: Understanding the status quo. In Cizek G. J., Wollack J. A. (Eds.), Handbook of quantitative methods for detecting cheating on tests (pp. 101-123). New York, NY: Routledge. [Google Scholar]
- Eckerly C., Babcock B., Wollack J. (2015, April). Preknowledge detection using a scale-purified deterministic gated IRT model. Paper presented at the annual meeting of the National Conference on Measurement in Education, Chicago, IL. [Google Scholar]
- Foster D. (2017). xgboostExplainer. Github Repository. Retrieved from https://github.com/AppliedDataSciencePartners/xgboostExplainer
- Holland P. W. (1996). Assessing unusual agreement between the incorrect answers of two examinees using the K-index: Statistical theory and empirical support. ETS Research Report Series, 1996(1), i-41. [Google Scholar]
- Jain A. (2016, March 1). Complete guide to parameter tuning in XGBoost (with codes in Python). Retrieved from https://www.analyticsvidhya.com/blog/2016/03/complete-guide-parameter-tuning-xgboost-with-codes-python/
- Kh R. (2018, February 22). Mitigating bias in machine learning datasets. Retrieved from https://dzone.com/articles/mitigating-biases-in-machine-learning-data-sets
- Kim D., Woo A., Dickison P. (2017). Identifying and investigating aberrant responses using psychometric-based and machine learning-based approaches. In Cizek G. J., Wollack J. A. (Eds.), Handbook of quantitative methods for detecting cheating on tests (pp. 70-98). New York, NY: Routledge. [Google Scholar]
- Knight W. (2017, October 3). Forget killer robots: Bias is the real AI danger. MIT Technology Review. Retrieved from https://www.technologyreview.com/s/608986/forget-killer-robotsbias-is-the-real-ai-danger/
- Lee S. Y. (2018). A mixture model approach to detect examinees with item preknowledge (Doctoral dissertation). Retrieved from ProQuest database. (Accession No. 10830593) [Google Scholar]
- Lemagnen K. (2018). Hyperparameter tuning in XGBoost. Retrieved from https://blog.cambridgespark.com/hyperparameter-tuning-in-xgboost-4ff9100a3b2f
- Man K., Sinharay S., Harring J. R. (2018, April). Use of data mining methods to detect test fraud. Paper presented at the annual meeting of National Council on Measurement in Education, New York, NY. [Google Scholar]
- Maynes D. D. (2005). M4: A new answer copying index. Unpublished manuscript, Caveon Test Security, Midvale, UT. [Google Scholar]
- McLeod L., Lewis C., Thissen D. (2003). A Bayesian method for the detection of item preknowledge in computerized adaptive testing. Applied Psychological Measurement, 27, 121-137. [Google Scholar]
- Mehta P., Bukov M., Wang C.-H., Day A. G., Richardson C., Fisher C. K., Schwab D. J. (2018). A high-bias, low-variance introduction to machine learning for physicists. Retrieved from https://arxiv.org/abs/1803.08823 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen D. (2016). Tree boosting with XGBoost: Why does XGBoost win “every” machine learning competition? (Master’s thesis, Norwegian University of Science and Technology, Trondheim, Norway: ). Retrieved from https://brage.bibsys.no/xmlui/handle/11250/2433761 [Google Scholar]
- O’Leary L. S., Smith R. W. (2017). Detecting candidate preknowledge and compromised content using differential person and item functioning. In Cizek G. J., Wollack J. A. (Eds.), Handbook of quantitative methods for detecting cheating on tests (pp. 151-163). New York, NY: Routledge. [Google Scholar]
- Qian H., Staniewska D., Reckase M., Woo A. (2016). Using response time to detect item preknowledge in computer-based licensure examinations. Educational Measurement: Issues and Practice, 35(1), 38-47. [Google Scholar]
- Rosso C. (2018, February 6). The human bias in the AI machine. Psychology Today. Retrieved from https://www.psychologytoday.com/us/blog/the-future-brain/201802/the-human-bias-in-the-ai-machine
- Saupe J. L. (1960). An empirical model for the corroboration of suspected cheating on multiple-choice tests. Educational and Psychological Measurement, 20, 475-489. [Google Scholar]
- Shu Z., Henson R., Luecht R. (2013). Using deterministic, gated item response theory model to detect test cheating due to item compromise. Psychometrika, 78, 481-497. [DOI] [PubMed] [Google Scholar]
- Sinharay S. (2017). Detection of item preknowledge using likelihood ratio test and score test. Journal of Educational and Behavioral Statistics, 42, 46-68. [Google Scholar]
- Sinharay S. (2018). A new person-fit statistic for the lognormal model for response times. Journal of Educational Measurement, 55, 457-476. [Google Scholar]
- Sotaridona L. S. (2003). Detecting answer copying (Unpublished doctoral dissertation). University of Twente, Enschede, Netherlands. [Google Scholar]
- Sotaridona L. S., Meijer R. R. (2002). Statistical properties of the K-index for detecting answer copying. Journal of Educational Measurement, 39, 115-132. [Google Scholar]
- Sotaridona L. S., Meijer R. R. (2003). Two new statistics to detect answer copying. Journal of Educational Measurement, 40, 53-69. [Google Scholar]
- Stan Development Team. (2018). RStan: the R interface to Stan (R package Version 2.17.3). Retrieved from http://mc-stan.org
- Stephen B. (2018, June 7). MIT fed an AI data from Reddit, and now it only thinks about murder. The Verge. Retrieved from https://www.theverge.com/2018/6/7/17437454/mit-ai-psychopathic-reddit-data-algorithmic-bias
- van der Linden W. J. (2006). A lognormal model for response times on test items. Journal of Educational and Behavioral Statistics, 31, 181-204. [Google Scholar]
- van der Linden W. J. (2007). A hierarchical framework for modeling speed and accuracy on test items. Psychometrika, 73, 287-308. [Google Scholar]
- van der Linden W. J., Guo F. (2008). Bayesian procedures for identifying aberrant response-time patterns in adaptive testing. Psychometrika, 73, 365-384. [Google Scholar]
- van der Linden W. J., Sotaridona L. (2006). Detecting answer copying when the regular response process follows a known response model. Journal of Educational and Behavioral Statistics, 31, 283-304. [Google Scholar]
- van der Linden W. J., van Krimpen-Stoop E. M. (2003). Using response times to detect aberrant responses in computerized adaptive testing. Psychometrika, 68, 251-265. [Google Scholar]
- Wang C., Xu G., Shang Z., Kuncel N. (2018). Detecting aberrant behavior and item preknowledge: A comparison of mixture modeling method and residual method. Journal of Educational and Behavioral Statistics, 43, 469-501. [Google Scholar]
- Wang X., Liu Y., Hambleton R. K. (2017). Detecting item preknowledge using a predictive checking method. Applied Psychological Measurement, 41, 243-263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wollack J. A. (1997). A nominal response model approach for detecting answer copying. Applied Psychological Measurement, 21, 307-320. [Google Scholar]
- Wollack J. A., Maynes D. D. (2017). Detection of test collusion using cluster analysis. In Cizek G. J., Wallock J. A. (Eds.), Handbook of quantitative methods for detecting cheating on tests (pp. 124-150). New York, NY: Routledge. [Google Scholar]
- Zhang V. S. (2015, August 31). Kaggle winning solution XGBoost algorithm: Let us learn from its author. Retrieved from https://www.slideshare.net/ShangxuanZhang/kaggle-winning-solution-xgboost-algorithm-let-us-learn-from-its-author