Abstract
Objective.
Deficits in the ability to perceive time have been proposed as an etiologic mechanism in the development of the cognitive and behavioral characteristics associated with ADHD. However, previous studies testing the presence of timing deficits have produced idiosyncratic results. This is in large part due to the under-utilization of insights from basic timing research, and from the inherent difficulty that arises when a single index of performance (i.e. reaction time or accuracy) is used to index the health of what is essentially a multiple component process. The current manuscript utilizes a diffusion model approach to isolate the component processes involved in timing (i.e. internal clock speed, decision making speed, speed/accuracy trade off strategies, and non-decision time) using a well-validated timing task.
Method.
Fifty children with ADHD and 32 non-ADHD controls aged 8–12 completed a temporal bisection procedure.
Results.
Diffusion model parameters indicated that both the internal clock and decision making speeds were slower among children with ADHD. However, the strength of evidence for slowed decision making far outweighed evidence for a slower internal clock.
Conclusions.
Slower evidence accumulation during decision-making is domain-general deficit in ADHD. Such slowing is consistent with adaptive-gain theories, which posit that a suboptimal ratio of neural signal-to-noise is characteristic of children with ADHD.
Keywords: ADHD, Timing, internal clock, diffusion model
Estimation of temporal intervals is an ability shared by people, animals, and even invertebrates (Boisvert & Sherry, 2006; Lejeune & Wearden, 1991; Wearden & Lejeune, 2008). The ubiquity of the ability to accurately estimate time suggests it serves a basic adaptive purpose, and as such has been theorized to underlie associative learning (Gallistel & Gibbon, 2000), optimal foraging patterns (Bateson, 2003), the fluid execution of complex motor movement, and the perception of speech (Mauk & Buonomano, 2004). Given the importance of intact temporal abilities for everyday activities, it is perhaps to be expected that poor timekeeping is associated with disruptions to adaptive functioning. Lack of orientation to time and date is used to indicate abnormal cognitive functioning (Akiskal, 2008), and more subtle disturbances in temporal abilities have been reported among people with a range of psychiatric and neurological disorders, including Attention-Deficit/Hyperactivity Disorder (ADHD; Allman, Teki, Griffiths, & Meck, 2014).
In fact, some (Barkley, 1997; Nigg & Casey, 2005; Rubia, Halari, Christakou, & Taylor, 2009) have suggested that poor execution of learned behavior seen in ADHD is in fact due to timing, although the level of detail provided with respect to mechanistic explanations differs across these conceptualizations. Studies of the structural, functional, and resting state activity of children and adults with ADHD (Bush, 2010; De La Fuente, Xia, Branch, & Li, 2013) have also identified structural and functional abnormalities in brain regions (including the prefrontal cortex, limbic system, and cerebellum) used during performance of timing procedures (Castellanos & Proal, 2012; Hart, Radua, Mataix-Cols, & Rubia, 2012; Wiener, Turkeltaub, & Coslett, 2010).
Recent reviews (Marx et al., 2017; Noreika, Falter, & Rubia, 2013) have found the performance of children with ADHD on timing tasks to be worse (i.e. less accurate or more variable) relative to unaffected peers, suggesting that group differences result from impairment in the internal clock. However, good performance on timing tasks depends on the health of the internal clock, as well as aspects of decision-making that are not specific to timing, such as utilizing the temporal information from the internal clock to make a decision, preparing and executing the motor response, and whether greater emphasis is placed on speed or accuracy of responses.
Moving forward requires the application of theory and methodology from timing research to determine if deficits in an internal timekeeping mechanism vs. associated non-timing cognitive processes (e.g. making a decision, emphasizing speed or accuracy) can explain differences in temporal task performance. This is the goal of the current study. Multiple paradigms have been developed to study timing, including: temporal production, verbal estimation, temporal reproduction, duration discrimination, and continuous tapping (Grondin, 2008). Of these, the bisection task is among the most commonly used and well-validated duration discrimination task in human and animal research (Church & Deluty, 1977; Kopec & Brody, 2010). During the task, participants are first trained to categorize auditory stimuli (often bursts of white noise) as “short” or “long” at two “anchor” lengths (e.g. 2 vs. 6s bursts). In the experimental trials, participants are then asked to classify auditory stimuli along a range of durations between and including the two anchor lengths.
In the traditional analysis of bisection task performance (Kopec & Brody, 2010), responses are collapsed across trials and the probability of responses being classified “long” is plotted for each of the trial durations, resulting in a sigmoidal function (See Figure 1). The interval at which subjects are equally likely to classify a stimulus as short or long is the bisection point (also known as the point of subjective equality or indifference point; Church & Deluty, 1977). A shift in the bisection point towards the “short” anchor is consistent with a slower running clock (i.e., the perception that most task durations are relatively short) and a shift towards the “long” anchor would be consistent with a faster running clock (i.e. most task durations are perceived as relatively long). Variability of response is measured using the slope of the probability function (i.e., the difference limen, see Figure 1). A steeper slope is indicative of reduced variability in performance and conversely, a shallower slope indicates greater variability. As the duration of the stimuli increases, the variability of an individual’s estimate of that duration also increases (Buhusi & Meck, 2005). Therefore, to produce the most accurate estimate of the precision with which a person can distinguish between durations of different lengths, the difference limen is often divided by the bisection point. The value thus obtained is known as the coefficient of variation (CV). Traditional analyses of the bisection task have used both the bisection point and CV as primary dependent variables. In turn, models of task performance have focused on accounting for the proportion of short and long responses of participants (Penney & Cheng, 2018).
Figure 1.
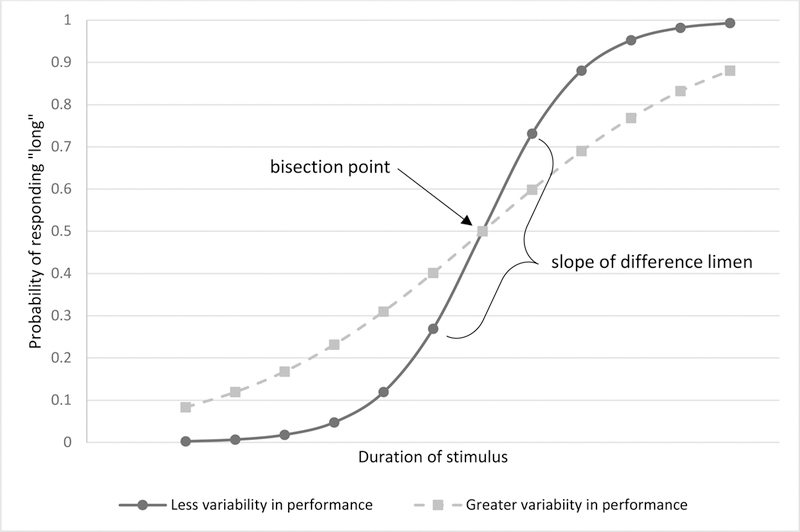
Example of a sigmoidal function describing performance on a bisection task. The bisection point is the duration which a participant is equally likely to classify as short or long. The difference limen is half the difference between durations characterized as long on 25% and 75% of trials. The CV is the bisection limen divided by the bisection point, and is measure of variability corrected for the magnitude of the durations used in the task. Greater variability in performance result in functions with shallower slopes.
Analysis of timing task performance has been recently expanded on the basis of the Ratcliff’s diffusion model framework (Ratcliff, 2006; Voss, Rothermund, & Voss, 2004), which is one of the best-known and well-validated models of simple perceptual choice behavior (Gold & Shadlen, 2001; Roitman & Shadlen, 2002). A unique advantage of this approach is that it utilizes response choices and response times, while measures of timing have traditionally relied on response choice alone (i.e., accuracy), which allows the identification of quantifiable domain general as well as timing-specific processes contributing to responses on a task.
The drift diffusion model (DDM) assumes simple decisions can be modeled as the accumulation of information favoring one response over the other (Figure 2). The rate of information accumulation in favor of a particular response is the drift rate, which increases with the quality or strength of evidence for a particular response option. The information accumulation process is bounded by two thresholds representing the response options, and a decision is made when the accumulated evidence exceeds one of thresholds. The distance between thresholds (boundary separation) reflects the degree to which individuals are conservative in selecting a response. The information accumulation process begins from a starting point that is typically assumed to be centered between the two boundaries. However, favoring one response option over the other, may shift the start point closer the corresponding boundary. Nondecision time reflects stimulus encoding, motor response time, and any other processes that contribute to response times but are not part of the decision process. Finally, the model also assumes some variability in parameters across trials.
Figure 2.

Two-stage diffusion process for interval timing (adapted from Balci & Simen, 2014). The first stage depicts the rate of temporal information accumulation (v1) when presented with an auditory stimulus of a “long” duration. When durations are longer, v1 will terminate closer to the “long” boundary, so that the start point of the decision stage is “biased” towards the long decision, and vice versa for shorter durations. v1 represents the speed of the internal clock and is calibrated to terminate after the long duration (or when the stimulus ends). After the tone offsets, the second “decision” stage begins. During the decision stage, the encoded tone is compared against tones stored in memory, and evidence that a duration is short or long drives the decision towards the corresponding boundary. The speed at which this evidence accumulation occurs is the drift rate of the decision process (v2). When the accumulation of evidence crosses either boundary, the decision stage is complete. Reaction time to the physical response of “long” or “short” is also influenced by an individual’s speed-accuracy trade off setting (i.e. boundary separation), as well as the time needed to plan and initiate the corresponding motor response (Ter).
Expanding on this model, the time-adaptive, opponent Poisson DDM (TOPDDM; Simen, Balci, deSouza, Cohen, & Holmes, 2011) has been developed to explain performance on timing tasks, including the bisection task (Balci & Simen, 2014). TOPDDM explains the bisection task within a two-stage diffusion model framework (Figure 2; Balci & Simen, 2014). The first stage (i.e. encoding of the stimulus duration) begins with the onset of the auditory tone (e.g., white noise), and ends when the tone offsets. The drift rate of the first stage, denoted v1, is the rate at which information about the duration of the auditory stimulus is gathered and encoded. TOPDDM assumes that in typical development v1 speed can be quickly calibrated (e.g. by an example: “This is a short (or long) tone: Listen.”). On the bisection task, the speed of v1 is calibrated such that accumulation of temporal information ceases after the long duration if the stimulus has not already ended. However, if v1 is too fast, slow, or highly variable, encoding of the auditory stimuli will be longer, shorter, or more variable than appropriate. In this way, the rate and variability of v1 reflects the speed and variability of the internal clock.
In the second stage, the encoded duration is compared against representations in memory, to determine whether to respond “Short” or “Long.” During this decision-making phase, evidence that a duration is short or long drives the decision process towards the corresponding boundary. Once the decision process reaches one of the boundaries, the associated response (i.e., “short” or “long”) is made. The starting point of the decision process, z, is determined by the endpoint of the first stage’s timing process, such that longer durations result in start points that are closer to, and therefore biased towards, the long boundary. The speed at which evidence for each decision is gathered is the drift rate of the decision process (v2). Similar to the standard diffusion model, easier decisions (i.e. durations closer to the short/long anchor points) have faster v2 rates; harder decisions (i.e. durations of intermediate length) have slower v2 rates. As with the traditional DM, an individual’s speed/accuracy trade off setting is captured in boundary separation (a), and motor response preparation and other unaccounted components are captured by a nondecision time (Ter) parameter. Finally, TOPDDM incorporates some degree of trial variability estimates in v2 (Sv), z (Sz), and Ter (St), which improves the model’s ability to account for the data.
From the perspective of the TOPDDM, ADHD deficits in the internal clock would be reflected in v1. Estimation of v1 is indirectly obtained from the start point of the decision stage, z; slower v1 speeds translate to a start point closer to the short decision boundary, while faster v1 speeds lead to a start point closer to the long decision boundary (Balci & Simen, 2014). Greater variability in v1 is expected to result in greater variability in the start point (Sz). In this way, z and Sz can be used as indices of an internal timekeeping mechanism. Poor task performance may also result from disruption in non-clock processes, which are reflected in the remaining DM parameters. Studies using diffusion modeling suggest that children with ADHD have slower drift rates during the decision-making stage (v2) compared to same-aged and IQ-matched peers, and may also exhibit differences in boundary separation and non-decision times (Fosco, White, & Hawk, 2017; Karalunas, Geurts, Konrad, Bender, & Nigg, 2014; Metin et al., 2013; Weigard & Huang-Pollock, 2017).
The current study seeks to better characterize the timing abilities of children with ADHD using a well-validated temporal decision-making task, and combined with the TOPDDM decomposition of the data to better capture variance associated with timing subprocesses. Consistent with prior studies, first, we anticipate children with ADHD will be less accurate and more variable on standard indices of performance on a bisection task (i.e., the bisection point and/or CV). Second, if performance is influenced by an impaired timing-specific mechanism (i.e. a faster, slower, or more variable internal clock), we would expect to see this reflected in increased start point variability (Sz), and/or start point (z) parameter. A more variable clock will result in greater Sz, a slower clock will result in a start point closer to the “short” boundary, and a fast clock will result in a start point closer to the “long” boundary. And third, based on prior studies, we also anticipate that group differences in performance will also be attributable to non-timing functions, including the v2 drift rate during decision making.
Methods
Sample
Children with ADHD (n=50) and non-ADHD controls (n=32), were recruited through advertisement via local schools, newspaper and radio ads, and fliers distributed throughout Centre and Dauphin counties in Pennsylvania. Children were between eight and 12 years of age and were ethnically representative of the region: 65.9% Caucasian/non-Hispanic; 11% Caucasian/Hispanic; 6.1% African-American/non-Hispanic; 1.2% African American/Hispanic; 3.7% Asian; 7.3% multiracial; 2.4% other; and 2.4% declined to report race/ethnicity. Children prescribed a non-stimulant psychoactive medication and those with a history of parent-reported head injuries, psychosis, neurological, developmental, intellectual, or sensorimotor disabilities, were excluded from the study.
Children with ADHD were required to meet full DSM-IV criteria for ADHD on the Diagnostic Interview Schedule for Children-IV (Shaffer, Fisher, Lucas, Dulcan, & Schwab-Stone, 2000) including duration, age of onset, and cross-situational impairment. Furthermore, at least one parent and one teacher report on the Attention, Hyperactivity, or ADHD subscales of the Behavioral Assessment Scale for Children (BASC-2; Reynolds & Kamphaus, 2004) or the Conners’ Rating Scales (Conners’; Conners, 2001) exceeded the 85th percentile (T-score>61). Following DSM-IV field trials (Lahey et al., 1994), final symptom counts were determined using an “or” algorithm to integrate parent report on DISC-IV and teacher reports on the ADHD Rating Scale (DuPaul, 1998). Children prescribed a psychostimulant medication (N=16) were required to abstain from their medication at least 24 hours in advance of the day of testing (mean/median washout duration=77.4/60.5 hours). Common childhood disorders, such as anxiety, depression, oppositional defiant disorder, and conduct disorder were assessed using the DISC-IV and behavioral rating scales, but were not exclusionary.
Non-ADHD controls did not meet criteria for ADHD on the DISC-IV, received fewer than 3 ADHD symptoms based on combined parent and teacher report, were below the 79th percentile (T-score≤58) on the rating scales listed above, and were never diagnosed or treated for ADHD in the past.
Procedure
The bisection procedure was administered within a larger test battery completed during two 3-hour test sessions. Data were collected in compliance with human subjects’ approval from the Pennsylvania State University Institutional Review Board (IRB#32126). Informed written consent from parents and verbal assent from children were obtained prior to participation. Children received a small prize for participation. Parents received monetary compensation and informal clinical feedback. A two-subtest short form of the Wechsler Intelligence Scale for Children-IV (WISC-IV; Wechsler, 2003) provided an estimated IQ. The correlation of the two-subtest short form with the full battery is 0.87 (Sattler & Dumont, 2004).
The bisection procedure.
The bisection procedure used in this task is variant of a commonly administered timing task in both the animal and human literatures (Church & Deluty, 1977; Mioni, Grondin, Mapelli, & Stablum, 2018; Penney & Cheng, 2018; Penney, Gibbon, & Meck, 2008). Children were presented with a computerized task in which they were asked to help “Bob the Alien” categorize bursts of white noise as short or long. There were eight blocks, each of which included 16 trials. Within each block, eight stimulus durations (between 2–6 s, divided equally among short and long trials), were presented twice. The differences in elapsed duration length between the four longest and four shortest stimuli were logarithmically equidistant (e.g., 2.00, 2.29, 5.23, and 6.00s), with the geometric mean of the anchors occurring at 3.46s. Stimuli were considered to be short if they were shorter than the geometric mean, and long if they were longer than the geometric mean. None of the presented stimuli durations was equal to the geometric mean. Reliability of performance accuracy across all eight blocks was acceptable (α = .76). Each trial started with the word “Listen” appearing onscreen for 500 ms, followed by the auditory burst. Following the burst of noise, children were given 3000 ms to respond. The next trial began immediately after a response was given (or after 3000 ms if no response made). After completing each block of trials participants were presented with feedback on their performance and the remaining number of blocks in the task (You got XX% of trials right on this round! Yay! # more rounds to go!) before beginning the following block. Reaction time and accuracy were the dependent variables.
Data Preparation and Modeling
To derive the bisection point and CV, the percent of “long” responses at each duration was calculated for each child and fit to a psychometric function using the quickpsy package in R (Linares & López-Moliner, 2016) (see Figure 3). Responses of two children with ADHD diverged from the sigmoidal pattern typically found in perceptual classification tasks such that a difference limen could not be calculated, and they were not included in further analyses of the bisection point or CV. There were therefore n = 48 children with ADHD, and n = 32 non-ADHD Controls for these analyses. There was no difference in the number of inattentive, F(1,48)=.82, p=.37, η2=.02, or hyperactive symptoms, F(1,48)=.65, p=.42, η2=.01, of the excluded vs. included children.
Figure 3.

Psychophysical functions of proportion “long” responses plotted against the comparison duration and the bisection point for each group.
To evaluate the effects of group the task on response times (RT), performance grouped by duration (short or long) and response (short or long). One child with ADHD and three non-ADHD controls made no “short” responses in the long duration condition (i.e. they did not classify any long duration as short) and therefore could not be included in analyses of responses times utilizing this condition. There were therefore n = 51 children with ADHD, and n = 29 non-ADHD Controls for the RT analyses.
For the TOPDDM analyses, parameter estimates were obtained using each participant’s response times and accuracy data. A single parameter was estimated for boundary separation (a), start point variability (Sz), drift rate variability (Sv) and non-decision time variability (St). Separate estimates for each response option (“short” or “long”) were obtained for drift rate (v2), start point (z), and non-decision time (Ter). Each of the short and long bins contained 64 trials, defined by whether the stimulus was shorter or longer than the geometric mean. Modeling was conducted using Dynamic Models of Choice (Heathcote et al., 2018; Heathcote, Lin, & Gretton, 2017) a free set of R functions for conducting model-based choice RT analyses in a Bayesian framework. A hierarchical approach was utilized in which individual-level and group-level parameters were estimated. Parameters were modeled separately for the ADHD and control groups, such that model parameters for each individual were unique but drawn from group-level distributions (Turner, Sederberg, Brown, & Steyvers, 2013; Wiecki, Sofer, & Frank, 2013). Samples were obtained from each group’s posterior distributions of mean parameter values, as well as parameter estimates for all individuals in the groups that are informed by these group-level distributions. Broad and uninformative priors were assigned for the group priors, and Markov chain Monte Carlo (MCMC) simulations were then used to draw samples from the joint posterior distribution across participant and group parameters. Visual examination of the trace plots and the Gelman-Rubin coefficient (Gelman & Rubin, 1992) suggested that chains were well mixed and remained stable. An additional 400 iterations from 30 chains of the group-level parameters were then obtained and used for subsequent analyses, resulting in a total of 12,000 posterior samples for analysis. Comparison of the cumulative distribution functions (Supplemental Figure 1) derived from the recovered parameters and the empirical data indicated the DM parameters captured participants’ response patterns.
Group differences in DM parameters were determined by evaluating the overlap among group-level sample distributions across diagnosis (ADHD vs. Control) and stimulus duration (short vs. long). Evidence for group differences in each DM parameter was quantified using odds ratios (OR). OR were computed as x/(1-x), where x denotes the probability that a sample from one distribution is larger than a sample from another distribution. OR values reflect relative evidence for a between- or within-group effect in a parameter relative to evidence for no difference, with greater values indicating more evidence for an effect. OR are reported as providing positive evidence (>3:1), substantial evidence (>10:1), strong evidence (>30:1), or decisive evidence (>100:1; Jeffreys, 1961).
Results
A comparison of children across both groups found no significant differences in sex, age, or estimated FSIQ. But as expected, children with ADHD had more inattention and hyperactive symptoms according to parent and teacher reports (See Table 1). No group differences were found in the bisection point, F(1,78)=.07, p=1.00, η2=.00, but children with ADHD had larger CVs, F(1,78)=10.94, p=.001, η2=.12 (Table 2 and Figure 3). Response times did not differ by stimulus duration, F(1,76)=.02, p=.88, η2=.00, response, F(1,76)= 1.10, p=.30, η2=.01, or ADHD status, F(1,76)= 3.24, p=.08, η2=.04. However, a group by response interaction was observed, F(1,76)=4.62, p=.035, n2=.06, such that correct responses were faster than incorrect responses among children with ADHD for both the short, t(49)=2.12, p=.039, η2=.02, and long stimuli, t(49)=2.13, p=.038, η2=.02, while children without ADHD showed faster responses when they correctly classified long, t(28)=2.37, p=.03, η2=.05, but not short durations, t(31)=.93, p=.36, η2=.01.
Table 1.
Sample demographics.
| M (SD) or n (%) | Control | ADHD | p | Effect size |
|---|---|---|---|---|
| N, # girls (% girls) | 32, 16 (50%) | 50, 19 (38%) | .28 | V=.12 |
| IQ | 104.03 (10.79) | 100.06 (14.72) | .55 | η2=.15 |
| Age (years) | 9.28 (1.17) | 9.26 (1.14) | 1.00 | η2=.01 |
| Parent BASC-Inattention t-score | 41.31 (6.33) | 66.36 (8.06) | <.001 | η2=.86 |
| Teacher BASC-Inattention t-score | 43.34 (5.92) | 61.15 (8.16) | <.001 | η2=.77 |
| Parent BASC-Hyperactivity t-score | 40.84 (4.42) | 66.94 (14.27) | <.001 | η2=.75 |
| Teacher BASC-Hyperactivity t-score | 43.71 (12.63) | 60.16 (12.95 | <.001 | η2=.62 |
| # DISC Inattentive Symptoms | .44 (.56) | 7.86 (1.82) | <.001 | η2=.93 |
| # DISC Hyperactive Symptoms | .16 (.37) | 5.82 (2.99) | <.001 | η2=.77 |
| # DISC ODD/CD diagnoses | 0 | 29 (58%) | <.001 | V=.59 |
| # DISC MDD/DD diagnoses | 0 | 5 (10%) | .07 | V=.20 |
| # GAD diagnoses | 0 | 6 (12%) | .04 | V=.23 |
Note. DISC = Diagnostic Interview Schedule for Children, ODD=Oppositional Defiant Disorder, CD=Conduct Disorder, MDD=Major Depressive Disorder, DD=Dysthymic Disorder, GAD=Generalized Anxiety Disorder.
Table 2.
Sample demographics and bisection task outcomes.
| M (SD) | Control | ADHD | P | Effect size |
|---|---|---|---|---|
| Bisection Point | 3.53 (.42) | 3.51 (.43) | 1.00 | η2=.00 |
| Difference Limen | 565.33 (275.53) | 800.44 (374.28) | .003 | η2=.11 |
| Bisection CV | .16 (.07) | .23 (.11) | .001 | η2=.12 |
| Response Times (secs) | 1.11 (.20) | 1.18 (.22) | .867 | η2=.00 |
Table 3a presents the median and 95% credible interval of the posterior distributions of the population means of the diffusion model parameters. Consistent with previous work (Balci & Simen, 2014; Simen, Vlasov, & Papadakis, 2016), comparison of parameters by duration found decisive evidence that relative to the short durations, start points for long duration stimuli were closer to the long duration boundary (OR>12,000; Table 3b). TOPDDM also predicts that motor preparation can occur during the v1 phase, so that longer stimuli can lead to shorter non-decision times, and vice versa. Indeed, we found positive evidence that nondecision times were longer for short durations (OR=5.68:1). There was also positive evidence that drift rates in the short duration condition were faster overall than for long durations (OR=6.39:1), though the TOPDDM is agnostic regarding such differences.
Table 3a.
Medians and 95% credible intervals (CI) of the posterior distributions of population-level means of the diffusion parameters by group.
| Control | ADHD | |
|---|---|---|
| v2 short | 1.04 [0.94, 1.14] | 0.85 [0.77, 0.94] |
| v2 long | 0.95 [0.84, 1.06] | 0.83 [0.73, 0.93] |
| z short | 0.50 [0.47, 0.52] | 0.47 [0.47, 0.48] |
| z long | 0.55 [0.53, 0.58] | 0.54 [0.52, 0.55] |
| Ter short | 0.25 [0.22, 0.28] | 0.27 [0.24, 0.30] |
| Ter long | 0.24 [0.21, 0.27] | 0.25 [0.23, 0.27] |
| a | 2.01 [1.82, 2.16] | 2.06 [1.97, 2.15] |
| Sv | 0.14 [0.07, 0.19] | 0.14 [0.07, 0.19] |
| Sz | 0.21 [0.11, 0.31] | 0.21 [0.11, 0.32] |
| St | 0.18 [0.10, 0.25] | 0.18 [0.09, 0.25] |
Note. short= short durations; long = long durations; v2 = drift rate; z = start point; Ter = nondecision time; a = boundary separation; Sv = variability of the drift rate; Sz = variability of the start point; St = variability of the nondecision time.
Table 3b.
Main effects across group (ADHD vs. Controls) and duration (short vs. long). Effects are expressed as the odds that parameter estimates from one group or condition are larger than the other.
| Parameter | Comparison | Direction | Odds (X-to-1) |
|---|---|---|---|
| v2 | Group | Control>ADHD | 856.14 |
| Duration | Short>Long | 6.39 | |
| z | Group | Control>ADHD | 47.79 |
| Duration | Long>Short | >12,000 | |
| Ter | Group | ADHD>Control | 5.37 |
| Duration | Short>Long | 5.68 | |
| a | Group | ADHD>Control | 2.34 |
| Sv | Group | ADHD>Control | 1.04 |
| Sz | Group | ADHD>Control | 1.01 |
| St | Group | Control>ADHD | 1.23 |
Note. OR are reported as providing positive evidence (>3:1), substantial evidence (>10:1), strong evidence (>30:1), or decisive evidence (>100:1) (Jeffreys, 1961). One non-negligible GroupxDuration interaction effect was observed and is reported in the main text. v2 = drift rate; z = start point; Ter = nondecision time; a = boundary separation; Sv = variability of the drift rate; Sz = variability of the start point; St = variability of the nondecision time.
Comparison of the DM parameters by group showed strong evidence (OR=47.79:1) that children with ADHD had start points (z) which were closer to the short decision boundary, and decisive evidence (OR=856.14:1) they had slower drift rates during the decision process (v2).
There was positive evidence that participants with ADHD had longer non-decision times (OR=5.37:1) and similarly positive evidence for an interaction effect of group and duration on drift rate (OR=3.12:1). When explored, this interaction revealed that controls showed faster drift rates for short durations than for long durations, while drift rate in the ADHD group did not vary by duration. No evidence was found for group-based differences in other parameters (a, Sv, Sz, St) or additional interaction effects between group and duration (z or Ter).
Discussion
Previous studies have found that children with ADHD are less accurate and more variable on timing tasks than non-ADHD peers. These results are commonly interpreted as evidence for a deficit in an internal timekeeping process. However, a straightforward interpretation of these findings is problematic because accurate timing also relies upon cognitive processes that are distinct from an internal clock. The combined use of a basic timing research framework and the TOPDDM in the current study allowed us to distinguish among the functioning of an internal clock mechanism as opposed to non-timing specific cognitive elements.
When examined with traditional indicators, and consistent with previous studies, we found that children with ADHD had a larger CV than non-ADHD controls (Marx et al., 2017; Smith, Taylor, Warner Rogers, Newman, & Rubia, 2002; Toplak & Tannock, 2005; Valko et al., 2010; Yang et al., 2007), but no group differences were found for the bisection point. Larger CVs occur when the accuracy of duration classifications decreases. It suggests a greater difficulty distinguishing between short and long durations, and therefore poorer temporal discrimination (Penney & Cheng, 2018). So, while children with ADHD are less precise in their judgment of time, there was no evidence of systematic under- or overestimation. In fact, the bisection point for both groups occurred at the anchor durations’ geometric mean, which is expected by decades of psychophysiological research (Wearden, 2016). Consequently, the processes governing the location of the bisection point appear to be functionally equivalent in both groups.
However, the difference limen, bisection point, and even choice reaction times are influenced by multiple processes. Applying the diffusion model allows us to identify the contribution of timing specific processes and domain general abilities during task performance. Following the TOPDDM framework, we found that children with ADHD exhibited a bias towards the short response option regardless of duration (i.e. z was closer to the short response option). A slower internal clock (v1) is expected to result in a start point closer to the short boundary. Therefore, this finding suggests that the temporal information accumulation process among children with ADHD is in fact slower than non-ADHD controls. Importantly, this difference was not identified using the bisection point as the traditional index of clock speed. This finding also explains why correct responses in the short condition were faster among children with ADHD, but not controls.
Though many theories positing impaired clock speed in ADHD do not specify the directionality that such a disturbance would take, some (Marx et al., 2017; Rubia et al., 2009; Smith et al., 2002) have suggested that a fast internal clock might contribute to the behavioral symptoms of ADHD. That is, a fast clock would result in accumulation of more temporal information during a given period, and consequently a subjective perception of a longer elapsed duration (e.g., the perception that an hour-long class is almost over when only 15 minutes have passed). This, in turn, would theoretically contribute to difficulties sustaining attention, task persistence, and impulsivity. However, our results support others (Hurks & Hendriksen, 2010; Wittmann & Paulus, 2008) who proposed that clocks that accumulate temporal information too slowly would lead to overly short estimates of time (believing you still have 10 minutes to get ready when you are already 5 minutes late), perhaps reflecting reduced attention to the passage of time.
A slower clock is also plausible in light of several findings relating to dopamine function in ADHD and timing. Both ADHD symptoms and timing ability are associated with the functioning of frontal and limbic regions, and dopamine rich pathways connecting these regions (De La Fuente et al., 2013; Hart et al., 2012; Konrad & Eickhoff, 2010; Rubia, Alegria, & Brinson, 2014; Wiener et al., 2010). Dopaminergic psychostimulants are known to increase the internal clock’s speed (Allman et al., 2014), are useful in treating ADHD symptoms (MTA Cooperative Group, 2004), normalize activity of brain regions involved in timing, and improve behavioral measures of performance (Rubia et al., 2009). And finally, adaptive gain models of ADHD suggest poor task performance (and slower drift rates) results from a suboptimal ability to transition between states of low and high arousal that balance distractibility and efficiency (Karalunas et al., 2014). Within this model, increased arousal promotes processing of information from relevant stimuli (signal) relative to distractions (noise), and slower drift rates suggests reflect this ratio of signal to noise may be smaller in children with ADHD. Increased neural noise may have also contributed to the slower v1 among children with ADHD as individuals with more neural noise have higher thresholds for detecting a stimulus (Aihara, Kitajo, Nozaki, & Yamamoto, 2008). Thus, both behavioral and pathophysiological evidence support the experimental finding of a slower clock among children with ADHD.
Importantly, the basic timing literature has a long history of distinguishing between clock and memory effects on task performance (Allman et al., 2014; Lustig & Meck, 2011), and has long proposed that the content of temporal memories can lead to problems with temporal performance. Although we cannot rule out the possibility that children with ADHD are unable to set their clock to a faster speed (due to some biological limitation), this seems unlikely given that children with ADHD perform well above chance (but typically worse than controls) in studies using longer durations (e.g., Barkley, Koplowitz, Anderson, & McMurray, 1997; Hurks & Hendriksen, 2010). Instead, slower temporal accumulation points to difficulties in the ability to “set” the clock’s speed. TOPDDM, supported by behavioral evidence from both animal and human studies, assumes the clock’s speed is typically established following a single presentation (i.e. exposure to the long anchor duration; Balci & Simen, 2014). Therefore, calibration to the correct speed would be rapid even if the temporal accumulation rate of children with ADHD were too slow during the task’s initial trials. However, an internal clock that remains too slow could arise if, in the encoding or retrieval process, durations are remembered as being shorter than their true length (e.g., 5.5s rather than 6s).
That being said, behavioral measures of performance were overwhelmingly dominated by slower drift rate in the decision-making stage (v2) among children with ADHD. Slower drift rates increase the probability of choosing an incorrect response during perceptual decision making (Ratcliff & McKoon, 2008), which would in turn increase the ADHD group’s CV and obscure differences in the bisection point. Slower v2 among children with ADHD is also in line with previous diffusion modeling studies, and has been found to account for ADHD-related deficits in vigilance and working-memory tasks (Huang-Pollock, Karalunas, Tam, & Moore, 2012; Karalunas et al., 2014; Metin et al., 2013; Weigard & Huang-Pollock, 2017), as well as improved performance following stimulant medication and reinforcement (Fosco et al., 2017). Together, this body of work suggests ADHD may be best characterized by a slower than average ability to accumulate task-relevant information during decision-making, which negatively impacts performance across multiple domains.
A central limitation of this study is the number of trials we were able to utilize for each participant. Recent diffusion modeling guidelines recommend using 200 trials as a rule of thumb (Voss, Voss, & Lerche, 2015), and studies of normative adults can include hundreds or thousands of trials (Klauer, Voss, Schmitz, & Teige-Mocigemba, 2007; Ratcliff & Van Dongen, 2009). This, of course, is not feasible when studying children, special populations, or both, as was the case in this study. To address the potential concern that parameters would not be adequately estimated, we utilized a hierarchical Bayesian approach, which improves parameter estimation by leveraging group-level similarities. Reassuringly, the similarity between our empirical and derived cumulative distribution functions indicates our DM parameters captured participants’ response patterns. Nonetheless, we encourage replication of our work using greater trial numbers so that our findings may be corroborated.
Summary and Conclusion
We found that children with ADHD performed worse than controls on a temporal discrimination task. Traditional measures indicated that children with ADHD showed no tendency to over- or underestimate durations, but rather showed less temporal precision overall. Further analyses provided evidence for slower information processing during decision making, and a bias towards responding “short” that is consistent with duration underestimation (i.e., a slower accumulation of temporal information). Therefore, at a functional level of behavior, temporal performance among children with ADHD is best accounted for by information processing deficits related to decision-making tasks rather than a core timing deficit.
Supplementary Material
Public Significance Statement.
The ability to accurately estimate the passage of time is fundamental to a range of adaptive processes, and some have suggested that timing is impaired among children with Attention Deficit Hyperactivity Disorder. Using cutting edge methodology, we find that while children with ADHD do have slower internal clocks, its influence on performance is far outweighed by evidence for slower decisional processing speed.
Acknowledgements
This work was supported in part by National Institute of Mental Health Grant R01 MH084947 to C.H-P. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of Mental Health or the National Institutes of Health. The authors thank the parents, teachers, and children who participated, and tireless research assistants who helped in the conduct of the study.
Footnotes
The authors have no conflicts of interest to report.
References
- Aihara T, Kitajo K, Nozaki D, & Yamamoto Y (2008). Internal noise determines external stochastic resonance in visual perception. Vision Research, 48(14), 1569–1573. doi: 10.1016/j.visres.2008.04.022 [DOI] [PubMed] [Google Scholar]
- Akiskal HS (2008). The Mental Status Examination In Fatemi SH& Clayton P(Eds.), The Medical Basis of Psychiatry (pp. 3–16): Humana Press. [Google Scholar]
- Allman MJ, Teki S, Griffiths TD, & Meck WH (2014). Properties of the internal clock: first- and second-order principles of subjective time. Annual Review of Psychology, 65(1), 743–771. doi: 10.1146/annurev-psych-010213-115117 [DOI] [PubMed] [Google Scholar]
- Balci F, & Simen P (2014). Decision processes in temporal discrimination. Acta Psychologica, 149, 157–168. doi: 10.1016/j.actpsy.2014.03.005 [DOI] [PubMed] [Google Scholar]
- Barkley RA (1997). Behavioral inhibition, sustained attention, and executive functions: Constructing a unifying theory of ADHD. Psychological Bulletin, 121(1), 65–94. [DOI] [PubMed] [Google Scholar]
- Barkley RA, Koplowitz S, Anderson T, & McMurray MB (1997). Sense of time in children with ADHD: Effects of duration, distraction, and stimulant medication. Journal of the International Neuropsychological Society, 3(4), 359–369. [PubMed] [Google Scholar]
- Boisvert MJ, & Sherry DF (2006). Interval timing by an invertebrate, the bumble bee Bombus impatiens. Current Biology, 16(16), 1636–1640. [DOI] [PubMed] [Google Scholar]
- Buhusi CV, & Meck WH (2005). What makes us tick? Functional and neural mechanisms of interval timing. Nature Reviews Neuroscience, 6(10), 755–765. doi: 10.1038/nrn1764 [DOI] [PubMed] [Google Scholar]
- Bush G (2010). Attention-Deficit Hyperactivity Disorder and Attention Networks. Neuropsychopharmacology, 35(1), 278–300. doi: 10.1038/npp.2009.120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castellanos FX, & Proal E (2012). Large-scale brain systems in ADHD: beyond the prefrontal-striatal model. Trends in Cognitive Sciences, 16(1), 17–26. doi : 10.1016/j.tics.2011.11.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Church RM, & Deluty MZ (1977). Bisection of temporal intervals. Journal of Experimental Psychology: Animal Behavior Processes, 3(3), 216–228. [DOI] [PubMed] [Google Scholar]
- Conners CK (2001). Conners’ Rating Scales--revised: CRS-R. North Tonawanda, NJ: Multi-Health Systems. [Google Scholar]
- De La Fuente A, Xia S, Branch C, & Li X (2013). A review of attention-deficit/hyperactivity disorder from the perspective of brain networks. Frontiers in Human Neuroscience, 7, 192. doi: 10.3389/fnhum.2013.00192 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DuPaul GJ (1998). ADHD rating scale-IV: checklists, norms, and clinical interpretation. New York: Guilford Press. [Google Scholar]
- Fosco WD, White CN, & Hawk LW Jr. (2017). Acute Stimulant Treatment and Reinforcement Increase the Speed of Information Accumulation in Children with ADHD. Journal of Abnormal Child Psychology, 45(5), 911–920. doi: 10.1007/s10802-016-0222-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallistel CR, & Gibbon J (2000). Time, rate, and conditioning. Psychological Review, 107(2), 289. [DOI] [PubMed] [Google Scholar]
- Gelman A, & Rubin DB (1992). Inference from Iterative Simulation Using Multiple Sequences. Statistical Science, 7(4), 457–472. [Google Scholar]
- Gold JI, & Shadlen MN (2001). Neural computations that underlie decisions about sensory stimuli. Trends in Cognitive Sciences, 5(1), 10–16. doi: 10.1016/S1364-6613(00)01567-9 [DOI] [PubMed] [Google Scholar]
- Grondin S (2008). Methods for studying psychological time In Grondin S(Ed.), Psychology of Time (1st ed., pp. 51–74). United Kingdom: Emerald Group Publishing Limited. [Google Scholar]
- Hart H, Radua J, Mataix-Cols D, & Rubia K (2012). Meta-analysis of fMRI studies of timing in attention-deficit hyperactivity disorder (ADHD). Neuroscience & Biobehavioral Reviews, 36(10), 2248–2256. doi: 10.1016/j.neubiorev.2012.08.003 [DOI] [PubMed] [Google Scholar]
- Heathcote A, Lin Y-S, Reynolds A, Strickland L, Gretton M, & Matzke D (2018). Dynamic models of choice. Behavior Research Methods. doi: 10.3758/s13428-018-1067-y [DOI] [PubMed] [Google Scholar]
- Heathcote A, Lin Y, & Gretton M (2017). DMC: Dynamic Models of Choice. Retrieved from osf.io/pbwx8. [Google Scholar]
- Huang-Pollock CL, Karalunas SL, Tam H, & Moore AN (2012). Evaluating vigilance deficits in ADHD: a meta-analysis of CPT performance. Journal of Abnormal Child Psychology, 121(2), 360–371. doi: 10.1037/a0027205 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hurks PPM, & Hendriksen JGM (2010). Retrospective and Prospective Time Deficits in Childhood ADHD: The Effects of Task Modality, Duration, and Symptom Dimensions. Child Neuropsychology, 17(1), 34–50. doi: 10.1080/09297049.2010.514403 [DOI] [PubMed] [Google Scholar]
- Jeffreys H (1961). Theory of probability (3rd ed.). Oxford, UK: Oxford University Press. [Google Scholar]
- Karalunas SL, Geurts HM, Konrad K, Bender S, & Nigg JT (2014). Annual research review: Reaction time variability in ADHD and autism spectrum disorders: measurement and mechanisms of a proposed trans-diagnostic phenotype. Journal of Child Psychology and Psychiatry, 55(6), 685–710. doi: 10.1111/jcpp.12217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klauer KC, Voss A, Schmitz F, & Teige-Mocigemba S (2007). Process Components of the Implicit Association Test: A Diffusion-Model Analysis. Journal of Personality and Social Psychology, 93(3), 353–368. doi: 10.1037/0022-3514.93.3.353 [DOI] [PubMed] [Google Scholar]
- Konrad K, & Eickhoff SB (2010). Is the ADHD Brain Wired Differently? A Review on Structural and Functional Connectivity in Attention Deficit Hyperactivity Disorder. Human Brain Mapping, 31(6), 904–916. doi: 10.1002/hbm.21058 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopec CD, & Brody CD (2010). Human performance on the temporal bisection task. Brain and Cognition, 74(3), 262–272. doi: 10.1016/j.bandc.2010.08.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lahey BB, Applegate B, McBurnett K, Biederman J, Greenhill L, Hynd GW, . . . Shaffer D (1994). DSM-IV field trials for attention deficit hyperactivity disorder in children and adolescents. American Journal of Psychiatry, 151(11), 1673–1685. doi: 10.1176/ajp.151.11.1673 [DOI] [PubMed] [Google Scholar]
- Lejeune H, & Wearden JH (1991). The comparative psychology of fixed-interval responding: some quantitative analyses. Learning and Motivation, 22(1), 84–111. [Google Scholar]
- Linares D, & López-Moliner J (2016). Quickpsy: An R package to fit psychometric functions for multiple groups. The R Journal, 8(1), 10. [Google Scholar]
- Lustig C, & Meck WH (2011). Modality differences in timing and temporal memory throughout the lifespan. Brain and Cognition, 77(2), 298–303. doi: 10.1016/j.bandc.2011.07.007 [DOI] [PubMed] [Google Scholar]
- Marx I, Weirich S, Berger C, Herpertz SC, Cohrs S, Wandschneider R, . . . Hassler F (2017). Living in the Fast Lane: Evidence for a Global Perceptual Timing Deficit in Childhood ADHD Caused by Distinct but Partially Overlapping Task-Dependent Cognitive Mechanisms. Frontiers in Human Neuroscience, 11, 122. doi: 10.3389/fnhum.2017.00122 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mauk MD, & Buonomano DV (2004). The neural basis of temporal processing. Annual Review of Neuroscience, 27(1), 307–340. doi: 10.1146/annurev.neuro.27.070203.144247 [DOI] [PubMed] [Google Scholar]
- Metin B, Roeyers H, Wiersema JR, van der Meere JJ, Thompson M, & Sonuga-Barke E (2013). ADHD Performance Reflects Inefficient but not Impulsive Information Processing: A Diffusion Model Analysis. Neuropsychology, 27(2), 193–200. doi: 10.1037/a0031533 [DOI] [PubMed] [Google Scholar]
- Mioni G, Grondin S, Mapelli D, & Stablum F (2018). A tRNS investigation of the sensory representation of time. Scientific reports, 8(1), 10364–10364. doi: 10.1038/s41598-018-28673-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- MTA Cooperative Group. (2004). National Institute of Mental Health Multimodal Treatment Study of ADHD Follow-up: 24-Month Outcomes of Treatment Strategies for Attention-Deficit/Hyperactivity Disorder. Pediatrics, 113(4), 754–761. doi: 10.1542/peds.113.4.754 [DOI] [PubMed] [Google Scholar]
- Nigg JT, & Casey BJ (2005). An integrative theory of attention-deficit/ hyperactivity disorder based on the cognitive and affective neurosciences. Development and Psychopathology, 17(3), 785–806. doi: 10.1017/s0954579405050376 [DOI] [PubMed] [Google Scholar]
- Noreika V, Falter CM, & Rubia K (2013). Timing deficits in attention-deficit/hyperactivity disorder (ADHD): Evidence from neurocognitive and neuroimaging studies. Neuropsychologia, 51(2), 235–266. doi: 10.1016/j.neuropsychologia.2012.09.036 [DOI] [PubMed] [Google Scholar]
- Penney TB, & Cheng X (2018). Duration Bisection: A User’s Guide In Vatakis A, Balci F, Di Luca M, & Correa Á (Eds.), Timing and Time Perception: Procedures, Measures, and Applications (pp. 98–126). Leiden, The Netherlands: Brill. [Google Scholar]
- Penney TB, Gibbon J, & Meck WH (2008). Categorical scaling of duration bisection in pigeons (Columba livia), mice (Mus musculus), and humans (Homo sapiens). Psychological Science, 19(11), 1103–1109. [DOI] [PubMed] [Google Scholar]
- Ratcliff R (2006). Modeling response signal and response time data. Cognitive Psychology, 53(3), 195–237. doi: 10.1016/j.cogpsych.2005.10.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & McKoon G (2008). The diffusion decision model: theory and data for two-choice decision tasks. Neural Computation, 20(4), 873–922. doi: 10.1162/neco.2008.12-06-420 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, & Van Dongen HPA (2009). Sleep deprivation affects multiple distinct cognitive processes. Psychonomic Bulletin & Review, 16(4), 742–751. doi: 10.3758/PBR.16.4.742 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reynolds CR, & Kamphaus RW (2004). BASC-2: Behavior Assessment System for Children (2nd ed.). Circle Pines, MN: American Guidance Service. [Google Scholar]
- Roitman JD, & Shadlen MN (2002). Response of Neurons in the Lateral Intraparietal Area during a Combined Visual Discrimination Reaction Time Task. Journal of Neuroscience, 22(21), 9475–9489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubia K, Alegria AA, & Brinson H (2014). Brain abnormalities in attention-deficit hyperactivity disorder: a review. Revista De Neurologia, 58, S3–S18. [PubMed] [Google Scholar]
- Rubia K, Halari R, Christakou A, & Taylor E (2009). Impulsiveness as a timing disturbance: neurocognitive abnormalities in attention-deficit hyperactivity disorder during temporal processes and normalization with methylphenidate. Philosophical Transactions of the Royal Society B: Biological Sciences, 364(1525), 1919–1931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaffer D, Fisher P, Lucas CP, Dulcan MK, & Schwab-Stone ME (2000). NIMH Diagnostic Interview Schedule for Children Version IV (NIMH DISC-IV): Description, Differences From Previous Versions, and Reliability of Some Common Diagnoses. Journal of the American Academy of Child & Adolescent Psychiatry, 39(1), 28–38. doi: 10.1097/00004583-200001000-00014 [DOI] [PubMed] [Google Scholar]
- Simen P, Balci F, deSouza L, Cohen JD, & Holmes P (2011). A Model of Interval Timing by Neural Integration. Journal of Neuroscience, 31(25), 9238–9253. doi: 10.1523/JNEUROSCI.3121-10.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simen P, Vlasov K, & Papadakis S (2016). Scale (in)variance in a unified diffusion model of decision making and timing. Psychological Review, 123(2), 151–181. doi: 10.1037/rev0000014 [DOI] [PubMed] [Google Scholar]
- Smith A, Taylor E, Warner Rogers J, Newman S, & Rubia K (2002). Evidence for a pure time perception deficit in children with ADHD. Journal of Child Psychology and Psychiatry, 43(4), 14. [DOI] [PubMed] [Google Scholar]
- Toplak ME, & Tannock R (2005). Time Perception: Modality and Duration Effects in Attention-Deficit/Hyperactivity Disorder (ADHD). Journal of Abnormal Child Psychology, 33(5), 639–654. doi: 10.1007/s10802-005-6743-6 [DOI] [PubMed] [Google Scholar]
- Turner BM, Sederberg PB, Brown SD, & Steyvers M (2013). A method for efficiently sampling from distributions with correlated dimensions. Psychological Methods, 18(3), 368–384. doi: 10.1037/a0032222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valko L, Schneider G, Doehnert M, Muller U, Brandeis D, Steinhausen HC, & Drechsler R (2010). Time processing in children and adults with ADHD. Journal of Neural Transmission, 117(10), 1213–1228. doi: 10.1007/s00702-010-0473-9 [DOI] [PubMed] [Google Scholar]
- Voss A, Rothermund K, & Voss J (2004). Interpreting the parameters of the diffusion model: An empirical validation. Memory & Cognition, 32(7), 1206–1220. [DOI] [PubMed] [Google Scholar]
- Voss A, Voss J, & Lerche V (2015). Assessing cognitive processes with diffusion model analyses: a tutorial based on fast-dm-30. Frontiers in Psychology, 6, 336. doi: 10.3389/fpsyg.2015.00336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wearden JH (2016). The Psychology of Time Perception. London: Palgrave Macmillan UK. [Google Scholar]
- Wearden JH, & Lejeune H (2008). Scalar properties in human timing: Conformity and violations. The Quarterly Journal of Experimental Psychology, 61(4), 569–587. doi: 10.1080/17470210701282576 [DOI] [PubMed] [Google Scholar]
- Wechsler D (2003). Wechsler intelligence scale for children-WISC-IV: Psychological Corporation. [Google Scholar]
- Weigard A, & Huang-Pollock C (2017). The role of speed in ADHD-related working memory deficits: A time-based resource-sharing and diffusion model account. Clinical Psychological Science, 5(2), 195–211. doi: 10.1177/2167702616668320 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiecki TV, Sofer I, & Frank MJ (2013). HDDM: hierarchical bayesian estimation of the drift-diffusion model in python. Frontiers in Neuroinformatics, 7, 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiener M, Turkeltaub P, & Coslett HB (2010). The image of time: a voxel-wise meta-analysis. NeuroImage, 49(2), 1728–1740. doi: 10.1016/j.neuroimage.2009.09.064 [DOI] [PubMed] [Google Scholar]
- Wittmann M, & Paulus MP (2008). Decision making, impulsivity and time perception. Trends in Cognitive Sciences, 12(1), 7–12. doi: 10.1016/j.tics.2007.10.004 [DOI] [PubMed] [Google Scholar]
- Yang B, Chan RCK, Zou X, Jing J, Mai J, & Li J (2007). Time perception deficit in children with ADHD. Brain Research, 1170, 90–96. doi: 10.1016/j.brainres.2007.07.021 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


