Optimizing the NIR Fluence Threshold for Nanobubble Generation by Controlled Synthesis of 10 - 40 nm Hollow Gold Nanoshells

Abstract

The laser fluence to trigger nanobubbles around hollow gold nanoshells (HGN) with near infrared light was examined through systematic modification of HGN size, localized surface plasmon resonance (LSPR), HGN concentration, and surface coverage. Improved temperature control during silver template synthesis provided monodisperse, silver templates as small as 9 nm. 10 nm HGN with < 2 nm shell thickness were prepared from these templates with a range of surface plasmon resonances from 600 – 900 nm. The fluence of picosecond near infrared (NIR) pulses to induce transient vapor nanobubbles decreased with HGN size at a fixed LSPR wavelength, unlike solid gold nanoparticles of similar dimensions that require an increased fluence with decreasing size. Nanobubble generation causes the HGN to melt with a blue shift of the LSPR. The nanobubble threshold fluence increases as the irradiation wavelength moves off the nanoshell LSPR. Surface treatment did not influence the threshold fluence. The threshold fluence increased with decreasing HGN concentration, suggesting that light localization through multiple scattering plays a role. The nanobubble threshold to rupture liposomes is 4 times smaller for 10 nm than for 40 nm HGN at a given LSPR, allowing us to use HGN size, LSPR, laser wavelength and fluence to control nanobubble generation.

Table of Contents Graphic

Introduction

One of the grand challenges of cell engineering is to initiate biological and/or chemical processes in living cells with spatial and temporal control ^[1]. Optically addressable surface plasmon-resonant metal nanoparticles are promising tools to address these challenges ^[2–13]. By controlling the size and shape of the metal nanoparticles ^[14–16], the local surface plasmon resonance (LSPR) can be red-shifted to the near infrared window, 650 – 950 nm, where biological materials are transparent ^[17]. Metal nanoparticles can be decorated with thiol-linked liposomes ^[3–6], siRNA ^[7–11], proteins ^[12] or small molecule drugs ^[13], as well as moieties to enhance colloidal stability and promote cell internalization via endocytosis ^{[7–9,12,18,19]}. The surface plasmon-resonant HGN can be triggered by irradiation with picosecond or shorter NIR light pulses; the HGN undergoes a rapid increase in temperature before any significant temperature change in the surroundings ^[16,20–23].

However, in the nanoseconds following light absorption, the hot HGN dissipates its thermal energy; if sufficient energy is available, a minute amount of water is vaporized, forming transient nanobubbles around the HGN ^{[3,7–10,12,19]}. The nanobubbles rapidly expand and collapse, similar to cavitation bubbles formed by ultrasound ^[3], without significantly changing the bulk temperature. Nanobubble generation requires a threshold energy; higher energies make the nanobubbles grow larger. Once formed, the mechanical forces generated by the expansion and collapse of the nanobubbles can lyse endosomes, liposomes, or cells, providing rapid contents release ^[3,7–9,12], cell poration ^[24,25], or even cell death ^[10,18,19]. Recent work has also shown that nanobubbles can be generated at steady state around gold nanoparticles heated by concentrated, continuous solar irradiation ^[26,27], which may provide new methods of solar energy harvesting ^[27,28].

How gold nanoparticle size, localized surface plasmon resonance (LSPR) wavelength, surface coating, concentration and irradiation wavelength (relative to the LSPR) influence the threshold fluence has not been systematically investigated. Here we show that an improved synthesis allowed us to create monodisperse hollow gold nanoshells of edge length as small as 10 nm with shell thickness less than 2 nm, to provide LSPR ranging from 650 – 900 nm ^{[15,16,21–23,29–31]}, in contradiction to recent reports stating such structures could not be made by galvanic replacement chemistry or were inherently unstable ^[32]. We made HGN of different sizes but the same LSPR, and the same diameter but different shell thicknesses, and therefore different LSPR ^[16,33]. This allows us to systematically test the threshold fluence as a function of HGN size at a given wavelength for particles with identical LSPR, and determine how the threshold fluence changes when the particles of the same size or different size are irradiated at wavelengths off resonance.

We find that generating a nanobubble requires sufficient energy to melt/anneal the HGN to solid nanoparticles as shown by the blue shift of the extinction spectra following irradiation at the nanobubble threshold fluence ^[16]. This suggests that the enthalpy of melting/solidification of the gold is necessary to induce nanobubble generation. The extinction spectra of the annealed solid nanoparticles confirm that the HGN made by galvanic replacement of silver templates are composed of a silver-gold alloy. We also find that the threshold fluence increases significantly as the irradiating wavelength moves off the LSPR; the threshold fluence tracks the extinction spectra of the HGN. For HGN with the same LSPR, there is a decrease in the threshold fluence for nanobubble generation as size is decreased from 40 to 10 nm. This is the opposite of solid gold nanoparticles that show a non-linear increase in threshold fluence as the nanoparticle size is decreased over this size range ^[21–23,31]. We also show that there is little effect of surface treatments, citrate-stabilized HGN and HGN covered with thiol-linked polyethylene glycols of molecular weights 750 – 5000 typically used for steric stabilization or for attaching liposomes or other cargo ^[3,8,9,12], have similar threshold fluence. Surprisingly, higher HGN concentrations have a lower threshold fluence than more dilute solutions, likely through a light localization process due to multiple scattering ^[34]. By synthesizing HGN via galvanic replacement with the appropriate combination of size and shell thickness, we find a strong HGN size dependence on the fluence necessary to rupture liposomes.

Results

The size and size distribution, and therefore the HGN LSPR, are determined by the size and shape distribution of the silver nanoparticles used as sacrificial templates, and the ratio of gold to silver in the subsequent galvanic replacement reaction ^[14,15]. Cubic silver templates greater than 20 nm in edge length were synthesized by reduction of silver trifluoroacetate in diethylene glycol in the presence of polyvinyl pyrrolidone in a sealed flask heated with a silicone oil bath to 150 °C as described by Xia and coworkers (Fig. 1A) ^[33]. This synthesis relies on a rapid burst of nucleation of silver crystal nuclei indicated by a color change to pale yellow about a minute after addition of the silver trifluoroacetate. This is followed by a slow, controlled growth of the nanoparticles ^[33]. Increasing the reaction time from 30 to 180 minutes increased the average nanocube size from 18 to 37 nm (Table 1).

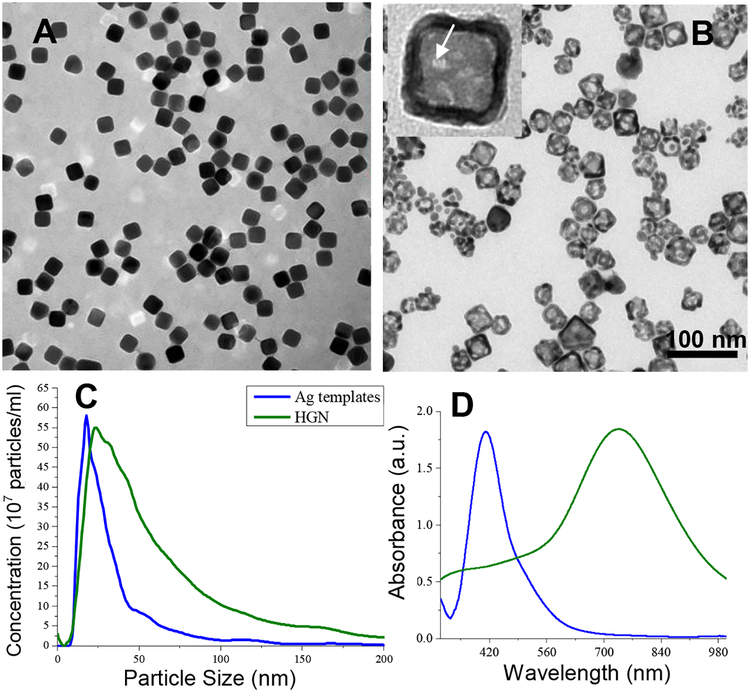
Figure 1.

(A) Transmission electron micrograph of silver nanocubes formed at a reaction time of 30 minutes. The cubes are monodisperse with well-defined sharp edges. (B) TEM image of hollow gold nanocubes (HGN) made from the silver templates in (A) by galvanic replacement. The inset shows the hollow shape with pores in the walls (arrow) (C) The mean size of the silver nanocubes from (A) determined by particle counting using a Nanosight Instrument is 18 nm, which agrees with the mean edge length measured from the TEM images. The mean size of the hollow gold nanocubes (HGN) increased to 23 °nm and the size distribution broadens somewhat consistent with the TEM images. This gives a wall thickness of 2–3 nm. (D) UV-vis extinction spectra of silver templates (from A) and HGN (from B). The plasmon resonance of the silver templates is shifted from ~ 400 nm to ~ 730 nm by the hollow shell structure, consistent with simulations in Fig. 4.

Table 1.

Reaction Time vs. Silver Nanoparticle Average Cube Edge Length

	Reaction time (min)	Ag Size [nm]	Au size [nm]
	8	9	10
	18	18	20
	30	20	22
	60	24	26
	90	25	28
	120	27	30
	150	32	35
	180	37	40

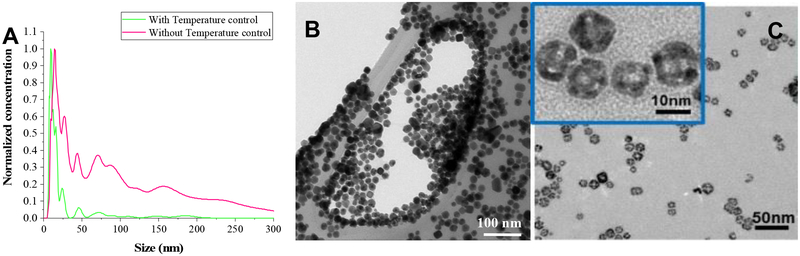
Previous work showed that decreasing the reaction time to less than 30 minutes decreased the size of the silver nanocubes, but at the cost of greatly increased polydispersity, which limited sizes to ≥ 18 nm ^[32,33]. Fig. 2A shows that for a reaction time of 10 minutes when heating the reaction flask with an oil bath, silver nanoparticles were formed with multiple sizes, with pronounced peaks at 14, 25, 45, 70 and 150 nm. During all syntheses, on addition of the silver trifluoroacetate, a drop in temperature to ~ 130 °C occurred, likely associated with the initial silver reduction or generation of silver crystal nuclei. The temperature recovered to 150 °C in about 4–5 minutes when heated by the oil bath. The multiple populations seen in the size distribution in Fig. 2A (red curve) suggest that multiple nucleation events occurred due to the temperature variation following CF₃COOAg injection. Previous work with cobalt nanoparticle synthesis has shown that minimizing the time recovering from the temperature drop following the initial reduction and nucleation steps can decrease the particle size and polydispersity ^[35]. By replacing the oil bath with variable current electrical resistance tape wrapped around a small 10 ml reaction beaker (Briskheat®, Sigma Aldrich), the heating rate could be rapidly adjusted so that the desired reaction temperature was recovered within a minute. The improved temperature control leads to more monodisperse population with a mean edge length of ~9 nm for 10 minutes of reaction (Fig. 2A, green curve). The 9 nm nanocubes are as monodisperse as the larger (>20 nm) nanocubes (Fig. 1C), and are about 50% smaller than the smallest previous silver nanocubes in the literature ^[33,36]. TEM images (Fig. 2B) show that the smaller silver templates are more rounded and less cubic than the larger silver templates, which has also been observed in previous studies of < 20 nm silver templates using other modified syntheses ^[36].

Figure 2.

(A) Reducing the reaction time to 10 minutes while heating with an oil bath causes the particle size to decrease but the polydispersity increases (red). The multiple peaks in the size distribution suggests multiple nucleation events due to the drop in temperature from 150 to 130 C and slow recovery (4–5 min) following injection of the silver trifluoroacetate when heating in an oil bath. When variable electrical resistance heating is used, the temperature recovers more rapidly (~ 1 min) decreasing both the mean size and the polydispersity (green). (B) TEM images of silver templates of mean size 10 nm (from temperature controlled synthesis in A). The silver templates have more rounded edges than those in Fig. 1, consistent with other syntheses to make smaller nanocube silver (C) TEM images of HGN of mean size 10 nm made from the 9 nm average size silver templates by the temperature controlled synthesis in (A).

Hollow Gold Nanoshell (HGN) Synthesis

HGN were prepared by galvanic replacement of the silver templates by gold (III) chloride hydrate (HAuCl₄). Silver (Ag⁺/Ag 0.8V, vs. SHE) has a lower redox potential than gold (AuCl₄⁻/Au 0.99V, vs. SHE), leading to the spontaneous plating of metallic gold onto the dissolving silver template ^[15,33] by the following stoichiometry:

$$3{\text{Ag}}_{(\text{s})}+{\text{AuCl}}_{4(\text{aq})}^{-}\to {\text{Au}}_{(\text{s})}+3{\text{Ag}}_{(\text{aq})}^{+}+4{\text{Cl}}_{(\text{aq})}^{-}$$

The gold plating on the silver template causes the nanoparticles to grow; the size distribution of the silver templates shown in Fig. 1C increases from an average of 18 nm to a mean size of 23 nm after the galvanic replacement reaction, suggesting a wall thickness of 2–3 nm. The oxidized Ag atoms dissolve into the solution as free Ag⁺ ions, which hollow out the template interior ^[33]. As the reaction proceeded, the solution color changed from yellow to blue, consistent with the red-shift of the localized surface plasmon resonance (LSPR) from 420 nm to 730 nm, as expected for a hollow particle with a thin metallic shell (Fig. 1D). During this process of oxidation and reduction, metallic silver and gold mix to form a gold/silver alloy in the walls of the HGN ^[33,37].

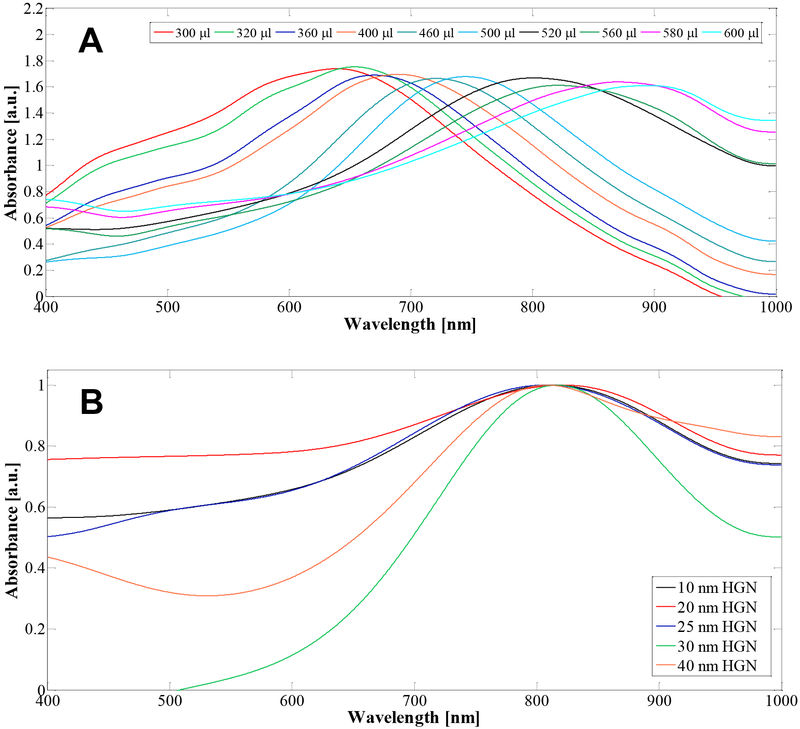
Fig. 3A shows UV-vis absorption spectra of HGN synthesized from 27 nm cubic silver templates (Table 1) following titration with increasing amounts of gold (III) chloride hydrate (HAuCl₄). The LSPR wavelength red-shifted from 650 nm to 900 nm as increasing volumes of 1 mM HAuCl₄ solution were added to 5 ml of the as-prepared silver template solution. The mean size of the HGN was ~ 30 nm following the galvanic replacement reaction. Increasing the amount of gold actually decreases the wall thickness of the HGN because silver is replaced by gold at a 3:1 stoichiometry. We also made HGN with the LSPR peak at 800 nm using silver templates of different sizes to vary the edge length of the HGN from 10 – 40 nm as shown in Fig. 3B to examine the effect of HGN size on the threshold fluence.

Figure 3.

(A) For a fixed silver nanocube template size of 27 nm, adding increasing amounts of 1 mM HAuCl₄ red-shifts the LSPR peak from 600 – 900 nm, without significantly altering the magnitude of the peak. (B) The LSPR peak can be adjusted to 800 nm for a wide range of silver template sizes by controlling the HAuCl₄ to silver ratio. The spectra in (B) were scaled to a peak height of 1.

The optical properties of the HGNs were modeled using full field electromagnetic simulations to confirm the observed trends ^[38–40]. The particles were modeled as consisting of 50% Ag – 50% Au alloys, and the inner and outer media were assumed to have the real permittivity of water. The optical properties of the gold or gold-silver alloy were described using a Drude function ^[41]. The actual complex permittivity of the metal may vary somewhat from these assumed parameters, as the composition of the alloy may not be exactly 50% Ag and 50% Au, the shell walls may contain pores (Fig. 1), and the complex permittivity of thin metal layers is often different from that of the bulk metal ^[42]. Nevertheless, these simulations illustrate the important trends in the optical properties of core-shell cubes ^[38].

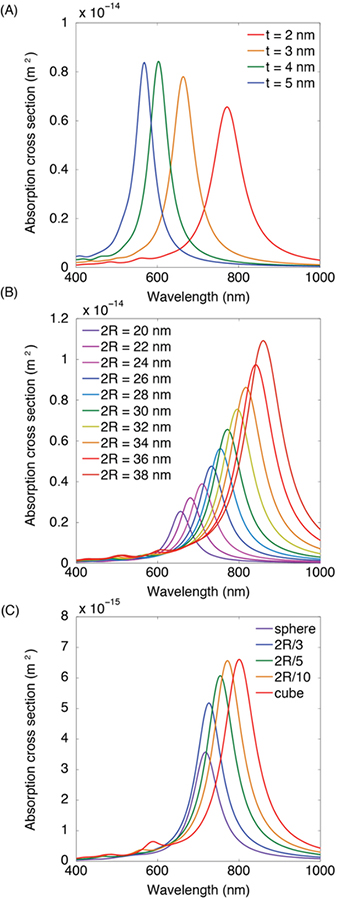
The LSPR is governed by the ratio of the inner radius to the outer radius of the HGN. For a fixed outer diameter of 30 nm, decreasing the shell thickness (which increases the ratio of the inner to outer radii) causes the resonance to red-shift to higher wavelengths (Fig. 4A) ^[14,43]. Similarly, for a fixed shell thickness, increasing the particle diameter red-shifts the resonance to higher wavelengths (which also increases the ratio of the inner to outer radii) (Fig. 4B). Cubic shapes are red-shifted relative to spherical shapes for the same diameter and shell thickness (Fig. 4C) ^[39]. The extent of the red-shift depends on the curvature at the corners of the cube, the sharper the edges, the greater the red-shift. Therefore, the LSPR wavelength can be tuned by changing the size of the template particle or the shell thickness, as in Fig. 3, or by controlling the shape of the resulting particle. Our calculations show that to achieve LSPR of 900 nm, the shells should be < 2 nm thick, even though a recent publication has suggested such nanoshells could not be grown by galvanic replacement chemistry ^[32].

Figure 4.

(A). Full field electromagnetic simulations of 50% Ag – 50% Au alloy 30 nm edge length HGN extinction spectra for different wall thickness of 2 – 5 nm. Decreasing the wall thickness red-shifts the LSPR. (B) Calculated extinction spectra for a constant wall thickness of 2 nm for various HGN edge lengths. Decreasing the wall thickness/edge length ratio red-shifts the spectra. (C). The extinction spectra red-shifts with the sharpness of the cube edge from a sphere to a sharp-edged cube. Intermediate spectra have corners rounded with various fractions of the overall HGN radius.

The experimental LSPR in Fig. 3 are much broader than the calculated LSPR in Fig. 4. Fig. 4 shows the sensitivity of the LSPR to small changes in the HGN geometry, which allows for significant tunability of the optical properties, but also implies that any polydispersity in shape, size and/or wall thickness will broaden the experimental extinction spectra. The increased linewidth can also arise because of increased radiation damping in large particles beyond the quasistatic limit as well as electron scattering at the surface of the metal shell; electron collisions cause a loss of electron phase coherence which results in a broadening of the LSPR spectra. This latter effect is not accounted for in these simulations in Fig. 4, which use bulk permittivity values and do not apply a correction for the increased damping likely in very thin materials ^[40].

Threshold Fluence

All HGN suspensions were diluted to an optical density (OD) of 1, which corresponds to a HGN density of ~ 10⁹ HGN/ml, and were pumped through a 200 μm ID square hollow glass capillary onto which was focused a variable wavelength, picosecond pulse pump laser. At this density, the HGN are separated by 6–10 μm and should be thermally isolated from each other ^[31,34]. A continuous wave probe laser was aligned collinearly with the pump laser, and the transmitted light was directed onto a photodetector ^[24]. The flow rate through the capillary was 18 μl/min, which gives a linear velocity of 7.5 mm/sec. The probe and pump beams were spread to 300 μm diameter so that ~ 30,000 HGN are in the irradiated volume; the linear velocity is matched to the beam size and pulse rate of 50 Hz so that each HGN is, on average, irradiated once. Even at the highest fluence used, ~ 100 mJ/cm², the measured temperature change of the irradiated suspensions was < 0.5 °C; nanobubble generation was not due to a change in the average suspension temperature.

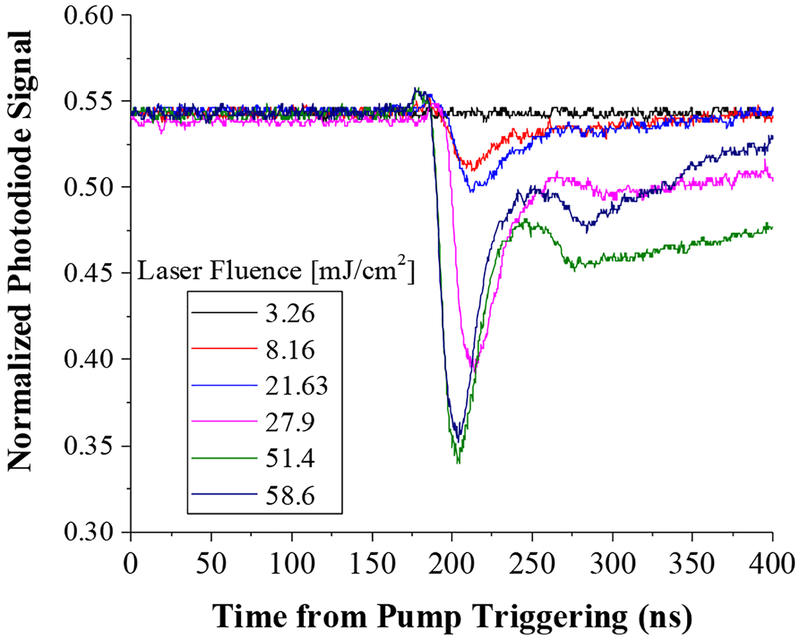
Detecting nanobubble generation was done by measuring the scatter of the probe laser by the nanobubbles; bubble generation results in less light reaching and being detected by the photodetector. The oscilloscope recordings of the photodetector signal show a dip as nanobubbles form; the signal is due to the collective generation of many nanobubbles. Fig. 5 shows that for 20 nm HGN irradiated at 800 nm (the LSPR peak for these HGN was ~ 780 nm), bubbles form for fluences ≥ 8 mJ/cm², and the amount of light scattered increases with increasing laser fluence, consistent with larger and longer-lasting nanobubbles ^[24]. A fluence of 3.5 mJ/cm² was not sufficient to induce bubbles as indicated by the flat trace of the optical signal. The bubble traces are asymmetric; the decay of the nanobubbles is slower than the nanobubble generation. This asymmetry agrees with simulation results from the Rayleigh-Plesset equations used to describe cavitation phenomena ^[22]. The extended tail of the trace is likely due to thermal disturbance of the liquid refractive index following nanobubble decay ^[24] or to generation of secondary bubbles at higher fluences ^[22,44].

Figure 5.

Vapor nanobubbles induce a change in refractive index leading to increased scattering of the probe laser, decreasing the signal at the photodiode as recorded by these oscilloscope tracings. We define the threshold fluence for nanobubble generation as the minimum fluence that leads to a dip in the photodiode signal. For a fluence of 3.5 mJ/cm² we see no deflection of the oscilloscope trace. However, for these 20 nm HGN irradiated at 800 nm, the threshold fluence is ≤ 8 mJ/cm² where we see the first dip in the tracings corresponding to nanobubble generation.

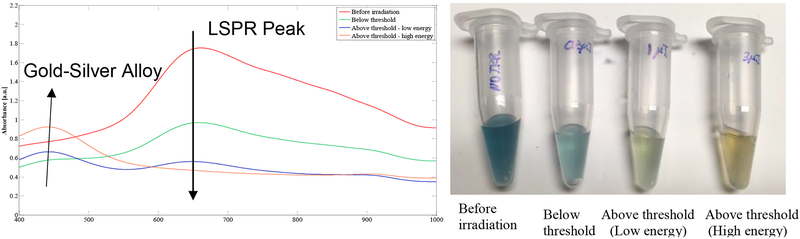
Irradiating the HGN at fluences at or above the nanobubble threshold leads to irreversible changes in the spectra and to the structure of the HGN ^[3,16]. Fig. 6 shows the extinction spectra of HGN with a LSPR at ~ 650 nm prior to and following irradiation with laser fluences below, just above, and well above the threshold laser fluence. Even below the nanobubble threshold, the LSPR peak (down arrow) at 650 nm decreases with increasing laser fluence and is eliminated at fluences well above threshold. Above the threshold fluence, a second peak at ~ 440 nm increases in intensity (up arrow). Solid nanoparticles of silver-gold alloys have a LSPR peak that depends on the silver fraction and is located between the 390 nm silver LSPR peak (compare to Fig. 1D) and the 520 nm gold LSPR peak ^[37,41]. This 440 nm peak is evidence that the hollow nanoshell structure melted into a solid core nanoparticle ^[3,16] with a roughly 50% silver- 50% gold alloy composition ^[37,41]. The absence of a peak at 390 or 520 nm shows that only the alloy is present in the nanoparticle. The color evolution of the irradiated HGN shows macroscopic evidence of the melting and reforming process. The near 50–50 alloy composition was also found by previous researchers making HGN by this synthesis ^[33]. Previous work has shown that HGN begin to anneal and change shape at 900 °C, close to the melting point of the gold-silver alloy of 1050 °C ^[20]. Recent theoretical simulations of nanobubble thresholds showed that for nanoparticles below 50 nm, melting and refreezing was necessary for nanobubble generation ^[22]. A consequence of this is that once a nanobubble is formed around an HGN, the melting and reforming process moves the LSPR peak out of the NIR; the greatly decreased cross section for absorption likely eliminates the generation of new nanobubbles around that melted HGN.

Figure 6.

UV-vis spectra of HGN before (red) and following irradiation with NIR fluences below (green), at (blue), and above (orange) the nanobubble threshold measured by optical scattering as in Fig. 5. The LSPR peak at ~ 650 nm, indicative of the hollow structure decreases with increasing laser fluence and disappears entirely for the highest laser fluence. A second peak at ~ 440 nm grows in with increasing laser fluence. The 440 nm peak is consistent with the LSPR of a roughly 50–50 silver-gold alloy solid core spherical nanoparticle, indicating that the nanobubble threshold correlates with melting and re-shaping the HGN into solid core nanoparticles. The absence of the pure silver LSPR at 390 nm and the pure gold LSPR at 520 nm shows that only the alloy is present. Photograph of cuvettes show the distinct color change on melting and reforming the HGN.

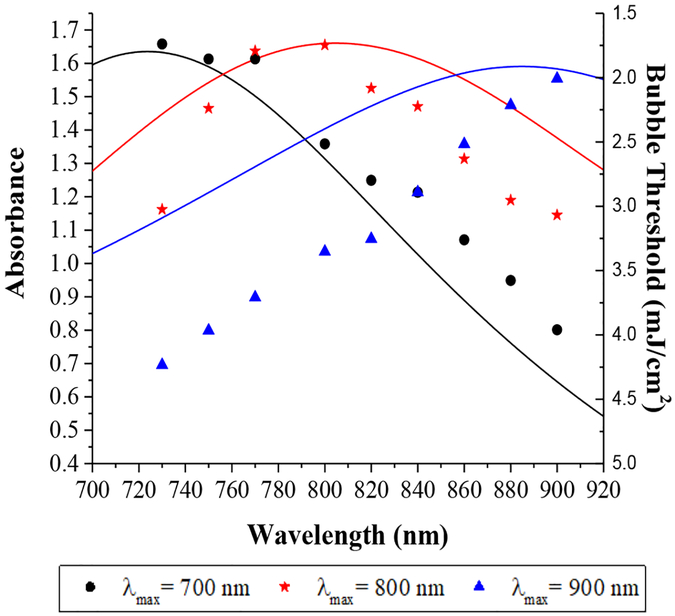
Figure 7A shows the UV-vis spectra of three different 30 nm HGN designed to have different LSPR peaks at wavelengths, λ_max, of 700, 800, and 900 nm. Irradiating suspensions at their λ_max gives a similar minimum threshold fluence, independent of λ_max and the irradiation wavelength. However, the threshold fluence increases as the irradiating wavelength moves off λ_max for all three HGN. When irradiating at 730 nm, it requires roughly twice the fluence to produce a nanobubble from HGN with λ_max of 800 nm compared to λ_max of 700, and about three times the fluence for an HGN with λ_max of 900 nm. However, these ratios are reversed when irradiating with 900 nm light. Hence, by gradually increasing the fluence, it is possible to induce nanobubbles in one population of HGN, then a second population, then a third, independently, depending on the choice of irradiation wavelength and λ_max.

Figure 7.

UV-vis spectra of 30 nm HGN with different LSPR peaks at 700 nm (black line), 800 nm (red line) and 900 nm (blue line). The nanobubble threshold fluence is proportional to the difference between the LSPR peak and the irradiation wavelength. Black circles refer to the threshold fluence for HGN with λ_max = 700 nm, red stars refer to HGN with λ_max = 800 nm, blue triangles refer to HGN with λ_max = 900 nm as a function of irradiating wavelength. The minimum fluence for picosecond pulsed irradiation at various wavelengths given by the individual symbols is ~ 2 mJ/cm² for all three sets of HGN of the same size when irradiated at their resonance wavelength. However, irradiating at wavelengths off the particular HGN LSPR peak (such as irradiating a HGN with λ_max = 700 nm at 900 nm) requires a significantly different fluence to initiate nanobubble generation. The order in which nanobubbles form with increasing fluence is reversed at 730 nm compared to 800 nm compared to 900 nm.

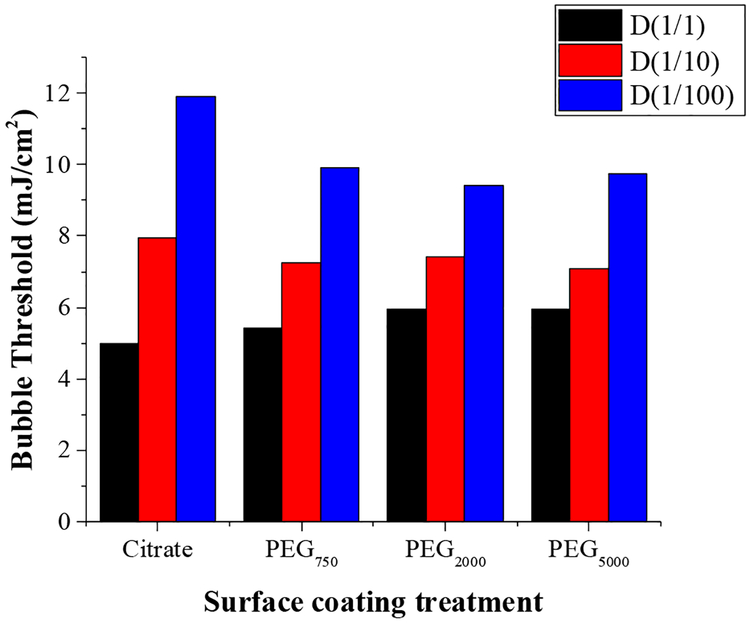
Various ligands are used to stabilize nanoparticles against aggregation or to tether the nanoparticles to proteins ^[12], genetic materials ^[7–9] or liposomes ^[3,4]. Figure 8 shows that the nanobubble threshold does not change significantly due to thiol-linked polyethylene glycol molecules of various molecular weights compared to citrate stabilized HGN. 40 nm HGN with a LSPR of 750 nm were reacted with thiol-terminated PEGs at a PEG:Au molar ratio of 1:10 to mimic typical tethers used for linking HGN to liposomes ^[3,4], proteins ^[12] or siRNA ^[7–9], or used as steric stabilizers. These HGN were irradiated with pulsed 750 nm NIR light, and there was no significant difference in the threshold fluence at a concentration corresponding to an OD =1 for any of the surface coatings. However, diluting the suspensions by a factor of 10 or 100 did increase the threshold fluence, but in the same way for all surface coatings. Diluting by a factor of 100 roughly doubled the threshold fluence independent of surface coating.

Figure 8.

Threshold fluence for 40 nm HGN with LSPR of 750 nm irradiated with 750 nm NIR pulsed light does not change significantly with surface modification by various molecular weight thiol-tethered polyethylene glycols and is the same as the citrate stabilized HGN. The undiluted samples (D(1/1) has an optical density of 1 which corresponds to ~ 10⁹ HGN/ml. D(1/10) refers to a dilution factor of 10 and D(1/100) refers to a dilution factor of 100. The threshold fluence increases with decreasing HGN concentration, doubling for a 100-fold dilution, but is independent of the PEG molecular weight.

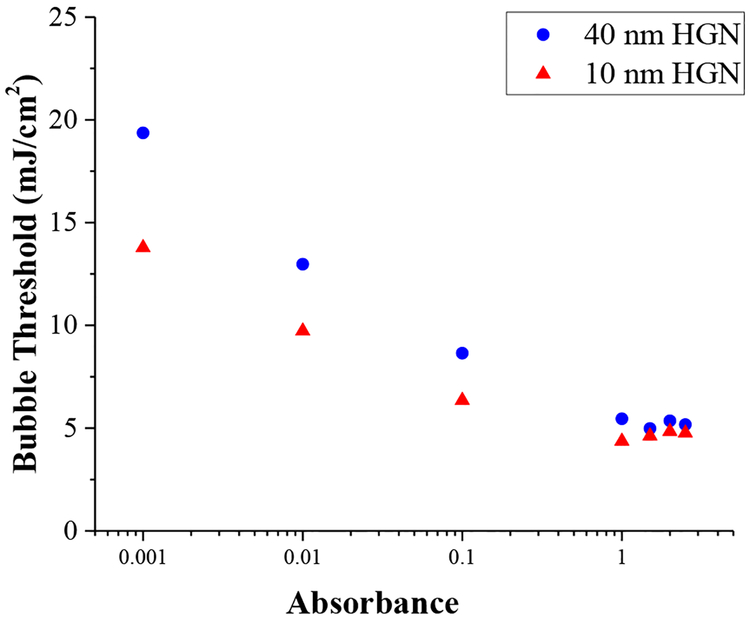
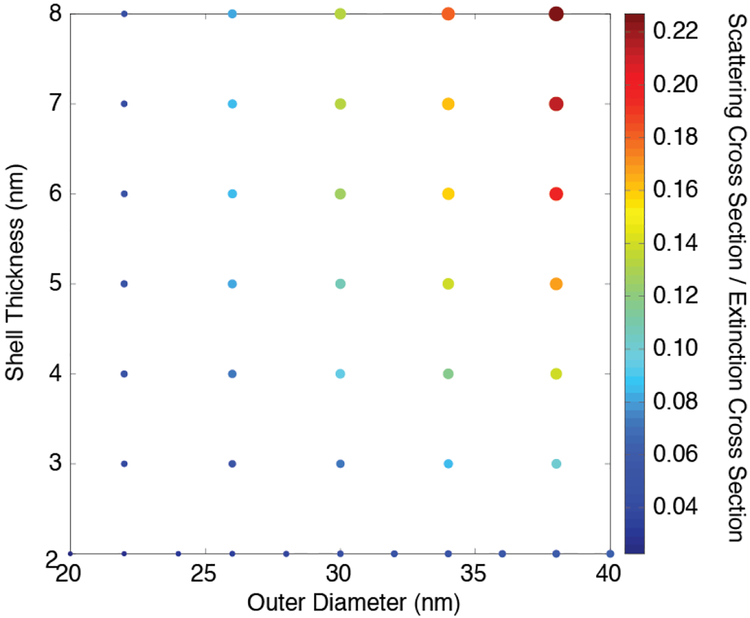
Fig. 9 shows how the threshold fluence for nanobubble generation depends on the HGN concentration and size for 10 and 40 nm HGN with LSPR of 800 nm. At the highest absorbance, the threshold fluence for 800 nm irradiation is similar for both 10 and 40 nm HGN and is relatively constant. However, as the HGN suspension is diluted, and the optical absorption decreases according to Beer’s law, the threshold fluence increases. This behavior is similar to that predicted for light localization through multiple scattering by Hogan et al. ^[34]. At high HGN concentrations, there is more scattering, especially for the larger HGN (See Fig. 10) and the path length of a given photon through the sample increases, increasing the probability it will be absorbed. The efficiency of the photons is increased, resulting in a lower fluence for nanobubble generation. This effect is smaller for the 10 nm HGN, which scatter less. Figure 10 shows the calculated fraction of the total extinction cross section due to scattering as a function of HGN outer diameter and shell thickness, indicating that the smaller nanoparticles scatter significantly less than the larger particles. This is consistent with the 10 nm HGN having a lower threshold fluence than 40 nm HGN at all concentrations, but the difference in threshold fluence decreases with increasing HGN concentration because of the larger scattering cross section for larger HGN.

Figure 9.

Concentration and size dependence of HGN of 10 and 40 nm edge length with LSPR at 800 nm irradiated at 800 nm. The concentration is in units of optical absorbance; a reduction of a factor of 10 in absorbance corresponds to a decrease of a factor of 10 in concentration according to Beer’s law. The threshold fluence for the 10 nm HGN is always less than that of the 40 nm HGN, but the difference decreases with increasing concentration. Multiple scattering events increase the average path length of the photons in the irradiated volume, which increases the average absorption probability, lowering the threshold fluence with concentration. The more highly scattering larger HGN show a stronger concentration dependence of threshold fluence than the less scattering, smaller HGN (See Fig 10).

Figure 10.

The calculated ratio of scattering to total cross sections for cuboidal HGN with a constant wall thickness and an increasing overall diameter. The color and size of the circles correspond to the different scattering to total cross section ratios as a function of overall HGN diameter and HGN thickness. As the HGN size and/or wall thickness increases, the fraction of the incident light that is scattered increases.

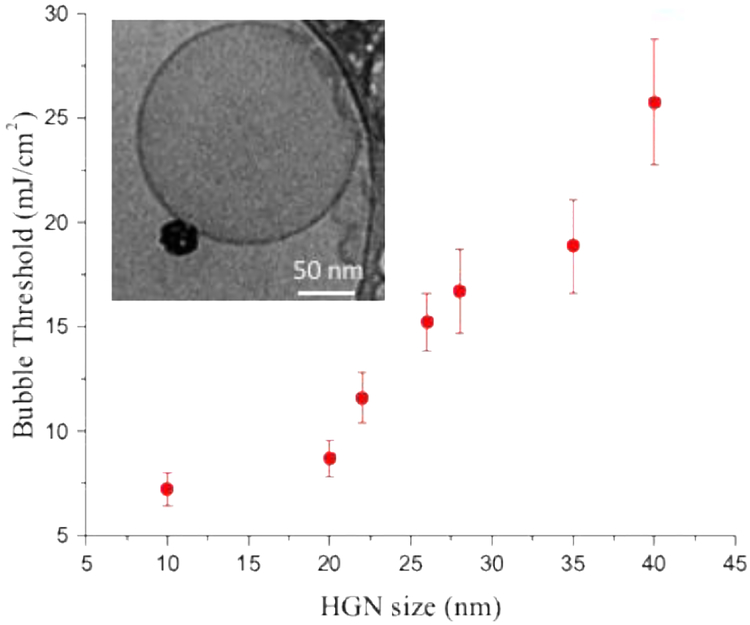
The factors that influence the threshold fluence can result in significant differences in HGN applications such as liposome rupture and contents release. HGN of different sizes but with the same 800 nm LSPR (see Fig. 3B) were attached to 100 nm dipalmitoylphosphatidylcholine liposomes via a 2000 Da thiol-PEG-lipid tether ^[4] prior to irradiation. Fig. 11 shows that the nanobubble threshold fluence increases significantly with HGN size when irradiated with resonant 800 nm light. This is the opposite of the behavior observed and predicted for solid gold nanoparticles of diameter < 60 nm ^[21–23]. In those studies, the fluence to induce nanobubble generation showed a minimum for 60 – 80 nm spherical solid gold nanoparticles, and increased for smaller or larger nanoparticles ^[23]. The greatly increased scattering relative to absorption with gold nanoparticle diameter is likely responsible for the observed increase ^[21–23] in threshold fluence for nanoparticles > 60 nm diameter. As in Fig. 9, the HGN, with their hollow core, appear to require a smaller threshold fluence as the size is decreased down to the smallest size of 10 nm. The liposome concentration was < 10⁸ liposomes/ml and on average, 1–3 HGN were tethered to each liposome (Fig. 11, inset). Previous work has shown that the nanobubble threshold correlates with liposome rupture and contents release ^[3]. Fig. 11 shows the benefits of smaller HGN at the dilute concentrations likely important in HGN applications.

Figure 11.

Minimum fluence required to initiate nanobubble generation on HGN tethered to 100 nm phospholipid liposomes. The inset cryo-TEM image shows a typical liposome coupled to an HGN via a 2000 Da thiol-PEG-lipid tether. The threshold fluence increases with HGN size, unlike that observed for solid metal nanoparticles. The HGN size and LSPR (Fig. 7) provide two independent ways to control the nanobubble threshold fluence. The threshold fluence correlates well with the minimum fluence needed to release the liposome contents.

Discussion

Decreasing the HGN size requires decreasing the silver template size, which we found required improved control of the reaction temperature during nanocube synthesis. The initial reduction of silver ions and generation of silver crystal nuclei is endothermic, which led to a temperature drop following the initial silver reduction, which in turn led to multiple nucleation events and increased polydispersity. Improved feedback temperature control, especially for the smallest silver nanocubes, led to monodisperse 9 nm templates, 50% smaller than the minimum size previously reported ^[33,36]. With this enhanced template control, the galvanic replacement of gold for silver can be tuned to provide control of the LSPR for any size HGN from 10 – 40 nm over the range of 600 – 900 nm. TEM images and electromagnetic simulations of these stable nanostructures show that the shell thickness is likely less than 2 nm for edge lengths of 10 nm ^[32,33,36]. These HGN are extremely stable and the spectra and nanostructure have remained unchanged for periods of more than a year, in contradiction to recent literature reports ^[32].

For successful nanobubble generation, this conversion of light energy to thermal energy must be faster than dissipation to the surrounding environment ^[16,20–23]. The minimum characteristic time for thermal dissipation is ${\tau }_D{~}^{\rho C_p{b}^2}{/}_k,$ in which ρC_p is the volumetric heat capacity of gold (2.5 × 10⁶ J-m⁻³-K⁻¹), k is the thermal conductivity of water (0.6 W-m⁻¹-K⁻¹), and b is a characteristic dimension of the HGN. For 5 ≤ b ≤ 30 nm, 100 ≤ τ_D ≤ 3750 psec. At the nanoscale, an energy mismatch of the vibrational modes at the gold-water interface can limit the energy transfer to the surroundings, which may be complicated by the presence of thiol-bound PEGs of various molecular weights. This interfacial resistance can greatly increase τ_D ^[45]. However, Fig. 8 shows that there is little effect of PEG coating on the threshold fluence. The thiol bond is quite labile under the rapid temperature changes that accompany nanobubble generation ^[7–9,46], and the PEG-thiol dissociates from the HGN at lower temperatures than nanobubble generation ^[7]. As a result, the vapor bubbles likely form at the actual gold-water interface as the thiol-linked PEGS have dissociated. The generation of a vapor layer at the gold-water interface acts as an insulating layer, which also decreases the rate of thermal diffusion to the surrounding water ^[26,28,45]. As the pulse length (28 psec) is less than our minimum estimate for τ_D, the light energy is initially confined to heating the nanoparticle. Hence, the initial temperature increase of the HGN is proportional to the light energy absorbed ^[20].

The absorption cross section for the hollow shells is proportional to the metal shell volume, ${\sigma }_{abs}\cong \xi R^{2}t,$ (Eqn. S3 and Supplemental Figure S1) and the energy absorbed is $Q={\sigma }_{abs}F\cong \xi R^{2}tF.$ For nanoscale bubbles, the surface tension at the bubble-water interface, γ, requires the water to be superheated to temperature, T, from its normal boiling point, T₀, at atmospheric pressure, P₀, as described by the Thomson equation:

$$\text{Δ}{H}_{vap}\left(\frac{T-T_0}{T{T}_0}\right)=bln\left(1+\frac{2\gamma }{R{P}_0}\right)$$ (1)

b is the gas constant and ΔH_vap is the latent heat of vaporization. Both γ and ΔH_vap decrease as the spinodal temperature is approached. For a bubble of radius 10 nm, water must be superheated to 272 °C ^[47]. However, at this temperature, water has essentially reached its spinodal temperature, T_S= 277 °C, at which the liquid becomes unstable and spontaneously converts to the vapor phase ^[23]. Recent simulations suggest that the pressure increase inside rapidly heated bubbles reaches the critical pressure and is independent of surface tension for all but the smallest (< 10 nm diameter) nanoparticles ^[45]. A rough estimate of the energy, Q, needed to heat the water in the hollow core to reach the spinodal temperature, T_s, is:

$$Q~R^3{\rho }_W{C}_{pW}\left(T_S-T_0\right)~\xi R^{2}tF$$ (2a)

$$F~R\left(\frac{{\rho }_W{C}_{pW}\left({\text{T}}_{\text{S}}-{\text{T}}_0\right)}{\xi t}\right)$$ (2b)

which is consistent with the laser fluence increasing with the radius, R, of the HGN (Fig. 9, 11). However, $\mathrm{\xi }$ depends on the wall thickness, t, the HGN radius, and the complex dielectric function, which, in turn, depends on the HGN composition. The only control over this we have is the ratio of gold salt to silver in the synthesis, so it is difficult to ascertain the contributions of any of these parameters in determining the LSPR. But these factors likely contribute to the non-linear behavior of the fluence threshold on R shown in Fig. 11. In addition to the multiple factors that influence the adsorption cross section and LSPR wavelength, the heat loss is highest for the particles with the largest surface area to volume ratio, which also likely increases the fluence threshold for the smallest HGN (Figs. 9, 11).

For the gold shell to heat water to the spinodal temperature, the shell must be heated well above this temperature by light absorption. The gold shell is heated to some maximum temperature, T_G, which causes energy to flow to the water in the core of the nanoshell, initially at T₀, causing the water temperature to rise and the shell temperature to fall until they are equalized. Hence the approximate maximum temperature that can be reached by the water in the core is (assuming no external losses):

$$T_{max}=\frac{\left[\left(4\pi R^{2}t\right)\rho C_p{T}_G\right]+\left[\left(\frac{4}{3}\pi R^3\right){\rho }_W{C}_{pw}{T}_0\right]}{\left(4\pi R^{2}t\right)\rho C_p+\left(\frac{4}{3}\pi R^3\right){\rho }_W{C}_{pW}}$$ (3a)

$$T_{max}=\frac{\left(\frac{t}{R}\right)3\rho C_p{T}_G+{\rho }_W{C}_{pW}{T}_0}{\left(\frac{t}{R}\right)3\rho C_p+{\rho }_W{C}_{pW}}$$ (3b)

ρ_WC_pW (4.2 J-cm⁻³-K⁻¹) is the volumetric heat capacity of water. The maximum water temperature depends on t/R, or the shell thickness to overall size, which varies from 0.1 – 0.25 for HGN absorbing in the near infrared (Fig. 4) ^[14]. Hence T_max will be roughly the same for all the HGN for a given T_G. For R = 10 nm and t = 2 nm, for T_max to reach the spinodal temperature of 277 °C, the gold-silver alloy shell must be heated to ~ 1000 °C, which is close to the melting point of the gold-silver alloy, ~ 1050 °C. As the nanoshell is also losing heat to the surrounding water, the metal shell must reach a higher temperature, which is consistent with our experimental observation in Fig. 6 that the gold nanoshells have to melt at the threshold fluence for nanobubble generation.

For solid spherical gold or silver-gold alloy nanoparticles, σ_abs=ζR³, and ζ is a function of the dielectric functions of water and gold ^[23,37]. The energy absorbed by the gold nanoparticle, Q=σ_absF≅ζR³F, in which F is the light fluence (mJ/cm²), hence $\delta T=\raisebox{1ex}{$\zeta R^{3}F$}\!\left/ \!\raisebox{-1ex}{$\rho C_p{R}^3$}\right.=\raisebox{1ex}{$\zeta F$}\!\left/ \!\raisebox{-1ex}{$\rho C_p$}\right.,$ and the ideal temperature increase for a solid core nanoparticle should be independent of the particle size. However, the heat loss is highest for the particles with the largest surface area to volume ratio, which is consistent with the observed increase in threshold energy with decreasing size ^[23]. Scattering increases relative to adsorption as the size of the spherical nanoparticles increases (Eqn. S4), which increases the threshold fluence for larger spherical nanoparticles. This is likely why solid core, spherical nanoparticles showed a minimum threshold fluence for 60 – 80 nm nanoparticles, and increased for both smaller or larger nanoparticles ^[23].

The extinction cross-section for nanoparticle interaction with light is made up of two contributions, absorption (Eqn. S3) and scattering (Eqn. S5). Fig. 10 shows the calculated ratio of scattering to total cross sections for cuboidal HGN with a constant wall thickness and an increasing overall diameter. The color and size of the circles correspond to the different ratios as a function of overall HGN diameter and HGN thickness. As the HGN size and/or wall thickness increases, the fraction of the incident light that is scattered increases. Hogan et al. showed that the multiple scattering of light by concentrated nanoparticles confined the light to smaller volumes, increasing the efficiency of converting the light to heat. Multiple scattering events increase the average path length of the photons in the irradiated volume, which increases the average absorption probability. This appears to be happening in the capillary tube during flow. As the concentration of the HGN increases, any light scattered has an increased probability of being absorbed by other HGN in the concentrated suspension. Based on these simulations, a 30 nm HGN with a 2 nm shell scatters approximately 4% of the light, whereas a 38 nm HGN with a 3 nm shell scatters approximately 9%. This increased scattering promotes the light localization effect we see in Fig. 9. At sufficiently high concentrations, increased HGN size and scattering have less effect on the threshold fluence than at lower concentrations as we see in Fig. 9 and in the liposomes in Fig. 11.

Conclusions

Vapor nanobubbles generated around hollow gold nanoparticles that strongly absorb near infrared light provide a unique tool for delivery of proteins ^[12] and genetic materials ^[8,9] to the cell cytoplasm, triggering release from endosomes ^[7], lysing liposomes ^[3], and even cancer cell ablation in vivo ^[18,19] with sub-cellular localization and millisecond time resolution. The rapid generation and disappearance of the nanobubbles can be used during flow processing of cells in high-throughput microfluidic devices to eliminate unwanted cell populations while simultaneously modifying other cell populations for cell and gene therapy ^[24,48] as the bulk temperature is unchanged during the process. The keys to these applications is to create optimized hollow gold nanoshells of the desired size and LSPR wavelength that form nanobubbles requiring the smallest possible laser fluence, combined with the ability to address different HGN populations (with different cargo or different functions) by modifying the sizes and LSPR wavelengths so that each population has a well-separated threshold fluence for a given irradiation wavelength.

Improved temperature control of the silver template synthesis reaction allowed us to make silver templates with edge lengths as small as 9 nm (50% smaller than any previous synthesis ^[36]), with low polydispersity of size and shape. HGN as small as 10 nm in diameter with shell thicknesses of < 2 nm were prepared from these templates by the galvanic replacement of silver by gold. Full field electromagnetic simulations confirm that the overall size and shell thickness, which determine the LSPR wavelength, could be controlled independently to provide a range of plasmon resonances from 650 – 900 nm for HGN of edge length 10 – 40 nm, in contradiction to recent reports suggesting that such HGN would be unstable ^[32].

With these size and LSPR optimized HGN, we determined the dependence of the laser fluence required to trigger transient nanobubble generation with picosecond pulsed near infrared light. We find that the fluence needed to induce vapor nanobubbles decreased with HGN size for HGN with the same LSPR, unlike solid metal nanoparticles that require an increased fluence with decreasing size ^[23]. This observation is consistent with a metal shell structure with water on both the interior and exterior of the HGN, with the interior water boiling to form the initial nanobubble. The nanobubbles likely form at temperatures at or near the spinodal decomposition temperature of water due to the superheating required for nanometer scale bubbles. This requires that the HGN heat to melting at the nanobubble fluence, which is confirmed by the blue shift of the extinction spectra from the NIR to ~ 440 nm, the LSPR of a roughly 50 – 50 gold-silver alloy. This means that once an HGN is irradiated sufficiently to form a nanobubble, its absorbance in the NIR is eliminated and it will no longer act as a future site for nanobubble generation. We find a significant increase in the nanobubble threshold fluence as the irradiation wavelength moves off the nanoshell resonance which allows the combination of LSPR and irradiation wavelength to address different HGN in solution independently.

Thiol-linked polyethylene glycols ranging from 750 to 5000 molecular weight made no significant difference on the threshold fluence. However, the threshold fluence increased with decreasing HGN concentration, suggesting that light localization through multiple scattering plays a role in determining the threshold fluence ^[34]. This may help minimize the laser fluence needed when HGN are used to deliver cargo in microfluidic devices at high concentrations ^[48], or distinguish between different HGN by size when the HGN are dilute as when tethered to liposomes. We show that both LSPR wavelength and HGN size can be used to tailor the fluence necessary for nanobubble generation. The appropriate choice of synthesis conditions to control HGN size, LSPR wavelength, combined with proper choice of laser irradiation wavelength and fluence, makes it possible to address different HGN with different cargoes in the same solution with high spatial and temporal resolution ^[8,12].

Experimental

Diethylene glycol (DEG, ReagentPlus® 99%, lot no.MKB59378V), silicon oil, sodium hydrosulfide hydrate (NaSH), hydrochloric acid (HCl, 37% by weight in water), silver trifluoroacetate (CF₃COOAg, ≥ 99.99%, lot no.MKBQ7429V), polyvinylpyrrolidone (PVP, powder, average MW 55,000, lot no. MKBN3006V), gold(III) chloride hydrate (HAuCl₄, ≥ 99.999%), sodium borohydride (NaBH₄, powder, ≥ 98.0%), and hydroxylamine hydrochloride (NH₂OH∙HCl, ReagentPlus® 99%) were obtained from Sigma-Aldrich (St. Louis, Mo). Silver nitrate (AgNO₃, crystalline, ≥ 99.7%) was purchased from Fisher scientific. Ethylene glycol (EG, AR®, trace metal basis) was obtained from Macron Fine Chemicals™. Silver nitrate solution (AgNO₃, 0.1M) was purchased from Fluka® Analytical. Methoxy-PEG-thiol of 750, 2000 and 5000 Da molecular weight and lipid-linked distearoylphosphatidylethanolamine linked to a 2000 Da PEG terminated in a thiol, DSPE-PEG-2000-SH, were purchased from Nanocs (New York, NY). Dipalmitoylphosphatidylcholine (DPPC) was purchased from Avanti Polar Lipids (Alabaster, Al). All chemicals were used as received. Water with a resistivity of 18.2 MΩ·cm at 25 °C was purified with a Millipore Direct Q 3UV-R (Billerica, MA) system.

Synthesis of cubic Ag templates ≥ 20 nm ^[33]

Cubic Ag templates ≥ 18 nm were prepared by heating diethylene glycol (5 ml) (DEG) in a 10 mL glass beaker (Pyrex®) to 150 °C in a silicon oil bath under magnetic stirring at 340 rpm ^[33]. After heating for 30 min, 30 mM NaSH (0.006 mL) in DEG was added. Four minutes later, 30 mM HCl (0.05 mL) in DEG was added, followed by 20 mg/ml polyvinylpyrrolidone (1.25 mL) (PVP) in DEG. The temperature dropped from 150 °C to ~ 120 °C on addition of PVP, but recovered quickly. After another 2 min, 282 mM CF₃COOAg (0.4 mL) in DEG was added which caused a drop in temperature to ~ 130 °C. The temperature recovered to 150 °C in 4–5 minutes.

The transparent solution became yellow one minute after CF₃COOAg injection indicating the generation of Ag nuclei during the time the temperature was dropping to ~ 130 °C. The size of the silver nanocubes was proportional to the length of time (30 minutes for 18 nm particles – 180 min for 32 nm particles ^[33]) following the addition of the CF₃COOAg. The solution went through three stages of dark reddish brown, reddish green, and bright yellowish green as the edge length of the cubic Ag seeds increased. The reaction solution was quenched by placing the beaker in a cold-water bath. The product was washed with acetone followed by centrifugation at 4000 rpm for 30 min to remove the remaining Ag precursor and DEG, and then washed with water followed by centrifugation at 13,000 rpm for 10 min (repeated three times) to remove excess PVP. The cubic Ag nanoparticles were dispersed in DI water.

Synthesis of cubic Ag templates < 20 nm

As previously reported, shorter reaction times using the synthesis described above led to smaller silver nanoparticles, but with much greater polydispersity ^[33]. We replaced the oil bath with an electrical resistance tape wrapped around the reaction beaker (Briskheat®, Sigma Aldrich). The beaker heater not only helps keep the reaction temperature constant, but can also supply heat to the sample at a rate such that the desired reaction temperature of 150 °C is recovered within a minute following addition of CF₃COOAg. The improved temperature control and uniformity leads to a single burst nucleation and a much more monodisperse population with a mean edge length of ~9 nm for 10 minutes of reaction (Fig. 2) and ~15 nm sized Ag templates for a reaction time of 15 min. The procedure for product collection was the same as the larger cubic Ag nanocubes. Table 1 shows the relationship between reaction time and nanocube average edge length for all these reactions as well as the gold nanoshells made from these silver templates.

Hollow Gold Nanoshell Synthesis

HGN were made via galvanic replacement chemistry from the appropriate batch of silver templates to create the desired size and shape HGN. A solution of Ag templates (5 mL) in Millipore treated water was slowly heated to 90 °C under magnetic stirring at 350 rpm and kept at 90 °C for 10 min. Then, the stirring speed was adjusted to 950 rpm and the appropriate volume of 1 mM HAuCl₄ in water was added dropwise into the reaction solution. The color changed from yellow to blue, suggesting the evolution of hollow gold nanoparticles. A UV-Vis spectrum from the reaction solution was used to determine the LSPR peak. The amount of HAuCl₄ was adjusted to fine tune the LSPR peak (Figs. 1–3). Once the reaction was complete, the samples were cooled, silver chloride was allowed to precipitate, and the supernatant containing the gold nanoshells was stored at 4°C until further use.

For a given size template, increasing the ratio of Au to Ag red-shifted the LSPR peak (Fig. 3A), which was associated with decreasing the thickness of the shell walls (Fig.4) ^[15,33]. For 5 ml of the as-prepared 30 nm cubic Ag templates, adding 300 – 600 μl of 1 mM HAuCl₄ solution increased the LSPR absorption maximum from 600 – 900 nm (Fig. 3A). HGN diameter and shell thickness was determined by spreading ~ 2 μl of sample suspension as onto lacey carbon TEM grids (Electron Microscopy Sciences), allowing the solvent to evaporate and imaging with transmission electron microscopy (FEI Technai Sphera G2). Silver template and HGN concentration and size distributions were measured using single particle tracking with a Nanosight NTA 2.3 particle-tracking device. The mean size given by TEM and particle tracking showed good agreement.

Steric Stabilization of Silver and Gold Nanoparticles

To minimize aggregation and settling during silver nanoparticle storage or during the galvanic replacement reaction, sodium citrate was added to make up a 5 mM solution after washing. The citrate binds to the Ag templates and provides an electrostatic barrier to aggregation. To stabilize the HGN after the galvanic replacement against aggregation, 750, 2000 and 5000 Da methoxy-PEG-thiol were allowed to bind to the HGN surface at a ratio of 1:10 mol PEG:Au overnight at room temperature. The excess PEG was removed by repeated washing and centrifugation steps. The PEGylated HGN were stable for weeks in water or saline.

Attaching HGN to Liposomes

Liposomes composed of dipalmitoylphosphatidylcholine (DPPC) (Avanti Polar Lipids; Alabaster, AI) and DSPE-PEG-2000-SH (Nanocs; New York, NY) were prepared by mixing at a 95:5 molar ratio at 25 mg/ml total concentration in chloroform in glass vials, and the solvent was removed overnight by evaporation under vacuum. The dried lipids were hydrated 30 minutes at 65℃ with TES buffer (51 mM NaCl, 50mM TES, NaN₃ 0.02 wt%, and 10 mM CaCl₂; pH 7.4) and extruded using an Avanti Mini-Extruder (Alabaster, AI) through Watson 100 nm polycarbonate filters. HGN were mixed with the thiol-PEG liposomes overnight at room temperature. Untethered HGN were removed by size-exclusion chromatography using a PD MidiTrap G-25 column (GE Healthcare) equilibrated with TES buffer at pH 7.4. HGN tethered liposomes were stored at 4 °C. The concentration of liposomes was adjusted by dilution with TES buffer to ~ 10⁸ liposomes/ml as determined by single-particle tracking with a Nanosight NTA 2.3 particle-tracking device. The mean size of the liposomes was 100 nm, also determined by Nanosight particle tracking and cryo-TEM imaging.

Nanobubble Generation and Detection in Flow

28 picosecond pulses of near infrared light of wavelengths 650 – 1000 nm of controlled fluence at a 50 Hz repetition rate were generated by pumping a PG403 optical parametric generator with a PL 2231 pulsed laser at 355 nm (Ekspla, Vilnius, Lithuania). A continuous wave Helium-Neon probe laser (632.8 nm,2 mW, polarized, HNL020L-JP, Thorlabs, Inc.) was used to detect the nanobubble generation. The pump and probe beams were focused onto a 0.2 mm ID square, hollow glass capillary of 0.1 mm wall thickness (#8320 Vitro Tubes, VitroCom, Mountain Lakes, NJ) in which the HGN suspension flowed. The pump beam diameter was set to 300 μm and was tilted at 15° so the pump beam would miss the lens used to collect the light from the probe beam, which was aligned normal to the capillary. The pump beam fluence was applied in the range 1–100 mJ/cm² and was measured by registering the image of the pump beam on the capillary and measuring the beam diameter at the sample plane with a photodetector/imaging device (Luka, Andor Technology, Northern Ireland). The pulse energy was measured using a pulse energy meter (Ophir Optronics, Ltd., Israel).

The continuous low power probe beam is scattered by the refractive index difference caused by the generation of nanobubbles around the HGN, and the light intensity measured by the photo-detector is collected by an oscilloscope (Teledyne LeCroy, Wavesufer MXs-8). A decrease in the transmitted light intensity is the characteristic signal of nanobubble generation and growth, followed by a rapid rise (100 nsec) in the transmitted intensity as the nanobubbles collapse. Nanobubbles are transient events, lasting a few hundred nanoseconds. The decrease in transmitted light intensity is due to the collective light scattering from a large number of nanobubbles being generated within the irradiated volume, rather than the scattering signal from single bubbles. We define the nanobubble threshold as an ~ 2% decrease in the normalized light intensity reaching the photodetector.

Silicone tubing (Ibidi®, I.D. 0.5 mm, wall thickness 0.8 mm) connected the optically transparent hollow glass capillary to a programmable Harvard Apparatus syringe pump 33 (Holliston, MA). All HGN suspensions were diluted to an optical density of 1 (OD =1) then pumped through the flow system at linear velocities of 3.8 – 42 mm/sec except as noted. Syringe pump settings were chosen to ensure a single pulse of the 50 Hz NIR light impinged on a given volume of the HGN suspension. After irradiation, the HGN suspension was passed through silicone tubing and collected in vials for further analysis. Operation of all hardware was controlled by a PC through custom software modules developed using the LabVIEW platform.

Electromagnetic simulations

Full-field finite-difference time-domain (FDTD) electromagnetic simulations were performed using numerical FDTD algorithms to extract the absorption and scattering cross sections ^[49]. The metal alloy was modeled following the data of Peña-Rodriguez et al. ^[41] for gold-silver alloys using the Drude model $\epsilon (\omega )={\epsilon }_{\infty }-\frac{{\omega }_p^2}{\left({\omega }^2+i\Gamma \omega \right)}$ where ε_∞ is the high-frequency dielectric constant, ω_p is the plasma frequency, and Γ is the damping parameter. To model alloys of different compositions with a Ag fraction of x_Ag, the complex permittivity followed the equation $\epsilon (\omega )=\left(8.6-4.6\ast x_{Ag}\right)-\frac{{\left(8.96+0.02x_{Ag}\right)}^2}{{\omega }^2+i\omega \left(0.06+0.47x_{Ag}-0.46x_{Ag}^2\right)}$ ^[41]. Water with a constant real permittivity of ℜ(ε)=1.77 was assumed to be both inside and outside the cube.