Cardiac ScoreCard: A Diagnostic Multivariate Index Assay System for Predicting a Spectrum of Cardiovascular Disease

Abstract

Clinical decision support systems (CDSSs) have the potential to save lives and reduce unnecessary costs through early detection and frequent monitoring of both traditional risk factors and novel biomarkers for cardiovascular disease (CVD). However, the widespread adoption of CDSSs for the identification of heart diseases has been limited, likely due to the poor interpretability of clinically relevant results and the lack of seamless integration between measurements and disease predictions. In this paper we present the Cardiac ScoreCard—a multivariate index assay system with the potential to assist in the diagnosis and prognosis of a spectrum of CVD. The Cardiac ScoreCard system is based on lasso logistic regression techniques which utilize both patient demographics and novel biomarker data for the prediction of heart failure (HF) and cardiac wellness. Lasso logistic regression models were trained on a merged clinical dataset comprising 579 patients with 6 traditional risk factors and 14 biomarker measurements. The prediction performance of the Cardiac ScoreCard was assessed with 5-fold cross-validation and compared with reference methods. The experimental results reveal that the ScoreCard models improved performance in discriminating disease versus non-case (AUC = 0.8403 and 0.9412 for cardiac wellness and HF, respectively), and the models exhibit good calibration. Clinical insights to the prediction of HF and cardiac wellness are provided in the form of logistic regression coefficients which suggest that augmenting the traditional risk factors with a multimarker panel spanning a diverse cardiovascular pathophysiology provides improved performance over reference methods. Additionally, a framework is provided for seamless integration with biomarker measurements from point-of-care medical microdevices, and a lasso-based feature selection process is described for the down-selection of biomarkers in multimarker panels.

1. Introduction

Cardiovascular disease (CVD) is a diverse class of diseases affecting the cardiovascular system. Although mortality rates are declining somewhat, CVD remains the leading cause of death and serious illness in the United States, accounting for nearly one of every three deaths (Go et al., 2014). With staggering direct and indirect costs, CVD is a major contributor to rising healthcare expenditure in the U.S. For instance, heart failure (HF) costs alone are projected to double by 2030, with every US taxpayer paying up to $244 each year (Heidenreich et al., 2013). The most common type of CVD is coronary artery disease (CAD), which is characterized by atherosclerotic plaque buildup that begins early in life and slowly progresses over time. About 50% of cardiovascular deaths occur due to sudden cardiac death, and a vast majority due to CAD (Mehta, Curwin, Gomes, & Fuster, 1997). In a significant proportion of these events, sudden cardiac death occurs without any history of CVD. These individuals may have only one, or none, of the traditional risk factors. Thus, novel biomarkers approaches may be necessary to supplement traditional risk factors in CVD diagnosis and prognosis. Early detection and frequent monitoring of both traditional risk factors and novel biomarkers has the potential to save lives and reduce unnecessary costs due to CVD morbidity and mortality.

To aid in disease identification and patient monitoring, clinical decision support systems (CDSSs) are being increasingly adopted to provide clinicians with personalized assessments or recommendations to assist in medical decisions. A popular topic in expert systems and artificial intelligence in medicine, a CDSS is defined as “any electronic system which aids in the clinical decision making process in which data from individual patients are used to generate personalized assessments or recommendations that are then presented to clinicians for consideration” (Kawamoto, Houlihan, Balas, & Lobach, 2005). The CDSSs have several advantages relative to standard of care including the potential for faster diagnosis, improved prediction performance, and reduced medical costs via elimination of unnecessary testing. However, clinicians may be reluctant to adopt certain CDSSs which are based on “black box” methods and provide results that are not easily interpreted in a clinical context. Likewise, lack of seamless integration between biomarker measurements and disease predictions may serve as a barrier to the broad-scale uptake of CDSS technologies. In an attempt to bridge this gap in this paper we present a CDSS for the prediction of a spectrum of CVD called the Cardiac ScoreCard. Based on a lasso logistic regression approach, the Cardiac ScoreCard algorithms combine patient demographics and novel protein biomarker data to form a single-valued “cardiac score” and clinically interpretable logistic regression coefficients. When fully developed, the Cardiac ScoreCard is intended to provide individualized assessments of cardiac health that are seamlessly integrated with biomarker measurements from point-of-care medical microdevices (McRae et al., 2015).

When fully developed, mass produced, and validated clinically, lab-on-a-chip systems have the potential to simplify lab analysis routines, reduce sample and reagent volumes, shorten analysis times, and lower the cost of healthcare. There is a strong need for these medical microdevices that are both cost-effective and analytically robust. The programmable bio-nano-chip (p-BNC) is a flexible detection platform that rivals established remote laboratory methods (Jokerst et al., 2011; McRae et al., 2015). Recent work has demonstrated the ‘macro’ laboratory based p-BNC’s multiplexed analyses of diverse analyte classes across several disease applications (Chou et al., 2012; Jokerst et al., 2010; Jokerst & McDevitt, 2009), for example, in the areas of HIV immune function (Rodriguez et al., 2005), cardiac heart disease (Christodoulides, Floriano, et al., 2005; Christodoulides, Mohanty, et al., 2005; Christodoulides et al., 2012; Floriano et al., 2009), ovarian cancer (Raamanathan et al., 2012), oral cancer (McDevitt et al., 2011), prostate cancer, and the detection of drugs of abuse (Christodoulides et al., 2015). While the p-BNC sensor platform offers a solution to the acquisition of cardiac biomarker measurements, the scope of this manuscript primarily covers the methods of converting biomarker and risk factor data streams into clinically usable and interpretable results. The various Cardiac ScoreCard models are intended to be used in conjunction with the p-BNC, but they may act as standalone calculators when provided the necessary input parameters.

The objective of this work is to develop predictive models for a spectrum of CVD and do so in a manner that can be integrated seamlessly with multi-parameter biomarker measurements. This paper will describe the process of developing the Cardiac ScoreCard and summarize the initial performance characteristics observed for two areas of cardiac disease, that is i) cardiac wellness and ii) HF diagnosis. The remainder of this paper is organized as follows. Section 2 reviews the literature for work related to CVD prediction models. Section 3 introduces the Cardiac ScoreCard approach and the role of biomarkers in CVD prediction. Descriptions of the clinical study data and the lasso logistic regression methods are provided in Section 4. Results and discussion for the cardiac wellness and HF models are covered in Section 5. Lastly, Section 6 concludes the paper with a brief summary of the models developed, their significance, and future directions.

2. Related work

2.1. Literature review

Clinical decision support tools are powerful expert systems with the potential to provide faster diagnoses, improved prediction performance, and reduced medical costs by eliminating unnecessary testing. Several clinical decision support systems and related prediction models for the identification of heart diseases have been developed over the years, implementing a variety of techniques. One of the most commonly used techniques is artificial neural networks (ANN) due to its superior prediction performance and ability to identify complex nonlinear patterns in the data (Kurt, Ture, & Kurum, 2008). In one of the first implementations for heart disease applications, an ANN was trained on chest pain patients presenting to the emergency room for the diagnosis of AMI (Baxt, 1991). Similarly, Furlong, Dupuy, & Heinsimer (1991) developed an ANN for diagnosing AMI using serial cardiac enzyme data. Yan, Jiang, Zheng, Peng, & Li (2006) implemented a multilayer perceptron-based model that can differentially diagnose five different cardiac outcomes. Mehrabi, Maghsoudloo, Arabalibeik, Noormand, & Nozari (2009) compared multilayer perceptron and radial basis function neural networks for the discrimination of HF and COPD in 266 patients and 42 clinical variables.

Aside from neural networks, various other techniques have been successfully implemented. Conforti & Guido (2005) used a Support Vector Machine (SVM) approach to classify AMI and non-case patients. Ion Titapiccolo et al. (2013) supported the use of random forest models in predicting cardiovascular outcomes in hemodialysis patients due to their ability to learn non-linear patterns in the feature space. Vila-Francés et al. (2013) employed a Bayesian network for the prediction of UA. Bayesian models are attractive for clinical use because the relationships among variables are represented by a graph and are, thus, easily interpreted by clinicians. Ensemble methods are a useful strategy for increasing the generalization performance by combining the posterior probabilities or predicted values from several base learners. Das, Turkoglu, & Sengur (2009) improved prediction performance using an ANN ensemble method for heart disease diagnosis on the Cleveland heart disease database. A. Wang, An, Chen, Li, & Alterovitz (2015) developed a low-cost and non-invasive screening system for hypertension based on a hybrid logistic regression and an ANN model using only simple demographic data from questionnaire responses.

Feature selection is an important step in developing predictive models that eliminates irrelevant or redundant input parameters, resulting in reduced model complexity and improved generalization ability. Various feature selection methods have been attempted within the context of diagnosing heart diseases. For example, Nahar, Imam, Tickle, & Chen (2013) identified several key risk factors which contribute to heart disease using an association rule mining approach. Shilaskar & Ghatol (2013) implemented a hybrid forward selection technique and SVM classifier which improved classification accuracy of various cardiovascular diseases. Shi et al. (2011) combined various feature selection approaches to identify a small subset of proteins and metabolites for the diagnosis of UA.

There are multiple scoring systems that profile CVD progression that have been widely adopted for risk estimation and clinical decision making. The Framingham 10-year CVD risk score (D’Agostino et al., 2008) and Reynolds score (Ridker, Buring, Rifai, & Cook, 2007; Ridker, Paynter, Rifai, Gaziano, & Cook, 2008) predict CVD risk. A multi-parameter model with carotid intima-media thickness, presence of plaque, and traditional risk factors improved coronary heart disease risk prediction in the Atherosclerosis Risk in Communities (ARIC) study (Nambi et al., 2010). Recently, the Pooled Cohort Risk Equations expand utility and improve generalizability by combining several large cohort studies and is currently recommended for estimating 10-year risk for a first atherosclerotic CVD event (Goff et al., 2013). The Thrombolysis in Myocardial Infarction (TIMI) risk score (Antman et al., 2000) estimates mortality for patients with unstable angina (UA) and non-ST elevation myocardial infarction (NSTEMI). The Seattle Heart Failure Model (Levy et al., 2006; Mozaffarian et al., 2007) and Framingham profiles (Kannel et al., 1999) estimate risk of congestive HF. Individually, these scores only provide narrow coverage across the broad spectrum of CVD progression. Additionally, many risk scores underutilize novel biomarker approaches, which, when combined with traditional risk factors, have been shown to boost prediction performance (Allen, 2010; Blankenberg et al., 2010; Kim et al., 2010). Despite the promise of increased performance, widespread adoption of multimarker assays and associated risk scores have not yet occurred, likely due to the absence of key technologies that seamlessly integrate biomarker measurements with disease prediction algorithms.

Some CDSSs for heart diseases have been applied to unique datasets with the inclusion of both patient demographic information and novel cardiac biomarker measurements. Notably, Eom, Kim, & Zhang (2008) performed differential heart disease diagnosis of normal, stable angina, UA, and AMI based on aptamer chip data using an ensemble with support vector machines, neural networks, decision trees, and Bayesian networks. Nambi et al. (2013) combined troponin T and N-terminal pro-B-type natriuretic peptide (NT-proBNP) with age and race in a gender-specific model to improve HF prediction performance in the ARIC study. Similarly, Blankenberg et al. (2010) used a lasso logistic regression approach with 30 biomarkers and demographics for 10-year cardiovascular risk estimation. However, to our knowledge no previous studies have documented a multivariate index assay system for a spectrum of CVD that takes into account the practicality of parameter selection in building point-of-care compatible multimarker panels. The bridge between model development/validation and integrated point-of-care testing represents a key step in moving these promising theoretical approaches into main stream clinical practice (McRae et al., 2015) and is made possible via novel biosensing technologies, such as the recently developed p-BNC platform (Fig. 1). The portable p-BNC system shown here, comprising disposable cartridges and a portable analyzer, automates complicated clinical measurement processes and analyses to provide intuitive “sample-to-answer” results in much less time than conventional methods. Compared to other CDSSs, the Cardiac ScoreCard system adds substantial value to clinicians and healthcare providers by streamlining patient sample collection, biomarker measurements, machine learning algorithms, electronic medical records, and intuitive health report cards.

Fig. 1.

The recently developed p-BNC platform streamlines multimarker measurements with disease-specific machine learning algorithms, such as the Cardiac ScoreCard, to provide intuitive indices of health status at the point-of-care. The p-BNC analyzer is shown both with (left) and without (right) the enclosure.

3. The Cardiac ScoreCard approach

Significant efforts over the past few decades have focused on translating biomarker assays to clinical practice. Most often, these efforts involve a long and uncertain pathway to discover, validate, and attain regulatory approval of a biomarker or panel of biomarkers for a specific application. However, this approach is enormously expensive and takes years to decades to complete (Rifai, Gillette, & Carr, 2006). Here, we describe a new cost- and time-effective pathway from discovery to clinical application through the development of the Cardiac ScoreCard. The Cardiac ScoreCard is an in vitro diagnostic multivariate index assay (IVDMIA), a device that uses multiple variables in an interpretation function to yield a single patient-specific result intended to diagnose, treat, or prevent disease and provides a result which cannot be independently derived by the end user (FDA, 2007). The ScoreCard features a multiplexed panel of 14 cardiac biomarkers that can be applied in many ways depending on setting, symptoms, and medical history (Fig. 2). Using measurements from a single chip format for multiple disease applications has the potential to significantly reduce time and costs associated with assay development and validation. This approach of making one chip for multiple applications leverages one of the key features of microelectronics whereby enormous scalability advantages are secured by using standardized fabrication strategies and chip architectures with capacity to scale. In the clinical diagnostics area, developing a broad range of capabilities through the creation of a platform that can service multiple related applications has potential to streamline the development and regulatory approval process. This holistic diagnostic tool development strategy described here underlies what may be a new paradigm in multi-parameter clinical diagnostics. It is in this capacity that the ScoreCard’s predictive algorithms encompass three cardiovascular states: cardiac wellness, AMI, and HF.

Fig. 2.

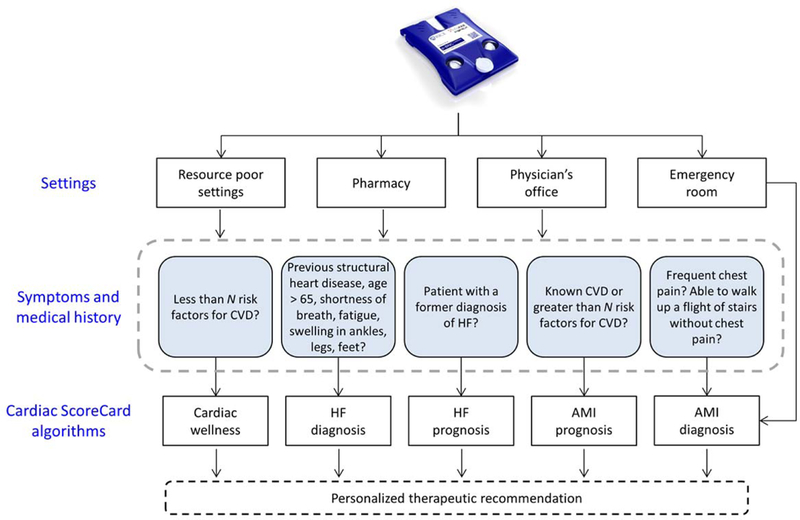
The Cardiac ScoreCard uses biomarker measurements and traditional risk factors to make predictions and therapeutic recommendations for a spectrum of cardiovascular disease (CVD). In this study, biomarker measurements were completed using standard methods including ELISA, LUMINEX, and Beckman Coulter Access; however, future measurements will be completed using the p-BNC (top figure). The choice of Cardiac ScoreCard model largely depends on the context of the test based on the individual’s setting, symptoms, and medical history. This study describes the development of Cardiac ScoreCard algorithms for cardiac wellness and heart failure (HF) diagnosis, while acute myocardial infarction (AMI) diagnosis and prognostic models for HF and AMI will be covered in future publications.

Currently, cardiac wellness testing relies in part on lipid profiling; however, nearly 50% of all heart attacks and strokes occur in patients with normal lipid levels (Ridker, Rifai, Rose, Buring, & Cook, 2002). Thus, there is need for a multimarker approach to risk profiling by supplementing lipid measurements with indicators of inflammation and plaque instability. The ScoreCard not only identifies high versus low risk individuals, but also provides a Cardiac Score that is indicative of overall cardiac health status. This wellness ScoreCard has potential in the future to be used by individuals in many settings such as pharmacies, clinics, workplaces, and homes. The ultimate goal of the cardiac wellness ScoreCard is CVD prevention by empowering individuals with a new tool to take control of their own heart health. Another advantageous feature of the wellness ScoreCard is that it uses the same panel as AMI (to be described in future publications) and HF ScoreCards, effectively creating an archive of baseline measurements for biomarkers of myocardial injury and hemodynamic stress.

Current guidelines recommend rapid response time in diagnosing AMI such that results are available as soon as possible, ideally within 60 minutes (Anderson et al., 2013). However, long delays in diagnosis often occur due to inefficiencies in central laboratory infrastructure. The AMI ScoreCard and the p-BNC have the potential to serve as a rapid point-of-care device that can diagnose AMI at the patient bedside within minutes. The AMI ScoreCard may also be used in ambulances, low-resource settings, and rural communities where timely diagnoses may significantly improve survival rates. Similarly, early and accurate diagnoses may improve outcomes for patients with HF (Roger et al., 2004). The condition of HF may be difficult to diagnose due to the presentation of non-specific symptoms. Furthermore, the differential diagnosis of HF often requires numerous expensive procedures to obtain surrogate measures of cardiac function. However, natriuretic peptides such as brain natriuretic peptide (BNP) or NT-proBNP assays have shown significant potential for detecting, monitoring, and even guiding treatment (Doust, Lehman, & Glasziou, 2006). Although models for AMI diagnosis, AMI prognosis, and HF prognosis are possible with these ScoreCard approaches, they are out of scope for the current study.

3.1. Biomarkers of CVD

Evidence has shown that employing a multimarker strategy with a pathobiologically diverse set of biomarkers adds substantial predictive information in the risk assessment of ACS (Morrow & Braunwald, 2003; Sabatine et al., 2002). Likewise, we hypothesize that by selecting a panel of biomarkers that are differentially expressed across all stages of CVD progression through different pathways, there will be opportunities to improve risk prediction. Also important is the relationship between biomarker levels. In general, a few uncorrelated predictors will perform better than many strongly correlated predictors. Since biomarkers from the same pathophysiology are often correlated with each other, it is advantageous to use uncorrelated biomarkers expressed in various stages of CVD through different pathophysiological pathways. Fig. 3 shows the biomarkers in this study grouped by their known CVD pathophysiology (Vasan, 2006) and relationships via Pearson correlation coefficient matrix generated using data from the current study, as described in Section 4. As plaque begins to form, mature, destabilize, and rupture, leading to the manifestation of ischemia, thrombosis, myocardial damage, and subsequent myocardial remodeling certain cardiac biomarkers are differentially expressed (Naghavi et al., 2003). The relative expression of these biomarkers forms a signature that may be used to pinpoint the status of an individual’s CVD pathophysiology.

Fig. 3.

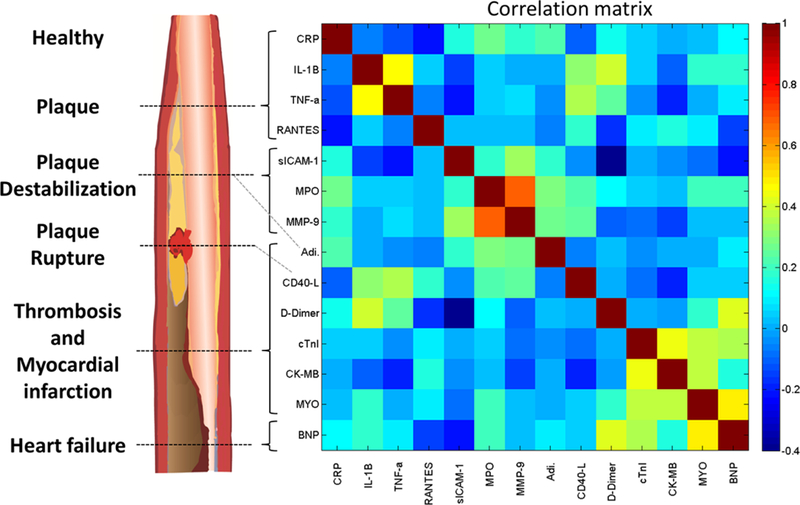
Cardiac biomarkers grouped by known CVD pathophysiology and Pearson correlation coefficient matrix. An idealized diagram (left) shows stages of atherosclerotic plaque development and associated biomarkers. A correlation matrix (right) shows the Pearson correlation coefficient matrix of evaluable data for all patients (N = 579). Correlations are derived from log-normalized, standardized, and imputed median serum biomarker concentrations across all time points for all patient outcomes in the current study. Details of the clinical studies and data handling procedures are described in Section 4.

It is important to note that some cardiac biomarkers are not specific to a single pathway, but may be expressed in multiple CVD pathways. For example, BNP is marker of hemodynamic stress that is released during ischemia and often monitored in patients with heart failure; however, it is also elevated upon ventricular wall stress and may be used as a predictor for other vascular events. Moreover, BNP is secreted almost exclusively from the heart and is thus more sensitive than non-specific markers that are secreted from other tissues (T. J. Wang, 2010). Similarly, cardiac troponins (cTn), first recognized as biomarkers for AMI (Cummins, Auckland, & Cummins, 1987), are the standard biomarkers for diagnosis of myocardial damage. However, recent developments in ultra-high sensitivity assay technology show that low levels of elevated troponin yield prognostic information for individuals without known cardiovascular disease (Eggers, Jaffe, Lind, Venge, & Lindahl, 2009; Zethelius, Johnston, & Venge, 2006; Kociol et al., 2010; Saunders et al., 2011). The information encoded in biomarkers from various CVD pathways has enormous potential for diagnostic and prognostic applications.

4. Data and Methods

4.1. Logistic regression

Logistic regression is well-suited for use in diagnostic models. For one, logistic regression allows the analysis of dichotomous outcomes with two mutually exclusive levels, e.g., disease and non-case, and the logistic regression is regarded as the standard method of analysis for this situation (Hosmer & Lemeshow, 2004; LaValley, 2008). Additionally, unlike most other classification models in statistical learning, logistic regression is probabilistic and is thus more intuitive than its non-probabilistic counterparts. Both the logistic regression’s interpretability and ability to function as a dichotomous classifier has given rise to its widespread popularity in the clinical community. Logistic regression models are fit using maximum likelihood given by

$$\underset{\beta ,{\beta }_0}{\max }\left\{\sum _{i=1}^N[y_i({\beta }_0+{\beta }^T{x}_i)-\log (1+e^{{\beta }_0+{\beta }^T{x}_i})]\right\}$$ (Eq. 1)

where x_i are the inputs, y_i are the responses, and β are the coefficients (Hastie, Tibshirani, & Friedman, 2009). In the following section, we apply a lasso penalty to the logistic regression to perform model shrinkage and selection.

4.2. Lasso penalty for model shrinkage and selection

When there are many correlated parameters in a logistic regression model, their coefficients may exhibit high variance. Imposing a size constraint, or shrinkage, on the coefficients alleviates this problem. The lasso penalty is a method for performing shrinkage that was originally introduced for use in least squares regression (Tibshirani, 1996); however, it may be applied to other methods such as the logistic regression. Perhaps the most notable property of the lasso is its ability to perform automatic parameter selection. The goal of parameter selection is to retain a subset of the relevant predictors and discard the rest. Alternative methods perform subset selection in a stepwise fashion, which is a discrete process (i.e., variables are either retained or discarded), and it often exhibits high variance and does not reduce prediction error of the full model (D. Wang, Zhang, & Bakhai, 2004). On the other hand, shrinkage methods like the lasso are more continuous and do not suffer as much from high variability (Hastie et al., 2009). Here, the lasso method makes a size constraint on parameters subject to the L₁ lasso penalty, $\sum _{j=1}^p|{\beta }_j|$ , and the log-likelihood can be written as:

$$\underset{\beta ,{\beta }_0}{\max }\left\{\sum _{i=1}^N[y_i({\beta }_0+{\beta }^T{x}_i)-\log (1+e^{{\beta }_0+{\beta }^T{x}_i})]-\lambda \sum _{j=1}^p|{\beta }_j|\right\}$$ (Eq. 2)

Here, λ is the complexity parameter that controls amount of shrinkage. Cross-validation is used to adaptively select an appropriate λ that minimizes the deviance. Fig. 4 demonstrates this concept through the L₁ regularization path for HF diagnosis as an example. The coefficients, β_j, are evaluated for each parameter as λ is varied between 0 and 1. When λ = 0, the coefficients are simply those given by logistic regression (Eq. 1). However, as λ increases, the coefficients shrink towards zero and towards each other. Increasing λ may also make some coefficients exactly zero; thus, the lasso performs a kind of continuous subset selection that is preferable over stepwise methods. Note that the intercept term β₀ is excluded from the L₁ penalty because penalization of the intercept would introduce bias dependent on the origin of y when selecting the penalty term. The cross-validated λ that minimizes the deviance of the test set is often selected for the final model; however, λ one standard error (SE) above the minimum deviance may be used to obtain a more sparse solution and to avoid the potential effects of an asymptotic deviance at low values of λ.

Fig. 4.

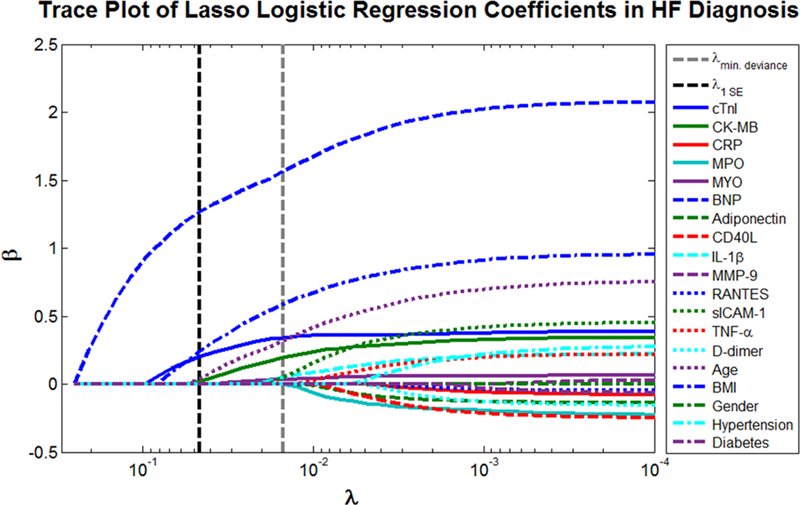
Trace plot of coefficients fit by lasso logistic regression for HF diagnosis. When λ is close to 0, the ordinary logistic regression estimates emerge. As λ increases, the coefficients shrink towards zero and towards each other.

4.3. Description of clinical studies

The Cardiac ScoreCard models were developed using data merged from two clinical studies. A cross-sectional biomarker discovery study at the University of Kentucky (UK) previously described (Christodoulides et al., 2012; Floriano et al., 2009) identified 13 relevant biomarkers for screening AMI. Serum and salivary samples were collected from AMI patients (N = 90) 0 to 48 hours from presentation to the emergency department (ED) and recruited healthy controls (N = 100). The primary outcomes of this study are ST segment elevation MI (STEMI), non-ST segment elevation MI (NSTEMI), and control. Biomarkers measured include cTnI, creatine kinase MB (CK-MB), C-reactive protein (CRP), myeloperoxidase (MPO), myoglobin (MYO), BNP, adiponectin, CD40 ligand (CD40L), interleukin-1 beta (IL-1β), matrix metalloproteinase 9 (MMP-9), regulated on activation normal T cell expressed and presumably secreted (RANTES), soluble intracellular adhesion molecule 1 (sICAM-1), and tumor necrosis factor alpha (TNF-α). These data were supplemented with preliminary data from a similar clinical study focusing on AMI diagnosis in the Texas Medical Center (TMC) in Houston, TX (clinical finding results to be published separately). Patients who presented to the ED with chest pain or AMI related symptoms (N = 389) and at least 21 years of age were enrolled. Serum samples were collected at 1, 3, 6, and 12 hours after presentation to the ED. Samples were assayed for the same 13 cardiac biomarkers and D-dimer via gold standard methods (e.g., ELISA, LUMINEX, and Beckman Coulter Access). The outcomes of this study were acute coronary syndrome (ACS) comprising STEMI, NSTEMI, and unstable angina (UA), indeterminate, unknown, non-case chest pain, congestive HF, and chronic kidney disease (CKD). The distributions of patient outcomes from the merged clinical studies are summarized in Table 1.

Table 1.

Number and percent of total patient outcomes (N = 579) from merged clinical study data.

Outcome	N (%)
Healthy control	100 (17)
Non-case chest pain	182 (31)
HF	81 (14)
ACS	145 (25)
Unstable angina	31 (5)
NSTEMI	48 (8)
STEMI	66 (11)
Indeterminate	17 (3)
Unknown	4 (1)
CKD	50 (9)

4.4. Cardiac wellness

Fig. 5 summarizes the flow of patient data for the development of the cardiac wellness model. A lasso logistic regression model was developed using data from two clinical studies, UK (N = 100) and TMC (N = 389). Here, only recruited healthy controls were included from the UK study whereas no healthy patients were enrolled in the TMC clinical study. Patients from UK presenting with UA, HF, CKD, indeterminate, or unknown status (N = 207) were excluded from the analysis. Patients with substantial data missing (> 50%) across the evaluated parameters were also excluded (N = 33). The remaining patients (N = 249) were dichotomized into two classifications, high risk (N = 154) and low risk (N = 95), according to the presence of morbidities associated with CVD risk described as follows.

Fig. 5.

Cardiac wellness model data flow and inclusion criteria.

One of the challenges in developing a model for cardiac wellness is the difficulty of obtaining relevant clinical endpoints which directly reflect health status. Long-term prospective studies like the Framingham Heart Study are particularly well-suited for gathering hard clinical endpoints such as morbidity and mortality; however, these studies are enormously expensive and take decades to complete. Here, to make immediate progress towards new model development, we use a risk stratification approach to develop a model of overall cardiac wellness. Several approaches to grouping patients by risk have been explored, such as counting risk factors for persons without known CVD or diabetes (Expert Panel on Detection, 2001) and grouping patients according to Framingham scores for low risk (< 6% in 10 years), medium risk (6–20% in 10 years), and high risk (> 20% in 10 years) (Greenland, Smith Jr., & Grundy, 2001). Here we classified subjects into low and high risk groups using the presence of hyperlipidemia, hypertension, stroke, diabetes, previous MI, and known CAD as risk factors. Patients with one or more risk factors were categorized as high risk for CVD while patients with zero risk factors were categorized as low risk. A logistic regression model with lasso penalty was trained using risk determination and a total of 18 parameters including age, gender, body mass index (BMI), smoking, and 14 cardiac biomarker measurements. Since the patient outcomes were defined by the number of risk factors present, it was necessary to exclude these factors as parameters in the model to avoid overfitting. Therefore, cholesterol, blood pressure, and diabetes were not included in the model parameters.

4.5. HF diagnosis

The development of the HF model follows a similar procedure. Fig. 6 reveals the flow of patient data for development of the HF diagnostic model. Again, a lasso logistic regression model was developed using data from two clinical studies, UK (N = 190) and TMC (N = 389). Patients presenting with UA, NSTEMI, STEMI, indeterminate, or unknown status (N = 171) were excluded from the analysis. Patients with substantial data missing (> 50%) across the evaluated parameters were also excluded (N = 52). The remaining patients (N = 356) were dichotomized into two classifications, HF (N = 83) and non-case (N = 273), according to history of HF or HF at admission. A total of 19 parameters were considered in this HF diagnostic model including diabetes, hypertension, gender, BMI, age, and 14 cardiac biomarker measurements.

Fig. 6.

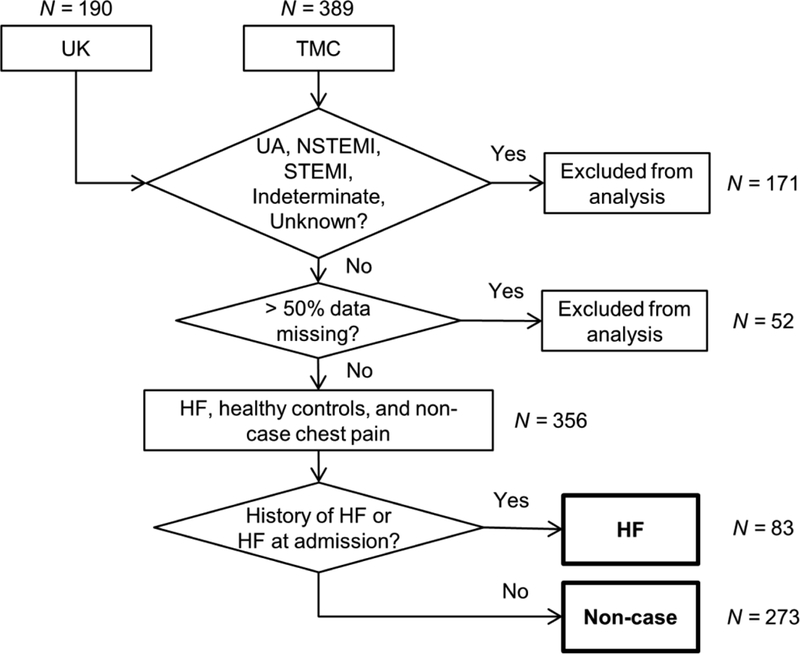
HF model data flow and inclusion criteria.

4.6. Data standardization and imputation

For both models continuous parameters, not including age and BMI, were transformed with natural log. Then, all data were standardized with zero mean and unit variance. Biomarker measurements that were below the limit of detection (LOD) were reassigned to their respective LOD, and biomarker concentrations recorded above assay range were set to the assay upper limit. Median biomarker concentrations across 1, 3, 6, and 12 hour time points were used for the models.

Missing data were imputed with a multiple imputation procedure in statistical software R using the multivariate imputation by chained equations (MICE) algorithm (Buuren & Groothuis-Oudshoorn, 2011). Multiple imputation is the preferred method for solving complex incomplete data problems (Buuren & Groothuis-Oudshoorn, 2011; Rubin, 1987), and it attempts to simulate the process that created the missing data and preserve relations in the data. Uncertainty regarding the relations between missing data are accounted for in the magnitude of differences between imputed data sets. The imputation procedure was performed in three main steps. For the purpose of this study, the data were assumed missing at random. First, a total of ten imputations were generated using predictive mean matching and logistic regression imputation models for numeric and categorical data, respectively. Then, model training and selection were performed on each individual imputed data set. Lastly, the performance of the trained models, including area under the receiver operating characteristic (ROC) curve (AUC), sensitivity, specificity, positive predictive value (PPV), and negative predictive value (NPV), were evaluated for pooled Cardiac ScoreCard estimates.

4.7. Model training and selection

The same model training and selection procedure was performed for cardiac wellness and HF models. The data were first partitioned using stratified 5-fold cross-validation, preserving the relative proportions of disease outcomes across each fold, with four folds for training and one fold for testing. For each iteration of cross-validation, models were trained for each m = 10 imputed datasets. Models were trained by fitting lasso penalized logistic regression coefficients using 50 log-linearly spaced λ values between 0 and 1. Deviance was estimated using 5-fold cross-validation within the training set, separating the data into four folds for the partial training set and one fold for validation set. Models were selected for λ that minimized deviance of the validation set (for cardiac wellness model) or for λ one SE above the minimum deviance (for HF model). The selected model was then retrained using the full training set, and the training error and test error were evaluated for each imputed dataset. The logistic regression probability, or “score”, was evaluated for the test set. The mean scores of the imputed datasets were evaluated for each fold. The mean score across each fold was evaluated, and predicted class labels were defined as “case” if the corresponding score was greater than the optimal cutoff given by ROC analysis.

4.8. Internal validation and performance metrics

Models were internally validated with 5-fold cross-validation, and performance was measured by AUC, sensitivity, specificity, PPV, and NPV. Discrimination improvement was determined by measuring difference in AUC of the ScoreCard and various reference methods using a one-sided test of significance with p = 0.05 (Hanley & McNeil, 1982). The cardiac wellness model discrimination was compared against the Framingham 10-year CVD risk score and a model comprising only the 14 biomarker panel. The Framingham risk score was calculated for each patient using methods described previously (D’Agostino et al., 2008), and the risk predictions were informed by the ROC’s optimal cutoff value. A lasso logistic regression model comprised of the 14 biomarkers was developed using the same approach as described. Cardiac wellness model calibration was performed by sorting patients into deciles of risk, and the Hosmer-Lemeshow goodness of fit statistic was used to determine whether the model adequately fits the data. The HF diagnosis model performance was compared with BNP, and the optimal cutoff from ROC analysis was used (67.0 pg/mL).

Hereafter, we refer to each model as a “ScoreCard” with the outcome of each model, or probability, denoted as the “Cardiac Score”. For the cardiac wellness model, Cardiac Score is treated as an indicator for overall cardiac wellness status, whereas in the HF model, Cardiac Score is used to generate disease predictions for diagnostic purposes and is evaluated as such. The difference in scoring procedure here employed reflects the anticipated end use criteria whereby the wellness model is expected to be used by the consumer wellness community and the HF model is projected to be used more directly by the clinical community.

5. Results and Discussion

5.1. Cardiac wellness results

A lasso logistic regression model for the prediction of cardiac wellness was developed. Fig. 7A shows ROC curves for Framingham 10-year CVD risk score, biomarker model, and the ScoreCard. The performance of each model is summarized in Table 2. The Framingham risk score shows satisfactory discrimination between risk groups (AUC = 0.7975 [95% CI, 0.7431, 0.8518]). The ScoreCard (AUC = 0.8403 [95% CI, 0.7924, 0.8881]) increases AUC over Framingham by 0.0428 (p = 0.1222). Biomarkers alone exhibited slightly worse discrimination than Framingham and the ScoreCard (AUC = 0.7664 [95% CI, 0.7087, 0.8241]). The ScoreCard significantly improves AUC over the biomarker model by 0.0739 (p = 0.0260), demonstrating the importance of traditional risk factors in new biomarker models. Fig. 7B shows good calibration of Cardiac Score with observed proportions of high risk patients across deciles of predicted risk. A non-significant result of the Hosmer-Lemeshow goodness of fit test suggests there is no evidence of a poor fit (p = 0.9754).

Fig. 7.

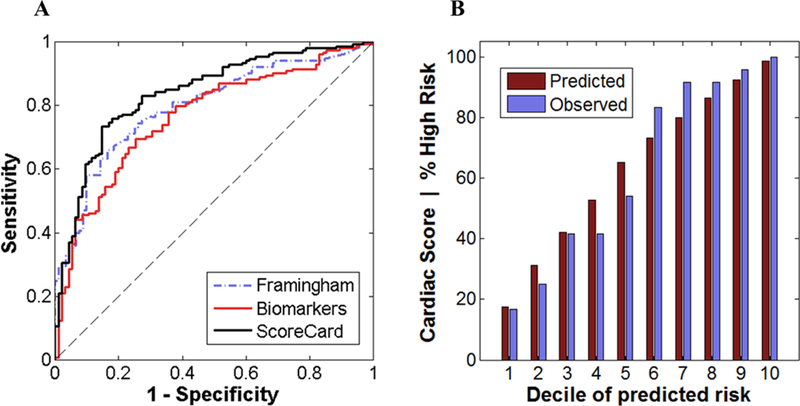
Cardiac wellness model discrimination and calibration. (A) The ROC curves for Framingham 10-year CVD risk score, a biomarker model, and the Cardiac ScoreCard. (B) Plot showing calibration for the wellness ScoreCard for patients sorted by deciles of predicted risk. Both discrimination and calibration results were generated using median diagnosis predictions and mean ScoreCard values across 10 imputations from stratified 5-fold cross-validated test sets.

Table 2.

Summary of performance for Framingham 10-year CVD risk, a model with only biomarkers, and Wellness ScoreCard. Sensitivity, specificity, PPV, and NPV (95% confidence intervals) are determined by optimal cutoff given by ROC analysis.

	Framingham	Biomarkers	Wellness ScoreCard
AUC	0.7975 (0.7431 – 0.8518)	0.7664 (0.7087 – 0.8241)	0.8403 (0.7924 – 0.8881)
Sensitivity	0.7403 (0.6803 – 0.7929)	0.6948 (0.6329 – 0.7508)	0.7597 (0.7009 – 0.8107)
Specificity	0.7474 (0.6878 – 0.7994)	0.7474 (0.6878 – 0.7994)	0.8211 (0.7665 – 0.8659)
PPV	0.8261 (0.7720 – 0.8703)	0.8168 (0.7619 – 0.8621)	0.8731 (0.8238 – 0.9111)
NPV	0.6396 (0.5763 – 0.6988)	0.6017 (0.5378 – 0.6625)	0.6783 (0.6158 – 0.7353)
Training error	-	-	0.2112
Test error	-	-	0.2429

Out of the 18 input parameters, the lasso penalty selected 15 (given by nonzero coefficient) with BMI (β_BMI = 0.8243), smoking (β_Smoking = 0.4711), age (β_Age = 0.4457), serum myoglobin (β_MYO = 0.3440), gender (β_Gender = 0.1939), and serum IL-1β (β_IL-1β = 0.1689) having the largest effect sizes (Table 3). These results suggest that, in addition to the important traditional risk factors, multiple biomarkers representing a diverse pathophysiology are necessary for assessing and predicting cardiac wellness.

Table 3.

Lasso logistic regression coefficients for Wellness and HF ScoreCards.

	Wellness ScoreCard	HF ScoreCard
β0 (intercept)	−0.0081	−1.6448
βcTnI	0.0986	0.2794
βCK-MB	0	0
βCRP	0.1450	0
βMPO	0.0026	0
βMYO	0.3440	0
βBNP	0.1046	1.5120
βAdiponectin	−0.0626	0
βCD40L	0	0
βIL-1β	0.1689	0
βMMP-9	0	0
βRANTES	−0.1021	0
βsICAM-1	−0.1642	0
βTNF-α	−0.0225	0
βD-dimer	0.0775	0
βAge	0.4457	0.0610
βBMI	0.8243	0.2485
βGender	0.1939	0
βSmoking	0.4711	*
βHypertension	*	0
βDiabetes	*	0

^*Parameter excluded from the model

The combination of multiple biomarkers and selected traditional risk factors into a multivariate index assay shows strong potential for discriminating high risk and low risk patients. However, one limitation in this study is that the models were trained using samples collected in the context of cardiac events. Thus, these models may need to be optimized further to service scenarios where preventative measurements are taken prior to an event. Also, our comparison of the Cardiac ScoreCard with the Framingham Risk Score is biased as the number of risk factors (presence of hyperlipidemia, hypertension, stroke, diabetes, previous MI, and known CAD) determined the high and low risk categories. Nonetheless, the acquisition of data using these convenient samples has provided quicker access to the initial models here presented.

5.2. HF diagnosis results

A lasso logistic regression model for the diagnosis of HF was developed. Fig. 8 shows ROC curves for BNP and Cardiac ScoreCard, and the performances of the ScoreCard and BNP are summarized in Table 4. The BNP values show adequate discrimination in diagnosing HF (AUC = 0.9320 [95% CI, 0.8936, 0.9704]). The ScoreCard (AUC = 0.9412 [95% CI, 0.9053, 0.9771]) shows slight improvements in AUC by 0.0092 (p = 0.3659).

Fig. 8.

The ROC curves for BNP and the HF ScoreCard. Results were generated using median diagnosis predictions across 10 imputations from stratified 5-fold cross-validated test sets.

Table 4.

Summary of performance for HF ScoreCard versus BNP. Sensitivity, specificity, PPV, and NPV (95% confidence intervals) are determined by optimal cutoff given by ROC analysis.

	BNP	HF ScoreCard
AUC	0.9320 (0.8936 – 0.9704)	0.9412 (0.9053 – 0.9771)
Sensitivity	0.8313 (0.7871 – 0.8684)	0.8554 (0.8133 – 0.8899)
Specificity	0.8959 (0.8580 – 0.9252)	0.9145 (0.8790 – 0.9410)
PPV	0.7113 (0.6604 – 0.7577)	0.7553 (0.7063 – 0.7988)
NPV	0.9451 (0.9145 – 0.9661)	0.9535 (0.9245 – 0.9727)
Training error	-	0.1614
Test error	-	0.1810

This lasso-based parameter selection approach resulted in a sparse model with four non-zero parameters: BNP (β_BNP = 1.5120), cTnI (β_cTnI = 0.2794), BMI (β_BMI = 0.2485), and age (β_Age = 0.0610) with all other parameter coefficients having no effect on the response (Table 3). As expected from the literature, BNP is the strongest indicator for presence of HF. From a practical standpoint, this sparse model of HF diagnosis prioritizes two out of the original 14 biomarkers, thus reducing costs and minimizing assay complexity.

Although improvements in discrimination were non-significant, the ScoreCard demonstrates its utility as a diagnostic indicator for HF. Here, sensitivity, specificity, PPV, and NPV are given for the optimal ROC cutoff, but the ScoreCard may be tuned for ruling in and ruling out HF in various clinical decision scenarios.

6. Conclusions

In this paper, we presented the Cardiac ScoreCard—a CDSS for the diagnosis and assessment of a spectrum of cardiovascular disease. There are several contributions that distinguish our approach from the previous work related to expert systems. (1) We combine patient demographics and novel biomarker measurements from a diverse pathophysiology to predict multiple CVD outcomes. One of the strengths of logistic regression is its ability to predict the presence of a disease based on independent variables which are continuous, categorical, or both. Our results suggest that augmenting the traditional risk factors (categorical) with a multimarker panel of protein biomarkers (continuous) provides improved performance over reference methods in both HF and wellness prediction. (2) To overcome issues with interpretability in CDSSs, we provide not only disease predictions, but also clinical insights in the form of logistic regression coefficients. Although other CDSSs that use “black box” methods (e.g., ANNs and SVMs) often outperform other more basic learners in terms of classification performance, they are not easily interpreted by clinicians because of their non-linear weights and feature mappings. In general, these methods do not provide interpretable rationale for diagnostic decisions, nor do they provide the requisite information needed to make patient-specific recommendations for treatment. (3) We provide a framework for the integration with point-of-care medical microdevices. The Cardiac ScoreCard leverages a single biomarker panel for multiple CVD applications. Consequently, this approach has the potential to greatly reduce costs and time associated with assay development, validation, and approval. While many CDSSs reported previously are largely decoupled from the data source, the Cardiac ScoreCard is intricately linked to the clinical testing method (McRae et al., 2015) and, as a result, may provide substantial added value to healthcare providers. Furthermore, the lasso-based parameter selection approach used in this study plays an important role in the down-selection of relevant biomarkers. In general, input variables should be highly correlated with the response, but uncorrelated with each other. Additionally, when developing a multiplexed immunoassay it is critically important to limit the total number of biomarkers assayed to a reasonable amount in order to alleviate the effects of non-specific binding and also to reduce cost associated with expensive antibody reagents. The lasso-based approach developed here plays a practical role in parameter reduction by selecting the relevant biomarkers for inclusion in multiplex panels.

Despite the unique contributions of the Cardiac ScoreCard approach, this study has several limitations. First, only a single classification technique was applied and compared to reference methods. As reported previously, the feature space of cardiac-related data may contain nonlinear patterns that would otherwise be undetectable without the use of nonlinear classification methods (Kurt et al., 2008). In future studies, a variety of techniques (e.g., ANNs, SVMs, decision trees, Bayesian networks, logistic regression, etc.) should be compared side-by-side. In addition, ensembles combining these base learners should be developed to further improve model performance and generalization. Second, model performance was estimated here using cross-validation. Validation using an external and independent test set will be necessary to show model generalizability. Another limitation of this study was the need to combine two datasets in order to provide enough samples for case and non-case discrimination in HF and wellness models. Lastly, longitudinal studies based on the Cardiac ScoreCard are needed to examine the effect on patient outcomes and to determine personalized treatments. Albeit preliminary and in need of further validation, initial results suggest the utility of the Cardiac ScoreCard in predicting cardiac wellness and HF.

Despite these limitations, these initial studies highlight key recommendations for future efforts in the areas of CVD prediction and multivariate index assay development. When developing CDSSs for CVD, researchers should consider incorporating models, such as decision trees, Bayesian networks, or logistic regression, which are easier to interpret and may provide better diagnostic support information to clinicians. Prioritizing interpretability may help minimize the clinical community’s reluctance to adopt these new clinical decision support tools. In addition, researchers should consider using practical parameter selection techniques when developing multiplexed immunoassays in order to retain a more manageable number of biomarkers, greatly simplify the assay chemistry, and reduce the cost of reagents. Lastly, researchers developing new algorithms for medical uses should not underestimate the importance of using real clinical data from the target population. While some publicly available datasets are perfect for testing new techniques and comparing performances with previous efforts, better prediction performance on these datasets does not necessarily generalize to future data. Thus, models should be developed using real clinical data, acquired in a way that replicates its targeted use, and validated using a similarly-derived independent test set.