Abstract
In this study, we demonstrate the use of cyclical low frequency signals with insulator-based dielectrophoresis (iDEP) devices for the separation of particles of similar characteristics and an experimental method for estimating particle DEP mobilities. A custom signal designer program was created using Matlab® and COMSOL Multiphysics® for the identification of specific low frequency signals aimed at separating particle mixtures by exploiting slight differences in surface charge (particle zeta potential) or particle size. For the separation by surface charge, a mixture of two types of 10 μm particles was analyzed and effectively separated employing both a custom step signal and a sawtooth left signal. Notably, these particles had the same shape, size, and surface functionalization as well as were made from the same substrate material. For the separation by size, a sample containing 2 μm and 5 μm particles was successfully separated using a custom step signal; these particles had the same shape, surface functionalization, were made from the same substrate materials, and had only a small difference in zeta potential (10 mV). Additionally, an experimental technique was developed to estimate the dielectrophoretic mobility of each particle type; this information was then utilized by the signal designer program. The technique developed in this study is readily applicable for designing signals capable of separating micron-sized particles of similar characteristics, such as microorganisms, where slight differences in cell size and the shape of surface charge could be effectively exploited. These findings open the possibility for applications in microbial screening using iDEP devices.
INTRODUCTION
There is a growing interest in the development of more selective and precise bioanalytical techniques for applications in the clinical and biomedical fields. In particular, assessments involving biological cells often require distinguishing subtle biophysical differences of size, shape, and electrical charge between similar cell species. The electrical phenotype of a cell is the collection of the electrical properties of the cell; differences in electrical phenotype could indicate significant changes in pathogenicity, antibiotic resistance, or gene transference between different strains.1,2 The development of microfluidic devices has enabled rapid growth in the study of cellular properties. Microfluidic techniques have the potential to substitute traditional bench scale methods employed in microbiological analysis by decreasing costs, sample size, and processing time.1,3
Microscale electrokinetic (EK) techniques offer an attractive option due to their flexibility, robustness, and ease of optimization. When designing electrokinetic microsystems, there is a series of parameters that can be fine-tuned for highly specific applications.4,5 Dielectrophoresis (DEP), the migration of particles due to polarization effects when exposed to nonuniform electric fields, is a label-free technique that can be utilized for the assessment and manipulation of a wide range of particles, including microorganisms. A majority of DEP based systems have employed either a series of electrodes or insulating structures to generate DEP forces on particles; the former is electrode based DEP (eDEP) and the latter is known as insulator-based DEP (iDEP). There are numerous reports illustrating the potential of iDEP for the separation, identification, and concentration of desired bioparticles.6–8 Fine-tuned iDEP assays have also shown promise for a point of care diagnosis using lab on a chip style devices for the inexpensive and rapid detection of various biomarkers.9,10
Carefully designed custom signals have numerous potential applications, as they can be used to manipulate a wide array of particles, from macromolecules to parasites.11 For example, the development of highly selective detection assays that employ functionalized polystyrene particles can enable challenging separations and isolation of low abundant particles.12 Regarding bioparticles, an effective manipulation allows for the production of concentrated mixtures of cells, DNA, mitochondria, and protein crystals, which have applications in several fields.13–16 There are a few reports in the literature on “ratcheting” behavior of particles using electric fields. Ajdari and Prost17 proposed a theoretical model to enhance the electrophoretic separation of DNA fragments by imposing an AC orthogonal electric field onto a conventional free flow electrophoretic system. Their model predicted the trapping of DNA fragments at periodic intervals which resulted in mostly forward motion.17 In a later report by the same group, Rousselet et al.18 explored the use of asymmetric periodic potentials to achieve the “pumping” of particles in an interdigitated electrode array. They reported the migration of a population of particles due to Brownian motion and EK effects under an applied signal of 5 V at 500 kHz.18 The study of iDEP devices has demonstrated successful particle separations utilizing both high frequency AC signals19 as well as DC5 signals but very few reports have focused on the use of low frequency signals.20–23 Our group reported the separation of particles, differing a half micrometer in diameter, using an electroosmotic flow (EOF) gradient and a low frequency AC signal (1–20 Hz).20
This study explores the use of low frequency cyclical electrical signals in iDEP devices for the separation of mixtures of polystyrene beads with similar characteristics based on surface charge or particle size differences. Four different types of particles were used in this study to create two distinct particle mixtures. The first mixture was aimed at demonstrating particle separation by exploiting charge differences, and the second mixture was selected for illustrating particle separation by size differences. This work, which relied on experimentation and simulation, required the design of specific low frequency electrical signals that were fine-tuned for a particular type of separation. In order to rapidly test and vary the large number of parameters defining a low frequency cyclical signal, a custom signal designer program was created to simulate particle migration inside an iDEP device. The program required information on the EK and DEP mobilities for each particle type. These mobilities were derived experimentally, and a new approach was developed for assessing particle DEP mobility. In order to test the accuracy of the signal designer program, the displacement of a single particle type was simulated with a specific signal. This signal was then used for an experiment, and the resulting simulated particle positions were compared with experimentally observed particle positions. Using the designer program, three signals, two custom and one conventional, were selected, and the defining parameters were optimized for the best particle separation. Once the two signals were simulated, experiments with iDEP devices with cylindrical posts verified the successful particle separations.
THEORETICAL BACKGROUND
The main forces acting on microparticles in iDEP devices [Fig. 1(a)] are divided into EK forces and DEP forces. The EK forces can be further divided into Stokes drag from electroosmotic flow (EOF) and electrophoresis (EP). The EK forces can be exploited for particle separations by taking advantage of differences in particle zeta potentials (ζparticle) and varying the electric field. The EK velocity is given by24,25
| (1) |
where is the medium permittivity, is the electric field, and is the viscosity of the medium. The DEP velocity of microparticles depends greatly on particle size, which is given by24,25
| (2) |
where rp is the radius of the particle, is the gradient of the electric field squared, and is the real part of the Clausius-Mossotti factor, which for frequencies below 100 kHz is given by26
| (3) |
where refers to real conductivity of the particle and the medium, and can vary from −0.5 to 1 for a spherical particle. The sign of depends on the relative polarizability of the particle with respect to the suspending medium. Particles exhibit positive DEP (pDEP) behavior when they are more polarizable than the medium and migrate toward the regions of higher electric field gradient. Negative DEP (nDEP) is the opposite effect. All particles in this study exhibited nDEP under the condition of low frequency electric fields.11 The particle conductivity depends on the conductivity of the bulk material and the surface conductance ,27
| (4) |
FIG. 1.
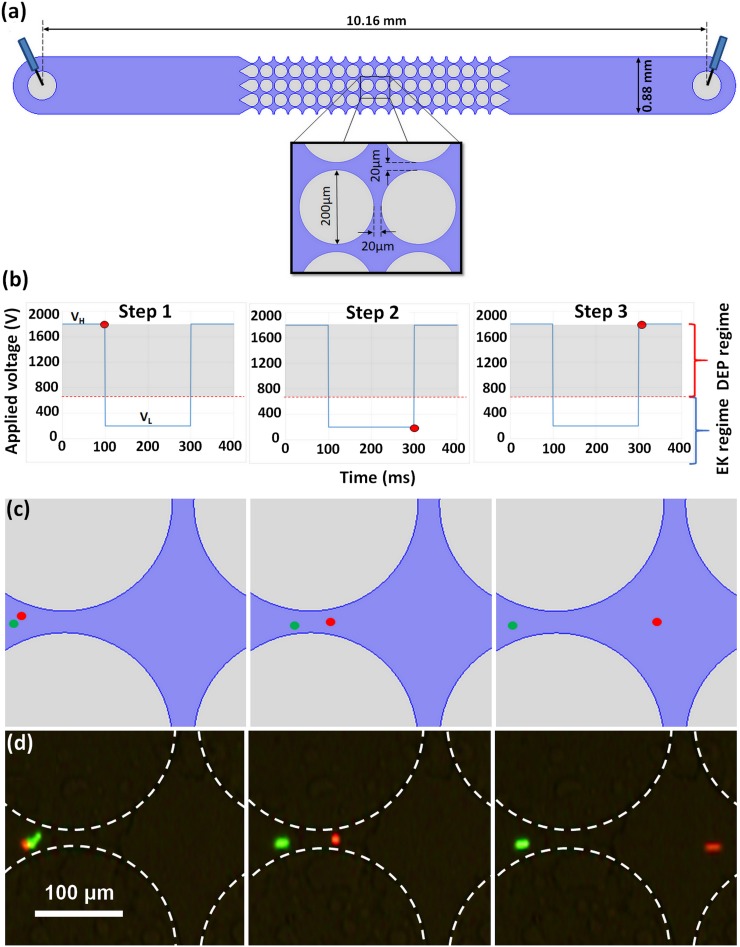
(a) Schematic of the channel with postdimensions. (b) Plot of a custom step signal used for demonstrating (c) and (d), the voltages are VH = 1800 V and VL = 200 V. (c) Cartoon of predicted particle position over time using signal shown in (b). (d) Experimental images of particle 5 (red) and 6 (green) demonstrating the 3-step particle separation by charge differences using signal shown in (b).
The overall particle velocity, accounting for EK and DEP, is given by the equation28–30
| (5) |
where and are the EK and DEP mobilities, respectively. Particle trapping occurs when , and Eq. (5) can be rearranged to estimate ,6
| (6) |
MATERIALS AND METHODS
Microdevices
Microchannels with cylindrical insulating posts [Fig. 1(a)] were made from polydimethylsiloxane (PDMS) employing standard soft lithography techniques.31 To create a device, PDMS (Dow Corning, Midland, MI) was cast onto a negative replica mold made with a silicon wafer (Silicon Inc., Boise, ID) and SU-8 3050 photoresist (MicroChem, Newton, MA). After curing, the PDMS slab was sealed with a PDMS-coated glass wafer, creating microchannels where all internal surfaces are PDMS and have same wall zeta potential (ζwall), ensuring consistent EOF. The microchannels were 10.16 mm long, 0.88 mm wide, and 40 μm deep and contained one inlet and one outlet liquid reservoir.
Microparticles
Four different types of particles were chosen for the separations characterized in this study (particles 1–4, Table I). An additional pair of particles (particles 5 and 6) was employed for feasibility demonstration. Two of the particles have the same size (10 μm) but differing zeta potentials. The other two particles have differing size (2 μm vs 5 μm) and similar zeta potentials. This particle selection was done to demonstrate the ability of our technique to exploit charge differences and size differences for achieving particle separations. Particle zeta potentials were experimentally measured in our laboratory by combining particle image velocimetry (PIV) and current monitoring assessments.32,33 Uncertainty in the determination of particle EK mobility and zeta potential were based on the standard deviation of particle velocity distribution as detailed in the study by Hidalgo-Caballero et al.33 Uncertainty in DEP mobility is the propagation of EK mobility uncertainty and uncertainty in trapping distance. Experimental errors of all measurements are reported in Table I. Particle suspensions were made of varying concentrations (1.8 × 106–2.0 × 108 particles/ml) based on the size.
TABLE I.
List of particles used for this study with the associated particle properties. The particle zeta potential, EK mobility, and DEP mobility were found experimentally. Reported uncertainties for ζparticle and μEK are one standard deviation. Reported uncertainties for μDEP are based on the accuracy of the image based determination of trapping distance and the uncertainty of μEK.
| No. | Brand | Color | Diameter (μm) | Surface funct. | ζparticle (mV) | μEK (m2 V−1 s−1) | μDEP (m4 V−2 s−1) |
|---|---|---|---|---|---|---|---|
| 1 | Magsphere | Green | 9.7 | Carboxylated | −60.9 ± 6 | 2.40 ± 0.30 × 10−8 | −2.80 ± 0.40 × 10−18 |
| 2 | Invitrogen | Red | 10.0 | Carboxylated | −19.1 ± 11 | 5.66 ± 0.20 × 10−8 | −7.58 ± 0.031 × 10−18 |
| 3 | Magsphere | Green | 2.0 | Carboxylated | −58.2 ± 15 | 2.61 ± 0.26 × 10−8 | −1.70 ± 0.19 × 10−18 |
| 4 | Magsphere | Red | 5.1 | Carboxylated | −48.3 ± 5 | 3.38 ± 0.35 × 10−8 | −4.63 ± 0.56 × 10−18 |
| 5 | Magsphere | Red | 5.1 | Carboxylated | 0.0 ± 8.1 | 7.58 ± 0.61 × 10−8 | −5.93 ± 0.47 × 10−18 |
| 6 | Magsphere | Green | 5.1 | Non-funct. | −35.5 ± 7.6 | 4.81 ± 0.63 × 10−8 | −3.14 ± 0.41 × 10−18 |
Equipment and software
Microparticle behavior was observed and recorded in the form of videos and pictures with a Leica DMi8 inverted microscope (Wetzlar, Germany) with a Leica DFC7000T camera and the software LASX. Periodic electric potentials were applied by employing a high voltage supply (HVS3000D, LabSmith, Livermore, CA). COMSOL Multiphysics 4.4 was used to model the electric field in the microchannel. Matlab 2016b was used to create the signal designer program. Full program details can be found in the supplementary material.
Suspending media
The suspending medium consisted primarily of deionized (DI) water with a conductivity of 20–25 μS/cm and a pH of 6.0–6.5. Tween 20 was added at a concentration of 0.05% (v/v) to minimize particle aggregation. A 0.1M KOH solution and a 0.1M KCl solution were used to adjust the medium conductivity and pH to the desired values. These media generate a wall zeta potential (ζwall) of −93.9 mV in our PDMS devices.
Experimental procedure
All iDEP experiments started with a clean PDMS device, preconditioned to ensure stable EOF. A sample of 1–10 μl of the selected particle suspension was added to the channel inlet, and platinum wire electrodes were placed in the channel reservoirs. After eliminating any pressure-driven flow, the desired signal was applied by employing the high voltage supply. Particle response was recorded in the form of pictures and videos that were used for further analysis.
FIG. 2.
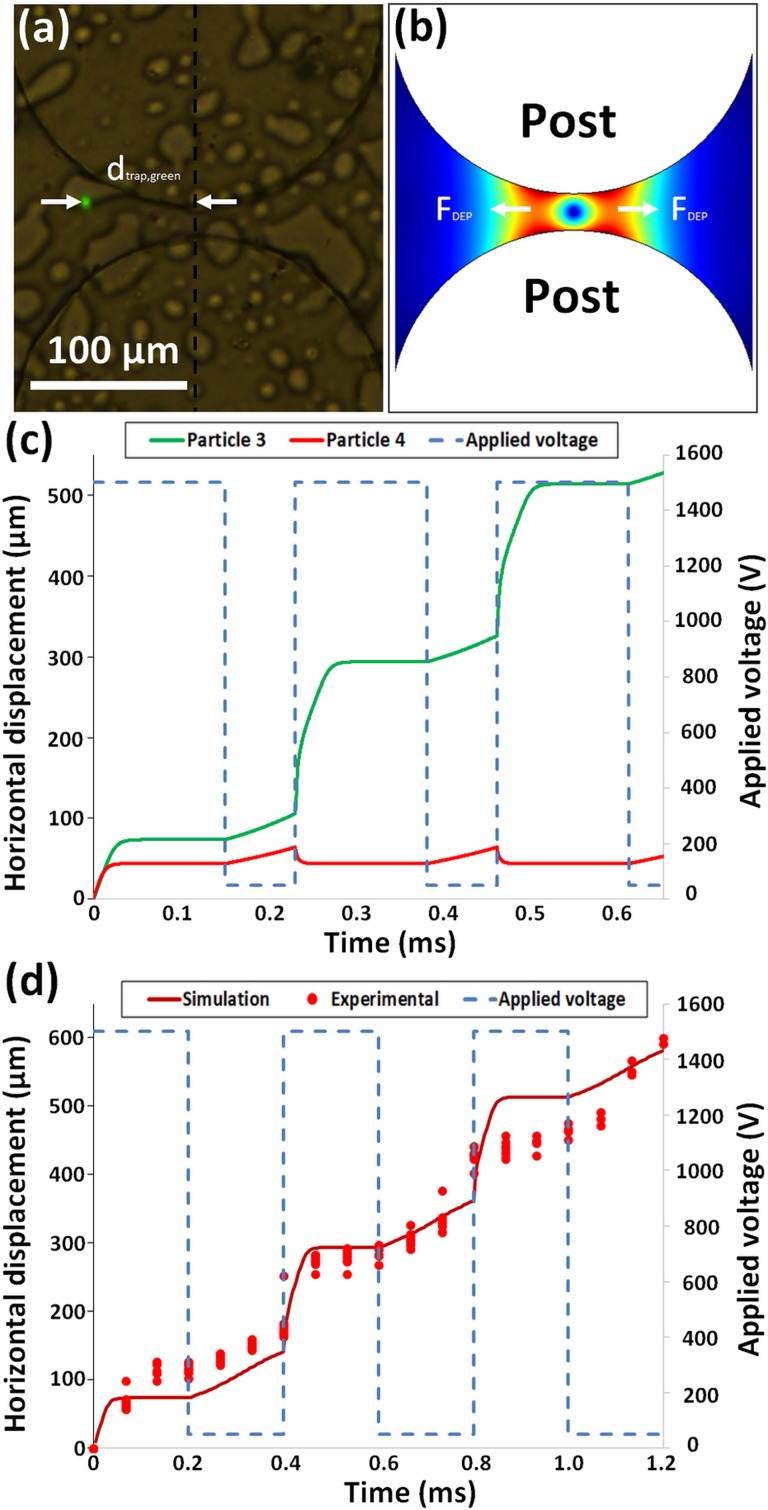
Model predictions. (a) Experimentally measured trapping distance for particle 1 (Table I, 9.7 μm green). (b) Gradient of the electric field squared and representation of the negative DEP forces in a postconstriction. (c) Predicted position of particle 3 (2 μm green) shown in green and particle 4 (5 μm red) shown in red when a custom signal, shown in blue, is applied. (d) Predicted position of particle 4 (5 μm red) vs time, experimentally found particle position vs time, and applied custom signal.
RESULTS AND DISCUSSION
In order to use a periodic electrical signal to separate the particle mixtures, a custom designer program was devised, which allowed for the rapid testing of various signal parameters. Without estimations provided by the simulation, which can test a given signal under 1 s, the search space required an unreasonable number of individual experiments to obtain a working signal. After simulating a variety of signals, two kinds of signals were chosen to demonstrate effective separations by exploiting charge or size differences between the particles [see Figs. 3(a)–5(a)]. The use of a custom step signal and a sawtooth left signal was found to be the most promising based on the simulation and experimental results.
FIG. 3.
(a) Plot of tracked particle positions, particle 1 (9.7 μm green) and particle 2 (10 μm red). Custom 2-step signal shown with dashed blue line. (b) Image of both particles trapped at 1000 V part of signal. (c) Image of particle 1 on the right side of constriction and particle 2 on the left side of constriction resulting in particle separation. Although the red particle appears to be larger than the green particle, both particles have similar diameters but different levels of fluorescence.
FIG. 4.
Separation of particle 1 (9.7 μm green) and 2 (10 μm red) by applying a sawtooth left signal. (a) Plot of experimental particle displacement of particle 1 shown in green and particle 2 shown in red. Linear curve fit for particle 1 shown with green dotted line and particle 2 shown with red dotted line. Equations for particle 1 and 2 curve fits are shown in green and red, respectively. Applied sawtooth left signal shown with dashed blue line. (b) Image of both particles trapped at a constriction between two posts. (c) Image of particle 1 (9.7 μm green) having migrated to the right side of postconstriction while particle 2 (10 μm red) is still on the left side of the constriction. Both particles are 10 μm in diameter but appear to be different sizes because of fluorescent intensity.
FIG. 5.
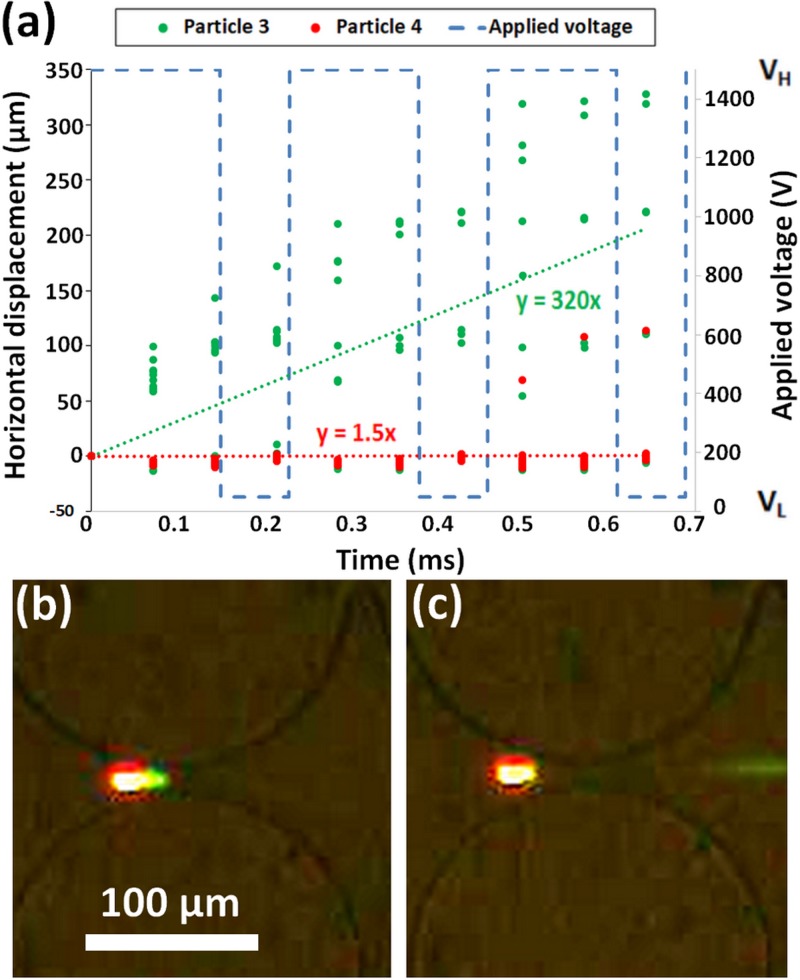
Separation of particles 3 (2 μm, green) and 4 (5 μm, red) from Table I using custom signal. (a) Plot of tracked particle positions, particle 3 shown in green and particle 4 shown in red. Custom signal shown with dashed blue line. (b) Image of both particles trapped during the application of VH (1500 V). (c) Image of particle 3 on the right side of constriction and particle 4 on the left side of constriction resulting in particle separation.
Mechanism behind particle separation with cyclical signals
By employing low frequency cyclical signals, particle migration can be carefully controlled within an iDEP channel [Fig. 1(a)]. The goal of this particular iDEP technique is to separate a mixture of particles by having particles of a certain characteristic (charge, size, or shape) effectively migrate forward, while other types of particles oscillate back and forth remaining in the same overall location. This mechanism works by switching between two iDEP regimes, trapping iDEP and streaming iDEP. Trapping iDEP is the capture of particles due to DEP forces overwhelming the EK forces exerted on a particle. Streaming iDEP34 is characterized by continuous particle motion because the EK forces are comparable to the DEP forces, and particles migrate under the influence of both forces.11,35 The mechanism exploited in this study relies on both particles being under the trapping iDEP step followed by both particles experiencing streaming iDEP. The separation occurs during the streaming iDEP step, because one type of particle will have a higher velocity. The particle type with the higher velocity will migrate to the downstream side of the postconstriction while the other particle type is on the upstream side of the constriction. At this moment, the cycle repeats and the particles experience trapping iDEP again but at distinct locations, with the lower velocity particle being pushed upstream and the faster particle being pushed downstream due to DEP forces. As this cycle repeats, the faster particle keeps migrating to the next constriction downstream at each cycle, and the slower particle will remain in the same constriction.
An example of a successful particle separation by exploiting charge differences with a cyclical signal is fully illustrated in Figs. 1(b)–1(d) as a three-step process. A step signal where the potential varies from VH = 1800 V to VL = 200 V is depicted in Fig. 1(b); the red circle in the signal corresponds to the signal magnitude for the results in Figs. 1(c)–1(d). The shaded region in the signal highlights the voltage magnitude at which DEP dominates the system and particles are trapped. The two particles in Fig. 1 are both 5 μm in diameter, spherical, and made from polystyrene; the only difference, besides their color, is a small difference in particle zeta potential (i.e., charge difference). The green particle has a higher magnitude of (−35.5 mV) which decreases the magnitude of its EK velocity; that is, under the same condition, the green particles migrate less than the red particles that have a lower magnitude of (−0.0 mV). Figure 1(c) shows a cartoon of the expected separation, and Fig. 1(d) illustrates the actual experiment depicting this 3-step separation. These experimental results confirm that by using a cyclical step signal, which varies from VH and VL, it is possible to separate two very similar particles with only a small difference in their particle zeta potentials.
Custom signal designer program
In order to find the correct combination of frequency, amplitude, DC bias, duty cycle, and signal type, a custom designer program was developed to predict the motion of particles within the iDEP channel. (Complete program is provided in the supplementary material.) By integrating the equation for particle velocity [Eq. (5)] using the Euler method, the particle location can be determined. In order to integrate Eq. (5), the following parameters had to be determined a priori with COMSOL and experimentation: , , , and .
Since both and vary with voltage and position, the electric field distribution within the device was simulated using COMSOL Multiphysics® at five different voltages. A “cutline” located halfway between two posts was used to extract the values of and , assuming the particle follows this path. Once these values were obtained an equation consisting of a second order polynomial for voltage multiplied by a tenth order polynomial for position was fitted to the dataset in order to have a smooth continuous function for the integration (supplementary material).
Both and are particle based parameters that were determined experimentally. The was found using the same process as Martínez-López et al.36 A new methodology was developed as part of this study for determining , which consisted on applying a voltage high enough to cause trapping iDEP and then measuring the distance from the particle center to the postcenterline as shown in Fig. 2(a). Particles are trapped when the DEP forces generated at the constriction between two posts, as represented in Fig. 2(b), are balanced with the EK forces. Knowing this trapping distance and trapping voltage, as well as the particle , allows for determining using Eq. (6).
After obtaining the necessary input data, the signal designer program was used to quickly test numerous frequencies, amplitudes, DC biases, and duty cycles to design custom signals that produce different displacements of particles 3 and 4 (Table I), as shown in Fig. 2(c). By selectively allowing a specific particle type to migrate further than the other particle type present in the mixture, an effective particle separation can be achieved. For example, the separation simulated in Fig. 2(c) illustrates that, under the custom step signal shown in blue, particle 3 (2 μm green) migrated ∼550 μm while particle 4 (5 μm red) stayed at the same position of ∼50 μm. This produced a separation distance between the two particle types of ∼500 μm in a time frame of only 0.6 s.
To test the accuracy of the signal designer program, a particle migration experiment with only one particle type was performed and the particle positions were tracked using ImageJ®. The starting position of each particle was then set to zero using the program detailed in the supplementary material. For comparison, the predicted particle positions as well as the experimental particle positions are shown in Fig. 2(d). The simulated and experimental particle positions are close, demonstrating that the code has a good agreement with experimental results. Some of the possible reasons why the predictions are not perfect are perhaps that the program does not account for additional factors, such as population distributions, particle-particle interactions, Joule heating, particle movement off the centerline, and other effects.35,37,38 Other contributions to the program inaccuracies may include expected experimental uncertainty in measuring trapping distance, trapping voltage, and EK mobility as well as variability in device geometry. The next three sections describe in detail how custom signals were selected for particle separation by charge and size differences.
Particle separation by exploiting charge differences with a custom step signal
The signal designer program was employed to identify a suitable signal for separating a mixture of two types of 10 μm particles (particles 1 and 2, Table I) that were roughly the same size, shape, and type of surface functionalization and both were made of polystyrene. The property utilized to separate particles 1 and 2 was the difference in surface charge, in terms of their zeta potentials as seen in Table I: −60.9 mV vs −19.1 mV. This surface charge difference exhibited itself as a difference in their EK mobilities. It was also found that the DEP mobilities of particle 1 and 2 also differ due to differences in surface conductance [Eq. (4)]. The higher magnitude of zeta potential of particle 1 increases the surface conductance,39 which, in turn, modifies the magnitude of [Eq. (4)] causing a lower magnitude of Re(fCM) [Eq. (3)], thus decreasing the DEP mobility [Eq. (2)]. The ability of particles with the same size and surface charge to have difference in surface conductance was demonstrated by Arnold et al.27
In order to exploit this surface charge difference, a voltage (VL) low enough to avoid trapping iDEP was applied to cause particle 1 (9.7 μm green) to migrate through the constriction while the slower moving particle 2 (10 μm red) does not progress all the way through the constriction. Once the faster particle is through the constriction but before the slower particle passes through, the voltage is increased to VH generating a dominating negative DEP force [Fig. 2(b)], which propels both particle types out of the constriction, but in opposite directions. The faster moving particle 1 (9.7 μm green) is pushed forward, while the slower moving particle 2 (10 μm red) is pushed backward.
The simplest signal designed with this methodology is the custom signal shown in Figs. 1(b) and 2(c), which is a step signal with a positive DC bias and negative duty cycle bias. The high voltage applied (VH) for the first part of the signal should be high enough to trap both particles [as shown in Fig. 2(b)] at a sufficient distance from the postcenterline shown in Fig. 2(a), such that the difference in particle EK mobilities can be exploited during the second part of the signal. However, as the voltage is increased, the effect on trapping distance is reduced as the particles move out of the constriction. By fine tuning the amplitude of VH, which traps the particles, it is possible to maximize the difference in the starting position of the two particle types. By balancing the trade-off between the trapping distance from the postcenterline and difference in particle trapping positions, an optimal VH can be found. It may be desirable to minimize the period of the higher voltage (VH) to reduce biological sample damage36,40 and Joule heating effects.41,42 Our current system featured potentials as high at 1800 V, which produced currents in the range of 40 μA; depending on the size of the biological cells being assessed, these conditions might need to be modified to preserve cell viability. It is important to note that the actual separation occurs during the application of VL (low voltage), and therefore, small changes in the amplitude and period of VL can easily ruin the separation. While designing a separation signal, if both particles had a net displacement, the amplitude or period of VL decreased and, if both particles had no net displacement, the amplitude or period of VL increased.
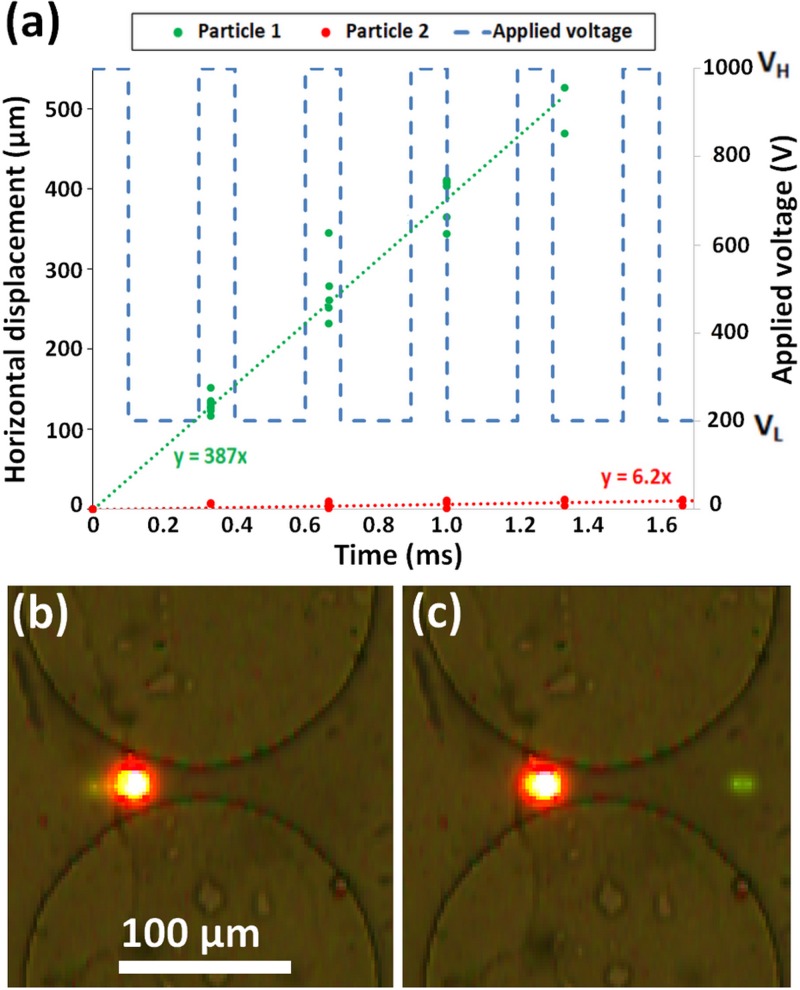
The signal designed for the separation by charge of particles 1 and 2 was a rectangular wave, shown in Fig. 3(a), with a frequency close to 3 Hz. The signal required a positive DC bias to avoid backward particle migration. The high voltage was set to VH = 1000 V in order to be in the trapping iDEP regime of both particles. The low voltage was set to VL = 200 V so that both particles experienced streaming iDEP. For these electrical potentials, the DEP force increases by a factor of 25 when the potential increases from VL to VH. With distinct particle velocities, a negative duty cycle bias was used because the time for which VL was applied was fine-tuned such that the two particles were at opposite sides of the constriction when VH started, and VH was applied only until the trapping of both particles stabilized. The result of the properly designed signal is a ratcheting behavior in which the faster moving particle will progress from one constriction entrance to the next during each signal cycle while the slower particle will oscillate back and forth in the same constriction. Figure 3(a) illustrates these results, where particle 1 (9.7 μm green) moved forward ∼500 mm, as depicted by the green line, and particle 2 (10 μm red) remained roughly at the same initial location, as illustrated by the red line. The plot also includes linear fits of particle displacement (y) as a function of time (x) for each particle type. The experimental trapping of both particles just prior to a constriction between to post is shown in Fig. 3(b), and an image of the actual separation when the green particle moves forward while the red particle is left behind is included in Fig. 3(c).
Particle separation by exploiting charge differences with a sawtooth left signal
In addition to the custom step signal developed in this study for particle separation by charge (Fig. 3), several conventional signals were tested in order to identify an additional signal for separation by charge differences. True AC signals were found to be counterproductive because, at the end of the positive part of the AC signal, the particles had a difference in position but, during the negative part of the signal, this difference was diminished, which hindered the separation. To avoid this, a DC bias equal to the half amplitude was used when testing sawtooth left, sawtooth right, sine, and triangular signals. After extensive experimental testing, it was found that a sawtooth left signal [Fig. 4(a)] provided the best separation of particles by charge differences.
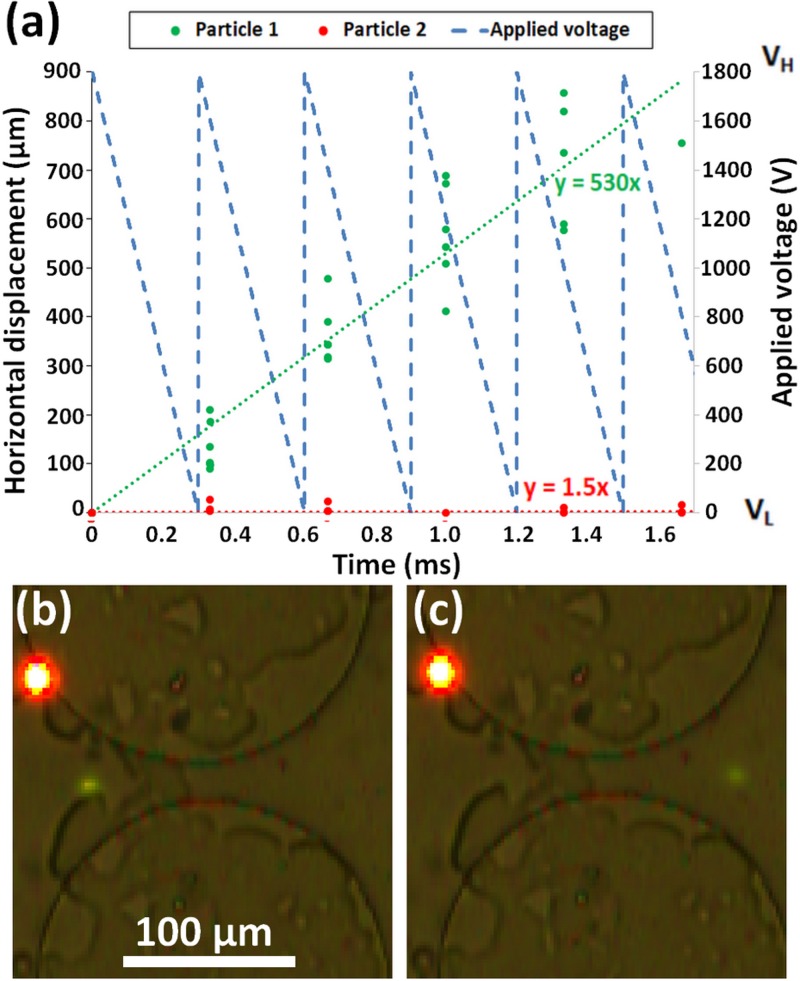
The successful sawtooth left signal, created by the signal designer program, used an amplitude of 1800 V so that both particles were trapped for a significant part of the signal, preventing both particles from migrating forward to the next constriction. The period of 0.3 s was selected so that as the voltage decreases, and particles switch from trapping to streaming iDEP, particle 1 (faster moving) will be on the downstream side of the constriction while particle 2 (slower moving) has to pass through the constriction. The success of this separation is illustrated in Fig. 4(a) in terms of the net particle displacement as a function of time. As it can be seen, during a time frame of 1.8 s, particle 1 (9.7 μm green) progressed ∼800 μm through the postarray while particle 2 (10 μm red) remained at the same constriction.
Let us explain these results, at the peak of the sawtooth signal, both particles will be trapped at distinct locations as seen in Fig. 4(b). As time progresses, and voltage linearly decreases, both particles will advance as the negative DEP force decreases faster than the EK force (DEP is a second order effect with respect to ), releasing the particles from the trapping iDEP. If the period is of proper length, the cycle will complete with particle 1 (9.7 μm green) having migrated to the right side of the constriction and particle 2 (10 μm red) still remains on the left side as shown in Fig. 4(c). As the voltage reaches zero and the signal starts over, particle 2 (red 10 μm) will become trapped at the same location while particle 1 (9.7 μm green) will be trapped at the next constriction, thus, achieving a separation. As the cycle repeats, the separation will become more evident as can be seen in Fig. 4(a) where the difference in particle displacement is ∼800 μm within 1.8 s. For the sawtooth left signal, the most important parameter to fine tune is the period, lengthening it if both particles fail to progress and shortening it if both particles progress.
While the sawtooth left and square signals both separated particles by charge, the speed of separation and the applied voltage make these different signals proficient for distinct applications. The average velocity of particle 1 (9.7 μm green) was faster using the sawtooth left signal [530 μm/s, Fig. 4(a)] than with the custom step signal [387 μm/s, Fig. 3(a)]. However, the required peak voltage (VH) was found to be 1800 V for the sawtooth left signal as opposed to the 1000 V for the custom step signal. These results illustrate that the sawtooth left signal [Fig. 4(a)] can be used when separation speed is of importance, while the custom step signal [Fig. 3(a)] can be used for separations requiring a lower voltage, such separations of biological cells.
Particles separation by exploiting size differences using a custom step signal
The signal designer program can also be used for identifying signals to be applied for separating particles with similar charge based on size differences: particles 3 (2 μm green, −58.2 mV) and 4 (5 μm red, −48.3 mV) from Table I resulting in a difference of 10 mV between particle zeta potential values. In this case, the fact that the smaller particle is the one with the higher magnitude of the negative zeta potential increases the difficulty of the separation, i.e., the separation would have been easier if the larger particle had a larger magnitude of negative zeta potential. Due to its smaller size, the 2 μm particle has a lower than the 5 μm particle. Consequently, there is a trade-off, since both EK and DEP forces are lower for the 2 μm particle than they are for the 5 μm particle. The signal predicted by simulations for this separation was a step custom signal similar to the one used previously, but with different periods and amplitudes [Fig. 5(a)]. As can be seen from the displacement plot, particle 3 (2 μm green) migrated at 320 μm/s on average while particle 4 (5 μm red) migrated at 1.5 μm/s on average resulting in a separation of ∼200 μm in a time frame of 0.65 s [Fig. 5(a)]. During the separation, some of the particles did not always follow the predicted movement, as shown by the migration of the red particle in Fig. 5(a). During the initial application of VH (1500 V), particles 3 and 4 were located roughly at the same position [Fig. 5(b)], which caused the separation to be more sensitive to changes in the VH and VL (50 V) amplitudes as well as VL period. By using the program to adjust VH, VL, and VL period, particle 3 (2 μm green) was able to migrate to the next constriction, due to the DEP force exerted on the particle decreasing by a factor of 900 when the voltage was switched from VH to VL. At the same time, particle 4 (5 μm red) remained in the same postconstriction as seen in Fig. 5(c), producing particle separation.
As mentioned above, while the size difference is significant (2 μm vs 5 μm), the small difference in zeta potential (−58.2 vs −48.3 mV) increases the difficulty in separating these particles. Based on the DEP mobility being proportional to the particle radius squared [Eq. (2)], the negative DEP mobility of particle 4 (5 μm red) was expected to be 6.5 times that of particle 3 (2 μm green). However, this was not the case, as can be seen in Table I, the difference between these experimentally measured mobilities was actually a factor of just 2.7. This discrepancy might be caused by distinct magnitudes of surface conductance between the two particle types [Eq. (4)].27 Particle 4, due its lower magnitude of , has a higher EK mobility and will move faster through the constriction during the application of VL. Therefore, the amplitude and period of VL had to be fine-tuned to exactly position particle 4 just to the left of the constriction while allowing particle 3 to cross the constriction centerline. This confirms that the higher magnitude of particle 3 is a hindrance during separation.
SUMMARY AND CONCLUSION
Reported here is the separation of polystyrene particles in an iDEP device by exploiting differences in surface charge and particle size using low frequency periodic signals. A total of three distinct separations were demonstrated; two separations by exploiting differences in surface charge and one separation by exploiting differences in particle size. A custom signal designer program was developed in order to identify cyclical low frequency electric signals that could be employed for specific particle separations. The signal designer program was employed to effectively explore the search space of varying signal type, frequency, amplitude, DC bias, and duty cycle. The program, which was developed with Matlab® and data exported from COMSOL Multiphysics, was used to simulate particle migration, and these predictions were compared to experimental results.
Furthermore, an experimental procedure, using the same iDEP device utilized for particle separation, was developed in order to determine the DEP mobility of the particles. The DEP mobility information is essential for both the signal designer program developed in this study and also for modeling other low frequency iDEP devices. The designer program was used to identify both a custom step signal and a sawtooth left signal, which were successfully tested experimentally for the separation of particles of the same size by exploiting surface charge differences. Additionally, the custom step signal was modified and employed for performing a separation of particles of similar charge based on size differences. These findings illustrate the potential of low frequency cyclical signals for achieving the separation of similar particles types, based on surface charge difference, particle size differences, or shape differences. The signal designer program could be employed for identifying suitable signals to be employed for the rapid screening of microorganisms with similar characteristics (charge or size), opening the possibilities for iDEP in applications for microbial analysis.
SUPPLEMENTARY MATERIAL
See the supplementary material for the two Matlab codes used in this study: (a) Matlab code for prediction of particle position and (b) Matlab code for particle image velocimetry data analysis.
ACKNOWLEDGMENTS
The authors would like to acknowledge the financial support provided by the National Science Foundation (NSF) (No. CBET-1705895).
Note: This article is part of the special topic, Festschrift for Professor Hsueh-Chia Chang.
REFERENCES
- 1.Ding J., Woolley C., and Hayes M. A., Anal. Bioanal. Chem. 409(27), 6405–6414 (2017). 10.1007/s00216-017-0582-5 [DOI] [PubMed] [Google Scholar]
- 2.Voldman J., Ann. Rev. Biomed. Eng. 8, 425–454 (2006). 10.1146/annurev.bioeng.8.061505.095739 [DOI] [PubMed] [Google Scholar]
- 3.Xuan X., “Recent advances in direct current electrokinetic manipulation of particles for microfluidic applications,” Electrophoresis (published online). 10.1002/elps.201900048 [DOI] [PubMed] [Google Scholar]
- 4.Kim D., Sonker M., and Ros A., Anal. Chem. 91(1), 277–295 (2019). 10.1021/acs.analchem.8b05454 [DOI] [PubMed] [Google Scholar]
- 5.Jones P. V., Salmon G. L., and Ros A., Anal. Chem. 89(3), 1531–1539 (2017). 10.1021/acs.analchem.6b03369 [DOI] [PubMed] [Google Scholar]
- 6.Wang Q., Jones A.-A. D., Gralnick J. A., Lin L., and Buie C. R., Sci. Adv. 5(1), eaat5664 (2019). 10.1126/sciadv.aat5664 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pethig R., J. Electrochem. Soc. 164(5), B3049–B3055 (2017). 10.1149/2.0071705jes [DOI] [Google Scholar]
- 8.Abdallah B. G., Roy-Chowdhury S., Coe J., Fromme P., and Ros A., Anal. Chem. 87(8), 4159–4167 (2015). 10.1021/acs.analchem.5b00589 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rohani A., Varhue W., Liao K.-T., Chou C.-F., and Swami N. S., Biomicrofluidics 10(3), 033109 (2016). 10.1063/1.4954933 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rohani A., Sanghavi B. J., Salahi A., Liao K.-T., Chou C.-F., and Swami N. S., Nanoscale 9(33), 12124–12131 (2017). 10.1039/C7NR02376F [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lapizco-Encinas B. H., Electrophoresis 40(3), 358–375 (2019). 10.1002/elps.201800285 [DOI] [PubMed] [Google Scholar]
- 12.Chen Q. and Yuan Y. J., RSC Adv. 9(9), 4963–4981 (2019). 10.1039/C8RA09017C [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kim D., Luo J., Arriaga E. A., and Ros A., Anal. Chem. 90(7), 4370–4379 (2018). 10.1021/acs.analchem.7b03774 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Camacho-Alanis F., Gan L., and Ros A., Sens. Actuator B Chem. 173(0), 668–675 (2012). 10.1016/j.snb.2012.07.080 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gan L., Chao T.-C., Camacho-Alanis F., and Ros A., Anal. Chem. 85(23), 11427–11434 (2013). 10.1021/ac402493u [DOI] [PubMed] [Google Scholar]
- 16.Rabbani M. T., Schmidt C. F., and Ros A., Anal. Chem. 89(24), 13235–13244 (2017). 10.1021/acs.analchem.7b03105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ajdari A. and Prost J., Proc. Natl. Acad. Sci. U.S.A. 88(10), 4468–4471 (1991). 10.1073/pnas.88.10.4468 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rousselet J., Salome L., Ajdari A., and Prost J., Nature 370(6489), 446–447 (1994). 10.1038/370446a0 [DOI] [PubMed] [Google Scholar]
- 19.Liao K.-T., Tsegaye M., Chaurey V., Chou C.-F., and Swami N. S., Electrophoresis 33(13), 1958–1966 (2012). 10.1002/elps.201100707 [DOI] [PubMed] [Google Scholar]
- 20.Gencoglu A., Olney D., LaLonde A., Koppula K. S., and Lapizco-Encinas B. H., Electrophoresis 35(2-3), 363–373 (2014). 10.1002/elps.201300385 [DOI] [PubMed] [Google Scholar]
- 21.Romero-Creel M., Goodrich E., Polniak D., and Lapizco-Encinas B., Micromachines 8(8), 239–253 (2017). 10.3390/mi8080239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Luo J., Muratore K. A., Arriaga E. A., and Ros A., Anal. Chem. 88(11), 5920–5927 (2016). 10.1021/acs.analchem.6b00837 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sano M. B., Caldwell J. L., and Davalos R. V., Biosens. Bioelectron. 30(1), 13–20 (2011). 10.1016/j.bios.2011.07.048 [DOI] [PubMed] [Google Scholar]
- 24.Hughes M. P., Nanoelectromechanics in Engineering and Biology (CRC Press, Boca Raton, FL, 2002). [Google Scholar]
- 25.Jones T. B., Electromechanics of Particles (Cambridge University Press, New York, 1995). [Google Scholar]
- 26.Markx G. H., Huang Y., Zhou X. F., and Pethig R., Microbiology 140, 585–591 (1994). 10.1099/00221287-140-3-585 [DOI] [Google Scholar]
- 27.Arnold W. M., Schwan H. P., and Zimmermann U., J. Phys. Chem. 91(19), 5093–5098 (1987). 10.1021/j100303a043 [DOI] [Google Scholar]
- 28.Zhu J., Canter R., Keten G., Vedantam P., Tzeng T.-R., and Xuan X., Microfluid. Nanofluidics 11(6), 743–752 (2011). 10.1007/s10404-011-0839-9 [DOI] [Google Scholar]
- 29.Zhu J. J. and Xuan X. C., J. Colloid Interface Sci. 340(2), 285–290 (2009). 10.1016/j.jcis.2009.08.031 [DOI] [PubMed] [Google Scholar]
- 30.Li M., Li S., Li W., Wen W., and Alici G., Electrophoresis 34(7), 952–960 (2013). 10.1002/elps.201200546 [DOI] [PubMed] [Google Scholar]
- 31.Duffy D. C., McDonald J. C., Schueller O. J. A., and Whitesides G. M., Anal. Chem. 70(23), 4974–4984 (1998). 10.1021/ac980656z [DOI] [PubMed] [Google Scholar]
- 32.Saucedo-Espinosa M. A. and Lapizco-Encinas B. H., Biomicrofluidics 10(3), 033104 (2016). 10.1063/1.4953183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hidalgo-Caballero S., Lentz C. J., and Lapizco-Encinas B. H., Electrophoresis 40(10), 1395–1399 (2019). 10.1002/elps.201800425 [DOI] [PubMed] [Google Scholar]
- 34.Cummings E. B., IEEE Eng. Med. Biol. Mag. 22(6), 75–84 (2003). 10.1109/MEMB.2003.1266050 [DOI] [PubMed] [Google Scholar]
- 35.Hill N. and Lapizco-Encinas B. H., “On the use of correction factors for the mathematical modeling of insulator based dielectrophoretic devices,” Electrophoresis (published online). 10.1002/elps.201900177 [DOI] [PubMed] [Google Scholar]
- 36.Martínez-López J. I., Moncada-Hernández H., Baylon-Cardiel J. L., Martínez-Chapa S. O., Rito-Palomares M., and Lapizco-Encinas B. H., Anal. Bioanal. Chem. 394(1), 293–302 (2009). 10.1007/s00216-009-2626-y [DOI] [PubMed] [Google Scholar]
- 37.Hossan M. R., Dillon R., Roy A. K., and Dutta P., J. Colloid Interface Sci. 394, 619–629 (2013). 10.1016/j.jcis.2012.12.039 [DOI] [PubMed] [Google Scholar]
- 38.Wang Q., Dingari N. N., and Buie C. R., Electrophoresis 38(20), 2576–2586 (2017). 10.1002/elps.201700144 [DOI] [PubMed] [Google Scholar]
- 39.Hughes M. P., Morgan H., and Flynn M. F., J. Colloid Interface Sci. 220(2), 454–457 (1999). 10.1006/jcis.1999.6542 [DOI] [PubMed] [Google Scholar]
- 40.Gallo-Villanueva R. C., Jesús-Pérez N. M., Martínez-López J. I., Pacheco A., and Lapizco-Encinas B. H., Microfluid. Nanofluidics 10(6), 1305–1315 (2011). 10.1007/s10404-010-0764-3 [DOI] [Google Scholar]
- 41.Kale A., Patel S., Hu G., and Xuan X., Electrophoresis 34(7), 674–683 (2013). 10.1002/elps.201200501 [DOI] [PubMed] [Google Scholar]
- 42.Gallo-Villanueva R. C., Sano M. B., Lapizco-Encinas B. H., and Davalos R., Electrophoresis 35(2–3), 352–361 (2014). 10.1002/elps.201300171 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See the supplementary material for the two Matlab codes used in this study: (a) Matlab code for prediction of particle position and (b) Matlab code for particle image velocimetry data analysis.